Analysis combustion of fuel droplets release to the atmosphere using homotopy analysis method

Abstract

In this paper, we investigate the model of combustion of polydisperse fuel spray that release to the atmosphere. The mathematical model using the well-known Eulerian–Lagrangian approach for transient flows of the fuel vapor–droplets mixture. The eddy breakup model is used to describe the combustion of the spray droplets as well as the k–$\mathit{ϵ}$ model is used to describe the turbulence of the process. In order to investigate the mathematical/physical model, we applied the well-known analytic approximate method, the homotopy analysis method (HAM). According to the theory of HAM, the convergence and the rate of solution series are dependent on the artificial convergent control parameter $ħ$.

Keywords:

• partial differential equations
• probability density function (PDF)
• homotopy analysis method (HAM)
• polydisperse fuel spray
• atmosphere

Public Interest Statement

In this paper, we applied the well-known semi-analytical method the homotopy analysis method in order to investigate the problem of combustion of polydisperse fuel spray that release to the atmosphere.

1. Introduction

Many chemical industries stored a large quantity of fuel at high pressure in liquid state. This phenomenon is dangerous for the environment and hence for people when a flammable substance released into the atmosphere. In many cases, two-phase outflow occurs so that the fuel cloud, which builds up in the atmosphere, contains a mixture of fuel vapor and liquid fuel droplets. A combustion/ignition of a mixture of fuel droplet–vapor–air cloud can cause shock-free combustion with the formation of a fireball (Makhviladze, Roberts, & Yakush, 1999a,1999b). Up to now, there are no many researches on the release of liquid fuel to the atmosphere. This paper is a natural continuous of the model presented in (Utyuzhnikov, 2002). In comparison to (Utyuzhnikov, 2002), we used with the operator $〈·〉$ which is an operation of averaging over the droplet sizes, i.e. the droplets size are presented using with a probability density function (PDF) n(r). The governing equations are divided to gas-phase equations and liquid-phase equations. The gas-phase equations are described by a system of Favre averaged Navier–Stokes equations completed by the k–$\mathit{ϵ}$ model of turbulence and eddy breakup model for turbulent combustion (Launder & Spalding, 1974). The liquid phase consists of liquid propane droplets. We take into account the influence of droplets on the gas using the relevant source terms in conservation equations of the model (Bradshaw, 1987).

When a fuel cloud is ignited the outcome can be shock-free which is giving rise to form a fireball, i.e. a large burning cloud. The combustion energy that released when an accident occur at the industry is of order $\approx {10}^{13}\text{J}$. This energy released during a short period of time 12–26 s. A significant proportion of this energy being emitted as a radiation, which can be very dangerous to people, equipment, environment, etc. This makes the research in this direction very important from practical point of view. The radiation is supposed to be emitted from the fireball surface with the total radiative power either being some fraction of the combustion rate or calculated from the Stefan–Boltzmann law with prescribed flame temperature and emissivity. In order to study the combustion of fireball, from analytical point of view, a simple geometrical shape should be assume, such as spherical symmetry (Fay & Lewis, 1976; Makhviladze, Roberts, & Yakush, 1999a,1999b).

The mathematical/physical model takes into account two-phase release. The Lagrangian approach is applied in order to describe the dispersion of droplets with the mass, momentum, and energy exchange between the gas and liquid phases via the source terms. In addition, the mathematical/physical model takes into account the radiative heat transfer as well as global kinetics soot formation and soot oxidation are applied in order to calculate the soot volume fraction. These two processes are necessary in order to calculate the absorption coefficient of hydrocarbon combustion product, (Makhviladze, Roberts, & Yakush, 1999c1999).

Many analytical methods have been developed in order to solve a system of differential equations (Salahshour, Ahmadian, Senu, Baleanu, & Agarwal, 2015; Zhang, Balochian, Agarwal, Bhatnagar, & Housheya, 2016).

One of the analytic approximate method that we applied in this paper is the well-known homotopy analysis method (HAM). In general, perturbation methods are widely used to investigate physical systems that can be exactly solved, but these systems need to contain small perturbations parameters in order to apply a different perturbation method. In contrast to the classical perturbation method, the HAM is always valid no matter whether there exist small physical parameters or not in the system (Kumar, Kumar, & Singh, 2016; Kumar, Kumar, Singh, & Singh, 2014; Xiang, Kumar, & Kumar, 2015). The HAM contains the auxiliary parameter called the artificial parameter $ħ$ (Shuijun, 2004). This means that this method does not involve perturbation series in power of physical parameters, and the convergence of approximate is controlled by $ħ$ which does not exist in the original physical model (Kumar, Kumar, & Baleneu, 2016). The biggest advantage of the HAM method, which is different from all other analytical methods, is that it provides us with a simple way to adjust and control the convergence region of solution series by choosing proper values of auxiliary parameter $ħ$, auxiliary function H and auxiliary linear operator L (for more information about the HAM refer to Behrouz, Heidar, and Ahmet (2013)–Yahaya and Simon (2015).

A comparison with experimental data enables one to validate the new model and the validity of the HAM method.

2. Governing equation of the model

The system of the governing equations describing the combustion of two phase releases of liquid fuel into the open atmosphere. The model take into account heat, mass, and momentum exchange between the gaseous and disperse phases, soot formation, and radiative heat transfer. The gas phase is described by a system of Favre-averaged Navier–Stokes equations with the k–$\mathit{ϵ}$ turbulence model and the eddy breakup model of turbulence combustion (Launder & Spalding, 1972). The gas is considered as a multicomponent mixture of ${\text{O}}_2,{\text{N}}_2,{\text{CO}}_2,{\text{H}}_2\text{O}$. The disperse phase consists of liquid fuel droplets moving with velocity $(u_d,v_d)$ and described in continuous way using a PDF n(R). We did not take into account the collisions between drops. The momentum equation includes the term of the drag force between the gas and the disperse phases. We assumed that there is no interaction between the droplets. The continuity and energy equations include evaporation of droplets and inter-phase energy exchange using the source terms. The reaction rate for individual component are $w_i=\pm {\mathit{\nu }}_{i}w$, where ${\mathit{\nu }}_i$ is the mass stoichiometric coefficient $({\mathit{\nu }}_F=1)$, the sign should be taken as negative for fuel and oxidizer and positive for combustion products. The radiative flux associated with kth gray gas is a function of the $U_k$, i.e. the kth gas radiative energy density and $U_k$, i.e. the black-body radiative energy density. The influence of turbulent fluctuation was neglected. The source terms in the gas phase determined by integrating over all droplets size.

Soot formation and oxidation were modeled using the two-step global scheme with large-scale flame. In order to apply the eddy breakup model, we use for calculation the mean flow characteristics. The radiation consists of infrared banded molecular radiation. The species having the strongest radiation bands being ${\text{CO}}_2$ and ${\text{H}}_2\text{O}$ and continuous spectra radiation from the soot particles. The optical thickness that corresponding to the k-th gray gas is determined by integrating the absorption coefficient along the vertical and horizontal lines of sight and taking the maximum of the resulting values overall all the computational domain. The model of volume emission is used for the gray gas. The radiative heat transfer calculations were based on the mean distribution of the temperature and concentration. In this way, one can neglect the influence of the turbulent fluctuations. The droplets are described by a Lagrangian approach. The volume fraction of the dispersed phase is negligible and there is no interaction between the droplets. This assumption can be made due to the spray dilute approximation. We take into account the effect of the turbulent fluctuations on the droplets motion in such a way that the gas velocity is represented as a sum of its average and fluctuating components. The evaporation rate of the droplets is described by the steady-state model in which the droplet temperature is determined by heat and mass balances with a Ranz–Marshal correction for the effect of the droplet motion. According to the assumptions above, the governing equations of the model are as follows (Makhviladze et al., 1999a,1999b; Utyuzhnikov, 2002):

continuity equation: (2.1) $$\begin{array}{c}\hfill \frac{\mathit{\partial }\mathit{\rho }}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}(\mathit{\rho }\overrightarrow{U})=〈S_m〉,\end{array}$$(2.1) momentum equation (2.2) $$\begin{array}{c}\hfill \frac{\mathit{\partial }(\mathit{\rho }\overrightarrow{U})}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}(\mathit{\rho }\overrightarrow{U}\overrightarrow{U})=-\overrightarrow{\mathrm{\nabla }}p+\mathrm{\nabla }\widehat{R}+(\mathit{\rho }-{\mathit{\rho }}_a)\overrightarrow{g}+〈{\overrightarrow{f}}_d〉,\end{array}$$(2.2) energy equation (2.3) $$\begin{array}{c}\hfill \frac{\mathit{\partial }(\mathit{\rho }h)}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}(\mathit{\rho }\overrightarrow{U}h)=\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{Pr}\overrightarrow{\mathrm{\nabla }}h\right)+w{Q}_c-S_R+〈S_h〉,\end{array}$$(2.3) species equation (2.4) $$\begin{array}{c}\hfill \frac{\mathit{\partial }(\mathit{\rho }{Y}_i)}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}(\mathit{\rho }\overrightarrow{U}{Y}_i)=\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}{Y}_i\right)+w_i+〈{\mathit{\delta }}_{i,F}{S}_m〉,\end{array}$$(2.4) turbulent kinetic energy (2.5) $$\begin{array}{c}\hfill \frac{\mathit{\partial }(\mathit{\rho }k)}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}(\mathit{\rho }\overrightarrow{U}k)=\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{{\mathit{\sigma }}_k}\overrightarrow{\mathrm{\nabla }}k\right)+G-\mathit{\rho }\mathit{ϵ}+〈S_t〉,\end{array}$$(2.5) dissipation equation (2.6) $$\begin{array}{c}\hfill \frac{\mathit{\partial }(\mathit{\rho }\mathit{ϵ})}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}(\mathit{\rho }\overrightarrow{U}\mathit{ϵ})=\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Pr}}\overrightarrow{\mathrm{\nabla }}\mathit{ϵ}\right)+\frac{\mathit{ϵ}}{k}(C_{1}G-C_2\mathit{\rho }\mathit{ϵ}+C_s〈S_t〉),\end{array}$$(2.6) particle concentration of soot equation (2.7) $$\begin{array}{cc}\hfill \frac{d{N}_s}{dt}& =\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}\frac{N_s}{\mathit{\rho }}\right)+g_0{N}_r\frac{(N_s+N_r)}{K}\hfill \\ \hfill & -A\frac{\mathit{ϵ}}{k}{N}_s\text{min}\left(1,\frac{{\mathit{\nu }}_s{\mathit{\rho }}_{O_2}}{{\mathit{\nu }}_s{m}_s{N}_s+{\mathit{\nu }}_O{\mathit{\rho }}_F}\right),\hfill \end{array}$$(2.7) particle concentration of radical equation (2.8) $$\begin{array}{cc}\hfill \frac{\text{d}{N}_r}{\text{dt}}& =\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}\frac{N_r}{\mathit{\rho }}\right)+A_s{Y}_F{e}^{-\frac{E}{RT}}+(f-g)N_r\frac{Y_F}{Y_{F_0}}\hfill \\ \hfill & -g_0{N}_r(N_s+N_r)-A\frac{\mathit{ϵ}}{k}{N}_s\text{min}\left(1,\frac{{\mathit{\nu }}_s{\mathit{\rho }}_{O_2}}{{\mathit{\nu }}_s{m}_s{N}_s+{\mathit{\nu }}_O{\mathit{\rho }}_F}\right),\hfill \end{array}$$(2.8) motion equation of a droplets (2.9) $$\begin{array}{cc}\hfill \frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^{3}n(r_d)\frac{\text{d}{\overrightarrow{U}}_d}{\text{dt}}〉& =C_D\frac{\mathit{\pi }}{8}\mathit{\rho }〈r_d^{2}n(r_d)||{\overrightarrow{U}}_g-{\overrightarrow{U}}_d||({\overrightarrow{U}}_g-{\overrightarrow{U}}_d)〉\hfill \\ \hfill & +\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^{3}n(r_d)〉\overrightarrow{g},\hfill \end{array}$$(2.9) evaporation of a droplets equation (2.10) $$\begin{array}{c}\hfill \frac{{\mathit{\rho }}_l\mathit{\pi }}{6}\frac{\text{d}}{\text{dt}}〈r_d^{3}n(r_d)〉=2\mathit{\pi }〈r_{d}n(r_d)〉\frac{\mathit{\lambda }}{C_p}\text{ln}(1+b)(1+0.3{\text{Re}}_i^{1/2}{\text{Pr}}^{1/3})\end{array}$$(2.10)

The following expressions are used in the above model:(2.11) $$\begin{array}{c}\hfill \widehat{R}=\mathit{\mu }(\overrightarrow{\mathrm{\nabla }}\overrightarrow{U}+\mathrm{\nabla }{\overrightarrow{U}}^T-\frac{2}{3}(\overrightarrow{\mathrm{\nabla }}\overrightarrow{U})I)-\frac{2}{3}\mathit{\rho }k\widehat{I},\end{array}$$(2.11) (2.12) $$\begin{array}{c}\hfill G={\mathit{\mu }}_t\left({(\overrightarrow{\mathrm{\nabla }}\overrightarrow{U}+\overrightarrow{\mathrm{\nabla }}{\overrightarrow{U}}^T)}^{ij}{\overrightarrow{\mathrm{\nabla }}}_i{\overrightarrow{U}}_j\right)-\frac{2}{3}\mathit{\rho }k\widehat{I}\overrightarrow{\mathrm{\nabla }}\overrightarrow{U}-\frac{{\mathit{\mu }}_t\overrightarrow{g}}{\mathit{\rho }}\overrightarrow{\mathrm{\nabla }\mathit{\rho }},\end{array}$$(2.12) (2.13) $$\begin{array}{c}\hfill w=\mathit{\rho }A\frac{\mathit{ϵ}}{k}\text{min}\left(Y_F,\frac{Y_O}{{\mathit{\nu }}_O},\frac{B{Y}_P}{{\mathit{\nu }}_P}\right),\end{array}$$(2.13) (2.14) $$\begin{array}{c}\hfill \overrightarrow{f_d}=-\frac{1}{\frac{4\mathit{\pi }}{3}〈r_d^{3}n(r_d)〉}{C}_D\frac{\mathit{\pi }}{8}\mathit{\rho }〈r_d^{2}n(r_d)||{\overrightarrow{U}}_g-{\overrightarrow{U}}_d||({\overrightarrow{U}}_g-{\overrightarrow{U}}_d)〉,\end{array}$$(2.14) (2.15) $$\begin{array}{c}\hfill 〈S_m〉=\frac{1}{\frac{4\mathit{\pi }}{3}〈r_d^{3}n(r_d)〉}\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}\frac{\text{d}}{\text{dt}}〈r_d^{3}n(r_d)〉,\end{array}$$(2.15) (2.16) $$\begin{array}{c}\hfill 〈S_h〉=-\frac{1}{\frac{4\mathit{\pi }}{3}〈r_d^{3}n(r_d)〉}\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}\frac{\text{d}}{\text{dt}}〈r_d^{3}n(r_d)〉(h-Q_v),\end{array}$$(2.16) (2.17) $$\begin{array}{c}\hfill 〈S_t〉=-\frac{1}{\frac{4\mathit{\pi }}{3}〈r_d^{3}n(r_d)〉}\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^3{n}_{r_d}\frac{\text{d}\overrightarrow{U}}{\text{dt}}\overrightarrow{U^{\prime }}〉,\end{array}$$(2.17) (2.18) $$\begin{array}{c}\hfill S_R=\sum _{i}4{\mathit{\kappa }}_i{a}_i\mathit{\sigma }(T^4-T_a^4),\end{array}$$(2.18) (2.19) $$\begin{array}{c}\hfill {\mathit{\mu }}_t=C_{\mathit{\mu }}\mathit{\rho }\frac{k^2}{\mathit{ϵ}},\end{array}$$(2.19)

where $\overrightarrow{I}$ is the unit tensor, $\mathit{\mu }={\mathit{\mu }}_l+{\mathit{\mu }}_t$, the total viscosity, is the sum of laminar and turbulent viscosities, respectively, $C_{\mathit{\mu }}$ is a constant in the turbulence model, $Q_v$ is the heat of evaporation, $\mathit{\kappa }$ is an absorption coefficient, a is a weight coefficient, $\overrightarrow{U^{\prime }}$ is the turbulent fluctuating velocity corresponding to the Gaussian probability distribution with the mean 2/3k.

2.1. The initial and boundary conditions

The initial and boundary conditions are as follows (Utyuzhnikov, 2002):

The problem is considered as an axisymmetric one in the cylindrical coordinate system (r, z). The fuel and the droplets are injected with constant temperature and pressure. The injection velocity is represented by a piecewise function of time. The spatial distribution of the velocity follows the Gaussian distribution with a maximum value of $U_{in}(0)=\sqrt{(2(p_0-p_a)/{\mathit{\rho }}_l)}$ (using the incompressible Bernoulli equation, where $p_0$ is the pressure in the tank and ${\mathit{\rho }}_l$ is the liquid propane density at the pressure $p_0$) on the z-axis and decrease in the velocity at the source boundary by the factor of $\sqrt{2}$. The initial size distribution of droplet follows the gamma distribution. The heat capacity and the heat of evaporation are assumed to be constant. The droplets do not reach the right and the upper boundaries since we assumed that these boundaries are located far enough. On the solid wall the following boundary conditions for k and $\mathit{ϵ}$ are $k=0$, $\mathrm{\nabla }\mathit{ϵ}·\overrightarrow{n}=0$, where $\overrightarrow{n}$ is the internal unit normal vector. For the radiative fluxes for optically thick gray gases, the following boundary conditions are used: $2{\overrightarrow{q}}_{R,k}·\overrightarrow{n}={(a_k{\overrightarrow{U}}_b-{\overrightarrow{U}}_k)}_{|w}$. Finally, we assumed that the ignition is spark like and takes place near the source surface in a small volume.

3. Preliminaries

In this section, we apply the HAM as presented in (Liao, 1998).

3.1. The basic idea of homotopy analysis method

Consider the following differential equation:(3.1) $$\begin{array}{c}\hfill N(u(\overrightarrow{r},t))=0.\end{array}$$(3.1)

where N is a nonlinear operator, $\overrightarrow{r}$ is a vector of spatial variables, t denotes time, and u is an unknown function.

3.1.1. Zero-order deformation equation

By means of generalizing the traditional concept of homotopy, Liao in (1998) constructs the so-called zero-order deformation equation:(3.2) $$\begin{array}{c}\hfill (1-p)\ell \left[\mathrm{\Phi }(\overrightarrow{r},t;p)-u_0(\overrightarrow{r},t)\right]=ħH(\overrightarrow{r},t)N(\mathrm{\Phi }(\overrightarrow{r},t;p)),\end{array}$$(3.2)

where $ħ$ is a non-zero auxiliary parameter, H is an auxiliary function, $\ell$ is an auxiliary linear operator, $u_0(·)$ is an initial guess of $u(·)$, $\mathrm{\Phi }$ is an unknown function. The degree of freedom is to choose the initial guess, the auxiliary linear operator, the auxiliary parameter, and the auxiliary function H. Expanding $\mathrm{\Phi }$ to a power series with respect to the embedding parameter p, one has(3.3) $$\begin{array}{c}\hfill \mathrm{\Phi }(\overrightarrow{r},t;p)=u_0(\overrightarrow{r},t)+\sum _{n=1}^{\infty }{u}_n(\overrightarrow{r},t)p^n,\end{array}$$(3.3)

where(3.4) $$\begin{array}{c}\hfill u_n(\overrightarrow{r},t)=\frac{1}{n!}\frac{{\mathit{\partial }}^n\mathrm{\Phi }(\overrightarrow{r},t;p)}{\mathit{\partial }{p}^n}{|}_{p=0}.\end{array}$$(3.4)

If the auxiliary linear operator, the initial guess, the auxiliary parameter, and the auxiliary function are so properly chosen that the above series converges at $p=1$, one has(3.5) $$\begin{array}{c}\hfill \mathrm{\Phi }(\overrightarrow{r},t)=\underset{p\to 1}{lim}\mathrm{\Phi }(\overrightarrow{r},t;p)=u_0(\overrightarrow{r},t)+\sum _{n=1}^{\infty }{u}_n(\overrightarrow{r},t),\end{array}$$(3.5)

which must be one of the solutions of the original nonlinear equation.

3.1.2. mth-order deformation

Define the vector:(3.6) $$\begin{array}{c}\hfill \overrightarrow{u_n}(\overrightarrow{r},t)=\{u_0(\overrightarrow{r},t),u_1(\overrightarrow{r},t),...,u_n(\overrightarrow{r},t)\}.\end{array}$$(3.6)

Differentiating Equation (3.2) m-times with respect to the embedding parameter p and then setting $p=0$ and finally dividing the terms by m!, we obtain the mth-order deformation equation in the form of:(3.7) $$\begin{array}{c}\hfill \ell [u_m(\overrightarrow{r},t)-{\mathit{\chi }}_m{u}_{m-1}(\overrightarrow{r},t)]=ħH(\overrightarrow{r},t)R_m(u_{m-1}(\overrightarrow{r},t)),\end{array}$$(3.7)

where(3.8) $$\begin{array}{c}\hfill R_m(u_{m-1}(\overrightarrow{r},t))=\frac{1}{(m-1)!}\frac{{\mathit{\partial }}^{m-1}N(\mathrm{\Phi }(\overrightarrow{r},t;p))}{\mathit{\partial }{p}^{m-1}}{|}_{p=0},\end{array}$$(3.8)

and ${\mathit{\chi }}_m$ is the unit step function. Applying the inverse operator ${\ell }^{-1}(·)$ on both side of Equation (3.7), we get(3.9) $$\begin{array}{c}\hfill u_m(\overrightarrow{r},t)={\mathit{\chi }}_m{u}_{m-1}(\overrightarrow{r},t)+ħ{\ell }^{-1}[H(\overrightarrow{r},t)R_m(u_{m-1}(\overrightarrow{r},t))].\end{array}$$(3.9)

In this way, it is easy to obtain $u_m$ for $m\ge 1$, at mth-order and finally get the solution as follows:(3.10) $$\begin{array}{c}\hfill u(\overrightarrow{r},t)=\sum _{n=0}^m{u}_n(\overrightarrow{r},t).\end{array}$$(3.10)

when $m\to \infty$, we get an accurate approximation of the original Equation (3.1). If Equation (3.1) admits unique solution, then this method will produce the unique solution. If Equation (3.1) does not possess unique solution, the HAM will give a solution among many other (possible) solutions.

The constants are as follows:(3.11) $$\begin{array}{cc}& C_{\mathit{\mu }}=0.09,C_1=1.44,C_2=1.92,C_s=1.5,{\mathit{\sigma }}_k=1,\text{Sc}=0.7\text{Pr}=0.7\hfill \\ \hfill & \text{Sc}=0.7,A=4B=0.5,K=5,g_0={10}^{-15}{\text{m}}^3/\text{s}.\hfill \end{array}$$(3.11)

The parameters are as follows:(3.12) $$\begin{array}{cc}& A_s=6.2\times {10}^{40}{\text{m}}^{-3}{\text{s}}^{-1},E=7.54\times {10}^5\text{J}/\text{mole},(f-g)={10}^2{\text{s}}^{-1},Y_{F0}=0.2,\hfill \\ \hfill & g_0={10}^{-15}{\text{m}}^3{\text{s}}^1,m_s={\mathit{\rho }}_s\mathit{\pi }{D}_s^3/6,{\mathit{\rho }}_s=2\times {10}^3\text{kg}/{\text{m}}^3,D_s=200\text{A}.\hfill \end{array}$$(3.12)

3.1.3. $ħ$-Curve

According to the theory of HAM, the convergence and the rate of solution series are dependent on the convergent control parameter $ħ$. This means that this parameter gives one a convenient way to adjust and to control the convergent region of the solutions. This subsection briefly describes how to choose this parameter based on (Liao, 2003).

Solving the mth-order deformation one obtains a family of solutions that depends on the auxiliary parameter $ħ$. So, regarding $ħ$ as independent variable, it is easy to plot the $ħ$-curves. For example, we can plot the following curves:(3.13) $$\begin{array}{cc}\hfill {\mathrm{{\rm Y}}}_1& =u{(\overrightarrow{r},t)}_{|\overrightarrow{r}=0,t=0},\text{or}{\mathrm{{\rm Y}}}_2=u^{\prime }{(\overrightarrow{r},t)}_{|\overrightarrow{r}=0,t=0},\text{or}{\mathrm{{\rm Y}}}_3=u^{″}{(\overrightarrow{r},t)}_{|\overrightarrow{r}=0,t=0},\hfill \\ \hfill {\mathrm{{\rm Y}}}_1& =v{(\overrightarrow{r},t)}_{|\overrightarrow{r}=0,t=0},\text{or}{\mathrm{{\rm Y}}}_2=v^{\prime }{(\overrightarrow{r},t)}_{|\overrightarrow{r}=0,t=0},\text{or}{\mathrm{{\rm Y}}}_3=v^{″}{(\overrightarrow{r},t)}_{|\overrightarrow{r}=0,t=0}\hfill \\ \hfill \end{array}$$(3.13)

The curves ${\mathrm{{\rm Y}}}_i(i=1,2,3)$ are a function of $ħ$ and thus can be plotted by a curve $\mathrm{{\rm Y}}\approx ħ$. According to (Liao, 2003), there exists a horizontal line segment (flat portion of the $ħ$-curve) in the figure of $\mathrm{{\rm Y}}\approx ħ$ and called the valid region of $ħ$ which corresponds to a region of convergence of the solutions. Thus, if we choose any value in the valid region of $ħ$, we are sure that the corresponding solution series are convergent. For given initial approximations $u_0(\overrightarrow{r},t)$, $v_0(\overrightarrow{r},t)$ the auxiliary linear operator $\ell$, and the auxiliary function $H(\overrightarrow{r},t)$, the valid region of $ħ$ for different special quantities is often nearly the same for a given problem. Hence, the so-called $ħ$-curve provides us with a convenient way to show the influence of $ħ$ on the convergence region of the solutions series.

As proved by (Shuijun, 2004) in general, if $ħ$ is properly chosen so that the series of solutions are convergent based on the following theorem:

Theorem 1

Suppose that $A\subset R$ be a Banach space donated with a suitable norm $\Vert ·\Vert$, over which the sequence $u_k(t)$ of $u(r,p)={\sum }_{k=0}^{\infty }{u}_k(r)p^k$ is defined for a prescribed value of $ħ$. Assume also that the initial approximation $u_0(t)$ remains inside the ball of the solution u(t). Taking $r\in R$ be a constant, the following statements hold true:

(1)	If $\Vert u_{k+1}(t)\Vert \le r\Vert u_k(t)\Vert$ for all k, given some $0<r<1$, then the series solution $u(t,p)={\sum }_{k=0}^{\infty }{u}_k(t)p^k$ converges absolutely at $p=1$ to $u(r)={\sum }_{k=0}^{\infty }{u}_k(r)$ over the domain of definition of t,
(2)	If $\Vert u_{k+1}(\overrightarrow{r},t)\Vert \ge r\Vert u_k(\overrightarrow{r},t)\Vert$ for all k, given some $r>1$, then the series solution $u(t,p)={\sum }_{k=0}^{\infty }{u}_k(t)p^k$ diverges at p = 1 over the domain of definition of t.

Proof

 

(1)

Let $S_n(t)$ denote the sequence of partial sum of the series $u(r)={\sum }_{k=0}^{\infty }{u}_k(r)$. We need to show that $S_n(t)$ is a Cauchy sequence in A, hence, consider, $$\Vert S_{n+1}(t)-S_n(t)\Vert =\Vert u_{n+1}(t)\Vert \le r\Vert u_n(t)\Vert \le r^2\Vert u_{n-1}(t)\Vert \le \cdots \le r^{n+1}\Vert u_0(t)\Vert .$$ It should be remarked that owing to these inequalities, all the approximations produced by the homotopy method will lie within the ball of u(t). In order to show the Cauchy sequence test let n, m be two natural numbers such that $n\ge m$. Using the above inequalities and the triangle inequality successively, we have, $$\begin{array}{cc}\hfill \Vert S_n(t)-S_m(t)\Vert & =\Vert S_n(t)-S_{n-1}(t)+S_{n-1}(t)-S_{n-2}(t)+\cdots +S_{m+1}(t)-S_m(t)\Vert \hfill \\ \hfill & \le \frac{(1-r^{n-m})r^{m+1}}{1-r}·\Vert u_0(t)\Vert ⟹\underset{n,m\to \infty }{lim}\Vert S_n(t)-S_m(t)\Vert =0.\hfill \end{array}$$ This means that $S_n(t)$ is a Cauchy sequence in the Banach space A, and this implies that the series solution $u(r)={\sum }_{k=0}^{\infty }{u}_k(r)$ is convergent. $\square$

(2)

Under the hypothesis supplied in (2), there exist a number d, $d>r>1$, so that the interval of convergence of the power series $u(r,p)={\sum }_{k=0}^{\infty }{u}_k(r)p^k$ is $|p|<\frac{1}{d}<1$ which excludes the case of $p=1$.

$\square$

Theorem 2

If the series solution defined by $u(r)={\sum }_{k=0}^{\infty }{u}_k(r)$ is convergent, then it converges to an exact solution of the nonlinear problem $N(u(r,t))=0$.

Proof

The proof presented in (Liao, 2003). $\square$

Theorem 3

Assume that the series solution ${\sum }_{n=0}^{\infty }{u}_n(t)$ is convergent to the solution u(t) for a prescribed value of $ħ$. If the truncated series ${\sum }_{n=0}^M{u}_n(t)$ is used as an approximation to the solution u(t) of the problem $N(u(r,t))=0$, then an upper bound for the error, $E_M(t)$, is estimated as $E_M(t)\le \frac{r^{M+1}}{1-r}\Vert u_0(t)\Vert$.

Proof

Using the inequality in the proof of Theorem 1, we receive$$\Vert u(t)-S_M(t)\Vert \le \frac{1-r^{n-M}}{1-r}{r}^{M+1}·\Vert u_0(t)\Vert .$$

Since $0<r<1$ then $(1-r^{n-M})<1$ which implies the desired upper bound for the error, $E_M(t)$.

$\square$

Remark 1

An optimal value of the convergence control parameter $ħ$ can be found by means of the exact square residual error integrated in the whole region of interest $\mathrm{\Gamma }$, at the order of approximation M, that is, $Res(ħ)={\int }_{\mathrm{\Gamma }}{\left[N\left({\sum }_{k=0}^M{u}_k(r)\right)\right]}^{2}dr$.

Hence, the more quickly $Res(ħ)$ decreases to zero, the faster the corresponding homotopy series solution $u(r)={\sum }_{k=0}^{\infty }{u}_k(r)$ converges to the exact solution of the problem $N(u(r,t))=0$. So, at the given order of approximation M, the corresponding optimal value of the convergence control parameter $ħ$ is given by the minimum of $Res(ħ)$, corresponding to a nonlinear algebraic equation of the form $\text{d}Res(ħ)/\text{dt}=0$ (see Table 4).

4. Analysis and results

In order to implement the HAM to the model (2.1)–(2.10), we write the expressions $R_m$ for each dynamical variables. The dynamical variables of the physical model are $\mathit{\rho }={\mathrm{\Phi }}^1,\overrightarrow{U}=\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right),h={\mathrm{\Phi }}^3,Y_i={\mathrm{\Phi }}_i^4,k={\mathrm{\Phi }}^5,\mathit{ϵ}={\mathrm{\Phi }}^6,N_s={\mathrm{\Phi }}^7,N_r={\mathrm{\Phi }}^8,{\overrightarrow{U}}_d=\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right),n={\mathrm{\Phi }}^{10}$. Hence, we defined the following series for the dynamical variables as follows:(4.1) $$\begin{array}{c}\hfill {\mathrm{\Phi }}_i=u_0(\mathit{\tau })+\sum _{m=1}^{\infty }{u}_m^{(i)}{p}^m.\end{array}$$(4.1)

According to our model the linear operator $\ell [·]$ will be in the form of:(4.2) $$\begin{array}{c}\hfill \ell [\mathrm{\Phi }(\mathit{\tau },p)]=\frac{\mathit{\partial }\mathrm{\Phi }(\mathit{\tau },p)}{\mathit{\partial }\mathit{\tau }},\end{array}$$(4.2)

and the nonlinear operator $N[·]$ as follows:(4.3) $$\begin{array}{c}\hfill N\left[{\mathrm{\Phi }}^1\right]=\frac{\mathit{\partial }{\mathrm{\Phi }}^1}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right))-〈S_m\left({\mathrm{\Phi }}^{10}\right)〉,\end{array}$$(4.3) (4.4) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^1{\mathrm{\Phi }}^2\right]& =\frac{\mathit{\partial }({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right))}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right)\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}^2\right))+\overrightarrow{\mathrm{\nabla }}p\hfill \\ \hfill & -\mathrm{\nabla }\widehat{R}\left(\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right),{\mathrm{\Phi }}^1,{\mathrm{\Phi }}^5\right)-\left({\mathrm{\Phi }}^1-{\mathit{\rho }}_a\right)\overrightarrow{g}\hfill \\ \hfill & -〈{\overrightarrow{f}}_d\left(\left({\mathrm{\Phi }}^{10},\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right)\right)\right.〉,\hfill \end{array}$$(4.4) (4.5) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^1{\mathrm{\Phi }}^3\right]& =\frac{\mathit{\partial }({\mathrm{\Phi }}^1{\mathrm{\Phi }}^3)}{\mathit{\partial }t}-\overrightarrow{\mathrm{\nabla }}({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right){\mathrm{\Phi }}^3)\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Pr}}\overrightarrow{\mathrm{\nabla }}{\mathrm{\Phi }}^3\right)-w{Q}_c-S_R\left({\mathrm{\Phi }}^3\right)-〈S_h\left(\left({\mathrm{\Phi }}^{10},{\mathrm{\Phi }}^3\right)\right.〉,\hfill \end{array}$$(4.5) (4.6) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^1{\mathrm{\Phi }}^3\right]& =\frac{\mathit{\partial }({\mathrm{\Phi }}^1{\mathrm{\Phi }}_i^4)}{\mathit{\partial }t}-\overrightarrow{\mathrm{\nabla }}({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right){\mathrm{\Phi }}_i^4)\hfill \\ \hfill & +\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}{\mathrm{\Phi }}_i^4\right)+w_i+〈{\mathit{\delta }}_{i,F}{S}_m\left(\left({\mathrm{\Phi }}^{10}\right)\right.〉,\hfill \end{array}$$(4.6) (4.7) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^1{\mathrm{\Phi }}^5\right]& =\frac{\mathit{\partial }({\mathrm{\Phi }}^1{\mathrm{\Phi }}^5)}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2{\mathrm{\Phi }}_2^2\right){\mathrm{\Phi }}^5)\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{{\mathit{\sigma }}_k}\overrightarrow{\mathrm{\nabla }}{\mathrm{\Phi }}^5\right)+G\left(\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right),{\mathrm{\Phi }}^1,{\mathrm{\Phi }}^5\right)\hfill \\ \hfill & +{\mathrm{\Phi }}^1{\mathrm{\Phi }}^6-〈S_t\left(\left({\mathrm{\Phi }}^{10},\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right)\right)\right.〉,\hfill \end{array}$$(4.7) (4.8) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^1{\mathrm{\Phi }}^6\right]& =\frac{\mathit{\partial }({\mathrm{\Phi }}^1{\mathrm{\Phi }}^6)}{\mathit{\partial }t}-\overrightarrow{\mathrm{\nabla }}({\mathrm{\Phi }}^1\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right){\mathrm{\Phi }}^6)\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Pr}}\overrightarrow{\mathrm{\nabla }}{\mathrm{\Phi }}^6\right)\hfill \\ \hfill & -\frac{{\mathrm{\Phi }}^6}{k}(C_{1}G\left(\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right),{\mathrm{\Phi }}^1,{\mathrm{\Phi }}^5\right)-C_2{\mathrm{\Phi }}^1{\mathrm{\Phi }}^6+C_s〈S_t\left({\mathrm{\Phi }}^{10},\left({\mathrm{\Phi }}_1^2,{\mathrm{\Phi }}_2^2\right)\right)〉),\hfill \end{array}$$(4.8) (4.9) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^7\right]& =\frac{\text{d}{\mathrm{\Phi }}^7}{\text{dt}}-\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}\frac{{\mathrm{\Phi }}^7}{{\mathrm{\Phi }}^1}\right)\hfill \\ \hfill & +g_0{\mathrm{\Phi }}^8\frac{({\mathrm{\Phi }}^7+{\mathrm{\Phi }}^8)}{K}-A\frac{\mathit{ϵ}}{k}{\mathrm{\Phi }}^7\text{min}\left(1,\frac{{\mathit{\nu }}_s{\mathit{\rho }}_{O_2}}{{\mathit{\nu }}_s{m}_s{N}_s+{\mathit{\nu }}_O{\mathit{\rho }}_F}\right),\hfill \end{array}$$(4.9) (4.10) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^8\right]& =\frac{\text{d}{\mathrm{\Phi }}^8}{\text{dt}}-\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}\frac{{\mathrm{\Phi }}^8}{\mathit{\rho }}\right)-A_s{\mathrm{\Phi }}_F^4{e}^{-\frac{E}{RT}}+(f-g){\mathrm{\Phi }}^8\frac{{\mathrm{\Phi }}_F^4}{Y_{F_0}}\hfill \\ \hfill & +g_0{\mathrm{\Phi }}^8({\mathrm{\Phi }}^7+{\mathrm{\Phi }}^8)+A\frac{{\mathrm{\Phi }}^6}{k}{\mathrm{\Phi }}^7\text{min}\left(1,\frac{{\mathit{\nu }}_s{\mathit{\rho }}_{O_2}}{{\mathit{\nu }}_s{m}_s{N}_s+{\mathit{\nu }}_O{\mathit{\rho }}_F}\right),\hfill \end{array}$$(4.10) (4.11) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^{10}\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right)\right]& =\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^3({\mathrm{\Phi }}^{10})\frac{\text{d}\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right)}{\text{dt}}〉\hfill \\ \hfill & -C_D\frac{\mathit{\pi }}{8}\mathit{\rho }〈r_d^2({\mathrm{\Phi }}^{10})||{\overrightarrow{U}}_g-\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right)||\left({\overrightarrow{U}}_g-\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right)\right)〉\hfill \\ \hfill & +\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^3({\mathrm{\Phi }}^{10})〉\overrightarrow{g},\hfill \end{array}$$(4.11) (4.12) $$\begin{array}{cc}\hfill N\left[{\mathrm{\Phi }}^{10}\right]& =\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}\frac{\text{d}}{\text{dt}}〈r_d^3({\mathrm{\Phi }}^{10})〉\hfill \\ \hfill & -2\mathit{\pi }〈r_d({\mathrm{\Phi }}^{10})〉\frac{\mathit{\lambda }}{C_p}\text{ln}(1+b)(1+0.3{\text{Re}}_i^{1/2}{\text{Pr}}^{1/3})\hfill \end{array}$$(4.12)

According to (Liao, 2009) let:(4.13) $$\begin{array}{c}\hfill D_{m-1}(·)=\frac{1}{(m-1)!}\frac{{\mathit{\partial }}^{m-1}(·)}{\mathit{\partial }{p}^{m-1}}{|}_{p=0},\end{array}$$(4.13)

then the expressions for $R_{m_{(·)}}$ are as follows:(4.14) $$\begin{array}{c}\hfill R_{m-1}\left({\mathrm{\Phi }}^1\right)=\frac{\mathit{\partial }{u}_m^{(1)}}{\mathit{\partial }t}+\overrightarrow{\mathrm{\nabla }}\left[\sum _{k=0}^m\left(u_k^{(1)}\left(u_{m-k}^{(2,1)},u_{m-k}^{(2,2)}\right)\right)\right]-〈S_m\left(u_m^{(10)}\right)〉,\end{array}$$(4.14) (4.15) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^1{\mathrm{\Phi }}^2\right)& =\frac{\mathit{\partial }}{\mathit{\partial }t}\left[\sum _{k=0}^m\left(u_k^{(1)}\left(u_{m-k}^{(2,1)},u_{m-k}^{(2,2)}\right)\right)\right]\hfill \\ \hfill & +\overrightarrow{\mathrm{\nabla }}\left[\sum _{k=0}^m\sum _{j=0}^k\left(u_j^{(1)}{u}_{k-j}^{(2,1)}{u}_{m-k}^{(2,1)}+u_j^{(1)}{u}_{k-j}^{(2,1)}{u}_{m-k}^{(2,2)}\right)\right]+\overrightarrow{\mathrm{\nabla }}p\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(u_m^{(2,1)},u_m^{(2,12)}\right)-\overrightarrow{\mathrm{\nabla }}{\left(u_m^{(2,1)},u_m^{(2,2)}\right)}^T+\frac{2}{3}\overrightarrow{\mathrm{\nabla }}\left[\left(u_m^{(2,1)},u_m^{(2,2)}\right)I\right]\hfill \\ \hfill & +\frac{2}{3}\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(5)}\widehat{I}-(u_m^{(1)}-{\mathit{\rho }}_a)\overrightarrow{g}-〈{\overrightarrow{f}}_d\left(\left(u_m^{(10)},\left(u_m^{(9,d_1)},u_m^{(9,d_2)}\right)\right)\right.〉,\hfill \end{array}$$(4.15) (4.16) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^1{\mathrm{\Phi }}^3\right)& =\frac{\mathit{\partial }}{\mathit{\partial }t}\left[\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(3)}\right]-\overrightarrow{\mathrm{\nabla }}\left[\sum _{k=0}^m\sum _{j=0}^k\left(u_j^{(1)}{u}_{k-j}^{(2,1)}{u}_{m-k}^{(3)},u_j^{(1)}{u}_{k-j}^{(2,2)}{u}_{m-k}^{(3)}\right)\right]\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Pr}}\overrightarrow{\mathrm{\nabla }}{u}_m^{(3)}\right)-w{Q}_c-S_R\left(u_m^{(3)}\right)-〈S_h\left(\left(u_m^{(10)},u_m^{(3)}\right)\right.〉,\hfill \end{array}$$(4.16) (4.17) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^1{\mathrm{\Phi }}^3\right)& =\frac{\mathit{\partial }}{\mathit{\partial }t}\left[\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(4,i)}\right]-\overrightarrow{\mathrm{\nabla }}\left[\sum _{k=0}^m\sum _{j=0}^k\left(u_j^{(1)}{u}_{k-j}^{(2,1)}{u}_{m-k}^{(4,i)},u_j^{(1)}{u}_{k-j}^{(2,2)}{u}_{m-k}^{(4,i)}\right)\right]\hfill \\ \hfill & +\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}{u}_m^{(4,i)}\right)+w_i+〈{\mathit{\delta }}_{i,F}{S}_m\left(\left(u_m^{(10)}\right)\right.〉,\hfill \end{array}$$(4.17) (4.18) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^1{\mathrm{\Phi }}^5\right)& =\frac{\mathit{\partial }}{\mathit{\partial }t}\left[\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(5)}\right]+\overrightarrow{\mathrm{\nabla }}\left[\sum _{k=0}^m\sum _{j=0}^k\left(u_j^{(1)}{u}_{k-j}^{(2,1)}{u}_{m-k}^{(5)},u_j^{(1)}{u}_{k-j}^{(2,2)}{u}_{m-k}^{(5)}\right)\right]\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{{\mathit{\sigma }}_k}\overrightarrow{\mathrm{\nabla }}{u}_m^{(5)}\right)+G\left(\left(u_m^{(2,1)},u_m^{(2,2)}\right),u_m^{(1)},u_m^{(5)}\right)\hfill \\ \hfill & +\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(6)}-〈S_t\left(\left(u_m^{(10)},\left(u_m^{(2,1)},u_m^{(2,2)}\right)\right)\right.〉,\hfill \end{array}$$(4.18) (4.19) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^1{\mathrm{\Phi }}^6\right)& =\frac{\mathit{\partial }}{\mathit{\partial }t}\left[\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(6)}\right]-\overrightarrow{\mathrm{\nabla }}\left[\sum _{k=0}^m\sum _{j=0}^k\left(u_j^{(1)}{u}_{k-j}^{(2,1)}{u}_{m-k}^{(6)},u_j^{(1)}{u}_{k-j}^{(2,2)}{u}_{m-k}^{(6)}\right)\right]\hfill \\ \hfill & -\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Pr}}\overrightarrow{\mathrm{\nabla }}{u}_m^{(6)}\right)-\frac{u_m^{(6)}}{k}(C_{1}G\left(\left(u_m^{(2,1)},u_m^{(2,2)}\right),u_m^{(1)},u_m^{(5)}\right)\hfill \\ \hfill & -C_2\left(\sum _{k=0}^m{u}_k^{(1)}{u}_{m-k}^{(6)}\right)+C_s〈S_t\left(u_m^{(10)},\left(u_m^{(2,1)},u_m^{(2,2)}\right)\right)〉,\hfill \end{array}$$(4.19) (4.20) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^7\right)& =\frac{\text{d}{u}_m^7}{\text{dt}}-\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}{u}_m^7\right)+g_0\sum _{k=0}^m{u}_k^{(8)}\frac{(u_{m-k}^{(7)}+u_{m-k}^{(8)})}{K}\hfill \\ \hfill & -A\frac{\mathit{ϵ}}{k}{u}_m^{(7)}\text{min}\left(1,\frac{{\mathit{\nu }}_s{\mathit{\rho }}_{O_2}}{{\mathit{\nu }}_s{m}_s{N}_s+{\mathit{\nu }}_O{\mathit{\rho }}_F}\right),\hfill \end{array}$$(4.20) (4.21) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^8\right)& =\frac{\text{d}{u}_m^{(8)}}{\text{dt}}-\overrightarrow{\mathrm{\nabla }}\left(\frac{\mathit{\mu }}{\text{Sc}}\overrightarrow{\mathrm{\nabla }}\frac{u_m^{(8)}}{\mathit{\rho }}\right)-A_s{u}_m^{(4,F)}{e}^{-\frac{E}{RT}}+(f-g)\sum _{k=0}^m{u}_k^{(7)}\frac{u_{m-k}^{(4,F)}}{Y_{F_0}}\hfill \\ \hfill & +g_0\sum _{k=0}^m{u}_k^{(8)}(u_{m-k}^{(7)}+u_k^{(8)})+\frac{A}{k}\sum _{k=0}^m{u}_k^{(6)}{u}_{m-k}^{(7)}\text{min}\left(1,\frac{{\mathit{\nu }}_s{\mathit{\rho }}_{O_2}}{{\mathit{\nu }}_s{m}_s{N}_s+{\mathit{\nu }}_O{\mathit{\rho }}_F}\right),\hfill \end{array}$$(4.21) (4.22) $$\begin{array}{cc}\hfill R_{m-1}\left({\mathrm{\Phi }}^{10}\left({\mathrm{\Phi }}_{d_1}^9,{\mathrm{\Phi }}_{d_2}^9\right)\right)& =\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^3\sum _{k=0}^m{u}_k^{(10)}\frac{\text{d}\left(u_{m-k}^{(9,d_1)},u_{m-k}^{(9,d_1)}\right)}{\text{dt}}〉\hfill \\ \hfill & -C_D\frac{\mathit{\pi }}{8}\mathit{\rho }〈r_d^2{u}_m^{(10)}||{\overrightarrow{U}}_g-\left(u_m^{(9,d_1)},u_m^{(9,d_2)}\right)||({\overrightarrow{U}}_g-\left(u_m^{(9,d_1)},u_m^{(9,d_2)}\right)〉\hfill \\ \hfill & +\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}〈r_d^3({\mathrm{\Phi }}^{10})〉\overrightarrow{g},\hfill \end{array}$$(4.22) (4.23) $$\begin{array}{c}\hfill R_{m-1}\left({\mathrm{\Phi }}^{10}\right)=\frac{{\mathit{\rho }}_l\mathit{\pi }}{6}\frac{\text{d}}{\text{dt}}〈(r_d^3{u}_m^{10})〉-2\mathit{\pi }〈(r_d{u}_m^{10})〉\frac{\mathit{\lambda }}{C_p}\text{ln}(1+b)(1+0.3{\text{Re}}_i^{1/2}{\text{Pr}}^{1/3})\end{array}$$(4.23)

Table 1. The error for different values of order approximation M and different values of the valid region of the convergence control parameter $ħ$

$ħ$	$M=10$	$M=20$	$M=30$	Error
$-$1.5	1.0724	1.8979	0.0008	$4.3998\times {10}^{-1}$
$-$1	1.0694	0.7484	0.0099	$3.9874\times {10}^{-3}$
$-$0.66	2.0199	0.7489	0.0006	$3.8343\times {10}^{-7}$
0.45	3.7688	1.3435	0.0036	$9.3848\times {10}^{-9}$
1	1.4001	0.0537	0.0022	$6.4737\times {10}^{-5}$

Table 2. The error for different values of order approximation M and different values of the valid region of the convergence control parameter $ħ$

$ħ$	$M=10$	$M=20$	$M=30$	Error
$-$2	2.0474	2.7943	0.0065	$4.64763\times {10}^{-4}$
$-$1.67	4.4683	0.2452	0.0554	$7.7479\times {10}^{-1}$
$-$0.07	3.2583	3.2425	0.0045	$6.4663\times {10}^{-10}$
1.25	3.4783	2.4889	0.0044	$1.6734\times {10}^{-4}$
1.97	1.7484	0.4667	0.0039	$2.4545\times {10}^{-8}$

Table 3. The error for different values of order approximation M and different values of the valid region of the convergence control parameter $ħ$

$ħ$	M=10	$M=20$	$M=30$	Error
$-$0.55	0.2348	0.0547	0.0001	$1.5789\times {10}^{-2}$
$-$0.068	0.0532	0.5948	0.0003	$4.7478\times {10}^{-2}$
$-$0.78	4.0852	0.0453	0.0005	$1.5347\times {10}^{-8}$
1.643	0.5936	0.5438	0.0004	$2.0999\times {10}^{-8}$
1.997	0.9548	0.4539	0.0009	$3.3245\times {10}^{-11}$

Table 4. Optimalvalues of $ħ$ for different values of order approximation M

Order of approximation M	Optimal value of $ħ$
10	$-$1.009
20	1.023
30	0.364

The results depend on the combination of the parameters k and $\mathit{ϵ}$ according to the form $\mathrm{\Gamma }\equiv \sqrt{k^3}/\mathit{ϵ}$. The effect of each of these parameters was weakly on the results. Another important parameter influencing on the results was the time which taken for the fireball to be visible. We denoted this time as $t_{FireBall}$. The connections between $\mathrm{\Gamma }$ and $t_{FireBall}$ is when $\mathrm{\Gamma }$ increase the $t_{FireBall}$ decrease (numerical values of these parameters: $\mathrm{\Gamma }=0.7m$ and $t_{FireBall}=4s$). The results of our calculations are presented in Figures 1 and 2. The injection period was about 0.2s. The fireball presented at the time instants $t=0.05,0.15,0.25,0.95,0.5,1.5,2.5,$ and 3.5. The dashed line in Figures 1 and 2 presented the visible fireball boundary in the experiment. Timely development of the fireball presented in these figures counterclockwise. The shape and location of the fireball are depends on the injection time. At the beginning of the process, the fireball is located close to the edge and it is small Figure 1. And as time progresses the location of the fireball approaches to the center and becomes more symmetric (Figure 1 counterclockwise). An interesting phenomenon occurs in Figure 2. The first three Figures 2(a)–(c) the fireball left at the center and is symmetric, but its length is shortened. In Figure 2(d), the fireball splits into two fireballs, this is because the high temperature and the breach diameter which effects on the shape of the fireball as long as the release time is relatively long. When applying the HAM we took into account different values of $ħ$. The flat portion of the $ħ$-curve called corresponds to a region of convergence of the solutions. Our simulations corresponds to 30th-order approximation (Figure 3). As shown in Figures 1 and 2 our calculations agree very well with experimental data.

Figure 1. Fireball. Temperature. Two-phase model for different time scale: t = 0.05 s, 0.15 s, 0.25 s, and 0.95 s. Simulations of experiment. The dashed line corresponds to the visible fireball in the experiment. The bar corresponds to the temperature.

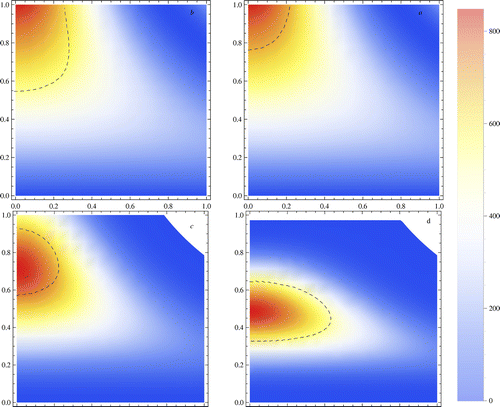
Figure 2. Fireball. Temperature. Two-phase model different time scale: t = 0.5 s, 1.5 s, 2.5 s, and 3.5 s. Simulations of experiment. The dashed line corresponds to the visible fireball in the experiment. The bar corresponds to the temperature.

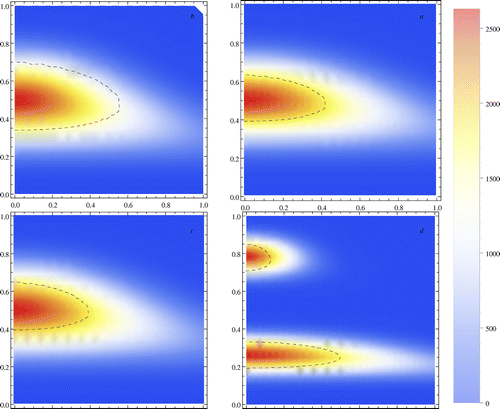
Figure 3. $ħ-curve$: the flat portion of the $ħ$-curve called the valid region of $ħ$ which corresponds to a region of convergence of the solutions. Simulations for 10th, 20th, and 30th-order approximations.

We compute the residual error according to the expression $Res(ħ)$ that corresponds to each nonlinear operator $N[·]$ given in Equations (4.3)–(4.12). The results for the error are summarized in Tables 1–3. As shown in these tables when the m-th order deformation is increase the error decrease.

5. Conclusions

A mathematical model was extended based on (Utyuzhnikov, 2002) by describing the droplets size using continuous model to simulate the combustion of polydisperse fuel spray vapor–droplets releases in the open atmosphere with hydrocarbon fuels at high pressures. The model takes into account two-phase clouds (fireball) combustion. The k–$\mathit{ϵ}$ model is used to described the turbulent processes. The two phase model was described using Eulerian–Lagrangian approach for the transient flows of fuel vapor–droplets mixture. We also take into account soot formation, radiative heat transfer mass transfer, and momentum exchange between the gaseous and the dispersed phase. The main process of the ignition of the fireball is the evolution from the reaction initiation until the total fuel is burnout.

$\mathit{\rho }$	=	density
${\mathit{\rho }}_a$	=	undisturbed atmosphere density
t	=	time
$U=(u,v)$	=	vector velocity
p	=	deviation
$\widehat{R}$	=	stress tensor
$\overrightarrow{g}=(0,-g)$	=	gravitational vector acceleration
${\overrightarrow{f}}_d$	=	drag force vector
h	=	enthalpy
$\mathit{\mu }$	=	total viscosities
$P_r$	=	Prandtl number
w	=	reaction rate
$w_i=\pm {\mathit{\nu }}_{i}w$	=	reaction rates for individual components
${\mathit{\nu }}_i$	=	mass stoichiometric coefficient of ith component
$Y_i=\text{Fuel},{\text{O}}_2,{\text{N}}_2,{\text{CO}}_2,{\text{H}}_2\text{O}$	=	the mass fractions
$\mathit{\delta }$	=	the Kronecker delta
Sc	=	Schmidt number
$〈·〉$	=	an operation of averaging over the droplet sizes
$S_h,S_t,S_m,S_R$	=	source term
$Q_c$	=	the heat of combustion
k	=	kinetic energy of turbulence
G	=	turbulence production term
$\mathit{ϵ}$	=	turbulent dissipation rate
${\mathit{\sigma }}_k$	=	constant in the turbulence model
$C_1,C_2,C_s$	=	constants
$N_s,N_r$	=	particle concentrations of soot and radicals
$g_0$	=	constant in the soot formation model
K, A	=	constants in the soot formation and eddy breakup model respectively
${\mathit{\nu }}_s$	=	mass stoichiometric coefficient of soot oxidation
$m_s$	=	mass of soot particle
$Y_F$	=	mass fraction of fuel
$Y_{F_0}$	=	constant in the soot formation model
$f-g$	=	net branching coefficient in the soot formation model
$A_s$	=	constant in the soot formation model
E	=	activation energy
R	=	universal gas constant
T	=	temperature
$r_d$	=	droplet radius
n	=	probability density function
$U_d=(u_d,v_d)$	=	droplet vector velocity
${\overrightarrow{U}}_g$	=	the local gas velocity
$C_D$	=	a function of droplet Reynolds number described by the empirical relationship (Kuo, 1986)
$\mathit{\lambda }$	=	molecular heat conductivity
$C_p$	=	specific heat capacity
b	=	mass transfer number in the droplet evaporation rate

In order to investigate the proposed model, we applied the well-known analytic approximate method the HAM and we compared the results to experimental data. An optimal value approach for the convergence control parameter has also been given. Via the theorems provided here, not only the question of the convergence of the homotopy series is answered, but also the region of validity of the space variable ensuring the convergence is determined. The calculations of the dynamic of the fireball as well as the radiative fraction of the total combustion energy are shown a good agreement with the experimental fireball data.

Acknowledgements

The author is very grateful to the referees for carefully reading the paper and for their comments and suggestions, which have improved the paper.

Additional information

Funding

The author received no direct funding for this research.

Notes on contributors

Ophir Nave

My research area is focused on all aspects of combustion of polydisperse and monodisperse fuel spray.

The models that describe the physical phenomena of these processes are systems of nonlinear partial differential equations. In order to investigate these models, we applied a semianalytical and asymptotic methods such as the homotopy analysis method (HAM), the method of integral invariant method (MIM), and singular perturbad homotopy analysis method (SPHAM).