A problem of thick circular plate in modified couple stress theory of thermoelastic diffusion

Abstract

The present investigation deals with an axisymmetric problem of thick circular plate in modified couple stress theory with mass diffusion. The Laplace and Hankel transforms technique have been used to investigate the problem. The displacements, stress components, temperature change, and chemical potential are obtained in the transformed domain subjected to thermal and chemical potential sources. Resulting quantities are obtained in the physical domain using a numerical inversion technique and depicted graphically. Comparisons are made with and without couple stress for both the Lord–Shulman (1967) and Green–Lindsay (1972) theories of thermoelasticity. Some particular cases of interest are also deduced.

Keywords:

• modified couple stress theory
• thermoelastic diffusion
• thermal and chemical potential sources
• Laplace and Hankel transforms

Public Interest Statement

The two dimensional problem of thick circular plate in modified couple stress theory with thermoelastic diffusion have many important applications in the field of material science, design of new materials, engineering, physics, geophysics, neuroradiology, and industry. Thermodiffusion plays an important role in the deformation of an elastic body due to thermal and chemical sources.

1. Introduction

Couple stress theory is an extended continuum theory that includes the effects of a couple per unit area on a material volume, in addition to the classical direct and shear forces per unit area. The existence of couple stress in materials was originally postulated by Voigt (1887). However, Cosserat and Cosserat (1909) were the first to develop a mathematical model to analyze materials with couple stresses.

Lacking an internal material length scale parameter, classical elasticity and plasticity cannot be used to interpret the size effect observed in numerous tests at micron and nanometer scales. However, higher order (non-local) continuum theories contain material length scale parameters and are capable of explaining microstructure related size (and other effects). Couple stress theories represent one class of such higher order theories. The classical couple stress elasticity theory (e.g. Koiter, 1964; Mindlin & Tiersten, 1962; Toupin, 1962) contains four material constants two classical and two additional for isotropic elastic materials. The couple stress theory can be viewed as a special format of strain gradient theory which uses rotation as a variable to describe curvature, while the strain gradient theory uses strain as variable to describe curvature.

The couple stress theory admits the possibility of asymmetric stress tensor since shear stress no longer have to be conjugate in order to ensure rotational equilibrium. The two additional constants are related to the underlying microstructure of the material and are inherently difficult to determine (e.g. Lakes, 1982; Lam, Yang, Chong, Wang, & Tong, 2003). Every physical theory possesses a certain domain of applicability outside which it fails to predict the physical phenomena with reasonable accuracy. Hence, there has been a need to develop higher order theories involving only one additional material length scale parameter.

Recently, Yang, Chong, Lam, and Tong (2002) developed a modified couple stress model, in which the couple stress tensor is symmetrical and only one material length parameter is needed to capture the size effect which is caused by micro-structure. Variational formulation of a modified couple stress theory and its application to a simple shear problem was studied by Ma, Gao, and Reddy (2008). Chen, Li, and Xu (2011) presented a modified couple stress model for bending analysis of composite laminated beams with first-order shear deformation. Asghari (2012) studied the geometrically nonlinear micro-plate formulation based on the modified couple stress theory. Şimşek and Reddy (2013) investigated the bending and vibration of functionally graded microbeams using a new higher order beam theory and the modified couple stress theory. Recently, the size-dependent buckling analysis of microbeams based on modified couple stress theory with high-order theories and general boundary conditions have been studied by Mohammad-Abadi and Daneshmehr (2014).

Beni, Mehralian, and Razavi (2015) discussed the problem of analysis of size-dependent shear deformable functionally graded cylindrical shell using modified couple stress theory. Results obtained using the modified couple stress theory are indicative of the considerable effect of the size parameter, particularly in bigger thicknesses and shorter lengths of nanotubes, on the natural frequency. In addition, Darijani and Shahdadi (2015) investigated the effect of shear deformation on the static bending and vibration responses of a simply supported microplate using modified couple stress theory and the governing Equations and related boundary conditions are solved simultaneously using Hamilton’s principle. Kumar and Devi (2015) presented the problem of hall current and rotation in a modified couple stress theory due to ramp type loading. Chen and Wang (2016) developed a new model of composite laminated Reddy plate of the global-local theory based on new modified couple stress theory. Reddy, Romanoff, and Loya (2016) discussed the problem of functionally graded circular plates with modified couple stress theory using finite element method.

Thermodiffusion in an elastic solid is due to the coupling of the fields of temperature, mass diffusion and strain. Heat and mass exchange with the environment during the process of the thermodiffusion in an elastic solid. The concept of thermodiffusion is used to describe the processes of thermomechanical treatment of metals (carboning, nitriding steel, etc.) and these processes are thermally activated, and their diffusing substances being, e.g. nitrogen, carbon, etc. They are accompanied by deformations of the solid.

Podstrigach Ia (1961) and Nowacki (1974a, 1974b, 1974c, 1976) developed the theory of thermoelastic with mass diffusion. In this theory, the coupled thermoelastic model is used. This implies infinite speeds of propagation of thermoelastic waves. Sherief et al. (2004) developed the theory of generalized thermoelastic diffusion that predicts finite speeds of propagation for thermoelastic and diffusive waves. Sherief and Saleh (2005) worked on a problem of a thermoelastic half space with a permeating substance in contact with the bounding plane in the context of the theory of generalized thermoelastic diffusion with one relaxation time. Recently, Kumar and Kansal (2008) derived the basic Equations in generalized thermoelastic diffusion for Green Lindsay (GL-model) theory and discussed the Lamb waves.

El-Maghraby and Abdel-Halim (2010) studied a problem of generalized thermoelasticity in Lord–Shulman theory (1967) a half space subjected to a known axisymmetric temperature distributions using Laplace and Hankel transforms technique. Tripathi, Kedar, and Deshmukh (2014) investigated the temperature distribution and thermal stresses in a semi-infinite cylinder with heat sources in thermoelastic theory with one relaxation time. Recently, Tripathi, Kedar, and Deshmukh (2015) discussed the problem of a thick circular plate with axisymmetric heat supply in a generalized thermoelastic diffusion using integral transform technique.

In the present paper, a problem of thick circular plate in modified couple stress theory by applying Laplace and Hankel transforms technique. The generalized theories of thermoelasticity developed by Sherief et al. (2004) and Kumar and Kansal (2008) are used to investigate the problem. The displacements, stress components, temperature change, and chemical potential are obtained numerically and represented graphically.

2. Governing equations

Following Yang et al. (2002), Kumar and Kansal (2008), the constitutive relations and the equations of motion in a modified couple stress generalized thermoelastic with mass diffusion in the absence of body forces, body couples, heat and mass diffusion sources are given by

(i) Constitutive relations(1) $$t_{ij}=\mathit{\lambda }{e}_{kk}{\mathit{\delta }}_{ij}+2\mathit{\mu }{e}_{ij}-\frac{1}{2}{e}_{kij}{m}_{lk,l}-{\mathit{\beta }}_1\left(1+{\mathit{\tau }}_1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)T{\mathit{\delta }}_{ij}-{\mathit{\beta }}_2\left(1+{\mathit{\tau }}^1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)C{\mathit{\delta }}_{ij},$$(1)

(2) $$m_{ij}=2\mathit{\alpha }{\mathit{\chi }}_{ij},$$(2)

(3) $${\mathit{\chi }}_{ij}=\frac{1}{2}\left({\mathit{\omega }}_{i,j}+{\mathit{\omega }}_{j,i}\right),$$(3)

(4) $${\mathit{\omega }}_i=\frac{1}{2}{e}_{ipq}{u}_{q,p},$$(4) (5) $$P=-{\mathit{\beta }}_2{e}_{kk}+b\left(1+{\mathit{\tau }}^1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)C-a\left(1+{\mathit{\tau }}_1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)T,$$(5)

(ii) Equations of motion(6) $$\left(\mathit{\lambda }+\mathit{\mu }+\frac{\mathit{\alpha }}{4}\mathrm{\Delta }\right)\mathrm{\nabla }\left(\mathrm{\nabla }·\mathit{u}\right)+\left(\mathit{\mu }-\frac{\mathit{\alpha }}{4}\mathrm{\Delta }\right){\mathrm{\nabla }}^2\mathit{u}-{\mathit{\beta }}_1\left(1+{\mathit{\tau }}_1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)\mathrm{\nabla }T-{\mathit{\beta }}_2\left(1+{\mathit{\tau }}^1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)\mathrm{\nabla }C=\mathit{\rho }\ddot{\mathit{u}},$$(6)

(iii) Equation of heat conduction(7) $$K^{*}\mathrm{\Delta }T-\mathit{\rho }{c}_e\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\tau }}_0\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)T-a{T}_0\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+\mathit{\gamma }\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)C=T_0{\mathit{\beta }}_1\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\tau }}_0{\mathit{\eta }}_0\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)\left(\mathrm{\nabla }.\mathit{u}\right),$$(7)

(iv) Equation of mass diffusion(8) $$D{\mathit{\beta }}_2\mathrm{\Delta }\left(\mathrm{\nabla }·\mathit{u}\right)+Da\left(1+{\mathit{\tau }}_1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)\mathrm{\Delta }T+\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\tau }}^0{\mathit{\eta }}_0\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right)C-Db\mathrm{\Delta }\left(1+{\mathit{\tau }}^1\frac{\mathit{\partial }}{\mathit{\partial }t}\right)C=0,$$(8)

where t_ij are the components of stress tensor, λ and μ are material constants, δ_ij is Kronecker’s delta, e_ij are the components of strain tensor, e_ijk is alternate tensor, m_ij are the components of couple stress, ${\mathit{\beta }}_1=\left(3\mathit{\lambda }+2\mathit{\mu }\right){\mathit{\alpha }}_t,{\mathit{\beta }}_2=\left(3\mathit{\lambda }+2\mathit{\mu }\right){\mathit{\alpha }}_c$. Here, ${\mathit{\alpha }}_t,{\mathit{\alpha }}_c$ are the coefficients of linear thermal expansion and diffusion expansion, respectively, T is the temperature change, C is the mass concentration, α is the couple stress parameter, χ_ij is symmetric curvature, w_i is the rotational vector, P is the chemical potential of the material per unit mass, b is the coefficient describing the measure of mass diffusion effects, and a is the coefficient describing the measure of thermoelastic diffusion.$\mathit{u}=\left(u_1,u_2,u_3\right)$ is the components of displacement vector, ρ is the density, Δ is the Laplacian operator, ∇ is del operator. K^* is the coefficient of the thermal conductivity, c_e is the specific heat at constant strain, and T₀ is the reference temperature assumed to be such that $\left|T/T_0\right|\ll 1$. D is the thermoelastic diffusion constant. Here, τ⁰, τ¹ are the diffusion relaxation times with τ¹ ≥ τ⁰ ≥ 0 and τ₀, τ₁ are thermal relaxation times with τ₁ ≥ τ₀ ≥ 0. Here, τ₁ = τ¹ = 0, η₀ = 1, γ = τ₀, for Lord–Shulman (L–S) model and ${\mathit{\eta }}_0=0,\mathit{\gamma }={\mathit{\tau }}^0$, for Green Lindsay (G–L) model.

3. Formulation of the problem

Let us consider a homogeneous isotropic, modified couple stress generalized thermodiffusion elastic thick plate of thickness 2d occupying the region defined by 0 ≤ r ≤ ∞, − d ≤ z ≤ d. Cylindrical polar coordinates (r, ϕ , z) having origin on the surface z = 0, between the lower and upper surfaces of the plate and the z-axis is assumed to be the axis of symmetry. Due to symmetry about z-axis, all the field quantities depend only on r, z, t.

The initial temperature in the thick plate is given by a constant temperature T₀ and the heat flux $g_{0}F\left(r,z\right)$ is prescribed on the upper and lower boundary surfaces. Under these conditions, thermodiffusion elastic quantities for a thick circular plate are required to be determined.

For the two-dimensional problem, we take the displacement vector $\mathit{u}=\left(u_r,0,u_z\right)$.

We define the dimensionless quantities:$$r^{\prime }=\frac{{\mathit{\omega }}^{*}}{c_1}r,z^{\prime }=\frac{{\mathit{\omega }}^{*}}{c_1}z,u_r^{\prime }=\frac{{\mathit{\omega }}^{*}}{c_1}{u}_r,u_z^{\prime }=\frac{{\mathit{\omega }}^{*}}{c_1}{u}_z,t^{\prime }={\mathit{\omega }}^{*}t,t_{ij}^{\prime }=\frac{t_{ij}}{{\mathit{\beta }}_1{T}_0},m_{ij}^{\prime }=\frac{{\mathit{\omega }}^{*}{m}_{ij}}{c_1{\mathit{\beta }}_1{T}_0},{\mathit{\gamma }}^{\prime }={\mathit{\omega }}^{*}\mathit{\gamma },$$$${\mathit{\tau }}_1^{\prime }={\mathit{\omega }}^{*}{\mathit{\tau }}_1,{\mathit{\tau }}_0^{\prime }={\mathit{\omega }}^{*}{\mathit{\tau }}_0,{\mathit{\tau }}^{0^{\prime }}={\mathit{\omega }}^{*}{\mathit{\tau }}^0,{\mathit{\tau }}^{1^{\prime }}={\mathit{\omega }}^{*}{\mathit{\tau }}^1,T^{\prime }=\frac{{\mathit{\beta }}_{1}T}{\mathit{\rho }{c}_1^2},C^{\prime }=\frac{{\mathit{\beta }}_{2}C}{\mathit{\rho }{c}_1^2},P^{\prime }=\frac{P}{{\mathit{\beta }}_2},$$(9) $$c_1^2=\frac{\mathit{\lambda }+2\mathit{\mu }}{\mathit{\rho }},{\mathit{\omega }}^{*2}=\frac{\mathit{\lambda }}{\left(\mathit{\mu }{t}^2+\mathit{\rho }\mathit{\alpha }\right)}.$$(9)

Upon introducing (9) in Equations (6)–(8), after suppressing the primes, we obtain:(10) $$a_1\frac{\mathit{\partial }e}{\mathit{\partial }r}+a_2\left({\mathrm{\nabla }}^2-\frac{1}{r^2}\right)u_r+a_3\mathrm{\Delta }\left(\frac{\mathit{\partial }e}{\mathit{\partial }r}-\left({\mathrm{\nabla }}^2-\frac{1}{r^2}\right)u_r\right)-{\mathit{\tau }}_t\frac{\mathit{\partial }T}{\mathit{\partial }r}-{\mathit{\tau }}_t^1\frac{\mathit{\partial }C}{\mathit{\partial }r}=\frac{{\mathit{\partial }}^2{u}_r}{\mathit{\partial }{t}^2},$$(10)

(11) $$a_1\frac{\mathit{\partial }e}{\mathit{\partial }z}+a_2{\mathrm{\nabla }}^2{u}_z+a_3\mathrm{\Delta }\left(\frac{\mathit{\partial }e}{\mathit{\partial }z}-{\mathrm{\nabla }}^2{u}_z\right)-{\mathit{\tau }}_t\frac{\mathit{\partial }T}{\mathit{\partial }z}-{\mathit{\tau }}_t^1\frac{\mathit{\partial }C}{\mathit{\partial }z}=\frac{{\mathit{\partial }}^2{u}_z}{\mathit{\partial }{t}^2},$$(11) (12) $${\mathrm{\nabla }}^{2}T-a_4{\mathit{\tau }}_t^{0}T-a_5{\mathit{\tau }}_{\mathit{\gamma }}^{0}C=a_6{\mathit{\tau }}_{{\mathit{\eta }}_0}^{0}e,$$(12)

(13) $$a_7{\mathrm{\nabla }}^{2}e+a_8{\mathit{\tau }}_t{\mathrm{\nabla }}^{2}T+{\mathit{\tau }}_t^{10}C-a_9{\mathit{\tau }}_t^1{\mathrm{\nabla }}^{2}C=0,$$(13)

where$$a_1=\frac{\left(\mathit{\lambda }+\mathit{\mu }\right)}{\mathit{\rho }{c}_1^2},a_2=\frac{\mathit{\mu }}{\mathit{\rho }{c}_1^2},a_3=\frac{\mathit{\alpha }{\mathit{\omega }}^{*2}}{4\mathit{\rho }{c}_1^4},a_4=\frac{\mathit{\rho }{c}_e{c}_1^2}{K^{*}{\mathit{\omega }}^{*}},a_5=\frac{a{T}_0{\mathit{\beta }}_1{c}_1^2}{{\mathit{\beta }}_2{K}^{*}{\mathit{\omega }}^{*}},a_6=\frac{T_0{\mathit{\beta }}_1^2}{\mathit{\rho }{K}^{*}{\mathit{\omega }}^{*}},a_7=\frac{{\mathit{\beta }}_2^{2}D{\mathit{\omega }}^{*}}{\mathit{\rho }{c}_1^4},a_8=\frac{a{\mathit{\beta }}_{2}D{\mathit{\omega }}^{*}}{{\mathit{\beta }}_1{c}_1^2},$$$$a_9=\frac{bD{\mathit{\omega }}^{*}}{c_1^2},{\mathit{\tau }}_t=\left(1+{\mathit{\tau }}_1\frac{\mathit{\partial }}{\mathit{\partial }t}\right),{\mathit{\tau }}_t^1=\left(1+{\mathit{\tau }}^1\frac{\mathit{\partial }}{\mathit{\partial }t}\right),{\mathit{\tau }}_t^0=\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\tau }}_0\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right),{\mathit{\tau }}_{{\mathit{\eta }}_0}^0=\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\eta }}_0{\mathit{\tau }}_0\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right),$$$${\mathit{\tau }}_{\mathit{\gamma }}^0=\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+\mathit{\gamma }\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right),{\mathit{\tau }}_t^{10}=\left(\frac{\mathit{\partial }}{\mathit{\partial }t}+{\mathit{\eta }}_0{\mathit{\tau }}^0\frac{{\mathit{\partial }}^2}{\mathit{\partial }{t}^2}\right),{\mathrm{\nabla }}^2=\frac{{\mathit{\partial }}^2}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}+\frac{{\mathit{\partial }}^2}{\mathit{\partial }{z}^2},e=\frac{u_r}{r}+\frac{\mathit{\partial }{u}_r}{\mathit{\partial }r}+\frac{\mathit{\partial }{u}_z}{\mathit{\partial }z}=\frac{1}{r}\frac{\mathit{\partial }}{\mathit{\partial }r}\left(r{u}_r\right)+\frac{\mathit{\partial }{u}_z}{\mathit{\partial }z}.$$

The displacement components u_r and u_z in terms of potential functions ϕ and ψ in dimensionless form are given by,(14) $$u_r=\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }r}+\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }r\mathit{\partial }z},u_z=\frac{\mathit{\partial }\mathit{\varphi }}{\mathit{\partial }z}-\left(\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\mathit{\psi }}{\mathit{\partial }r}\right).$$(14)

We define Laplace and Hankel transforms as:$$\overline{f}(r,z,s)=\underset{0}{\overset{\infty }{\int }}f(r,z,t)e^{-st}dt$$(15) $$\overline{f}(\mathit{\eta },z,s)=H\left[\overline{f}(r,z,s)\right]=\underset{0}{\overset{\infty }{\int }}\overline{f}(r,z,s)r{J}_n\left(\mathit{\eta }r\right)dr$$(15)

where s is the Laplace transform parameter, $\mathit{\eta }$ is the Hankel transform parameter and J_n ( ) is the Bessel function of the first kind of order n.

Making use of (14) in (10)–(13) and applying the Laplace and Hankel transforms defined by (15) on the resulting equation (after simplification), we obtain:(16) $$\left[D^6+G_1{D}^4+G_2{D}^2+G_3\right]\left(\widehat{\mathit{\varphi }},\widehat{T},\widehat{C}\right)=0,$$(16) (17) $$\left[D^4-B_1{D}^2+B_2\right]\widehat{\mathit{\phi }}=0,$$(17)

where G₁, G₂, G₃, B₁, and B₂ are given in Appendix (1).

The general solution of Equation (16) can be written as:(18) $$\widehat{\mathit{\varphi }}={\widehat{\mathit{\varphi }}}_1+{\widehat{\mathit{\varphi }}}_2+{\widehat{\mathit{\varphi }}}_3,$$(18)

where $\widehat{{\mathit{\varphi }}_i}$ is a general solution of the homogeneous differential equation given by:(19) $$\left(D^2-m_i^2\right)\widehat{{\mathit{\varphi }}_i}=0,i=1,2,3.$$(19)

where m₁, m₂, and m₃ are the roots of the characteristic equation(20) $$D^6+G_1{D}^4+G_2{D}^2+G_3=0.$$(20)

The complete solution of Equation (19) can be written as:(21) $$\widehat{\mathit{\varphi }}=\sum _{i=1}^3{A}_{i}cosh(m_{i}z),$$(21)

Solving Equation (17), we get:(22) $$\widehat{\mathit{\psi }}={\widehat{\mathit{\psi }}}_4+{\widehat{\mathit{\psi }}}_5,$$(22)

where $\widehat{{\mathit{\psi }}_i}(i=4,5)$ is a solution of the homogeneous differential equation given by:(23) $$\left(D^2-m_i^2\right)\widehat{{\mathit{\psi }}_i}=0,i=4,5.$$(23)

The solution of the Equation (17), yield:(24) $$\widehat{\mathit{\psi }}=\sum _{i=4}^5{A}_{i}sinh(m_{i}z),$$(24)

where m₄ and m₅ are the roots of the characteristic equation(25) $$D^4-B_1{D}^2+B_2=0.$$(25)

The solution of the Equation (16) is(26) $$\left(\widehat{\mathit{\varphi }},\widehat{T},\widehat{C}\right)(\mathit{\eta },z,s)=\sum _{i=1}^3(1,R_i,S_i)A_{i}cosh(m_{i}z),$$(26)

where R_i and S_i are given in Appendix (2).

4. Boundary conditions

The appropriate boundary conditions for this problem are:

(1)	(27) $$\frac{\mathit{\partial }T}{\mathit{\partial }z}=\pm g_{0}F\left(r,z\right)\text{at}z=\pm d,$$(27)
(2)	(28) $$t_{zz}=t_{zr}=m_{z\mathit{\varphi }}=0\text{at}z=\pm d,$$(28)
(3)	(29) $$P=\mathit{\delta }(t)f(r)\text{at}z=\pm d$$(29)

where(30) $$F\left(r,z\right)=z^2{e}^{-\mathit{\omega }r},\mathit{\omega }>0.$$(30)

(31) $$f\left(r\right)=H\left(a-r\right),$$(31)

and δ( ) is the Dirac delta function, H( ) is the Heavy side unit step function.

Applying Laplace and Hankel transforms defined by (15) on (30) and (31), we obtain:(32) $$\widehat{F}(\mathit{\eta },z)=\frac{z^2\mathit{\omega }}{{\left({\mathit{\omega }}^2+{\mathit{\alpha }}^2\right)}^{\frac{3}{2}}},$$(32)

(33) $$\widehat{f}(\mathit{\eta })=\frac{a{J}_1(\mathit{\eta }a)}{\mathit{\eta }},$$(33)

The non-dimensional values of t_zz, t_zr, m_zϕ, and P are given by (1)–(5) and (9), (14) as:(34) $$t_{zz}=a_{10}{\mathrm{\nabla }}^2\mathit{\varphi }+2a_{11}\left\{\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }{z}^2}-\frac{{\mathit{\partial }}^3\mathit{\psi }}{\mathit{\partial }{r}^2\mathit{\partial }z}+\frac{1}{r}\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }r\mathit{\partial }z}\right\}-a_{12}\left\{{\mathit{\tau }}_{t}T+{\mathit{\tau }}_t^{1}C\right\},$$(34) (35) $$t_{zr}=a_{11}\left(2\frac{{\mathit{\partial }}^2\mathit{\varphi }}{\mathit{\partial }r\mathit{\partial }z}+\frac{\mathit{\partial }}{\mathit{\partial }r}\left(\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{z}^2}-\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{r}^2}-\frac{1}{r}\frac{\mathit{\partial }\mathit{\psi }}{\mathit{\partial }r}\right)\right)-a_{13}\left[\frac{\mathit{\partial }}{\mathit{\partial }r}\left(\frac{{\mathit{\partial }}^2}{\mathit{\partial }{r}^2}+\frac{{\mathit{\partial }}^2}{\mathit{\partial }{z}^2}\right)\left(\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{z}^2}+\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\mathit{\psi }}{\mathit{\partial }r}\right)\right],$$(35)

(36) $$m_{z\mathit{\varphi }}=2a_{13}\frac{{\mathit{\partial }}^2}{\mathit{\partial }r\mathit{\partial }z}\left(\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{z}^2}+\frac{{\mathit{\partial }}^2\mathit{\psi }}{\mathit{\partial }{r}^2}+\frac{1}{r}\frac{\mathit{\partial }\mathit{\psi }}{\mathit{\partial }r}\right),$$(36)

(37) $$P=-{\mathrm{\nabla }}^2\mathit{\varphi }+a_{14}{\mathit{\tau }}_t^{1}C-a_{15}{\mathit{\tau }}_{t}T,$$(37)

where$$a_{10}=\frac{\mathit{\lambda }}{{\mathit{\beta }}_1{T}_0},a_{11}=\frac{\mathit{\mu }}{{\mathit{\beta }}_1{T}_0},a_{12}=\frac{\mathit{\rho }{c}_1^2}{{\mathit{\beta }}_1{T}_0},a_{13}=\frac{\mathit{\alpha }{\mathit{\omega }}^{*2}}{4c_1^2{\mathit{\beta }}_1{T}_0},a_{14}=\frac{b\mathit{\rho }{c}_1^2}{{\mathit{\beta }}_2^2},a_{15}=\frac{a\mathit{\rho }{c}_1^2}{{\mathit{\beta }}_1{\mathit{\beta }}_2}s.$$

Substituting the values of $\widehat{\mathit{\varphi }},\widehat{T},\widehat{C}$ and $\widehat{\mathit{\phi }}$ from (24) and (26) in the boundary conditions (27)–(29) and with the aid of (15) and (32)–(37), we obtain the expressions for displacement components, stresses, temperature change, chemical potential, and concentration as(38) $${\widehat{u}}_r=-\mathit{\eta }\left[\sum _{i=1}^3{A}_{i}cosh(m_{i}d)+\sum _{i=4}^5{A}_i{m}_{i}cosh(m_{i}d)\right],$$(38)

(39) $${\widehat{u}}_z=\sum _{i=1}^3{m}_i{A}_{i}sinh(m_{i}d)+{\mathit{\eta }}^2\left(\sum _{i=4}^5{A}_{i}sinh(m_{i}d)\right),$$(39)

(40) $$\widehat{T}=\sum _{i=1}^3{R}_i{A}_{i}cosh(m_{i}d),$$(40) (41) $$\widehat{t}{}_{\text{zz}}=\sum _{i=1}^3{M}_i{A}_{i}cosh(m_{i}d)+\sum _{i=4}^5{M}_i{A}_{i}cosh(m_{i}d),$$(41) (42) $$\widehat{t}{}_{\text{zr}}=-\mathit{\eta }\left[\sum _{i=1}^3{N}_i{A}_{i}sinh(m_{i}d)+\sum _{i=4}^5{N}_i{A}_{i}sinh(m_{i}d)\right],$$(42)

(43) $$\widehat{P}=\sum _{i=1}^3{K}_i{A}_{i}cosh(m_{i}d)+\sum _{i=4}^5{K}_i{A}_{i}cosh(m_{i}d),$$(43) (44) $$\widehat{m}{}_{\text{z}\mathit{\varphi }}=-2\mathit{\eta }{a}_{14}\left[\sum _{i=4}^5{Q}_i{A}_{i}cosh(m_{i}d)\right],$$(44) (45) $$\widehat{C}=\sum _{i=1}^3{S}_i{A}_{i}cosh(m_{i}d),$$(45)

where

A₁, A₂, A₃, A₄, and A₅, ${\sum }_{i=1}^3{M}_i,{\sum }_{i=1}^3{N}_i,{\sum }_{i=1}^3{K}_i,{\sum }_{i=4}^5{M}_i,{\sum }_{i=4}^5{N}_i,{\sum }_{i=4}^5{K}_i,{\sum }_{i=4}^5{Q}_i$ are given in Appendix (3).

5. Particular cases

(1)	If α = 0, in Equations (38)–(45), we obtain the components of displacement and stresses for a generalized thermoelastic with mass diffusion model. The results obtain are similar as given by Tripathi et al. (2015) with the changed value of

$$\widehat{F}(\mathit{\eta },z)=\frac{z^2\mathit{\omega }}{{\left({\mathit{\omega }}^2+{\mathit{\alpha }}^2\right)}^{\frac{3}{2}}}.$$

(2)	In the absence of diffusion ($a=D={\mathit{\tau }}_t^1=0)$, in Equations (38)–(45), we obtain the components of displacement and stresses in a modified couple stress thermoelastic medium.
(3)	If ${\mathit{\tau }}_1={\mathit{\tau }}^1=0,{\mathit{\eta }}_0=1,\mathit{\gamma }={\mathit{\tau }}_0$ in Equations (38)–(45), we obtain the corresponding results for modified couple stress thermoelastic with mass diffusion for Lord Shulman (L–S) model.
(4)	If ${\mathit{\eta }}_0=0,\mathit{\gamma }={\mathit{\tau }}^0$ in Equations (38)–(45), we obtain the corresponding results for modified couple stress thermoelastic with mass diffusion for Green Lindsay (G–L) model.

6. Numerical inversion of the transforms

The solution is obtained in physical domain, we must invert the transforms in (38)–(45), for all the theories. Here, the displacement components, stresses, temperature change, mass concentration, and chemical potential are functions of z, the parameters of Laplace and Hankel transforms s and η, respectively, and hence are of the form $\widehat{f}(\mathit{\eta },z,s)$ and f(r, z, t) is a known function of r, z, and t. To obtain the solution of the problem in the physical domain, we invert the Laplace and Hankel transforms using the method described by Kumar and Deswal (2007).

7. Numerical results and discussion

For numerical computations, following Daliwal and Singh (1980), we take the magnesium material (thermoelastic diffusion solid) as:$$\mathit{\lambda }=2.696\times {10}^{10}\text{kg}{\text{m}}^{-1}{\text{s}}^{-2},\mathit{\mu }=1.639\times {10}^{10}\text{kg}{\text{m}}^{-1}{\text{s}}^{-2},T_0=0.293\times {10}^3\text{K},$$$$c_e=1.04\times {10}^3\text{J}{\text{Kg}}^{-1}{\text{K}}^{-1},{\mathit{\alpha }}_t=1.78\times {10}^{-5}{\text{K}}^{-1},{\mathit{\alpha }}_c=1.98\times {10}^{-4}{\text{m}}^3{\text{kg}}^{-1},$$$$a=1.02\times {10}^4{\text{m}}^2{\text{s}}^{-2}{\text{K}}^{-1},b=9\times {10}^5{\text{kg}}^{-1}{\text{m}}^5{\text{s}}^{-2},D=0.85\times {10}^{-8}\text{Kg}\text{s}{\text{m}}^{-3},$$$$\mathit{\rho }=1.74\times {10}^3\text{Kg}{\text{m}}^{-3},K^{*}=1.7\times {10}^2\text{W}{\text{m}}^{-1}{\text{K}}^{-1},\mathit{\alpha }=1\text{kg}\text{m}{\text{s}}^{-2},$$$$t=1\text{s},\mathit{\omega }=10{\text{s}}^{-1},{\mathit{\tau }}_0=0.01\text{s},{\mathit{\tau }}^0=0.03\text{s},{\mathit{\tau }}_1=0.02\text{s},{\mathit{\tau }}^1=0.04\text{s}.$$

The software Matlab 7.10.4 has been used to determine the normal stress, tangential stress, temperature change, mass concentration, and couple stress for different values of α for both L–S and G–L theories are computed numerically and shown graphically in Figures 1–5, respectively.

Figure 1. Variation of normal stress with distance.

Figure 2. Variation of tangential stress with distance.

Figure 3. Variation of temperature change with distance.

In Figures 1–4, solid line (–) corresponds to L–S α = 0, solid line with center symbol (–*–) corresponds to L–S α = 1, small dash line (----) corresponds to G–L α = 0 and small dash line with center symbol (---*---) corresponds to G–L α = 1.

Figure 4. Variation of chemical potential with distance.

Figure 5. Variation of couple stress with distance.

Similarly, in Figure 5, solid line (–) corresponds to L–S α = 1, solid line with center symbol (–*–) corresponds to L–S α = 2, small dash line (----) corresponds to G–L α = 1 and small dash line with center symbol (---*---) corresponds to G–L α = 2, respectively.

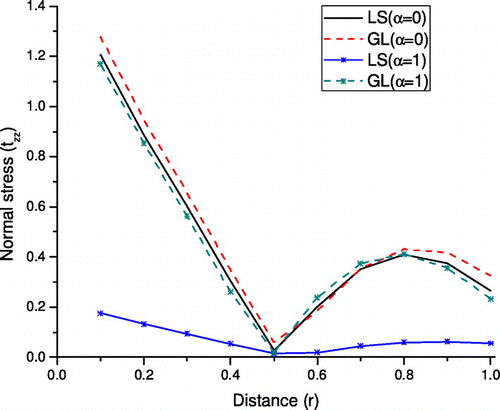
Figure 1 shows that the variations of normal stress t_zz with r. The value of normal stress decreases rapidly in the range 0 ≤ r < 0.6 and oscillatory behavior is noticed for the remaining range for both values of α and both theories of thermodiffusion elastic media. On the other hand, the values of normal stress for G–L theory is more in comparison to L–S theory for with and without α.

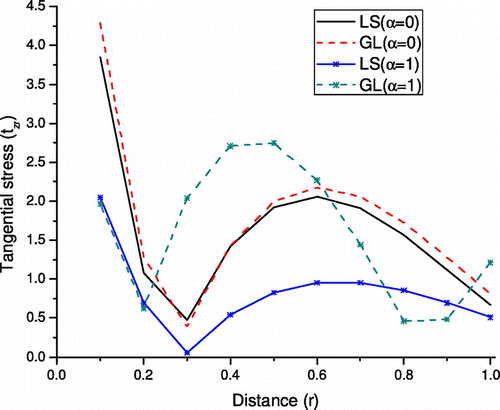
Figure 2 depicts that the variation of tangential stress t_zr with r. Oscillatory behavior is shown for both cases and both L–S and G–L theories. Similarly, the values of tangential stress for L–S (α = 0) is greater in comparison to L–S (α = 1) and similar behavior is noticed for both values of α for G–L theory.

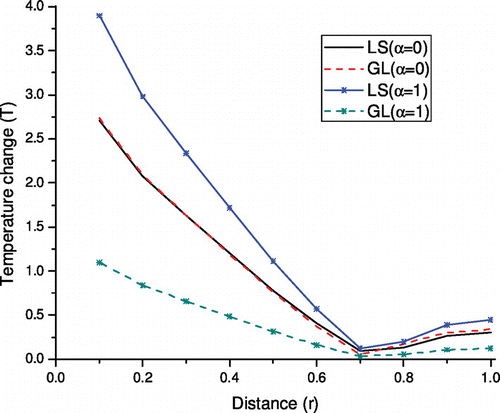
Figure 3 depicts the variation of temperature change with r for α = 0, 1. It is noticed that the behavior of α = 0, 1 is similar for both the theories of thermodiffusion elastic. It is noticed that the values of temperature change decreases in the range 0 ≤ r < 0.8 and increases in the remaining values of r for both values of α = 0, 1 and both L–S and G–L theories. In the presence of couple stress, the values of T for L–S theory is higher in comparison to G–L theory, whereas in the absence of couple stress, reverse behavior is observed.

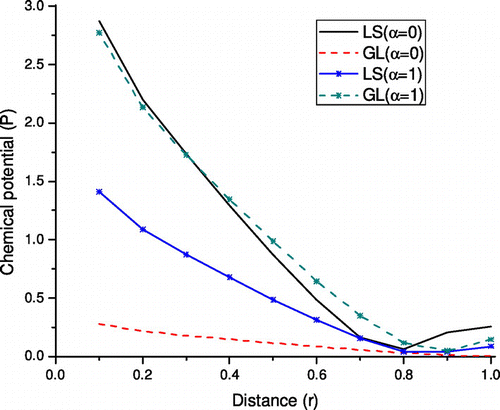
Figure 4 shows that the variations of chemical potential with r. Similar behavior is noticed for both values of α. Also, the values of chemical potential P increases due to the presence of couple stress and decreases in the absence of couple stress for G–L theory in comparison to L–S theory.

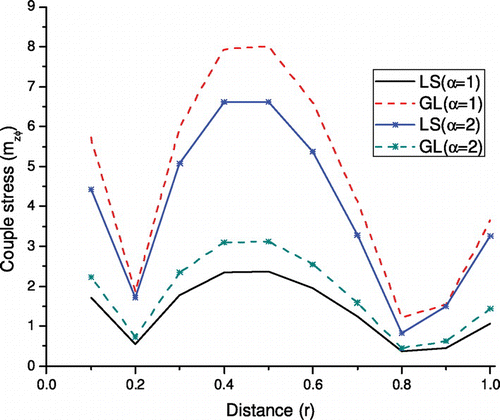
Figure 5 represents that the variation of couple stress m_zϕ with r. Similar trend is noticed for both the values of α and both theories of thermodiffusion elastic. On the other hand, the values of m_zϕ for L–S theory is less in comparison to G–L theory for α = 1 and opposite behavior is noticed for α = 2.

8. Conclusions

A problem of thick circular plate in modified couple stress theory is a significant problem of continuum mechanics. The result obtained from above study is summarized as.

The resulting quantities depicted graphically are observed to be very sensitive towards the couple stress parameters. It is evident that the physical quantities are also effected by the different non-classical theories of thermodiffusion elasticity. It is observed that couple stress increase the values of normal stress t_zz and chemical potential P for G–L theory in comparison to L–S theory and reverse behavior is observed for temperature change T. Couple stress parameter α dominate the values of t_zr and m_zϕ for both theories of thermodiffusion elastic. Due to relaxation time the value of couple stress increases. The effect of couple stress and thermo elastic diffusion plays a significant role on the physical quantities. The stresses, temperature change and chemical potential gives a better information which lead to the understanding of material structure. The result presented may be beneficial to the researchers working in material science, engineers and physicists as well as those working in the hyperbolic thermoelastic diffusion solid.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Rajneesh Kumar

Rajneesh Kumar is the author of the manuscript and a well-known professor in Department of Mathematics, Kurukshetra University, Kurukshetra (Haryana, India). He received his PhD in Applied Mathematics from Guru Nanak Dev University, Amritsar (Punjab, India) in 1986. He has 30 years of teaching experience and published 460 research papers in international journals with high impact factors. He has guided 23 PhD students and 7 PhD students are working under his supervision. His area of interests include micropolar elasticity, thermoelastic with diffusion, poroelasticity, thermoelastic with voids, magneto-piezothermoelasticity, microstretch, microtemperature, viscoelasticity, fractional-order thermoelasticity, modified couple stress theory, and bio heat transfer. He is a reviewer of many international journals and a member of many academic and professional bodies. The problem investigated in this study analyzes the response of various sources in a modified couple stress theory, being a significant problem of continuum mechanics with various applications in geophysics and engineering.

Appendix (1)

$$G=\left(\mathit{\delta }{a}_9-a_7\right){\mathit{\tau }}_t^{22},$$$$G_1=\left[-3{\mathit{\eta }}^2\mathit{\delta }{a}_9{\mathit{\tau }}_t^{22}-\left\{s^2{a}_9{\mathit{\tau }}_t^{22}+\mathit{\delta }\left({\mathit{\tau }}_t^{66}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}+a_4{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{33}\right)\right\}-{\mathit{\tau }}_t^{11}\left(a_6{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{55}+a_5{a}_7{\mathit{\tau }}_t^{44}\right)-{\mathit{\tau }}_t^{22}\left(a_6{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{55}-a_4{a}_7{\mathit{\tau }}_t^{33}-3a_7{\mathit{\eta }}^2\right)\right]/G,$$$$G_2=\left[3{\mathit{\eta }}^4\mathit{\delta }{a}_9{\mathit{\tau }}_t^{22}+2{\mathit{\eta }}^2\left\{s^2{a}_9{\mathit{\tau }}_t^{22}+\mathit{\delta }\left({\mathit{\tau }}_t^{66}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}+a_4{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{33}\right)\right\}+s^2\left({\mathit{\tau }}_t^{66}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}+a_4{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{33}\right)+a_4\mathit{\delta }{\mathit{\tau }}_t^{33}{\mathit{\tau }}_t^{66}+{\mathit{\tau }}_t^{11}\left\{a_6{\mathit{\tau }}_t^{55}{\mathit{\tau }}_t^{66}+2{\mathit{\eta }}^2\left(a_6{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{55}+a_5{a}_7{\mathit{\tau }}_t^{44}\right)\right\}-{\mathit{\tau }}_t^{22}\left(3a_7{\mathit{\eta }}^4-2{\mathit{\eta }}^2\left(a_6{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{55}-a_4{a}_7{\mathit{\tau }}_t^{33}\right)\right)\right]/G,$$$$G_3=\left[-\mathit{\delta }{a}_9{\mathit{\tau }}_t^{22}{\mathit{\eta }}^6-{\mathit{\eta }}^4\left\{s^2{a}_9{\mathit{\tau }}_t^{22}+\mathit{\delta }\left({\mathit{\tau }}_t^{66}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}+a_4{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{33}\right)\right\}-{\mathit{\eta }}^2\left\{s^2\left({\mathit{\tau }}_t^{66}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}+a_4{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{33}\right)+a_4\mathit{\delta }{\mathit{\tau }}_t^{33}{\mathit{\tau }}_t^{66}\right\}-s^2{a}_4{\mathit{\tau }}_t^{33}{\mathit{\tau }}_t^{66}-{\mathit{\tau }}_t^{11}\left(a_6{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{55}{\mathit{\tau }}_t^{66}{\mathit{\eta }}^2+{\mathit{\eta }}^4\left(a_6{a}_9{\mathit{\tau }}_t^{22}{\mathit{\tau }}_t^{55}+a_5{a}_7{\mathit{\tau }}_t^{44}\right)\right)-{\mathit{\tau }}_t^{22}\left(-a_7{\mathit{\eta }}^6+{\mathit{\eta }}^4\left(a_6{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{55}-a_4{a}_7{\mathit{\tau }}_t^{33}\right)\right)\right]/G.$$$$B_1=\frac{a_2+2a_3{\mathit{\eta }}^2}{a_3},B_2=\frac{a_3{\mathit{\eta }}^4+a_2{\mathit{\eta }}^2+s^2}{a_3},{\mathit{\tau }}_t^{11}=\left(1+{\mathit{\tau }}_{1}s\right),{\mathit{\tau }}_t^{22}=\left(1+{\mathit{\tau }}^{1}s\right),{\mathit{\tau }}_t^{33}=\left(s+{\mathit{\tau }}_0{s}^2\right),$$$${\mathit{\tau }}_t^{44}=\left(s+\mathit{\gamma }{s}^2\right),{\mathit{\tau }}_t^{55}=\left(s+{\mathit{\eta }}_0{\mathit{\tau }}_0{s}^2\right),{\mathit{\tau }}_t^{66}=\left(s+{\mathit{\eta }}_0{\mathit{\tau }}^0{s}^2\right),\mathit{\delta }=\left(a_1+a_2\right),e={\mathrm{\nabla }}^2\mathit{\varphi }.$$

Appendix (2)

$$R_i=\sum _{i=1}^3\frac{a_6{\mathit{\tau }}_t^{55}\left(m_i^2-{\mathit{\eta }}^2\right)\left\{{\mathit{\tau }}_t^{66}-a_9\left(m_i^2-{\mathit{\eta }}^2\right){\mathit{\tau }}_t^{22}\right\}-a_5{a}_7{\mathit{\tau }}_t^{44}{\left(m_i^2-{\mathit{\eta }}^2\right)}^2}{\left[\left(-\left(m_i^2-{\mathit{\eta }}^2\right)+a_4{\mathit{\tau }}_t^{33}\right)\left({\mathit{\tau }}_t^{66}-\left(m_i^2-{\mathit{\eta }}^2\right)\left(a_9{\mathit{\tau }}_t^{22}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}\right)\right)\right]},$$$$S_i=\sum _{i=1}^3\frac{{\left(m_i^2-{\mathit{\eta }}^2\right)}^2\left[a_6{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{55}+a_7{\left(m_i^2-{\mathit{\eta }}^2\right)}^2\left(\left(m_i^2-{\mathit{\eta }}^2\right)-a_4{\mathit{\tau }}_t^{33}\right)\right]}{\left[\left(-\left(m_i^2-{\mathit{\eta }}^2\right)+a_4{\mathit{\tau }}_t^{33}\right)\left({\mathit{\tau }}_t^{66}-\left(m_i^2-{\mathit{\eta }}^2\right)\left(a_9{\mathit{\tau }}_t^{22}+a_5{a}_8{\mathit{\tau }}_t^{11}{\mathit{\tau }}_t^{44}\right)\right)\right]},i=1,2,3.$$

Appendix (3)

$$A_1=\frac{{\mathrm{\Delta }}_1}{\mathrm{\Delta }},A_2=\frac{{\mathrm{\Delta }}_2}{\mathrm{\Delta }},A_3=\frac{{\mathrm{\Delta }}_3}{\mathrm{\Delta }},A_4=\frac{{\mathrm{\Delta }}_4}{\mathrm{\Delta }},A_5=\frac{{\mathrm{\Delta }}_5}{\mathrm{\Delta }},$$$$\mathrm{\Delta }=R_1{m}_1{g}_1[M_2{h}_2(N_3{K}_5{g}_3{h}_5-N_5{K}_3{g}_5{h}_3+N_3{K}_4{g}_3{h}_4-N_4{K}_3{g}_4{h}_3)-M_3{h}_3(N_2{K}_5{g}_2{h}_5-N_5{K}_2{g}_5{h}_2+N_2{K}_4{g}_2{h}_4-N_4{K}_2{g}_4{h}_2)+M_4{h}_4(N_2{K}_3{g}_2{h}_3-N_3{K}_2{g}_3{h}_2)+M_5{h}_5(N_2{K}_3{g}_2{h}_3-N_3{K}_2{g}_3{h}_2)]+R_2{m}_2{g}_2[M_1{h}_1(N_3{K}_5{g}_3{h}_5-N_5{K}_3{g}_5{h}_3-N_3{K}_4{g}_3{h}_4+N_4{K}_3{g}_4{h}_3)-M_3{h}_3(N_1{K}_5{g}_1{h}_5-N_5{K}_1{g}_5{h}_1-N_1{K}_4{g}_1{h}_4+N_4{K}_1{g}_4{h}_1)+M_5{h}_5(N_1{K}_3{g}_1{h}_3-N_3{K}_1{g}_3{h}_1)?+M{?}_4{h}_4(N_3{K}_1{g}_3{h}_1-N_1{K}_3{g}_1{h}_3)]+R_3{m}_3{g}_3[M_1{h}_1(N_2{K}_5{g}_2{h}_5-N_5{K}_2{g}_5{h}_2+N_2{K}_4{g}_2{h}_4-N_4{K}_2{g}_4{h}_2)-M_2{h}_2(N_1{K}_5{g}_1{h}_5-N_5{K}_1{g}_5{h}_1+N_1{K}_4{g}_1{h}_4-N_4{K}_1{g}_4{h}_1)+M_4{h}_4(N_1{K}_2{g}_1{h}_2-N_2{K}_1{g}_2{h}_1)+M_5{h}_5(N_1{K}_2{g}_1{h}_2-N_2{K}_1{g}_2{h}_1)]$$$$g_1=sinh\left(m_{1}d\right),g_2=sinh\left(m_{2}d\right),g_3=sinh\left(m_{3}d\right),g_4=sinh\left(m_{4}d\right),$$

$$g_5=sinh\left(m_{5}d\right),h_1=cosh\left(m_{1}d\right),h_2=cosh\left(m_{2}d\right),h_3=cosh\left(m_{3}d\right),$$

$$h_4=cosh\left(m_{4}d\right),h_5=cosh\left(m_{5}d\right),$$

Δ_i (i = 1, $\dots$, 5) are obtain by replacing 1st, 2nd, 3rd, 4th and 5th column by ${\left[g_0\widehat{F}(\mathit{\eta }z),0,0,\left(\widehat{F}(\mathit{\eta })\right)\right]}^T$ in Δ_i.

and$$\sum _{i=1}^3{M}_i=\sum _{i=1}^3\left[a_{10}\left(m_i^2-{\mathit{\eta }}^2\right)+2a_{11}{m}_i^2-a_{12}\left({\mathit{\tau }}_t^{11}{R}_i+{\mathit{\tau }}_t^{22}{S}_i\right)\right],$$$$\sum _{i=4}^5{M}_i=\sum _{i=4}^5\left[2\left(a_{10}+a_{11}\right){\mathit{\eta }}^2{m}_i\right],$$$$\sum _{i=1}^3{N}_i=\sum _{i=1}^3\left(2a_{11}{m}_i\right),$$$$\sum _{i=4}^5{N}_i=\sum _{i=4}^5\left[a_{11}\left(m_i^2+{\mathit{\eta }}^2\right)-a_{13}{\left(m_i^2-{\mathit{\eta }}^2\right)}^2\right],\sum _{i=4}^5{Q}_i=\sum _{i=4}^5{m}_i\left(m_i^2-{\mathit{\eta }}^2\right),$$$$\sum _{i=1}^3{K}_i=\sum _{i=1}^3\left[-\left(m_i^2+{\mathit{\eta }}^2\right)+a_{14}{\mathit{\tau }}_t^{22}{S}_i-a_{15}{\mathit{\tau }}_t^{66}{R}_i\right],\sum _{i=4}^5{K}_i=\sum _{i=4}^5\left(-2{\mathit{\eta }}^2{m}_i\right).$$