The combined reproducing kernel method and Taylor series to solve nonlinear Abel’s integral equations with weakly singular kernel

Abstract

The reproducing kernel method and Taylor series to determine a solution for nonlinear Abel’s integral equations are combined. In this technique, we first convert it to a nonlinear differential equation by using Taylor series. The approximate solution in the form of series in the reproducing kernel space is presented. The advantages of this method are as follows: First, it is possible to pick any point in the interval of integration and as well the approximate solution. Second, numerical results compared with the existing method show that fewer nodes are required to obtain numerical solutions. Furthermore, the present method is a reliable method to solve nonlinear Abel’s integral equations with weakly singular kernel. Some numerical examples are given in two different spaces.

Keywords:

• reproducing kernel
• Taylor series
• Abel’s integral

2010 Mathematics subject classifications:

• 46E22
• 45G05

Public Interest Statement

In mathematical modeling of real-life problems, we need to deal with functional equations, e.g. partial differential equations, integral and integro-differential equation, stochastic equations and others. Several numerical methods have been developed for the solution of the integral equations. Recently, the applications of reproducing kernel method (RKM) have become of great interest for scholars. Reproducing kernel Hilbert space-based regularization approach is a computationally efficient method with a wide range of applications.

1. Introduction

Abel’s integral equation, linear or nonlinear, arises in many branches of scientific fields (Singh, Pandey, & Singh, 2009), such as seismology, microscopy, radio astronomy, atomic scattering, electron emission, radar ranging, X-ray radiography, plasma diagnostics, and optical fiber evaluation. A variety of numerical and analytic methods for solving these equations are presented. In Liu and Tao (2007) mechanical quadrature methods, wavelet Galerkin method (Maleknjad, Nosrati, & Najafi, 2012), homotopy analysis method (Jafarian, Ghaderi, Golmankhaneh, & Baleanu, 2014), modified new iterative method (Gupta, 2012), a jacobi spectral collocation scheme (Abdelkawy, Ezz-Eldien, & Amin, 2015), a collocation method (Saadatmandi & Dehghan, 2008), block-pulse functions approach (Nosrati Sahlan, Marasi, & Ghahramani, 2015, Bernstein polynomials (Alipour & Rostamy, 2011) and Legendre wavelets (Yousefi, 2006). For further see Kilbas and Saigo (1999), Kumar, Singh, and Dixit (2011), Pandey, Singh, and Singh (2009), Wang, Zhu, and Fečkan (2014).

Table 1. Numerical results of Ex. 1

Node	$|u_N{(x)-u(x)|}_{W_2^6}$	$|u_N{(x)-u(x)|}_{W_2^8}$
0.0	3.02630E$-$10	1.79190E$-$12
0.1	3.06130E$-$10	1.81322E$-$12
0.2	3.09631E$-$10	1.83364E$-$12
0.3	3.13138E$-$10	1.85496E$-$12
0.4	3.16652E$-$10	1.87672E$-$12
0.5	3.20175E$-$10	1.89715E$-$12
0.6	3.23709E$-$10	1.91758E$-$12
0.7	3.27254E$-$10	1.93801E$-$12
0.8	3.30814E$-$10	1.96110E$-$12
0.9	3.34385E$-$10	1.98153E$-$12
1.0	3.37971E$-$10	2.00195E$-$12

The reproducing kernel functions have been used as basis functions of the reproducing kernel method for approximating the solution of different types of differential and integral equations such as singular integral equation with cosecant kernel (Du & Shen, 2008), Fredholm integro-differential equations with weak singularity (Du Zhao, & Zhao, 2014), Fredholm integral equation of the first kind (Du & Cui, 2008), multiple solutions of nonlinear boundary value problems (Abbasbandy, Azarnavid, & Alhuthali, 2015), nonlinear delay differential equations of fractional order (Ghasemi, Fardi, & Ghaziani, 2015), nonlinear Volterra integro-differential equations of fractional order (Jiang & Tian, 2015) and singularly perturbed boundary value problems with a delay (Geng & Qian, 2015). For further see Alvandi, Lotfi, and Paripour (2016), Geng, Qian, and Li (2014), Jordão and Menegatto (2014), Moradi, Yusefi, Abdollahzadeh, and Tila (2014), Xu and Lin (2016).

Table 2. Numerical results of Ex. 2

Node	$|u_N{(x)-u(x)|}_{W_2^5}$	$|u_N{(x)-u(x)|}_{W_2^7}$
0.0	1.54000E$-$9	3.08260E$-$11
0.1	1.39704E$-$9	2.79418E$-$11
0.2	1.29331E$-$9	2.58670E$-$11
0.3	1.21641E$-$9	2.43285E$-$11
0.4	1.15773E$-$9	2.31558E$-$11
0.5	1.11194E$-$9	2.22403E$-$11
0.6	1.07561E$-$9	2.15113E$-$11
0.7	1.04614E$-$9	2.09222E$-$11
0.8	1.02112E$-$9	2.04518E$-$11
0.9	9.97839E$-$10	2.01288E$-$11
1.0	9.73064E$-$10	2.00633E$-$11

The aim of this paper is to introduce the reproducing kernel method to solve nonlinear Abel’s integral equation. The standard form of equation (Wazwaz, 1997) is given by(1.1) $$\begin{array}{c}\hfill f(x)=\underset{0}{\overset{x}{\int }}\frac{1}{\sqrt{x-t}}F(u(t))\text{d}t,0<x\le 1,\end{array}$$(1.1)

where the function f(x) is a given real-valued function, and F(u(x)) is a nonlinear function of u(x). Recall that the unknown function u(x) occurs only inside the integral sign for the Abel’s integral equation.

Figure 1. The comparisons between exact and numerical solution for $m=8$.

Figure 2. The absolute errors in spaces $W_2^6[0,1],W_2^8[0,1]$, respectively.

Figure 3. The comparisons between numerical and exact solution for $m=7$.

Figure 4. The absolute errors in space $W_2^5[0,1]$ and $W_2^7[0,1]$, respectively.

Figure 5. The comparisons between numerical and exact solution for $m=7$.

Figure 6. The absolute errors in spaces $W_2^5[0,1],W_2^7[0,1]$, respectively.

Figure 7. The comparisons between numerical and exact solution for $m=8$.

Figure 8. The absolute errors in space $W_2^5[0,1]$ and $W_2^8[0,1]$, respectively.

This paper is organized as six sections including the introduction. In the next section, we introduce construction of the method in the reproducing kernel space for solving Equation (1.1). The analytical solution is presented in Section 3. The implementations of the method is provided in Section 4. Numerical findings demonstratig the accuracy of the new numerical scheme are reported in Section 5. The last section is a brief conclusion.

2. Construction of the method

In this section, we construct the space $W_2^m[0,1]$ and then formulate the reproducing kernel function $R_x(y)$ in the space $W_2^m[0,1]$. The dimensional space is finite. First, we present some necessary definitions from reproducing kernel theory.

Definition 2.1

Let $\mathbb{H}=\{u(x)|u(x)$ is a real-valued function or complex function, $x\in X$, X is a abstract set $\}$ be a Hilbert space, with inner product$$\begin{array}{c}\hfill {⟨u(x),v(x)⟩}_{\mathbb{H}},(u(x),v(x)\in \mathbb{H}).\end{array}$$

Definition 2.2

A function space $W_2^m[0,1]$ is defined by $W_2^m[0,1]=\{u^{(m-1)}(x)$ is an absolutely continuous real-valued function on [0, 1] and $u^{(m)}(x)\in L^2[0,1]\}$.

The inner product and norm in $W_2^m[0,1]$ are given respectively by(2.1) $$\begin{array}{c}\hfill {⟨u,v⟩}_{W_2^m}=\sum _{i=0}^{m-1}{u}^{(i)}(0)v^{(i)}(0)+\underset{0}{\overset{1}{\int }}{u}^{(m)}(x)v^{(m)}(x)\text{d}x,\end{array}$$(2.1)

and(2.2) $$\begin{array}{c}\hfill {\Vert u\Vert }_{W_2^m}={\sqrt{⟨u,u⟩}}_{W_2^m},u,v\in W_2^m[0,1].\end{array}$$(2.2)

Definition 2.3

If $\forall x\in X$, there exists a unique function $R_x(y)$ in $\mathbb{H}$, for each fixed $y\in X$ then $R_x(y)\in \mathbb{H}$ and any $u(x)\in \mathbb{H}$, which satisfies ${⟨u(y),R_x(y)⟩}_{W_2^m}=u(x)$. Then, Hilbert space $\mathbb{H}$ is called the reproducing kernel space and $R_x(y)$ is called the reproducing kernel of $\mathbb{H}$.

Corollary 2.1

The space $W_2^m[0,1]$ is a reproducing kernel space.

The reproducing kernel $R_x(y)$ can be denoted by(2.3) $$\begin{array}{c}\hfill R_x(y)=\left\{\begin{array}{cc}R(x,y)=\sum _{i=1}^{2m}{p}_i(y)x^{i-1},\hfill & x\le y,\hfill \\ R(y,x)=\sum _{i=1}^{2m}{q}_i(y)x^{i-1},\hfill & x>y,\hfill \end{array}\right.\end{array}$$(2.3)

where coefficients $p_i(y),q_i(y),\{i=1,2,\dots ,2m\}$, could be obtained by solving the following equations(2.4) $$\begin{array}{cc}& \frac{{\mathit{\partial }}^i{R}_y(x)}{\mathit{\partial }{x}^i}\left|{}_{x=y^{+}}\right.=\frac{{\mathit{\partial }}^i{R}_y(x)}{\mathit{\partial }{x}^i}\left|{}_{x=y^{-}}\right.,i=0,1,2,\dots ,2m-2,\hfill \end{array}$$(2.4) (2.5) $$\begin{array}{cc}& {(-1)}^m\left(\frac{{\mathit{\partial }}^{2m-1}{R}_y(x)}{\mathit{\partial }{x}^{2m-1}}\left|{}_{x=y^{+}}-\frac{{\mathit{\partial }}^{2m-1}{R}_y(x)}{\mathit{\partial }{x}^{2m-1}}\left|{}_{x=y^{-}}\right)\right.\right.=1,\hfill \end{array}$$(2.5) (2.6) $$\begin{array}{cc}& \left\{\begin{array}{cc}\frac{{\mathit{\partial }}^i{R}_y(0)}{\mathit{\partial }{x}^i}-{(-1)}^{m-i-1}\frac{{\mathit{\partial }}^{2m-i-1}{R}_y(0)}{\mathit{\partial }{x}^{2m-i-1}}=0,\hfill & i=0,1,\dots ,m-1,\hfill \\ \frac{{\mathit{\partial }}^{2m-i-1}{R}_y(1)}{\mathit{\partial }{x}^{2m-i-1}}=0,\hfill & i=0,1,\dots ,m-1.\hfill \end{array}\right.\hfill \end{array}$$(2.6)

For more details, see Minggen and Yingzhen (2009).

2.1. A transformation of the Equation (1.1)

Using modified Taylor series, the nonlinear Abel’s integral equations with weakly singular kernel transform into nonlinear differential equations that can be solved easily.

With the Taylor series expansion of F(u(t)) expanded about the given point x belonging to the interval [0, 1], we have the Taylor series approximation of F(u(t)) in the following form(2.7) $$\begin{array}{c}\hfill F(u(t))=F(u(x))+F^{\prime }(u(x))u^{\prime }(x)(t-x)+\cdots .\end{array}$$(2.7)

We use the truncated Taylor series and substitute it instead of the nonlinear term of Equation (1.1),(2.8) $$\begin{array}{c}\hfill f(x)=\underset{0}{\overset{x}{\int }}\frac{1}{\sqrt{x-t}}F(u(t))\text{d}t=H(x,u(x),u^{\prime }(x),\dots ,u^{(n)}(x)).\end{array}$$(2.8)

3. The analytical solution

In this section, we present a nonlinear differential operator and a normal orthogonal system of the space $W_2^m[0,1]$. After that, an iterative method of obtaining the solution is introduced in the space $W_2^m[0,1]$.

First of all, we define an invertible bounded linear operator as(3.1) $$\begin{array}{c}\hfill \mathbb{L}:W_2^m[0,1]⟶W_2^{m-n}[0,1],\end{array}$$(3.1)

such that(3.2) $$\begin{array}{c}\hfill \mathbb{L}u(x)=u(x)f(x)=u(x)H(x,u(x),u^{\prime }(x),\dots ,u^{(n)}(x))=G(x,u(x),u^{\prime }(x),\dots ,u^{(n)}(x)).\end{array}$$(3.2)

Next, we construct an orthogonal function system of $W_2^m[0,1]$.

Let ${\mathit{\varphi }}_i(x)=f(x_i)R_{x_i}(x)$ and ${\mathit{\psi }}_i(x)={\mathbb{L}}^{\ast }{\mathit{\varphi }}_i(x)$, where ${\left\{x_i\right\}}_{i=1}^{\infty }$ is dense on [0, 1] and ${\mathbb{L}}^{\ast }$ is the adjoint operator of $\mathbb{L}$. From the properties of the reproducing kernel function $R_x(y)$, we have $⟨u(x),{\mathit{\varphi }}_i(x)⟩=u(x_i)$ for every $u(x)\in W_2^m[0,1]$.

Theorem 3.1

If ${\left\{x_i\right\}}_{i=1}^{\infty }$ is dense in the interval [0, 1] , then ${\left\{{\mathit{\psi }}_i(x)\right\}}_{i=1}^{\infty }$ is the complete system of $W_2^m[0,1]$.

Proof

Note that ${\left\{x_i\right\}}_{i=1}^{\infty }$ is dense in the interval [0, 1] . For $u(x)\in W_2^m[0,1]$, if(3.3) $$\begin{array}{c}\hfill ⟨u(x),{\mathit{\psi }}_i(x)⟩=⟨u(x),{\mathbb{L}}^{\ast }{\mathit{\varphi }}_i(x)⟩=⟨\mathbb{L}u(x),{\mathit{\varphi }}_i(x)⟩=⟨u(x),{\mathit{\varphi }}_i(x)⟩=u(x_i)=0,(i=1,2,\dots ),\end{array}$$(3.3)

from the density of ${\left\{x_i\right\}}_{i=1}^{\infty }$ and continuity of u(x) , then we have $u(x)\equiv 0$.

The orthonormal system ${\{{\overline{\mathit{\psi }}}_i(x)\}}_{i=1}^{\infty }$ of $W_2^m[0,1]$ is constructed from ${\{{\mathit{\psi }}_i(x)\}}_{i=1}^{\infty }$ by using the Gram–Schmidt algorithm, and then the approximate solution will be obtained by calculating a truncated series based on these functions, such that(3.4) $$\begin{array}{c}\hfill {\overline{\mathit{\psi }}}_i(x)=\sum _{k=1}^i{\mathit{\beta }}_{ik}{\mathit{\psi }}_k(x),({\mathit{\beta }}_{ii}>0,i=1,2,\dots ),\end{array}$$(3.4)

where ${\mathit{\beta }}_{ik}$ are orthogonal coefficients. However, Gram–Schmidt algorithm has some drawbacks such as high volume of computations and numerical instability, to fix these flaws see Moradi et al. (2014).

Theorem 3.2

Let ${\left\{x_i\right\}}_{i=1}^{\infty }$ be dense in the interval [0, 1]. If the Equation (1.1) has a unique solution, then the solution satisfies the form(3.5) $$\begin{array}{c}\hfill u(x)=\sum _{i=1}^{\infty }\sum _{k=1}^i{\mathit{\beta }}_{ik}G(x_k,u(x_k),u^{\prime }(x_k),\dots ,u^{(n)}(x_k)){\overline{\mathit{\psi }}}_i(x).\end{array}$$(3.5)

Proof

Let u(x) be the solution of Equation (1.1) u(x) is expanded in Fourier series, it has$$\begin{array}{cc}\hfill u(x)& =\sum _{i=1}^{\infty }⟨u(x),{\overline{\mathit{\psi }}}_i(x)⟩{\overline{\mathit{\psi }}}_i(x)=\sum _{i=1}^{\infty }\sum _{k=1}^i{\mathit{\beta }}_{ik}⟨u(x),{\mathit{\psi }}_k(x)⟩{\overline{\mathit{\psi }}}_i(x)\hfill \\ \hfill & =\sum _{i=1}^{\infty }\sum _{k=1}^i{\mathit{\beta }}_{ik}⟨u(x),{\mathbb{L}}^{\ast }{\mathit{\phi }}_k(x)⟩{\overline{\mathit{\psi }}}_i(x)=\sum _{i=1}^{\infty }\sum _{k=1}^i{\mathit{\beta }}_{ik}⟨\mathbb{L}u(x),{\mathit{\phi }}_k(x)⟩{\overline{\mathit{\psi }}}_i(x)\hfill \\ \hfill & =\sum _{i=1}^{\infty }\sum _{k=1}^i{\mathit{\beta }}_{ik}⟨G(x,u(x),u^{\prime }(x),\dots ,u^{(n)}(x)),{\mathit{\phi }}_k(x)⟩{\overline{\mathit{\psi }}}_i(x)\hfill \\ \hfill & =\sum _{i=1}^{\infty }\sum _{k=1}^i{\mathit{\beta }}_{ik}G(x_k,u(x_k),u^{\prime }(x_k),\dots ,u^{(n)}(x_k)){\overline{\mathit{\psi }}}_i(x).\hfill \end{array}$$

The proof is complete. $\square$

The Equation (3.2) is nonlinear, that is $G(x,u(x),u^{\prime }(x),\dots ,u^{(n)}(x))$ depend on u and its derivatives, then its solution can be obtained by the following iterative method.

Table 3. Numerical results of Ex. 3

Node	$|u_N{(x)-u(x)|}_{W_2^5}$	$|u_N{(x)-u(x)|}_{W_2^7}$
0.0	7.65597E$-$10	7.65610E$-$13
0.1	7.74042E$-$10	7.74047E$-$13
0.2	7.82533E$-$10	7.82485E$-$13
0.3	7.91071E$-$10	7.91145E$-$13
0.4	7.99655E$-$10	7.99583E$-$13
0.5	8.08287E$-$10	8.08242E$-$13
0.6	8.16966E$-$10	8.16902E$-$13
0.7	8.25692E$-$10	8.25784E$-$13
0.8	8.34466E$-$10	8.34444E$-$13
0.9	8.43288E$-$10	8.43325E$-$13
1.0	8.52157E$-$10	8.52207E$-$13

Table 4. Numerical results of Ex. 4

Node	$|u_N{(x)-u(x)|}_{W_2^5}$	$|u_N{(x)-u(x)|}_{W_2^8}$
0.0	3.76495E$-$7	2.47265E$-$9
0.1	3.92670E$-$7	2.63038E$-$9
0.2	4.07560E$-$7	2.77181E$-$9
0.3	4.21260E$-$7	2.89812E$-$9
0.4	4.33761E$-$7	3.01038E$-$9
0.5	4.45059E$-$7	3.10962E$-$9
0.6	4.55221E$-$7	3.19679E$-$9
0.7	4.64218E$-$7	3.27280E$-$9
0.8	4.72314E$-$7	3.33846E$-$9
0.9	4.79246E$-$7	3.39458E$-$9
1.0	4.85486E$-$7	3.44188E$-$9

By truncating the series of the left-hand side of (3.5), we obtain the approximate solution of Equation (1.1)(3.6) $$\begin{array}{c}\hfill u_N(x)=\sum _{i=1}^N\sum _{k=1}^i{\mathit{\beta }}_{ik}G(x_k,u(x_k),u^{\prime }(x_k),\dots ,u^{(n)}(x_k)){\overline{\mathit{\psi }}}_i(x).\end{array}$$(3.6) $u_N(x)$ in (3.6) is the N-term intercept of u(x) in (3.5), so $u_N(x)⟶u(x)$ in $W_2^m[0,1]$ as $N⟶\infty$.

4. Implementations of the method

Let $x_1=0$ and $u^{(i)}(x_1)=0,(i=1,2\dots n)$, then $G(x_1,u(x_1),u^{\prime }(x_1),\dots ,u^{(n)}(x_1))$ is known. We put(4.1) $$\begin{array}{cc}\hfill G(x_1,u_0(x_1),u_0^{\prime }(x_1),\dots ,u_0^{(n)}(x_1))& =G(x_1,u(x_1),u^{\prime }(x_1),\dots ,u^{(n)}(x_1)).\hfill \\ \hfill u_N(x)& =\sum _{i=1}^N{B}_i{\overline{\mathit{\psi }}}_i(x),\hfill \end{array}$$(4.1)

where$$\begin{array}{c}\hfill B_i=\sum _{k=1}^i{\mathit{\beta }}_{ik}G(x_k,u_i(x_k),u_i^{\prime }(x_k),\dots ,u_i^{(n)}(x_k)).\end{array}$$

Let$$\begin{array}{cc}\hfill B_1& ={\mathit{\beta }}_{11}G(x_1,u_0(x_1),u_0^{\prime }(x_1),\dots ,u_0^{(n)}(x_1)),\hfill \\ \hfill u_1(x)& =B_1{\overline{\mathit{\psi }}}_1(x),\hfill \\ \hfill B_2& =\sum _{k=1}^2{\mathit{\beta }}_{2k}G(x_k,u_1(x_k),u_1^{\prime }(x_k),\dots ,u_1^{(n)}(x_k)),\hfill \\ \hfill u_2(x)& =B_1{\overline{\mathit{\psi }}}_1(x)+B_2{\overline{\mathit{\psi }}}_2(x),\hfill \\ \hfill & ⋮\hfill \\ \hfill B_N& =\sum _{k=1}^N{\mathit{\beta }}_{Nk}G(x_k,u_{N-1}(x_k),u_{N-1}^{\prime }(x_k),\dots ,u_{N-1}^{(n)}(x_k)),\hfill \\ \hfill u_N(x)& =\sum _{i=1}^N{B}_i{\overline{\mathit{\psi }}}_i(x).\hfill \end{array}$$

Next, the convergence of $u_N(x)$ will be proved.

4.1. Convergence of method

Theorem 4.1

Suppose $\Vert u_N{(x)\Vert }_{W_2^m}$ is bounded in (4.1), if ${\{x_i\}}_{i=1}^{\infty }$ is dense in [0, 1],  then the N-term approximate solution $u_N(x)$ converges to the exact solution u(x) of Equation (1.1) and the exact solution is expressed as(4.2) $$\begin{array}{c}\hfill u(x)=\sum _{i=1}^{\infty }{B}_i{\overline{\mathit{\psi }}}_i(x),\end{array}$$(4.2)

where $B_i$ is given by (4.1).

Proof

The convergence of $u_N(x)$ will be proved. From (4.1), one gets(4.3) $$\begin{array}{c}\hfill u_N(x)=u_{N-1}(x)+B_N{\overline{\mathit{\psi }}}_N(x).\end{array}$$(4.3)

From the orthogonality of ${\{{\overline{\mathit{\psi }}}_i(x)\}}_{i=1}^{\infty },$ it follows that(4.4) $$\begin{array}{c}\hfill \Vert u_N{(x)\Vert }_{W_2^m}^2=\Vert u_{N-1}{(x)\Vert }_{W_2^m}^2+{\Vert B_N\Vert }^2.\end{array}$$(4.4)

The sequence $\Vert u_N{(x)\Vert }_{W_2^m}$ is monotone increasing. Due to $\Vert u_N{(x)\Vert }_{W_2^m}$ being bounded, $\{\Vert u_N(x){\Vert }_{W_2^m}\}$ is convergent as $N⟶\infty .$ Then there is a constant c such that(4.5) $$\begin{array}{c}\hfill \sum _{i=1}^{\infty }{B}_i^2=c.\end{array}$$(4.5)

It implies that$$\begin{array}{c}\hfill B_i=\sum _{k=1}^i{\mathit{\beta }}_{ik}G(x_k,u_i(x_k),u_i^{\prime }(x_k),\dots ,u_i^{(n)}(x_k)).\end{array}$$

let $m>N$, in view of $(u_m-u_{m-1})\perp (u_{m-1}-u_{m-2})\perp \cdots \perp (u_{N+1}-u_N),$ it follows that(4.6) $$\begin{array}{cc}\hfill \Vert (u_m-u_N){\Vert }_{W_2^m}^2& =\Vert u_m-u_{m-1}+u_{m-1}-u_{m-2}+\cdots +u_{N+1}-u_N{\Vert }_{W_2^m}^2\hfill \\ \hfill & =\Vert u_m-u_{m-1}{\Vert }_{W_2^m}^2+\Vert u_{m-1}-u_{m-2}{\Vert }_{W_2^m}^2+\cdots +{\Vert u_{N+1}-u_N\Vert }_{W_2^m}^2\hfill \\ \hfill & =\sum _{i=N+1}^m{(B_i)}^2⟶0,(N⟶\infty ).\hfill \end{array}$$(4.6)

Considering the completeness of $W_2^m[0,1]$, it has$$\begin{array}{c}\hfill u_N(x)\stackrel{{\Vert ·\Vert }_{W_2^m}}{⟶}u(x),(N⟶\infty ).\end{array}$$

It is proved that u(x) is the solution of Equation (1.1).

Hence$$\begin{array}{c}\hfill u(x)=\sum _{i=1}^{\infty }{B}_i{\overline{\mathit{\psi }}}_i(x).\end{array}$$

The proof is complete. $\square$

Theorem 4.2

If $u_N(x)\stackrel{{\Vert ·\Vert }_{W_2^m}}{⟶}u(x)$ and $x_N⟶y(N⟶\infty )$, then(4.7) $$\begin{array}{c}\hfill G(x_N,u_N(x_N),u_N^{\prime }(x_N),\dots ,u_N^{(n)}(x_N))⟶G(y,u(y),u^{\prime }(y),\cdots ,u^{(n)}(y))(N⟶\infty ).\end{array}$$(4.7)

Proof

We will prove $u_N^{(i)}(x_N)⟶u^{(i)}(y),(N⟶\infty )$ and $i=0,1,2,\dots ,n$. Observing that$$\begin{array}{cc}\hfill \left|u_N^{(i)}(x_N)-u^{(i)}(y)\right|& =\left|u_N^{(i)}(x_N)-u_N^{(i)}(y)+u_N^{(i)}(y)-u^{(i)}(y)\right|\hfill \\ \hfill & \le \left|u_N^{(i)}(x_N)-u_N^{(i)}(y)\right|+\left|u_N^{(i)}(y)-u^{(i)}(y)\right|\hfill \end{array}$$

It follows that$$\begin{array}{cc}\hfill \left|u_N^{(i)}(x_N)-u_N^{(i)}(y)\right|& =\left|⟨u_N(x),\frac{{\mathit{\partial }}^i}{\mathit{\partial }{y}^i}(R_{x_N}(x)-R_y(x))⟩\right|\hfill \\ \hfill & \le {∥u_N(x)∥}_{W_2^m}{∥\frac{{\mathit{\partial }}^i}{\mathit{\partial }{y}^i}(R_{x_N}(x)-R_y(x))∥}_{W_2^m}.\hfill \end{array}$$

From the convergence of $u_N(x)$, there exist constants $M_1\in \mathbb{N}$ and $M\in \mathbb{R}$, such that$$\begin{array}{c}\hfill \Vert u_N^{(i)}{(x)\Vert }_{W_2^m}\le M{\Vert u(x)\Vert }_{W_2^m},\text{for}N\ge M_1\text{and}i=0,1,2,\dots ,n.\end{array}$$

Since$$\begin{array}{c}\hfill \Vert R_{x_N}(x)-R_y{(x)\Vert }_{W_2^m}⟶0(N⟶\infty ).\end{array}$$

It follows that $|u_N^{(i)}(x_N)-u^{(i)}(y)|⟶0$ as $x_N⟶y$ from $\Vert u_N^{(i)}{(x)\Vert }_{W_2^m}\le M{\Vert u(x)\Vert }_{W_2^m}.$

Hence, as $x_N⟶y$ it shows that$$\begin{array}{c}\hfill u_N^{(i)}(x_N)⟶u^{(i)}(y)(N⟶\infty ).\end{array}$$

It follows that(4.8) $$\begin{array}{c}\hfill G(x_N,u_N(x_N),u_N^{\prime }(x_N),\dots ,u_N^{(n)}(x_N))⟶G(y,u(y),u^{\prime }(y),\dots ,u^{(n)}(y))(N⟶\infty ).\end{array}$$(4.8)

Consequently, the method mentioned is convergent. $\square$

5. Applications and numerical results

The reproducing kernel method for solving nonlinear Abel’s integral equations with weakly singular kernel will be illustrated by studying the following examples. For solving these examples, $N=10$ and $m>n$ are considered, where N is the number of terms of the Fourier series of the unknown function u(x) and n is the number of terms of the Taylor series. The approximate solutions obtained of Equation (4.1) are compared with the exact solution of each example which are found to be in good agreement with each other. The examples are computed using Mathematica 8.0.

Example 5.1

Consider the following nonlinear Abel integral equation (Wazwaz, 2011):$$\begin{array}{c}\hfill \frac{2}{3}{x}^{\frac{1}{2}}(3+2x)=\underset{0}{\overset{x}{\int }}\frac{1}{\sqrt{x-t}}ln(u(t))\text{d}t,\end{array}$$

the exact solution of this problem is $u(x)=e^{x+1}$.

The approximate solution by the proposed method for $n=2$ is computed. The Taylor series approximation of $ln(u(t))$ is used in the following form(5.1) $$\begin{array}{c}\hfill ln(u(t))=ln(u(x))+\frac{u^{\prime }(x)(t-x)}{u(x)}+\frac{(-{(u^{\prime }(x))}^2+u(x)u^{″}(x)){(t-x)}^2}{2{(u(x))}^2}.\end{array}$$(5.1)

The absolute errors obtained in spaces $W_2^6[0,1]$, $W_2^8[0,1]$ are given in Table 1. This is an indication of accuracy on the reproducing Kernel space. However, by increasing m , the approximate solution improves.

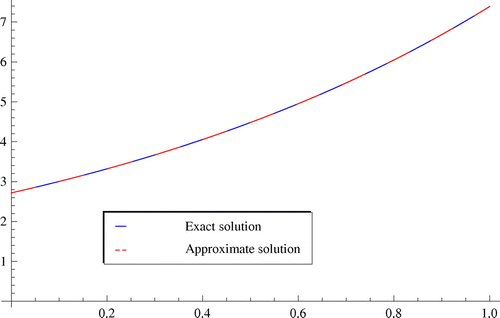
The comparisons between the exact solution and the numerical solutions for $m=8$ are shown in Figure 1. We can see clearly that the numerical solutions and exact solution coincide completely. Figure 2 reveals the absolute errors in spaces $W_2^6[0,1],W_2^8[0,1]$, respectively.

Example 5.2

In the second example, we solve the nonlinear Abel integral equation (Wazwaz, 2011):$$\begin{array}{c}\hfill \frac{2}{3}{x}^{\frac{1}{2}}(3+2x)=\underset{0}{\overset{x}{\int }}\frac{1}{\sqrt{x-t}}{cos}^{-1}(u(t))\text{d}t,\end{array}$$

the exact solution is $u(x)=cos(x+1)$.

The approximate solution by the proposed method for $n=1$ is computed. The Taylor series approximation of ${cos}^{-1}(u(t))$ is used in the following form(5.2) $$\begin{array}{c}\hfill {cos}^{-1}(u(t))={cos}^{-1}(u(x))-\frac{u^{\prime }(x)(t-x)}{\sqrt{1-u^2(x)}}.\end{array}$$(5.2)

The absolute errors obtained in spaces $W_2^5[0,1]$, $W_2^7[0,1]$ are given in Table 2. This is an indication of accuracy on the reproducing Kernel space. However, by increasing m , the approximate solution improves.

The comparisons between the exact solution and the numerical solutions for $m=7$ are shown in Figure 3. We can see clearly that the numerical solutions and exact solution coincide completely. Figure 4 reveals the absolute errors in spaces $W_2^5[0,1],W_2^7[0,1]$, respectively.

Example 5.3

Let us consider the nonlinear Abel integral equation (Wazwaz, 2011):$$\begin{array}{c}\hfill \frac{1}{15}{x}^{\frac{1}{2}}(30+40x+16x^2)=\underset{0}{\overset{x}{\int }}\frac{1}{\sqrt{x-t}}{u}^2(t)\text{d}t,\end{array}$$

the exact solution of this problem is $u(x)=1+x$.

The approximate solution by the proposed method for $n=2$ is computed. The Taylor series approximation of $u^2(t)$ is used in the following form(5.3) $$\begin{array}{c}\hfill u^2(t)=u^2(x)+{(u^2)}^{\prime }(x)(t-x)+\frac{1}{2}{(u^2)}^{″}(x){(t-x)}^2.\end{array}$$(5.3)

The absolute errors obtained in spaces $W_2^5[0,1]$, $W_2^7[0,1]$ are given in Table 3. This is an indication of accuracy on the reproducing Kernel space. However, by increasing m , the approximate solution improves.

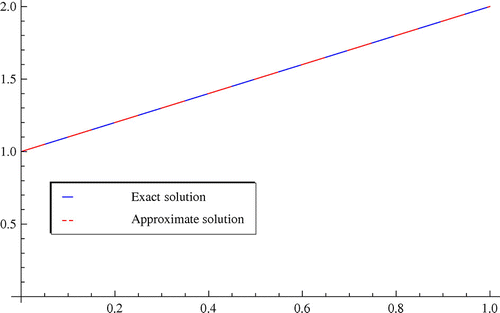
The comparisons between the exact solution and the numerical solutions for $m=7$ are shown in Figure 5. We can see clearly that the numerical solutions and exact solution coincide completely. Figure 6 reveals the absolute errors in spaces $W_2^5[0,1],W_2^7[0,1]$, respectively.

Example 5.4

Now, we consider the singular nonlinear Abel integral equation (Wazwaz, 2011):$$\begin{array}{c}\hfill \frac{2}{3}e{x}^{\frac{1}{2}}(3+2x)=\underset{0}{\overset{x}{\int }}\frac{1}{\sqrt{x-t}}{e}^{u(t)}\text{d}t,\end{array}$$

the exact solution is $u(x)=1+ln(x+1)$.

The approximate solution by the proposed method for $n=1$ is computed. The Taylor series approximation of $e^{u(t)}$ is used in the following form(5.4) $$\begin{array}{c}\hfill e^{u(t)}=e^{u(x)}+e^{u(x)}{u}^{\prime }(x)(t-x).\end{array}$$(5.4)

The absolute errors obtained in spaces $W_2^5[0,1]$, $W_2^8[0,1]$ are given in Table 4. This is an indication of accuracy on the reproducing Kernel space. However, by increasing m , the approximate solution improves.

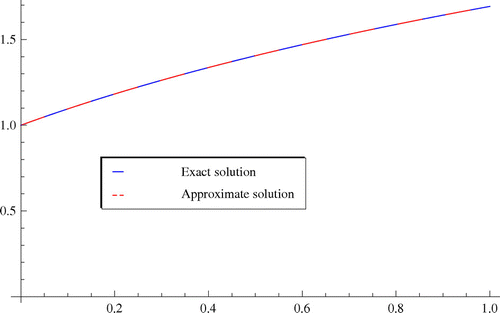
The comparisons between the exact solution and the numerical solutions for $m=8$ are shown in Figure 7. We can see clearly that the numerical solutions and exact solution coincide completely. Figure 8 reveals the absolute errors in spaces $W_2^5[0,1],W_2^8[0,1]$, respectively.

6. Conclusions

To numerically solve nonlinear Abel’s integral equations by means of the reproducing kernel method, the reproducing kernel functions as a basis and Taylor series to remove singularity were used. The absolute errors in two spaces were computed. By increasing m, the accuracy of the approximate solution improves. So, to get the more accurate result, it is sufficient to increase m . As seen from the examples, the method can be accurate and stable.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Azizallah Alvandi

Azizallah Alvandi is currently PhD degree student under the supervision of Dr Mahmoud Paripour in Department of Mathematics, Hamedan Branch, Islamic Azad University, Hamedan, Iran. His research interests include numerical analysis, Integral equations.

Mahmoud Paripour

Mahmoud Paripour is Assistant Professor in Applied Mathematics, Hamedan University of Technology, Hamedan, Iran. His research interests are mainly in the area of numerical analysis, Integral equations, Partial differential equations, Orthogonal functions, Fuzzy integral equations, Fuzzy linear systems.