Parameter estimations for mixed generalized exponential distribution based on progressive type-I interval censoring

Abstract

This paper considers the estimation of parameters based on a progressively type-I interval-censored data from a mixed generalized exponential distribution. The maximum likelihood estimation is used but an analytic form cannot be obtained. The EM algorithm is applied to obtain the maximum likelihood estimates. The performance of the estimates is judged by a simulating study and a real data is presented to illustrate the method of estimation developed here.

Keywords:

• progressive type-I interval censoring
• mixed generalized exponential distribution
• maximum likelihood estimation
• EM algorithm

Public Interest Statement

Progressive type-I interval censoring data in survival analysis and reliability analysis are a kind of interested and popular data type. This work is modeling for this kind of data with a more flexible Mixed Generalized Exponential Distribution including the exponential distribution and Weibull distribution. And the result of this paper can apply to the lifetime analysis in clinical trial, engineering and so on.

1. Introduction

In the life testing, reliability studies and survival analysis, it is extremely common that items are lost or removed from experiments before failure. The most popular censoring schemes are type-I and type-II censoring. Under type-I censoring, the test is continued until a pre-specified time. In type-II censoring, the test is continued up to a pre-specified number of failures. Progressive type-II censoring is an extension of the traditional type-II censoring scheme and it has been studied such as Balakrishnan and Aggarwala (2000), Balakrishnan, Kannan, Lin, and Wu (2004) and so on. Sometimes it is impossible to observe the whole life test process continuously due to time and cost constraint. Only the number of failures is observed in an interval instead of observing the failure time exactly and this is called interval censoring. As the mixture of the interval censoring and progressive censoring, Aggarwala (2001) introduced progressive type-I interval censoring scheme and developed the statistical inference for the exponential distribution based on progressively type-I interval-censored data. Ng and Wang (2009) discussed statistical inference for Weibull distribution under progressive type-I interval censoring. They have compared with different estimation methods for the parameters of Weibull distribution via simulation. Lin, Wu, and Balakrishnan (2009) considered determination of optimum life testing plan with progressively type-I interval-censored data from the log-normal distribution. Chen and Lio (2010) considered parameter estimations for generalized exponential distribution under progressive type-I interval censoring. They have obtained the estimates of unknown parameters using EM algorithm, midpoint approximation method and method of moments. Further, Lio, Chen, and Tsai (2011) presented the parameter estimations of the generalized Rayleigh distribution at the same censoring scheme. Peng and Yan (2011) considered the MLEs and moments estimators of the parameters for gamma distribution based on progressive type-I interval censoring and compared with the biases and mean square errors through simulation. Pradhan and Gijo (2013) considered inference for the unknown parameters of log-normal distribution based on progressively type-I interval-censored data through both frequency and Bayesian approaches.

In most simple life tests, the experimental data come from one population and have only one type of failure. In fact, a mixed distribution can provide a flexible candidate to depict the time to failure. Especially in the analysis of biased life data, the failure hazard in the beginning is quite high and the failure rate is decreased or constant as the age increases. On this occasion, population is not homogeneous but is made up from sub-populations. There are many researches for the mixed distribution, such as McClean (1986), Soliman (2006), Tian, He, and Chen (2008), Tian, Tian and Chen (2012), Tian, Tian, and Zhu (2014), Tian, Zhu and Tian (2013) and so on. Nevertheless, to our best knowledge, no published papers address maximum likelihood estimation of the mixed generalized exponential distribution (MGED) under progressive type-I interval censoring. In this work, we consider the estimation for parameters of the MGED based on progressively type-I interval-censored data. This paper gives the likelihood equations of the unknown parameters. It is observed that there is no closed form of MLEs. Therefore, it is suggested to use the EM algorithm to compute the MLEs and present the performance of the estimates by simulations.

The rest of the paper is organized as follows. The model and data description are provided in Section 2. The maximum likelihood estimators of the unknown parameters are obtained in Section 3. The EM algorithm procedure is given in Section 4. The performance of the estimators is investigated via simulation in Section 5. A data-set is analyzed in Section 6. Section 7 includes some conclusion remarks.

2. The description of the model and data

Consider the MGED with m components with its probability density function, cumulative distribution function and hazard function as follows(2.1) $$f(t;P,\mathit{\alpha },\mathit{\lambda })=\sum _{k=1}^m{P}_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k{\left(1-e^{-{\mathit{\lambda }}_{k}t}\right)}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_{k}t},t>0$$(2.1) (2.2) $$F\left(t;P,\mathit{\alpha },\mathit{\lambda }\right)=\sum _{k=1}^m{p}_k{\left(1-e^{-{\mathit{\lambda }}_{k}t}\right)}^{{\mathit{\alpha }}_k},t\ge 0$$(2.2)

(2.3) $$h\left(t;P,\mathit{\alpha },\mathit{\lambda }\right)=\frac{\sum _{k=1}^m{p}_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k{\left(1-e^{-{\mathit{\lambda }}_{k}t}\right)}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_{k}t}}{1-\sum _{k=1}^m{p}_k{\left(1-e^{-{\mathit{\lambda }}_{k}t}\right)}^{{\mathit{\alpha }}_k}},t\ge 0$$(2.3)

where $P=\left(p_1,p_2,\dots ,p_{m-1}\right)$, $\mathit{\alpha }=\left({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_m\right)$, $\mathit{\lambda }=\left({\mathit{\lambda }}_1,\dots ,{\mathit{\lambda }}_m\right)$, 0 < p_k < 1, k = 1, …, m − 1, $p_m=1-\sum _{k=1}^{m-1}{p}_k$, α_k > 0 are the shape parameters, ${\mathit{\lambda }}_k>0$ are the scale parameters, the number of the parameters is 3m − 1.

Then, progressive type-I interval censoring scheme is as follows. Let n identical items be placed on a test at time t₀ = 0 and pre-specify N inspection times t₁ < t₂ < ⋯ < t_N, where t_N is the scheduled termination time of the experiment. Suppose X_i is the failure number within the interval of (t_i−1, t_i], Y_i is the survival items numbers at time t_i and R_i is the number of items randomly removed from the surviving items at time t_i. R₁, R₂, …, R_N can be pre-specified by the percentage of the remaining surviving items. Therefore, for the pre-specified percentage $p_i^{\prime },R_i=⌊Y_i{p}_i^{\prime }⌋,i=1,2,\dots ,N,p_N^{\prime }=1$. Alternatively R₁, R₂, …, R_m can also be pre-specified positive integers. In this case, there must be at least R_i units available for removal. The proportions of surviving units to be removed at the monitoring and censoring points have been given in the simulation. And the progressively type-I interval-censored data are given by {X_i, R_i, t_i}, i = 1, 2, …, N, where the sample size $n={\sum }_{i=1}^N(X_i+R_i)$. If R_i = 0, i = 1, 2, …, N – 1, then progressive type-I interval censoring is reduced to the traditional interval-censored data, X₁, X₂, …, X_N, X_N+1 = R_N.

3. Maximum likelihood estimation

Given a progressively type-I interval-censored data, {X_i, R_i, t_i}, i = 1, 2, …, N which sample size is n, from a lifetime distribution with distribution function F(T, θ) and θ is the parameter vector. Then, the likelihood function is (Aggarwala, 2001)(3.1) $$L(\mathit{\theta })\propto {\left[F(t_1,\mathit{\theta })\right]}^{X_1}{[1-F(t_1,\mathit{\theta })]}^{R_1}\times {[F(t_2,\mathit{\theta })-F(t_1,\mathit{\theta })]}^{X_2}{[1-F(t_2,\mathit{\theta })]}^{R_2}\times \cdots \times {[F(t_N,\mathit{\theta })-F(t_{N-1},\mathit{\theta })]}^{X_N}{[1-F(t_N,\mathit{\theta })]}^{R_N}=\prod _{i=1}^N{[F(t_i,\mathit{\theta })-F(t_{i-1},\mathit{\theta })]}^{X_i}{[1-F(t_i,\mathit{\theta })]}^{R_i}$$(3.1)

where t₀ = 0. We can obtain the MLEs of the parameters by maximizing the likelihood function in (3.1).

Given the MGED by the Equation (2.2), the above likelihood function can be specified as follows:$$L(P,\mathit{\alpha },\mathit{\lambda })\propto \prod _{i=1}^N{\left[\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}\right]}^{X_i}{\left[1-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}\right]}^{R_i}$$

And the log-likelihood function is$$l(P,\mathit{\alpha },\mathit{\lambda })=lnL(P,\mathit{\alpha },\mathit{\lambda })=\text{constant}+\sum _{i=1}^N\left\{X_{i}ln\left[\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}\right]+R_{i}ln\left[1-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}\right]\right\}$$

Taking derivatives of the log-likelihood function with respective to $p_k,{\mathit{\alpha }}_k,{\mathit{\lambda }}_k$ to zero, the following score equations are obtained:$$\sum _{i=1}^N\frac{X_i\left[{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}-{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}\right]}{\left[\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}\right]}-\sum _{i=1}^N\frac{R_i{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}}{1-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}}=0$$$$\sum _{i=1}^N\left\{\frac{X_i[p_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}ln(1-e^{-{\mathit{\lambda }}_k{t}_i})-p_k{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}ln(1-e^{-{\mathit{\lambda }}_k{t}_i})]}{\left[\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}\right]}\right\}-\sum _{i=1}^N\left[\frac{R_i{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}ln(1-e^{-{\mathit{\lambda }}_k{t}_i})}{1-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}}\right]=0$$

$$\sum _{i=1}^N\left\{\frac{X_i\left[p_k{\mathit{\alpha }}_k{t}_i{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_k{t}_i}-p_k{\mathit{\alpha }}_k{t}_{i-1}{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_k{t}_{i-1}}\right]}{\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}}\right\}-\sum _{i=1}^N\left[\frac{R_i{p}_k{\mathit{\alpha }}_k{t}_i{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_k{t}_i}}{1-\sum _{k=1}^m{p}_k{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}}\right]=0$$

Obviously, the equations are quite complex and there is no closed form for the solutions to the above equations and the EM algorithm introduced as follows to find the MLEs of $p_k,{\mathit{\alpha }}_k,{\mathit{\lambda }}_k$, k = 1, 2, …, m.

4. EM algorithm

The Expectation Maximization (EM) Algorithm (Dempster, Laird, & Rubin, 1977) is a useful tool to estimate the parameters of the distribution based on an incomplete data. Here, some notations are similar to that in the Tian et al. (2014). In order to estimate the MGED models under progressive type-I interval censoring, EM algorithm is applied to estimate the unknown parameters. Suppose τ₁, τ₂, …, τ_n are n independent identically distributed (iid) samples from the MGED model and denote

$$f_{ki}={\mathit{\alpha }}_k{\mathit{\lambda }}_k{(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_i})}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_k{\mathit{\tau }}_i}{f}_i=\sum _{k=1}^m{p}_k{f}_{ki}$$

$$S_{ki}=1-{(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_i})}^{{\mathit{\alpha }}_k}{S}_i=\sum _{k=1}^m{p}_k{S}_{ki}$$

where k = 1, 2, …, m, i = 1, 2, …, n.

Here, the sample τ_i, i = 1, 2, …, n is divided into two components that consist of τ_ij and ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$. Let τ_ij, j = 1, 2, …, X_i be the lifetimes within interval (t_i−1, t_i] and ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$, j^′ = 1, 2, …, R_i be the lifetimes for those withdrawn items at t_i for i = 1, 2, …, N and the number of the τ_ij and ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$ are $\sum _{i=1}^N{X}_i$, $\sum _{i=1}^N{R}_i$, respectively. Introduce an indicator vector I_ij = (I_ij1, I_ij2, …, I_ijm) of τ_ij, $I_{i{j}^{\prime }}=(I_{i{j}^{\prime }1},I_{i{j}^{\prime }2},\dots ,I_{i{j}^{\prime }m})$of ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$, $I_{ijk}(I_{i{j}^{\prime }k})$ is a binary random variable only taking the value 1 if τ_ij(${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$) comes the k-th component, and 0 otherwise for k = 1, 2, …, m. Also denote $I=(I_{ij},I_{i{j}^{\prime }}),$ i = 1, 2, …, N, j = 1, 2, …, X_i, j^′ = 1, 2, …, R_i as an indicator matrix composed of n indicator vectors of all life variables τ_ij and ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$. Evidently random vector I_ij = (I_ij1, I_ij2, …, I_ijm) and $I_{i{j}^{\prime }}=(I_{i{j}^{\prime }1},I_{i{j}^{\prime }2},\dots ,I_{i{j}^{\prime }m})$ follows the multinomial distribution. However, we may not know which component the variate comes from. Namely, I cannot be observed, thus regard it as the missing data in the EM algorithm. In the following paper, denote $I_{ij}^{(1)}=(I_{ij1}^{(1)},I_{ij2}^{(1)},\dots ,I_{ijm}^{(1)})$, $I_{i{j}^{\prime }}^{(2)}=(I_{i{j}^{\prime }1}^{(2)},I_{i{j}^{\prime }2}^{(2)},\dots ,I_{i{j}^{\prime }m}^{(2)})$ as the indicator vectors of the data τ_ij and ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$, respectively.

As to the the lifetimes τ_ij within interval (t_i−1, t_i], the joint density of τ_ij and $I_{ij}^{(1)}$ is $g({\mathit{\tau }}_{ij},I_{ij}^{(1)}|P,\mathit{\alpha },\mathit{\lambda })=\prod _{k=1}^m{[p_k(S_{ki-1}-S_{ki})]}^{I_{ijk}^{(1)}}$. Given τ_ij, the conditional density of $I_{ij}^{(1)}$ is $p(I_{ijk}^{(1)}=1|{\mathit{\tau }}_{ij},P,\mathit{\alpha },\mathit{\lambda })=\frac{p_k(S_{ki-1}-S_{ki})}{(S_{i-1}-S_i)},k=1,2,\dots ,m$.

Where, $S_{ki}=1-{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}$, $S_{ki-1}=1-{(1-e^{-{\mathit{\lambda }}_k{t}_{i-1}})}^{{\mathit{\alpha }}_k}$, $S_i=\sum _{k=1}^m{p}_k{S}_{ki}$, $S_{i-1}=\sum _{k=1}^m{p}_k{S}_{ki-1}$

For the right-censored data ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$, the joint density of ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$ and ${I_{i{j}^{\prime }}}^{(2)}$ is given by $g({\mathit{\tau }}_{i{j}^{\prime }}^{\ast },{I_{i{j}^{\prime }}}^{(2)}|P,\mathit{\alpha },\mathit{\lambda })=\prod _{k=1}^m{[p_k{S}_{ki}]}^{{I_{i{j}^{\prime }k}}^{(2)}}$. Given ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$, the conditional density of ${I_{i{j}^{\prime }}}^{(2)}$ is $p({I_{i{j}^{\prime }k}}^{(2)}=1|{\mathit{\tau }}_{i{j}^{\prime }}^{\ast },P,\mathit{\alpha },\mathit{\lambda })=\frac{p_k{S}_{ki}}{S_i},k=1,2,\dots ,m$. Where $S_{ki}=1-{(1-e^{-{\mathit{\lambda }}_k{t}_i})}^{{\mathit{\alpha }}_k}$, $S_i=\sum _{k=1}^m{p}_k{S}_{ki}.$

In Section 2, denote the progressively type-I interval-censored sample as {X_i, R_i, t_i}, i = 1, 2, …, N. In the progressive type-I interval censoring experiments, we can only observe the failure numbers X_i within the intervals (t_i−1, t_i] and R_i, the number of the censored items withdrawn at the censoring time t_i for i = 1, 2, …, N. Then, the observed values can be simply denoted as Y = (t₁, t₂, …, t_N, X₁, X₂, …, X_N, R₁, R₂, …, R_N). However, the true failure time within the interval (t_i−1, t_i] denoted as τ_ij, i = 1, 2, …, N, j = 1, 2, …, X_i and the true failure time of censored units at t_i denoted as ${\mathit{\tau }}_{i{j}^{\prime }}^{\ast }$, i = 1, 2, …, N, j^′ = 1, 2, …, R_i can not be observed in life experiments. Consequently, $\mathit{\tau }=({\mathit{\tau }}_{ij},{\mathit{\tau }}_{i{j}^{\prime }}^{\ast };i=1,2,\dots ,N,j=1,2,\dots ,X_i,j^{\prime }=1,2,\dots ,R_i)$ can be regarded as missing data. All the missing data can be denoted (τ, I) and all the complete data can be denoted as W = (τ, I, Y). The following procedure will give the MLEs of all unknown parameters via the EM algorithm consisting of two steps: E-step and M-step.

First of all, the likelihood function of the MGED model under the complete data W is given by$$l(P,\mathit{\alpha },\mathit{\lambda }|W)=\prod _{i=1}^N\left\{\prod _{j=1}^{X_i}\prod _{k=1}^m{\left[p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k{(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}})}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}}\right]}^{{I_{ijk}}^{(1)}}\times \prod _{j^{\prime }=1}^{R_i}\prod _{k=1}^m{\left[p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k{(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }})}^{{\mathit{\alpha }}_k-1}{e}^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }}\right]}^{{I_{i{j}^{\prime }k}}^{(2)}}\right\}$$

The log-likelihood function of the complete data is

$$lnl(P,\mathit{\alpha },\mathit{\lambda }|W)=\sum _{i=1}^N\sum _{k=1}^m\left\{\sum _{j=1}^{X_i}{I_{ijk}}^{(1)}\left[ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)+({\mathit{\alpha }}_k-1)ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}})-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}\right]+\sum _{j^{\prime }=1}^{R_i}{I_{i{j}^{\prime }k}}^{(2)}\left[ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)+({\mathit{\alpha }}_k-1)ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }})-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }\right]\right\}$$

Given initial values $P^{(0)},{\mathit{\alpha }}^{(0)},{\mathit{\lambda }}^{(0)}$ of the unknown parameter vectors, we can obtain parameter estimates of model (2.1) based on EM algorithm via the following two steps. Of course, estimation performance has a great relationship with the choice of the initial values. Generally, different initial values may be lead to different convergence rate. In the simulation, it is suggest to choose some groups of initial values to compare the estimation results.

E-step: suppose the (h − 1)-th iteration values are $P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)}$, then the Q function of the h-th iteration is obtained by$$Q(P,\mathit{\alpha },\mathit{\lambda }|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},Y)=E\left[lnl(P,\mathit{\alpha },\mathit{\lambda }|W)|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},Y\right]=\sum _{i=1}^N\sum _{k=1}^{m}E\left\{\sum _{j=1}^{X_i}{I_{ijk}}^{(1)}\left[ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)+({\mathit{\alpha }}_k-1)ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}})-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}\right]+\sum _{j^{\prime }=1}^{R_i}{I_{i{j}^{\prime }k}}^{(2)}\left[ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)+({\mathit{\alpha }}_k-1)ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }})-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }\right]\right\}=\sum _{i=1}^N\sum _{k=1}^m\left\{\sum _{j=1}^{X_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)E({I_{ijk}}^{(1)})+({\mathit{\alpha }}_k-1)\sum _{j=1}^{X_i}E\left[ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}}){I_{ijk}}^{(1)}\right]-{\mathit{\lambda }}_k\sum _{j=1}^{X_i}E({\mathit{\tau }}_{ij}{I_{ijk}}^{(1)})+\sum _{j^{\prime }=1}^{R_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)E({I_{i{j}^{\prime }k}}^{(2)})+({\mathit{\alpha }}_k-1)\sum _{j^{\prime }=1}^{R_i}E\left[ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }}){I_{i{j}^{\prime }k}}^{(2)}\right]-{\mathit{\lambda }}_k\sum _{j^{\prime }=1}^{R_i}E({\mathit{\tau }}_{i{j}^{\prime }}^{\ast }{I_{i{j}^{\prime }k}}^{(2)})\right\}=\sum _{i=1}^N\sum _{k=1}^m\left\{\sum _{j=1}^{X_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)E[E({I_{ijk}}^{(1)}|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},\mathit{\tau },Y)]+({\mathit{\alpha }}_k-1)\sum _{j=1}^{X_i}E\left[E(ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}}){I_{ijk}}^{(1)}|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},\mathit{\tau },Y)\right]-{\mathit{\lambda }}_k\sum _{j=1}^{X_i}E[E({\mathit{\tau }}_{ij}·{I_{ijk}}^{(1)}|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},\mathit{\tau },Y)]+\sum _{j^{\prime }=1}^{R_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)E\left[E({I_{i{j}^{\prime }k}}^{(2)}|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},\mathit{\tau },Y)\right]+({\mathit{\alpha }}_k-1)\sum _{j^{\prime }=1}^{R_i}E\left[E(ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }}){I_{i{j}^{\prime }k}}^{(2)}|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},\mathit{\tau },Y)\right]-{\mathit{\lambda }}_k\sum _{j^{\prime }=1}^{R_i}E\left[E({\mathit{\tau }}_{i{j}^{\prime }}^{\ast }{I_{i{j}^{\prime }k}}^{(2)}|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},\mathit{\tau },Y)\right]\right\}=\sum _{i=1}^N\sum _{k=1}^m\left\{\sum _{j=1}^{X_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)E\left[a_{kij}^{(h-1)}({\mathit{\tau }}_{ij})\right]+({\mathit{\alpha }}_k-1)\sum _{j=1}^{X_i}E\left[ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}})a_{kij}^{(h-1)}({\mathit{\tau }}_{ij})\right]-{\mathit{\lambda }}_k\sum _{j=1}^{X_i}E\left[{\mathit{\tau }}_{ij}·a_{kij}^{(h-1)}({\mathit{\tau }}_{ij})\right]+\sum _{j^{\prime }=1}^{R_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)E[b_{ki{j}^{\prime }}^{(h-1)}({\mathit{\tau }}_{i{j}^{\prime }}^{\ast })]+({\mathit{\alpha }}_k-1)\sum _{j^{\prime }=1}^{R_i}E\left[ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }})b_{ki{j}^{\prime }}^{(h-1)}({\mathit{\tau }}_{i{j}^{\prime }}^{\ast })\right]-{\mathit{\lambda }}_k\sum _{j^{\prime }=1}^{R_i}E\left[{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }·b_{ki{j}^{\prime }}^{(h-1)}({\mathit{\tau }}_{i{j}^{\prime }}^{\ast })\right]\right\}=\sum _{i=1}^N\sum _{k=1}^m\left\{\sum _{j=1}^{X_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})+({\mathit{\alpha }}_k-1)\sum _{j=1}^{X_i}E\left[ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{ij}})a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})\right]-{\mathit{\lambda }}_k\sum _{j=1}^{X_i}E\left[{\mathit{\tau }}_{ij}·a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})\right]+R_i·ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)·b_{ki}^{(h-1)}(t_i)+({\mathit{\alpha }}_k-1)\sum _{j^{\prime }=1}^{R_i}E\left[ln(1-e^{-{\mathit{\lambda }}_k{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }})b_{ki}^{(h-1)}(t_i)\right]-{\mathit{\lambda }}_k\sum _{j^{\prime }=1}^{R_i}E\left[{\mathit{\tau }}_{i{j}^{\prime }}^{\ast }·b_{ki}^{(h-1)}(t_i)\right]\right\}$$

where,$$a_{kij}^{(h-1)}({\mathit{\tau }}_{ij})=\frac{p_k^{(h-1)}(S_{ki-1}^{(h-1)}(t_{i-1})-S_{ki}^{(h-1)}(t_i))}{(S_{i-1}^{(h-1)}(t_{i-1})-S_i^{(h-1)}(t_i))}\widehat{=}{a}_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})$$

$$b_{ki{j}^{\prime }}^{(h-1)}({\mathit{\tau }}_{i{j}^{\prime }}^{\ast })=\frac{p_k^{(h-1)}·S_{ki}^{(h-1)}(t_i)}{S_i^{(h-1)}(t_i)}\widehat{=}{b}_{ki}^{(h-1)}(t_i)$$$$S_{ki-1}^{(h-1)}(t_{i-1})=1-{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}{t}_{i-1}})}^{{\mathit{\alpha }}_k^{(h-1)}}$$$$S_{ki}^{(h-1)}(t_i)=1-{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}{t}_i})}^{{\mathit{\alpha }}_k^{(h-1)}}$$$$S_{i-1}^{(h-1)}(t_{i-1})=\sum _{k=1}^m{p}_k^{(h-1)}{S}_{ki-1}^{(h-1)}(t_{i-1})$$$$S_i^{(h-1)}(t_i)=\sum _{k=1}^m{p}_k^{(h-1)}{S}_{ki}^{(h-1)}(t_i)$$$$k=1,2,\dots ,m,i=1,2,\dots ,N,j=1,2,\dots ,X_i,j^{\prime }=1,2,\dots ,R_i$$

Then,

$$Q(P,\mathit{\alpha },\mathit{\lambda }|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},Y)=\sum _{i=1}^N\sum _{k=1}^m\left[\sum _{j=1}^{X_i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})+({\mathit{\alpha }}_k-1)\sum _{j=1}^{X_i}\underset{t_{i-1}}{\overset{t_i}{\int }}ln(1-e^{-{\mathit{\lambda }}_{k}x})a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})p_{ij}(x)\text{d}x-{\mathit{\lambda }}_k\sum _{j=1}^{X_i}\underset{t_{i-1}}{\overset{t_i}{\int }}x·a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})p_{ij}(x)\text{d}x+R_i·ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)b_{ki}^{(h-1)}(t_i)+({\mathit{\alpha }}_k-1)\sum _{j^{\prime }=1}^{R_i}\underset{t_i}{\overset{\infty }{\int }}ln(1-e^{-{\mathit{\lambda }}_{k}x})b_{ki}^{(h-1)}(t_i)p_{i{j}^{\prime }}(x)\text{d}x-{\mathit{\lambda }}_k\sum _{j^{\prime }=1}^{R_i}\underset{t_i}{\overset{\infty }{\int }}x·b_{ki}^{(h-1)}(t_i)p_{i{j}^{\prime }}(x)\text{d}x\right]=\sum _{i=1}^N\sum _{k=1}^m\left[X_{i}ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)\mathrm{\Delta }{1}_{kij}^{(h-1)}+({\mathit{\alpha }}_k-1)X_i\mathrm{\Delta }{2}_{kij}^{(h-1)}-{\mathit{\lambda }}_k{X}_i\mathrm{\Delta }{3}_{kij}^{(h-1)}+R_i·ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)\mathrm{\Delta }{4}_{ki}^{(h-1)}+({\mathit{\alpha }}_k-1)R_i\mathrm{\Delta }{5}_{ki{j}^{\prime }}^{(h-1)}-{\mathit{\lambda }}_k{R}_i\mathrm{\Delta }{6}_{ki{j}^{\prime }}^{(h-1)}\right]=\sum _{i=1}^N\sum _{k=1}^m\left[(X_i\mathrm{\Delta }{1}_{kij}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)+({\mathit{\alpha }}_k-1)(X_i\mathrm{\Delta }{2}_{kij}^{(h-1)}+R_i\mathrm{\Delta }{5}_{ki{j}^{\prime }}^{(h-1)})-{\mathit{\lambda }}_k(X_i\mathrm{\Delta }{3}_{kij}^{(h-1)}+R_i\mathrm{\Delta }{6}_{ki{j}^{\prime }}^{(h-1)})\right]$$

where$$\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}=a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1}),\mathrm{\Delta }{2}_{kij}^{(h-1)}=\underset{t_{i-1}}{\overset{t_i}{\int }}ln(1-e^{-{\mathit{\lambda }}_{k}x})a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})p_{ij}(x)\text{d}x$$

$$\mathrm{\Delta }{3}_{kij}^{(h-1)}=\underset{t_{i-1}}{\overset{t_i}{\int }}x{a}_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})p_{ij}(x)\text{d}x,\mathrm{\Delta }{4}_{ki}^{(h-1)}=b_{ki}^{(h-1)}(t_i)$$$$\mathrm{\Delta }{5}_{ki{j}^{\prime }}^{(h-1)}=\underset{t_i}{\overset{\infty }{\int }}ln(1-e^{-{\mathit{\lambda }}_{k}x})b_{ki}^{(h-1)}(t_i)p_{i{j}^{\prime }}(x)\text{d}x,\mathrm{\Delta }{6}_{ki{j}^{\prime }}^{(h-1)}=\underset{t_i}{\overset{\infty }{\int }}x{b}_{ki}^{(h-1)}(t_i)p_{i{j}^{\prime }}(x)\text{d}x$$$$p_{ij}(x|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},Y)=\frac{\sum _{k=1}^m{p}_k^{(h-1)}{\mathit{\alpha }}_k^{(h-1)}{\mathit{\lambda }}_k^{(h-1)}{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}x})}^{{\mathit{\alpha }}_k^{(h-1)}-1}{e}^{-{\mathit{\lambda }}_k^{(h-1)}x}}{\sum _{k=1}^m{p}_k^{(h-1)}{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}{t}_i})}^{{\mathit{\alpha }}_k^{(h-1)}}-\sum _{k=1}^m{p}_k^{(h-1)}{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}{t}_{i-1}})}^{{\mathit{\alpha }}_k^{(h-1)}}},$$$$x\in (t_{i-1},t_i),\text{and}$$$$p_{i{j}^{\prime }}(x|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},Y)=\frac{\sum _{k=1}^m{p}_k^{(h-1)}{\mathit{\alpha }}_k^{(h-1)}{\mathit{\lambda }}_k^{(h-1)}{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}x})}^{{\mathit{\alpha }}_k^{(h-1)}-1}{e}^{-{\mathit{\lambda }}_k^{(h-1)}x}}{1-\sum _{k=1}^m{p}_k^{(h-1)}{(1-e^{-{\mathit{\lambda }}_k^{(h-1)}{t}_i})}^{{\mathit{\alpha }}_k^{(h-1)}}},$$$$x\in (t_i,+\infty ).$$

M-step: we maximize the approximate Q function numerically in E-step with respect to unknown parameters $P,\mathit{\alpha },\mathit{\lambda }$ to update estimates which are denoted as $P^{(h)},{\mathit{\alpha }}^{(h)},{\mathit{\lambda }}^{(h)}$.

In order to obtain the estimates of unknown parameters more conveniently in M-step, use $\tilde{\mathrm{\Delta }}{2}_{kij}^{(h-1)},\tilde{\mathrm{\Delta }}{5}_{ki{j}^{\prime }}^{(h-1)}$ instead of $\mathrm{\Delta }{2}_{kij}^{(h-1)},\mathrm{\Delta }{5}_{ki{j}^{\prime }}^{(h-1)}$, respectively. Here, $\tilde{\mathrm{\Delta }}{2}_{kij}^{(h-1)},\tilde{\mathrm{\Delta }}{5}_{ki{j}^{\prime }}^{(h-1)}$ have the following expressions:

$$\tilde{\mathrm{\Delta }}{2}_{kij}^{(h-1)}=\underset{t_{i-1}}{\overset{t_i}{\int }}ln(1-e^{-{\mathit{\lambda }}_k^{(h-1)}x})a_{k,i,i-1}^{(h-1)}(t_i,t_{i-1})p_{ij}(x)\text{d}x$$

$$\tilde{\mathrm{\Delta }}{5}_{ki{j}^{\prime }}^{(h-1)}=\underset{t_i}{\overset{\infty }{\int }}ln(1-e^{-{\mathit{\lambda }}_k^{(h-1)}x})b_{ki}^{(h-1)}(t_i)p_{i{j}^{\prime }}(x)\text{d}x$$

Then the above Q function is:

$$Q(P,\mathit{\alpha },\mathit{\lambda }|P^{(h-1)},{\mathit{\alpha }}^{(h-1)},{\mathit{\lambda }}^{(h-1)},Y)\approx \sum _{i=1}^N\sum _{k=1}^m\left[(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})ln(p_k{\mathit{\alpha }}_k{\mathit{\lambda }}_k)+({\mathit{\alpha }}_k-1)(X_i\tilde{\mathrm{\Delta }}{2}_{kij}^{(h-1)}+R_i\tilde{\mathrm{\Delta }}{5}_{ki{j}^{\prime }}^{(h-1)})-{\mathit{\lambda }}_k(X_i\mathrm{\Delta }{3}_{kij}^{(h-1)}+R_i\mathrm{\Delta }{6}_{ki{j}^{\prime }}^{(h-1)})\right]$$

Then, take the derivatives of unknown parameters and let(4.1) $$\frac{\mathit{\partial }Q}{\mathit{\partial }{\mathit{\alpha }}_k}\approx \sum _{i=1}^N\left[\frac{1}{{\mathit{\alpha }}_k}(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})+X_i\tilde{\mathrm{\Delta }}{2}_{kij}^{(h-1)}+R_i\tilde{\mathrm{\Delta }}{5}_{ki{j}^{\prime }}^{(h-1)}\right]=0k=1,\dots ,m$$(4.1) (4.2) $$\frac{\mathit{\partial }Q}{\mathit{\partial }{\mathit{\lambda }}_k}\approx \sum _{i=1}^N\left[\frac{1}{{\mathit{\lambda }}_k}(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})-(X_i\mathrm{\Delta }{3}_{kij}^{(h-1)}+R_i\mathrm{\Delta }{6}_{ki{j}^{\prime }}^{(h-1)})\right]=0k=1,\dots ,m$$(4.2) (4.3) $$\frac{\mathit{\partial }Q}{\mathit{\partial }{p}_k}=\frac{1}{p_k}\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})-\frac{1}{1-\sum _{j=1}^{m-1}{p}_j}\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{m,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{mi}^{(h-1)})=0k=1,\dots ,m-1.$$(4.3)

Solve the Equations (4.1) and (4.2), there are

(4.4) $${\widehat{\mathit{\alpha }}}_k^{(h)}\approx -\frac{\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})}{\sum _{i=1}^N(X_i\tilde{\mathrm{\Delta }}{2}_{kij}^{(h-1)}+R_i\tilde{\mathrm{\Delta }}{5}_{ki{j}^{\prime }}^{(h-1)})},k=1,\dots ,m$$(4.4)

(4.5) $${\widehat{\mathit{\lambda }}}_k^{(h)}\approx \frac{\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})}{\sum _{i=1}^N(X_i\mathrm{\Delta }{3}_{kij}^{(h-1)}+R_i\mathrm{\Delta }{6}_{ki{j}^{\prime }}^{(h-1)})},k=1,\dots ,m$$(4.5)

Solve the Equation (4.3), there is

$$p_k\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{m,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{mi}^{(h-1)})+\sum _{j=1}^{m-1}{p}_j·\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)})$$

(4.6) $$=\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{k,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{ki}^{(h-1)}),k=1,2,\dots ,m-1$$(4.6)

From Equation (4.6), obtain the h-th iteration values of parameters p₁, …, p_m−1 which are the solutions of the linear equation group denoted by AP = b, where P, A, b are given respectively as follows$$P={(p_1,p_2,\dots ,p_{m-1})}^T$$$$A_{m-1}=(a_{ls}),a_{ls}=\left\{\begin{array}{cc}\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{l,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{li}^{(h-1)})+\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{m,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{mi}^{(h-1)}),& l=s\\ \sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{l,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{li}^{(h-1)}),& l\ne s\end{array}\right.$$$$b={\left(\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{1,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{1i}^{(h-1)}),\cdots ,\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{m-1,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{m-1i}^{(h-1)})\right)}^T$$

Since $\sum _{i=1}^N(X_i\mathrm{\Delta }{1}_{l,i,i-1}^{(h-1)}+R_i\mathrm{\Delta }{4}_{li}^{(h-1)})>0,l=1,2,\dots ,m-1$, it is easy to testify that the rank of matrix A is m − 1, i.e. A is a invertible matrix. Therefore, the unique solution of parameter vector P of the h-th iteration in the M-step is obtained

(4.7) $${\widehat{p}}^{(h)}={(p_1^{(h)},p_2^{(h)},\dots ,p_{m-1}^{(h)})}^T=A^{-1}b$$(4.7)

From the above Equations (4.4), (4.5) and (4.7), we can update ${\widehat{P}}^{(h)},{\widehat{\mathit{\alpha }}}^{(h)},{\widehat{\mathit{\lambda }}}^{(h)}$ by repeating E-step and M-step till the total error of all estimated parameters approaches the supposed restraint.

5. Simulation study

The purpose of simulation study is to investigate the performance of the estimates for the MGED parameters in modeling progressive type-I interval censoring lifetime data. Here, we use some similar algorithm steps proposed in Aggarwala (2001). The simulation is conducted in R language. To be self-contained, the algorithm is re-produced as follows.

Firstly, generate the numbers, X_i, of failed items in each subinterval (t_i−1, t_i], i = 1, 2, …, N, from a sample of size n putting on life testing at time t_i = 0. A progressively type-I interval-censored data,(X_i, R_i, t_i), i = 1, 2, …, N, from MGED which has distribution (2.2) can be generated using the fact that(5.1) $$X_1\sim \text{Binom}[n,F(T_1)]$$(5.1)

and let X₀ = 0 and R₀ = 0 for i = 1, 2, …, N,

$$X_i|X_{i-1},\dots ,X_1,R_{i-1},\dots ,R_1$$

$$\sim r\text{Binom}\left[n-\sum _{j=1}^{i-1}(X_j+R_j),\frac{F(T_i)-F(T_{i-1})}{1-{\sum }_{j=1}^{i-1}[F(T_j)-F(T_{j-1})]}\right]$$

(5.2) $$=r\text{Binom}\left[n-\sum _{j=1}^{i-1}(X_i+R_i),\frac{F(T_i)-F(T_{i-1})}{1-F(T_{i-1})}\right]$$(5.2)

(5.3) $$R_i=floor\left[p_i^{\prime }\times \left(n-\sum _{j=1}^{i-1}(X_j+R_j)-X_i\right)\right]$$(5.3)

where floor() returns the largest integer not greater than the argument in R language and 0 = t₀ < t₁ < ⋯ < t_N < ∞ are pre-scheduled times.

In this paper, we just consider the MGED model with two components under the progressive type-I interval censoring scheme. Suppose that the true values of model parameters are $p_1=0.6,{\mathit{\alpha }}_1=0.9,{\mathit{\lambda }}_1=0.13,{\mathit{\alpha }}_2=1,{\mathit{\lambda }}_2=1.3$, while the initial values are taken as $p_1^{(0)}=0.4,{\mathit{\alpha }}_1^{(0)}=0.8$, ${\mathit{\lambda }}_1^{(0)}=0.1,{\mathit{\alpha }}_2^{(0)}=0.9,{\mathit{\lambda }}_2^{(0)}=1$. Each replication of the simulation generates a progressively type-I interval-censored data of size n = 60, 120, 180, 300, 500 with N = 10, pre-specified inspection times t₁ = 1, t₂ = 2, t₃ = 3, t₄ = 4, t₅ = 5, t₆ = 6, t₇ = 7, t₈ = 8, t₉ = 9 and t₁₀ = 10 and t₁₀ = 10 as the time to terminate the experiment.

In this paper, we consider the following progressive interval censoring

Schemes:

Scheme 1: $p_{(1)}^{\prime }=(0.05,0.05,0.05,0.05,0.1,0.1,0.1,0.1,0.1,1)$

Scheme 2: $p_{(2)}^{\prime }=(0.05,0.05,0.05,0.05,0.1,0.1,0,0,0,1)$

Scheme 3: $p_{(3)}^{\prime }=(0,0,0,0.1,0.05,0.1,0.15,0.05,0.05,1)$

Scheme 4: $p_{(4)}^{\prime }=(0,0,0,0,0,0,0,0,0,1)$

where censoring in $p_{(1)}^{\prime }$ in lighter for the first four intervals and heavier for the next five intervals. The censoring pattern is reversed in $p_{(2)}^{\prime }$. $p_{(3)}^{\prime }$ is no censoring in the first three interval and then some censoring afterwards. $p_{(4)}^{\prime }$ is the conventional interval censoring where no removals prior to the experiment termination.

Repeat the simulation experiments 1,000 times for the sample sizes n = 60, 120, 180, 300, 500. Denote the h-th estimates as ${\mathrm{\Theta }}^{(h)}=(p_1^{(h)},{\mathit{\alpha }}_1^{(h)},{\mathit{\lambda }}_1^{(h)},{\mathit{\alpha }}_2^{(h)},{\mathit{\lambda }}_2^{(h)}),$ h = 1, …, s, s = 1,000. The final average bias and mean square errors (MSEs) of the estimates are given respectively as $\text{Bias}({\mathit{\theta }}_j)=(1/s){\sum }_{h=1}^s({\widehat{\mathit{\theta }}}_j^{(h)}-{\mathit{\theta }}_j)$ and $\text{MSE}({\mathit{\theta }}_j)=(1/s){\sum }_{h=1}^s{({\widehat{\mathit{\theta }}}_j-{\mathit{\theta }}_j)}^2$, where ${\widehat{\mathit{\theta }}}_j$ is the j-th coordinate of the unknown parameter vector Θ. The computation results for four different censoring schemes are illustrated in Tables 1–4, respectively.

Table 1. Average biases, MSE(s) of estimators for scheme 1 when the sample sizes are n = 60, 120, 180, 300, 500

n		${\widehat{p}}_1$	${\widehat{\mathit{\alpha }}}_1$	${\widehat{\mathit{\lambda }}}_1$	${\widehat{\mathit{\alpha }}}_2$	${\widehat{\mathit{\lambda }}}_2$
60	Bias	−0.0598	0.0293	−0.0384	0.0597	0.1282
	MSE	0.0237	0.0029	0.0046	0.0054	0.1485
120	Bias	−0.0942	0.0507	−0.0483	0.0738	0.1209
	MSE	0.0197	0.0034	0.0042	0.0061	0.0802
180	Bias	−0.1083	0.0598	−0.0527	0.0793	0.1283
	MSE	0.0189	0.0041	0.0038	0.0067	0.0575
300	Bias	−0.1148	0.0623	−0.0539	0.0819	0.1339
	MSE	0.0177	0.0042	0.0037	0.0069	0.0423
500	Bias	−0.1169	0.0666	−0.0559	0.0836	0.1310
	MSE	0.0163	0.0046	0.0036	0.0071	0.0327

Table 2. Average biases, MSE(s) of estimators for scheme 2 when the sample sizes are n = 60, 120, 180, 300, 500

n		${\widehat{p}}_1$	${\widehat{\mathit{\alpha }}}_1$	${\widehat{\mathit{\lambda }}}_1$	${\widehat{\mathit{\alpha }}}_2$	${\widehat{\mathit{\lambda }}}_2$
60	Bias	−0.0899	0.0363	−0.0427	0.0654	0.1428
	MSE	0.0015	0.0002	0.0002	0.0029	0.0098
120	Bias	−0.0791	0.0459	−0.0472	0.0716	0.1371
	MSE	0.0008	0.0002	0.0002	0.0003	0.0040
180	Bias	−0.1091	0.0613	−0.0554	0.0780	0.1507
	MSE	0.0009	0.0002	0.0002	0.0003	0.0025
300	Bias	−0.1096	0.0681	−0.0557	0.0825	0.1034
	MSE	0.0008	0.0002	0.0002	0.0004	0.0012
500	Bias	−0.1126	0.0660	−0.0498	0.08726	0.1505
	MSE	0.0007	0.0002	0.0001	0.0004	0.0019

Table 3. Average biases, MSE(s) of estimators for scheme 3 when the sample sizes are n = 60, 120, 180, 300, 500

n		${\widehat{p}}_1$	${\widehat{\mathit{\alpha }}}_1$	${\widehat{\mathit{\lambda }}}_1$	${\widehat{\mathit{\alpha }}}_2$	${\widehat{\mathit{\lambda }}}_2$
60	Bias	−0.0106	−0.0156	−0.0205	−0.0180	0.0406
	MSE	0.0209	0.0033	0.0032	0.0016	0.1572
120	Bias	−0.0217	−0.0055	−0.0230	−0.0148	0.0504
	MSE	0.0109	0.0017	0.0021	0.0007	0.0904
180	Bias	−0.0314	−0.0008	−0.0245	−0.0135	0.0433
	MSE	0.0085	0.0011	0.0016	0.0005	0.0583
300	Bias	−0.0319	0.0004	−0.0255	−0.0132	0.0563
	MSE	0.0058	0.0007	0.0013	0.0003	0.0382
500	Bias	−0.0322	0.0020	−0.0252	−0.0126	0.0653
	MSE	0.0036	0.0004	0.0009	0.0003	0.2480

Table 4. Average biases, MSE(s) of estimators for scheme 4 when the sample sizes are n = 60, 120, 180, 300, 500

n		${\widehat{p}}_1$	${\widehat{\mathit{\alpha }}}_1$	${\widehat{\mathit{\lambda }}}_1$	${\widehat{\mathit{\alpha }}}_2$	${\widehat{\mathit{\lambda }}}_2$
60	Bias	−0.0018	−0.0198	−0.0171	−0.0276	0.0231
	MSE	0.0209	0.0043	0.0032	0.0025	0.1468
120	Bias	−0.0096	−0.0113	−0.0169	−0.0250	0.0553
	MSE	0.0112	0.0022	0.0016	0.0011	0.0839
180	Bias	−0.0155	−0.0062	−0.0191	−0.0229	0.0542
	MSE	0.0070	0.0013	0.0012	0.0008	0.0594
300	Bias	−0.0164	−0.0028	−0.0190	−0.0203	0.0708
	MSE	0.0048	0.0009	0.0008	0.0006	0.0365
500	Bias	−0.0203	−0.0007	−0.0200	−0.0192	0.0694
	MSE	0.0029	0.0005	0.0007	0.0005	0.0247

From Tables 1–4, we can see that the EM algorithm is very effective in dealing with parameter estimation of the MGED for the given four sampling schemes under the progressive type-I interval censoring. The number of the specified inspection is fixed. For the given one scheme, it is obvious that the simulation results are changed as n increases, but the range is very small. It is easy to understand the phenomenon that the estimation of the unknown parameters is biased slightly when the number of the items withdrawn from the experiment is increasing. It is obvious that the simulation results are mainly decided by the sample size n and the censoring proportion. For different censoring schemes, the smaller censoring proportion we design in life testing, the better estimation results we will get. Therefore, the scheme 4 presents the most precise estimation. Further, for fixed N as n increases, on the whole, the biases, the MSEs decrease.

6. Data analysis

In order to illustrate the effectiveness of the model and algorithm, we analyze a real data-set bellow. A data-set which describe the survival times for surgery of a group of 374 patients who underwent operations in connection with a type of malignant disease (Berkson & Gage, 1950; Lawless, 2003). The data are given in Table 5.

Table 5. Survival time in interval form for the patients who underwent operations in connection with a type of malignant disease

Interval	dj	Ri
[0, 1)	90	0
[1, 2)	76	0
[2, 3)	51	0
[3, 4)	25	12
[4, 5)	20	5
[5, 6)	7	9
[6, 7)	4	9
[7, 8)	1	3
[8, 9)	3	5
[9, 10)	2	5
[10, ∞)	47	0

According to the data above, d_js in the first five intervals are significantly different with the last intervals and think that the data may not come from the homogenous population. Thus, consider two components of the MGED (1.1) to analyze this data-set. Through the method discussed above, we can obtain that the parameter estimates are ${\widehat{p}}_1=0.4213$, ${\widehat{\mathit{\alpha }}}_1=0.9216$, ${\widehat{\mathit{\lambda }}}_1=0.0886$, ${\widehat{\mathit{\alpha }}}_2=0.9118$, ${\widehat{\mathit{\lambda }}}_2=0.4017$, respectively. And the survival function and the hazard rate function of the model (1.1) are as follow:(6.1) $$\widehat{S}(x)=1-[0.4213\times {(1-e^{-0.0886x})}^{0.9216}+0.5787\times {(1-e^{-0.4017x})}^{0.9118}],x\ge 0$$(6.1) (6.2) $$\widehat{h}(x)=\frac{0.0344\times {(1-e^{-0.0886x})}^{-0.0784}{e}^{-0.0886x}+0.2119\times {(1-e^{-0.4017x})}^{-0.0882}{e}^{-0.4017x}}{1-[0.4213\times {(1-e^{-0.0886x})}^{0.9216}+0.5787\times {(1-e^{-0.4017x})}^{0.9118}]},x\ge 0$$(6.2)

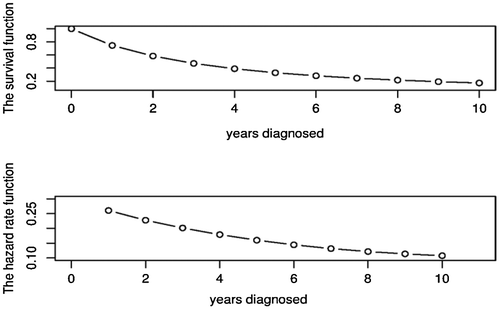
From (6.1) and (6.2), we can get the fitted survival function and hazard rate function of the real data as in Figure 1. For Figure 1, the hazard rate function is monotone decreasing function. There is great change in the first few years and then tends to be gentle after eight years. Therefore, for this disease, the risk rate of patients after operation in the short time is higher. In order to avoid the recurrence in the recovery stage after the operation, we suggest to check regularly.

Figure 1. The fitted survival function and hazard rate function of the real data.

In order check the validity of the model, we adopt the Kolmogorov-Smirnov goodness-of-fit test statistic for the fitted distribution $\widehat{F}(x)$. Define the maximum distance in Kolmogorov-Smirnov goodness-of-fit test:

(6.3) $$D_n(F)=\underset{0\le x<\infty }{sup}|{\widehat{F}}_n(x)-F(x|\widehat{\mathit{\theta }})|,$$(6.3)

as the distance between the empirical distribution ${\widehat{F}}_n(x)$, of the given complete data-set and the fitted distribution function $F(x|\widehat{\mathit{\theta }})$ with $\widehat{\mathit{\theta }}$ as the MLE of unknown parameter vector θ. When a progressively type-I interval-censored data are given, the empirical distribution is replaced by the following (6.4) in the formula D_n(F).(6.4) $$\widehat{F}(x_i)=1-\prod _{j=1}^i(1-{\widehat{p}}_j),i=1,\dots ,N$$(6.4)

where ${\widehat{p}}_j=\frac{d_j}{n-{\sum }_{k=0}^{j-1}{d}_k-{\sum }_{k=0}^{j-1}{R}_k},j=1,\dots ,N.$

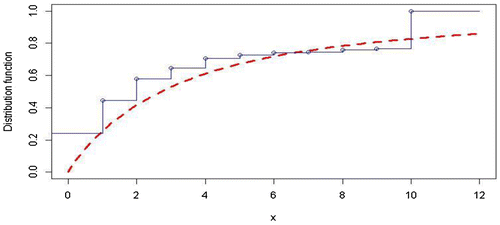
Fit the data-set in Table 5, we obtain the K-S distance 0.2406. So it is reasonable to say that the MGED provides a good fit for the given data-set in Table 5. Figure 2 is given to compare the empirical distribution function with the fitted distribution function.

Figure 2. The empirical and fitted distribution function.

Note: Fold line represents the empirical distribution function, dotted line represents the fitted distribution function.

7. Conclusion and remarks

This article considers the estimation of parameters based on a progressively type-I interval-censored data from a MGED. Because the data in this paper are not complete, the EM algorithm is used to obtain the maximum likelihood estimates. Then the performance of the estimates is presented by a simulating study in different setups and gets effective results. Lastly, a surgery data of a group of 374 patients who underwent operations in connection with a type of malignant disease are presented to illustrate the method of estimation developed here.

Additional information

Funding

This research was partially supported by National Science Foundation of China (NSFC) [grant numbers 11301037, 11671054 and 11571051] and The Education Department of Jilin Province, "13th Five-Year" project planning 2016317.

Notes on contributors

Chunjie Wang

Chunjie Wang obtained her PhD degree in Probability and Mathematics Statistics from the School of Mathematics, Jilin University, Changchun, China. She is currently working in Changchun University of Technology (CCUT), Changchun, China, as an associate professor. Her research interests include Survival analysis, Mathematical Statistics.

Shuying Wang

Shuying Wang is currently doing her PhD from Jilin University, Changchun, China. Her research interests include Mathematical Statistics and Survival analysis.

Dehui Wang

Dehui Wang is currently working as professor in the School of Mathematics in Jilin University, Changchun, China. His research interests include Mathematical Statistics, Time Series, and Survival Analysis.

Chunjing Li

Chunjie Li is currently doing her PhD from Jilin University, Changchun, China. Her research interests include Mathematical Statistics and Survival Analysis.

Xiaogang Dong

Xiaogang Dong obtained his PhD degree in Statistics from Jilin University, Changchun, China. He is currently working in Changchun University of Technology (CCUT), Changchun, China, as a professor. His research interests include High frequency data analysis, Survival analysis, Mathematical Statistics, and Applied Statistics.