The improved F-expansion method with Riccati equation and its applications in mathematical physics

Abstract

The improved F-expansion method combined with Riccati equation is one of the most effective analytical methods in finding the exact traveling wave solutions to non-linear evolution equations in mathematical physics. In this article, this method is implemented to investigate new exact solutions to the Drinfel’d–Sokolov–Wilson (DSW) equation and the Burgers equation. The performance of this method is reliable, direct, and simple to execute compared to other existing methods. The obtained solutions in this work are imperative and significant for the explanation of some practical physical phenomena.

Keywords:

• improved F-expansion method
• DSW equation
• Burgers equation
• exact solution
• non-linear evolution equations

AMS subject classifications:

• 35C07
• 35C08
• 35P99
• 5K05

Public Interest Statement

The modeling of most of the real world phenomena leads to non-linear evolution equations (NLEEs). For better understanding the intricate phenomena, closed form solutions play a vital role. Therefore, diverse group of researchers developed and extended different methods to examine closed form solutions to NLEEs. In this article, we use the improved F-expansion method combined with Riccati equation to investigate closed form wave solutions to the Drinfel’d–Sokolov–Wilson (DSW) equation and the Burgers equation. Thus, we obtain abundant closed form wave solutions of these two equations among them some are new solutions. We expect that the new closed form solutions will be helpful to elucidate the associated phenomena.

1. Introduction

In the field of non-linear science, the investigation of the traveling wave solutions to non-linear evolution equations (NLEEs) plays a significant role in several aspects of mathematical and physical phenomena. Non-linear wave phenomena appear in various scientific and engineering fields such as fluid mechanics, meteorology, optical fibers, biology, solid state physics, chemical kinematics, chemical physics, and geochemistry. Non-linear wave phenomena of dispersion, dissipation, diffusion, reaction, and convection are very significant in non-linear wave equations. Therefore, finding exact solutions to NLEEs has long been one of the most essential areas of research in mathematics and physics. With the development of symbolic computation software like Maple and Mathematica, diverse group of researchers have established many powerful and effective methods in finding analytical and numerical solutions of non-linear equations. The exact solutions of the non-linear equations facilitate the verification of the numerical solvers and aid in the stability analysis of the solutions.

A significant number of methods for the solution of partial differential equations (PDEs) have been established over the last three decades from both theoretical and practical points of view. Improvements in numerical techniques, combine with the advancement of computer technology have meant that many of the PDEs arising from engineering and scientific applications, which were previously intractable, can now be easily solved (Wang, Li, & Zhang, 2008). In the last several decades a wide range of methods have been developed to construct traveling solutions to NLEEs such as, the homogeneous balance method (Wang, 1996; Wang, Zhou, & Li, 1996), the auxiliary equation method (Sirendaoreji, 2003; Zhang & Xia, 2007), the Exp-function method (Wu & He, 2007, 2008), the Darboux transformation method (Hu, Tang, Lou, & Liu, 2004; Leble & Ustinov, 1993), the tanh-function method (Abdusalam, 2005), the modified extended tanh-function method (Lee & Sakthivel, 2011), the Jacobi elliptic function method (Liu, Fu, Liu, & Zhao, 2001; Parkes, Duffy, & Abbott, 2002), the first integral method (Abbasbandy & Shirzadi, 2010; Bekir & Ünsal, 2012), the modified simple equation method (Jawad, Petkovic, & Biswas, 2010; Khan & Akbar, 2013a, 2014), the $(G^{\prime }/G)$-expansion method (Islam, Khan, Akbar, & Islam, 2013; Khan & Akbar, 2014a; Kim & Sakthivel, 2012; Wang et al., 2008), the homotopy perturbation method (Changbum & Rathinasamy, 2010; Mohyud-Din, 2007; Mohyud-Din & Noor, 2009; Mohyud-Din, Yildrim, & Sariaydin, 2010; Rathinasamy, Changbum, & Jonu, 2010), the $exp(-\mathit{\Phi }(\mathit{\xi }))$-expansion method (Khan & Akbar, 2013b), the variational iteration method (Molliq, Noorani, & Hashim, 2009) and the F-expansion method (Hua, 2006; Islam, Khan, Akbar, & Mastroberardino, 2014; Zhao, 2013) etc.

The objective of this article is to implement the improved F-expansion method in constructing the traveling wave solutions to NLEEs in the mathematical physics via the DSW equation and the Burgers equation in terms of functions that satisfy the Riccati equation $F^{\prime }(\mathit{\xi })=k+F^2(\mathit{\xi })$.

The Burgers equation is the lowest order approximation for the one-dimensional propagation of weak waves in a fluid. It is also used in vehicle density in high way traffic. It is one of the fundamental PDEs in fluid mechanics. Burgers equation is completely integrable. The wave solutions of Burgers equation are single and multiple-front solutions (Wazwaz, 2009). The DSW equation is an important wave model in physics (Inc, 2006).

The organization of this article is as follows: In Section 2, we will illustrate the improved F-expansion method in detail. In Section 3, the improved F-expansion method is applied to search for the many exact solutions of the DSW equations and the Burgers equation. In Section 4, explanation and graphical representation of some of the attained solutions will be discussed. In Section 5, we include the comparison and conclusions are given in Section 6.

2. The improved F-expansion method

In this section, we describe the improved F-expansion method ornately for seeking the exact traveling wave solutions to NLEEs.

Let us consider a general non-linear evolution equation in the form,(1) $$P(u,u_x,u_y,u_t,u_{xx},u_{xy},u_{xt},\dots )=0,$$(1)

where $u=u(x,y,t)$ is an unknown function, P is a polynomial of $u(x,y,t)$ and its partial derivatives in which the highest order partial derivatives and the non-linear terms are involved and the subscripts stands for the partial derivatives.

We introduce the leading steps of the method as follows:

Step-1: In the first step, we make known the traveling wave transformation,(2) $$u(x,t)=u(\mathit{\xi })\mathit{\xi }=x+y\pm \mathit{\lambda }t,$$(2)

where $\mathit{\lambda }\in \Re -\{0\}$ is the celerity of the traveling wave. The traveling wave transformation (2), transforms Equation (1) into an ordinary differential equation (ODE) for $u=u(\mathit{\xi })$:(3) $$Q(u,u^{\prime },u^{″},u^{‴},\dots )=0,$$(3)

where Q is a polynomial of u and its derivatives and the superscripts indicate the ordinary derivatives with respect to ξ.

Step-2: Equation (3) can possibly be integrated term by term one or more times, to yield constants of integration. The integral constant may be zero for straightforwardness.

Step-3: We assume the traveling wave solution of Equation (3) can be expressed by a polynomial in $F\left(\mathit{\xi }\right)$ as follows:(4) $$u(\mathit{\xi })=\sum _{i=0}^N{\mathit{\alpha }}_i{\left(m+F(\mathit{\xi })\right)}^i+\sum _{i=1}^N{\mathit{\beta }}_i{\left(m+F(\mathit{\xi })\right)}^{-i},$$(4)

where either α_N or β_N may be zero, but both of them could not be zero at time, ${\mathit{\alpha }}_i(i=0,1,2,\dots ,N)$ and ${\mathit{\beta }}_i(i=0,1,2,\dots ,N)$ and m are arbitrary constants to be determined later.

We consider the well-known Riccati equation(5) $$F^{\prime }(\mathit{\xi })=k+F^2(\mathit{\xi }),$$(5)

where the prime stands for derivatives with respect to ξ; k is the real parameter.

We now represent the three cases of the general solution of the Riccati equation (5) as follows:

Case-I: When k < 0, the general solutions are:$$F_1=-\sqrt{-k}tanh(\sqrt{-k}\mathit{\xi }),$$$$F_2=-\sqrt{-k}coth(\sqrt{-k}\mathit{\xi }).$$

Case-II: When k > 0, the general solutions are:$$F_4=\sqrt{k}tan(\sqrt{k}\mathit{\xi }),$$$$F_5=-\sqrt{k}cot(\sqrt{k}\mathit{\xi }).$$

Case-III: When k = 0, the general solution is:$$F_3=-\frac{1}{\mathit{\xi }}$$

Step-4: The positive integer Nis usually obtained by taking the homogeneous balance between the highest order non-linear terms and the derivatives of the highest order appearing in (3). If the degree of u(ξ) is D[u(ξ)] = N, then the degree of the other expressions will be as follows:(6) $$D\left[\frac{d^{p}u(\mathit{\xi })}{d{\mathit{\xi }}^p}\right]=N+p,D\left[u^p{\left(\frac{d^{q}u(\mathit{\xi })}{d{\mathit{\xi }}^q}\right)}^s\right]=Np+s(N+p).$$(6)

Therefore, we can find the value of N from (4), using Equation (6).

Step-5: Substituting (4) including with Equation (5) into Equation (3) together with the value of Nattained in step 3, we get a polynomials in ${(m+F)}^i$ and ${(m+F)}^{-i}(i=1,2,3,\dots N)$, then collect each coefficient of the resulted polynomial to zero, yields an over-determined set of algebraic equations for α_N, β_N, m and $\mathit{\lambda }$.

Step-6: Suppose the value of the constants ${\mathit{\alpha }}_N,{\mathit{\beta }}_N,m$ and $\mathit{\lambda }$ can be determined by solving the algebraic equations attained in step 4. Since the general solution of Equation (5) is well known to us, inserting the value of ${\mathit{\alpha }}_N,{\mathit{\beta }}_N,m$ and $\mathit{\lambda }$ into Equation (4), we attain more general type and new exact traveling wave solutions of the non-linear partial differential Equation (1).

3. Applications

In this section, we will make use of the improved F-expansion method to find the exact traveling wave solution to the DSW equations and the Burgers equation.

Example 3.1

The Drinfel’d–Sokolov–Wilson (DSW) equation

Let us consider the Drinfel’–-Sokolov–Wilson (DSW) (Khan, Akbar, & Nur Alam, 2013) equation in the form:(7) $$\begin{array}{c}{u}_t+pv{v}_x=0,\hfill \\ v_t+q{v}_{xxx}+ru{v}_x+s{u}_{x}v=0,\hfill \end{array}$$(7)

where $p,q,r$ and s are real parameters. This equation was introduced as an important wave model in physics.

We utilize the traveling wave variable $u(\mathit{\xi })=u(x,t),v(\mathit{\xi })=v(x,t),\mathit{\xi }=x+\mathit{\lambda }t$ to transform the PDE (7) into the ODE,(8) $$\mathit{\lambda }{u}^{\prime }+pv{v}^{\prime }=0,$$(8) (9) $$\mathit{\lambda }{v}^{\prime }+q{v}^{‴}+ru{v}^{\prime }+s{u}^{\prime }v=0,$$(9)

where by integrating Equation (8) with respect to ξ once and neglecting the constant of integration, we obtain(10) $$u=-\frac{p{v}^2}{2\mathit{\lambda }}.$$(10)

Inserting Equation (9) into Equation (8. 2), we obtain(11) $$2\mathit{\lambda }q{v}^{‴}+2{\mathit{\lambda }}^2{v}^{\prime }-p(r+2s)v^2{v}^{\prime }=0$$(11)

Integrating Equation (11) with respect to ξ once and setting the constant of integration to zero, we obtain(12) $$2\mathit{\lambda }q{v}^{″}+2{\mathit{\lambda }}^{2}v-\frac{p(r+2s)v^3}{3}=0$$(12)

Taking the homogeneous balance between the highest order non-linear term u³ and the derivative term u″ from Equation (12), yields 3 N = N + 2, which gives N = 1.

Hence for N = 1, Equation (4) reduces to(13) $$u(\mathit{\xi })={\mathit{\alpha }}_0+{\mathit{\alpha }}_1(m+F(\mathit{\xi }))+{\mathit{\beta }}_1{(m+F(\mathit{\xi }))}^{-1}.$$(13)

Now substituting (13) including Equation (5) into Equation (12), we get a polynomial in $F(\mathit{\xi })$. Equating the coefficient of the same power of $F(\mathit{\xi })$, we attain the following system of algebraic equations:$$-12q\mathit{\lambda }{\mathit{\alpha }}_1+pr{\mathit{\alpha }}_1^2+2ps{\mathit{\alpha }}_1^2=0$$$$-36q\mathit{\lambda }{\mathit{\alpha }}_{1}m+6pr{\mathit{\alpha }}_1^{3}m+6ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2+12ps{\mathit{\alpha }}_1^{3}m+3pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2=0$$$$-12q\mathit{\lambda }{\mathit{\alpha }}_{1}k+6ps{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1+3pr{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1+30ps{\mathit{\alpha }}_1^3{m}^2+30ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1^{2}m+15pr{\mathit{\alpha }}_1^3{m}^2+15pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1^{2}m+3pr{\mathit{\alpha }}_1^2{\mathit{\beta }}_1-36q\mathit{\lambda }{\mathit{\alpha }}_1{m}^2+6ps{\mathit{\alpha }}_1^3{\mathit{\beta }}_1-6{\mathit{\lambda }}^2{\mathit{\alpha }}_1=0$$$$12pr{\mathit{\alpha }}_1^2{\mathit{\beta }}_{1}m+30pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^2+24ps{\mathit{\alpha }}_0^2{\mathit{\alpha }}_{1}m+24ps{\mathit{\alpha }}_1^2{\mathit{\beta }}_{1}m-24{\mathit{\lambda }}^2{\mathit{\alpha }}_{1}m-6{\mathit{\lambda }}^2{\mathit{\alpha }}_0+12ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1{\mathit{\beta }}_1+60ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^2+20pr{\mathit{\alpha }}_1^3{m}^3-36q\mathit{\lambda }{\mathit{\alpha }}_{1}km+12q\mathit{\lambda }{\mathit{\beta }}_{1}m-12q\mathit{\lambda }{\mathit{\alpha }}_1{m}^3+12pr{\mathit{\alpha }}_0^2{\mathit{\alpha }}_{1}m+6pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1{\mathit{\beta }}_1+40ps{\mathit{\alpha }}_1^3{m}^3+2ps{\mathit{\alpha }}_0^3+pr{\mathit{\alpha }}_0^3=0$$$$30pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^3-36q\mathit{\lambda }{\mathit{\alpha }}_{1}k{m}^2+36ps{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1{m}^2+18pr{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1{m}^2+3pr{\mathit{\alpha }}_0^2{\mathit{\beta }}_1+15pr{\mathit{\alpha }}_1^3{m}^4-6{\mathit{\lambda }}^2{\mathit{\beta }}_1+3pr{\mathit{\alpha }}_1{\mathit{\beta }}_1^2+36ps{\mathit{\alpha }}_0{\mathit{\alpha }}_{1}m{\mathit{\beta }}_1-18{\mathit{\lambda }}^2{\mathit{\alpha }}_{0}m+3pr{\mathit{\alpha }}_0^{3}m+6ps{\mathit{\alpha }}_1{\mathit{\beta }}_1^2-36{\mathit{\lambda }}^2{\mathit{\alpha }}_1{m}^2+6ps{\mathit{\alpha }}_0^{3}m+36ps{\mathit{\alpha }}_1^2{m}^2{\mathit{\beta }}_1+18pr{\mathit{\alpha }}_1^2{m}^2{\mathit{\beta }}_1+60ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^3+6ps{\mathit{\alpha }}_0^2{\mathit{\beta }}_1+30ps{\mathit{\alpha }}_1^3{m}^4+18pr{\mathit{\alpha }}_0{\mathit{\alpha }}_{1}m{\mathit{\beta }}_1-12q\mathit{\lambda }{\mathit{\beta }}_{1}k=0$$$$36ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1{\mathit{\beta }}_1{m}^2-12{\mathit{\lambda }}^2{\mathit{\beta }}_{1}m+3pr{\mathit{\alpha }}_0{\mathit{\beta }}_1^2+12ps{\mathit{\alpha }}_1^3{m}^5-18{\mathit{\lambda }}^2{\mathit{\alpha }}_0{m}^2+15pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^4+30ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^4+12ps{\mathit{\alpha }}_{1}m{\mathit{\beta }}_1^2-12q\mathit{\lambda }{\mathit{\alpha }}_{1}k{m}^3+6ps{\mathit{\alpha }}_0^3{m}^2+6ps{\mathit{\alpha }}_0{\mathit{\beta }}_1^2-24{\mathit{\lambda }}^2{\mathit{\alpha }}_1{m}^3+12ps{\mathit{\alpha }}_0^2{\mathit{\beta }}_{1}m+6pr{\mathit{\alpha }}_{1}m{\mathit{\beta }}_1^2+24ps{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1{m}^3+3pr{\mathit{\alpha }}_0^3{m}^2+18pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1{\mathit{\beta }}_1{m}^2+12pr{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1{m}^3+24ps{\mathit{\alpha }}_1^2{m}^3{\mathit{\beta }}_1+6pr{\mathit{\alpha }}_0^2{\mathit{\beta }}_{1}m+6pr{\mathit{\alpha }}_1^3{m}^5+12pr{\mathit{\alpha }}_1^2{m}^3{\mathit{\beta }}_1+12q\mathit{\lambda }{\mathit{\beta }}_{1}km=0$$$$-12q\mathit{\lambda }{\mathit{\beta }}_1{k}^2+pr{\mathit{\alpha }}_1^3{m}^6+2ps{\mathit{\alpha }}_1^3{m}^6+pr{\mathit{\beta }}_1^3+2ps{\mathit{\beta }}_1^3+6ps{\mathit{\alpha }}_1^2{m}^4{\mathit{\beta }}_1+6ps{\mathit{\alpha }}_1{m}^2{\mathit{\beta }}_1^2+3pr{\mathit{\alpha }}_1^2{m}^4{\mathit{\beta }}_1+3pr{\mathit{\alpha }}_1{m}^2{\mathit{\beta }}_1^2+3pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^5+3pr{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1{m}^4+6ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1^2{m}^5+6ps{\mathit{\alpha }}_0^2{\mathit{\alpha }}_1{m}^4+3pr{\mathit{\alpha }}_0{\mathit{\beta }}_1^{2}m+3pr{\mathit{\alpha }}_0^2{\mathit{\beta }}_1{m}^2+6ps{\mathit{\alpha }}_0{\mathit{\beta }}_1^{2}m+6ps{\mathit{\alpha }}_0^2{\mathit{\beta }}_1{m}^2-6{\mathit{\lambda }}^2{\mathit{\alpha }}_0{m}^3-6{\mathit{\lambda }}^2{\mathit{\beta }}_1{m}^2-6{\mathit{\lambda }}^2{\mathit{\alpha }}_1{m}^4+6pr{\mathit{\alpha }}_0{\mathit{\alpha }}_1{m}^3{\mathit{\beta }}_1+12ps{\mathit{\alpha }}_0{\mathit{\alpha }}_1{m}^3{\mathit{\beta }}_1+2ps{\mathit{\alpha }}_0^3{m}^3+pr{\mathit{\alpha }}_0^3{m}^3=0$$

From the above system of equations, we get the values of ${\mathit{\alpha }}_0,{\mathit{\alpha }}_1,{\mathit{\beta }}_1,m$ and $\mathit{\lambda }$:

Set-01: $m=0,\mathit{\lambda }=-2qk,{\mathit{\alpha }}_0=0,{\mathit{\alpha }}_1=0,{\mathit{\beta }}_1=\pm \frac{2I\sqrt{6}q{k}^{\frac{3}{2}}}{\sqrt{p(r+2s)}}.$

Set-02: $m=m,\mathit{\lambda }=-2qk,{\mathit{\alpha }}_0=\mp \frac{2\sqrt{-6k}qm}{\sqrt{p(r+2s)}},{\mathit{\alpha }}_1=\pm \frac{2\sqrt{-6k}q}{\sqrt{p(r+2s)}},{\mathit{\beta }}_1=0.$

Set-03: $m=0,\mathit{\lambda }=-8qk,{\mathit{\alpha }}_0=0,{\mathit{\alpha }}_1=\pm \frac{4\sqrt{-6k}q}{\sqrt{p(r+2s)}},{\mathit{\beta }}_1=\mp \frac{4I\sqrt{6}q{k}^{\frac{3}{2}}}{\sqrt{p(r+2s)}}.$

Set-04: $m=0,\mathit{\lambda }=4qk,{\mathit{\alpha }}_0=0,{\mathit{\alpha }}_1=\pm \frac{4\sqrt{3k}q}{\sqrt{p(r+2s)}},{\mathit{\beta }}_1=\pm \frac{4\sqrt{3}q{k}^{\frac{3}{2}}}{\sqrt{p(r+2s)}}.$

Set-05: $m=\pm \frac{1}{12}\frac{I\sqrt{6p(r+2s)}{\mathit{\alpha }}_0}{q\sqrt{k}},\mathit{\lambda }=-2qk,{\mathit{\alpha }}_0={\mathit{\alpha }}_0,{\mathit{\alpha }}_1=0,$$${\mathit{\beta }}_1=\mp \frac{1}{2}\frac{24k^2{q}^2-2ps{\mathit{\alpha }}_0^2-pr{\mathit{\alpha }}_0^2}{q\sqrt{-6kp(r+2s)}}.$$

Case-I: when k < 0, we get the following solutions in terms of hyperbolic functions:

Family-01: $v_{1,2}(\mathit{\xi })=\mp \frac{2\sqrt{6}qk}{\sqrt{p(r+2s)}}coth(\sqrt{-k}\mathit{\xi }),$$$u_1(\mathit{\xi })=\frac{6qk}{(r+2s)}{coth}^2(\sqrt{-k}\mathit{\xi }),$$$$v_{3,4}(\mathit{\xi })=\mp \frac{2\sqrt{6}qk}{\sqrt{p(r+2s)}}tanh(\sqrt{-k}\mathit{\xi }),$$$$u_2(\mathit{\xi })=\frac{6qk}{(r+2s)}{tanh}^2(\sqrt{-k}\mathit{\xi }),$$

where $\mathit{\xi }=x-2qkt.$

Family-02: $v_{5,6}(\mathit{\xi })=\pm \frac{2\sqrt{6}qk}{\sqrt{p(r+2s)}}tanh(\sqrt{-k}\mathit{\xi }),$$$u_3(\mathit{\xi })=\frac{6qk}{(r+2s)}{tanh}^2(\sqrt{-k}\mathit{\xi }),$$$$v_{7,8}(\mathit{\xi })=\pm \frac{2I\sqrt{6}qk}{\sqrt{p(r+2s)}}coth(\sqrt{-k}\mathit{\xi }),$$$$u_4(\mathit{\xi })=\frac{6qk}{(r+2s)}{coth}^2(\sqrt{-k}\mathit{\xi }),$$

where $\mathit{\xi }=x-2qkt.$

Family-03: $v_{9,10}(\mathit{\xi })=\pm \frac{4\sqrt{6}qk}{\sqrt{p(r+2s)}}(tanh(\sqrt{-k}\mathit{\xi })+coth(\sqrt{-k}\mathit{\xi })),$$$u_5(\mathit{\xi })=\frac{6qk}{(r+2s)}({tanh}^2(\sqrt{-k}\mathit{\xi })+{coth}^2(\sqrt{-k}\mathit{\xi })+2),$$$$v_{11,12}(\mathit{\xi })=\pm \frac{4\sqrt{6}qk}{\sqrt{p(r+2s)}}(tanh(\sqrt{-k}\mathit{\xi })+coth(\sqrt{-k}\mathit{\xi })),$$$$u_6(\mathit{\xi })=\frac{6qk}{(r+2s)}({tanh}^2(\sqrt{-k}\mathit{\xi })+{coth}^2(\sqrt{-k}\mathit{\xi })+2),$$

where $\mathit{\xi }=x-8qkt.$

Family-04: $v_{13,14}(\mathit{\xi })=\mp \frac{4\sqrt{3}qk}{\sqrt{p(r+2s)}}(tanh(\sqrt{-k}\mathit{\xi })-coth(\sqrt{-k}\mathit{\xi })),$$$u_7(\mathit{\xi })=\frac{6qk}{(r+2s)}({tanh}^2(\sqrt{-k}\mathit{\xi })+{coth}^2(\sqrt{-k}\mathit{\xi })-2),$$$$v_{15,16}(\mathit{\xi })=\mp \frac{4\sqrt{3}qk}{\sqrt{p(r+2s)}}(coth(\sqrt{-k}\mathit{\xi })-tanh(\sqrt{-k}\mathit{\xi })),$$$$u_8(\mathit{\xi })=\frac{6qk}{(r+2s)}({tanh}^2(\sqrt{-k}\mathit{\xi })+{coth}^2(\sqrt{-k}\mathit{\xi })-2),$$

where $\mathit{\xi }=x+4qkt.$

Family-05: $v_{17,18}(\mathit{\xi })=-\frac{2qk\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right)\pm 12q{k}^2\right)\sqrt{6}}{\sqrt{-kp(r+2s)}\left(12q{(-k)}^{\frac{3}{2}}tanh\left(\sqrt{-k}\right)\pm \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)},$$$u_9(\mathit{\xi })=-\frac{6q{\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right)\pm 12q{k}^2\right)}^2}{(r+2s){\left(12q{\left(-k\right)}^{\frac{3}{2}}tanh\left(\sqrt{-k}\right)\pm \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)}^2},$$$$v_{19,20}(\mathit{\xi })=-\frac{2qk\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right)\pm 12q{k}^2\right)\sqrt{6}}{\sqrt{-kp(r+2s)}\left(12q{\left(-k\right)}^{\frac{3}{2}}coth\left(\sqrt{-k}\right)\pm \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)},$$$$u_{10}(\mathit{\xi })=-\frac{6q{\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right)\pm 12q{k}^2\right)}^2}{(r+2s){\left(12q{(-k)}^{\frac{3}{2}}coth\left(\sqrt{-k}\right)\pm \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)}^2},$$

where $\mathit{\xi }=x-2qkt.$

Case-II: when k > 0, we get the following trigonometric function solutions:

Family-06: $v_{21,22}(\mathit{\xi })=\pm \frac{2I\sqrt{6}qk}{\sqrt{p(r+2s)}}cot\left(\sqrt{k}\mathit{\xi }\right),$$$u_{11}(\mathit{\xi })=-\frac{6qk}{(r+2s)}{cot}^2\left(\sqrt{k}\mathit{\xi }\right),$$$$v_{23,24}(\mathit{\xi })=\mp \frac{2I\sqrt{6}qk}{\sqrt{p(r+2s)}}tan\left(\sqrt{k}\mathit{\xi }\right),$$$$u_{12}(\mathit{\xi })=-\frac{6qk}{(r+2s)}{tan}^2\left(\sqrt{k}\mathit{\xi }\right),$$

where $\mathit{\xi }=x-2qkt.$

Family-07: $v_{25,26}(\mathit{\xi })=\pm \frac{2I\sqrt{6}qk}{\sqrt{p(r+2s)}}tan\left(\sqrt{k}\mathit{\xi }\right),$$$u_{13}(\mathit{\xi })=-\frac{6qk}{(r+2s)}{tan}^2\left(\sqrt{k}\mathit{\xi }\right),$$$$v_{27,28}(\mathit{\xi })=\pm \frac{2I\sqrt{6}qk}{\sqrt{p(r+2s)}}cot\left(\sqrt{k}\mathit{\xi }\right),$$$$u_{14}(\mathit{\xi })=-\frac{6qk}{(r+2s)}{cot}^2\left(\sqrt{k}\mathit{\xi }\right),$$

where $\mathit{\xi }=x-2qkt.$

Family-08: $v_{29,30}(\mathit{\xi })=\pm \frac{4I\sqrt{6}qk}{\sqrt{p(r+2s)}}\left(tan\left(\sqrt{k}\mathit{\xi }\right)-coth\left(\sqrt{k}\mathit{\xi }\right)\right),$$$u_{15}(\mathit{\xi })=-\frac{6qk}{(r+2s)}\left({tan}^2\left(\sqrt{k}\mathit{\xi }\right)+{cot}^2\left(\sqrt{k}\mathit{\xi }\right)-2\right),$$$$v_{31,32}(\mathit{\xi })=\mp \frac{4\sqrt{6}qk}{\sqrt{p(r+2s)}}\left(cot\left(\sqrt{k}\mathit{\xi }\right)-tan\left(\sqrt{k}\mathit{\xi }\right)\right),$$$$u_{16}(\mathit{\xi })=-\frac{6qk}{(r+2s)}\left({cot}^2\left(\sqrt{k}\mathit{\xi }\right)+{tan}^2\left(\sqrt{k}\mathit{\xi }\right)-2\right),$$

where $\mathit{\xi }=x-8qkt.$

Family-09: $v_{33,34}(\mathit{\xi })=\pm \frac{4\sqrt{3}qk}{\sqrt{p(r+2s)}}csc\left(\sqrt{k}\mathit{\xi }\right)sec\left(\sqrt{k}\mathit{\xi }\right),$$$u_{17}(\mathit{\xi })=-\frac{6qk}{(r+2s)}{csc}^2\left(\sqrt{k}\mathit{\xi }\right){sec}^2\left(\sqrt{k}\mathit{\xi }\right),$$$$v_{35,36}(\mathit{\xi })=\mp \frac{4\sqrt{3}qk}{\sqrt{p(r+2s)}}csc\left(\sqrt{k}\mathit{\xi }\right)sec\left(\sqrt{k}\mathit{\xi }\right),$$$$u_{18}(\mathit{\xi })=-\frac{6qk}{(r+2s)}{csc}^2\left(\sqrt{k}\mathit{\xi }\right){sec}^2\left(\sqrt{k}\mathit{\xi }\right),$$

where $\mathit{\xi }=x+4qkt.$

Family-10: $v_{37,38}(\mathit{\xi })=\frac{2qk\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{k}tan\left(\sqrt{k}\mathit{\xi }\right)\mp 12q{k}^2\right)\sqrt{6}}{\sqrt{-kp(r+2s)}\left(12q{k}^{\frac{3}{2}}tan\left(\sqrt{k}\right)\pm \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)},$$$u_{19}(\mathit{\xi })=-\frac{6q{\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{k}tan\left(\sqrt{k}\mathit{\xi }\right)\mp 12q{k}^2\right)}^2}{(r+2s){\left(12q{k}^{\frac{3}{2}}tan\left(\sqrt{k}\right)\pm \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)}^2},$$$$v_{39,40}(\mathit{\xi })=\frac{2qk\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{k}cot\left(\sqrt{k}\mathit{\xi }\right)\pm 12q{k}^2\right)\sqrt{6}}{\sqrt{-kp(r+2s)}\left(12q{k}^{\frac{3}{2}}cot\left(\sqrt{k}\right)\mp \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)},$$$$u_{20}(\mathit{\xi })=-\frac{6q{\left(\sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\sqrt{k}cot\left(\sqrt{-k}\mathit{\xi }\right)\pm 12q{k}^2\right)}^2}{(r+2s){\left(12q{k}^{\frac{3}{2}}cot\left(\sqrt{k}\right)\mp \sqrt{6}\sqrt{-kp(r+2s)}{\mathit{\alpha }}_0\right)}^2},$$

where $\mathit{\xi }=x-2qkt.$

Remark

All of these obtained solutions have been verified with Maple by substituting them into the original equations and were found correct.

Example 3.2

The Burgers equation

In this subsection, we consider the Burgers equation (Khan & Akbar, 2014b) in the form:(14) $$u_t-u{u}_x-u_{xx}-u_{yy}=0$$(14)

Burgers introduced this equation to capture some of the features of turbulent fluid in a channel by the interaction of the opposite effects of convection and diffusion. It is also used to describe the structure of shock waves, traffic flow, and acoustic transmission. Burgers equation is completely integrable. The wave solutions of Burgers equation are single and multiple-front solutions.

We substitute the traveling wave transformation $u(\mathit{\xi })=u(x,y,t),\mathit{\xi }=x+y-\mathit{\lambda }t$ into Equation (14) and obtained the ordinary differential equation:(15) $$\mathit{\lambda }{u}^{\prime }+u{u}^{\prime }+2u^{″}=0$$(15)

where prime denotes the derivative with respect to ξ.

Integrating once with respect to ξ, Equation (15) becomes(16) $$4u^{\prime }+u^2+2\mathit{\lambda }u+p=0$$(16)

where p is the integration constant. Balancing the highest order derivative u′ and the non-linear term u², we obtain N = 1.

Hence for N = 1 Equation (5) reduces to(17) $$u(\mathit{\xi })={\mathit{\alpha }}_0+{\mathit{\alpha }}_1(m+F(\mathit{\xi }))+{\mathit{\beta }}_1{(m+F(\mathit{\xi }))}^{-1}.$$(17)

Utilizing (17) including (5) into Equation (16), we get a polynomial in $F(\mathit{\xi })$. Equating the coefficient of the same power of $F(\mathit{\xi })$ to zero, we attain the following system of algebraic equations:$$4{\mathit{\alpha }}_1+{\mathit{\alpha }}_1^2=0$$$$2\mathit{\lambda }{\mathit{\alpha }}_1+8{\mathit{\alpha }}_{1}m+4{\mathit{\alpha }}_1^{2}m+2{\mathit{\alpha }}_0{\mathit{\alpha }}_1=0$$$$6\mathit{\lambda }{\mathit{\alpha }}_{1}m-4{\mathit{\beta }}_1+4{\mathit{\alpha }}_1{m}^2+2\mathit{\lambda }{\mathit{\alpha }}_0+6{\mathit{\alpha }}_0{\mathit{\alpha }}_{1}m+6{\mathit{\alpha }}_1^2{m}^2+{\mathit{\alpha }}_0^2+4{\mathit{\alpha }}_{1}k+p+2{\mathit{\alpha }}_1{\mathit{\beta }}_1=0$$$$2\mathit{\lambda }{\mathit{\beta }}_1+4{\mathit{\alpha }}_{1}m{\mathit{\beta }}_1+2{\mathit{\alpha }}_0^{2}m+6{\mathit{\alpha }}_0{\mathit{\alpha }}_1{m}^2+8{\mathit{\alpha }}_{1}km+2pm+2{\mathit{\alpha }}_0{\mathit{\beta }}_1+6\mathit{\lambda }{\mathit{\alpha }}_1{m}^2+4{\mathit{\alpha }}_1^2{m}^3+4\mathit{\lambda }{\mathit{\alpha }}_{0}m=0$$$$-4{\mathit{\beta }}_{1}k+{\mathit{\beta }}_1^2+2{\mathit{\alpha }}_0{\mathit{\alpha }}_1{m}^3+2\mathit{\lambda }{\mathit{\alpha }}_0{m}^2+2{\mathit{\alpha }}_0{\mathit{\beta }}_{1}m+2{\mathit{\alpha }}_1{m}^2{\mathit{\beta }}_1+{\mathit{\alpha }}_0^2{m}^2+2\mathit{\lambda }{\mathit{\beta }}_{1}m+{\mathit{\alpha }}_1^2{m}^4+2\mathit{\lambda }{\mathit{\alpha }}_1{m}^3+4{\mathit{\alpha }}_{1}k{m}^2+p{m}^2=0$$

Solving the above system of equations for ${\mathit{\alpha }}_0,{\mathit{\alpha }}_1,{\mathit{\beta }}_1,m$ and $\mathit{\lambda }$ we get the following values:

Set-01: $m=m,p=16k+16m^2+8m{\mathit{\alpha }}_0+{\mathit{\alpha }}_0^2,\mathit{\lambda }=-(4m+{\mathit{\alpha }}_0)t,{\mathit{\alpha }}_0={\mathit{\alpha }}_0,{\mathit{\alpha }}_1=0$$${\mathit{\beta }}_1=4(k+m^2).$$

Set-02: $m=m,p=16m^2-8m{\mathit{\alpha }}_0+{\mathit{\alpha }}_0^2+16k,\mathit{\lambda }=4m-{\mathit{\alpha }}_0,{\mathit{\alpha }}_0={\mathit{\alpha }}_0,{\mathit{\alpha }}_1=-4,{\mathit{\beta }}_1=0.$

Set-03: $m=0,p=64k+{\mathit{\alpha }}_0^2,\mathit{\lambda }=-{\mathit{\alpha }}_0,{\mathit{\alpha }}_0={\mathit{\alpha }}_0,{\mathit{\alpha }}_1=-4,{\mathit{\beta }}_1=4k.$

Case-I: When k < 0, we get the following hyperbolic function solutions:

Family-01: $u_1(\mathit{\xi })=\frac{m{\mathit{\alpha }}_0-{\mathit{\alpha }}_0\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right)+4k+4m^2}{m-\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right)},$$$u_2(\mathit{\xi })=\frac{m{\mathit{\alpha }}_0-{\mathit{\alpha }}_0\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right)+4k+4m^2}{m-\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right)},$$

where $\mathit{\xi }=x+y+(4m+{\mathit{\alpha }}_0)t.$

Family-02: $u_3(\mathit{\xi })={\mathit{\alpha }}_0-4m+4\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right),$$$u_4(\mathit{\xi })={\mathit{\alpha }}_0-4m+4\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right),$$

where $\mathit{\xi }=x+y-(4m-{\mathit{\alpha }}_0)t.$

Family-03: $u_5(\mathit{\xi })=\frac{{\mathit{\alpha }}_0\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right)-4k{tanh}^2\left(\sqrt{-k}\mathit{\xi }\right)-4k}{\sqrt{-k}tanh\left(\sqrt{-k}\mathit{\xi }\right)},$$$u_6(\mathit{\xi })=\frac{{\mathit{\alpha }}_0\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right)-4k{coth}^2\left(\sqrt{-k}\mathit{\xi }\right)-4k}{\sqrt{-k}coth\left(\sqrt{-k}\mathit{\xi }\right)},$$

where $\mathit{\xi }=x+y+{\mathit{\alpha }}_{0}t.$

Case-II: When k > 0, we get the following trigonometric function solutions:

Family-04: $u_7(\mathit{\xi })=\frac{m{\mathit{\alpha }}_0+{\mathit{\alpha }}_0\sqrt{k}tan\left(\sqrt{k}\mathit{\xi }\right)+4k+4m^2}{m+\sqrt{k}tan\left(\sqrt{k}\mathit{\xi }\right)},$$$u_8(\mathit{\xi })=\frac{m{\mathit{\alpha }}_0-{\mathit{\alpha }}_0\sqrt{k}cot\left(\sqrt{k}\mathit{\xi }\right)+4k+4m^2}{m-\sqrt{k}cot\left(\sqrt{k}\mathit{\xi }\right)},$$

where $\mathit{\xi }=x+y+(4m+{\mathit{\alpha }}_0)t.$

Family-05: $u_9(\mathit{\xi })={\mathit{\alpha }}_0-4m-4\sqrt{k}tan\left(\sqrt{k}\mathit{\xi }\right),$$$u_{10}(\mathit{\xi })={\mathit{\alpha }}_0-4m+4\sqrt{k}cot\left(\sqrt{k}\mathit{\xi }\right),$$

where $\mathit{\xi }=x+y-(4m-{\mathit{\alpha }}_0)t.$

Family-06: $u_{11}(\mathit{\xi })=\frac{{\mathit{\alpha }}_{0}tan\left(\sqrt{k}\mathit{\xi }\right)-4\sqrt{k}{tan}^2\left(\sqrt{k}\mathit{\xi }\right)-4\sqrt{k}}{tan\left(\sqrt{k}\mathit{\xi }\right)},$$$u_{12}(\mathit{\xi })=\frac{{\mathit{\alpha }}_{0}cot\left(\sqrt{k}\mathit{\xi }\right)+4\sqrt{k}{cot}^2\left(\sqrt{k}\mathit{\xi }\right)-4\sqrt{k}}{cot\left(\sqrt{k}\mathit{\xi }\right)},$$

where $\mathit{\xi }=x+y+{\mathit{\alpha }}_{0}t.$

Case-III: When k = 0, we get the following rational function solutions:

Family-07: $u_{13}(\mathit{\xi })=\frac{{\mathit{\alpha }}_{0}m\mathit{\xi }-{\mathit{\alpha }}_0+4m^2\mathit{\xi }}{m\mathit{\xi }-1},$

where $\mathit{\xi }=x+y+(4m+{\mathit{\alpha }}_0)t.$

Family-08: $u_{14}(\mathit{\xi })=\frac{{\mathit{\alpha }}_0\mathit{\xi }-4m\mathit{\xi }+4}{\mathit{\xi }},$

where $\mathit{\xi }=x+y-(4m-{\mathit{\alpha }}_0)t.$

Family-09: $u_{15}(\mathit{\xi })=\frac{{\mathit{\alpha }}_0\mathit{\xi }+4}{\mathit{\xi }},$

where $\mathit{\xi }=x+y+{\mathit{\alpha }}_{0}t.$

Remark

Again, all of these solutions have been verified with Maple by substituting them into the original equations and were found to be correct.

4. Explanation and graphical representations of the obtained solutions

4.1. Explanation of the obtained solutions

In this section, we will discuss the physical interpretation of the obtained results of the DSW equation and Burgers equation.

4.1.1. Drinfel’d–Sokolov–Wilson equation

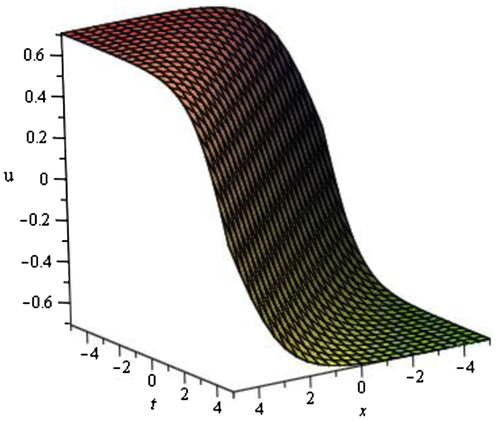
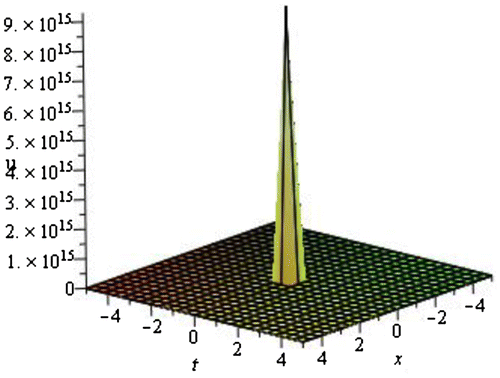
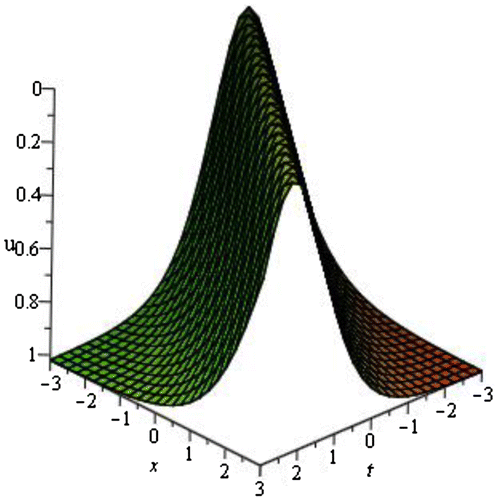
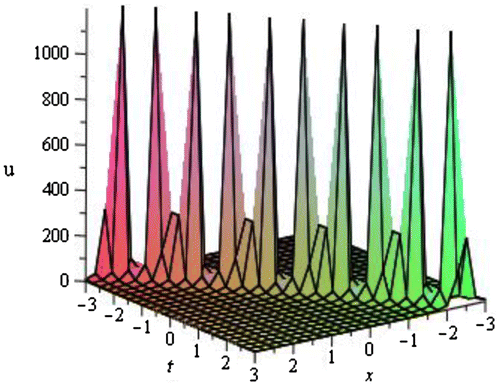
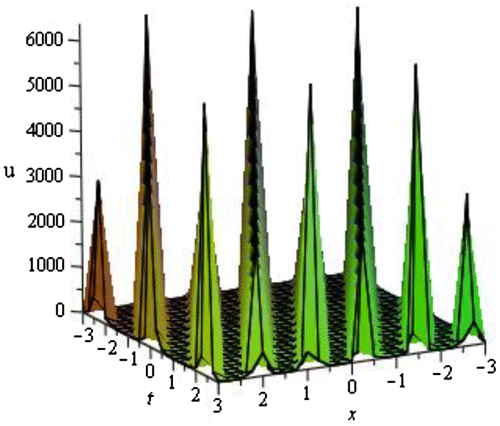
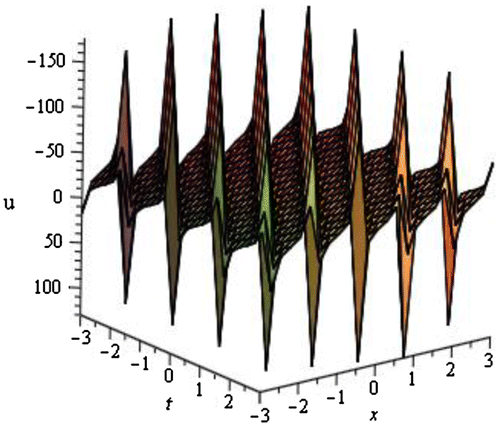
We have obtained total of 60 traveling wave solutions in terms of some unknown parameters. These solutions are subdivided into ten families according to the negative and positive values of v and u. The solutions are combinations of hyperbolic functions, trigonometric functions, and rational functions. If we put the particular values of the unknown parameters in each traveling wave solutions, then the solitary waves can be obtained. We have depicted some figure of the solitary waves by setting particular values of unknown parameters.

•	For the particular values of $p=1,q=-3,r=2,s=3,k=-0.25$ within the interval $-3\le x,t\le 3$ Figure 1 is singular kink solution (shows the shape of $v_2(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=3,q=-2,r=2,s=1,k=-0.25$ within the interval $-5\le x,t\le 5$ Figure 2 is kink shaped solution (shows the shape of $v_4(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=1,q=-2,r=3,s=1,k=0.50$ within the interval $-5\le x,t\le 5$ Figure 3 is single soliton solution (shows the shape of $v_{21}(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=1,q=-2,r=1,s=3,k=0.40$ within the interval $-5\le x,t\le 5$ Figure 4 is periodic solution (shows the shape of $v_{24}(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=3,q=-2,r=2,s=1,k=-0.05$ within the interval $-3\le x,t\le 3$ Figure 5 is singular soliton solution (shows the shape of $u_1(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=3,q=-2,r=2,s=1,k=-0.34$ within the interval $-3\le x,t\le 3$ Figure 6 is Bell-shaped soliton solution (shows the shape of $u_2(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=3,q=-2,r=2,s=1,,k=0.20$ within the interval $-3\le x,t\le 3$ Figure 7 is singular soliton solution (shows the shape of $u_{11}(\mathit{\xi })$ for DSW equation).
•	For the particular values of $p=3,q=-2,r=2,s=1,k=7$ within the interval $-3\le x,t\le 3$ Figure 8 is periodic solution (shows the shape of $u_{12}(\mathit{\xi })$ for DSW equation).

Figure 1. Singular kink solution $v_2(\mathit{\xi })$ of DWS equation for $p=1,q=-3,r=2,s=3,k=-0.25$ within the interval $-3\le x,t\le 3$.

Figure 2. Kink shaped solution $v_4\left(\mathit{\xi }\right)$ of DWS equation for $p=3,q=-2,r=2,s=1,k=-0.25$ within the interval $-5\le x,t\le 3$.

Figure 3. Single soliton solution $v_{21}(\mathit{\xi })$ of DWS equation for $p=1,q=-2,r=3,s=1,k=0.50$ within the interval $-5\le x,t\le 5$.

Figure 4. Periodic solution $v_{24}(\mathit{\xi })$ of DWS equation for $p=1,q=-2,r=1,s=3,k=0.40$ within the interval $-5\le x,t\le 5$.

Figure 5. Singular soliton solution $u_1(\mathit{\xi })$ of DWS equation for $p=3,q=-2,r=2,s=1,k=-0.05$ within the interval $-3\le x,t\le 3$.

Figure 6. Bell-shaped soliton $u_2(\mathit{\xi })$ of DWS equation for $p=3,q=-2,r=2,s=1,k=-0.34$ within the interval $-3\le x,t\le 3$.

Figure 7. Singular soliton $u_{11}(\mathit{\xi })$ of DWS equation for $p=3,q=-2,r=2,s=1,k=0.20$ within the interval $-3\le x,t\le 3$.

Figure 8. Periodic solution $u_{12}(\mathit{\xi })$ of DWS equation for $p=3,q=-2,r=1,s=1,k=7$ within the interval $-3\le x,t\le 3$.

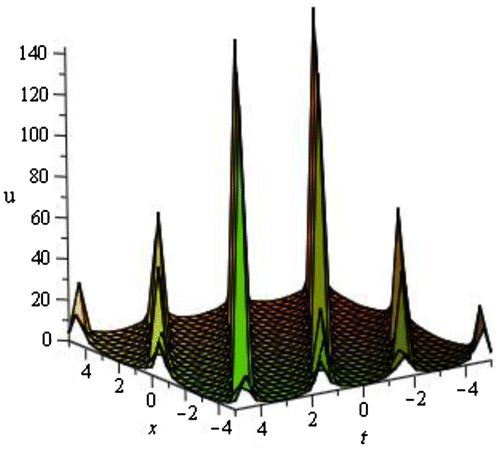
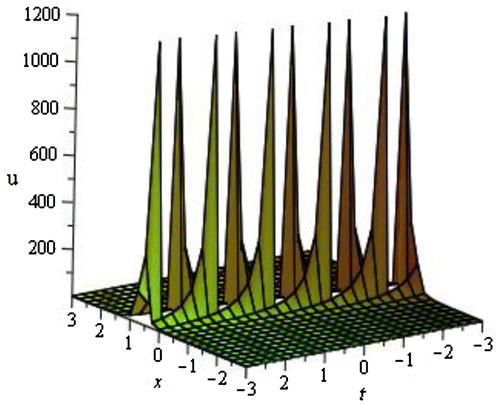
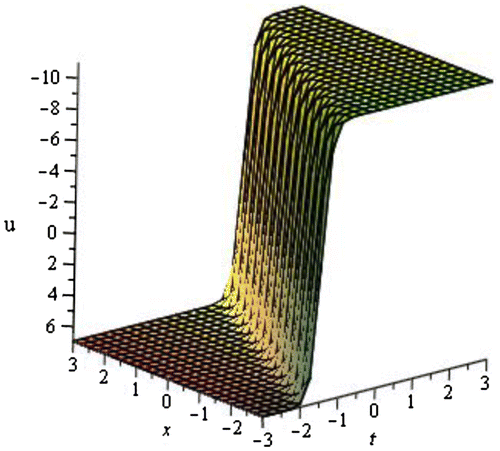
4.1.2. Burgers equation

Now we will discuss about the obtained results of the Burgers equation and their graphical representation.

•	For the particular values of $y=0,m=1,{\mathit{\alpha }}_0=2,k=-5$ within the interval $-3\le x,t\le 3$ Figure 9 is kink shaped soliton solution (shows the shape of $u_3(\mathit{\xi })$ for Burgers equation).
•	For the particular values of $y=0,m=7,{\mathit{\alpha }}_0=5,k=7$ within the interval $-3\le x,t\le 3$ Figure 10 is periodic solution (shows the shape of $u_9(\mathit{\xi })$ for Burgers equation).

Figure 9. Kink shaped soliton $u_3(\mathit{\xi })$ of Burgers equation for $y=0,m=1,{\mathit{\alpha }}_0=2,k=-5$ within the interval $-3\le x,t\le 3$.

Figure 10. Periodic solution $u_9(\mathit{\xi })$ of Burgers equation for $y=0,m=7,{\mathit{\alpha }}_0=5,k=7$ within interval $-3\le x,t\le 3$.

4.2. Graphical representation of the obtained solutions

The graphical illustrations of the solutions of DSW equations are depicted in Figures 1–8 and the solutions of Burgers equations are represented in Figures 9 and 10 with the aid of commercial software Maple.

5. Comparison

In this section, we will discuss the effectiveness of the improved F-expansion method compared to other existing methods.

5.1. DSW equation with the MSE method

In Khan et al. (2013), Khan and Akbar investigated exact solutions of the DSW equations throughout the modified simple equation method and attained 12 solutions (see Appendix A). On the other hand, by adopting the improved F-expansion method in this article we attained 60 solutions. It is remarkable to point out that some of our solutions correspond well with some of the solutions available in the literature, if we put particular values of the parameters which substantiate our solutions. Likewise, if we put $k=1,q=-\frac{1}{2}$ in our solutions $v_{3,4}(\mathit{\xi })$ (family-01) and $v_{5,6}(\mathit{\xi })$ (family-02) correspond with the Equation (A. 1). Also our solutions $v_{1,2}(\mathit{\xi })$ (family-01) correspond with the Equation (A. 2) attained by Khan et al. (2013) in place of $\mathit{\omega }=1,q=-\frac{1}{2}$. Congruently, for the conditions $k=1,q=\frac{1}{2}$ our solutions of $v_{25,26}(\mathit{\xi })$ and $u_{27,28}(\mathit{\xi })$ (family-07) correspond with the Equations (A. 3) and (A. 4), respectively, attained by Khan et al. (2013) in place of $\mathit{\omega }=1,q=\frac{1}{2}$. Yet again if put $k=1,q=-\frac{1}{2}$ in our solutions $u_1(\mathit{\xi })$ and $u_2(\mathit{\xi })$ (family-01) correspond with the Equations (A. 5) and (A. 6), respectively, attained by Inc (2006) in place of $\mathit{\omega }=1,q=-\frac{1}{2}$. Congruently, for the conditions $k=1,q=\frac{1}{2}$ our solutions of $u_3(\mathit{\xi })$ and $u_4(\mathit{\xi })$ (family-04) correspond with the Equations (A. 7) and (A. 8), respectively, attained by Khan et al. (2013) in place of $\mathit{\omega }=1,q=\frac{1}{2}$.

5.2. Burgers equation with modified simple equation method

In Khan and Akbar (2014b) Khan and Akbar studied exact solutions of the Burgers equation by the use of the modified simple equation and attained five solutions (see Appendix B). On the other hand by the improved F-expansion method in this article, we attained 15 solutions. If we put ${\mathit{\alpha }}_0=-1,m=0,k=-\frac{1}{16}$ into our solutions $u_3(\mathit{\xi })$ and $u_4(\mathit{\xi })$ correspond with the Equations (B. 1) and (B. 2), respectively, attained by Khan and Akbar (2014b) in place of ω = 1.Congruently, if we put ${\mathit{\alpha }}_0=-1,m=0,k=\frac{1}{16}$ into our solutions $u_{10}(\mathit{\xi })$ that coincide with Equation (B. 3) attained by Khan and Akbar (2014b) in place of ω = 1.

6. Conclusions

The improved F-expansion method combined with Riccati equation is used in this article for seeking abundant exact traveling wave solutions to the Drinfel’d–Sokolov–Wilson equation and the Burgers equation with the aid of symbolic computation, such as Maple. The obtained solutions are presented in terms of the hyperbolic functions, the trigonometric functions and the rational functions. Furthermore, our constructed solutions show that the solution procedure of this method is very modest, consistent, and straightforward. If the parameters take special values, we get the existing solitary wave solutions, singular soliton solution, periodic solutions, and kink solutions. The result reveal that the improved F-expansion method is a promising instrument since it can provide a variety of solutions of distinctive physical configurations. This method can also be applied to other non-linear evolution equations (NLEEs) in mathematical physics.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

M. Ali Akbar

M. Ali Akbar is an Associate Professor at the Department of Applied Mathematics, University of Rajshahi, Bangladesh. He received his PhD in Mathematics from the Department of Mathematics, University of Rajshahi, Bangladesh. He is actively involved in research in the field of nonlinear differential equations and fractional calculus. He has published more than 150 research articles of which 55 articles are published in ISI (Thomson Reuter) indexed journals and other 14 articles published in Scopus indexed journals.

Norhashidah Hj. Mohd. Ali

Norhashidah Hj. Mohd. Ali received her Bachelor of Science (Maths) with a minor in Information Sciences in 1984 from Western Illinois University, USA. In 1986, she received her MSc in Applied Mathematics from Virginia Tech, USA. She completed her PhD in Industrial Computing from Universiti Kebangsaan Malaysia in 1998. She is currently a professor at the School of Mathematical Sciences, Universiti Sains Malaysia. Her research interests include numerical differential equations and parallel processing.

Appendix A

Khan et al. (2013) examined the exact solutions of the DSW equation via the modified Simple equation method. They obtained the following solutions(A.1) $$v_{1,2}(\mathit{\xi })=\pm \mathit{\omega }\sqrt{\frac{6}{p(r+2s)}}tanh\left(\sqrt{\left(\frac{w}{2q}\right)}(x+\mathit{\omega }t)\right),$$(A.1) (A. 2) $$v_{3,4}(\mathit{\xi })=\pm \mathit{\omega }\sqrt{\frac{6}{p(r+2s)}}coth\left(\sqrt{\left(\frac{w}{2q}\right)}\left(x+\mathit{\omega }t\right)\right),$$(A. 2) (A. 3) $$v_{5,6}(\mathit{\xi })=\pm I\mathit{\omega }\sqrt{\frac{6}{p(r+2s)}}tan\left(\sqrt{\left(\frac{w}{2q}\right)}\left(x-\mathit{\omega }t\right)\right),$$(A. 3) (A. 4) $$v_{7,8}(\mathit{\xi })=\pm I\mathit{\omega }\sqrt{\frac{6}{p(r+2s)}}cot\left(\sqrt{\left(\frac{w}{2q}\right)}(x-\mathit{\omega }t)\right),$$(A. 4) (A. 5) $$u_1(\mathit{\xi })=-\frac{3\mathit{\omega }}{r+2s}{tanh}^2\left(\sqrt{\left(\frac{w}{2q}\right)}(x+\mathit{\omega }t)\right),$$(A. 5) (A. 6) $$u_2(\mathit{\xi })=-\frac{3\mathit{\omega }}{r+2s}{coth}^2\left(\sqrt{\left(\frac{w}{2q}\right)}(x+\mathit{\omega }t)\right),$$(A. 6) (A. 7) $$u_3(\mathit{\xi })=-\frac{3\mathit{\omega }}{r+2s}{tan}^2\left(\sqrt{\left(\frac{w}{2q}\right)}(x-\mathit{\omega }t)\right),$$(A. 7) (A. 8) $$u_4(\mathit{\xi })=-\frac{3\mathit{\omega }}{r+2s}{cot}^2\left(\sqrt{\left(\frac{w}{2q}\right)}(x-\mathit{\omega }t)\right).$$(A. 8)

Appendix B

Khan & Akbar (2014b) studied the exact solutions of the Burgers equation with the support of the modified simple equation method. They projected the following solutions,(B. 1) $$u_1(\mathit{\xi })=-\mathit{\omega }\left(1-tanh\left(\frac{\mathit{\omega }}{4}(x+y-\mathit{\omega }t)\right)\right),$$(B. 1) (B. 2) $$u_2(\mathit{\xi })=-\mathit{\omega }\left(1-coth\left(\frac{\mathit{\omega }}{4}(x+y-\mathit{\omega }t)\right)\right),$$(B. 2) (B. 3) $$u_3(\mathit{\xi })=-\mathit{\omega }\left(1-cot\left(\frac{\mathit{\omega }}{4}(x+y-\mathit{\omega }t)\right)\right),$$(B. 3) (B. 4) $$u_4(\mathit{\xi })=-\mathit{\omega }\left(1-tan\left(\frac{\mathit{\omega }}{4}(x+y-\mathit{\omega }t)\right)\right),$$(B. 4) (B.5) $$u_5(\mathit{\xi })=-2\mathit{\omega }+\frac{4\mathit{\omega }{c}_1(1+tanh(\mathit{\omega }(x+y-\mathit{\omega }t)/2))}{2c_1(1+tanh(\mathit{\omega }(x+y-\mathit{\omega }t)/2))+c_2\mathit{\omega }sech(\mathit{\omega }(x+y-\mathit{\omega }t)/2)}.$$(B.5)