Mathematical analysis of delayed HIV-1 infection model for the competition of two viruses

Abstract

In this research article, a new mathematical delayed human immunodeficiency virus (HIV-1) infection model with two constant intracellular delays, is investigated. The analysis of the model is thoroughly discussed by the basic reproduction numbers $R_0$ and $R_s$. For $R_0<1$, the infection-free equilibrium $(E^0)$ is shown to be locally as well as globally stable. Similarly, the single-infection equilibrium $(E^s)$ is proved to be locally as well as globally asymptotically stable if $1<R_0<R_s$. Our derived results show that the incorporation of even small intracellular time delay can control the spread of HIV-1 infection and can better the quality of the life of the patient. Finally, numerical simulations are used to illustrate the derived theoretical results.

Keywords:

• HIV-1 model
• intracellular delay
• recombinant virus
• Lyapunov functional
• LaSalle’s invariance principle
• Hopf bifurcation

Public Interest Statement

Time delays are usually incorporated into the mathematical models for the purpose of accurate representations of HIV-1 infection process. There are time delays between initial viral entry into a cell and subsequent viral production. Therefore, discrete delays are used in mathematical models to prove that large time delays can help to eliminate the virus and control the infection of HIV-1.

1. Introduction

Human immunodeficiency virus (HIV-1) is a lentivirus that causes acquired immunodeficiency syndrome (AIDS). HIV attacks CD4 cells and weakens the immune system. This infection passes though three different phases: the primary infection, the chronic infection and and AIDS is the last stage of HIV-1 infection. To control this infection, many scientists and researchers have been focusing on it but in spite of this, there is no effective way to cure AIDS. In the recent research, recombinant virus is used for controlling the infection of HIV-1 (see for example, Nolan, 1997; Wagner & Hewlett, 1999). Revilla and Garcya-Ramos (2003) established a five-dimensional ordinary differential equation system to investigate the control of the infection by introducing a recombinant virus. Jiang, Yu, Yuan, and Zou (2009), introduced a constant injection rate of the recombinant virus and presented various bifurcation patterns. A control strategy of the HIV-1 epidemic model was given in Yu and Zou (2012). In Revilla and Garcya-Ramos (2003), the authors analyzed the structure of equilibrium solutions and presented some simulations. Jiang et al. (2009), presented the stability of all possible equilibrium solutions and bifurcations between these equilibria, as well as proved the existence of Hopf bifurcation. Yu and Zou (2012), incorporated a control parameter $\mathit{\eta }$ to measure the injection rate of the recombinant for controlling/eliminating the HIV virus.

The following system of differential equations is standard and classic in-host model for HIV-1 infection (Perelson & Nelson, 1999)(1) $$\begin{array}{cc}\hfill \dot{x}(t)& =\mathit{\lambda }-dx(t)-\mathit{\beta }x(t)v(t),\hfill \\ \hfill \dot{y}(t)& =\mathit{\beta }x(t)v(t)-ay(t),\hfill \\ \hfill \dot{v}(t)& =ky(t)-pv(t),\hfill \end{array}$$(1)

where x(t), y(t) and v(t) represent the densities of uninfected cells, infected cells and the free virus, respectively, at time t. The constant parameters in system (1) are explained as below: the positive constant $\mathit{\lambda }$ is the rate at which new target cells are generated, d is their specific death rate and $\mathit{\beta }$ is the constant rate at which a T-cell is contacted by the virus. It is assumed that once cells are infected, they may die at rate a due to the immune system or the virus. In the mean time, each of the infected cells produces new virus particles at a rate k. In Revilla and Garcya-Ramos (2003), a second virus is added into model (1) which may cause the infected cells to have a second infection. Then, these cells are called double-infected cells. The system (1) is modified to the following form:(2) $$\begin{array}{cc}\hfill \dot{x}(t)& =\mathit{\lambda }-dx(t)-\mathit{\beta }x(t)v(t),\hfill \\ \hfill \dot{y}(t)& =\mathit{\beta }x(t)v(t)-ay(t)-\mathit{\alpha }w(t)y(t),\hfill \\ \hfill \dot{z}(t)& =aw(t)y(t)-bz(t),\hfill \\ \hfill \dot{v}(t)& =ky(t)-pv(t),\hfill \\ \hfill \dot{w}(t)& =cz(t)-qw(t).\hfill \end{array}$$(2)

Here w(t) and z(t) represent the density of genetically modified (recombinant) virus describes and double-infected cells, respectively. The rate of infection of double-infected cells is denoted by $\mathit{\alpha }$. The recombinant are removed at a rate qw. The double-infected cells die at a rate of bz and release recombinant virus at a rate cz.

Tian, Bai, and Yu (2014) and Perelson and Nelson (1999) introduced the time delay in the system (2). Because, time is required for the virus to contact a target cell and then the contacted cells to become infected. They introduced the time lag into model (2) and modified the model as follows:(3) $$\begin{array}{cc}\hfill \dot{x}(t)& =\mathit{\lambda }-dx(t)-\mathit{\beta }x(t)v(t),\hfill \\ \hfill \dot{y}(t)& =\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })-ay(t)-\mathit{\alpha }w(t)y(t),\hfill \\ \hfill \dot{z}(t)& =aw(t)y(t)-bz(t),\hfill \\ \hfill \dot{v}(t)& =ky(t)-pv(t),\hfill \\ \hfill \dot{w}(t)& =cz(t)-qw(t),\hfill \end{array}$$(3)

where $\mathit{\tau }$ stands for the average time needed for a viral particle to go through the eclipse phase. Here a is the constant death rate of those infected cells which are not virus-producing cells yet. Therefore, $e^{-a\mathit{\tau }}$ is the probability of surviving of cells in the time period from $t-\mathit{\tau }$ to t (see also Ali, Zaman, & Algahtani,, 2016; Culshaw, Ruan, & Webb, 2003; Herz, Bonhoeffer, Anderson, May, & Nowak, 1996; Lv & Yuan, 2009; Miao & Abdurahman, 2013; Mittler, Markowitz, Ho, & Perelson, 1999; Nelson, Murray, & Perelson, 2000; Nelson & Perelson, 2002; Tian et al., 2014; Wang, 2015). However, the case where the contact process between the uninfected cells and pathogen virus is not instantaneous (see Tian et al., 2014) also should be examined (Tian et al., 2014). Here, we assume the same values of delays in both terms. This assumption is for simplicity and that it is valuable to analyze the case where the two types of time delays do not have the same values. This process was considered directly in the work of Tian et al. (2014). Also, in Miao and Abdurahman (2013) the authors considered delays in the model dealing with the investigations of global dynamics for a system of delay differential equations which describe a virus–immune interaction but ignored delay in rate of contact between virus and target cells. But our proposed model investigates both the local and global dynamic for a system of delay differential equations and discuss the effect of recombinant virus. In this paper, we introduce time delay, similar to the disease transmission term, in the rate of contact term. By introducing delay in the mentioned term, our proposed model becomes(4) $$\begin{array}{cc}\hfill \dot{x}(t)& =\mathit{\lambda }-dx(t)-\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau }),\hfill \\ \hfill \dot{y}(t)& =\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })-ay(t)-\mathit{\alpha }w(t)y(t),\hfill \\ \hfill \dot{z}(t)& =\mathit{\alpha }w(t)y(t)-bz(t),\hfill \\ \hfill \dot{v}(t)& =ky(t)-pv(t),\hfill \\ \hfill \dot{w}(t)& =cz(t)-qw(t),\hfill \end{array}$$(4)

We will study the dynamical behavior of the proposed model, and will show how delays influence stability of the model. We will discuss the well-posdeness of the solutions of model and the stability of all equilibrium points. Moreover, the basic reproduction numbers will be found. It will be shown that infection-free equilibrium $E^0$ is locally as well as globally asymptotically stable. We also show that the $E^s$ (recombinant absent equilibrium) is locally as well as globally asymptotically stable.

The rest of this paper is organized as follows. The Section 2 is devoted to preliminarily results. In Section 3, local stability is discussed. Section 4 is devoted to global stability. Numerical simulation is discussed in Section 5. Finally, conclusion and discussion are drawn in Section 6.

2. Preliminary results

In this section, we will discuss the well-posedness, basic reproduction numbers, and the existence of equilibria of the proposed model (4).

Theorem 2.1

Under the given initial conditions (5), all the solutions of the system (4) are non-negative and bounded.

Proof

Let $B=C([-\mathit{\tau },0];R^5)$ be the Banach space of continuous mapping from $[-\mathit{\tau },0]$ to $R^5$ equipped with the sup-norm. The following initial conditions(5) $$\begin{array}{c}\hfill x(\mathit{\varphi })\ge 0,y(\mathit{\varphi })\ge 0,z(\mathit{\varphi })\ge 0,v(\mathit{\varphi })\ge 0,w(\mathit{\varphi })\ge 0,\mathit{\varphi }\in [-\mathit{\tau },0].\end{array}$$(5)

are satisfied for the system (4), where $(x(\mathit{\varphi }),x(\mathit{\varphi }),x(\mathit{\varphi }),x(\mathit{\varphi }),x(\mathit{\varphi }))\in B$. The fundamental theory of functional differential equations (see e.g. Hale & Verduyn Lunel, 1993), implies that there exists a unique solution $(x(t),y(t),z(t),v(t),w(t)$ for the given initial conditions in (5).

Using constant of variation formula, we get the following solutions of system (4).$$\begin{array}{cc}\hfill x(t)& =x(0)e^{-{\int }_0^t(d+\mathit{\beta }v(\mathit{\zeta }))d\mathit{\zeta }}+\mathit{\lambda }\underset{0}{\overset{t}{\int }}\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })e^{-{\int }_{\mathit{\eta }}^t(d+\mathit{\beta }v(\mathit{\zeta }))d\mathit{\zeta }}d\mathit{\eta },\hfill \\ \hfill y(t)& =y(0)e^{-{\int }_0^t(a+\mathit{\alpha }z(\mathit{\zeta }))d\mathit{\zeta }}+\underset{0}{\overset{t}{\int }}(\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau }))e^{-{\int }_{\mathit{\eta }}^t(a+\mathit{\alpha }v(\mathit{\zeta }))d\mathit{\zeta }}d\mathit{\eta },\hfill \\ \hfill z(t)& =z(0)e^{-bt}+\underset{0}{\overset{t}{\int }}\mathit{\alpha }w(t)y(t)e^{-{\int }_{\mathit{\eta }}^t-b(t-\mathit{\zeta })d\mathit{\zeta }}d\mathit{\eta },\hfill \\ \hfill v(t)& =v(0)e^{-pt}+{\int }_0^{t}k{e}^{-p(t-\mathit{\eta })}d\mathit{\eta },\hfill \\ \hfill w(t)& =w(0)e^{-qt}+{\int }_0^{t}cz(\mathit{\eta })e^{-q(t-\mathit{\eta })}d\mathit{\eta }.\hfill \end{array}$$

Which clearly indicate that all the solutions are positive.

Let us define the following function to show the boundedness of the solution $(x(t),y(t),z(t),v(t),w(t))$:(6) $$\begin{array}{c}\hfill \mathrm{\Omega }(t)=ckx(t)+cky(t)+ckz(t)+\frac{ac}{2}v(t)+\frac{bk}{2}w(t).\end{array}$$(6)

Calculating the derivative of Equation (6), we obtain$$\begin{array}{cc}\hfill \frac{\text{d}\mathrm{\Omega }(t)}{\text{d}t}& =ck\left(\mathit{\lambda }-dx(t)-\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })\right)\hfill \\ \hfill & +ck\left(\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })-ay(t)-\mathit{\alpha }w(t)y(t)\right)\hfill \\ \hfill & +ck\left(aw(t)y(t)-bz(t)\right)+\frac{ac}{2}\left(ky(t)-pv(t)\right)+\frac{bk}{2}\left(cz(t)-qw(t)\right)\hfill \\ \hfill & =ck\mathit{\lambda }-\left(dckx(t)+\frac{a}{2}cky(t)+\frac{b}{2}ckz(t)+q\frac{bk}{2}w(t)+p\frac{ac}{2}v(t)\right)\hfill \\ \hfill & \le ck\mathit{\lambda }{e}^{-a\mathit{\tau }}-\mathrm{{\rm Y}}\mathrm{\Omega }(t).\hfill \end{array}$$

Here $\mathrm{{\rm Y}}=min\left\{d,\frac{a}{2},\frac{b}{2},q,p\right\}$. This means that $\mathrm{\Omega }(t)$ is bounded, so all the solutions $x(t),y(t),z(t),v(t)\text{and}w(t)$ are bounded.

The system (4) has the following three possible biologically meaningful equilibria: disease-free equilibrium $E^0(x_0,y_0,z_0,v_0,w_0)$, single-infection equilibrium $E^s(x_1,y_1,z_1,v_1,w_1)$ and double-infection equilibrium $E^d(x_2,y_2,z_2,v_2,w_2)$, which are given by$$\begin{array}{cc}\hfill E^0& =\left(\frac{\mathit{\lambda }}{d},0,0,0,0\right),\hfill \\ \hfill E^s& =\left(\frac{ap}{\mathit{\beta }k{e}^{-a\mathit{\tau }}},\frac{\mathit{\lambda }k\mathit{\beta }{e}^{-a\mathit{\tau }}-adp}{ka\mathit{\beta }{e}^{-a\mathit{\tau }}},0,\frac{\mathit{\lambda }k\mathit{\beta }{e}^{-a\mathit{\tau }}-adp}{pa\mathit{\beta }{e}^{-a\mathit{\tau }}},0\right),\hfill \\ \hfill E^d& =\left(\frac{(\mathit{\alpha }\mathit{\lambda }c+\mathit{\gamma }bq)p}{\mathit{\alpha }cdp+\mathit{\beta }kqb{e}^{-a\mathit{\tau }}},\frac{bq}{\mathit{\alpha }c},\frac{q}{\mathit{\alpha }c}\left(\frac{ck\mathit{\lambda }\mathit{\alpha }\mathit{\beta }{e}^{-a(\mathit{\tau })}-a\mathit{\alpha }cdp-abqk\mathit{\beta }{e}^{-a\mathit{\tau }}}{\mathit{\alpha }cdp+bkq\mathit{\beta }{e}^{-a\mathit{\tau }}}\right),\right.\hfill \\ \hfill & \left.\frac{kqb}{\mathit{\alpha }cp},\frac{\mathit{\alpha }ck\mathit{\beta }\mathit{\lambda }{e}^{-a(\mathit{\tau })}-a\mathit{\alpha }cdp-abqk\mathit{\beta }{e}^{-a\mathit{\tau }}}{\mathit{\alpha }(\mathit{\alpha }cdp+bkq\mathit{\beta }{e}^{-a\mathit{\tau }})}\right).\hfill \end{array}$$

The interpretation of each equilibrium point can be described as: $E^0$ is an infection-free equilibrium corresponding to maximal levels of healthy CD$+4$ T cells. The second equilibrium $E^s$ corresponds to positive levels of healthy CD$+4$ T cells, infected cells, pathogen virus, but not to recombinant virus. $E^d$ represent positive levels of healthy CD$+4$ T cells, infected cells, and both pathogen and recombinant virus.

The basic reproduction number (see Perelson & Nelson, 1999), can be defined as$$\begin{array}{c}\hfill R_0=\frac{k\mathit{\beta }\mathit{\lambda }{e}^{-a\mathit{\tau }}}{adp},\end{array}$$

where $\frac{\mathit{\lambda }}{d}$ is the density of healthy cells available for infection, $\frac{\mathit{\beta }{e}^{-a\mathit{\tau }}}{a}$ is the average number of host cells that each HIV infects and $\frac{k}{p}$ is the average number of virons that an infected cell produces. If $R_0<1$, then $E^0$ is the only biologically meaningful equilibrium. If $R_0>1$, there is another equilibrium $E^s$ but $E^d$ exists if and only if $R_d>1$, where$$\begin{array}{c}\hfill R_d=\frac{\mathit{\alpha }\mathit{\beta }\mathit{\lambda }ck{e}^{-a\mathit{\tau }}-\mathit{\alpha }cdpa}{\mathit{\beta }bkqa{e}^{-a\mathit{\tau }}}=\frac{a\mathit{\alpha }cdp}{\mathit{\beta }bkq{e}^{-a\mathit{\tau }}}(R_0-1).\end{array}$$

Let $R_s=1+\frac{\mathit{\beta }bkq{e}^{-a\mathit{\tau }}}{\mathit{\alpha }cdp}$, then $R_d>1$ if and only if $R_0>R_s$,

3. Local stability

In this section, we will show the local dynamical behavior of the system (4).

Theorem 3.1

When $R_0<1$, then the disease-free equilibrium $E^0$ is locally asymptotically stable while for $R_0>1$, $E^0$ becomes unstable and the single infection equilibrium $E^s$ occurs.

Proof

The linearized system of model (4) around $E^0$ can be written as(7) $$\begin{array}{cc}\hfill \dot{x}(t)& =-dx(t)-\mathit{\beta }{e}^{-a\mathit{\tau }}\frac{\mathit{\lambda }}{d}v(t-\mathit{\tau }),\hfill \\ \hfill \dot{y}(t)& =\mathit{\beta }{e}^{-a\mathit{\tau }}\frac{\mathit{\lambda }}{d}v(t-\mathit{\tau })-ay(t),\hfill \\ \hfill \dot{z}(t)& =-bz(t),\hfill \\ \hfill \dot{v}(t)& =ky(t)-pv(t),\hfill \\ \hfill \dot{w}(t)& =cz(t)-qw(t).\hfill \end{array}$$(7)

The characteristic equation corresponding to the Jacobian matrix of linearized system (7) is given by(8) $$\begin{array}{c}\hfill (b+\mathit{\rho })(d+\mathit{\rho })(q+\mathit{\rho })\left[(a+\mathit{\rho })(p+\mathit{\rho })-\frac{\mathit{\lambda }}{d}\mathit{\beta }k{e}^{-\mathit{\tau }(\mathit{\rho }+a)}\right].\end{array}$$(8)

where $\mathit{\rho }$ stands for eigne value. The three negative roots of the characteristic Equation (8) are $-b,-d$, and $-q$ and the remaining roots can be determined from the following equation:(9) $$\begin{array}{c}\hfill (a+\mathit{\rho })(p+\mathit{\rho })=\frac{\mathit{\lambda }}{d}\mathit{\beta }k{e}^{-\mathit{\tau }(\mathit{\rho }+a)}.\end{array}$$(9)

If $\mathit{\rho }$ has non-negative real part, then modulus of the left-hand side of Equation (9) satisfies$$\begin{array}{c}\hfill \left|(a+\mathit{\rho })(p+\mathit{\rho })\right|\ge ap.\end{array}$$

While modulus of the right hand side of (9) satisfies$$\begin{array}{c}\hfill \frac{\mathit{\lambda }}{d}\mathit{\beta }k|e^{-\mathit{\tau }(\mathit{\rho }+a)}|=|ap{R}_0|<ap.\end{array}$$

This leads to contradiction. Thus, when $R_0<1$, then all the eigne values have negative real part. Therefore, the infection free state $E^0$ is locally asymptotically stable. For $R_0>1$, we have$$\begin{array}{c}\hfill g(\mathit{\rho })=(a+\mathit{\rho })(p+\mathit{\rho })-\frac{\mathit{\lambda }}{d}\mathit{\beta }k{e}^{-\mathit{\tau }(\mathit{\rho }+a)}.\end{array}$$

Now $g(0)=ap(1-R_0)<0$ and ${lim}_{\mathit{\rho }\to \infty }g(\mathit{\rho })=+\infty$. By the continuity of $g(\mathit{\rho })$ there exists at least one positive root of $g(\mathit{\rho })=0$. Thus, the infection-free equilibrium $E^0$ is unstable if $R_0>1$.

Theorem 3.2

If $1<R_0<R_s$, then the recombinant present equilibrium $E^s$ is locally asymptotically stable while $E^s$ become unstable for $R_0>R_s$.

Proof

The linearized system of model (4) at $E^s(x_1,y_1,z_1,v_1,w_1)$ is given by(10) $$\begin{array}{cc}\hfill \dot{x}(t)& =-dx(t)-\mathit{\beta }{e}^{-a\mathit{\tau }}(x_{1}v(t-\mathit{\tau })+v_{1}x(t-\mathit{\tau })),\hfill \\ \hfill \dot{y}(t)& =\mathit{\beta }{e}^{-a\mathit{\tau }}(x_{1}v(t-\mathit{\tau })+v_{1}x(t-\mathit{\tau })-ay(t)-\mathit{\alpha }{y}_{1}w(t),\hfill \\ \hfill \dot{z}(t)& =\mathit{\alpha }{y}_{1}w(t)-bz(t),\hfill \\ \hfill \dot{v}(t)& =ky(t)-pv(t),\hfill \\ \hfill \dot{w}(t)& =cz(t)-qw(t).\hfill \end{array}$$(10)

The characteristic equation corresponding to the Jacobian matrix of system (10) can be written in simplified form as $f_1(\mathit{\rho })f_2(\mathit{\rho })=0$, where$$\begin{array}{cc}\hfill f_1(\mathit{\rho })& ={\mathit{\rho }}^2+(b+q)\mathit{\rho }+bq-\frac{c\mathit{\alpha }(\mathit{\lambda }k\mathit{\beta }{e}^{-a\mathit{\tau }}-adp)}{ak\mathit{\beta }{e}^{-a\mathit{\tau }}},\hfill \\ \hfill f_2(\mathit{\rho })& ={\mathit{\rho }}^3+\left(a+p+\frac{k\mathit{\beta }\mathit{\lambda }}{ap}{e}^{-a\mathit{\tau }}\right){\mathit{\rho }}^2+\left[\frac{k\mathit{\beta }\mathit{\lambda }}{ap}{e}^{-a\mathit{\tau }}(a+p)+ap\right]\mathit{\rho }\hfill \\ \hfill & +k\mathit{\beta }\mathit{\lambda }{e}^{-a\mathit{\tau }}-a(\mathit{\rho }+d)p{e}^{-\mathit{\rho }\mathit{\tau }}.\hfill \end{array}$$

Now $f_1(\mathit{\rho })$ can be simplified as$$f_1(\mathit{\rho })={\mathit{\rho }}^2+(b+q)\mathit{\rho }+bq(1-R_d),$$

which indicates that $f_1(\mathit{\rho })=0$ has two roots with negative real part if and only if $R^d<1$ (i.e. $R_0<R^s$), or one positive and one negative root if $R_2>1$ (i.e. $R_0>R_s$). Therefore, if $R_0>R_s$, then single-infection equilibrium $E_d$ is unstable. After some simplification $f_2(\mathit{\rho })=0$, can be written as(11) $$\begin{array}{c}\hfill {\mathit{\rho }}^3+a_2(\mathit{\tau }){\mathit{\rho }}^2+a_1(\mathit{\tau })\mathit{\rho }+a_0(\mathit{\tau })-(c_1\mathit{\rho }+c_2)e^{-\mathit{\rho }\mathit{\tau }}=0,\end{array}$$(11)

where$$\begin{array}{cc}\hfill a_2(\mathit{\tau })& =a+p+\frac{k\mathit{\beta }\mathit{\lambda }}{ap}{e}^{-a\mathit{\tau }},a_1(\mathit{\tau })=\frac{k\mathit{\beta }\mathit{\lambda }}{ap}{e}^{-a\mathit{\tau }}(a+p)+ap,\hfill \\ \hfill a_0(\mathit{\tau })& =k\mathit{\beta }\mathit{\lambda }{e}^{-a\mathit{\tau }},c_1=ap,c_2=apd.\hfill \end{array}$$

It is easy to see that $\mathit{\rho }=0$ is not a root of (11) if $R_0>1$, since$$a_0(\mathit{\tau })-c_2=k\mathit{\beta }\mathit{\lambda }{e}^{-a\mathit{\tau }}-apd=apd(R_0-1)>0.$$

When $\mathit{\tau }=0$, then (11) becomes(12) $$\begin{array}{c}\hfill {\mathit{\rho }}^3+a_2(0){\mathit{\rho }}^2+(a_1(0)-c_1)\mathit{\rho }+a_0(0)-c_2=0,\end{array}$$(12)

Applying the Routh–Hurwitz criterion (see Gantmacher, 1959), we know that all the roots of (12) have negative real part, because$$\begin{array}{cc}& a_2(0)=a+p+\frac{k\mathit{\beta }\mathit{\lambda }}{ap}>0,\hfill \\ \hfill & a_1(0)-c_1=\frac{k\mathit{\beta }\mathit{\lambda }}{ap}(a+p)>0,\hfill \\ \hfill & a_0(0)-c_2=apd(R_0{|}_{\mathit{\tau }=0}-1)>0.\hfill \end{array}$$

Similarly,$$\begin{array}{c}\hfill a_2(0)(a_1(0)-c_1)-(a_0(0)-c_2)=\frac{k^2{\mathit{\beta }}^2{\mathit{\lambda }}^2}{(a^2{p}^2}(a+p)+\frac{k\mathit{\beta }\mathit{\lambda }}{ap}{(a+p)}^2+apd>0\end{array}$$

Thus, any root of (11) has negative real part when $\mathit{\tau }=0$. Now, we consider the distribution of the roots when $\mathit{\tau }>0$. Let $\mathit{\rho }=i\mathit{\kappa }(\mathit{\kappa }>0)$ be the purely imaginary root of (11), then$$-i{\mathit{\kappa }}^3-a_2(\mathit{\tau }){\mathit{\kappa }}^2+i{a}_1(\mathit{\tau })\mathit{\kappa }+a_0(\mathit{\tau })-(i{c}_1\mathit{\kappa }+c_2)e^{-i\mathit{\kappa }\mathit{\tau }}=0.$$

The modula of the above equation result in(13) $$\begin{array}{c}\hfill G({\mathit{\kappa }}^2)={\mathit{\kappa }}^6+[a_2^2(\mathit{\tau })-2a_1(\mathit{\tau })]{\mathit{\kappa }}^4+[a_1^2(\mathit{\tau })-2a_0(\mathit{\tau })a_2(\mathit{\tau })-c_1^2]{\mathit{\kappa }}^2+a_0^2(\mathit{\tau })-c_2^2=0.\end{array}$$(13)

Since$$\begin{array}{cc}& a_2^2(\mathit{\tau })-2a_1(\mathit{\tau })]=a^2+p^2+d^2{R}_0^2>0,\hfill \\ \hfill & a_1^2(\mathit{\tau })-2a_0(\mathit{\tau })a_2(\mathit{\tau })-c_1^2=d^2[(a^2+p^2]R_0^2>0,\hfill \\ \hfill & a_0^2(\mathit{\tau })-c_2^2=a^2{p}^2{d}^2(R_0^2-1)>0,\hfill \end{array}$$

Thus, all the coefficients of $G({\mathit{\kappa }}^2)$ are positive. Therefore, the function $G({\mathit{\kappa }}^2)$ is monotonically increasing for $0\le {\mathit{\kappa }}^2<\infty$ with $G(0)>0$. This implies that Equation (13) has no positive roots if $R_0>1$. Hence, all the roots of (11) have negative real parts for $\mathit{\tau }>0$ if $R_0>1$.

4. Global stability

In this section, we will study the global stability of equilibria of system (4) by using suitable Lyapunov functionals and LaSalles invariant principle.

Theorem 4.1

When $R_0<1$ the disease-free equilibrium $E_0$ is globally asymptotically stable.

Proof

Let us consider the following Lyapunov functional(14) $$\begin{array}{cc}\hfill V_i(t)& =\frac{1}{2}{\left(x(t)-\frac{\mathit{\lambda }}{d}\right)}^2+\frac{\mathit{\lambda }}{d}y(t)+\frac{\mathit{\lambda }}{d}z(t)+\frac{a\mathit{\lambda }}{kd}v(t)+\frac{b\mathit{\lambda }}{cd}w(t)\hfill \\ \hfill & +\frac{\mathit{\beta }\mathit{\lambda }}{d}{e}^{-a\mathit{\tau }}{\int }_{t-\mathit{\tau }}^{t}x(\mathit{\zeta })v(\mathit{\zeta })d(\mathit{\zeta }),\hfill \\ \hfill \end{array}$$(14)

where $V_i(t)$ stands for Lyapunov functional at $E^0$, the derivative of (14) and the use of (4), yield the following equation$$\begin{array}{cc}\hfill \dot{V_i}(t)& =\left(x(t)-\frac{\mathit{\lambda }}{d}\right)\left(\mathit{\lambda }-dx(t)-\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })\right)\hfill \\ \hfill & +\frac{\mathit{\lambda }}{d}\left(\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })-ay(t)-\mathit{\alpha }w(t)y(t)\right)\hfill \\ \hfill & +\frac{\mathit{\lambda }}{d}\left(\mathit{\alpha }w(t)y(t)-bz(t)\right)+\frac{a\mathit{\lambda }}{kd}\left(ky(t)-pv(t)\right)+\frac{b\mathit{\lambda }}{cd}\left(cz(t)-qw(t)\right)\hfill \\ \hfill & +\frac{\mathit{\beta }\mathit{\lambda }}{d}{e}^{-a\mathit{\tau }}{\int }_{t-\mathit{\tau }}^{t}x(\mathit{\zeta })v(\mathit{\zeta })d(\mathit{\zeta })\hfill \\ \hfill \end{array}$$

After further simplification, the above equation becomes(15) $$\begin{array}{cc}\hfill \dot{V_i}(t)& =-\left(x(t)-\frac{\mathit{\lambda }}{d}\right)\left(\left(x(t)-\frac{\mathit{\lambda }}{d}\right)+\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })\right)+\frac{ap\mathit{\lambda }}{dk}\left(\frac{k\mathit{\beta }\mathit{\lambda }{e}^{-a\mathit{\tau }}}{adp}-1\right)v(t)-\frac{qb\mathit{\lambda }}{cd}w(t),\hfill \\ \hfill & =-\left(x(t)-\frac{\mathit{\lambda }}{d}\right)\left(\left(x(t)-\frac{\mathit{\lambda }}{d}\right)+\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })\right)-\frac{ap\mathit{\lambda }}{dk}(1-R_0)v(t)-\frac{qb\mathit{\lambda }}{cd}w(t).\hfill \end{array}$$(15)

Thus, when $R_0<1$, then Equation (15) implies that $\dot{V_i}(t)<0$ and the equality holds if and only if $x_0=\frac{\mathit{\lambda }}{d}$, $y(t)=0$, $z(t)=0$, $v(t)=0$, $w(t)=0$. Therefore, by LaSalle’s invariance principle (see LaSalle, 1976), we conclude that $E_0$ is globally asymptotically stable when $R_0<1$.

Theorem 4.2

For $1<R_0<R_s$, the single infection equilibrium $E^s$ is globally asymptotically stable.

Proof

Let us construct the Lyapunove functional(16) $$\begin{array}{cc}\hfill V_s(t)& =(x-x_{1}lnx)+(y-y_{1}lny)+z+\frac{a}{k}(v-v_{1}lnv)+\frac{b}{c}w\hfill \\ \hfill & +x_1{v}_1\mathit{\beta }{e}^{-a\mathit{\tau }}\underset{t-\mathit{\tau }}{\overset{t}{\int }}\left(\frac{x(\mathit{\theta })v(\mathit{\theta })}{v_{1}x(\mathit{\theta }+\mathit{\tau })}-lnx(\mathit{\theta })v(\mathit{\theta })\right)d\mathit{\theta }.\hfill \end{array}$$(16)

where $V_s(t)$ stands for Lyapunov function at single infection equilibrium $E^s$. The derivative of Equation (16) yields(17) $$\begin{array}{cc}\hfill \dot{V_s}(t)& =\left(1-\frac{x_1}{x}\right)\dot{x}+\left(1-\frac{y_1}{y}\right)\dot{y}+\dot{z}+\frac{a+\mathit{\gamma }}{k}\left(1-\frac{v_1}{v}\right)\dot{v}+\frac{b}{c}\dot{w}+x_1{v}_1\mathit{\beta }{e}^{-a\mathit{\tau }}\left(\frac{x(t)v(t)}{x(t+\mathit{\tau })v_1}\right.\hfill \\ \hfill & \left.-\frac{x(t-\mathit{\tau })v(t-\mathit{\tau })}{x(t)v_1}-ln(x(t)v(t))+ln(x(t-\mathit{\tau })v(t-\mathit{\tau }))\right)\hfill \\ \hfill & =\left(1-\frac{x_1}{x}\right)(\mathit{\lambda }-dx(t)-\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })+\mathit{\gamma }y(t))\hfill \\ \hfill & +\left(1-\frac{y_1}{y}\right)(\mathit{\beta }{e}^{-a\mathit{\tau }}x(t-\mathit{\tau })v(t-\mathit{\tau })-(a+\mathit{\gamma })y(t)-\mathit{\alpha }w(t)y(t))\hfill \\ \hfill & +\mathit{\alpha }w(t)y(t)-bz(t)+\frac{a}{k}\left(1-\frac{v_1}{v}\right)(ky(t)-pv(t))+\frac{b}{c}(cz(t)-qw(t))\hfill \\ \hfill & +x_1{v}_1\mathit{\beta }{e}^{-a\mathit{\tau }}\left(\frac{x(t)v(t)}{x(\mathit{\tau }+t)v_1}-\frac{x(t-\mathit{\tau })v(t-\mathit{\tau })}{x(t)v_1}+ln\frac{x(t-\mathit{\tau })v(t-\mathit{\tau }))}{(x(t)v(t)}\right).\hfill \end{array}$$(17)

The model (4) at single-infection equilibrium $E^s(x_1,y_1,z_1,v_1,w_1)$ becomes$$\begin{array}{c}\hfill \mathit{\lambda }=d{x}_1+\mathit{\beta }{e}^{-a\mathit{\tau }}{x}_1{v}_1,\mathit{\beta }{e}^{-a\mathit{\tau }}{x}_1{v}_1=a{y}_1,k{y}_1=p{v}_1.\end{array}$$

If $\mathit{\tau }$ is very large, i.e. when delay in contact of targeted cells with virus and the latent period is very large, then the rate of infection will be very small and contrarily if $\mathit{\tau }$ is very small, then the infection will spread more rapidly. Therefore, we suppose that delay is very large, then(18) $$\begin{array}{c}\hfill \underset{\mathit{\tau }\to \infty }{lim}(x(t+\mathit{\tau }))=x(t).\end{array}$$(18)

Therefore, Equation (17) becomes(19) $$\begin{array}{cc}\hfill \dot{V_s}(t)& =d{x}_1\left(2-\frac{x}{x_1}-\frac{x_1}{x}\right)+\mathit{\beta }{e}^{-a\mathit{\tau }}{x}_1{v}_1\left(3-\frac{x_1}{x}-\frac{y{v}_1}{y_{1}v}-\frac{y_{1}x(t-\mathit{\tau })v(t-\mathit{\tau })}{y{x}_1{v}_1}\right.\hfill \\ \hfill & \left.+ln\frac{x(t-\mathit{\tau })v(t-\mathit{\tau })}{xv}\right)+\frac{\mathit{\alpha }dp}{\mathit{\beta }k}(R_0-R_1)w(t).\hfill \end{array}$$(19)

The following inequalities hold$$\begin{array}{cc}& 2-\frac{x}{x_1}-\frac{x_1}{x}\le 0,\hfill \\ \hfill & 3-\frac{x_1}{x}-\frac{y{v}_1}{y_{1}v}-\frac{y_{1}x(t-\mathit{\tau })v(t-\mathit{\tau })}{y{x}_1{v}_1}+ln\frac{x(t-\mathit{\tau })v(t-\mathit{\tau })}{xv}\le 0.\hfill \end{array}$$

By using the above inequalities, Equation (19) implies that $\frac{\text{d}{V}_s}{\text{d}t}<0$ when $R_0<R_s$, and the equality holds when $x=x_1,y=y_1,z=0,v=v_1,w=0$. Then, by LaSalle’s invariance principle (LaSalle, 1976), we conclude that $E^s$ is globally asymptotically stable.

5. Numerical simulation

In this section, we illustrate the theoretical results obtained in previous sections numerically. We discuss some numerical results and simulations by using dde23 from the software MATLAB R2010a. These results show that delays play an important role in determining the dynamic behavior of the HIV-1 modeling. The delay can change the dynamic behavior quantitatively.

For numerical simulation, we have taken some of the values estimated and some of them experimental. $\mathit{\lambda }=2$ (Density of CD$4+$ T cells in the healthy human blood is $\acute{X}=1,000cell/m{m}^3$ (Michie, McLean, Alcock, & Beverly, 1992). Assumed equilibrium, their production $\acute{\mathit{\lambda }}$ equal loss $\acute{\mathit{\lambda }}=\acute{X}d$. Assumed that a fraction $\mathit{\mu }=0.2$ of new generated cells are activated $\mathit{\lambda }=\acute{\mathit{\lambda }}\mathit{\mu }=2$ (Herelle, 1926)). $d=0.01$ (Average life span of CD4+T cell is two years, so $d=0:0014$ (Michie et al., 1992). From modeling, $d=0.01$ (Stafford et al., 2000)). $\mathit{\beta }=0.004{\text{mm}}^3/\text{vir}$ (Assumed indirectly as a small value that preserves both infections. For single infection $\mathit{\beta }=0:00027$ (Michie et al., 1992)), $\mathit{\beta }=0:00065$ (Stafford et al., 2000)). $a=0.5$ (Based on life span of HIV-1 infected cells of three days (Michie et al., 1992). Also, Other estimates: $a=0.49$ (Perelson, Neumann, Markowitz, Leonard, & Ho, 1996), $a=0.39$ (Michie et al., 1992)). $\mathit{\alpha }=0.004$ (Estimated indirectly as a small value that preserves the double infection. Taken identical to $\mathit{\beta }$). $b=2$ (Based on observations of virus release within 8 h of infection before lysis (Schnell, Johnson, Buonocore, & Rose, 1997)). $p=3$ (Based on life span of 1 / 2 day (Michie et al., 1992). Another value, $p=3$ (Perelson et al., 1996)). $k=50\text{vir/cell}$ ($k=n_{1}a$. $n_1$ is total number of infectious HIV-1 produced by a cell: $n_1\sim 140$ (Ali, Zaman, & Chohan, 2016; Layne, Spouge, & Dembo, 1989). $c=2,000\text{vir/cell}$ ($c=n_{2}b$. $n_2$ is total number of infectious re-combinant produced by a double-infected cell. In vitro total number of recombinants per cell is $\sim 3333$ (Schnell et al., 1997). Assumed $n_2=1,000$). $q=p$ (estimated identical to p). $\mathit{\tau }=1.0\sim 1.5$ days (Estimated).

Figure 1. Simulation of system (4) for $\mathit{\tau }=1.5$.

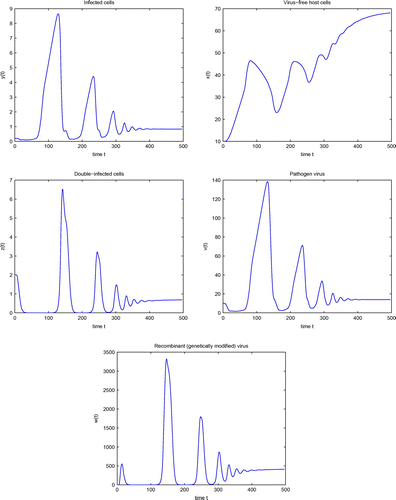
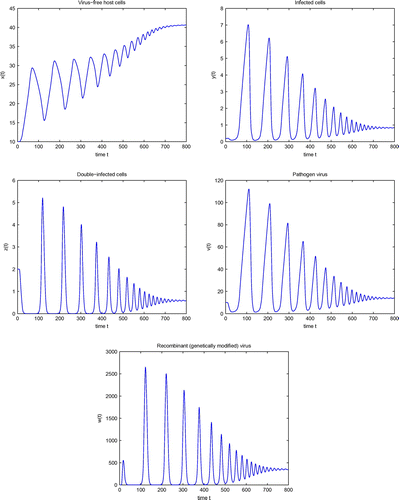
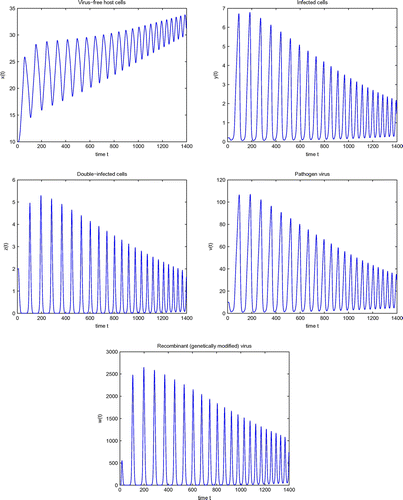
Figure 1 shows the simulation of system (4) at $\mathit{\tau }=1.5$ and represents convergence to the stable equilibrium $E^s$. If we decrease the value further, i.e. $\mathit{\tau }=0.7$, then $E^s$ will lose its stability and the double-infection equilibrium $E^d$ will occur, which is shown in Figure 2. Simulation of system (4) for $\mathit{\tau }=0.4$ are shown in Figure 3. Comparing the results in Figure 3 with that in Figure 1 shows that the solution trajectory takes longer to converge to its steady-state value, as we see that all the components have more oscillating behaviors having amplitude very large, and they take longer time to converge to $E^d$. Also, it can be noted that the amplitudes of the oscillations increases. Therefore, the incorporation of even small delay in model (4) can produce significant quantitative changes in its solutions. This significance of delay can not be seen from the model without delay. Hence, time delays are very important for the modeling of HIV-1 infection and cannot be ignored.

Figure 2. Simulation of system (4) for $\mathit{\tau }=0.7$.

Figure 3. Simulation of system (4) for $\mathit{\tau }=0.4$.

6. Conclusion

In this paper, a delayed HIV-1 model is presented. It has been shown that our proposed model with delay has three equilibrium solutions: the disease-free equilibrium $E^0$, single-infection equilibrium $E^s$, and double-infection equilibrium $E^d$. Also, we have shown that a series of bifurcations occur as the basic reproduction number $R_0$ is increased. It is noted that to reduce the density of pathogen virus, a strategy should aim to reduce the value of $R_0$ to below one. From the derived formula for $R_0$, we see that $R_0$ can be decreased by increasing either of the time delays. Also, the incorporation of intracellular delay plays a positive role in preventing the virus. It is observed that keeping all other parameters fixed, larger $\mathit{\tau }$ can bring $R_0$ to a level lower than one, making the infection-free equilibrium point globally asymptotically stable. It has been shown that $E^0$ is locally as well as globally asymptotically stable for $R_0\in (0,1)$, and becomes unstable at the transcritical bifurcation point $R_0=1$, and bifurcates into $E^s$, which is stable for $R_0\in (1,R_s)$. Time delay may change dynamic behavior quantitatively and qualitatively even in the normal range of values. Therefore, time delay is a very important fact and cannot be ignored for reducing the infection of HIV-1.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Nigar Ali

Nigar Ali has done his MSc mathematics from university of peshawer, Pakistan and MPhil in Mathematics from Malakand University, Pakistan. He is a PhD scholar in Department of Mathematics, UOM, Pakistan. His area of interest includes biomathematics, fractional differential equations, and fluid mechanics.

Gul Zaman

Gul Zaman is working as an associate professor in Department of Mathematics, UOM, Pakistan. He has many research papers and attended several national and international conferences and seminars. His area of interest includes biomathematics, fractional differential equations, and fluid mechanics.

Muhammad Ikhlaq Chohan

Muhammad Ikhlaq Chohan is an assistant professor at Department of Business Administration and Accounting, Buraimi University College, AlBuraimi, Oman. His area of interest includes biomathematics and applied mathematics.