New group iterative schemes in the numerical solution of the two-dimensional time fractional advection-diffusion equation

Abstract

Numerical schemes based on small fixed-size grouping strategies have been successfully researched over the last few decades in solving various types of partial differential equations where they have been proven to possess the ability to increase the convergence rates of the iteration processes involved. The formulation of these strategies on fractional differential equations, however, is still at its infancy. Appropriate discretization formula will need to be derived and applied to the time and spatial fractional derivatives in order to reduce the computational complexity of the schemes. In this paper, the design of new group iterative schemes applied to the solution of the 2D time fractional advection-diffusion equation are presented and discussed in detail. The Caputo fractional derivative is used in the discretization of the fractional group schemes in combination with the Crank–Nicolson difference approximations on the standard grid. Numerical experiments are conducted to determine the effectiveness of the proposed group methods with regard to execution times, number of iterations, and computational complexity. The stability and convergence properties are also presented using a matrix method with mathematical induction.The numerical results will be proven to agree with the theoretical claims.

Keywords:

• group methods
• two-dimensional problem
• time fractional advection-diffusion
• Caputo fractional derivative
• Crank–Nicolson difference schemes
• stability & convergence analysis

Public Interest Statement

Many phenomena in science and engineering can be modelled as two dimensional fractional advection-diffusion equations satisfying appropriate initial and boundary conditions. With the advent of computing technology, effective numerical methods have been extensively formulated in solving these equations due to their simplicity and accuracy. In particular, finite difference formulas, are oftenly used to numerically discretize the differential equations to produce sparse systems of linear equations which may be suitably solved by iterative solvers. However, iterative solvers have the disadvantage of being too slow to converge which may increase the computation timings. To overcome this problem, suitable small fixed-size grouping strategies are applied to the mesh points of the solution domain following the discretization of the differential equation which results in schemes with faster convergence and lower computational complexity with comparable accuracies. This is very useful to engineers and scientists who are involved in time consuming simulation modeling processes.

1. Introduction

Fractional calculus, which is the calculus of integrals and derivatives in random order, dates back as far as the more popular integer calculus, and has been gaining significant interest over the past few years with its history and development being explored in detail by Oldham and Spanier (1974), Miller and Ross (1993), Samko, Kilbas, and Marichev (1993) and Podlubny (1998). Fractional differential equations (FDEs) can be used to model many problems in a wide field of applications. They are defined as equations that utilize fractional derivatives and considered as powerful tools that can describe the memory and hereditary characteristics of various materials. Several researchers have explored the use of FDEs in the fields of chemistry (Gorenflo, Mainardi, Moretti, Pagnini, & Paradisi, 2002; Seki, Wojcik, & Tachiya, 2003), physics (Henry & Wearne, 2000; Metzler, Barkai, & Klafter, 1999; Metzler & Klafter, 2000; Wyss, 1986) and other scientific and engineering spheres (Baeumer, Benson, Meerschaert, & Wheatcraft, 2001; Benson, Wheatcraft, & Meerschaert, 2000; Cushman & Ginn, 2000; Mehdinejadiani, Naseri, Jafari, Ghanbarzadeh, & Baleanu, 2013). Since there are at most no exact solutions to the majority of fractional differential equations, it is necessary to resort to approximation and numerical methods (Abdelkawy, Zaky, Bhrawy, & Baleanu, 2015; Balasim & Ali, 2015; Baleanu, Agheli, & Al Qurashi, 2016; Bhrawy & Baleanu, 2013). Over the past decade, there has been an influx of numerical methods development for solving various types of FDEs (Agrawal, 2008; Ali, Abdullah, & Mohyud-Din, 2017; Chen, Deng, & Wu, 2013; Chen & Liu, 2008; Chen, Liu, Anh, & Turner, 2011; Chen, Liu, & Burrage, 2008; Leonenko, Meerschaert, & Sikorskii, 2013; Li, Zeng, & Liu, 2012; Liu, Zhuang, Anh, Turner, & Burrage, 2007; Shen, Liu, & Anh, 2011; Sousa & Li, 2015; Su, Wang, & Wang, 2011; Uddin & Haq, 2011; Zhang, Huang, Feng, & Wei, 2013; Zheng, Li, & Zhao, 2010; Zhuang, Gu, Liu, Turner, & Yarlagadda, 2011; Zhuang, Liu, Anh, & Turner, 2009).

Chen et al. (2008) used implicit and explicit difference techniques to solve time fractional reaction-diffusion equations, while Liu et al. (2007) proposed for these techniques to be employed in solving the space-time fractional advection-dispersion equation by replacing the first-order time derivative by the Caputo fractional derivative, and the first-order and second-order space derivatives by the Riemman–Liouville fractional derivatives. The use of radial basis function (RBF) approximation method was discussed in Uddin and Haq (2011) to solve the time fractional advection-dispersion equation in a bounded domain. The application of finite element method was also seen in Zheng et al. (2010), in solving the space fractional advection-diffusion equation under non-homogeneous initial boundary conditions. In Chen et al. (2011), a numerical method with first-order temporal accuracy and second-order spatial accuracy was established for solving the variable order Galilei advection-diffusion equation with a nonlinear source term, while Zhuang et al. (2009) used the explicit and implicit Euler approximation to solve a variable order fractional advection-diffusion equation with a nonlinear source term. A new numerical solution for the 2D fractional advection-dispersion equation with variable coefficients in a finite field was also introduced by Chen and Liu (2008). In 2011, Shen et al. (2011) proposed the explicit and implicit finite difference approximations for the space-time Riesz–Caputo fractional advection-diffusion equation where the implicit scheme was proven to be unconditionally stable, while the explicit scheme exhibits a conditionally stable property. The development of an implicit meshless method was also seen in Zhuang et al. (2011) in solving the time-dependent fractional advection-diffusion equation where a discretized system of equations was obtained using the moving least squares (MLS) meshless shape functions.

In general, finding numerical solutions to FDEs using iterative finite difference schemes is not a straightforward process and can be a challenging task due to several reasons. Firstly, all the earlier solutions have to be saved if the current solution is to be computed, making the calculations even more complex and costly in terms of CPU usage time in cases where traditional point implicit difference approaches are used. Secondly, although the point implicit techniques are stable, a significant amount of CPU usage time is required when many unknowns are involved. In recent decades, grouping strategies have been proven to possess characteristics that are able to reduce the spectral radius of the generated matrix resulting from the finite difference discretization of the differential equation, and therefore increase the convergence rates of the iterative algorithms. They have been shown to reduce the computational timings compared to their point wise counterparts in solving several types of partial differential equation (Ali & Kew, 2012; Evans & Yousif, 1986; Kew & Ali, 2015; Ng & Ali, 2008; Othman & Abdullah, 2000; Tan, Ali, & Lai, 2012; Yousif & Evans, 1995). These group methods are also easy to implement and suitable to be implemented on parallel computers due to their explicit nature. However, till date these strategies have not been tested on solving FDEs, particularly for the 2D cases. Therefore, in this study, the formulation of new group iterative methods is presented in solving the following 2Dl time fractional advection diffusion equation(1) $$\begin{array}{c}\hfill \frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}=a_x\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+a_y\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}-b_x\frac{\mathit{\partial }u}{\mathit{\partial }x}-b_y\frac{\mathit{\partial }u}{\mathit{\partial }y}+f\left(x,y,t\right),\end{array}$$(1)

where $0<\mathit{\alpha }<1,a_x,a_y,b_x,b_y$ are positive constants and f(x, y, t) is nonhomogeneous term subjected to the following initial and Dirichlet boundary conditions$$\begin{array}{cc}& u(x,y,0)=g(x,y)\hfill \\ \hfill & u(0,y,t)=g_1(y,t)u(1,y,t)=g_2(y,t)\hfill \\ \hfill & u(x,0,t)=g_3(x,t)u(x,1,t)=g_4(x,t)\hfill \end{array}$$

This equation plays an important role in describing transport dynamics in complex systems which are governed by anomalous diffusion and non-exponential relaxation patterns (Zhuang, Gu, Liu, Turner, & Yarlagadda, 2011). This paper is outlined as follows. Section 2 presents the proposed group iterative methods obtained from the Crank–Nicolson difference approximation followed by the stability and convergence analysis of the difference schemes in Sections 3 and 4, respectively. Section 5 presents the discussion on the computational effort involved in solving Equation (1) using the proposed methods with regard to the arithmetic operations for each iteration. Finally, the results of the numerical experiments are presented and discussed in Section 6.

2. Standard approximation schemes for fractional advection-diffusion equations

The Caputo fractional derivative, $D^{\mathit{\alpha }}$, of the order-$\mathit{\alpha }$ is expressed as follows (Li, Qian, & Chen, 2011):(2) $$\begin{array}{c}\hfill D^{\mathit{\alpha }}=\frac{1}{\mathrm{\Gamma }(m-\mathit{\alpha })}\underset{0}{\overset{x}{\int }}\frac{f^m(t)}{{(x-t)}^{\mathit{\alpha }-m+1}}dt,\mathit{\alpha }>0,m-1<\mathit{\alpha }<m,m\in N,x>0,\end{array}$$(2)

where $\mathrm{\Gamma }(·)$ is the Euler Gamma function. Further details on the definitions and properties of fractional derivatives are available in Podlubny (1998).

We need to apply appropriate finite difference approximations to the time and space derivaties of (1), let $h>0$ be the space step and $k>0$ be the time step. The domain is assumed to be uniform in both x and y directions. Define $x_i=ih,y_j=jh$, $\{i,j=0,1,$...$,n\},$ and a mesh size of $h=\frac{1}{n}$, where n is an arbitrary positive integer and $t_k=k\mathit{\tau },k=0,1,$..., l. various approximations formulas could be obtained for (1) at the point of $(x_i,y_j,t_k)$. By taking the average of the central difference approximations to the left side of (1) at the points $(i,j,k+1)$ and $(i,j,k)$, the Caputo time fractional approximation (2) can be transformed to the following form (Karatay, Kale, & Bayramoglu, 2013)(3) $$\begin{array}{c}\hfill \begin{array}{c}\frac{{\mathit{\partial }}^{\mathit{\alpha }}u(x_i,y_j,t_{k+1})}{\mathit{\partial }{t}^{\mathit{\alpha }}}=w_1{u}^k+{\sum }_{s=1}^{k-1}\left[w_{k-s+1}-w_{k-s}\right]u_{i,j}^s-w_k{u}_{i,j}^0+\mathit{\sigma }\frac{\left(u_{i,j}^{k+1}-u_{i,j}^k\right)}{2^{1-\mathit{\alpha }}}\hfill \\ +O({\mathit{\tau }}^{2-\mathit{\alpha }}),\hfill \end{array}\end{array}$$(3)

where $\mathit{\sigma }=\frac{1}{{\mathit{\tau }}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha })},w_s=\mathit{\sigma }({(s+\frac{1}{2})}^{1-\mathit{\alpha }}-{(s-\frac{1}{2})}^{1-\mathit{\alpha }})$.

Using (3) in combination with the second-order Crank–Nicolson difference scheme for the right side of (1) will result in the following fractional standard point (FSP) formula(4) $$\begin{array}{c}\hfill \begin{array}{c}{w}_1{u}^k+{\sum }_{s=1}^{k-1}\left[w_{k-s+1}-w_{k-s}\right]u_{i,j}^s-w_k{u}_{i,j}^0+\mathit{\sigma }\frac{\left(u_{i,j}^{k+1}-u_{i,j}^k\right)}{2^{1-\mathit{\alpha }}}\hfill \\ =\frac{a_x}{2}\left(\frac{u_{i-1,j}^{k+1}-2u_{i,j}^{k+1}+u_{i+1,j}^{k+1}}{h^2}+\frac{u_{i-1,j}^k-2u_{i,j}^k+u_{i+1,j}^k}{h^2}\right)\hfill \\ +\frac{a_y}{2}\left(\frac{u_{i,j-1}^{k+1}-2u_{i,j}^{k+1}+u_{i,j+1}^{k+1}}{h^2}+\frac{u_{i,j-1}^k-2u_{i,j}^k+u_{i,j+1}^k}{h^2}\right)-\frac{b_x}{2}\left(\frac{u_{i+1,j}^{k+1}-u_{i-1,j}^{k+1}}{2h}+\frac{u_{i+1,j}^k-u_{i-1,j}^k}{2h}\right)\hfill \\ -\frac{b_y}{2}\left(\frac{u_{i,j+1}^{k+1}-u_{i,j-1}^{k+1}}{2h}+\frac{u_{i,j+1}^k-u_{i,j-1}^k}{2h}\right)+f_{i,j}^{k+\frac{1}{2}}+O({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2).\hfill \end{array}\end{array}$$(4)

Equation (4) can be simplified to become as follows(5) $$\begin{array}{c}\hfill \begin{array}{c}\left(1+s_x+s_y\right)u_{i,j}^{k+1}=(\frac{s_x}{2}+\frac{c_x}{4})u_{i-1,j}^{k+1}+(\frac{s_x}{2}-\frac{c_x}{4})u_{i+1,j}^{k+1}+(\frac{s_y}{2}+\frac{c_y}{4})u_{i,j-1}^{k+1}\hfill \\ +(\frac{s_y}{2}-\frac{c_y}{4})u_{i,j+1}^{k+1}+\left(1-2^{1-\mathit{\alpha }}{w}_1^{\ast }-s_x-s_y\right)u_{i,j}^k+(\frac{s_x}{2}+\frac{c_x}{4})u_{i-1,j}^k\hfill \\ +(\frac{s_x}{2}-\frac{c_x}{4})u_{i+1,j}^k+(\frac{s_y}{2}+\frac{c_y}{4})u_{i,j-1}^k+(\frac{s_y}{2}-\frac{c_y}{4})u_{i,j+1}^k+2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j}^0\hfill \\ +2^{1-\mathit{\alpha }}{\sum }_{s=1}^{k-1}\left[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }\right]u_{i,j}^s+m_0{f}_{i,j}^{k+1/2}\hfill \end{array}\end{array}$$(5)

where $m_0=2^{1-\mathit{\alpha }}{t}^{\mathit{\alpha }}\mathrm{\Gamma }(2-\mathit{\alpha }),w_s^{\ast }=\left({(s+1/2)}^{1-\mathit{\alpha }}-{(s-1/2)}^{1-\mathit{\alpha }}\right)$, $s_x=\frac{a_x{m}_0}{h^2},s_y=\frac{a_y{m}_0}{h^2},c_x=\frac{b_x{m}_0}{h},c_y=\frac{b_y{m}_0}{h}.$

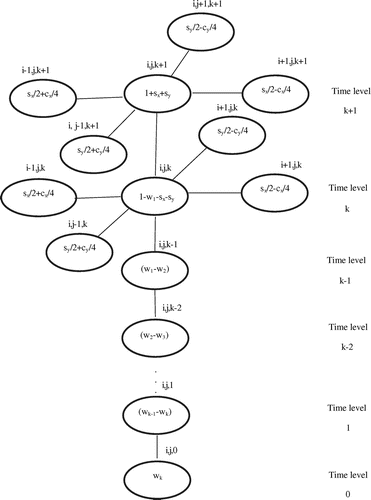
Figure 1 shows the computational molecule for Equation (5).

Figure 1. Computational molecule of the standard point approximation.

2.1. Fractional explicit group method

In formulating the fractional explicit group (FEG) method, (5) is applied to any group of four points in the solution domain to generate a $4\times 4$ system of equation as follows(6) $$\begin{array}{c}\hfill \left(\begin{array}{cccc}D& -a_1& 0& -b_1\\ -a_2& D& -b_1& 0\\ 0& -b_2& D& -a_2\\ -b_2& 0& -a_1& D\end{array}\right)\left(\begin{array}{c}{u}_{i,j}\\ u_{i+1,j}\\ u_{i+1,j+1}\\ u_{i,j+1}\end{array}\right)=\left(\begin{array}{c}rh{s}_{i,j}\\ rh{s}_{i+1,j}\\ rh{s}_{i+1,j+1}\\ rh{s}_{i,j+1}\end{array}\right),\end{array}$$(6)

where $D=1+s_x+s_y,a_1=\left(\frac{s_x}{2}-\frac{c_x}{4}\right),b_1=\left(\frac{s_y}{2}-\frac{c_y}{4}\right),a_2=\left(\frac{s_x}{2}+\frac{c_x}{4}\right),b_2=\left(\frac{s_y}{2}+\frac{c_y}{4}\right),$$R=(1-2^{1-\mathit{\alpha }}{w}_1^{\ast }-s_x-s_y),$$$\begin{array}{cc}\hfill rh{s}_{i,j}=& a_2(u_{i-1,j}^{k+1}+u_{i-1,j}^k)+b_2(u_{i,j-1}^{k+1}+u_{i,j-1}^k)+a_1{u}_{i+1,j}^k+b_1{u}_{i,j+1}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j}^0+R{u}_{i,j}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i.j}^s+m_0{f}_{i,j}^{k+1/2},\hfill \\ \hfill rh{s}_{i+1,j}=& a_1(u_{i+2,j}^{k+1}+u_{i+2,j}^k)+b_2(u_{i+1,j-1}^{k+1}+u_{i+1,j-1}^k)+b_1{u}_{i+1,j+1}^k+a_2{u}_{i,j}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i+1,j}^0+R{u}_{i+1,j}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i+1,j}^s+m_0{f}_{i+1,j}^{k+1/2},\hfill \\ \hfill rh{s}_{i+1,j+1}=& a_1(u_{i+2,j+1}^{k+1}+u_{i+2,j+1}^k)+b_1(u_{i+1,j+2}^{k+1}+u_{i+1,j+2}^k)+b_2{u}_{i+1,j}^k+a_2{u}_{i,j+1}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i+1,j+1}^0+R{u}_{i+1,j+1}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i+1,j+1}^s+m_0{f}_{i+1,j+1}^{k+1/2},\hfill \\ \hfill rh{s}_{i,j+1}=& a_2(u_{i-1,j+1}^{k+1}+u_{i-1,j+1}^k)+b_1(u_{i,j+2}^{k+1}+u_{i,j+2}^k)+a_1{u}_{i+1,j+1}^k+b_2{u}_{i,j}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j+1}^0+R{u}_{i,j+1}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i,j+1}^s+m_0{f}_{i,j+1}^{k+1/2}.\hfill \end{array}$$

Mathematical software can be used to easily invert (6) to obtain the FEG formula(7) $$\begin{array}{c}\hfill \left(\begin{array}{c}{u}_{i,j}\hfill \\ u_{i+1,j}\hfill \\ u_{i+1,j+1}\hfill \\ u_{i,j+1}\hfill \end{array}\right)=\frac{1}{r}\left(\begin{array}{cccc}{r}_1\hfill & r_2\hfill & r_3\hfill & r_4\hfill \\ r_5\hfill & r_1\hfill & r_4\hfill & r_6\hfill \\ r_7\hfill & r_8\hfill & r1\hfill & r_5\hfill \\ r_8\hfill & r_9\hfill & r_2\hfill & r_1\hfill \end{array}\right)\left(\begin{array}{c}rh{s}_{i,j}\hfill \\ rh{s}_{i+1,j}\hfill \\ rh{s}_{i+1,j+1}\hfill \\ rh{s}_{i,j+1}\hfill \end{array}\right),\end{array}$$(7)

where$$\begin{array}{cc}\hfill r=& \frac{1}{256}(c_x^4+c_y^4+8c_y^2\left(4+5s_x^2+8s_y+3s_y^2+8s_x\left(1+s_y\right)\right)+16[9s_x^4+48s_x^3\left(1+s_y\right)\hfill \\ \hfill +& {\left(4+8s_y+3s_y^2\right)}^2+2s_x^2\left(44+88s_y+39s_y^2\right)+16s_x\left(4+12s_y+11s_y^2+3s_y^3\right)]\hfill \\ \hfill +& c_x^2\left(-2c_y^2+8\left(4+3s_x^2+8s_y+5s_y^2+8s_x\left(1+s_y\right)\right)\right)),\hfill \\ \hfill r_1=& \frac{1}{16}\left(1+s_x+s_y\right)\left(c_{\text{x}}^2+c_y^2+4\left(4+3s_x^2+8s_y+3s_y^2+8s_x\left(1+s_y\right)\right)\right),\hfill \\ \hfill r_2=& -\frac{1}{64}\left({\text{c}}_{\text{x}}-2{\text{s}}_{\text{x}}\right)\left({\text{c}}_{\text{x}}^2-{\text{c}}_{\text{y}}^2+4\left(4+3{\text{s}}_{\text{x}}^2+8{\text{s}}_{\text{y}}+5{\text{s}}_{\text{y}}^2+8{\text{s}}_{\text{x}}\left(1+{\text{s}}_{\text{y}}\right)\right)\right),\hfill \\ \hfill r_3=& \frac{1}{8}\left({\text{c}}_{\text{x}}-2{\text{s}}_{\text{x}}\right)\left({\text{c}}_{\text{y}}-2{\text{s}}_{\text{y}}\right)\left(1+{\text{s}}_{\text{x}}+{\text{s}}_{\text{y}}\right),\hfill \\ \hfill r_4=& -\frac{1}{64}\left({\text{c}}_{\text{y}}-2{\text{s}}_{\text{y}}\right)\left(-{\text{c}}_{\text{x}}^2+{\text{c}}_{\text{y}}^2+4\left(4+5{\text{s}}_{\text{x}}^2+8{\text{s}}_{\text{y}}+3{\text{s}}_{\text{y}}^2+8{\text{s}}_{\text{x}}\left(1+{\text{s}}_{\text{y}}\right)\right)\right),\hfill \\ \hfill r_5=& \frac{1}{64}\left({\text{c}}_{\text{x}}+2{\text{s}}_{\text{x}}\right)\left({\text{c}}_{\text{x}}^2-{\text{c}}_{\text{y}}^2+4\left(4+3{\text{s}}_{\text{x}}^2+8{\text{s}}_{\text{y}}+5{\text{s}}_{\text{y}}^2+8{\text{s}}_{\text{x}}\left(1+{\text{s}}_{\text{y}}\right)\right)\right),\hfill \\ \hfill r_6=& -\frac{1}{8}\left({\text{c}}_{\text{x}}+2{\text{s}}_{\text{x}}\right)\left({\text{c}}_{\text{y}}-2{\text{s}}_{\text{y}}\right)\left(1+{\text{s}}_{\text{x}}+{\text{s}}_{\text{y}}\right),\hfill \\ \hfill r_7=& \frac{1}{8}\left({\text{c}}_{\text{x}}+2{\text{s}}_{\text{x}}\right)\left(1+{\text{s}}_{\text{x}}+{\text{s}}_{\text{y}}\right)\left({\text{c}}_{\text{y}}+2{\text{s}}_{\text{y}}\right),\hfill \\ \hfill r_8=& \frac{1}{64}\left({\text{c}}_{\text{y}}+2{\text{s}}_{\text{y}}\right)\left(-{\text{c}}_{\text{x}}^2+{\text{c}}_{\text{y}}^2+4\left(4+5{\text{s}}_{\text{x}}^2+8{\text{s}}_{\text{y}}+3{\text{s}}_{\text{y}}^2+8{\text{s}}_{\text{x}}\left(1+{\text{s}}_{\text{y}}\right)\right)\right),\hfill \\ \hfill r_9=& -\frac{1}{8}\left({\text{c}}_{\text{x}}-2{\text{s}}_{\text{x}}\right)\left(1+{\text{s}}_{\text{x}}+{\text{s}}_{\text{y}}\right)\left({\text{c}}_{\text{y}}+2{\text{s}}_{\text{y}}\right).\hfill \end{array}$$

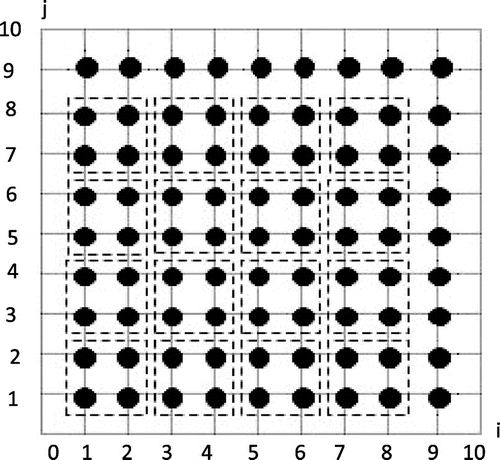
Figure 2 shows the construction of blocks of four points in the solution domain for the case n = 10. Note that if n is even, there will be ungrouped points near the upper and right sides of the boundary. The FEG method proceeds with the iterative evaluation of solutions in these blocks of four points using Equation (7) throughout the whole solution domain until convergence is achieved. For the case of even n, the solutions at the ungrouped points near the boundaries are computed using (5).

Figure 2. Grouping of the points for the FEG method (n = 10).

Figure 3. Grouping of the points for the FMEG method (n = 10).

2.2. The fractional modified explicit group method

In this new method, we consider the nodal points with grid size spacing $2\mathit{h}=\frac{2}{n}$. The standard fractional formula is generated through the application specific finite difference approximations with 2h-spaced points. Using the Caputo time fractional approximation (3) at the left-hand side of (1) and the second order Crank–Nicolson difference scheme with 2h-spaced points at the right hand side of (1), the following approximation formula is obtained:(8) $$\begin{array}{c}\hfill \begin{array}{c}{w}_1{u}^k+{\sum }_{s=1}^{k-1}\left[w_{k-s+1}-w_{k-s}\right]u_{i,j}^s-w_k{u}_{i,j}^0+\mathit{\sigma }\frac{\left(u_{i,j}^{k+1}-u_{i,j}^k\right)}{2^{1-\mathit{\alpha }}}\hfill \\ =\frac{a_x}{2}\left(\frac{u_{i-2,j}^{k+1}-2u_{i,j}^{k+1}+u_{i+2,j}^{k+1}}{{4h}^2}+\frac{u_{i-2,j}^k-2u_{i,j}^k+u_{i+2,j}^k}{{4h}^2}\right)\hfill \\ +\frac{a_y}{2}\left(\frac{u_{i,j-2}^{k+1}-2u_{i,j}^{k+1}+u_{i,j+2}^{k+1}}{{4h}^2}+\frac{u_{i,j-2}^k-2u_{i,j}^k+u_{i,j+2}^k}{{4h}^2}\right)-\frac{b_x}{2}\left(\frac{u_{i+2,j}^{k+1}-u_{i-2,j}^{k+1}}{4h}+\frac{u_{i+2,j}^k-u_{i-2,j}^k}{4h}\right)\hfill \\ -\frac{b_y}{2}\left(\frac{u_{i,j+2}^{k+1}-u_{i,j-2}^{k+1}}{4h}+\frac{u_{i,j+2}^k-u_{i,j-2}^k}{4h}\right)+f_{i,j}^{k+1/2}+O({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2).\hfill \end{array}\end{array}$$(8)

On simplification, we obtain the following(9) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \left(1+\frac{s_x+s_y}{4}\right)u_{i,j}^{k+1}=(\frac{s_x}{8}+\frac{c_x}{8})u_{i-2,j}^{k+1}+(\frac{s_x}{8}-\frac{c_x}{8})u_{i+2,j}^{k+1}+(\frac{s_y}{8}+\frac{c_y}{8})u_{i,j-2}^{k+1}\\ \hfill +(\frac{s_y}{8}-\frac{c_y}{8})u_{i,j+2}^{k+1}+\left(1-2^{1-\mathit{\alpha }}{w}_1^{\ast }-\frac{s_x+s_y}{4}\right)u_{i,j}^k+(\frac{s_x}{2}+\frac{c_x}{8})u_{i-2,j}^k\\ \hfill +(\frac{s_x}{8}-\frac{c_x}{8})u_{i+2,j}^k+(\frac{s_y}{8}+\frac{c_y}{8})u_{i,j-2}^k+(\frac{s_y}{8}-\frac{c_y}{8})u_{i,j+2}^k+2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j}^0\\ \hfill +2^{1-\mathit{\alpha }}\sum _{s=1}^{k-1}\left[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }\right]u_{i,j}^s+m_0{f}_{i,j}^{k+1/2}.\end{array}\end{array}$$(9)

Applying (9) to any group of four points (i, j), (i + 2, j), (i + 2, j + 2) and (i, j + 2) in the solution domain will result in the following $4\times 4$ system(10) $$\begin{array}{c}\hfill \left(\begin{array}{cccc}{D}_1& -a_{11}& 0& -b_{11}\\ -a_{22}& D_1& -b_{11}& 0\\ 0& -b_{22}& D_1& -a_{22}\\ -b_{22}& 0& -a_{11}& D_1\end{array}\right)\left(\begin{array}{cc}& u_{i,j}\\ & u_{i+2,j}\\ & u_{i+2,j+2}\\ & u_{i,j+2}\end{array}\right)=\left(\begin{array}{c}rh{s}_{i,j}\hfill \\ rh{s}_{i+2,j}\hfill \\ rh{s}_{i+2,j+2}\hfill \\ rh{s}_{i,j+2}\hfill \end{array}\right),\end{array}$$(10)

where, $D_1=(1+\frac{s_x+s_y}{4}),a_{11}=\left(\frac{s_x}{8}-\frac{c_x}{8}\right),b_{11}=\left(\frac{s_y}{8}-\frac{c_y}{8}\right),a_{22}=\left(\frac{s_x}{8}+\frac{c_x}{8}\right),b_{22}=\left(\frac{s_y}{8}+\frac{c_y}{8}\right),Q=\left(1-2^{1-\mathit{\alpha }}{w}_1^{\ast }-\frac{s_x+s_y}{4}\right)$,$$\begin{array}{cc}\hfill rh{s}_{i,j}=& a_{22}(u_{i-2,j}^{k+1}+u_{i-2,j}^k)+b_{22}(u_{i,j-2}^{k+1}+u_{i,j-2}^k)+a_{11}{u}_{i+2,j}^k+b_{11}{u}_{i,j+2}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j}^0+Q{u}_{i,j}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i.j}^s+m_0{f}_{i,j}^{k+1/2},\hfill \\ \hfill rh{s}_{i+2,j}=& a_{11}(u_{i+4,j}^{k+1}+u_{i+4,j}^k)+b_{22}(u_{i+2,j-2}^{k+1}+u_{i+2,j-2}^k)+b_{11}{u}_{i+2,j+2}^k+a_{22}{u}_{i,j}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i+2,j}^0+Q{u}_{i+2,j}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i+2,j}^s+m_0{f}_{i+2,j}^{k+1/2},\hfill \\ \hfill rh{s}_{i+2,j+2}=& a_{11}(u_{i+4,j+2}^{k+1}+u_{i+4,j+2}^k)+b_{11}(u_{i+2,j+4}^{k+1}+u_{i+2,j+4}^k)+b_{22}{u}_{i+2,j}^k+a_{22}{u}_{i,j+2}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i+2,j+2}^0+q{u}_{i+2,j+2}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i+2,j+2}^s+m_0{f}_{i+2,j+2}^{k+1/2},\hfill \\ \hfill rh{s}_{i,j+2}=& a_{22}(u_{i-2,j+2}^{k+1}+u_{i-2,j+2}^k)+b_{11}(u_{i,j+4}^{k+1}+u_{i,j+4}^k)+a_{11}{u}_{i+2,j+2}^k+b_{22}{u}_{i,j}^k\hfill \\ \hfill & +2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j+2}^0+Q{u}_{i,j+2}^k+\sum _{s=1}^{k-1}{2}^{1-\mathit{\alpha }}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]u_{i,j+2}^s+m_0{f}_{i,j+2}^{k+1/2}.\hfill \end{array}$$

The four-point FMEG equation below is obtained by inverting (10), as follows(11) $$\begin{array}{c}\hfill \left(\begin{array}{c}{u}_{i.j}^{k+1}\hfill \\ u_{i+2,j}^{k+1}\hfill \\ u_{i+2,j+2}^{k+1}\hfill \\ u_{i,j+2}^{k+1}\hfill \end{array}\right)=\frac{1}{\mathit{const}}\left(\begin{array}{cccc}{r}_{11}\hfill & r_{22}\hfill & r_{33}\hfill & r_{44}\hfill \\ r_{55}\hfill & r_{11}\hfill & r_{44}\hfill & r_{66}\hfill \\ r_{77}\hfill & r_{88}\hfill & r_{11}\hfill & r_{55}\hfill \\ r_{88}\hfill & r_{99}\hfill & r_{22}\hfill & r_{11}\hfill \end{array}\right)\left(\begin{array}{c}rh{s}_{i,j}\hfill \\ rh{s}_{i+2,j}\hfill \\ rh{s}_{i+2,j+2}\hfill \\ rh{s}_{i,j+2}\hfill \end{array}\right),\end{array}$$(11) $$\begin{array}{cc}\hfill cons=& \frac{1}{4096}\left(4096+c_x^4+c_y^4+4096s_x+1408s_x^2+192s_x^3+9s_x^4+4096s_y\right.\hfill \\ \hfill & +3072s_x{s}_y+704s_x^2{s}_y+48s_x^3{s}_y+1408s_y^2+704s_x{s}_y^2+78s_x^2{s}_y^2+192s_y^3\hfill \\ \hfill & +48s_x{s}_y^3+9s_y^4+2c_y^2\left(64+5s_x^2+32s_y+3s_y^2+8s_x\left(4+s_y\right)\right)\hfill \\ \hfill & +2c_x^2\left(64-c_y^2+3s_x^2+32s_y+5s_y^2+8s_x\left(4+s_y\right)\right)),\hfill \\ \hfill r_{11}=& \frac{1}{256}\left(4+s_x+s_y\right)\left(64+c_x^2+c_y^2+32s_x+3s_x^2+32s_y+8s_x{s}_y+3s_y^2\right),\hfill \\ \hfill r_{22}=& -\frac{1}{512}\left(c_x-s_x\right)\left(64+c_x^2-c_y^2+32s_x+3s_x^2+32s_y+8s_x{s}_y+5s_y^2\right),\hfill \\ \hfill r_{33}=& -\frac{1}{512}\left(c_x-s_x\right)\left(64+c_x^2-c_y^2+32s_x+3s_x^2+32s_y+8s_x{s}_y+5s_y^2\right),\hfill \\ \hfill r_{44}=& -\frac{1}{512}\left(c_y-s_y\right)\left(64-c_x^2+c_y^2+32s_x+5s_x^2+32s_y+8s_x{s}_y+3s_y^2\right),\hfill \\ \hfill r_{55}=& \frac{1}{512}\left(c_x+s_x\right)\left(64+c_x^2-c_y^2+32s_x+3s_x^2+32s_y+8s_x{s}_y+5s_y^2\right),\hfill \\ \hfill r_{66}=& -\frac{1}{128}\left(c_x+s_x\right)\left(c_y-s_y\right)\left(4+s_x+s_y\right),\hfill \\ \hfill r_{77}=& \frac{1}{128}\left(c_x+s_x\right)\left(c_y+s_y\right)\left(4+s_x+s_y\right),\hfill \end{array}$$$$\begin{array}{cc}\hfill r_{88}=& \frac{1}{512}\left(c_y+s_y\right)\left(64-c_x^2+c_y^2+32s_x+5s_x^2+32s_y+8s_x{s}_y+3s_y^2\right),\hfill \\ \hfill r_{99}=& -\frac{1}{128}\left(c_x-s_x\right)\left(c_y+s_y\right)\left(4+s_x+s_y\right).\hfill \end{array}$$

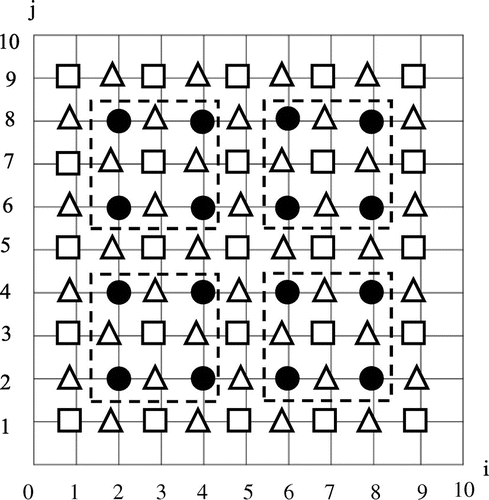
To use this method, the grid points in the solution domain are divided into three types of points, denoted by the symbols $\square ,▵$ and $\bullet$ in alternate ordering as shown in Figure 3. Note that the evaluation of (11) require points of type $\bullet$ only. Thus, we can construct the FMEG method by generating the iterations on this type of points only, followed by the evaluation of solutions directly once on points of type $\square$ and $▵$ . The FMEG algorithm can then be summarized as follows:

(1)	Divide the grid points into three types $\square ,▵$ and $\bullet$ in alternate order as depicted in Figure 3.
(2)	Set the initial guess for the iterations.
(3)	Evaluate the solutions at points $\bullet$ using Equation (11) iteratively at the time level $k+1$.
(4)	Step 5 is performed if the iteration converges. Otherwise, Step 3 is repeated until a convergence is attained.
(5)	The steps below are performed directly once for points $\square$ and $▵$ in Figure 3 at the time level $k+1$: (a) For type $\square$ points, the rotated $h-spaced$ five-point approximation formula derived by rotating the $x-y$ axis clockwise at ${45}^{\circ }$ was used (Tan, Ali, & Lai, 2012). This approximation formula was applied to the right side of Equation (1), in combination with (3) being applied to the left side of (1), to obtain the following rotated C-N formula: $$\begin{array}{cc}\hfill \left(1+\frac{s_x+s_y}{2}\right)u_{i,j}^{k+1}& =(\frac{s_x}{4}+\frac{c_x-c_y}{8})u_{i-1,j+1}^{k+1}+(\frac{s_x}{4}-\frac{c_x+c_y}{8})u_{i+1,j+1}^{k+1}+(\frac{s_y}{4}+\frac{c_y-c_x}{8})u_{i+1,j-1}^{k+1}\hfill \\ \hfill & +(\frac{s_y}{4}+\frac{c_x+c_y}{8})u_{i-1,j-1}^{k+1}+\left(1-2^{1-\mathit{\alpha }}{w}_1^{\ast }-\frac{s_x+s_y}{2}\right)u_{i,j}^k+(\frac{s_x}{4}+\frac{c_x-c_y}{8})u_{i-1,j+1}^k\hfill \\ \hfill & +(\frac{s_x}{4}-\frac{c_x+c_y}{8})u_{i+1,j+1}^k+(\frac{s_y}{4}+\frac{c_y-c_x}{8})u_{i+1,j-1}^k+(\frac{s_y}{4}+\frac{c_x+c_y}{8})u_{i-1,j-1}^k+2^{1-\mathit{\alpha }}{w}_k^{\ast }{u}_{i,j}^0\hfill \\ \hfill & +2^{1-\mathit{\alpha }}\sum _{s=1}^{k-1}\left[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }\right]u_{i,j}^s+m_0{f}_{i,j}^{k+1/2}.\hfill \end{array}$$ (b) For type $▵$ points, the typical $h-spaced$ formula (5) is used. Note that formula (5) involve points of type $▵$ only.

 

3. Stability analysis

A scheme is considered to be stable if the errors cease to increase with the passing of time, and gradually become inconsequential as the computation progresses. Even though the spacing is different, Equation (5) gives rise to both the FEG and FMEG methods. Therefore, the stability of both methods can be analyzed in similar ways. Here, we will show the stability of the FMEG scheme using eigenvalues of the generated matrices with mathematical induction.

Form (10) we obtain(12) $$\begin{array}{cc}\hfill A{U}^1& =BUk=0\hfill \\ \hfill A{U}^{k+1}& =B{U}^k-C_1{U}^k+{\sum }_{s=1}^{k-1}{C}_{k-s}{U}^s+C_k{U}^o+bk>0\hfill \end{array}$$(12)

where $A=\left(\begin{array}{ccccc}{R}_1\hfill & R_2\hfill & & 0\hfill & 0\hfill \\ R_3\hfill & R_1\hfill & R_2\hfill & & 0\hfill \\ \hfill & & \ddots \hfill & & \\ 0\hfill & & R_3\hfill & R_1\hfill & R_2\hfill \\ 0\hfill & 0\hfill & & R_3\hfill & R_1\hfill \end{array}\right)$, $B=\left(\begin{array}{ccccc}{S}_1\hfill & S_2\hfill & & 0\hfill & 0\hfill \\ S_3\hfill & S_1\hfill & S_2\hfill & & 0\hfill \\ \hfill & & \ddots \hfill & & \\ 0\hfill & & S_3\hfill & S_1\hfill & S_2\hfill \\ 0\hfill & 0\hfill & & S_3\hfill & S_1\hfill \end{array}\right)$ , $b=\left(\begin{array}{c}{W}_1\hfill \\ W_1\hfill \\ ⋮\hfill \\ W_1\hfill \\ W_1\hfill \end{array}\right)$$R_1=\left(\begin{array}{ccccc}{G}_1\hfill & G_3\hfill & & & \\ G_2\hfill & G_1\hfill & G_3\hfill & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & G_2\hfill & G_1\hfill & G_3\hfill \\ \hfill & & & G_2\hfill & G_1\hfill \end{array}\right),$$R_2=\left(\begin{array}{ccccc}{G}_5\hfill & & & & \\ \hfill & G_5\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & G_5\hfill & \\ \hfill & & & & G_5\hfill \end{array}\right)$$R_3=\left(\begin{array}{ccccc}{G}_4\hfill & & & & \\ \hfill & G_4\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & G_4\hfill & \\ \hfill & & & & G_4\hfill \end{array}\right),$$S_1=\left(\begin{array}{ccccc}{H}_1\hfill & H_3\hfill & & & \\ H_2\hfill & H_1\hfill & H_3\hfill & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & H_2\hfill & H_1\hfill & H_3\hfill \\ \hfill & & & H_2\hfill & H_1\hfill \end{array}\right)$$S_2=\left(\begin{array}{ccccc}{H}_5\hfill & & & & \\ \hfill & H_5\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & H_5\hfill & \\ \hfill & & & & H_5\hfill \end{array}\right),$$S_3=\left(\begin{array}{ccccc}{H}_4\hfill & & & & \\ \hfill & H_4\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & H_4\hfill & \\ \hfill & & & & H_4\hfill \end{array}\right)$$C_k=\left(\begin{array}{ccccc}{M}_k\hfill & & & & \\ \hfill & M_k\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & M_k\hfill & \\ \hfill & & & & M_k\hfill \end{array}\right)$,

$C_{k-s}=\left(\begin{array}{ccccc}{M}_{k-s}\hfill & & & & \\ \hfill & M_{k-s}\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & M_{k-s}\hfill & \\ \hfill & & & & M_{k-s}\hfill \end{array}\right),s=1,...,k-1$

$C_1=\left(\begin{array}{ccccc}{M}_1\hfill & & & & \\ \hfill & M_1\hfill & & & \\ \hfill & & \ddots \hfill & & \\ \hfill & & & M_1\hfill & \\ \hfill & & & & M_1\hfill \end{array}\right),$$W_1=\left(\begin{array}{c}{L}_1\hfill \\ L_1\hfill \\ ⋮\hfill \\ L_1\hfill \\ L_1\hfill \end{array}\right),$$G_1=\left(\begin{array}{cccc}{D}_1\hfill & -a_{11}\hfill & 0\hfill & -b_{11}\hfill \\ -a_{22}\hfill & D_1\hfill & -b_{11}\hfill & 0\hfill \\ 0\hfill & -b_{22}\hfill & D_1\hfill & -a_{22}\hfill \\ -b_{22}\hfill & 0\hfill & -a_{11}\hfill & D_1\hfill \end{array}\right)$$G_2=\left(\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & -b_{22}\hfill \\ 0\hfill & 0\hfill & -b_{22}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right),$$G_3=\left(\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & -b_{11}\hfill & 0\hfill & 0\hfill \\ -b_{11}\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right)$$G_4=\left(\begin{array}{cccc}0\hfill & -a_{22}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & -a_{22}\hfill & 0\hfill \end{array}\right),$$G_5=\left(\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & 0\hfill \\ -a_{11}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & -a_{11}\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right)$, $H_1=\left(\begin{array}{cccc}Q\hfill & a_{11}\hfill & 0\hfill & b_{11}\hfill \\ a_{22}\hfill & Q\hfill & b_{11}\hfill & 0\hfill \\ 0\hfill & b_{22}\hfill & Q\hfill & a_{22}\hfill \\ b_{22}\hfill & 0\hfill & a_{11}\hfill & Q\hfill \end{array}\right),$$H_2=\left(\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & b_{22}\hfill \\ 0\hfill & 0\hfill & b_{22}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right)$$H_3=\left(\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & b_{11}\hfill & 0\hfill & 0\hfill \\ b_{11}\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right),$$H_4=\left(\begin{array}{cccc}0\hfill & a_{22}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & a_{22}\hfill & 0\hfill \end{array}\right),$$H_5=\left(\begin{array}{cccc}0\hfill & 0\hfill & 0\hfill & 0\hfill \\ a_{11}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & a_{11}\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right)$$M_{k-s}=\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}\left(\begin{array}{cccc}(w_{{}_{k-s}}^{\ast }-w_{{}_{k-s+1}}^{\ast })\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & (w_{{}_{k-s}}^{\ast }-w_{{}_{k-s+1}}^{\ast })\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & (w_{{}_{k-s}}^{\ast }-w_{{}_{k-s+1}}^{\ast })\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & (w_{{}_{k-s}}^{\ast }-w_{{}_{k-s+1}}^{\ast })\hfill \end{array}\right),$$M_1=\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}\left(\begin{array}{cccc}{w}_{{}_1}^{\ast }\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & w_{{}_1}^{\ast }\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & w_{{}_1}^{\ast }\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & w_{{}_1}^{\ast }\hfill \end{array}\right)$, $M_k=\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}\left(\begin{array}{cccc}{w}_{{}_k}^{\ast }& 0& 0& 0\\ 0& w_{{}_k}^{\ast }& 0& 0\\ 0& 0& w_{{}_k}^{\ast }& 0\\ 0& 0& 0& w_{{}_k}^{\ast }\end{array}\right),$$L_1=2^{1-\mathit{\alpha }}\mathrm{\Gamma }[2-\mathit{\alpha }]\left(\begin{array}{c}{f}_{i,j}\hfill \\ f_{i+2,j}\hfill \\ f_{i+2,j+2}\hfill \\ f_{i,j+2}\hfill \end{array}\right),i,j=2,6,...,n-2$.

The following lemma is important to prove the stability.

Lemma 1

[Karatay, Kale, & Bayramoglu, 2013] In (12), the coefficients $w_s^{\ast },s=1,2,...,k$ satisfy the following $1-w_{k-s}^{\ast }>w_{k-s+1}^{\ast },s=1,2,...,k$. $2-{\sum }_{S=1}^{k-1}[w_{k-s}^{\ast }-w_{k-s+1}^{\ast }]+w_k^{\ast }=w_1^{\ast },s=1,2,...,k$.

For simplicity, we assume $s_x=s_y=S=\frac{\mathrm{\Gamma }(2-\mathit{\alpha })2^{1-\mathit{\alpha }}}{h^2},c_x=c_y=C=\frac{\mathrm{\Gamma }(2-\mathit{\alpha })2^{1-\mathit{\alpha }}}{h},D_1=\frac{1}{t\mathit{\alpha }}+\frac{S}{2}$ and $Q=\frac{1}{t\mathit{\alpha }}-2^{1-\mathit{\alpha }}{w}_1^{\ast }-\frac{S}{2}$

Theorem 1

If $\left(\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2}-\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }+\frac{\sqrt{-C^2+S^2}}{4}\right)>0$ then the FMEG scheme (10) is stable.

To prove the stability of (10), we suppose that $u_{i,j}^k,i,j=1,2,...,n,k=1,2,...,l$ are the approximate solutions to the exact solution $U_{i,j}^k$ of (1), the error ${\mathit{\epsilon }}_{i,j}^k=U_{i,j}^k-u_{i,j}^k$ be the error at time level k. From (12), the error satisfies(13) $$\begin{array}{c}\hfill \begin{array}{cc}A{E}^1=BE\hfill & k=0\hfill \\ A{E}^{k+1}=B{E}^k-C_1{E}^k+{\sum }_{s=1}^{k-1}{C}_{k-s}{U}^s+C_k{E}^o\hfill & k>0\hfill \end{array}\end{array}$$(13)

where $E^{k+1}=\left(\begin{array}{c}{E}_1^{k+1}\hfill \\ E_1^{k+1}\hfill \\ ⋮\hfill \\ E_1^{k+1}\hfill \\ E_1^{k+1}\hfill \end{array}\right),E_1^{k+1}=\left(\begin{array}{c}{\mathit{\epsilon }}_2^{k+1}\hfill \\ {\mathit{\epsilon }}_4^{k+1}\hfill \\ ⋮\hfill \\ {\mathit{\epsilon }}_{m-4}^{k+1}\hfill \\ {\mathit{\epsilon }}_{m-2}^{k+1}\hfill \end{array}\right),{\mathit{\epsilon }}_i^{k+1}=\left[\begin{array}{c}{\mathit{\epsilon }}_{i,j}^{k+1}\hfill \\ {\mathit{\epsilon }}_{i+2,j}^{k+1}\hfill \\ {\mathit{\epsilon }}_{i+2,j+2}^{k+1}\hfill \\ {\mathit{\epsilon }}_{i,j+2}^{k+1}\hfill \end{array}\right],i=2,6,...,n-2,j=2,6,...,n-2$.

From the above equations, the following are obtained:(14) $$\begin{array}{cc}& A=G_4+G_2+G_1+G_3+G_5\hfill \\ \hfill & B=H_4+H_2+H_1+H_3+H_5\hfill \\ \hfill & C_1=M_1\hfill \\ \hfill & C_{k-s}=M_{k-s}\hfill \\ \hfill & C_k=M_k\hfill \end{array}$$(14)

It is worthy to note that, from (14), the eigenvalues of the matrices $A,B,C_1,C_{k-s}$ and $C_k$ are $a_k,b_k,c_1,c_{k-s}$ and $c_k$ respectively, where$$\begin{array}{cc}& a_k=\left\{\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2},\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2},\frac{1}{4}\left(\frac{4}{t^{\mathit{\alpha }}}+2S-\sqrt{-C^2+S^2}\right),\frac{1}{4}\left(\frac{4}{t^{\mathit{\alpha }}}+2S+\sqrt{-C^2+S^2}\right)\right\}\hfill \\ \hfill & b_k=\left\{\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2},\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2},\frac{1}{4}\left(\frac{4}{t^{\mathit{\alpha }}}-2S-\sqrt{-C^2+S^2}\right),\frac{1}{4}\left(\frac{4}{t^{\mathit{\alpha }}}-2S+\sqrt{-C^2+S^2}\right)\right\}\hfill \\ \hfill & c_1=\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }\hfill \\ \hfill & c_{k-s}=\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}(w_{k-s}^{\ast }-w_{k-s+1}^{\ast })\hfill \\ \hfill & c_k=\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_k^{\ast }\hfill \end{array}$$

For $k=0$$$\begin{array}{cc}& E^1=A^{-1}B{E}^0\hfill \\ \hfill & ∥E^1∥\le \mathit{\rho }(A^{-1}B)∥E^0∥=\left|\frac{\left(\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2}+\frac{\sqrt{-C^2+S^2}}{4}\right)}{\left(\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2}+\frac{\sqrt{-C^2+S^2}}{4}\right)}\right|∥E^0∥\hfill \\ \hfill & \therefore ∥E^1∥\le ∥E^0∥\hfill \end{array}$$

Supposing that: $∥E^s∥\le ∥E^0∥,s=1,...,k.$

Need to prove this inequality holds for $s=k+1$.$$\begin{array}{cc}\hfill E^{k+1}& =A^{-1}(B-C_1)E^k+\sum _{s=1}^{k-1}{A}^{-1}{C}_{k-s}{E}^s+A^{-1}{C}_k{E}^0\hfill \\ \hfill & \le \mathit{\rho }(A^{-1}(B-C_1))∥E^0∥+\sum _{s=1}^{k-1}\mathit{\rho }(A^{-1}{C}_{k-s})∥E^0∥+\mathit{\rho }(A^{-1}{C}_k)∥E^0∥\hfill \end{array}$$

Using Lemma 1, we get$$\begin{array}{cc}\hfill ∥E^{k+1}∥& \le \frac{\left|\left(\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2}-\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }+\frac{\sqrt{-C^2+S^2}}{4}\right)\right|}{\left(\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2}+\frac{\sqrt{-C^2+S^2}}{4}\right)}∥E^0∥+\frac{\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }}{\left(\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2}+\frac{\sqrt{-C^2+S^2}}{4}\right)}∥E^0∥\hfill \\ \hfill & \therefore ∥E^{k+1}∥\le ∥E^0∥\hfill \\ \hfill \end{array}$$

Therefore, under the conditions $\left(\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2}-\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }+\frac{\sqrt{-C^2+S^2}}{4}\right)>0$ the FMEG iterative scheme (10) is stable. $\square$

4. Convergence analysis

Theorem 2

The finite difference FMEG scheme (10) is convergent and the following estimate hold $∥e^{k+1}∥\le C_k^{-1}({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2)$ if $\left(\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2}-\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }+\frac{\sqrt{-C^2+S^2}}{4}\right)>0$.

Let us denote the truncation error at $(x_i,y_j,t_{k+1})$ by $R^{k+1}$. From (8), we have, $∥R^{k+1/2}∥\le c({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2)$ Define ${\mathit{\eta }}^{k+1}=U(x_i,y_j,t_{k+1})-u_{i,j}^{k+1}$$i,j=1,2,..,n$, $k=1,2,...,l$ and $e^{k+1}={(e_1^{k+1},e_1^{k+1},...,e_1^{k+1})}^T,$ using $e^0=0$ , where $e_1^{k+1}=\left(\begin{array}{c}{\mathit{\eta }}_2^{k+1}\hfill \\ {\mathit{\eta }}_4^{k+1}\hfill \\ ⋮\hfill \\ {\mathit{\eta }}_{m-4}^{k+1}\hfill \\ {\mathit{\eta }}_{m-2}^{k+1}\hfill \end{array}\right),{\mathit{\epsilon }}_i^{k+1}=\left[\begin{array}{c}{\mathit{\eta }}_{i,j}^{k+1}\hfill \\ {\mathit{\eta }}_{i+2,j}^{k+1}\hfill \\ {\mathit{\eta }}_{i+2,j+2}^{k+1}\hfill \\ {\mathit{\eta }}_{i,j+2}^{k+1}\hfill \end{array}\right],\{i,j\}=2,6,...,n-2$. Substitution into (12) produces:$$\begin{array}{cc}& A{e}^1=R^{\frac{1}{2}}\hfill \\ \hfill & A{e}^{k+1}=B{e}^k-C_1{e}^k+{\sum }_{s=1}^{k-1}{C}_{k-s}{e}^{{}_{s-1}}+R^{k+\frac{1}{2}}.\hfill \end{array}$$

Using mathematical induction to prove the above theorem, set $∥C_0^{-1}∥=1$. For $k=0$$$\begin{array}{cc}& A{e}^1=R^{\frac{1}{2}}\hfill \\ \hfill & ∥e^1∥\le \mathit{\rho }(A^{-1})∥R∥\le ∥C_0^{-1}∥({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2).\hfill \end{array}$$

Assume that $∥e^k∥\le ∥C_{k-1}^{-1}∥∥R^{k+\frac{1}{2}}∥$.

Need to prove it hold for $s=k+1$$A{e}^{k+1}=(B-C_1)e^k+\sum _{s=1}^{k-1}{C}_{k-s}{e}^{s-1}+R^{k+\frac{1}{2}}$$$\begin{array}{cc}& ∥e^{k+1}∥\le \mathit{\rho }(A^{-1}(B-C_1))∥e^k∥+\sum _{s=1}^{k-1}\mathit{\rho }(A^{-1}{C}_{k-s})∥e^{s-1}∥+\mathit{\rho }(A^{-1})∥R^{k+\frac{1}{2}}∥\hfill \\ \hfill & ∥e^{k+1}∥\le \left(\frac{\left|\left(\frac{1}{t^{\mathit{\alpha }}}-\frac{S}{2}-\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }+\frac{\sqrt{-C^2+S^2}}{4}\right)\right|}{\left(\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2}+\frac{\sqrt{-C^2+S^2}}{4}\right)}+\frac{\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_1^{\ast }}{\left(\frac{1}{t^{\mathit{\alpha }}}+\frac{S}{2}+\frac{\sqrt{-C^2+S^2}}{4}\right)}\right)∥C_k^{-1}∥∥R^{k+\frac{1}{2}}∥\hfill \\ \hfill & \le ∥C_k^{-1}∥∥R^k∥\hfill \\ \hfill & ={(\frac{2^{1-\mathit{\alpha }}}{t^{\mathit{\alpha }}}{w}_k^{{}^{\ast }})}^{-1}({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2)\hfill \\ \hfill & =\frac{k^{\mathit{\alpha }}{k}^{-\mathit{\alpha }}{\mathit{\tau }}^{\mathit{\alpha }}}{2^{1-\mathit{\alpha }}({(k+\frac{1}{2})}^{1-\mathit{\alpha }}-{(k-\frac{1}{2})}^{1-\mathit{\alpha }})}({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2)\hfill \\ \hfill & =\frac{1}{2^{1-\mathit{\alpha }}(1-\mathit{\alpha })}({\mathit{\tau }}^{2-\mathit{\alpha }}+{(△x)}^2+{(△y)}^2)\hfill \end{array}$$

Since $\underset{k\to \infty }{lim}\frac{k^{-\mathit{\alpha }}}{{(k+\frac{1}{2})}^{1-\mathit{\alpha }}-{(k-\frac{1}{2})}^{1-\mathit{\alpha }}}=\frac{1}{1-\mathit{\alpha }}$. $\square$  

5. Computational complexity

This section presents an analysis of the computational complexity with regard to the three techniques described for solving (1), which is the number of arithmetic operations per iteration. For simplicity, we assume $s_x=s_y,c_x=c_y$. Suppose $m^2$ internal points exist within the solution, with $m=n-1$, where n has an even mesh size, then the ungrouped points will be found close to the right/upper boundaries. Internal mesh points have two main types, namely, the iteration points that participate in the iteration process and the direct points that are directly calculated once using the rotated and standard difference formulas following the attainment of the iteration convergence. Table 1 lists the number of internal mesh points for the three earlier methods, whereas Table 2 provides a summary of the number of arithmetic operations that are needed for each iteration and the direct solution following the convergence, not only for the explicit group methods, but also for the fractional standard point (FSP) method.

Table 1. Number of various types of mesh points for the point and explicit group methods

	Number of points
Point types	FSP	FEG	FMEG
Iterative group points	$m^2$	${(m-1)}^2$	$\frac{{(m-1)}^2}{4}$
Iterative ungrouped points	–	2m-1	–
Total iterative points	$m^2$	$m^2$	$\frac{{(m-1)}^2}{4}$
Direct h-spaced rotated points	–	–	$\frac{{(m+1)}^2}{4}$
Direct h-spaced standard points	–	–	$\frac{m^2-1}{4}$
Total direct points	–	–	$\frac{3m^2+2m-1}{4}$

Table 2. Computational complexity for the point and explicit group methods

	Per iteration		After convergence
Methods	Additional	Multiplication	Additional	Multiplication
SFP	$(14+13(k-1))m^2$	$(10+(k-1))m^2$	–	–
FEG	$(15+13(k-1)){(m-1)}^2+(14+13(k-1))(2m-1)$	$(14+(k-1)){(m-1)}^2+(10+(k-1))(2m-1)$	–	–
FMEG	$\frac{((15+13(k-1)){(m-1)}^2)}{4}$	$\frac{((14+(k-1)){(m-1)}^2)}{4}$	$(14+13(k-1))\times \frac{(3m^2+2m-1)}{4}$	$(10+(k-1))\times \frac{(3m^2+2m-1)}{4}$

Table 3. Comparison of the number of iterations, Execution times, average, and maximum error for different time step and mesh size at $\mathit{\alpha }=0.75$ and $\mathit{\alpha }=0.95$

Example 1				$\mathit{\alpha }=0.75$				$\mathit{\alpha }=0.95$
h	$▵t$	Method	Time	Ite.	Ave	Max	Time	Ite.	Ave	Max
		FSP	9.18	11	6.485E-4	1.030E-3	6.16	8	6.125E-4	9.761E-4
1/6	1/100	FEG	7.25	8	6.458E-4	1.029E-3	5.49	6	6.120E-4	9.763E-4
		FMEG	1.13	2	2.063E-3	3.375E-3	1.15	2	1.986E-3	3.252E-3
		FSP	350.37	11	2.480E-4	4.409E-4	195.31	6	2.581E-4	4.664E-4
1/10	1/350	FEG	367.80	8	2.094E-4	3.807E-4	172.19	5	2.031E-4	3.681E-4
		FMEG	54.55	4	6.899E-4	1.27E-3	54.30	4	6.709E-4	1.240E-3
		FSP	3924.31	10	2.172E-4	4.353E-4	2032.86	5	2.506E-4	5.002E-4
1/14	1/850	FEG	2941.31	7	1.346E-4	4.353E-4	2024.52	5	9.522E-5	1.801E-4
		FMEG	700.02	4	3.402E-4	6.539E-4	604.66	3	3.317E-4	6.372E-4
		FSP	22,323.3	9	2.923E-4	6.114E-4	12224.3	5	1.599E-4	3.242E-4
1/18	1/1620	FEG	17,268.0	6	1.613E-4	3.212E-4	10,499.4	4	7.361E-5	1.471E-4
		FMEG	4330.99	4	2.208E-4	4.015E-4	3786.52	3	1.966E-4	3.887E-4

Figure 4. A comparison of the numerical solution of the example 1 at $\mathit{\alpha }$ = 0.75, y = 1/6, t = 1 between, (A) FSP and FMEG (B) FEG and FMEG.

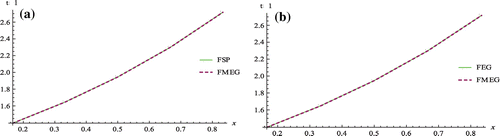
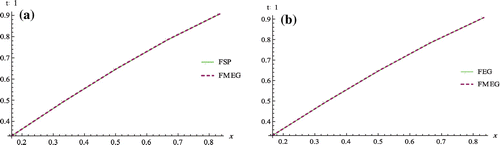
Figure 5. A comparison of the numerical solution of the example 2 at $\mathit{\alpha }$ = 0.75, y = 1/6, t = 1 between,(A) FSP and FMEG (B) FEG and FMEG.

Figure 6. Experimental results for the mesh size against the Time at $\mathit{\alpha }$ = 0:75, (A) Example 1, (B) Example 2.

Figure 7. Experimental results for the mesh size against the Ite. at $\mathit{\alpha }$ = 0:75, (A) Example 1, (B) Example 2.

6. Numerical experiments and discussion of results

Several numerical examples are presented in this section to prove the effectiveness of the fractional explicit group methods in solving the 2-D TFADE (1) with a Dirichlet boundary condition. A computer with Windows 7 Professional and Mathematica software having a Core i7 GHZ and 4 GB of RAM was used for conducting the experiments.

Table 4. Comparison of the number of iterations, Execution times, average and maximum error for different time step and mesh size at $\mathit{\alpha }=0.75$ and $\mathit{\alpha }=0.95$

Example 2			$\mathit{\alpha }=0.75$				$\mathit{\alpha }=0.95$
h	$▵t$	Method	Time	Ite.	Ave	Max	Time	Ite.	Ave	Max
		FSP	7.81	9	4.320E-4	6.690E-3	5.2	6	4.326E-4	6.702E-4
1/6	1/100	FEG	6.53	7	4.359E-4	6.759E-4	4.83	5	4.372E-4	6.781E-4
		FMEG	1.17	2	1.364E-3	2.276E-3	1.32	2	1.369E-3	2.283E-3
		FSP	294.69	9	1.173E-4	1.974E-4	169.2	5	1.126E-4	1.835E-4
1/10	1/350	FEG	230.39	6	1.269E-4	2.192E-4	155.22	4	1.334E-4	2.238E-4
		FMEG	55.13	4	5.190E-4	9.475E-4	48.40	3	5.205E-4	9.504E-4
		FSP	3,267.46	8	1.577E-5	2.441E-5	1,772.2	4	1.321E-5	3.995E-5
1/14	1/850	FEG	2621.1	6	5.451E-5	9.851E-5	1718.99	4	6.546E-5	1.202E-4
		FMEG	690.99	4	2.643E-4	4.999E-4	596.96	3	2.652E-4	5.017E-4
		FSP	17,647.9	7	5.607E-5	1.264E-4	10,034.0	4	1.780E-5	4.500E-5
1/18	1/1620	FEG	13,574.3	5	4.239E-6	1.0105E-5	9,708.83	3	1.494E-5	3.291E-5
		FMEG	4,351.54	4	1.584E-4	3.057E-4	3,764.74	3	1.591E-4	3.072E-4

Example 1

The time fractional initial boundary value problem below was considered (Zhuang, Gu, Liu, Turner, & Yarlagadda, 2011) $\frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}-\frac{\mathit{\partial }u}{\mathit{\partial }x}-\frac{\mathit{\partial }u}{\mathit{\partial }y}+0.5\mathrm{\Gamma }\left(3+\mathit{\alpha }\right)t^2{e}^{x+y}$ where $\mathrm{\Omega }=\left\{\left(x,y\right)|0\le x\le 1,0\le y\le 1\right\}$ is the solution domain with the exact solution being $t^{2+\mathit{\alpha }}{e}^{x+y}$.

Example 2

The following time fractional advection-diffusion equation was also considered (Mohebbi & Abbaszadeh, 2013) $\frac{{\mathit{\partial }}^{\mathit{\alpha }}u}{\mathit{\partial }{t}^{\mathit{\alpha }}}=\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{x}^2}+\frac{{\mathit{\partial }}^{2}u}{\mathit{\partial }{y}^2}-\frac{\mathit{\partial }u}{\mathit{\partial }x}-\frac{\mathit{\partial }u}{\mathit{\partial }y}+\frac{t^{1-\mathit{\alpha }}(sinx+siny)}{\mathrm{\Gamma }\left(2-\mathit{\alpha }\right)}+t(cosx+sinx+cosy+siny)$

with the initial and boundary conditions are given as $u\left(x,y,0\right)=0$$u\left(0,y,t\right)=tsiny$, $u(1,y,t)=t(sin1+siny)$, $u\left(x,0,t\right)=tsinx$, $u\left(x,1,t\right)=t(sinx\text{+sin}1)$, $0<t<1$, $0<x,y<1.$

Different mesh sizes of 6, 10, 14, and 18 and various time steps, which satisfy the stability conditions, with a fixed relaxation factor (Gauss–Seidel relaxation scheme) of 1.0 were used to run the experiments. During all the experiments, the norm for the convergence criteria was ${\mathit{\iota }}_{\infty }$, while error tolerance was set at $\mathit{\epsilon }={10}^{-5}$. Numerical results were obtained using of the methods described in Section 2 for different values of $\mathit{\alpha }$. 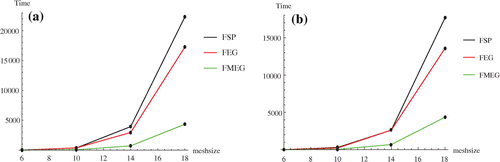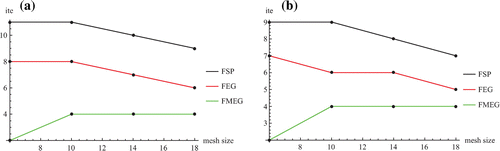The number of iterations, the execution time, and the error analysis are presented in Tables 3 and 4 and Figures 4–7 for the fractional point method and the fractional group methods. Figure 6 shows the execution times for various mesh sizes for both Examples 1 & 2. Its clear that when fractional group methods are used, the results are just as accurate as the FSP method. From the results obtained, it is observed that the execution timings were reduced by as much as 20 and 80 % of the FSP method when the FEG and FMEG methods were used respectively. In contrast to the other tested methods, the fractional group methods, specifically the FMEG method, took a least times to compute the solutions. As shown in Tables 3 & 4 and Figure 6 the time taken for FMEG to be executed was only approximately 15.6–32.5$\%$ of the FEG method, and was 12.3–23.9% of the FSP method. To gauge the computational complexity, obtaining an approximation of the amount of calculations involved for each method is necessary. The estimation for the amount of computational work involved was determined by arithmetic operations that were performed for a single iteration (as outlined in Section 5). With the help of Tables 1 & 2, and based on the assumption that an approximately equal amount of time was needed for adding, subtracting, multiplying, dividing and assigning, a summary of the total number of operations involved in the iterative methods is presented in Table 5. This shows that the FMEG requires the least number of operations, thus confirming the theoretical complexity analysis.

Table 5. Total computing operations involved for the point and grouping methods

			Total operations Example 1		Total operations Example 2
h	$▵t$	Method	$\mathit{\alpha }=0.75$	$\mathit{\alpha }=0.95$	$\mathit{\alpha }=0.75$	$\mathit{\alpha }=0.95$
		FSP	196,625	143,000	160,875	107,250
1/6	1/100	FEG	143,704	107,778	125,741	89 815
		FMEG	23,002	23,002	23,002	23,002
		FSP	2,196,315	1,197,990	1,796,985	998,325
1/10	1/350	FEG	1,600,140	1,000,090	1,200,100	800,068
		FMEG	341,462	341,462	341,462	301,934
		FSP	10,080,850	5,040,425	8,064,680	4,032,340
1/14	1/850	FEG	7,062,140	5,044,390	6,053,260	4,035,510
		FMEG	1,766,910	1,551,970	1,766,910	1,551,970
		FSP	29,534,355	16,711,425	26,229,420	14,988,240
1/18	1/1620	FEG	19,698,000	13,374,800	18,743,200	11,245,900
		FMEG	5,828,950	5,196,200	6,672,190	5,836,220

7. Conclusion

This paper presented the development and formulation of new fractional explicit group iterative methods for solving the 2D-TFADE. The C-N difference schemes with h spacing and 2h spacing gave rise to the FEG and FMEG methods, respectively. The stability and convergence of the proposed methods were analyzed using the matrix form with mathematical induction. Through the numerical experiments, the FMEG method stood out amongst all the other tested methods when it comes to its execution time and number of iterations, as it requires the least number of operation counts. It is noted that in terms of accuracy, the FMEG method is just as good as the FSP method and the FEG method. This work confirms the suitability and feasibility of the grouping strategies in solving the 2D time fractional advection-diffusion equation. The implementation of similar group methods on solving other fractional differential equations will be reported soon.

Additional information

Funding

This work was supported by the Research University Individual (RUI) under [grant number 1001/PMATHS/8011016].

Notes on contributors

Alla Tareq Balasim

Alla Tareq Balasim is a lecture at the Department of Mathematics Almustansiria University, Iraq. He received his Master in Mathematics from the Department of Mathematics, Baghdad University, Iraq. He is currently a PhD student and his research interests are numerical deferential equations and dynamical system.

Norhashidah Hj. Mohd. Ali

Norhashidah Hj. Mohd. Ali is a Professor at the School of Mathematical Sciences, Universiti Sains Malaysia. She received her PhD in Industrial Computing from Universiti Kebangsaan Malaysia. Her areas of expertise include numerical differential equations and parallel numerical algorithms. She has over 25 years teaching and research experiences and has written more than 100 articles in these areas.