Existence of infinitely many solutions for a class of difference equations with boundary value conditions involving p(k)-Laplacian operator

Abstract

The existence of infinitely many solutions was investigated for an anisotropic discrete non-linear problem involving p(k)-Laplacian operator with Dirichlet boundary value condition. The technical approach is based on a local minimum theorem for differentiable functionals in finite dimensional space.

Keywords:

• discrete non-linear boundary value problem
• infinitely many solutions
• variational methods
• critical point theory

AMS Subject Classifications:

• 39F20
• 34B15
• 39A10
• 39A12
• 39A70
• 65Q10

Public Interest Statement

Theory of difference equations is the inclusion of a great number of applications in different fields of research, such as mechanical engineering, control systems, economics, social sciences, computer science, physics, artificial or biological neural networks, cybernetics and ecology. There is increasing interest in the existence of infinitly many solutionsto boundary value problems for finite difference equations with p(k)-Laplacian operator and their applications in many fields.

1. Introduction

One of the reasons for the huge development of the theory of difference equations is the inclusion of a great number of applications in different fields of research, such as mechanical engineering, control systems, economics, social sciences, computer science, physics, artificial or biological neural networks, cybernetics and ecology. There seems to be increasing interest in the existence of results to boundary value problems for finite difference equations with p(k)-Laplacian operator because of their applications in many fields. Results on this topic are usually achieved using various fixed point theorems in cone; see Avci (2016), Avci and Pankov (2015), and Liu and Ge (2003) and references therein for details. Another tool in the study of non-linear difference equations is upper and lower solution techniques; see, for instance, Chu and Jiang (2005), Henderson and Thompson (2002) and references therein. It is well known that critical point theory is an important tool to deal with the problems for differential equations. More, recently, in Bonanno and Candito (2009), Candito and D’Aguì (2010), Chu and Jiang (2005), Candito and Giovannelli (2008), Khaleghi Moghadam and Avci (2017), Khaleghi Moghadam, Heidarkhani, and Henderson (2014), Khaleghi Moghadam and Henderson (2017), and Khaleghi Moghadam, Li, and Tersian (2018) by starting from the seminal paper Agarwal, Perera, and O’Regan (2005), the existence and multiplicity of solutions for non-linear discrete boundary value problems have been investigated by adopting variational methods.

The main goal of the present paper is to establish the existence of infinitely many solutions for the following discrete anisotropic problem(1.1) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathrm{\Delta }(w(k-1)|\mathrm{\Delta }u(k-1)|}^{p(k-1)-2}{\mathrm{\Delta }u(k-1))+q(k)|u(k)|}^{p(k)-2}u(k)=\lambda f(k,u(k)),\hfill \\ u(0)=u(T+1)=0,\hfill \end{array}\right.\end{array}$$(1.1)

for any $k\in [1,T]$, where T is a fixed positive integer, [1, T] is the discrete interval $\{1,...,T\}$, $f:[1,T]\times \mathbb{R}\to \mathbb{R}$ is a continuous function, $\lambda >0$ is a parameter and $w:[0,T]\to [1,\infty )$ is a fix function and $\mathrm{\Delta }u(k)=u(k+1)-u(k)$ is the forward difference operator and the function $p:[0,T+1]\to [2,\infty )$ is bounded and the function $q:[0,T+1]\to [1,\infty )$ is bounded, we denote for short$$\begin{array}{c}\hfill q^{-}:=\underset{k\in [1,T+1]}{min}q(k)\ge 1,q^{+}:=\underset{k\in [1,T+1]}{max}q(k),\end{array}$$$$p^{+}:=\underset{k\in [0,T+1]}{max}p(k),\text{and}{p}^{-}:=\underset{k\in [0,T+1]}{min}p(k),$$$$\begin{array}{c}\hfill w^{-}:=\underset{k\in [0,T]}{min}w(k),w^{+}:=\underset{k\in [0,T]}{max}w(k).\end{array}$$

We want to remark that problem (1.1) is the discrete variant of the variable exponent anisotropic problem(1.2) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\sum }_{i=1}^N\frac{\partial }{\partial x_i}(w_i(x)|\frac{\partial u}{\partial x_i}{|}^{p_i(x)-2}\frac{\partial u}{\partial x_i}{)+q(x)|u|}^{p_i(x)-2}u=\lambda f(x,u),x\in \mathrm{\Omega },\hfill \\ u=0,x\in \partial \mathrm{\Omega },\hfill \end{array}\right.\end{array}$$(1.2)

where $\mathrm{\Omega }\subset {\mathbb{R}}^N$, $N\ge 3$ is a bounded domain with smooth boundary, $f\in C(\overline{\mathrm{\Omega }}\times \mathbb{R},\mathbb{R})$ is a given function that satisfies certain properties and $p_i(x)$, $w_i(x)\ge 1$ and $q(x)\ge 1$ are continuous functions on $\overline{\mathrm{\Omega }}$ with $2\le p_i(x)$ for each $x\in \mathrm{\Omega }$ and every $i\in \{1,2,\cdots ,N\}$, $\lambda >0$ is real number.

In this article, in the framework of variational methods, we look for the existence of infinitely many solutions to problem (1.1) based on a recent local minimum theorem obtained (Theorem 2.1) which is given in finite dimensional spaces in Bonanno and Candito (2014) due to Bonanno, Candito and D’Aguì. We ensure exact intervals of the parameter $\lambda$, in which the problem (1.1) admits infinitely solutions.

In this article, after presenting a main tools theorem (Theorem 2.1) and an applicable lemma (Lemma 2.1), we present a lemma ( Lemma 2.2) which is fundamental to our aims where $\lambda$ lies in a well-defined half-line. Bearing in mind a fundamental lemma, we obtain our results where the existence of an unbounded sequence of solutions (Theorem 3.1) converges to infinity depending on the non-linear term having suitable behaviours at infinity.

Moreover, we also emphasize that by strong maximum principle, if f is non-negative and $f(k,0)=0$ for all $k\in [1,T]$, our results guarantee infinitely many positive solutions (Remark 3.3).

Further, as an example, we point out a special case of our main results with respect to Theorem 3.1, in the following theorem.

Theorem 1.1

Let $f:\mathbb{R}\to \mathbb{R}$

be a continuous function and$$\begin{array}{c}\hfill \underset{s\to +\infty }{lim\; inf}\frac{{max}_{|t|\le s}{\int }_0^{t}f(\xi )d\xi }{\frac{{|s|}^3}{T(T+4){(2T+2)}^2}-\frac{2T+2}{T(T+4)}}<+\infty ,\end{array}$$$$\begin{array}{c}\hfill \underset{s\to \infty }{lim\; sup}\frac{{max}_{|t|\le s}{\int }_0^{t}f(\xi )d\xi }{{|s|}^{T+4}}=+\infty .\end{array}$$

Then, for any$$\lambda \in \left]0,\frac{1}{{lim\; inf}_{s\to +\infty }\frac{{max}_{|t|\le s}{\int }_0^{t}f(\xi )d\xi }{\frac{{|s|}^3}{T(T+4){(2T+2)}^2}-\frac{2T+2}{T(T+4)}}}\right[,$$

the problem(1.3) $$\begin{array}{c}\hfill \left\{\begin{array}{c}-{\mathrm{\Delta }(|\mathrm{\Delta }u(k-1)|}^k{\mathrm{\Delta }u(k-1))+|u(k)|}^{k+1}u(k)=\lambda f(u(k)),k\in [1,T],\hfill \\ u(0)=u(T+1)=0,\hfill \end{array}\right.\end{array}$$(1.3)

admits an unbounded sequence of solutions $u_n$ such that$$\underset{n\to +\infty }{lim}{\left\{\sum _{k=1}^{T+1}|\mathrm{\Delta }{u}_n{(k-1)|}^3+{|u_n(k)|}^3\right\}}^{1/3}=\infty .$$

The local minimum theorem (Theorem 2.1) due to Bonanno, Candito and D’Aguì (2014) is also successfully employed to the existence of infinitely solutions for two-point boundary value problems in Bonanno and Candito (2009), Bonanno and Molica Bisci (2009), Khaleghi Moghadam et al. (2014), Salari, Caristi, Barilla, and Puglisi (2000).

The remainder of this paper is arranged as follows. In Section 2, we recall the main tools (Theorem 2.1) and give some basic knowledge. In Section 3, we state and prove our main results of the paper that contains several theorems and corollaries, and prove a special case of our main result (Theorem 1.1) and illustrate the results by giving concrete examples as applications to (1.1).

2. Preliminaries

Our main tool is the following infinitely many critical points theorem. Assume that:

(H) Let $(X,\Vert ·\Vert )$ be a real finite dimensional Banach space and let $\mathrm{\Phi },\mathrm{\Psi }:X⟶\mathbb{R}$ be two continuously Gateaux differentiable functionals with $\mathrm{\Phi }$ coercive and such that$$\underset{X}{inf}\mathrm{\Phi }=\mathrm{\Phi }(0)=\mathrm{\Psi }(0)=0.$$

Put$$\phi (r):=\frac{{sup}_{{\mathrm{\Phi }}^{-1}(]0,r])}\mathrm{\Psi }}{r},$$

for all $r>0$,$${\phi }_{\infty }:=\underset{r\to +\infty }{lim\; inf}\phi (r).$$

Theorem 2.1

([Theorem 4.3] Bonanno, Candito, & DAgu‘i, 2014). The following property holds:

Assume that ${\phi }_{\infty }<+\infty$ and for each $\lambda \in ]0,\frac{1}{{\phi }_{\infty }}[$ the function $I_{\lambda }=\mathrm{\Phi }-\lambda \mathrm{\Psi }$ is unbounded from below. Then, there is a sequence $\{u_n\}$ of critical points (local minima) of $I_{\lambda }$ such that $li{m}_{n\to +\infty }\mathrm{\Phi }(u_n)=+\infty$.

Remark 2.2

Theorem 2.1 is the finite dimensional version of [Bonanno, 2012, Theorem 7.4] (see also [Ricceri, 2000, Theorem 2.3] and observations in Remark 3.1).

Let $T\ge 2$ be a fixed positive integer, [1, T] denote a discrete interval $\{1,...,T\}$. Define T-dimensional function space by$$W:=\{u:[0,T+1]\to \mathbb{R}:u(0)=u(T+1)=0\},$$

which is a Hilbert space under the norm$$\Vert u\Vert ={\left\{\sum _{k=1}^{T+1}{w(k-1)|\mathrm{\Delta }u(k-1)|}^{p^{-}}+q(k){|u(k)|}^{p^{-}}\right\}}^{1/p^{-}}.$$

Since W is finite-dimensional, we can also define the following equivalent norm on W $${\Vert u\Vert }_{+}={\left\{\sum _{k=1}^{T+1}{w(k-1)|\mathrm{\Delta }u(k-1)|}^{p^{+}}+q(k){|u(k)|}^{p^{+}}\right\}}^{1/p^{+}}.$$

Now, let $\psi :W\to \mathbb{R}$ be given by the formula(2.1) $$\begin{array}{c}\hfill \psi (u):=\sum _{k=1}^{T+1}{[w(k-1)|\mathrm{\Delta }u(k-1)|}^{p(k-1)}+q(k){|u(k)|}^{p(k)}].\end{array}$$(2.1)

In the sequel, we will use the following inequalities.

Lemma 2.3 (Lemma 2.1-2.2)

[Lemma 2.1-2.2] Khaleghi Moghadam and Henderson (2017) For any $u\in W$, there exist two positive constants $C_1$ and $C_2$ such that(2.2) $$\begin{array}{c}\hfill \Vert u\Vert <1\Rightarrow {\Vert u\Vert }_{+}^{p^{+}}\le \psi (u)\le {\Vert u\Vert }^{p^{-}},\end{array}$$(2.2) (2.3) $$\begin{array}{c}\hfill \Vert u\Vert \ge 1\Rightarrow {\Vert u\Vert }^{p^{-}}-C_1\le \psi (u)\le {\Vert u\Vert }_{+}^{p^{+}}+C_1,\end{array}$$(2.3) (2.4) $$\begin{array}{c}\hfill C_2{\Vert u\Vert }^{p^{+}}\le {\Vert u\Vert }_{+}^{p^{+}}\le 2^{\frac{p^{+}-p^{-}}{p^{-}}}{C}_2{\Vert u\Vert }^{p^{+}},\end{array}$$(2.4) (2.5) $$\begin{array}{c}\hfill {\Vert u\Vert }_{\infty }:=\underset{k\in [1,T]}{max}|u(k)|\le {(2T+2)}^{\frac{p^{-}-1}{p^{-}}}\Vert u\Vert ,\end{array}$$(2.5)

where$$C_1=(T+1)(w^{+}+q^{+})\in ]1,+\infty [,C_2=\{(2T+2)max\{w^{+},q^{+}\}{\}}^{\frac{p^{-}-p^{+}}{p^{-}}}\in ]0,1].$$

Let $\mathrm{\Phi }$ and $\mathrm{\Psi }$ be as in the following(2.6) $$\begin{array}{cc}\hfill \mathrm{\Phi }(u)& :=\sum _{k=1}^{T+1}\left[\frac{w(k-1)}{p(k-1)}{|\mathrm{\Delta }u(k-1)|}^{p(k-1)}+\frac{q(k)}{p(k)}{|u(k)|}^{p(k)}\right],\hfill \\ \hfill \mathrm{\Psi }(u)& :=\sum _{k=1}^{T}F(k,u(k)),\hfill \end{array}$$(2.6)

where $F(k,t):={\int }_0^{t}f(k,\xi )d\xi$ for every $(k,t)\in [1,T]\times \mathbb{R}$.

To study the problem (1.1), we consider the functional $I_{\lambda ,\mu }:W\to \mathbb{R}$ defined by(2.7) $$\begin{array}{cc}\hfill I_{\lambda }(u)& =\sum _{k=1}^{T+1}\left[\frac{w(k-1)}{p(k-1)}{|\mathrm{\Delta }u(k-1)|}^{p(k-1)}+\frac{q(k)}{p(k)}{|u(k)|}^{p(k)}\right]\hfill \\ \hfill & -\hfill & \hfill \lambda \sum _{k=1}^{T}F(k,u).\end{array}$$(2.7)

We want to remark that since problem (1.1) is settled in a finite-dimensional Hilbert space W, it is not difficult to verify that the functional $I_{\lambda }$ satisfies the regularity properties. Therefore, $I_{\lambda }$ is of class $C^1$ on W (see, e.g., Jiang & Zhou (2008)) with the derivative$$\begin{array}{cc}\hfill I_{\lambda }^{\prime }(u)(v)& =\sum _{k=1}^{T+1}\left[{w(k-1)|\mathrm{\Delta }u(k-1)|}^{p(k-1)-2}\mathrm{\Delta }u(k-1)\mathrm{\Delta }v(k-1)\right]\hfill \\ \hfill & +\sum _{k=1}^{T}q(k){|u(k)|}^{p(k)-2}u(k)v(k)\hfill \\ \hfill & -\hfill & \hfill \sum _{k=1}^T\left[\lambda f(k,u(k))\right]v(k),\end{array}$$

for all $u,v\in W$.

It is clear that the critical points of $I_{\lambda }$ and the solutions of the problem (1.1) are exactly equal.

Now we give two lemmas and the following notation. Put$$A:=\left(w(0)+w(T)+\sum _{k=1}^{T}q(k)\right),$$

and$$B^{\infty }:=\underset{s\to \infty }{lim\; sup}\frac{{\sum }_{k=1}^{T}F(k,s)}{{|s|}^{p^{+}}}.$$

Lemma 2.4

If $0<B^{\infty }$, then $I_{\lambda }$ is unbounded from below for each $\lambda \in ]\frac{A}{p^{-}{B}^{\infty }},+\infty [$.

Fix l such that $B^{\infty }>l>\frac{A}{p^{-}\lambda }$ and let $d_n$ be a sequence of positive numbers, with $li{m}_{n\to \infty }{d}_n=+\infty$, such that for each $n\in \mathbb{N}$ large enough. Set(2.8) $$\begin{array}{c}\hfill w_n(k):=\left\{\begin{array}{cc}{d}_n^{\frac{p^{-}}{p^{+}}},\hfill & k\in [1,T];\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\right.\end{array}$$(2.8)

Clearly, $w_n\in W$. Bearing in mind $p^{-}\le p(k)\le p^{+}$, we obtain(2.9) $$\begin{array}{cc}\hfill \mathrm{\Phi }(w_n)& \le \frac{1}{p^{-}}\psi (d_n^{\frac{p^{-}}{p^{+}}})\hfill \\ \hfill & \le \frac{A{d}_n^{p^{-}}}{p^{-}},\hfill \end{array}$$(2.9)

from ${lim\; sup}_{n\to \infty }\frac{{\sum }_{k=1}^{T}F(k,d_n^{\frac{p^{-}}{p^{+}}})}{|d_n^{\frac{p^{-}}{p^{+}}}{|}^{p^{+}}}>l$, there is $\nu \in \mathbb{N}$ such that ${\sum }_{k=1}^{T}F(k,d_n^{\frac{p^{-}}{p^{+}}})>l{|d_n|}^{p^{-}}$ for all $n\ge \nu$.

Therefore,$$\mathrm{\Psi }(w_n)=\sum _{k=1}^{T}F(k,w_n(k))=\sum _{k=1}^{T}F(k,d_n^{\frac{p^{-}}{p^{+}}})>l{|d_n|}^{p^{-}}.$$

Thus, one has$$\begin{array}{cc}\hfill I_{\lambda }(w_n)& =\mathrm{\Phi }(w_n)-\lambda \mathrm{\Psi }(w_n)<\frac{d_n^{p^{-}}A}{p^{-}}-\lambda l{d}_n^{p^{-}}\hfill \\ \hfill & =d_n^{p^{-}}\left(\frac{A}{p^{-}}-\lambda l\right)\to -\infty ,\text{as}n\to +\infty ,\hfill \end{array}$$

that is, ${lim}_{n\to +\infty }{I}_{\lambda }(w_n)=-\infty .$

3. Main results

First, put$$\begin{array}{c}\hfill B_{\infty }:=\underset{s\to +\infty }{lim\; inf}\frac{{\sum }_{k=1}^T{max}_{|t|\le s}F(k,t)}{\frac{{|s|}^{p^{-}}}{p^{+}{(2T+2)}^{p^{-}-1}}-\frac{C_1}{p^{+}}}.\end{array}$$

We state our main result as follows.

Theorem 3.1

Assume that $0\le B_{\infty }<\infty$ and $B^{\infty }=\infty$ and $f:[1,T]\times \mathbb{R}\to \mathbb{R}$ is a continuous function. Then, for any$$\lambda \in \mathrm{\Lambda }:=\left]0,\frac{1}{B_{\infty }}\right[,$$

the problem (1.1) admits an unbounded sequence of solutions.

Our aim is to apply Theorem 2.1 to our problem. To this end, first, we observe that due to $0\le B_{\infty }<\infty$, the interval $\mathrm{\Lambda }$ is non-empty, so fix $\overline{\lambda }$ in $\mathrm{\Lambda }$.

To settle the variational framework of problem (1.1), take $X=W$, and put $\mathrm{\Phi },\mathrm{\Psi }$ as defined in (2.6), for every $u\in W$. Again, because W is finite dimensional, an easy computation ensures that $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are of class $C^1$ on W with the derivatives$$\begin{array}{cc}\hfill {\mathrm{\Phi }}^{\prime }(u)(v)& =\sum _{k=1}^{T+1}w(k-1){|\mathrm{\Delta }u(k-1)|}^{p(k-1)-2}\mathrm{\Delta }u(k-1)\mathrm{\Delta }v(k-1)\hfill \\ \hfill & +\sum _{k=1}^{T}q(k){|u(k)|}^{p(k)-2}u(k)v(k)\hfill \\ \hfill & =-\sum _{k=1}^T{\mathrm{\Delta }(w(k-1)|\mathrm{\Delta }u(k-1)|}^{p(k-1)-2}\mathrm{\Delta }u(k-1))v(k)\hfill \\ \hfill & +\sum _{k=1}^{T}q(k){|u(k)|}^{p(k)-2}u(k)v(k),\hfill \end{array}$$

and$${\mathrm{\Psi }}^{\prime }(u)(v)=\sum _{k=1}^{T}f(k,u(k))v(k),$$

for all $u,v\in W$. Also $\mathrm{\Phi }$ is coercive. Indeed, let $u\in W$ be such that $\Vert u\Vert >1$. From (2.3), we have$$\mathrm{\Phi }(u)\ge \frac{1}{p^{+}}\psi (u)\ge \frac{{\Vert u\Vert }^{p^{-}}}{p^{+}}-\frac{C_1}{p^{+}}.$$

Therefore, $\mathrm{\Phi }(u)\to \infty$ as $\Vert u\Vert \to \infty$, i.e. $\mathrm{\Phi }$ is coercive. It is clear that ${inf}_X\mathrm{\Phi }=\mathrm{\Phi }(0)=\mathrm{\Psi }(0)=0$. Therefore, we observe that the regularity assumptions on $\mathrm{\Phi }$ and $\mathrm{\Psi }$, as requested in Theorem 2.1, are verified, i.e. condition (H) holds.

Standard arguments show that $I_{\overline{\lambda }}:=\mathrm{\Phi }-\overline{\lambda }\mathrm{\Psi }\in C^1(W,\mathbb{R})$ as well as that critical points of $I_{\overline{\lambda }}$ are exactly the solutions of the problem (1.1).

Next, we prove ${\phi }_{\infty }<+\infty$. Let $\{d_n\}$ be a real sequence such that $d_n\to \infty$ as $n\to \infty$. Put$$\begin{array}{c}\hfill r_n:=min\{r_{1,n},r_{2,n}\},\end{array}$$

where$$\begin{array}{c}\hfill r_{1,n}:=\frac{d_n^{p^{+}}}{p^{+}},r_{2,n}:=\frac{1}{p^{+}}\left(\frac{d_n^{p^{-}}}{{(2T+2)}^{p^{-}-1}}-C_1\right),\end{array}$$

Clearly, $r_n\to \infty$ as $n\to \infty$ and for n enough large $r_n=\frac{1}{p^{+}}(\frac{d_n^{p^{-}}}{{(2T+2)}^{p^{-}-1}}-C_1)$. For all $u\in W$ such that $\mathrm{\Phi }(u)<r_n$, we consider two cases (1) $\Vert u\Vert <1$, (2) $\Vert u\Vert \ge 1$. In first case, taking (2.1) and (2.2) into account, one has$$\begin{array}{c}\hfill r_{1,n}\ge r_n>\mathrm{\Phi }(u)\ge \frac{1}{p^{+}}\psi (u)\ge \frac{{\Vert u\Vert }_{+}^{p^{+}}}{p^{+}}\ge \frac{{|u(k)|}^{p^{+}}}{p^{+}},\forall k\in [1,T],\end{array}$$

so(2.10) $$\begin{array}{c}\hfill \underset{k\in [1,T]}{max}|u(k)|<{(p^{+}{r}_{1,n})}^{\frac{1}{p^{+}}}=d_n.\end{array}$$(2.10)

In second case, $\Vert u\Vert >1$, taking (2.1) and (2.3) into account, one has$$\begin{array}{c}\hfill r_{2,n}\ge r_n>\mathrm{\Phi }(u)\ge \frac{1}{p^{+}}\psi (u)\ge \frac{1}{p^{+}}{(\Vert u\Vert }^{p^{-}}-C_1),\end{array}$$

so $\Vert u\Vert <{(p^{+}{r}_{2,n}+C_1)}^{\frac{1}{p^{-}}}.$ By (2.5), we obtain(3.1) $$\begin{array}{c}\hfill \underset{k\in [1,T]}{max}|u(k)|\le {(2T+2)}^{\frac{p^{-}-1}{p^{-}}}\Vert u\Vert <{(2T+2)}^{\frac{p^{-}-1}{p^{-}}}{(p^{+}{r}_{2,n}+C_1)}^{\frac{1}{p^{-}}}=d_n.\end{array}$$(3.1)

Therefore, by (3.1) and (3.2), we have for $i=1,2$$$\begin{array}{cc}\hfill \underset{u\in {\mathrm{\Phi }}^{-1}(]-\infty ,r_n[)}{sup}\mathrm{\Psi }(u)& \le \underset{u\in {\mathrm{\Phi }}^{-1}(]-\infty ,r_{i,n}[)}{sup}\mathrm{\Psi }(u)=\underset{u\in {\mathrm{\Phi }}^{-1}(]-\infty ,r_{i,n}[)}{sup}\sum _{k=1}^{T}F(k,u(k))\hfill \\ \hfill & \le \sum _{k=1}^T\underset{|\xi |\le d_n}{max}F(k,\xi ).\hfill \end{array}$$

Therefore,$$\begin{array}{cc}\hfill \varphi (r_n)& =\frac{{sup}_{u\in {\mathrm{\Phi }}^{-1}]-\infty ,r_n[}\mathrm{\Psi }(u)}{r_n}\le \frac{{\sum }_{k=1}^{k=T}{max}_{|\xi |\le d_n}F(k,\xi )}{r_n}\hfill \\ \hfill & =\frac{p^{+}{\sum }_{k=1}^{k=T}{max}_{|\xi |\le d_n}F(k,\xi )}{\frac{d_n^{p^{-}}}{{(2T+2)}^{p^{-}-1}}-C_1}.\hfill \end{array}$$

Hence,(3.2) $$\begin{array}{cc}\hfill {\phi }_{\infty }& =\underset{r\to +\infty }{lim\; inf}\varphi (r)=\underset{n\to +\infty }{lim\; inf}\varphi (r_n)\hfill \\ \hfill & \le \underset{n\to +\infty }{lim\; inf}\frac{p^{+}{\sum }_{k=1}^{k=T}{max}_{|\xi |\le d_n}F(k,\xi )}{\frac{d_n^{p^{-}}}{{(2T+2)}^{p^{-}-1}}-C_1}=B_{\infty }.\hfill \end{array}$$(3.2)

Hence, bearing in mind $B_{\infty }<\infty$, ${\phi }_{\infty }<\infty$ follows.

Also by Lemma 2.4, since $B^{\infty }=\infty$, $I_{\lambda }$ is unbounded from below for all $\lambda \in ]0,\frac{1}{{\phi }_{\infty }}[\subseteq ]0,+\infty [$, hence, the problem (1.1) admits an unbounded sequence of solutions $u_n$ for all $\lambda \in \mathrm{\Lambda }\subseteq ]0,\frac{1}{{\phi }_{\infty }}[$ such that$$\underset{n\to \infty }{lim}\mathrm{\Phi }(u_n)=+\infty ,$$

and the proof is complete. $\square$

Corollary 3.2

If $u_n$ are the ensured solutions in the conclusions of Theorem 3.1, then ${lim}_{n\to +\infty }\Vert u_n\Vert =\infty$.

We must have $\Vert u_n\Vert \ge 1$. Indeed, if $\Vert u_n\Vert <1$, from (2.2), we have $\mathrm{\Phi }(u_n)\le \frac{\psi (u_n)}{p^{-}}\le \frac{\Vert u_n{\Vert }^{p^{-}}}{p^{-}}<\frac{1}{p^{-}}$; this is in contradiction with ${lim}_{n\to \infty }\mathrm{\Phi }(u_n)=+\infty$,

Hence, taking (2.3) and (2.4) into account, one has$$\begin{array}{c}\hfill \mathrm{\Phi }(u_n)\le \frac{\psi (u_n)}{p^{-}}\le \frac{1}{p^{-}}(\Vert u_n{\Vert }_{+}^{p^{+}}+C_1)\le \frac{1}{p^{-}}(2^{\frac{p^{+}-p^{-}}{p^{-}}}{C}_2\Vert u_n{\Vert }^{p^{+}}+C_1),\end{array}$$

so, bearing in mind $\mathrm{\Phi }(u_n)\to \infty$ as $n\to \infty$, the assertion concludes. $\square$

Remark 3.3

Under the condition $B_{\infty }=0$, Theorem 3.1 concludes that for every $\lambda >0$ the problem (1.1) admits an unbounded sequence of solutions in W.

Figure 1. The graph of the function F(k, t)

Example 3.4

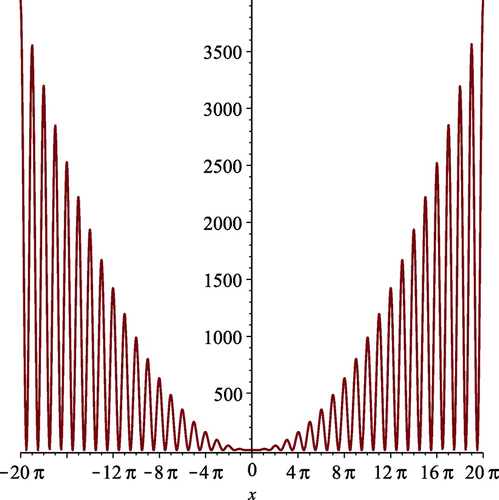
Let $T=2$, $p(k)=\frac{1}{3}k+2$, $q(k)=w(k)=1$ and $f(k,x)=\frac{d}{\mathit{dx}}(x^2(1+x^2({cos}^{2}x)))$ for $k=1,2$ and $x\in \mathbb{R}$. Hence, $p^{-}=2$, $p^{+}=3$, $A=T+2=4$ and $C_1=(T+1)(w^{+}+q^{+})=6$. Simple calculations show that (see the graph of function F(k, t) in Figure 1).$$\begin{array}{cc}\hfill B^{\infty }& =\underset{s\to \infty }{lim\; sup}\frac{{\sum }_{k=1}^{T}F(k,s)}{{|s|}^{p^{+}}}\hfill \\ \hfill & =\underset{s\to \infty }{lim\; sup}\frac{{\sum }_{k=1}^T{s}^2(1+s^2({cos}^{2}s))}{{|s|}^3}=\infty ,\hfill \end{array}$$$$\begin{array}{cc}\hfill B_{\infty }& =\underset{s\to +\infty }{lim\; inf}\frac{{\sum }_{k=1}^T{max}_{|\xi |\le s}{\xi }^2(1+{\xi }^2({cos}^2\xi ))}{\frac{{|s|}^{p^{-}}}{p^{+}{(2T+2)}^{p^{-}-1}}-\frac{C_1}{p^{+}}}\hfill \\ \hfill & =\underset{s\to \infty }{lim\; inf}\frac{2{max}_{|\xi |\le s}{\xi }^2(1+{\xi }^2({cos}^2\xi ))}{\frac{{|s|}^2}{3(6)}-\frac{6}{3}}=36.\hfill \end{array}$$

Then, by Theorem 3.1, for every$$\lambda \in \mathrm{\Lambda }:=\left]0,\frac{1}{36}\right[,$$

the problem$$\left\{\begin{array}{c}-{\mathrm{\Delta }(|\mathrm{\Delta }u(k-1)|}^{\frac{1}{3}(k-1)}{\mathrm{\Delta }u(k-1))+|u(k)|}^{\frac{1}{3}k}u(k)=\lambda \left(f(k,u(k))\right),\hfill \\ u(0)=u(3)=0,\hfill \end{array}\right.$$

for every $k\in [1,2]$, admits an unbounded sequence of solutions.

Remark 3.5

The proof of Theorem 1.1 coincides with the proof of Theorem 3.1 and Corollary 3.2, with $q(k)=w(k)=1$ and $p(k)=k+3$.

Remark 3.6

By the strong maximum principle [Lemma 2.3] Agarwal et al. (2005) (see also ([Theorem 2.2] Bonanno & Candito, 2009), if f is non-negative and $f(k,0)=0$ for all $k\in [0,T]$, then the ensured solutions in the conclusions of Theorem 3.1 are positive (for more illustration see Khaleghi Moghadam et al., 2018).

Additional information

Funding

This work was supported by the Sari Agricultural Sciences and Natural Resources University [grant number 05-1395-04].

Notes on contributors

M. Khaleghi Moghadam

M. Khaleghi Moghadam is an Assistant Professor of Mathematics, Department of Basic Sciences, Sari Agricultural Sciences and Natural Resources University, 578 Sari. The author key research activities are: Nonlinear Analysis: Variational Principles, Critical Point Theory, Variational Inequalities Difference Equations: Fractional Difference Equations, Theory, Applications Partial and Ordinary Differential Equations: Semilinear and Quasilinear, Elliptic Boundary Value Problems.