Modelling the impact of mass administration of ivermectin in the treatment of onchocerciasis (river blindness)

Abstract

Onchocerciasis (river blindness) is a disease spread from black flies to humans. This disease is responsible for chronic morbidity in sub-Saharan Africa. The principal strategy to achieve onchocerciasis elimination is through mass drug administration with ivermectin, a drug that is effective in the short term but wanes quickly. Ivermectin kills the skin-dwelling microfilariae. It may also kill and/or sterilize adult worms. This treatment protocol occurs bi-annually. Consequently, a system of impulsive differential equations is introduced to model both fixed and non-fixed mass drug administration with ivermectin. We determine the threshold for the proportion of treated individuals that reduces the infection in the human population. In the absence of impulsive mass drug administration with ivermectin, we determine the threshold for eradication $R_0$ and carry out stability analysis. The sensitivity analysis results reveal that the disease is unlikely to be eradicated without extremely low transmission levels or strong vector control. If treatment is included, then treatment at fixed intervals can control but not eradicate the disease. Treatment at non-fixed intervals may produce bursts of infection. Thus, bi-annual mass drug administration with ivermectin that is tailored to eradicate onchocerciasis, can only lead to significant reduction of onchocerciasis. However, to achieve 2020/2025 onchocerciasis elimination goals set by World Health Organization, the human-vector contact should be sufficiently reduced and vector control programmes implemented to supplement an intensive and effective mass drug administration with ivermectin.

Keywords:

• onchocerciasis; ivermectin; World Health Organization; mathematical model; impulsive differential equations; reproduction number; sensitivity; simulation

Public Interest Statement

Impulsive differential equations are very helpful in studying many biological systems and population dynamics that have sudden change in their states. In epidemiology, impulsive differential equations assess the vaccination and or treatment program that consists of periodical repetitions of impulsive vaccinations and or treatment in a population, on all the age cohorts. The results from the pulse control strategy support the fact that eradication of onchocerciasis is possible with tolerable regularity of mass drug administration with ivermectin.

1. Introduction

Onchocerciasis (also known as river blindness) is a neglected tropical disease caused by the filarial nematode Onchocerca volvulus in human hosts (Feasey, Wansbrough-Jones, Mabey, & Solomon, 2009). The disease is transmitted by the black fly (Simulium damnosum) (Turner, Basáñez, Walker, & Churcher, 2014). Simulium breeds close to oxygen-rich flowing streams and rivers in inter-tropical zones (Crosskey, 1990; Kealey, 2010). Onchocerciasis endemic areas thus tend to include the most agriculturally fertile land available. The infection of onchocerciasis begins at the third larvae stage in the human host after the vector’s blood meal. The larvae develop into adult filariae in the subcutaneous tissues from which microfilariae migrate throughout the body, predominantly within the skin (Lustigman, MacDonald, & Abraham, 2003). This produces an intense itching of the skin and a chronic dermatitis that leads to skin atrophy and depigmentation (Cox, 2002). The migration of microfilariae through the anterior and posterior segments of the eye precipitates inflammatory reactions that lead to loss of vision and sometimes blindness (Kealey, 2010; Mopecha & Thieme, 2003).

Various onchocerciasis control strategies have achieved dramatic success in reducing onchocerciasis transmission (Traoré et al., 2009; Winnen et al., 2002). The strategies have employed both the use of larvicide spraying at black fly breeding sites and the periodic mass drug administration with ivermectin to the affected human populations. The control programmes have been spearheaded by three international programmes: the Onchocerciasis Control Program, the Onchocerciasis Elimination Programme in the Americas and the African Program for Onchocerciasis Control (APOC). Transmission of onchocerciasis was interrupted in Guatemala and in several hyper-endemic foci of Mali and Senegal following six-monthly mass drug administration with ivermectin (Gonzalez et al., 2009). In 2014, Columbia and Ecuador were declared free of onchocerciasis following the implementation of the control strategies for decades by the WHO (Global Health Observatory, 2016).

Mass drug administration with ivermectin is the main strategy used to achieve elimination of onchocerciasis in sub-Saharan Africa by 2020/2025 as articulated by the 2012 Roadmap of World Health Organization (WHO) (Hopkins & Boatin, 2011; Winnen et al., 2002; World Health Organization, 2012). Ivermectin kills the skin dwelling microfilariae that are the progeny of adult Onchocerca volvulus and are infectious to biting black fly species vectors. Ivermectin may also kill and/or sterilize adult worms (Gardon, Boussinesq, Kamgno, Gardon-Wendel, & Duke, 2002). Multiple rounds of mass treatment are effective in lowering the prevalence and intensity of onchocerciasis. Furthermore, if given for long enough at high enough coverage, it can lead to the interruption of transmission and elimination of the infection (Lovato et al., 2014). Mass treatment with ivermectin was initially carried out annually. However, a change in strategy to six monthly mass treatments was adopted to increase the probability of disease eradication (Barrett & Stanberry, 2009; Winnen et al., 2002).

Although substantial epidemiological work has been done on the study of onchocerciasis transmission dynamics, little has been done to model the disease using impulsive differential equations. Our aim is to examine the effects of mass drug administration with ivermectin using a mathematical model of impulsive differential equations. The model focuses on the effect of fixed and non-fixed mass drug administration with ivermectin in the treatment of onchocerciasis to account for the reduction of infection of onchocerciasis in the human population. Thus, we endeavour to address the following research questions: (1) Can we determine the critical threshold for the proportion of individuals with ochocerciasis that will reduce the infection of the onchocerciasis in the population? (2) Can mass drug administration with ivermectin eradicate onchocerciasis? (3) Does control of onchocerciasis depend on mass drug administration with ivermectin occurring at fixed times? Thus, the potential effect of mass treatment on onchocerciasis transmission dynamics is of great interest.

In this manuscript, our work is organized as follows: related literature is provided in Section 2. In Section 3, we formulate the mathematical model. In Section 4, we analyse the non-impulsive version of the model by calculating the basic reproduction number and carrying out stability analysis. In Section 5, we analyse the model with impulses and determine the effectiveness of mass drug administration with ivermectin for the regular mass treatment. Numerical simulation results are then presented in Section 6. In Section 7, we conclude our project and give relevant recommendation.

2. Related literature

A number of epidemiological models have been formulated and mathematically analysed to describe the behaviour of onchocerciasis in the population. Walker et al. (2017) tested the EPIONCHO and ONCHOSIM models against epidemiological data. The data were collected over two decades from 27 sentinel communities in two onchocerciasis foci in Mali and Senegal where the observed prevalence of infection was brought to zero circa 2007–2009 after 15–17 years of mass treatment with ivermectin. They simulated the models using programmatic information on the frequency and coverage of mass treatments and trained the model projections using longitudinal parasitological data, evaluating the projected outcome of elimination (local parasite extinction) or resurgence. Their findings suggested that meeeting onchocerciasis elimination goals of 2020/2025 depends on when an intervention began; how intensively and effectively it was implemented and on the local transmission conditions. Furthermore, in areas where the prevailing ecological conditions are highly propitious to transmission, elimination by 2020 or 2025 may be unfeasible with ivermectin alone. Thus, they suggested that localized low-cost vector control should be considered as a complement to mass treatment with ivermectin alongside other alternative treatment strategies that include anti-wolbachial therapies to accelerate progress towards the 2020/2025 goals.

Authors in Lont et al. (2017), Golden et al. (2016) extended ONCHOSIM model with new output on the Ov16 antibody serostatus of individuals based on their history of infection. They then used ONCHOSIM simulation model to explore for different transmission settings how the Ov16 antibody prevalence in children 1 year after the last mass drug administration with ivermectin round is related to the duration and coverage of mass drug administration with ivermectin, the microfilariae prevalence in the population and the probability that onchocerciasis is eventually eliminated. The results suggested that the post mass administration of ivermectin microfilariae prevalence in the population aged 5 years and above and the Ov16 antibody prevalence in children aged 0-9 years decline with increasing duration and treatment coverage.

Mopecha and Thieme (2003) developed a model to account for both human and bovine onchocerciasis. They considered cross-reactive immunity in response to inocculation of cattle by larvae. They showed that if parasites are wasted on the “wrong" hosts, then the reproduction number is lowered, while cross-reactive immunity can lead to classical competition phenomena. Basáñez and Boussinesq (1999), Basáñez and Ricárdez-Esquinca (2001) developed a model to describe the population biology and control of human onchocerciasis. Their aim was to evaluate various interventions combining the removal of adult worms (nodulectomy) and the microfilaricidal and sterilizing effects of ivermectin. They derived a threshold condition for disease control involving the vector biting rate and the basic reproduction number. They estimated that the annual biting rate for the Simulium onchraceum s.l is 7665 bites per person per year. This is the minimum below which human onchocerciasis would be unable to become endemic in Central America since the basic reproduction number, $R_0$, would be less than unity. They recommended that if the worm is sterilised and the vector population is condensed, then the epidemic could be restricted. In Africa, several field studies have achieved significant reduction in the transmission of infection by repeated annual mass treatment with ivermectin (Guillet et al., 1995; Plaisier, Alley, Van Oortmarssen, Boatin, & Habbema, 1997; Remme, De Sole, & Van Oortmarssen, 1990).

Alley et al. (2001) used a microsimulation model to examine the possibility of switching treatment from the microfilaricide ivermectin to a hypothetical macrofilaricide. They showed that elimination was possible using a macrofilaricide, but that high coverage levels were critical. Filipe et al. (2005) developed an age and sex structured model for intensity of infection with parasite regulation within humans and vectors. They showed that heterogeneous age and sex exposure could explain location specific infection patterns of onchocerciasis. Poolman and Galvani (2006) incorporated host heterogeneity into a model in order to evaluate intervention strategies targeting specific populations for treatment with ivermectin. They found that targeted allocation of ivermectin in a highly heterogeneous population could reduce the public health burden of onchocerciasis using 20–25% of the doses of untargeted allocation. Over the years, a very large literature on mathematical modelling of onchocerciasis has been produced and other several reviews pertinent to this study are available (Basáñez, Walker, Turner, Coffeng, de Vlas, & Stolk, 2016; Coffeng et al., 2017; Lovato et al., 2014; Oguoma & Acho, 2014; OHanlon et al., 2016; Omondi, Orwa, & Nyabadza, 2017; Omondi, Nyabadza, Bonyah, & Badu, 2017).

This paper is motivated by the work in Omondi (2016) and was done as an Msc. research project by the first author. Stopping the transmission chain of onchocerciasis remains the only viable form of control against the spread of infection. The potential effect of mass administration of ivermectin is thus of great interest. We focus on the application of impulsive differential equations to model the periodic mass administration of ivermectin tailored towards eradicating onchocerciasis. To the author?s best knowledge, impulsive differential equation has not been applied to onchocerciasis disease transmission.

3. The mathematical model

3.1. Model formulation

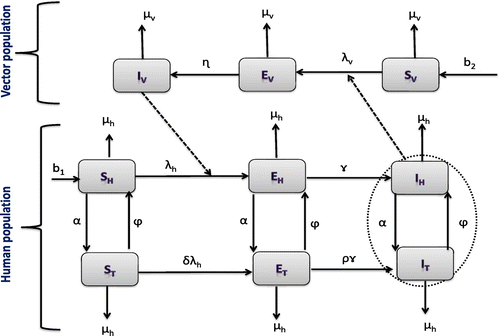
We develop a model to better understand the transmission dynamics of onchocerciasis and its treatment. We consider a habitat with two interacting populations. The two populations are humans (hosts) and black flies (vectors). The total human population is partitioned into six compartments: the susceptible human compartment, $S_H$, referring to individuals not infected with onchocerciasis but who are at risk of infection; the exposed compartment, $E_H$, referring to the individuals that have been exposed to onchocerciaisis through bites; the infectious compartment, $I_H$, referring to individuals with onchocerciaisis infection; susceptible humans undergoing ivermectin treatment, $S_T$; exposed humans undergoing ivermectin treatment, $E_T$; and the infectious humans undergoing ivermectin treatment, $I_T$. The black fly population is partitioned into three compartments: susceptible vectors, $S_V$, referring to black flies that have not picked up microfilariae but are at risk of picking up microfilariae during a blood meal; the exposed vector compartment, $E_V$, referring to black flies that have picked up microfilariae from an infected human during blood meal; and the infected vector compartment, $I_V$.

The total human and vector populations at any given time, t, are respectively given by;(1) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill N(t)& =S_H(t)+E_H(t)+I_H(t)+S_T(t)+E_T(t)+I_T(t),\hfill \\ \hfill V(t)& =S_V(t)+E_V(t)+I_V(t).\hfill \end{array}\right\}\end{array}$$(1)

We assume that the transmission of onchocerciaisis in susceptible hosts is only through contact with an infectious vector. We also assume that susceptible vectors become infectious as a result of contact with infectious hosts during a blood meal. The population under study is assumed to be large enough to be modelled deterministically. The recruitment of new susceptible individuals and susceptible vectors is given by $b_1$ and $b_2$, respectively. Assuming $\beta$ is the blackfly biting rate, that is, the average number of bites per black fly per unit, the rate of infection per susceptible black fly can be represented by(2) $$\begin{array}{c}\hfill {\lambda }_v(t)=\frac{q\beta (I_H+\kappa I_T)}{N},\end{array}$$(2)

where q is the transmission probability from infectious human to black flies and $\kappa$ is the modification parameter which measures the relative ability of individuals in class $I_T$ to cause new infections relative to those in class $I_H$. We assume here that the individuals under treatment have a slightly lower probability to initiate new infections, thus, $0\le \kappa \le 1$. Assuming that the total number of bites made by black flies equals the number of bites received by humans, then the average number of bites per human receives per unit time is $\frac{\beta V}{N}$. Assuming that the transmission probability per bite from infectious black flies to human is p, the rate of infection per susceptible human is given by(3) $$\begin{array}{c}\hfill {\lambda }_h(t)=\frac{p\beta V}{N}\frac{I_V}{V}=\frac{p\beta I_V}{N}.\end{array}$$(3)

We then introduce ${\beta }_h=p\beta$ and ${\beta }_v=q\beta$ parameters to simplify the infection rates per susceptible human and vector respectively. Individuals in class $E_H$ progress to class $I_H$ at rate $\gamma$. Individuals undergoing ivermectin treatment in class $S_T$ acquire infection at the rate $\delta {\lambda }_h$, where $\delta$ defines the reduced effect of infection of the susceptible individuals as a result of treatment. Individuals in class $E_T$ progress to class $I_T$ at the rate $\rho \gamma$, where $\rho$ is the reduced effect of progression to class $I_T$ as a result of treatment. Immediately following treatment, infection in the human population is assumed to be reduced by some proportion $\alpha$. This therefore results in a system of impulsive differential equations (Bainov & Simeonov, 1993; Lakshmikantham, Bainov, & Simeonov, 1989). It is assumed that individuals undergoing treatment relapse due to waning of the drug at the rate $\phi$. We include natural mortality rates given by ${\mu }_h$ and ${\mu }_v$ for the human and vector populations respectively.

We further assume that individuals under treatment have no immunity to the disease upon treatment. In addition, we assume that infected vectors and human do not recover from the infection during the modelling time. The dynamics in the host and vector populations are represented in the schematic diagram in Figure 1.

Figure 1. A compartmental representation of the epidemics and treatment of onchocerciasis. It is important to note that the model proposed here is an extension of the previous model studied in Omondi et al. (2017).

3.2. Model equations

The following system of non-linear ordinary differential equations, with non-negative initial conditions, describes the dynamics of onchocerciasis epidemics:(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4)

subject to the following initial conditions:(5) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill S_H(0)& >0,E_H(0)>0,I_H(0)>0,S_T(0)>0,E_T(0)>0,I_T(0)>0,\hfill \\ \hfill S_V(0)& >0,E_V(0)>0,I_V(0)>0.\hfill \end{array}\right\}\end{array}$$(5)

The impulsive conditions are(6) $$\begin{array}{c}\hfill \left.\begin{array}{cc}△S_H\hfill & =-\alpha S_H,△E_H=-\alpha E_H,△I_H=-\alpha I_H,\hfill \\ △S_T\hfill & =+\alpha S_H,△E_T=+\alpha E_H,△I_T=+\alpha I_H,\hfill \end{array}\right\},t=t_k.\end{array}$$(6)

Treatment may occur at either fixed or non-fixed intervals.

4. System without impulses

4.1. Well-posedness

System (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) describes a human-vector population, so it is therefore necessary to prove that the solutions of system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) with non-negative initial conditions remain non-negative for all time $t\ge 0$ and are bounded in the region(7) $$\begin{array}{c}\hfill \mathrm{\Omega }=\left\{(S_H,E_H,I_H,S_T,E_T,I_T)\in {\mathbb{R}}_{+}^6:N\le \frac{b_1}{{\mu }_h},(S_V,E_V,I_V)\in {\mathbb{R}}_{+}^3:V\le \frac{b_2}{{\mu }_v}\right\}.\end{array}$$(7)

Theorem 4.1

Let $S_H\ge 0,E_H\ge 0,I_H\ge 0,S_T\ge 0,E_T\ge 0,I_T\ge 0,S_V\ge 0,E_V\ge 0,I_V\ge 0$. Then the solutions $S_H(t),E_H(t),I_H(t),S_T(t),E_T(t),I_T(t),S_V(t),E_V(t),I_V(t)$ of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) are positive for all $t\ge 0$. In addition, the region $\mathrm{\Omega }$ is positively invariant and all solutions starting in $\mathrm{\Omega }$ approach, enter or stay in $\mathrm{\Omega }$.

Proof

Let $t^{\ast }=\text{sup}\{t>0:S_H(t)>0,E_H(t)>0,I_H(t)>0,S_T(t)>0,E_T(t)>0,I_T(t)>0,S_V(t)>0,E_V(t)>0,I_V(t)>0\}$. Thus $t^{\ast }\ge 0$. Then, from the first equation of our system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ), we obtain$$\begin{array}{cc}\hfill \dot{S_H}& =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H\ge -({\lambda }_h+{\mu }_h)S_H,\hfill \\ \hfill S_H(t^{\ast })& \ge S_H(0)exp\{-\left({\int }_0^{t^{\ast }}{\lambda }_h(m)dm+{\mu }_h{t}^{\ast }\right)\}.\hfill \end{array}$$

Similarly, one can show that $E_H\ge 0,I_H\ge 0,S_T\ge 0,E_T\ge 0,I_T\ge 0,S_V\ge 0,E_V\ge 0,I_V\ge 0$. This completes the proof for positivity.

The total population of the humans N and that of the vector population V is governed by(8) $$\begin{array}{cc}\hfill \dot{N}& =b_1-{\mu }_{h}N,\dot{V}=b_2-{\mu }_{v}V.\hfill \end{array}$$(8)

Hence(9) $$\begin{array}{c}\hfill \underset{t\to \infty }{lim}supN\le \frac{b_1}{{\mu }_h}\text{and}\underset{t\to \infty }{lim}supV\le \frac{b_2}{{\mu }_v}.\end{array}$$(9)

Therefore, N(t) and V(t) are bounded and the domain of biological significance is positively invariant and attracting. Thus, all solutions starting in $\mathrm{\Omega }$ remain in $\mathrm{\Omega }$.

4.2. Maximal solution

Next, we overestimate the number of infectious individuals in the population. From the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ), we have established that the total human (host) population is bounded above by $\frac{b_1}{{\mu }_h}$. Thus, from the fifth equation of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) we have$$\begin{array}{c}\hfill \frac{d{E}_T}{\mathit{dt}}=\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T.\end{array}$$

If we bound $S_T$ by the total human population and $I_V$ by the total vector population, we have(10) $$\begin{array}{c}\hfill \frac{d{E}_T}{\mathit{dt}}\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v}-(\rho \gamma +\phi +{\mu }_h)E_T.\end{array}$$(10)

Solving the inequality in (10(10) $$\begin{array}{c}\hfill \frac{d{E}_T}{\mathit{dt}}\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v}-(\rho \gamma +\phi +{\mu }_h)E_T.\end{array}$$(10) ), we obtain(11) $$\begin{array}{c}\hfill E_T\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}+\left[E_T(0)-\frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]e^{-(\rho \gamma +\phi +{\mu }_h)t}.\end{array}$$(11)

As t approaches infinity, then the solution in (11(11) $$\begin{array}{c}\hfill E_T\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}+\left[E_T(0)-\frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]e^{-(\rho \gamma +\phi +{\mu }_h)t}.\end{array}$$(11) ) is bounded by(12) $$\begin{array}{c}\hfill E_T\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}.\end{array}$$(12)

Substituting the expression in (12(12) $$\begin{array}{c}\hfill E_T\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}.\end{array}$$(12) ) into the sixth equation of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ), we have$$\begin{array}{c}\hfill \frac{d{I}_T}{\mathit{dt}}\le \frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}-(\phi +{\mu }_h)I_T,\end{array}$$

whose solution can be expressed as(13) $$\begin{array}{c}\hfill I_T\le \frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}.\end{array}$$(13)

Using the solutions obtained in (12(12) $$\begin{array}{c}\hfill E_T\le \frac{\delta {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}.\end{array}$$(12) ) and (13(13) $$\begin{array}{c}\hfill I_T\le \frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}.\end{array}$$(13) ) in the second and third equations in the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) respectively, we have(14) $$\begin{array}{cc}\hfill E_H\le & \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right],\hfill \end{array}$$(14) (15) $$\begin{array}{cc}\hfill I_H\le & \gamma \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]+\phi \left[\frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}\right].\hfill \end{array}$$(15)

The significance of these inequalities is that they overestimate the number of people with onchocerciasis in the population without necessarily solving the original systems of the differential equations. We will make use of these overestimates shortly.

4.3. Stability of the model equilibria

4.3.1. Disease-free equilibrium

The disease-free equilibrium for the system without impulses is given by(16) $$\begin{array}{c}\hfill E_0=({\widehat{S}}_H,{\widehat{E}}_H,{\widehat{I}}_H,{\widehat{S}}_T,{\widehat{E}}_T,{\widehat{I}}_T,{\widehat{S}}_V,{\widehat{E}}_V,{\widehat{I}}_V)=\left(\frac{b_1}{{\mu }_h},0,0,0,0,0,\frac{b_2}{{\mu }_v},0,0\right).\end{array}$$(16)

4.3.2. The basic reproduction number

The basic reproduction number for the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) is obtained using the next-generation method described in Van den Driessche and Watmough (2002). It is given by$$\begin{array}{c}\hfill R_0=\sqrt{{\mathcal{R}}_0}=\sqrt{\frac{b_2\gamma \eta {\beta }_h{\beta }_v}{b_1{\mu }_v^2\left(\gamma +{\mu }_h\right)\left(\eta +{\mu }_v\right)}}.\end{array}$$

Note that this expression is a threshold, not necessarily the average number of secondary infections (Li, Blakeley, & Smith?, 2011).

Theorem 4.2

The disease-free equilibrium, $E_0$, given in (16(16) $$\begin{array}{c}\hfill E_0=({\widehat{S}}_H,{\widehat{E}}_H,{\widehat{I}}_H,{\widehat{S}}_T,{\widehat{E}}_T,{\widehat{I}}_T,{\widehat{S}}_V,{\widehat{E}}_V,{\widehat{I}}_V)=\left(\frac{b_1}{{\mu }_h},0,0,0,0,0,\frac{b_2}{{\mu }_v},0,0\right).\end{array}$$(16) ) of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) is globally stable if ${\mathcal{R}}_0<1$ otherwise unstable.

Proof

Let $V={\theta }_1{E}_H+{\theta }_2{I}_H+{\theta }_3{E}_T+{\theta }_4{I}_T+{\theta }_5{E}_V+{\theta }_6{I}_V$ be a candidate Lyapunov function. The constants ${\theta }_1$ for $i=1,2,3,4,5,6$ are non-negative. We can find the constants ${\theta }_i$ such that the Lyapunov candidate is positive definite. The derivative of the Lyapunov function is given by$$\begin{array}{cc}\hfill \frac{\mathit{dV}}{\mathit{dt}}& ={\theta }_1\frac{d{E}_H}{\mathit{dt}}+{\theta }_2\frac{d{I}_H}{\mathit{dt}}+{\theta }_3\frac{d{E}_T}{\mathit{dt}}+{\theta }_4\frac{d{I}_T}{\mathit{dt}}+{\theta }_5\frac{d{E}_V}{\mathit{dt}}+{\theta }_6\frac{d{I}_V}{\mathit{dt}},\hfill \\ \hfill & ={\theta }_1\left[\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-Q_1{E}_H\right]+{\theta }_2[\gamma E_H+\phi I_T-{\mu }_h{I}_H]+{\theta }_3\left[\frac{\delta {\beta }_h{I}_V{S}_T}{N}-Q_3{E}_T\right]\hfill \\ \hfill & +{\theta }_4[\rho \gamma E_T-Q_2{I}_T]+{\theta }_5\left[\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-Q_4{E}_V\right]+{\theta }_6[\eta E_V-{\mu }_v{I}_V],\hfill \\ \hfill & =[{\theta }_2\gamma -{\theta }_1{Q}_1]E_H+\left[\frac{{\theta }_5{\mu }_h{b}_2{\beta }_v}{{\mu }_v{b}_1}-{\theta }_2{\mu }_h\right]I_H+[{\theta }_1\phi +{\theta }_4\rho \gamma -{\theta }_3{Q}_3]E_T\hfill \\ \hfill & +\left[{\theta }_2\phi +\frac{{\theta }_5\kappa {\beta }_v{\mu }_h{b}_2}{{\mu }_v{b}_1}-{\theta }_4{Q}_2\right]I_T+[{\theta }_6\eta -{\theta }_5{Q}_4]E_V+[{\theta }_1{\beta }_h-{\theta }_6{\mu }_v]I_V,\hfill \end{array}$$

where$$\begin{array}{c}\hfill Q_1=\gamma +{\mu }_h,Q_2=\phi +{\mu }_h,Q_3=\rho \gamma +\phi +{\mu }_h,Q_4=\eta +{\mu }_v.\end{array}$$

Setting the coefficients to $I_H,E_T,I_T,E_V\text{and}{I}_V$ to zero, we obtain(17) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\theta }_1& =\frac{Q_4{\mu }_v}{{\beta }_h},{\theta }_2=\frac{b_2{\beta }_v\eta }{b_1{\mu }_v},{\theta }_3=\frac{b_2\eta \kappa \rho \gamma {\mu }_h{\beta }_v}{b_1{Q}_2{Q}_3{\mu }_v}+\frac{b_2\eta \rho \gamma \phi {\beta }_v}{b_1{Q}_2{Q}_3{\mu }_v}+\frac{Q_4\phi {\mu }_v}{Q_3{\beta }_h},\hfill \\ \hfill {\theta }_4& =\frac{b_2{\beta }_v\eta (\kappa {\mu }_h+\phi )}{Q_2{b}_1{\mu }_v},{\theta }_5=\eta ,{\theta }_6=Q_4.\hfill \end{array}\end{array}$$(17)

We then use the coefficients obtained in (17(17) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\theta }_1& =\frac{Q_4{\mu }_v}{{\beta }_h},{\theta }_2=\frac{b_2{\beta }_v\eta }{b_1{\mu }_v},{\theta }_3=\frac{b_2\eta \kappa \rho \gamma {\mu }_h{\beta }_v}{b_1{Q}_2{Q}_3{\mu }_v}+\frac{b_2\eta \rho \gamma \phi {\beta }_v}{b_1{Q}_2{Q}_3{\mu }_v}+\frac{Q_4\phi {\mu }_v}{Q_3{\beta }_h},\hfill \\ \hfill {\theta }_4& =\frac{b_2{\beta }_v\eta (\kappa {\mu }_h+\phi )}{Q_2{b}_1{\mu }_v},{\theta }_5=\eta ,{\theta }_6=Q_4.\hfill \end{array}\end{array}$$(17) ) into the candidate Lyapunov function. The derivative of the resulting Lyapunov function becomes(18) $$\begin{array}{c}\hfill \frac{\mathit{dV}}{\mathit{dt}}=\frac{Q_1{Q}_4{\mu }_v}{{\beta }_h}[{\mathcal{R}}_0-1].\end{array}$$(18)

We note that, whenever ${\mathcal{R}}_0<1$, then $\frac{\mathit{dV}}{\mathit{dt}}<0$. Therefore, by LaSalle’s Invariance principle (LaSalle, 1976), the disease-free equilibrium is globally stable whenever ${\mathcal{R}}_0<1$. $\square$

4.3.3. Endemic equilibrium

The endemic equilibrium point, $E_1$, is found by equating the right-hand of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) to zero. Expressing all the variables in terms of $I_H$, we get$$\begin{array}{c}\hfill \begin{array}{cc}\hfill S_H^{\ast }& =b_1\left(\frac{1}{{\mu }_h}-\frac{b_2\eta {\beta }_h{I}_H^{\ast }{\beta }_v}{b_1{Q}_4{\mu }_v\left(b_1{\mu }_v+{\mu }_h{I}_H^{\ast }{\beta }_v\right)+b_2\eta {\beta }_h{\mu }_h{I}_H^{\ast }{\beta }_v}\right),\hfill \\ \hfill E_H^{\ast }& =\frac{b_1{b}_2\eta {\beta }_h{\mu }_h{I}_H^{\ast }{\beta }_v}{Q_1\left(b_1{Q}_4{\mu }_v\left(b_1{\mu }_v+{\mu }_h{I}_H^{\ast }{\beta }_v\right)+b_2\eta {\beta }_h{\mu }_h{I}_H^{\ast }{\beta }_v\right)},S_T^{\ast }=E_T^{\ast }=I_T^{\ast }=0,\hfill \\ \hfill S_V^{\ast }& =\frac{b_1{b}_2}{{\beta }_v{\mu }_h{I}_H^{\ast }+b_1{\mu }_v},E_V^{\ast }=\frac{b_2{\beta }_v{\mu }_h{I}_H^{\ast }}{Q_4({\beta }_v{\mu }_h{I}_H^{\ast }+b_1{\mu }_v)},I_V^{\ast }=\frac{b_2{\beta }_v{\mu }_h\eta I_H^{\ast }}{Q_4{\mu }_v({\beta }_v{\mu }_h{I}_H^{\ast }+b_1{\mu }_v)}.\hfill \end{array}\end{array}$$

After some algebraic manipulations, we either have $I_H^{\ast }=0$ or(19) $$\begin{array}{c}\hfill I_H^{\ast }=\frac{Q_1{Q}_4{b}_1^2{\mu }_v^2}{Q_1{\beta }_v{\mu }_h(b_2{\beta }_h\eta +Q_4{b}_1{\mu }_v)}\left[{\mathcal{R}}_0-1\right].\end{array}$$(19)

The case where $I_H^{\ast }=0$, gives the disease-free equilibrium, treated earlier. From expression (19(19) $$\begin{array}{c}\hfill I_H^{\ast }=\frac{Q_1{Q}_4{b}_1^2{\mu }_v^2}{Q_1{\beta }_v{\mu }_h(b_2{\beta }_h\eta +Q_4{b}_1{\mu }_v)}\left[{\mathcal{R}}_0-1\right].\end{array}$$(19) ), one sees that when ${\mathcal{R}}_0<1$, then $I_H^{\ast }<0$, implying that the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) has no positive solution. However, when ${\mathcal{R}}_0>1$, then $I_H^{\ast }>0$ and a unique endemic equilibrium exists.

Theorem 4.3

If ${\mathcal{R}}_0>0$, then $E_0$ is unstable and the unique endemic equilibrium $E_1$ is locally asymptotically stable in the interior of the feasible region $\mathrm{\Omega }$.

Proof

The stability and the direction of bifurcation ${\mathcal{R}}_0=1$ of the endemic equilibrium is proved by the direct use of the Center Manifold Theory (CMT) as described in Castillo-Chavez and Song (2004). We avoid re-stating the theorem and adopting notations as described in Castillo-Chavez and Song (2004), we compute the values of $\mathbf{a}$ and $\mathbf{b}$ whose signs determine local dynamics of the model (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ). The basic reproduction of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) is established to be(20) $$\begin{array}{c}\hfill {\mathcal{R}}_0=\frac{b_2\gamma \eta {\beta }_h{\beta }_v}{b_1{\mu }_v^2\left(\gamma +{\mu }_h\right)\left(\eta +{\mu }_v\right)}.\end{array}$$(20)

Suppose, we choose $\theta ={\beta }_h$ as the bifurcation parameter so that when ${\mathcal{R}}_0=1$, we have(21) $$\begin{array}{c}\hfill \theta =\frac{b_1{\mu }_v^2\left(\gamma +{\mu }_h\right)\left(\eta +{\mu }_v\right)}{b_2\gamma \eta {\beta }_v}\end{array}$$(21)

In order to apply the Center Manifold Theory (CMT), it is necessary to make the following changes to the state variables, we let $S_H=x_1,E_H=x_2,I_H=x_3,S_T=x_4,E_T=x_5,I_T=x_6,S_V=x_7,E_V=x_8,I_V=x_9$. The system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) can now be written in the form $\frac{\mathit{df}}{\mathit{dx}}=f(x)$, where $x=(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,x_9)$. The system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) therefore becomes(22) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \dot{x_1}& =b_1+\phi x_4-\frac{{\beta }_h{x}_9{x}_1}{N}-{\mu }_h{x}_1,\hfill \\ \hfill \dot{x_2}& =\frac{{\beta }_h{x}_9{x}_1}{N}+\phi x_5-Q_1{x}_2,\hfill \\ \hfill \dot{x_3}& =\gamma x_2+\phi x_6-{\mu }_h{x}_3,\hfill \\ \hfill \dot{x_4}& =-\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_2{x}_4,\hfill \\ \hfill \dot{x_5}& =\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_3{x}_5,\hfill \\ \hfill \dot{x_6}& =\rho \gamma x_5-Q_2{x}_6,\hfill \\ \hfill \dot{x_7}& =b_2-\frac{{\beta }_v{x}_3{x}_7}{N}-\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-{\mu }_v{x}_7,\hfill \\ \hfill \dot{x_8}& =\frac{{\beta }_v{x}_3{x}_7}{N}+\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-Q_4{x}_8,\hfill \\ \hfill \dot{x_9}& =\eta x_8-{\mu }_v{x}_9.\hfill \end{array}\right\}\end{array}$$(22) The system (22(22) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \dot{x_1}& =b_1+\phi x_4-\frac{{\beta }_h{x}_9{x}_1}{N}-{\mu }_h{x}_1,\hfill \\ \hfill \dot{x_2}& =\frac{{\beta }_h{x}_9{x}_1}{N}+\phi x_5-Q_1{x}_2,\hfill \\ \hfill \dot{x_3}& =\gamma x_2+\phi x_6-{\mu }_h{x}_3,\hfill \\ \hfill \dot{x_4}& =-\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_2{x}_4,\hfill \\ \hfill \dot{x_5}& =\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_3{x}_5,\hfill \\ \hfill \dot{x_6}& =\rho \gamma x_5-Q_2{x}_6,\hfill \\ \hfill \dot{x_7}& =b_2-\frac{{\beta }_v{x}_3{x}_7}{N}-\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-{\mu }_v{x}_7,\hfill \\ \hfill \dot{x_8}& =\frac{{\beta }_v{x}_3{x}_7}{N}+\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-Q_4{x}_8,\hfill \\ \hfill \dot{x_9}& =\eta x_8-{\mu }_v{x}_9.\hfill \end{array}\right\}\end{array}$$(22) ) with the bifurcation point $\theta$, has a simple zero eigenvalue. Thus, it enables us to use the Center Manifold Theory to analyse the stability of the system (22(22) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \dot{x_1}& =b_1+\phi x_4-\frac{{\beta }_h{x}_9{x}_1}{N}-{\mu }_h{x}_1,\hfill \\ \hfill \dot{x_2}& =\frac{{\beta }_h{x}_9{x}_1}{N}+\phi x_5-Q_1{x}_2,\hfill \\ \hfill \dot{x_3}& =\gamma x_2+\phi x_6-{\mu }_h{x}_3,\hfill \\ \hfill \dot{x_4}& =-\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_2{x}_4,\hfill \\ \hfill \dot{x_5}& =\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_3{x}_5,\hfill \\ \hfill \dot{x_6}& =\rho \gamma x_5-Q_2{x}_6,\hfill \\ \hfill \dot{x_7}& =b_2-\frac{{\beta }_v{x}_3{x}_7}{N}-\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-{\mu }_v{x}_7,\hfill \\ \hfill \dot{x_8}& =\frac{{\beta }_v{x}_3{x}_7}{N}+\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-Q_4{x}_8,\hfill \\ \hfill \dot{x_9}& =\eta x_8-{\mu }_v{x}_9.\hfill \end{array}\right\}\end{array}$$(22) ) near ${\beta }_h=\theta$. Therefore, a right eigenvector w associated with zero eigenvalue has components(23) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill w_1& =-\frac{b_1{\mu }_v^2\left(\gamma +{\mu }_h\right)\left(\eta +{\mu }_v\right)}{b_2\gamma \eta {\mu }_h{\beta }_v},w_2=\frac{b_1{\mu }_v^2\left(\eta +{\mu }_v\right)}{b_2\gamma \eta {\beta }_v},w_3=\frac{b_1{\mu }_v^2\left(\eta +{\mu }_v\right)}{b_2\eta {\mu }_h{\beta }_v},\hfill \\ \hfill w_4& =w_5=w_6=0,w_7=-\frac{(\eta +{\mu }_v)}{\eta },w_8=\frac{{\mu }_v}{\eta },w_9=1.\hfill \end{array}\end{array}$$(23)

Similarly, the corresponding left eigenvector v associated with zero eigenvalue has components(24) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill v_1& =v_4=v_7=0,v_2=1,v_3=\frac{Q_1}{\gamma },\hfill \\ \hfill v_5& =\frac{Q_1\kappa {\beta }_v\rho \gamma {\mu }_h+{\beta }_v\phi (\gamma (\rho \gamma +\phi )+{\mu }_h(\gamma +\rho \gamma ))}{Q_2{Q}_3{\beta }_v\gamma },\hfill \\ \hfill v_6& =\frac{Q_1{\beta }_v(\kappa {\mu }_h+\phi )}{Q_2{\beta }_v\gamma },v_8=\frac{Q_1{b}_1{\mu }_v}{b_2{\beta }_v\gamma },v_9=\frac{Q_1{Q}_4{b}_1{\mu }_v}{b_2{\beta }_v\eta \gamma }.\hfill \end{array}\end{array}$$(24)

We now compute $\mathbf{a}$ and $\mathbf{b}$ as outlined in Castillo-Chavez and Song (2004). From the system (22(22) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\hfill \dot{x_1}& =b_1+\phi x_4-\frac{{\beta }_h{x}_9{x}_1}{N}-{\mu }_h{x}_1,\hfill \\ \hfill \dot{x_2}& =\frac{{\beta }_h{x}_9{x}_1}{N}+\phi x_5-Q_1{x}_2,\hfill \\ \hfill \dot{x_3}& =\gamma x_2+\phi x_6-{\mu }_h{x}_3,\hfill \\ \hfill \dot{x_4}& =-\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_2{x}_4,\hfill \\ \hfill \dot{x_5}& =\frac{\delta {\beta }_h{x}_9{x}_4}{N}-Q_3{x}_5,\hfill \\ \hfill \dot{x_6}& =\rho \gamma x_5-Q_2{x}_6,\hfill \\ \hfill \dot{x_7}& =b_2-\frac{{\beta }_v{x}_3{x}_7}{N}-\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-{\mu }_v{x}_7,\hfill \\ \hfill \dot{x_8}& =\frac{{\beta }_v{x}_3{x}_7}{N}+\frac{\kappa {\beta }_v{x}_6{x}_7}{N}-Q_4{x}_8,\hfill \\ \hfill \dot{x_9}& =\eta x_8-{\mu }_v{x}_9.\hfill \end{array}\right\}\end{array}$$(22) ), the non-zero partial derivatives of f(x) associated with $\mathbf{a}$ are given by(25) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \frac{{\partial }^2{f}_2}{\partial x_1\partial x_9}=\frac{\theta {\mu }_h}{b_1},\frac{{\partial }^2{f}_8}{\partial x_3\partial x_7}=\frac{{\beta }_v{\mu }_h}{b_1},\frac{{\partial }^2{f}_8}{\partial x_6\partial x_7}=\frac{\kappa {\beta }_v{\mu }_h}{b_1}.\end{array}\end{array}$$(25)

Thus, the expression for $\mathbf{a}$ is given by(26) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbf{a}& =v_2{w}_1{w}_9\frac{{\partial }^2{f}_2}{\partial x_1\partial x_9}+v_8{w}_3{w}_7\frac{{\partial }^2{f}_8}{\partial x_3\partial x_7}+v_8{w}_6{w}_7\frac{{\partial }^2{f}_8}{\partial x_6\partial x_7},\hfill \\ \hfill & =-\left(\frac{b_1{\mu }_v^3\left(\gamma +{\mu }_h\right){\left(\eta +{\mu }_v\right)}^2\left({\mu }_v\left(\gamma +{\mu }_h\right)+\gamma \kappa {\beta }_v\right)}{b_2^2{\gamma }^2{\eta }^2{\beta }_v^2}\right)<0.\hfill \end{array}\end{array}$$(26)

We finally compute the value of $\mathbf{b}$. The non-zero partial derivatives of f(x) associated with b is given by(27) $$\begin{array}{c}\hfill \frac{{\partial }^2{f}_2}{\partial x_9\partial \theta }=1.\end{array}$$(27)

Therefore the expression for $\mathbf{b}$ is given by(28) $$\begin{array}{c}\hfill \mathbf{b}=v_2{w}_9\frac{{\partial }^2{f}_2}{\partial x_9\partial \theta }=1>0.\end{array}$$(28)

Since, $\mathbf{a}<0$ and $\mathbf{b}>0$, we conclude from item (iv) of Center Manifold Theorem (Castillo-Chavez & Song, 2004) that the established endemic equilibrium $E_1$ is locally asymptotically stable for ${\mathcal{R}}_0>1$ and there exists a positive unstable equilibrium. This completes the proof.

5. Model with impulses

In this section, we present and analyse the system with pulse treatment of onchocerciasis with ivermectin. Treatment occurs every six months. We, therefore, first examine the case of fixed times $t_k$, with individuals treated at rate $\alpha$. This results in system of impulsive differential equations (Bainov & Simeonov, 1993; Lakshmikantham, Bainov, & Simeonov, 1989; Samoilenko, Perestyuk, & Chapovsky, 1995). The administration of ivermectin is thus approximated by an instantaneous change.

5.1. General solution

Here, we overestimate the number of people infected with onchocerciasis in the population. Suppose the maximal number of individuals infected with onchocerciasis is given by inequality (15(15) $$\begin{array}{cc}\hfill I_H\le & \gamma \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]+\phi \left[\frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}\right].\hfill \end{array}$$(15) ). Then the one-dimensional impulsive differential equation given by(29) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{d{I}_H}{\mathit{dt}}& =\gamma \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]+\phi \left[\frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}\right]-{\mu }_h{I}_H,t\ne t_k,\hfill \\ \hfill △I_H& =-\alpha I_H,t=t_k,\hfill \end{array}\end{array}$$(29)

overestimates the number of infected individuals.

Letting $I=I_H$ for notational simplicity, from (29(29) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{d{I}_H}{\mathit{dt}}& =\gamma \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]+\phi \left[\frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}\right]-{\mu }_h{I}_H,t\ne t_k,\hfill \\ \hfill △I_H& =-\alpha I_H,t=t_k,\hfill \end{array}\end{array}$$(29) ) we have$$\begin{array}{c}\hfill \begin{array}{cc}\hfill I^{+}-I^{-}& =-\alpha I,\hfill \\ \hfill I^{+}& =(1-\alpha )I^{-}.\hfill \end{array}\end{array}$$

Let $Q_5={\beta }_h{b}_2\gamma [\delta \rho \phi +Q_2(\delta \phi +Q_3)]$ and denote $I_k^{+}=I(t_k^{+})$ and $I_k^{-}=I(t_k^{-})$. Here, $I(t_k^{-})$ is the population proportion of infected individuals immediately before the impulse and $I(t_k^{+})$ is the value immediately after the impulse. Hence, for a single impulsive cycle $t_k\le t\le t_k+1$, we have$$\begin{array}{c}\hfill \begin{array}{cc}\hfill I^{\prime }(t)+{\mu }_{h}I(t)& =\frac{Q_5}{Q_2{Q}_3{\mu }_v},\hfill \\ \hfill \frac{d}{\mathit{dt}}\left(e^{{\mu }_{h}t}I\right)& =\frac{Q_5}{Q_2{Q}_3{\mu }_v}\left(e^{{\mu }_{h}t}I\right),\hfill \\ \hfill e^{{\mu }_{h}t}I(t)-e^{{\mu }_h{t}_k}I(t_k^{+})& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}{e}^{{\mu }_{h}t}-\frac{Q_5}{Q_2{Q}_3{\mu }_h^2{\mu }_v}{e}^{{\mu }_h{t}_k},\hfill \\ \hfill I(t)& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(1-e^{{\mu }_h(t_k-t)}\right)+I(t_k^{+})e^{{\mu }_h(t_k-t)}.\hfill \end{array}\end{array}$$

It therefore follows that(30) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_{k+1}^{-}& =\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)(1-e^{{\mu }_h(t_{k+1}-t_k)})+I_k^{+}{e}^{{\mu }_h(t_{k+1}-t_k)},\hfill \\ \hfill & =\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)(1-e^{-{\mu }_h(t_{k+1}-t_k)})+(1-\alpha )I_k^{-}(e^{-{\mu }_h(t_{k+1}-t_k)}).\hfill \end{array}\end{array}$$(30)

The solution obtained in (30(30) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_{k+1}^{-}& =\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)(1-e^{{\mu }_h(t_{k+1}-t_k)})+I_k^{+}{e}^{{\mu }_h(t_{k+1}-t_k)},\hfill \\ \hfill & =\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)(1-e^{-{\mu }_h(t_{k+1}-t_k)})+(1-\alpha )I_k^{-}(e^{-{\mu }_h(t_{k+1}-t_k)}).\hfill \end{array}\end{array}$$(30) ) at the impulse points satisfies$$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_1^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v},I_1^{+}=(1-\alpha )\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right),\hfill \\ \hfill I_2^{-}& =(1-\alpha )\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)e^{-{\mu }_h(t_2-t_1)}+\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)\left(1-e^{{\mu }_h(t_2-t_1)}\right),\hfill \\ \hfill I_2^{+}& =(1-\alpha )I_2^{-}={(1-\alpha )}^2\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)e^{-{\mu }_h(t_2-t_1)}\hfill \\ \hfill & +(1-\alpha )\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)\left(1-e^{{\mu }_h(t_2-t_1)}\right),\hfill \\ \hfill I_3^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}({(1-\alpha )}^2{e}^{-{\mu }_h(t_3-t_1)}+(1-\alpha )e^{-{\mu }_h(t_3-t_2)}\hfill \\ \hfill & +1-(1-\alpha )e^{-{\mu }_h(t_3-t_1)}-e^{-{\mu }_h(t_3-t_2)}),\hfill \\ \hfill I_3^{+}& =(1-\alpha )I_3^{-}=\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}({(1-\alpha )}^3{e}^{-{\mu }_h(t_3-t_1)}\hfill \\ \hfill & +{(1-\alpha )}^2{e}^{-{\mu }_h(t_3-t_2)}+(1-\alpha )-{(1-\alpha )}^2{e}^{-{\mu }_h(t_3-t_1)}-(1-\alpha )e^{-{\mu }_h(t_3-t_2)}),\hfill \\ \hfill I_4^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}({(1-\alpha )}^3{e}^{-{\mu }_h(t_4-t_1)}+{(1-\alpha )}^2{e}^{-{\mu }_h(t_4-t_2)}+(1-\alpha )e^{-{\mu }_h(t_4-t_3)}\hfill \\ \hfill & +1-{(1-\alpha )}^2{e}^{-{\mu }_h(t_4-t_1)}-(1-\alpha )e^{-{\mu }_h(t_4-t_2)}-e^{-{\mu }_h(t_4-t_3)}),I_4^{+}=(1-\alpha )I_4^{-}.\hfill \end{array}\end{array}$$

Thus, the general solution becomes(31) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_n^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}({(1-\alpha )}^{(n-1)}{e}^{-{\mu }_h(t_n-t_1)}+{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(t_n-2)}+\cdots \hfill \\ \hfill & +(1-\alpha )e^{-{\mu }_h(t_n-t_{n-1})}+1-{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(t_n-t_1)}\hfill \\ \hfill & -{(1-\alpha )}^{(n-3)}{e}^{-{\mu }_h(t_n-t_2)}-\cdots -e^{-{\mu }_h(t_n-t_{n-1})}).\hfill \end{array}\end{array}$$(31)

The general solution obtained in (31(31) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_n^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}({(1-\alpha )}^{(n-1)}{e}^{-{\mu }_h(t_n-t_1)}+{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(t_n-2)}+\cdots \hfill \\ \hfill & +(1-\alpha )e^{-{\mu }_h(t_n-t_{n-1})}+1-{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(t_n-t_1)}\hfill \\ \hfill & -{(1-\alpha )}^{(n-3)}{e}^{-{\mu }_h(t_n-t_2)}-\cdots -e^{-{\mu }_h(t_n-t_{n-1})}).\hfill \end{array}\end{array}$$(31) ) defines the maximal number of people with onchocerciasis immediately before the mass treatment with ivermectin. This solution depends on the human and vector recruitment rates, the human-vector transmission contact rate, the incubation period in the human, the waning rate of ivermectin, human and vector death rates, treatment times and the treatment effectiveness. A similar approach can be employed to calculate the maximal number of latently infected individuals using the overestimate obtained in (14(14) $$\begin{array}{cc}\hfill E_H\le & \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right],\hfill \end{array}$$(14) ). For fixed mass administration of ivermectin, (31(31) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_n^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}({(1-\alpha )}^{(n-1)}{e}^{-{\mu }_h(t_n-t_1)}+{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(t_n-2)}+\cdots \hfill \\ \hfill & +(1-\alpha )e^{-{\mu }_h(t_n-t_{n-1})}+1-{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(t_n-t_1)}\hfill \\ \hfill & -{(1-\alpha )}^{(n-3)}{e}^{-{\mu }_h(t_n-t_2)}-\cdots -e^{-{\mu }_h(t_n-t_{n-1})}).\hfill \end{array}\end{array}$$(31) ) does not depend on time.

5.2. Fixed administration of ivermectin

For a fixed time period $\tau =t_{n+1}-t_n$, we have$$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_n^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1+(1-\alpha )e^{{\mu }_h\tau }+{(1-\alpha )}^2{e}^{-2{\mu }_h\tau }+\cdots +{(1-\alpha )}^{(n-1)}{e}^{-{\mu }_h(n-1)\tau }\hfill \\ \hfill & -e^{-{\mu }_h\tau }(1+(1-\alpha )e^{-{\mu }_h\tau }+\cdots +{(1-\alpha )}^{(n-2)}{e}^{-{\mu }_h(n-2)\tau })),\hfill \\ \hfill & =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(\frac{1-{(1-\alpha )}^n{e}^{{\mu }_{h}n\tau }}{1-(1-\alpha )e^{{\mu }_h\tau }}-\frac{1-{(1-\alpha )}^{(n-1)}{e}^{-{\mu }_h(n-1)\tau }}{1-(1-\alpha )e^{{\mu }_h\tau }}{e}^{-{\mu }_h\tau }\right).\hfill \end{array}\end{array}$$

Thus(32) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{n\to \infty }{lim}{I}_n^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(\frac{1}{1-(1-\alpha )e^{-{\mu }_h\tau }}-\frac{1}{1-(1-\alpha )e^{-{\mu }_h\tau }}{e}^{-{\mu }_h\tau }\right)\hfill \\ \hfill & =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(\frac{1-e^{-{\mu }_h\tau }}{1-(1-\alpha )e^{-{\mu }_h\tau }}\right).\hfill \end{array}\end{array}$$(32)

The solution obtained in (32(32) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{n\to \infty }{lim}{I}_n^{-}& =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(\frac{1}{1-(1-\alpha )e^{-{\mu }_h\tau }}-\frac{1}{1-(1-\alpha )e^{-{\mu }_h\tau }}{e}^{-{\mu }_h\tau }\right)\hfill \\ \hfill & =\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(\frac{1-e^{-{\mu }_h\tau }}{1-(1-\alpha )e^{-{\mu }_h\tau }}\right).\hfill \end{array}\end{array}$$(32) ) is the maximum population of the infected individuals. Note that$$\begin{array}{c}\hfill \underset{\begin{array}{c}\tau \to 0\\ n\to \infty \end{array}}{lim}{I}_n^{-}=0,\end{array}$$

implying that the total number of infected humans shrinks to zero as the frequency of mass treatment with ivermectin increases (although note that the impulsive assumptions would break down in this limit). In order to keep the infected individuals under a threshold $\widehat{I}$, we have$$\begin{array}{c}\hfill \widehat{I}<\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\left(\frac{1-e^{-{\mu }_h\tau }}{1-(1-\alpha )e^{-{\mu }_h\tau }}\right),\end{array}$$

which implies that(33) $$\begin{array}{c}\hfill \tau <\frac{1}{{\mu }_h}ln\left[\frac{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v(1-\alpha )}{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}\right]={\tau }_{\text{max}}(\alpha ).\end{array}$$(33)

The expression in (33(33) $$\begin{array}{c}\hfill \tau <\frac{1}{{\mu }_h}ln\left[\frac{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v(1-\alpha )}{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}\right]={\tau }_{\text{max}}(\alpha ).\end{array}$$(33) ) gives the maximum period of mass administration of ivermectin in the population to keep the infection of onchocerciasis below $\widehat{I}$. If we restrict $\tau$ to $0\le \tau <{\tau }_{\text{max}}$, then the disease can be controlled below the threshold $\widehat{I}$ (but not necessarily eradicated).

5.3. Non-fixed administration of ivermectin

In this section, we consider a situation in which the mass administration of ivermectin is carried out at non-fixed times. However, this would require that the entire history of mass drug administration with ivermectin is known, which is unlikely to be the case (Figure 2). Thus, we will assume that mass drug administration with ivermectin occurring more than two events previously has a negligible effect on the number of currently treated individuals. That is,$$\begin{array}{c}\hfill e^{-{\mu }_h(t_n-t_k)}\approx 0\text{for}k>2.\end{array}$$

It then follows from (30(30) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_{k+1}^{-}& =\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)(1-e^{{\mu }_h(t_{k+1}-t_k)})+I_k^{+}{e}^{{\mu }_h(t_{k+1}-t_k)},\hfill \\ \hfill & =\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)(1-e^{-{\mu }_h(t_{k+1}-t_k)})+(1-\alpha )I_k^{-}(e^{-{\mu }_h(t_{k+1}-t_k)}).\hfill \end{array}\end{array}$$(30) ) that$$\begin{array}{c}\hfill \begin{array}{cc}\hfill I_n^{-}& <\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-e^{-{\mu }_h(t_n-t_{n-1})}),\hfill \\ \hfill I_{n+1}^{-}& <\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-e^{-{\mu }_h(t_n-t_{n-1})})+(1-\alpha )I_n^{-}{e}^{-{\mu }_h(t_n-t_{n-1})},\hfill \\ \hfill & <\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-e^{-{\mu }_h(t_{n+1}-t_n)})\hfill \\ \hfill & +(1-\alpha )\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-\alpha e^{-{\mu }_h(t_n-t_{n-1})})e^{-{\mu }_h(t_{n+1}-t_n)}.\hfill \end{array}\end{array}$$

The above inequality can be approximated as(34) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{I}& \equiv \frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-e^{-{\mu }_h(t_{n+1}-t_n)})\hfill \\ \hfill & +(1-\alpha )\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-\alpha e^{-{\mu }_h(t_n-t_{n-1})})e^{-{\mu }_h(t_{n+1}-t_n)}.\hfill \end{array}\end{array}$$(34)

The expression in (34(34) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{I}& \equiv \frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-e^{-{\mu }_h(t_{n+1}-t_n)})\hfill \\ \hfill & +(1-\alpha )\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1-\alpha e^{-{\mu }_h(t_n-t_{n-1})})e^{-{\mu }_h(t_{n+1}-t_n)}.\hfill \end{array}\end{array}$$(34) ) gives the number of infected humans that will be below $\widehat{I}$ based on knowing the two previous mass administration times. Then the “next best” mass drug administration with ivermectin satisfies the following:$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}(1+(1-\alpha ))-\widehat{I}& =e^{-{\mu }_h(t_{n+1}-t_n)}\left(\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}\right)\hfill \\ \hfill & (1+\alpha (1-\alpha )e^{-{\mu }_h(t_{n+1}-t_n)}),\hfill \\ \hfill e^{-{\mu }_h(t_{n+1}-t_n)}& =\frac{2-\alpha -Q_5/Q_2{Q}_3{\mu }_h{\mu }_v}{1+\alpha (1-\alpha )e^{-{\mu }_h(t_{n+1}-t_n)}},\hfill \\ \hfill t_{n+1}& =t_n-\frac{1}{{\mu }_h}ln\left(\frac{2-\alpha -Q_5/Q_2{Q}_3{\mu }_h{\mu }_v}{1+\alpha (1-\alpha )e^{-{\mu }_h(t_{n+1}-t_n)}}\right).\hfill \end{array}\end{array}$$

Next, we compare fixed and non-fixed mass drug administration with ivermectin. Assuming that the mass treatment times in the non-fixed case are constant, $\widehat{\tau }$, then from (33(33) $$\begin{array}{c}\hfill \tau <\frac{1}{{\mu }_h}ln\left[\frac{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v(1-\alpha )}{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}\right]={\tau }_{\text{max}}(\alpha ).\end{array}$$(33) ), we have(35) $$\begin{array}{c}\hfill \begin{array}{c}\hfill \widehat{\tau }=\frac{1}{{\mu }_h}ln\left(\frac{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v(1-\alpha )}{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}\right),\\ \hfill \end{array}\end{array}$$(35) (36) $$\begin{array}{c}\hfill \widehat{\tau }{|}_{\alpha =0}=\frac{1}{{\mu }_h}ln\left(\frac{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}\right)=0,\end{array}$$(36) (37) $$\begin{array}{c}\hfill \widehat{\tau }{|}_{\alpha =1}=\frac{1}{{\mu }_h}ln\left(\frac{Q_5}{Q_5-\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v}\right).\end{array}$$(37)

If there is no impulse, then from (29(29) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{d{I}_H}{\mathit{dt}}& =\gamma \left[\frac{{\beta }_h{b}_2}{{\mu }_v}+\frac{\delta \phi {\beta }_h{b}_2}{{\mu }_v(\rho \gamma +\phi +{\mu }_h)}\right]+\phi \left[\frac{\delta {\beta }_h\rho \gamma b_2}{{\mu }_v(\phi +{\mu }_h)(\rho \gamma +\phi +{\mu }_h)}\right]-{\mu }_h{I}_H,t\ne t_k,\hfill \\ \hfill △I_H& =-\alpha I_H,t=t_k,\hfill \end{array}\end{array}$$(29) ), we have ${lim}_{t\to \infty }I=\frac{Q_5}{Q_2{Q}_3{\mu }_h^2{\mu }_v}$. Thus, we can assume that $\widehat{I}=\frac{Q_5}{Q_2{Q}_3{\mu }_h{\mu }_v}$. Hence,(38) $$\begin{array}{c}\hfill 0<1-\frac{Q_2{Q}_3{\mu }_h{\mu }_v\widehat{I}}{Q_5}<1,\end{array}$$(38)

therefore, ${\widehat{\tau }}_{\alpha =1}>0$. Assuming that non-fixed mass treatment with ivermectin occurs indefinitely and further letting ${\tau }_{\text{max}}\equiv t_{n+1}-t_n=t_n-t_{n-1}$, then the minimum treatment effectiveness satisfies(39) $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tau }_{\text{max}}& =\frac{1}{{\mu }_h}ln\left(\frac{2-\alpha -\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v/Q_5}{1+\alpha (1-\alpha )e^{-{\mu }_h{\tau }_{\text{max}}}}\right).\hfill \end{array}\end{array}$$(39)

If ${\tau }_{\text{max}}=0$, then it follows that (39) becomes$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{1}{{\mu }_h}ln\left(\frac{2-\alpha -\widehat{I}{Q}_2{Q}_3{\mu }_h{\mu }_v/Q_5}{1+\alpha (1-\alpha )}\right)=0,\hfill \\ \hfill & 2-\alpha -\widehat{I}\frac{Q_2{Q}_3{\mu }_h{\mu }_v}{Q_5}=1+\alpha (1-\alpha ),\hfill \\ \hfill & \alpha =1\pm \sqrt{\frac{Q_2{Q}_3{\mu }_h{\mu }_v}{Q_5}}.\hfill \end{array}\end{array}$$

The larger root exceeds 1 and hence can be discounted. It follows that the smaller root ${\alpha }_0=1-\sqrt{\frac{Q_2{Q}_3{\mu }_h{\mu }_v}{Q_5}}$, satisfies $0<{\alpha }_0<1$ as stated in (38(38) $$\begin{array}{c}\hfill 0<1-\frac{Q_2{Q}_3{\mu }_h{\mu }_v\widehat{I}}{Q_5}<1,\end{array}$$(38) ). This implies that the mass treatment is only effective in the range ${\alpha }_0<\alpha \le 1$.

Figure 2. Comparison of the actual infected individuals and the estimated infected individuals.

6. Numerical simulations

In this section, we carry out parameter estimation, sensitivity analysis of the model parameters and numerical simulations for system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) to demonstrate the theoretical results. The simulations are performed using the fourth order Runge-Kutta scheme in Matlab 2014a with the set of parameter values given in Table 1. We consider the parameters in realistic ranges with guidance from past literature on onchocerciasis epidemics in Ghana.

6.1. Parameter estimation

We consider average parameter values that encompass features of onchocerciasis disease including the rate of infection, the incubation period and the length of infections period in the vector and host populations. Although estimates of some parameters are given in Table 1, here we give additional explanations and descriptions of some of the parameters.

(1)	The average birthrate in Ghana was estimated to be 31.09 births/1,000 population in 2015 and 30.60 births/1,000 population in 2014 according to the World Fact Book by Central Intelligence Agency (2016) and Ghana Statistical Service report on Demographic and Health Survey (2016), respectively. Owing to unchecked immigration, the recruitment rate is, therefore, estimated to be in the range $(0.0000819\le b_1\le 0.00108)N$ per day.
(2)	The natural human death rate is estimated based on average life of 50–70 years in accordance with Central Intelligence Agency data and 2014 demographic data released by Ghana Statistical Service estimates of life expectancy at birth (Central Intelligence Agency: The World Fact Book, 2016; Ghana Statistical Service, 2016). The average black fly lifespan is 2–3 weeks (Hopkins & Boatin, 2011; Simulium spp., 2016).
(3)	It takes $\frac{3}{4}$ to 2 years for the worm to mature and release enough microfilariae to be detectable in the skin of the human host (Animal Diversity Web, 2016; Hopkins & Boatin, 2011; Onchocerciasis, 2016; Nguyen et al., 2005). Therefore a reasonable estimate of the incubation rate $\gamma$ is $0.00137\le \gamma \le 0.00365$ per day. On the other hand, the average incubation period in the blackfly is 1–2 weeks (Animal Diversity Web, 2016; Hopkins & Boatin, 2011; How is Onchocerciasis Spread?, 2016; Onchocerciasis, 2016). Thus, a reasonable value for $\eta$ is $0.0714\le \eta \le 0.1667$ per day.
(4)	The modification parameters ($\kappa ,\delta \text{and}\rho$) are strictly between 0 and 1 due to the reduced ability of individuals to cause infections following ivermectin treatment.
(5)	The mass administration rate $\alpha$ is estimated to be between 0 and $100\%$.

For illustration purpose, we consider the parameter values estimates given in Table 1 with $N=200,000$ and $V=10,000$.

Table 1. Estimated parameter values in the model for onchocerciasis case. The rates are given per day

Parameter	Range	Point value (assumed)	Source
$b_1$	0.0000819–0.001085	0.00009/N	Estimated
${\mu }_h$	0.0000391–0.0000548	0.000052	Central Intelligence Agency: The World Fact Book (2016), Ghana Statistical Service (2016)
${\beta }_h$	0–0.01	0.00198	Assumed
$\gamma$	0.00137–0.00365	0.00139	Animal Diversity Web (2016), Hopkins and Boatin (2011), Onchocerciasis (2016), Nguyen et al. (2005)
$\alpha$	0–1	[0.1, 0.65]	Turner et al. (2015), Winnen et al. (2002)
$\phi$	0.01–0.1	0.0015	Turner et al. (2015)
$\kappa$	0–1	0.0083	Assumed
$\rho$	0–0.1	0.001	Assumed
$\delta$	0–1	0.002	Assumed
$b_2$	0.0214–0.4	0.144/V	Assumed
${\beta }_v$	0–0.01	0.00079	Assumed
$\eta$	0.0714–0.1667	0.078	Animal Diversity Web (2016), Hopkins and Boatin (2011), How is Onchocerciasis Spread? (2016), Onchocerciasis (2016)
${\mu }_v$	0.0118–0.0714	0.068	Hopkins and Boatin (2011), Simulium spp. (2016)

6.2. Sensitivity analysis

Sensitivity analysis is the study of how uncertainty in the output of a system can be apportioned to different sources of uncertainty in the model input (Saltelli et al., 2008a, b). It is a technique for systematically varying model inputs and determining their effect on the model output. We perform sensitivity analysis in order to investigate the contribution of vital parameters on the model dynamics, specifically to establish the parameters that have significant influence on the onchocerciasis dynamics. We use Latin Hypercube Sampling (LHS), a stratified Monte Carlo sampling scheme applicable to many parameters from a multidimensional distribution (Saltelli et al., 2008a, b). It allows for simultaneous determination of an unbiased estimate of the model output for a given set of model input. We perform the sensitivity analysis by computing the Partial Rank Correlation Coefficients (PRCCs) for each parameter value, sampled by the LHS scheme (Blower & Dowlatabadi, 1994). Parameters with positive PRCCs will increase $R_0$ when they are increased, whereas parameters with negative PRCCs will decrease $R_0$ when they are increased. The outcome is the reproduction number $R_0$ derived from the theoretical model. We determine PRCCs with 1000 simulations per run to determine parameters that have a significant influence on $R_0$.

Figure 3. Tornado plots of partial rank correlation coefficients (PRCCs) of the parameters that influence $R_0$ for the input parameters using the values in Table 1. Parameters with PRCC $>0$ increase $R_0$ when they are increased whereas parameters with PRCC $<0$ decrease $R_0$ when they are increased.

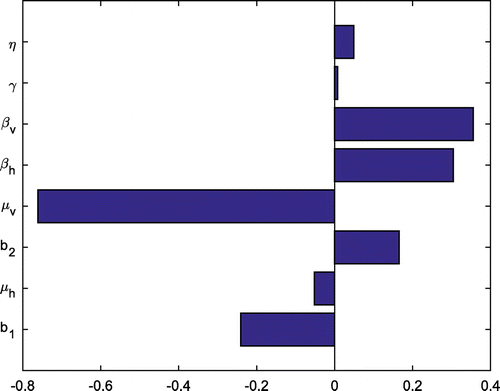
The PRCCs results in Figure 3 illustrate the degree of the effect that each parameter has on the outcome. The three parameters with the most influence on $R_0$ are the transmission contact rate in humans, ${\beta }_h$, the vector transmission contact rate, ${\beta }_v$, and the vector death rate ${\mu }_v$.

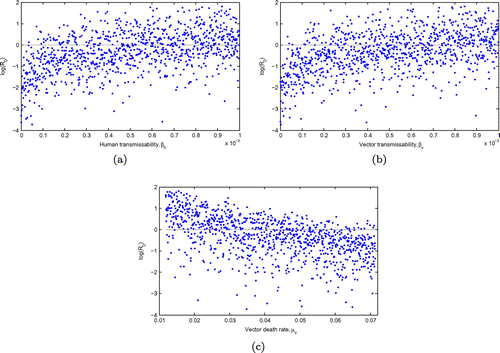
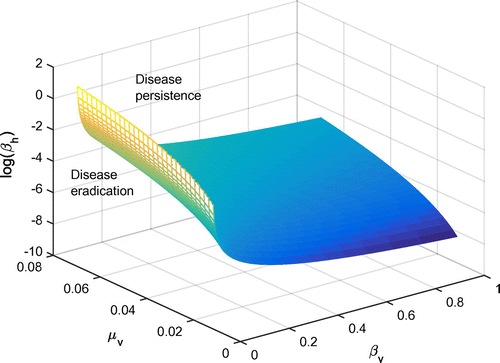
Figure 4 displays 1000 Monte Carlo simulations for the input parameters with the most effect on the basic reproduction number. Scatter plots show that $R_0$ is monotone increasing with increasing values of ${\beta }_h$ and ${\beta }_v$ and monotone decreasing with increasing vector mortality rate, ${\mu }_v$. However, $R_0$ is only guaranteed to be less than unity when the human–vector and vector-human contact rates are sufficiently small. These results also suggest that, even if vector death rate is extremely high, eradication is not possible.

Figure 4. The Monte Carlo simulations for the three parameters with the greatest influence on the $R_0$: the transmission contact rate in humans, the transmission contact rate in the vector and the vector death rate for the input parameters using the values in Table 1 and 1,000 simulations per run. Eradication is only possible if the transmissibilities are extremely small or if the vector death rate is extremely high.

In order to gain more insight into the three parameters with the greatest influence on the basic reproduction number, $R_0$, all other parameters were fixed at their sample values. A surface plot for $R_0=1$ is shown in Figure 5.

Figure 5. Eradication threshold for the three parameters with the greatest influence on $R_0$.

6.3. Simulation results

The results presented in this section demonstrate the dynamics of onchocerciasis for the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) obtained using Matlab ODE45 solver, which employs simultaneously the fourth and fifth order Runge-Kutta schemes. Unless otherwise stated, parameters are as stated in Table 1. We give results of system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) with impulses for both the cases when $R_0<1$ and when $R_0>1$ as shown in Figures 8–11 and Figures 6–7, respectively. In addition, we numerically make a comparison between fixed and non-fixed mass administration of ivermectin in the treatment of onchocerciasis. In order to illustrate the effectiveness of ivermectin, we vary the reduction rate $(\alpha )$ for both the cases of $R_0$.

First, we examine the behaviour of the system (4(4) $$\begin{array}{c}\hfill \left.\begin{array}{cc}\dot{S_H}\hfill & =b_1+\phi S_T-\frac{{\beta }_h{I}_V{S}_H}{N}-{\mu }_h{S}_H,\hfill \\ \dot{E_H}\hfill & =\frac{{\beta }_h{I}_V{S}_H}{N}+\phi E_T-(\gamma +{\mu }_h)E_H,\hfill \\ \dot{I_H}\hfill & =\gamma E_H+\phi I_T-{\mu }_h{I}_H,\hfill \\ \dot{S_T}\hfill & =-\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\phi +{\mu }_h)S_T,\hfill \\ \dot{E_T}\hfill & =\frac{\delta {\beta }_h{I}_V{S}_T}{N}-(\rho \gamma +\phi +{\mu }_h)E_T,\hfill \\ \dot{I_T}\hfill & =\rho \gamma E_T-(\phi +{\mu }_h)I_T,\hfill \\ \dot{S_V}\hfill & =b_2-\frac{{\beta }_v{I}_H{S}_V}{N}-\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-{\mu }_v{S}_V,\hfill \\ \dot{E_V}\hfill & =\frac{{\beta }_v{I}_H{S}_V}{N}+\frac{\kappa {\beta }_v{I}_T{S}_V}{N}-(\eta +{\mu }_v)E_V,\hfill \\ \dot{I_V}\hfill & =\eta E_V-{\mu }_v{I}_V.\hfill \end{array}\right\},t\ne t_k,\end{array}$$(4) ) when the basic reproduction number, $R_0$, 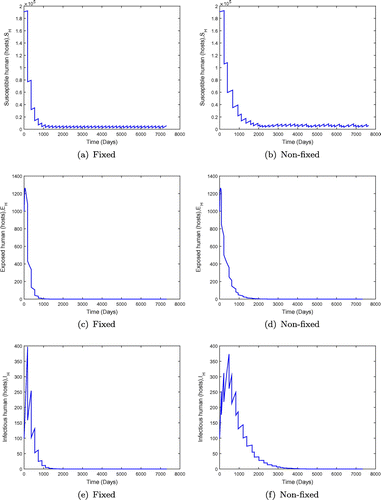is greater than unity for the fixed and non-fixed mass administration of ivermectin. 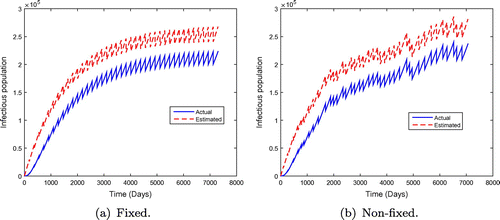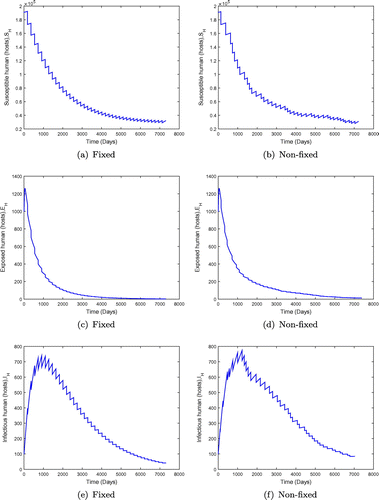It is seen in Figure 6 that when the effectiveness of ivermectin is low, that is, $\alpha =0.10$, the disease spreads in the population. However, the results in Figure 7 show that the endemicity of the disease is reduced when the effectiveness rate of mass administration of ivermectin is increased. We also observe that fixed mass treatment yields a better outcome compared to non-fixed mass administration.

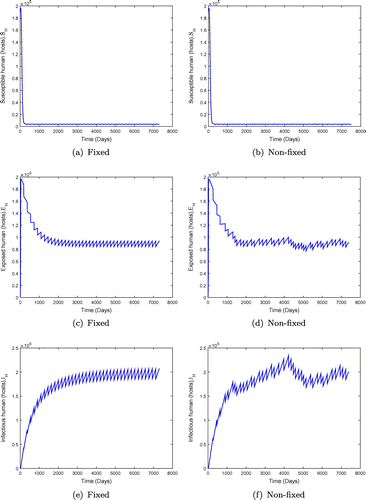
We then examine the case when the basic reproduction number is below unity for both the fixed and non-fixed mass drug administration with ivermectin. We examine two cases of $R_0<1$: when $R_0$ is close to unity and where $R_0$ is significantly less than unity. We observe in Figure 8 that when $R_0$ is less than but close to one, the disease may persist in the population when the value of $\alpha$ is small. However an increment in the value of $\alpha$ moves the system towards a disease-free state, but there is no eradication. This is shown in Figure 9 with $\alpha =0.65$. The results in Figure 10 show the dynamics of the population under both fixed and non-fixed mass administration of ivermectin at $\alpha =0.1$ keeping the interval $\tau =182.5$ days (6 monthly interval) for fixed mass administration of ivermectin. We observe that the system with impulses attains its disease-free state, suggesting that onchocerciasis dies out. These results are consistent with theorem (). However, when the ivermectin effectiveness is increased, the system attains the disease free equilibrium much faster as shown in Figure 11.

Figure 6. System behaviour for fixed and non-fixed mass administration of ivermectin with $\alpha =0.10,R_0=1.2412,b_1=0.0009,b_2=0.35,{\beta }_h=0.00562,{\beta }_v=0.00243,\phi =0.025,{\mu }_v=0.012$.

Figure 7. System behaviour for fixed and non-fixed mass administration of ivermectin with $\alpha =0.65,R_0=1.2412,b_1=0.0009,b_2=0.35,{\beta }_h=0.00562,{\beta }_v=0.00243,\phi =0.025,{\mu }_v=0.012$. Note that increasing $\alpha$ improves the outcome but does not lead to eradication.

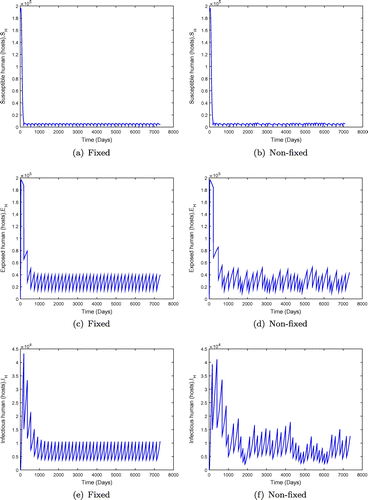
Figure 8. System behaviour for fixed and non-fixed mass administration of ivermectin with $\alpha =0.10,R_0=0.9352,b_1=0.0009,b_2=0.35,{\beta }_h=0.00443,\phi =0.025,{\beta }_v=0.00175,{\mu }_v=0.012$. Non-fixed adminsitration may produce lower overall numbers of infected individuals, but the outcome is not predictable.

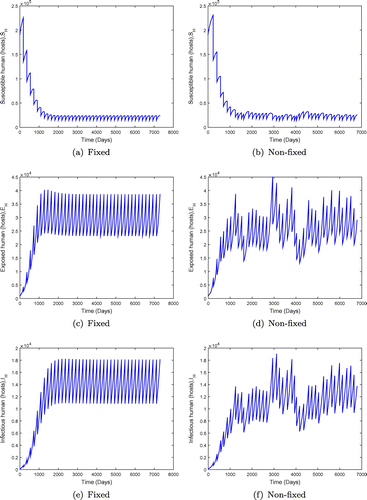
Figure 9. System behaviour for fixed and non-fixed mass administration of ivermectin with $\alpha =0.65,R_0=0.9352,b_1=0.0009,b_2=0.35,{\beta }_h=0.00443,\phi =0.025,{\beta }_v=0.00175,{\mu }_v=0.012$. Non-fixed administration may produces bursts of infection, even if the disease would be otherwise kept at low levels.

Figure 10. System behaviour for fixed and non-fixed mass administration of ivermectin with $\alpha =0.1,R_0=0.1181$ using parameter values in Table 1. Note that non-fixed administration may have a delaying or preventative effect on eradication.

Figure 11. System behaviour for fixed and non-fixed mass administration of ivermectin with $\alpha =0.65,R_0=0.1181$ using parameter values in Table 1. Increasing $\alpha$ hastens eradication, in both the fixed and non-fixed case.

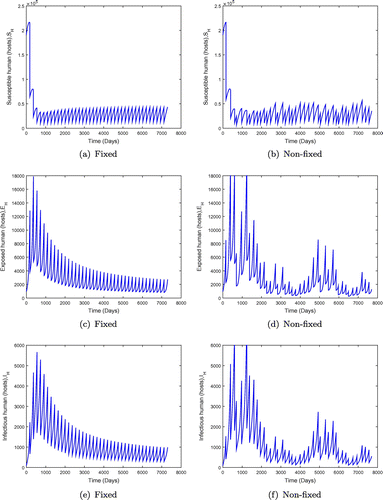
7. Conclusion

Onchocerciasis is one of the neglected tropical diseases that is still to be eradicated. In connection with the WHO’s plan of onchocerciasis elimination, mass drug administration with ivermectin is the most efficient approach towards this effort. This is spearheaded by APOC in Sub-Saharan Africa where the disease is endemic. In order to investigate the effectiveness of ivermectin in the control of onchocerciasis, we formulated a deterministic model that captures the dynamics of this disease in humans and blackflies. The analysis of the model without pulse mass administration of ivermectin shows that, the disease-free state exists and is stable if $R_0<1$. On the other hand, if $R_0>1$, the disease-free state loses its stability and the system tends towards the endemic state. Then, sensitivity analysis, we have computed the Partial Rank Correlation Coefficients between $R_0$ and each parameter of the model. The results show that the parameters ${\beta }_h$ , the transmission contact of infection from an infected vector to a susceptible human and ${\beta }_v$, the transmission of infection from an infected human to a susceptible vector, have the highest influence on $R_0$. The other parameter with an important effect ${\mu }_v$, the vector removal rate.

We have provided the estimates for the necessary frequency and strength of mass drug administration with ivermectin. We may conclude that the disease can be controlled through mass drug administration with ivermectin with needed frequency and high strength of ivermectin. Furthermore, our results suggest that reducing human-vector contact can be one way of reducing but not eradicating onchocerciasis from the population. This can be done by implementing personal protection practices such as wearing insect repellent, wearing long sleeves and long pants during the day when blackflies bite. In addition, application of insecticides can be effective in reducing the presence of vector in the environment.

To assess the impact of combination of different controls, we have conducted several simulations, using the called “pulse control" technique. We have observed from our numerical results that the eradication of onchocerciasis is possible with tolerable regularity of mass drug administration with ivermectin provided the basic reproduction number is kept (far) below unity. We can conclude that, in the presence of mass administration of ivermectin with six month intervals, the disease can be controlled. Furthermore, if the frequency of mass administration is increased, the system moves towards a better outcome. Our modelling results show that mass administration of ivermectin at regular interval is an effective method of onchocerciaisis eradication if other parameters can be sufficiently controlled. However, emerging new treatment options as suggested in Kuesel (2016), particularly moxidectin which is similar but more efficacious than ivermectin, present promising alternatives (Awadzi, Opoku, Attah, Lazdins-Helds, & Kuesel, 2014; Turner et al., 2015).

The model presented in this paper has a number of limitations. Mass administration of ivermectin is assumed to occur instantaneously. However, in reality, there is usually a small delay as mass treatment reaches it maximum coverage. It is important to note that the delays do not affect the impulsive assumptions, provided the time interval of mass administration of ivermectin is significantly larger than the instantaneous approximation. Unavailability of experiential data poses a challenge for model verification. Despite the shortcomings, the model still provides some useful insights into the control of onchocerciasis through the implementation of regular mass administration of ivermectin in conjunction with transmission reduction and the implementation of vector control measures.

Acknowledgements

The authors are grateful to the University of Stellenbosch, DST/NRF South African Centre for Epidemiological Modelling and Analysis (SACEMA) and the African Institute for Mathematical Sciences (AIMS) for their support during the preparation of the manuscript. RJS? is supported by an NSERC Discovery Grant. For citation purposes, please note that the question mark in “Smith” is part of his name.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

E.O. Omondi

E.O. Omondi is currently pursuing his PhD in mathematics at Strathmore University in Kenya. He holds Bsc degree in Applied Statistics with Computing from the University of Eldoret in Kenya, Msc in Mathematical Sciences from African Institute for Mathematical Sciences (AIMS), South Africa and Masters of science (Msc) in Mathematics from University of Stellenbosch in South Africa. His area of interest includes biomathematics and applied statistics.

F. Nyabadza

F. Nyabadza is is a professor in the Department of Mathematical Sciences of Stellenbosch University, South Africa. He has written many research articles and attended several international conferences and seminars. He has supervised several master’s and PhD students as well as post-docs. His area of interest includes Mathematical Epidemiology and specifically the application of mathematics to disease dynamics. He focuses on control dynamics and the investigation of the impact of interventions in human diseases for the purpose of informing public health policy.

R.J. Smith?

R.J. Smith note that the question mark is part of his name) is a professor in Department of Mathematics and Statistics of University of Ottawa in Canada. He has many research articles and attended several international conferences and seminars. He has supervised several masters and PhD students as well as post-docs. His fields of interest include Mathematical modelling of infectious diseases and Impulsive differential equations.