Remarks on kernel Bayes’ rule

Abstract

The kernel Bayes’ rule has been proposed as a nonparametric kernel-based method to realize Bayesian inference in reproducing kernel Hilbert spaces. However, we demonstrate both theoretically and experimentally that the way of incorporating the prior in the kernel Bayes’ rule is unnatural. In particular, we show that under some reasonable conditions, the posterior in the kernel Bayes’ rule is completely unaffected by the prior, which seems to be irrelevant in the context of Bayesian inference. We consider that this phenomenon is in part due to the fact that the assumptions in the kernel Bayes’ rule do not hold in general.

Keywords:

• Kernel method
• Bayes’ rule
• reproducing kernel Hilbert space

Public interest statement

This paper examines the validity of the kernel Bayes’ rule, a recently proposed nonparametric framework for Bayesian inference. The researchers on the kernel Bayes’ rule are aiming to apply this method to a wide range of Bayesian inference problems. However, as we demonstrate in this paper, the way of incorporating the prior in the kernel Bayes’ rule seems wrong in the context of Bayesian inference. Several theorems of the kernel Bayes’ rule rely on a strong assumption which does not hold in general.

The problems of the kernel Bayes’ rule seem to be nontrivial and difficult, and we have currently no idea to solve them. We hope that this study would trigger reexamination and correction of the basic framework of the kernel Bayes’ rule.

1. Introduction

The kernel Bayes’ rule has recently emerged as a novel framework for Bayesian inference (Fukumizu, Song, & Gretton, 2013; Song, Fukumizu, & Gretton, 2014; Song, Huang, Smola, & Fukumizu, 2009). It is generally agreed that, in this framework, we can estimate the kernel mean of the posterior distribution, given kernel mean expressions of the prior and likelihood distributions. Since the distributions are mapped and nonparametrically manipulated in infinite-dimensional feature spaces called reproducing kernel Hilbert spaces (RKHS), it is believed that the kernel Bayes’ rule can accurately evaluate the statistical features of high-dimensional data and enable Bayesian inference even if there were no appropriate parametric models. To date, several applications of the kernel Bayes’ rule have been reported (Fukumizu et al., 2013; Kanagawa et al., 2014). However, the basic theory and the algorithm of the kernel Bayes’ rule might need to be modified because of the following reasons:

(1)	The posterior in the kernel Bayes’ rule is in some cases completely unaffected by the prior.
(2)	The posterior in the kernel Bayes’ rule considerably depends upon the choice of the parameters to regularize covariance operators.
(3)	It does not hold in general that conditional expectation functions are included in the RKHS, which is an essential assumption of the kernel Bayes’ rule.

This paper is organized as follows. We begin in Section 2 with a brief review of the kernel Bayes’ rule. In Section 3, we theoretically address the three arguments described above. Numerical experiments are performed in Section 4 to confirm the theoretical results in Section 3. In Section 5, we summarize the theoretical and experimental results and present our conclusions. Some of the proofs for Sections 2 and 3 are given in Section 6.

2. Kernel Bayes’ rule

In this section, we briefly review the kernel Bayes’ rule following (Fukumizu et al., 2013). Let $\mathcal{X}$ and $\mathcal{Y}$ be measurable spaces, $(X,Y)$ be a random variable with an observed distribution P on $\mathcal{X}\times \mathcal{Y}$, U be a random variable with the prior distribution $\mathrm{\Pi }$ on $\mathcal{X}$, and $(Z,W)$ be a random variable with the joint distribution Q on $\mathcal{X}\times \mathcal{Y}$. Note that Q is defined by the prior $\mathrm{\Pi }$ and the family $\{P_{\mathcal{Y}|x}|x\in \mathcal{X}\}$, where $P_{\mathcal{Y}|x}$ denotes the conditional distribution of Y given $X=x$. For each $y\in \mathcal{Y}$, let $Q_{\mathcal{X}|y}$ represent the posterior distribution of Z given $W=y$. The aim of the kernel Bayes’ rule is to derive the kernel mean of $Q_{\mathcal{X}|y}$.

Definition 1

Let $k_{\mathcal{X}}$ and $k_{\mathcal{Y}}$ be measurable positive definite kernels on $\mathcal{X}$ and $\mathcal{Y}$ such that $E[k_{\mathcal{X}}(X,X)]<\infty$ and $E[k_{\mathcal{Y}}(Y,Y)]<\infty$, respectively, where $E[·]$ denotes the expectation operator. Let ${\mathcal{H}}_{\mathcal{X}}$ and ${\mathcal{H}}_{\mathcal{Y}}$ be the RKHS defined by $k_{\mathcal{X}}$ and $k_{\mathcal{Y}}$, respectively. We consider two bounded linear operators $C_{\mathit{YX}}:{\mathcal{H}}_{\mathcal{X}}\to {\mathcal{H}}_{\mathcal{Y}}$ and $C_{\mathit{XX}}:{\mathcal{H}}_{\mathcal{X}}\to {\mathcal{H}}_{\mathcal{X}}$ such that(1) $$\begin{array}{c}\hfill {⟨g,C_{\mathit{YX}}f⟩}_{{\mathcal{H}}_{\mathcal{Y}}}=E\left[f(X)g(Y)\right]\text{and}{⟨f_1,C_{\mathit{XX}}{f}_2⟩}_{{\mathcal{H}}_{\mathcal{X}}}=E\left[f_1(X)f_2(X)\right]\end{array}$$(1)

for any $f,f_1,f_2\in {\mathcal{H}}_{\mathcal{X}}$ and $g\in {\mathcal{H}}_{\mathcal{Y}}$, where ${⟨·,·⟩}_{{\mathcal{H}}_{\mathcal{X}}}$ and ${⟨·,·⟩}_{{\mathcal{H}}_{\mathcal{Y}}}$ denote inner products on ${\mathcal{H}}_{\mathcal{X}}$ and ${\mathcal{H}}_{\mathcal{Y}}$, respectively. The integral expressions for $C_{\mathit{YX}}$ and $C_{\mathit{XX}}$ are given by$$\begin{array}{c}\hfill (C_{\mathit{YX}}f)(·)={\int }_{\mathcal{X}\times \mathcal{Y}}{k}_{\mathcal{Y}}(·,y)f(x)dP(x,y)\text{and}(C_{\mathit{XX}}f)(·)={\int }_{\mathcal{X}}{k}_{\mathcal{X}}(·,x)f(x)d{P}_{\mathcal{X}}(x),\end{array}$$

where $P_{\mathcal{X}}$ denotes the marginal distribution of X. Let $C_{\mathit{XY}}$ be the bounded linear operator defined by$$\begin{array}{c}\hfill {⟨f,C_{\mathit{XY}}⟩}_{{\mathcal{H}}_{\mathcal{X}}}=E\left[f(X)g(Y)\right]\end{array}$$

for any $f\in {\mathcal{H}}_{\mathcal{X}}$ and $g\in {\mathcal{H}}_{\mathcal{Y}}$. Then $C_{\mathit{XY}}$ is the adjoint of $C_{\mathit{YX}}$.

Theorem 1

(Fukumizu et al., 2013, Theorem 1)    If $E[g(Y)|X=·]\in {\mathcal{H}}_{\mathcal{X}}$ for $g\in {\mathcal{H}}_{\mathcal{Y}}$, then $C_{\mathit{XX}}E[g(Y)|X=·]=C_{\mathit{XY}}g$.

Definition 2

Let $Q_{\mathcal{Y}}$ denote the marginal distribution of W. Assuming that $E[k_{\mathcal{X}}(U,U)]<\infty$ and $E[k_{\mathcal{Y}}(W,W)]<\infty$, we can define the kernel means of $\mathrm{\Pi }$ and $Q_{\mathcal{Y}}$ by$$\begin{array}{c}\hfill m_{\mathrm{\Pi }}=E[k_{\mathcal{X}}(·,U)]\text{and}{m}_{Q_{\mathcal{Y}}}=E[k_{\mathcal{Y}}(·,W)],\end{array}$$

respectively. Due to the reproducing properties of ${\mathcal{H}}_{\mathcal{X}}$ and ${\mathcal{H}}_{\mathcal{Y}}$, the kernel means satisfy ${⟨f,m_{\mathrm{\Pi }}⟩}_{{\mathcal{H}}_{\mathcal{X}}}=E[f(U)]$ and ${⟨g,m_{Q_{\mathcal{Y}}}⟩}_{{\mathcal{H}}_{\mathcal{Y}}}=E[g(W)]$ for any $f\in {\mathcal{H}}_{\mathcal{X}}$ and $g\in {\mathcal{H}}_{\mathcal{Y}}$.

Theorem 2

(Fukumizu et al., 2013, Theorem 2) If $C_{\mathit{XX}}$ is injective, $m_{\mathrm{\Pi }}\in \mathrm{R}an(C_{\mathit{XX}})$, and $E[g(Y)|X=·]\in {\mathcal{H}}_{\mathcal{X}}$ for any $g\in {\mathcal{H}}_{\mathcal{Y}}$, then(2) $$\begin{array}{c}\hfill m_{Q_{\mathcal{Y}}}=C_{\mathit{YX}}{C}_{\mathit{XX}}^{-1}{m}_{\mathrm{\Pi }},\end{array}$$(2)

where $\mathrm{R}an(C_{\mathit{XX}})$ denotes the range of $C_{\mathit{XX}}$.

Here we have, for any $x\in \mathcal{X}$(3) $$\begin{array}{c}\hfill E\left[k_{\mathcal{Y}}(·,Y)|X=x\right]=C_{\mathit{YX}}{C}_{\mathit{XX}}^{-1}{k}_{\mathcal{X}}(·,x)\end{array}$$(3)

by replacing $m_{\mathrm{\Pi }}$ in Equation (2) for $k_{\mathcal{X}}(·,x)$. It is noted in Fukumizu et al. (2013) that the assumption $m_{\mathrm{\Pi }}\in \mathrm{R}an(C_{\mathit{XX}})$ does not hold in general. In order to remove this assumption, ${(C_{\mathit{XX}}+ϵI)}^{-1}$ has been suggested to be used instead of $C_{\mathit{XX}}^{-1}$, where $ϵ$ is a regularization constant and I is the identity operator. Thus, the approximations of Equations (2) and (3) are respectively given by$$\begin{array}{c}\hfill m_{Q_{\mathcal{Y}}}^{\text{reg}}=C_{\mathit{YX}}{\left(C_{\mathit{XX}}+ϵI\right)}^{-1}{m}_{\mathrm{\Pi }}\text{and}{E}^{\text{reg}}\left[k_{\mathcal{Y}}(·,Y)|X=x\right]=C_{\mathit{YX}}{\left(C_{\mathit{XX}}+ϵI\right)}^{-1}{k}_{\mathcal{X}}(·,x).\end{array}$$

Similarly, for any $y\in \mathcal{Y}$, the approximation of $m_{Q_{\mathcal{X}|y}}$ is provided by(4) $$\begin{array}{c}\hfill m_{Q_{\mathcal{X}|y}}^{\text{reg}}=E^{\text{reg}}\left[k_{\mathcal{X}}(·,Z)|W=y\right]=C_{\mathit{ZW}}{\left(C_{\mathit{WW}}+\delta I\right)}^{-1}{k}_{\mathcal{Y}}(·,y),\end{array}$$(4)

where $\delta$ is a regularization constant and the linear operators $C_{\mathit{ZW}}$ and $C_{\mathit{WW}}$ will be defined below.

Definition 3

We consider the kernel means $m_Q=m_{(ZW)}$ and $m_{(WW)}$ such that$$\begin{array}{c}\hfill {⟨m_{(ZW)},g\otimes f⟩}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{X}}}=E\left[f(Z)g(W)\right]\text{and}{⟨m_{(WW)},g_1\otimes g_2⟩}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}}=E\left[g_1(W)g_2(W)\right]\end{array}$$

for any $f\in {\mathcal{H}}_{\mathcal{X}}$ and $g,g_1,g_2\in {\mathcal{H}}_{\mathcal{Y}}$, where $\otimes$ denotes the tensor product. Let $C_{(YX)X}:{\mathcal{H}}_{\mathcal{X}}\to {\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{X}}$ and $C_{(YY)X}:{\mathcal{H}}_{\mathcal{X}}\to {\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}$ be bounded linear operators which respectively satisfy(5) $$\begin{array}{cc}\hfill {⟨g\otimes f,C_{(YX)X}h⟩}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{X}}}& =E\left[g(Y)f(X)h(X)\right],\hfill \\ \hfill {⟨g_1\otimes g_2,C_{(YY)X}f⟩}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}}& =E\left[g_1(Y)g_2(Y)f(X)\right]\hfill \end{array}$$(5)

for any $f,h\in {\mathcal{H}}_{\mathcal{X}}$ and $g,g_1,g_2\in {\mathcal{H}}_{\mathcal{Y}}$.

From Theorem 2, Fukumizu et al. (2013) proposed that $m_{(ZW)}$ and $m_{(WW)}$ can be given by$$\begin{array}{c}\hfill m_{(ZW)}=C_{(YX)X}{C}_{\mathit{XX}}^{-1}{m}_{\mathrm{\Pi }}\in {\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{X}}\text{and}{m}_{(WW)}=C_{(YY)X}{C}_{\mathit{XX}}^{-1}{m}_{\mathrm{\Pi }}\in {\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}.\end{array}$$

In case $m_{\mathrm{\Pi }}$ is not included in $\mathrm{R}an(C_{\mathit{XX}})$, they suggested that $m_{(ZW)}$ and $m_{(WW)}$ could be approximated by$$\begin{array}{c}\hfill m_{(ZW)}^{\text{reg}}=C_{(YX)X}{\left(C_{\mathit{XX}}+ϵI\right)}^{-1}{m}_{\mathrm{\Pi }}\text{and}{m}_{(WW)}^{\text{reg}}=C_{(YY)X}{\left(C_{\mathit{XX}}+ϵI\right)}^{-1}{m}_{\mathrm{\Pi }}.\end{array}$$

Remark 1

(Fukumizu et al., 2013, p. 3760)    $m_{(ZW)}$ and $m_{(WW)}$ can respectively be identified with $C_{\mathit{ZW}}$ and $C_{\mathit{WW}}$.

Here, we introduce the empirical method for estimating the posterior kernel mean $m_{Q_{\mathcal{X}|y}}$ following (Fukumizu et al., 2013).

Definition 4

Suppose we have an independent and identically distributed (i.i.d.) sample ${\{(X_i,Y_i)\}}_{i=1}^n$ from the observed distribution P on $\mathcal{X}\times \mathcal{Y}$ and a sample ${\{U_j\}}_{j=1}^l$ from the prior distribution $\mathrm{\Pi }$ on $\mathcal{X}$. The prior kernel mean $m_{\mathrm{\Pi }}$ is estimated by(6) $$\begin{array}{c}\hfill {\widehat{m}}_{\mathrm{\Pi }}=\sum _{j=1}^l{\gamma }_j{k}_{\mathcal{X}}(·,U_j),\end{array}$$(6)

where ${\gamma }_1,\dots ,{\gamma }_l$ are weights. Let us put ${\widehat{\mathit{m}}}_{\mathrm{\Pi }}={({\widehat{m}}_{\mathrm{\Pi }}(X_1),\dots ,{\widehat{m}}_{\mathrm{\Pi }}(X_n))}^{\mathrm{T}}$, $G_X={(k_{\mathcal{X}}(X_i,X_j))}_{1\le i,j\le n}$, and $G_Y={(k_{\mathcal{Y}}(Y_i,Y_j))}_{1\le i,j\le n}$.

Proposition 1

(Fukumizu et al., 2013, Proposition 3, revised)   Let $I_n$ denote the identity matrix of size n. The estimates of $C_{\mathit{ZW}}$ and $C_{\mathit{WW}}$ are given by$$\begin{array}{c}\hfill {\widehat{C}}_{\mathit{ZW}}=\sum _{i=1}^n{\widehat{\mu }}_i{k}_{\mathcal{X}}(·,X_i)\otimes k_{\mathcal{Y}}(·,Y_i)\text{and}{\widehat{C}}_{\mathit{WW}}=\sum _{i=1}^n{\widehat{\mu }}_i{k}_{\mathcal{Y}}(·,Y_i)\otimes k_{\mathcal{Y}}(·,Y_i),\end{array}$$

respectively, where $\widehat{\mathit{\mu }}={({\widehat{\mu }}_1,\dots ,{\widehat{\mu }}_n)}^{\mathrm{T}}={(G_X+nϵI_n)}^{-1}{\widehat{\mathit{m}}}_{\mathrm{\Pi }}$.

The proof of this revised proposition is given in Section 6.1. It is suggested in Fukumizu et al. (2013) that Equation (4) can be empirically estimated by$$\begin{array}{c}\hfill {\widehat{m}}_{Q_{\mathcal{X}|y}}={\widehat{C}}_{\mathit{ZW}}{\left({\widehat{C}}_{\mathit{WW}}^2+\delta I_n\right)}^{-1}{\widehat{C}}_{\mathit{WW}}{k}_{\mathcal{Y}}(·,y).\end{array}$$

Theorem 3

(Fukumizu et al., 2013, Proposition 4)    Given an observation $y\in \mathcal{Y}$, ${\widehat{m}}_{Q_{\mathcal{X}|y}}$ can be calculated by$$\begin{array}{c}\hfill {\widehat{m}}_{Q_{\mathcal{X}|y}}={\mathit{k}}_X^{\mathrm{T}}{R}_{X|Y}{\mathit{k}}_Y(y),R_{X|Y}=\mathrm{\Lambda }{G}_Y{\left({(\mathrm{\Lambda }{G}_Y)}^2+\delta I\right)}^{-1}\mathrm{\Lambda },\end{array}$$

where $\mathrm{\Lambda }=\text{diag}(\widehat{\mathit{\mu }})$ is the diagonal matrix with the elements of $\widehat{\mathit{\mu }}$, ${\mathit{k}}_X={\left(k_{\mathcal{X}}(·,X_1),\dots ,k_{\mathcal{X}}(·,X_n)\right)}^{\mathrm{T}}$, and ${\mathit{k}}_Y={\left(k_{\mathcal{Y}}(·,Y_1),\dots ,k_{\mathcal{Y}}(·,Y_n)\right)}^{\mathrm{T}}$.

If we want to know the posterior expectation of a function $f\in {\mathcal{H}}_{\mathcal{X}}$ given an observation $y\in \mathcal{Y}$, it is estimated by$$\begin{array}{c}\hfill {⟨f,{\widehat{m}}_{Q_{\mathcal{X}|y}}⟩}_{{\mathcal{H}}_{\mathcal{X}}}={\mathit{f}}_X^{\mathrm{T}}{R}_{X|Y}{\mathit{k}}_{\mathcal{Y}}(y),\end{array}$$

where ${\mathit{f}}_X={(f(X_1),\dots ,f(X_n))}^{\mathrm{T}}$.

3. Theoretical arguments

In this section, we theoretically support the three arguments raised in Section 1. First, we show in Section 3.1 that the posterior kernel mean ${\widehat{m}}_{Q_{\mathcal{X}|y}}$ is completely unaffected by the prior distribution $\mathrm{\Pi }$ under the condition that $\mathrm{\Lambda }$ and $G_Y$ are non-singular. This implies that, at least in some cases, $\mathrm{\Pi }$ does not properly affect ${\widehat{m}}_{Q_{\mathcal{X}|y}}$. Second, we mention in Section 3.2 that the linear operators $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$ are not always surjective, and address the problems associated with the setting of the regularization parameters $ϵ$ and $\delta$. Third, we demonstrate in Section 3.3 that conditional expectation functions are not generally contained in the RKHS, which means that Theorems 1, 2, and 5–8 in Fukumizu et al. (2013) do not work in some situations.

3.1. Relations between the posterior ${\widehat{m}}_{Q_{\mathcal{X}|y}}$ and the prior $\mathrm{\Pi }$

Let us review Theorem 3. Assume that $G_Y$ and $\mathrm{\Lambda }$ are non-singular matrices. (This assumption is not so strange, as shown in Section 6.2.) The matrix $R_{X|Y}=\mathrm{\Lambda }{G}_Y{({(\mathrm{\Lambda }{G}_Y)}^2+\delta I)}^{-1}\mathrm{\Lambda }$ tends to $G_Y^{-1}$ as $\delta$ tends to 0. Furthermore, if we set $\delta =0$ from the beginning, we obtain $R_{X|Y}=G_Y^{-1}$. This implies that the posterior kernel mean ${\widehat{m}}_{Q_{\mathcal{X}|y}}={\mathit{k}}_X^{\mathrm{T}}{R}_{X|Y}{\mathit{k}}_Y(y)$ never depends on the prior distribution $\mathrm{\Pi }$ on $\mathcal{X}$, which seems to be a contradiction to the nature of Bayes’ rule.

Some readers may argue that, even in this case, we should not set $\delta =0$. Then, however, there is ambiguity about why and how the regularization parameters are introduced in the kernel Bayes’ rule, since Fukumizu et al. originally used the regularization parameters just to solve inverse problems as an analog of ridge regression (Fukumizu et al., 2013, p. 3758). They seem to support the validity of the regularization parameters by Theorems 5, 6, 7, and 8 in Fukumizu et al. (2013), however, these theorems do not work without the strong assumption that conditional expectation functions are included in the RKHS, as will be discussed in Section 3.2. In addition, since the theorems work only when ${\delta }_n$, etc. decay to zero sufficiently slowly, it seems that we have no principled way to choose values for the regularization parameters, except for cross-validation or similar techniques. It is worth mentioning that, in our simple experiments in Section 4.2, we could not obtain a reasonable result with the kernel Bayes’ rule using any combination of values for the regularization parameters.

3.2. The inverse of the operators $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$

As noted by Fukumizu et al. (2013), the linear operators $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$ are not surjective in some usual cases, the proof of which is given in Section 6.3. Therefore, they proposed an alternative way of obtaining a solution $f\in {\mathcal{H}}_{\mathcal{X}}$ of the equation $C_{\mathit{XX}}f=m_{\mathrm{\Pi }}$, that is, a regularized inversion $f={(C_{\mathit{XX}}+ϵI)}^{-1}{m}_{\mathrm{\Pi }}$ as an analog of ridge regression, where $ϵ$ is a regularization parameter and I is an identity operator. One of the disadvantages of this method is that the solution $f={(C_{\mathit{XX}}+ϵI)}^{-1}{m}_{\mathrm{\Pi }}$ depends upon the choice of $ϵ$. In Section 4.2, we numerically show that the prediction using the kernel Bayes’ rule considerably depends on the regularization parameters $ϵ$ and $\delta$. Theorems 5–8 in Fukumizu et al. (2013) seem to support the appropriateness of the regularized inversion. However, these theorems work under the condition that conditional expectation functions are contained in the RKHS, which does not hold in some cases as proved in Section 3.3. Furthermore, since we need to assume sufficiently slow decay of the regularization constants $ϵ$ and $\delta$ in these theorems, it is practically difficult to set appropriate values for $ϵ$ and $\delta$. A cross-validation procedure seems to be useful for tuning the parameters and we may obtain good experimental results, however, it seems to lack theoretical background.

Instead of the regularized inversion method, we can compute generalized inverse matrices of $G_X$ and $\mathrm{\Lambda }{G}_Y$, given a sample ${\{(X_i,Y_i)\}}_{i=1}^n$. Below, we briefly introduce a generalization of a matrix inverse. For more details, see Horn and Johnson (2013).

Definition 5

Let A be a matrix of size $m\times n$ over the complex number space $\mathbb{C}$. We say that a matrix $A^{\times }$ of size $n\times m$ is a generalized inverse matrix of A if $A{A}^{\times }A=A$. We also say that a matrix $A^{†}$ of size $n\times m$ is the Moore-Penrose generalized inverse matrix of A if $A{A}^{†}$ and $A^{†}A$ are Hermitian, $A{A}^{†}A=A$, and $A^{†}A{A}^{†}=A^{†}$.

Remark 2

In fact, any matrix A has the Moore-Penrose generalized inverse matrix $A^{†}$. Note that $A^{†}$ is uniquely determined by A. If A is square and non-singular, then $A^{\times }=A^{†}=A^{-1}$. For a generalized inverse matrix $A^{\times }$ of size $n\times m$, $A{A}^{\times }v=v$ for any vector $v\in {\mathbb{C}}^m$ if v is contained in the image of A. In particular, $A^{\times }v$ is a vector contained in the preimage of v under A.

In the calculation of ${\widehat{m}}_{Q_{\mathcal{X}|y}}={\mathit{k}}_X^{\mathrm{T}}{R}_{X|Y}{\mathit{k}}_Y(y)$, we numerically compare the case $R_{X|Y}={({\mathrm{\Lambda }}^{\prime }{G}_Y)}^{†}{\mathrm{\Lambda }}^{\prime }$ with the original case $R_{X|Y}=\mathrm{\Lambda }{G}_Y{({(\mathrm{\Lambda }{G}_Y)}^2+\delta I)}^{-1}\mathrm{\Lambda }$ in Section 4.2, where ${\mathrm{\Lambda }}^{\prime }=\text{diag}(G_X^{†}{\widehat{\mathit{m}}}_{\mathrm{\Pi }})$.

3.3. Conditional expectation functions and RKHS

In this subsection, we show that conditional expectation functions are in some cases not contained in the RKHS.

Definition 6

For $p\in [1,\infty )$, we define the spaces $L^p(\mathbb{R})$, $L^p(\mathbb{R},\mathbb{C})$, and $L^p({\mathbb{R}}^2,\mathbb{R})$ as$$\begin{array}{cc}& L^p(\mathbb{R}):=\left\{\begin{array}{cc}f:\mathbb{R}\to \mathbb{R}|& {\int }_{-\infty }^{\infty }{|f(x)|}^{p}dx<\infty \end{array}\right\},\hfill \\ \hfill & L^p(R,C):=\{f:R\to C|{\int }_{-\infty }^{\infty }{|f(x)|}^{p}dx<\infty \}\hfill & \hfill L^p({\mathbb{R}}^2,\mathbb{R}):=\left\{\begin{array}{cc}f:{\mathbb{R}}^2\to \mathbb{R}|& {\int }_{{\mathbb{R}}^2}{|f(x_1,x_2)|}^{p}d{x}_{1}d{x}_2<\infty \end{array}\right\}.\end{array}$$

We also define the $L^p$ norm for $f\in L^p(\mathbb{R})$ or $f\in L^p(\mathbb{R},\mathbb{C})$ as$$\begin{array}{c}\hfill {\Vert f\Vert }_p:={\left({\int }_{-\infty }^{\infty }{|f(x)|}^{p}dx\right)}^{\frac{1}{p}},\end{array}$$

and the $L^p$ norm for $f\in L^p({\mathbb{R}}^2,\mathbb{R})$ as$$\begin{array}{c}\hfill {\Vert f\Vert }_p:={\left({\int }_{{\mathbb{R}}^2}{|f(x_1,x_2)|}^{p}d{x}_{1}d{x}_2\right)}^{\frac{1}{p}}.\end{array}$$

Definition 7

For a function $f\in L^1(\mathbb{R},\mathbb{C})\cap L^2(\mathbb{R},\mathbb{C})$, we define its Fourier transform as$$\begin{array}{c}\hfill \widehat{f}(t):=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f(x)exp(-\sqrt{-1}tx)dx.\end{array}$$

We can uniquely extend the Fourier transform to an isometry $\widehat{}:L^2(\mathbb{R},\mathbb{C})\to L^2(\mathbb{R},\mathbb{C})$. We also define the inverse Fourier transform $\stackrel{ˇ}{}:L^2(\mathbb{R},\mathbb{C})\to L^2(\mathbb{R},\mathbb{C})$ as an isometry uniquely determined by$$\begin{array}{c}\hfill \check{f}(t):=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f(x)exp(\sqrt{-1}tx)dx\end{array}$$

for $f\in L^1(\mathbb{R},\mathbb{C})\cap L^2(\mathbb{R},\mathbb{C})$.

Definition 8

Let us define a Gaussian kernel $k_G$ on $\mathbb{R}$ by$$\begin{array}{c}\hfill k_G(x,y):=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{{(x-y)}^2}{2{\sigma }^2}\right).\end{array}$$

As described in Fukumizu (2014), the RKHS of real-valued functions and complex-valued functions corresponding to the positive definite kernel $k_G$ are given by$$\begin{array}{cc}\hfill {\mathcal{H}}_G& :=\left\{\begin{array}{cc}f\in L^2(\mathbb{R})& {\int }_{-\infty }^{\infty }{\left|\widehat{f}(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt<\infty \end{array}\right\},\hfill \\ \hfill {\mathcal{H}}_G\left(\mathbb{R},\mathbb{C}\right)& :=\left\{\begin{array}{cc}f\in L^2(\mathbb{R},\mathbb{C})& {\int }_{-\infty }^{\infty }{\left|\widehat{f}(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt<\infty \end{array}\right\},\hfill \end{array}$$

respectively, and the inner product of $f,g\in {\mathcal{H}}_G$ or $f,g\in {\mathcal{H}}_G\left(\mathbb{R},\mathbb{C}\right)$ on the RKHS is calculated by(7) $$\begin{array}{c}\hfill ⟨f,g⟩={\int }_{-\infty }^{\infty }\widehat{f}(t)\overline{\widehat{g}(t)}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt,\end{array}$$(7)

where the overline denotes the complex conjugate. Remark that ${\mathcal{H}}_G$ is a real Hilbert subspace contained in the complex Hilbert space ${\mathcal{H}}_G(\mathbb{R},\mathbb{C})$.

Fukumizu et al. (2013) mentioned that the conditional expectation function $E[g(Y)|X=·]$ is not always included in ${\mathcal{H}}_{\mathcal{X}}$. Indeed, if the variables X and Y are independent, then $E[g(Y)|X=·]$ becomes a constant function on $\mathcal{X}$, the value of which might be non-zero. In the case that $\mathcal{X}=\mathbb{R}$ and $k_{\mathcal{X}}=k_G$, the constant function with non-zero value is not contained in ${\mathcal{H}}_{\mathcal{X}}={\mathcal{H}}_G$.

Additionally, in order to prove Theorems 5 and 8 in Fukumizu et al. (2013), they made the assumption that $E[k_{\mathcal{Y}}(Y,\tilde{Y})|X=x,\tilde{X}=\tilde{x}]\in {\mathcal{H}}_{\mathcal{X}}\otimes {\mathcal{H}}_{\mathcal{X}}$ and $E[k_{\mathcal{X}}(Z,\tilde{Z})|W=y,\tilde{W}=\tilde{y}]\in {\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}$, where $(\tilde{X},\tilde{Y})$ and $(\tilde{Z},\tilde{W})$ are independent copies of the random variables $(X,Y)$ and $(Z,W)$ on $\mathcal{X}\times \mathcal{Y}$, respectively. We also see that this assumption does not hold in general. Suppose that X and Y are independent and that so are $\tilde{X}$ and $\tilde{Y}$. Then $E[k_{\mathcal{Y}}(Y,\tilde{Y})\mid X=x,\tilde{X}=\tilde{x}]$ is a constant function of $(x,\tilde{x})$, the value of which might be non-zero. In the case that $\mathcal{X}=\mathbb{R}$ and $k_{\mathcal{X}}=k_G$, the constant function having non-zero value is not contained in ${\mathcal{H}}_{\mathcal{X}}\otimes {\mathcal{H}}_{\mathcal{X}}={\mathcal{H}}_G\otimes {\mathcal{H}}_G$. Note that ${\mathcal{H}}_G\otimes {\mathcal{H}}_G$ is isomorphic to the RKHS corresponding to the kernel $k((x_1,x_2),({\tilde{x}}_1,{\tilde{x}}_2))=k_G(x_1,{\tilde{x}}_1)k_G(x_2,{\tilde{x}}_2)$ on ${\mathbb{R}}^2$, that is,$$\begin{array}{c}\hfill {\mathcal{H}}_G\otimes {\mathcal{H}}_G=\left\{\begin{array}{cc}f\in L^2({\mathbb{R}}^2,\mathbb{R})& {\int }_{{\mathbb{R}}^2}{\left|\widehat{f}(t_1,t_2)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}(t_1^2+t_2^2)\right)d{t}_{1}d{t}_2<\infty \end{array}\right\},\end{array}$$

where the Fourier transform of $f:{\mathbb{R}}^2\to \mathbb{R}$ is defined by$$\begin{array}{c}\hfill \widehat{f}(t_1,t_2):=\underset{n\to \infty }{lim}{\left(\frac{1}{\sqrt{2\pi }}\right)}^2{\int }_{x_1^2+x_2^2<n}f(x_1,x_2)exp\left(-\sqrt{-1}(t_1{x}_1+t_2{x}_2)\right)d{x}_{1}d{x}_2.\end{array}$$

Thus, the assumption that conditional expectation functions are included in the RKHS does not hold in general. Since most of the theorems in Fukumizu et al. (2013) require this assumption, the kernel Bayes’ rule may not work in several cases.

4. Numerical experiments

In this section, we perform numerical experiments to illustrate the theoretical results in Sections 3.1 and 3.2. We first introduce probabilistic classifiers in Section 4.1 based on conventional Bayes’ rule assuming Gaussian distributions (BR), the original kernel Bayes’ rule (KBR1), and the kernel Bayes’ rule using Moore-Penrose generalized inverse matrices (KBR2). In Section 4.2, we apply the three classifiers to a binary classification problem with computer-simulated data sets. Numerical experiments are implemented in version 2.7.6 of the Python software (Python Software Foundation, Wolfeboro Falls, NH, USA).

4.1. Algorithms of the three classifiers, BR, KBR1, and KBR2

Let $(X,Y)$ be a random variable with a distribution P on $\mathcal{X}\times \mathcal{Y}$, where $\mathcal{X}=\{C_1,\dots ,C_g\}$ is a family of classes and $\mathcal{Y}={\mathbb{R}}^d$. Let $\mathrm{\Pi }$ and Q be the prior and the joint distributions on $\mathcal{X}$ and $\mathcal{X}\times \mathcal{Y}$, respectively. Suppose we have an i.i.d. training sample ${\{(X_i,Y_i)\}}_{i=1}^n$ from the distribution P. The aim of this subsection is to derive algorithms of the three classifiers, BR, KBR1, and KBR2, which respectively calculate the posterior probability for each class given an observation $y\in \mathcal{Y}$, that is, $Q_{\mathcal{X}|y}(C_1),\dots ,Q_{\mathcal{X}|y}(C_g)$.

4.1.1. The algorithm of BR

In BR, we estimate the posterior probability of j-th class $(j=1,\dots ,g)$ given a test value $y\in \mathcal{Y}$ by$$\begin{array}{c}\hfill {\widehat{Q}}_{\mathcal{X}|y}(C_j)=\frac{{\widehat{P}}_{\mathcal{Y}|C_j}(y)\mathrm{\Pi }(C_j)}{{\sum }_{k=1}^g{\widehat{P}}_{\mathcal{Y}|C_k}(y)\mathrm{\Pi }(C_k)},\end{array}$$

where ${\widehat{P}}_{\mathcal{Y}|C_j}(·)$ is the density function of the d-dimensional normal distribution $\mathcal{N}({\widehat{M}}_j,{\widehat{S}}_j)$ defined by$$\begin{array}{c}\hfill {\widehat{P}}_{\mathcal{Y}|C_j}(·)=\frac{1}{\sqrt{{(2\pi )}^d\left|{\widehat{S}}_j\right|}}exp\left(-\frac{1}{2}{(·-{\widehat{M}}_j)}^{\mathrm{T}}{\widehat{S}}_j^{-1}(·-{\widehat{M}}_j)\right).\end{array}$$

The mean vector ${\widehat{M}}_j\in {\mathbb{R}}^d$ and the covariance matrix ${\widehat{S}}_j\in {\mathbb{R}}^{d\times d}$ are calculated from the training data of the class $C_j$.

4.1.2. The algorithm of KBR1

Let us define positive definite kernels $k_{\mathcal{X}}$ and $k_{\mathcal{Y}}$ as$$\begin{array}{c}\hfill k_{\mathcal{X}}(X,X^{\prime })=\left\{\begin{array}{cc}1& (X=X^{\prime })\\ 0& (X\ne X^{\prime })\end{array}\right.\text{and}{k}_{\mathcal{Y}}(Y,Y^{\prime })=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{{∥Y-Y^{\prime }∥}^2}{2{\sigma }^2}\right)\end{array}$$

for $X,X^{\prime }\in \mathcal{X}$ and $Y,Y^{\prime }\in \mathcal{Y}$, and the corresponding RKHS as ${\mathcal{H}}_{\mathcal{X}}$ and ${\mathcal{H}}_{\mathcal{Y}}$, respectively. Here we set $∥Y∥=\sqrt{{\sum }_{i=1}^d{y}_i^2}$ for $Y={(y_1,y_2,\dots ,y_d)}^{\mathrm{T}}\in \mathcal{Y}={\mathbb{R}}^d$. Then, the prior kernel mean is given by$$\begin{array}{c}\hfill {\widehat{m}}_{\mathrm{\Pi }}(·)=\sum _{j=1}^g\mathrm{\Pi }(C_j)k_{\mathcal{X}}(·,C_j),\end{array}$$

where ${\sum }_{j=1}^g\mathrm{\Pi }(C_j)=1$. Let us put $G_X={(k_{\mathcal{X}}(X_i,X_j))}_{1\le i,j\le n}$, $G_Y={(k_{\mathcal{Y}}(Y_i,Y_j))}_{1\le i,j\le n}$, $D={(1_{\{C_i\}}(X_j))}_{1\le i\le g,1\le j\le n}\in {\{0,1\}}^{g\times n}$, ${\widehat{\mathit{m}}}_{\mathrm{\Pi }}={({\widehat{m}}_{\mathrm{\Pi }}(X_1),\dots ,{\widehat{m}}_{\mathrm{\Pi }}(X_n))}^{\mathrm{T}}$, $\widehat{\mathit{\mu }}={({\widehat{\mu }}_1,\dots ,{\widehat{\mu }}_n)}^{\mathrm{T}}={(G_X+nϵI_n)}^{-1}{\widehat{\mathit{m}}}_{\mathrm{\Pi }}$, $\mathrm{\Lambda }=\text{diag}(\widehat{\mathit{\mu }})$, ${\mathit{k}}_X(·)={\left(k_{\mathcal{X}}(·,X_1),\dots ,k_{\mathcal{X}}(·,X_n)\right)}^{\mathrm{T}}$, ${\mathit{k}}_Y(·)={\left(k_{\mathcal{Y}}(·,Y_1),\dots ,k_{\mathcal{Y}}(·,Y_n)\right)}^{\mathrm{T}}$, and $R_{X|Y}=\mathrm{\Lambda }{G}_Y{({(\mathrm{\Lambda }{G}_Y)}^2+\delta I_n)}^{-1}\mathrm{\Lambda }$, where $I_n$ is the identity matrix of size n and $ϵ,\delta \in \mathbb{R}$ are heuristically set regularization parameters. Note that $1_A$ stands for the indicator function of a set A described as $$\begin{array}{c}\hfill 1_A(t):=\left\{\begin{array}{cc}1& (t\in A)\\ 0& (t\notin A)\end{array}\right..\end{array}$$

Following Theorem 3, the posterior kernel mean given a test value $y\in \mathcal{Y}$ is estimated by$$\begin{array}{c}\hfill {\widehat{m}}_{Q_{\mathcal{X}|y}}={\mathit{k}}_X^{\mathrm{T}}{R}_{X|Y}{\mathit{k}}_Y(y).\end{array}$$

Here, we estimate the posterior probabilities for classes given a test value $y\in \mathcal{Y}$ by $$\begin{array}{c}\hfill \left(\begin{array}{c}{\widehat{Q}}_{\mathcal{X}|y}(C_1)\\ ⋮\\ {\widehat{Q}}_{\mathcal{X}|y}(C_g)\end{array}\right)=\left(\begin{array}{c}{〈1_{\{C_1\}},{\widehat{m}}_{Q_{\mathcal{X}|y}}〉}_{{\mathcal{H}}_{\mathcal{X}}}\\ ⋮\\ {〈1_{\{C_g\}},{\widehat{m}}_{Q_{\mathcal{X}|y}}〉}_{{\mathcal{H}}_{\mathcal{X}}}\end{array}\right)=D{R}_{X|Y}{\mathit{k}}_Y(y).\end{array}$$

4.1.3. The algorithm of KBR2

Let $G_X^{†}$ denote the Moore-Penrose generalized inverse matrix of $G_X$. Let us put ${\widehat{\mathit{\mu }}}^{\prime }={({\widehat{\mu }}_1^{\prime },\dots ,{\widehat{\mu }}_n^{\prime })}^{\mathrm{T}}=G_X^{†}{\widehat{\mathit{m}}}_{\mathrm{\Pi }}$, ${\mathrm{\Lambda }}^{\prime }=\text{diag}({\widehat{\mathit{\mu }}}^{\prime })$, and $R_{X|Y}^{\prime }={\left({\mathrm{\Lambda }}^{\prime }{G}_Y\right)}^{†}{\mathrm{\Lambda }}^{\prime }$. Replacing $R_{X|Y}$ in Section 4.1.2 for $R_{X|Y}^{\prime }$, the posterior probabilities for classes given a test value $y\in \mathcal{Y}$ is estimated by$$\begin{array}{c}\hfill {\left({\widehat{Q}}_{\mathcal{X}|y}(C_1),\dots ,{\widehat{Q}}_{\mathcal{X}|y}(C_g)\right)}^{\mathrm{T}}=D{R}_{X|Y}^{\prime }{\mathit{k}}_Y(y).\end{array}$$

4.2. Probabilistic predictions by the three classifiers

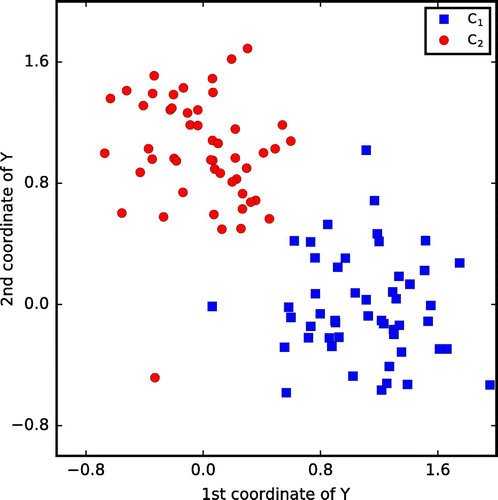
Here, we apply the three classifiers defined in Section 4.1 to a binary classification problem using computer-simulated data-sets, where $\mathcal{X}=\{C_1,C_2\}$ and $\mathcal{Y}={\mathbb{R}}^2$. In the first step, we independently generate 100 sets of training samples with each training sample being ${\{(X_i,Y_i)\in \mathcal{X}\times \mathcal{Y}\}}_{i=1}^{100}$, where $X_i=C_1$ and $Y_i\sim \mathcal{N}(M_1,S_1)$ if $1\le i\le 50$, $X_i=C_2$ and $Y_i\sim \mathcal{N}(M_2,S_2)$ if $51\le i\le 100$, $M_1={(1,0)}^{\mathrm{T}}$, $M_2={(0,1)}^{\mathrm{T}}$, and $S_1=S_2=\text{diag}(0.1,0.1)$. Here, ${\{Y_i\}}_{i=1}^{50}$ and ${\{Y_i\}}_{i=51}^{100}$ are sampled i.i.d. from $\mathcal{N}(M_1,S_1)$ and $\mathcal{N}(M_2,S_2)$, respectively. Individual Y-values of one of the training samples are plotted in Figure 1.

Figure 1. Individual Y-values of a training sample.

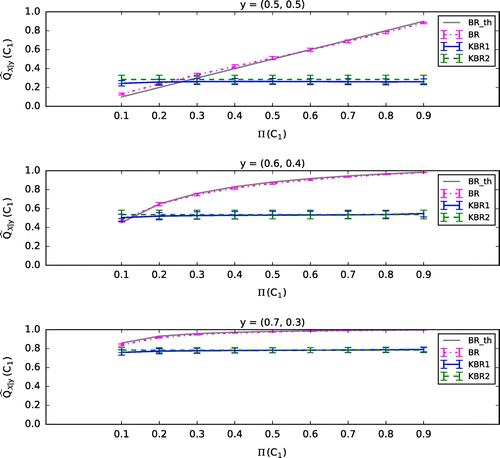
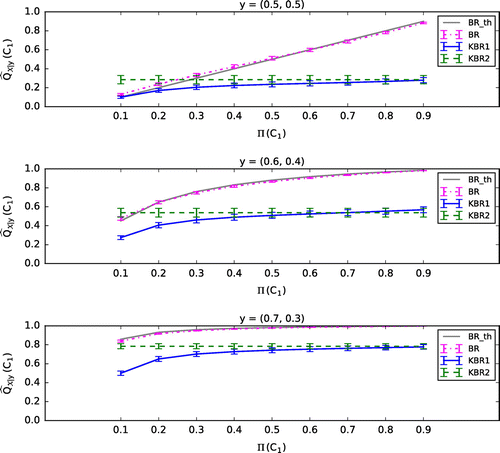
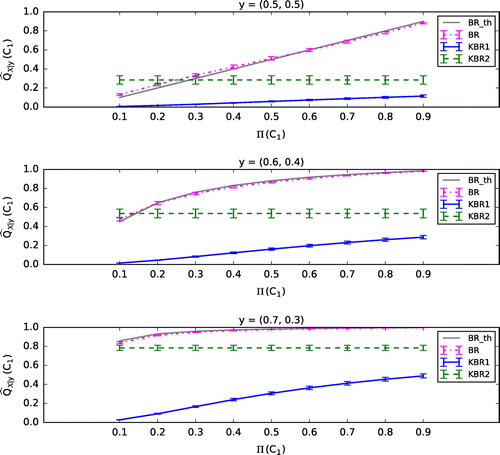
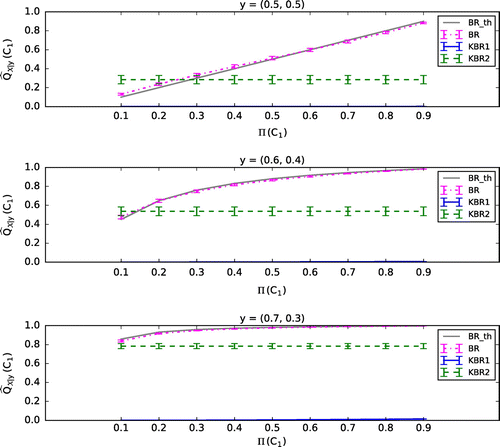
With each of the 100 training samples and a simulated prior probability of $C_1$, or $\mathrm{\Pi }(C_1)\in \{0.1,0.2,\dots ,0.9\}$, the classifiers defined in Section 4.1 estimate the posterior probability of $C_1$ given a test value $y\in \{(0.5,0.5),(0.6,0.4),(0.7,0.3)\}$, that is, $Q_{\mathcal{X}|y}(C_1)$. Figures 2–5 show the mean (plus or minus standard error of the mean, SEM) of the 100 values of ${\widehat{Q}}_{\mathcal{X}|y}(C_1)$ calculated by each of the classifiers, BR, KBR1, and KBR2. Here we show the case where $\sigma$ in KBR1 and KBR2 is fixed to 0.1, and the regularization parameters of KBR1 are set to be $ϵ=\delta ={10}^{-7}$ (Figure 2), $ϵ=\delta ={10}^{-5}$ (Figure 3), $ϵ=\delta ={10}^{-3}$ (Figure 4), and $ϵ=\delta ={10}^{-1}$ (Figure 5). In Figures 2–5, BR_th represents the theoretical value of BR, which coincides with BR if the parameters ${\widehat{M}}_1$, ${\widehat{M}}_2$, ${\widehat{S}}_1$, and ${\widehat{S}}_2$ are set to be $M_1$, $M_2$, $S_1$, and $S_2$, respectively.

Figure 2. The case $ϵ=\delta ={10}^{-7}$.

Consistent to Section 3.1, ${\widehat{Q}}_{\mathcal{X}|y}(C_1)$ calculated by KBR1 is poorly influenced by $\mathrm{\Pi }(C_1)$ compared with that by BR when $ϵ$ and $\delta$ are set to be small (see Figures 2 and 3). In addition, ${\widehat{Q}}_{\mathcal{X}|y}(C_1)$ calculated by KBR2 also seems to be uninfluenced by $\mathrm{\Pi }(C_1)$. When $ϵ$ and $\delta$ are set to be larger, the effect of $\mathrm{\Pi }(C_1)$ on ${\widehat{Q}}_{\mathcal{X}|y}(C_1)$ becomes apparent in KBR1, however, the value of ${\widehat{Q}}_{\mathcal{X}|y}(C_1)$ becomes too small (see Figures 4 and 5). These results suggest that in the kernel Bayes’ rule, the posterior does not depend on the prior if $ϵ$ and $\delta$ are negligible, which might be a contradiction to the nature of Bayes’ theorem. Moreover, even though the prior affects the posterior when $ϵ$ and $\delta$ become larger, the posterior seems too much dependent on $ϵ$ and $\delta$, which are initially defined just for the regularization of matrices.

We have also tested all possible combinations of the following values for the parameters in KBR1 and/or KBR2: $ϵ\in \{{10}^{-1},{10}^{-3},{10}^{-5},{10}^{-7},{10}^{-9},{10}^{-11},{10}^{-13},{10}^{-15}\}$, $\delta \in \{{10}^{-1},{10}^{-3},{10}^{-5},{10}^{-7},{10}^{-9},{10}^{-11},{10}^{-13},{10}^{-15}\}$, and $\sigma \in \{0.01,0.1,1,10,100\}$. All the experimental results have been evaluated in a similar manner as above, and none of the results are found to be reasonable in the context of Bayesian inference (see Supplementary material).

Figure 3. The case $ϵ=\delta ={10}^{-5}$.

Figure 4. The case $ϵ=\delta ={10}^{-3}$.

Figure 5. The case $ϵ=\delta ={10}^{-1}$.

5. Conclusions

One of the important features of Bayesian inference is that it provides a reasonable way of updating the probability for a hypothesis as additional evidence is acquired. The kernel Bayes’ rule has been expected to enable Bayesian inference in RKHS. In other words, the posterior kernel mean has been considered to be reasonably estimated by the kernel Bayes’ rule, given kernel mean expressions of the prior and likelihood. What is “reasonable" depends on circumstances, however, some of the results in this paper seem to show obviously unreasonable aspects of the kernel Bayes’ rule, at least in the context of Bayesian inference.

First, as shown in Section 3.1, when $\mathrm{\Lambda }$ and $G_Y$ are non-singular matrices and so we set $\delta =0$, the posterior kernel mean ${\widehat{m}}_{Q_{\mathcal{X}|y}}$ is entirely unaffected by the prior distribution $\mathrm{\Pi }$ on $\mathcal{X}$. This means that, in Bayesian inference with the kernel Bayes’ rule, prior beliefs are in some cases completely neglected in calculating the kernel mean of the posterior distribution. Numerical evidence is also presented in Section 4.2. When the regularization parameters $ϵ$ and $\delta$ are set to be small, the posterior probability calculated by the kernel Bayes’ rule (KBR1) is almost unaffected by the prior probability in comparison with that by conventional Bayes’ rule (BR). Consistently, when the regularized inverse matrices in KBR1 are replaced for the Moore-Penrose generalized inverse matrices (KBR2), the posterior probability is also uninfluenced by the prior probability, which seems to be unsuitable in the context of Bayesian updating of a probability distribution.

Second, as discussed in Sections 3.2 and 4.2, the posterior estimated by the kernel Bayes’ rule considerably depends upon the regularization parameters $ϵ$ and $\delta$, which are originally introduced just for the regularization of matrices. A cross-validation approach is proposed in Fukumizu et al. (2013) to search for the optimal values of the parameters. However, theoretical foundations seem to be insufficient for the correct tuning of the parameters. Furthermore, in our experimental settings, we are not able to obtain a reasonable result using any combination of the parameter values, suggesting the possibility that there are no appropriate values for the parameters in general. Thus, we consider it difficult to solve the problem that $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$ are not surjective by just adding regularization parameters.

Third, as shown in Section 3.3, the assumption that conditional expectation functions are included in the RKHS does not hold in general. Since this assumption is necessary for most of the theorems in Fukumizu et al. (2013), we believe that the assumption itself may need to be reconsidered.

In summary, even though current research efforts are focused on the application of the kernel Bayes’ rule (Fukumizu et al., 2013; Kanagawa et al., 2014), it might be necessary to reexamine its basic framework of combining new evidence with prior beliefs.

6. Proofs

In this section, we provide some proofs for Sections 2 and 3.

6.1. Estimation of $C_{\mathit{ZW}}$ and $C_{\mathit{WW}}$

Here we give the proof of Proposition 1.

Proof

Let ${\widehat{C}}_{\mathit{XX}}$, ${\widehat{C}}_{(YX)X}$, and ${\widehat{C}}_{(YY)X}$ denote the estimates of $C_{\mathit{XX}}$, $C_{(YX)X}$, and $C_{(YY)X}$, respectively. We define the estimates of $m_{(ZW)}$ and $m_{(WW)}$ as$$\begin{array}{c}\hfill {\widehat{m}}_{(ZW)}={\widehat{C}}_{(YX)X}{\widehat{C}}_{\mathit{XX}}^{-1}{\widehat{m}}_{\mathrm{\Pi }}\text{and}{\widehat{m}}_{(WW)}={\widehat{C}}_{(YY)X}{\widehat{C}}_{\mathit{XX}}^{-1}{\widehat{m}}_{\mathrm{\Pi }},\end{array}$$

and put $h={\widehat{C}}_{\mathit{XX}}^{-1}{\widehat{m}}_{\mathrm{\Pi }}\in {\mathcal{H}}_{\mathcal{X}}$. According to Equation (5), for any $f\in {\mathcal{H}}_{\mathcal{X}}$ and $g\in {\mathcal{H}}_{\mathcal{Y}}$,$$\begin{array}{cc}& {〈{\widehat{m}}_{(ZW)},g\otimes f〉}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{X}}}={〈{\widehat{C}}_{(YX)X}h,g\otimes f〉}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{X}}}=\widehat{E}\left[f(X)g(Y)h(X)\right]\hfill \\ \hfill & =\frac{1}{n}\sum _{i=1}^{n}f(X_i)g(Y_i)h(X_i)={〈\frac{1}{n}\sum _{i=1}^{n}h(X_i)k_{\mathcal{X}}(·,X_i)\otimes k_{\mathcal{Y}}(·,Y_i),f\otimes g〉}_{{\mathcal{H}}_{\mathcal{X}}\otimes {\mathcal{H}}_{\mathcal{Y}}},\hfill \end{array}$$

where $\widehat{E}[·]$ represents the empirical expectation operator. Thus, from Remark 1,(8) $$\begin{array}{c}\hfill {\widehat{C}}_{\mathit{ZW}}={\widehat{m}}_{(ZW)}=\frac{1}{n}\sum _{i=1}^{n}h(X_i)k_{\mathcal{X}}(·,X_i)\otimes k_{\mathcal{Y}}(·,Y_i).\end{array}$$(8)

Similarly, for any $g_1,g_2\in {\mathcal{H}}_{\mathcal{Y}}$,$$\begin{array}{cc}& {〈{\widehat{m}}_{(WW)},g_1\otimes g_2〉}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}}={〈{\widehat{C}}_{(YY)X}h,g_1\otimes g_2〉}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}}=\widehat{E}\left[g_1(Y)g_2(Y)h(X)\right]\hfill \\ \hfill & =\frac{1}{n}\sum _{i=1}^n{g}_1(Y_i)g_2(Y_i)h(X_i)={〈\frac{1}{n}\sum _{i=1}^{n}h(X_i)k_{\mathcal{Y}}(·,Y_i)\otimes k_{\mathcal{Y}}(·,Y_i),g_1\otimes g_2〉}_{{\mathcal{H}}_{\mathcal{Y}}\otimes {\mathcal{H}}_{\mathcal{Y}}}.\hfill \end{array}$$

Thus, from Remark 1,(9) $$\begin{array}{c}\hfill {\widehat{C}}_{\mathit{WW}}={\widehat{m}}_{(WW)}=\frac{1}{n}\sum _{i=1}^{n}h(X_i)k_{\mathcal{Y}}(·,Y_i)\otimes k_{\mathcal{Y}}(·,Y_i).\end{array}$$(9)

Next, we will derive $h(X_1),\dots ,h(X_n)$. Since $C_{\mathit{XX}}$ is a self-adjoint operator,$$\begin{array}{cc}\hfill {〈h,{\widehat{C}}_{\mathit{XX}}f〉}_{{\mathcal{H}}_{\mathcal{X}}}& ={〈{\widehat{C}}_{\mathit{XX}}h,f〉}_{{\mathcal{H}}_{\mathcal{X}}}={〈{\widehat{m}}_{\mathrm{\Pi }},f〉}_{{\mathcal{H}}_{\mathcal{X}}}=\sum _{j=1}^l{\gamma }_{j}f(U_j)\hfill \end{array}$$

for any $f\in {\mathcal{H}}_{\mathcal{X}}$. On the other hand, from Equation (1),$$\begin{array}{c}\hfill {〈h,{\widehat{C}}_{\mathit{XX}}f〉}_{{\mathcal{H}}_{\mathcal{X}}}=\widehat{E}\left[f(X)h(X)\right]=\frac{1}{n}\sum _{i=1}^{n}f(X_i)h(X_i)\end{array}$$

for any $f\in {\mathcal{H}}_{\mathcal{X}}$. Hence, we have(10) $$\begin{array}{c}\hfill \sum _{j=1}^l{\gamma }_{j}f(U_j)=\frac{1}{n}\sum _{i=1}^{n}f(X_i)h(X_i)\end{array}$$(10)

for any $f\in {\mathcal{H}}_{\mathcal{X}}$. Replacing f in Equation (10) for $k_{\mathcal{X}}(X_1,·),\dots ,k_{\mathcal{X}}(X_n,·)\in {\mathcal{H}}_{\mathcal{X}}$, we have(11) $$\begin{array}{c}\hfill \left(\begin{array}{ccc}{k}_{\mathcal{X}}(X_1,U_1)& \cdots & k_{\mathcal{X}}(X_1,U_l)\\ ⋮& \ddots & ⋮\\ k_{\mathcal{X}}(X_n,U_1)& \cdots & k_{\mathcal{X}}(X_n,U_l)\end{array}\right)\left(\begin{array}{c}{\gamma }_1\\ ⋮\\ {\gamma }_l\end{array}\right)=\frac{1}{n}{G}_X\left(\begin{array}{c}h(X_1)\\ ⋮\\ h(X_n)\end{array}\right).\end{array}$$(11)

Using Equation (6), the left hand side of Equation (11) is given by$$\begin{array}{c}\hfill \left(\begin{array}{c}{〈{\sum }_{j=1}^l{\gamma }_j{k}_{\mathcal{X}}(·,U_j),k_{\mathcal{X}}(·,X_1)〉}_{{\mathcal{H}}_{\mathcal{X}}}\\ ⋮\\ {〈{\sum }_{j=1}^l{\gamma }_j{k}_{\mathcal{X}}(·,U_j),k_{\mathcal{X}}(·,X_n)〉}_{{\mathcal{H}}_{\mathcal{X}}}\end{array}\right)=\left(\begin{array}{c}{\sum }_{j=1}^l{\gamma }_j{k}_{\mathcal{X}}(X_1,U_j)\\ ⋮\\ {\sum }_{j=1}^l{\gamma }_j{k}_{\mathcal{X}}(X_n,U_j)\end{array}\right)=\left(\begin{array}{c}{\widehat{m}}_{\mathrm{\Pi }}(X_1)\\ ⋮\\ {\widehat{m}}_{\mathrm{\Pi }}(X_n)\end{array}\right).\end{array}$$

Therefore, we have$$\begin{array}{c}\hfill \frac{1}{n}\left(\begin{array}{c}h(X_1)\\ ⋮\\ h(X_n)\end{array}\right)=G_X^{-1}\left(\begin{array}{c}{\widehat{m}}_{\mathrm{\Pi }}(X_1)\\ ⋮\\ {\widehat{m}}_{\mathrm{\Pi }}(X_n)\end{array}\right)\approx {\left(G_X+nϵI\right)}^{-1}{\widehat{\mathit{m}}}_{\mathrm{\Pi }}=\widehat{\mathit{\mu }}.\end{array}$$

Replacing $\frac{1}{n}{(h(X_1),\dots ,h(X_n))}^{\mathrm{T}}$ for $\widehat{\mathit{\mu }}={({\widehat{\mu }}_1,\dots ,{\widehat{\mu }}_n)}^{\mathrm{T}}$, Equations (8) and (9) become$$\begin{array}{c}\hfill {\widehat{C}}_{\mathit{ZW}}=\sum _{i=1}^n{\widehat{\mu }}_i{k}_{\mathcal{X}}(·,X_i)\otimes k_{\mathcal{Y}}(·,Y_i)\text{and}{\widehat{C}}_{\mathit{WW}}=\sum _{i=1}^n{\widehat{\mu }}_i{k}_{\mathcal{Y}}(·,Y_i)\otimes k_{\mathcal{Y}}(·,Y_i),\end{array}$$

respectively. $\square$

6.2. Non-singularity of $G_Y$ and $\mathrm{\Lambda }$

Here we show that the assumption in Section 3.1 holds under reasonable conditions.

Definition 9

Let f be a real-valued function defined on a non-empty open domain $\text{Dom}(f)\subseteq {\mathbb{R}}^d$. We say that f is analytic if f can be described by a Taylor expansion on a neighborhood of each point of $\text{Dom}(f)$.

Proposition 2

Let k be a positive definite kernel on ${\mathbb{R}}^d$. Let $\nu$ be a probability measure on ${\mathbb{R}}^d$ which is absolutely continuous with respect to Lebesgue measure. Assume that k is an analytic function on ${\mathbb{R}}^d\times {\mathbb{R}}^d$ and that the RKHS corresponding to k is infinite dimensional. Then for any i.i.d. random variables $X_1,X_2,\dots ,X_n$ with the same distribution $\nu$, the Gram matrix $G_X={(k(X_i,X_j))}_{1\le i,j\le n}$ is non-singular almost surely with respect to ${\nu }^n=\nu \times \nu \times \cdots \times \nu \text{(n times)}$.

Proof

Let us put $f(x_1,x_2,\dots ,x_n):=det{(k(x_i,x_j))}_{1\le i,j\le n}$. Since the RKHS corresponding to k is infinite dimensional, there are ${\xi }_1,{\xi }_2,\dots ,{\xi }_n\in {\mathbb{R}}^d$ such that ${\{k(·,{\xi }_i)\}}_{1\le i\le n}$ are linearly independent. Then $f({\xi }_1,{\xi }_2,\dots ,{\xi }_n)\ne 0$ and hence f is a non-zero analytic function. Note that any non-trivial subvarieties of the euclidean spaces defined by analytic functions have Lebesgue measure zero. By this fact, the subvariety$$\begin{array}{c}\hfill \mathcal{V}(f):=\left\{\begin{array}{cc}(x_1,x_2,\dots ,x_n)\in {({\mathbb{R}}^d)}^n& f(x_1,x_2,\dots ,x_n)=0\end{array}\right\}\subset {({\mathbb{R}}^d)}^n\end{array}$$

has Lebesgue measure zero. Since $\nu$ is absolutely continuous, ${\nu }^n(\mathcal{V}(f))=0$. This completes the proof. $\square$

From Proposition 2, we easily obtain the following corollary.

Corollary 1

Let k be a Gaussian kernel on ${\mathbb{R}}^d$ and let $X_1,X_2,\dots ,v{X}_n$ be i.i.d. random variables with the same normal distribution on ${\mathbb{R}}^d$. Then the Gram matrix $G_X={(k(X_i,X_j))}_{1\le i,j\le n}$ is non-singular almost surely.

Proposition 3

Let k be a positive definite kernel on $\mathcal{X}={\mathbb{R}}^d$, $\nu$ a probability measure on $\mathcal{X}$ which is absolutely continuous with respect to Lebesgue measure. Assume that k is an analytic function on $\mathcal{X}\times \mathcal{X}$ and that the RKHS $\mathcal{H}$ corresponding to k is infinite dimensional. Then for any $(ϵ,{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_l,U_1,U_2,\dots ,U_l)\in {\mathbb{R}}_{+}\times {\mathbb{R}}^l\times {({\mathbb{R}}^d)}^l$ except Lebesgue measure zero, and for any i.i.d. random variables $X_1,X_2,\dots ,X_n$ with the same distribution $\nu$, each ${\mu }_i$ for $i=1,2,\dots ,n$ is (defined almost surely and) non-zero almost surely, where ${({\mu }_1,{\mu }_2,\dots ,{\mu }_n)}^T={(G_X+nϵI_n)}^{-1}{\widehat{\mathit{m}}}_{\mathrm{\Pi }}$, ${\widehat{\mathit{m}}}_{\mathrm{\Pi }}={({\widehat{m}}_{\mathrm{\Pi }}(X_1),{\widehat{m}}_{\mathrm{\Pi }}(X_2),\dots ,{\widehat{m}}_{\mathrm{\Pi }}(X_n))}^T$, and ${\widehat{m}}_{\mathrm{\Pi }}(·)={\sum }_{j=1}^l{\gamma }_{j}k(·,U_j)$. Here ${\mathbb{R}}_{+}$ denotes the set of positive real numbers.

Proof

Let us put $\mathcal{S}:={\mathbb{R}}_{+}\times {\mathbb{R}}^l\times {({\mathbb{R}}^d)}^l$, $\mathcal{T}:={\mathcal{X}}^n\times \mathcal{S}$, and$$\begin{array}{c}\hfill f_i(x_1,x_2,\dots ,x_n,ϵ,{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_l,U_1,U_2,\dots ,U_l):={\mu }_i(i=1,2,\dots ,n)\end{array}$$

for $(x_1,x_2,\dots ,x_n)\in {\mathcal{X}}^n$ and $(ϵ,{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_l,U_1,U_2,\dots ,U_l)\in \mathcal{S}$. Since the RKHS corresponding to k is infinite- dimensional, we can obtain ${\xi }_1,{\xi }_2,\dots ,{\xi }_n\in \mathcal{X}$ such that ${\{k(·,{\xi }_i)\}}_{1\le i\le n}$ are linearly independent. The Gram matrix ${(k({\xi }_i,{\xi }_j))}_{1\le i,j\le n}={({⟨k(·,{\xi }_i),k(·,{\xi }_j)⟩}_{\mathcal{H}})}_{1\le i,j\le n}$ is positive definite, and its eigenvalues are all positive. Hence $det({(k({\xi }_i,{\xi }_j))}_{1\le i,j\le n}+nϵI_n)>0$ for each $ϵ\in {\mathbb{R}}_{+}$, and $det(G_X+nϵI_n)=det({(k(x_i,x_j))}_{1\le i,j\le n}+nϵI_n)$ is a non-zero analytic function on ${\mathcal{X}}^n$ for each $ϵ\in {\mathbb{R}}_{+}$.

For $(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)\in \mathcal{S}$, let us define a closed measure-zero set $\mathcal{V}(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l):=\{(x_1,x_2,\dots ,x_n)\in {\mathcal{X}}^n\mid det(G_X+nϵI_n)=0\}\subset {\mathcal{X}}^n$. Then $f_i(\ast ,ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)$ is defined on ${\mathcal{X}}^n\backslash \mathcal{V}(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)$ for each $i\in \{1,2,\dots ,n\}$. Using Cramer’s rule,$$\begin{array}{c}\hfill {\mu }_i=\frac{det\left({\eta }_1,{\eta }_2,\dots ,{\eta }_{i-1},{\widehat{\mathit{m}}}_{\mathrm{\Pi }},{\eta }_{i+1},\dots ,{\eta }_n\right)}{det\left(G_X+nϵI_n\right)},\end{array}$$

where ${\eta }_m$ stands for the m-th column vector of $G_X+nϵI_n$. Here we denote by $g_i$ the numerator of ${\mu }_i$, that is, $g_i={\mu }_{i}det(G_X+nϵI_n)$.

It is easy to see that $g_i({\xi }_1,{\xi }_2,\dots ,{\xi }_n,\ast )$ is a non-zero analytic function of $\ast$ on $\mathcal{S}$. Indeed, if $ϵ\to +0$, $U_1={\xi }_i$, ${\gamma }_1=1$, and ${\gamma }_2={\gamma }_3=\cdots ={\gamma }_l=0$, then $g_i\to det{({⟨k(·,{\xi }_i),k(·,{\xi }_j)⟩}_{\mathcal{H}})}_{1\le i,j\le n}\ne 0$. Hence ${\mathcal{Z}}_i:=\{\ast \in \mathcal{S}\mid g_i({\xi }_1,{\xi }_2,\dots ,{\xi }_n,\ast )=0\}$ is a closed subset of $\mathcal{S}$ with Lebesgue measure zero for each $i\in \{1,2,\dots ,n\}$. For any $(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)\in \mathcal{S}\backslash ({\cup }_{i=1}^n{\mathcal{Z}}_i)$,$$\begin{array}{c}\hfill {\mathcal{F}}_i(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l):=\left\{\begin{array}{cc}\ast \in {\mathcal{X}}^n& g_i\left(\ast ,ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l\right)=0\end{array}\right\}\end{array}$$

is a closed subset of ${\mathcal{X}}^n$ with Lebesgue measure zero for each $i\in \{1,2,\dots ,n\}$, since $g_i(\ast ,ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)$ is a non-zero analytic function of $\ast$ on ${\mathcal{X}}^n$. Therefore, ${\mu }_i=f_i(\ast ,ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)$ is defined and non-zero for $i=1,2,\dots ,n$ and for $\ast \in {\mathcal{X}}^n\backslash (\mathcal{V}(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)\cup ({\cup }_{j=1}^n{\mathcal{F}}_j(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)))$ if $(ϵ,{\gamma }_1,\dots ,{\gamma }_l,U_1,\dots ,U_l)\in \mathcal{S}\backslash ({\cup }_{i=1}^n{\mathcal{Z}}_i)$. This completes the proof. $\square$

The following corollary directly follows from Proposition 3.

Corollary 2

Let k be a Gaussian kernel on ${\mathbb{R}}^d$ and let $X_1,X_2,\dots ,X_n$ be i.i.d. random variables with the same normal distribution on ${\mathbb{R}}^d$. All other notations are as in Proposition 3. Then $\mathrm{\Lambda }:=\text{diag}({\mu }_1,{\mu }_2,\dots ,{\mu }_n)$ is non-singular almost surely for any $(ϵ,{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_l,U_1,U_2,\dots ,U_l)\in {\mathbb{R}}_{+}\times {\mathbb{R}}^l\times {({\mathbb{R}}^d)}^l$ except for those in a set of Lebesgue measure zero.

6.3. Non-surjectivity of $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$

The covariance operators $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$ are not surjective in general. This can be verified by the fact that they are compact operators. (If the operators are surjective on the corresponding RKHS which is infinite-dimensional, then they cannot be compact because of the open mapping theorem.) Here we present some easy examples where $C_{\mathit{XX}}$ and $C_{\mathit{WW}}$ are not surjective. Let us consider for simplicity the case $\mathcal{X}=\mathbb{R}$. Let X be a random variable on $\mathbb{R}$ with a normal distribution $\mathcal{N}(\mu ,{\sigma }_0^2)$. We prove that $C_{\mathit{XX}}$ is not surjective under the usual assumption that the positive definite kernel on $\mathbb{R}$ is Gaussian. In order to demonstrate this, we use the symbols defined in Section 3.3 and several proven results on function spaces and Fourier transforms (see Rudin, 1987, for example). Note that the following three propositions are introduced without proofs.

Proposition 4

Let us put $f(x)=exp(-(a{x}^2+bx+c))$ for $a,b,c\in \mathbb{R}$, where $a>0$. Then$$\begin{array}{c}\hfill \widehat{f}(t)=\frac{1}{\sqrt{2a}}exp\left(-\frac{t^2-2\sqrt{-1}bt-b^2+4ac}{4a}\right).\end{array}$$

Proposition 5

For $f\in L^2(\mathbb{R},\mathbb{C})$, $\widehat{\overline{f}}(t)=\overline{\widehat{f}(-t)}$ almost everywhere. In particular, if $f\in L^2(\mathbb{R})$, then $\overline{\widehat{f}(t)}=\widehat{f}(-t)$ almost everywhere.

Proposition 6

For $f\in L^2(\mathbb{R},\mathbb{C})$, put $f_a(x):=f(x-a)$. Then ${\widehat{f}}_a(t)=exp\left(-\sqrt{-1}at\right)\widehat{f}(t)$.

Definition 10

Let $p(·)$ denote the density function of the normal distribution $\mathcal{N}(\mu ,{\sigma }_0^2)$ on $\mathbb{R}$, that is,$$\begin{array}{c}\hfill p(·)=\frac{1}{\sqrt{2\pi }{\sigma }_0}exp\left(-\frac{{(·-\mu )}^2}{2{\sigma }_0^2}\right).\end{array}$$

Let X be a random variable on $\mathbb{R}$ with $\mathcal{N}(\mu ,{\sigma }_0^2)$. The linear operator $C_{\mathit{XX}}:{\mathcal{H}}_G\to {\mathcal{H}}_G$ is defined by ${⟨C_{\mathit{XX}}f,g⟩}_{{\mathcal{H}}_G}=E[f(X)g(X)]$ for any $f,g\in {\mathcal{H}}_G$, which is also described as$$\begin{array}{c}\hfill (C_{\mathit{XX}}f)(·)={\int }_{-\infty }^{\infty }f(x)k(·,x)p(x)dx\end{array}$$

for any $f\in {\mathcal{H}}_G$.

Proposition 7

If $f,g\in {\mathcal{H}}_G$, then ${〈f,g〉}_{{\mathcal{H}}_G}\in \mathbb{R}$

Proof

From Proposition 5, $\overline{\widehat{f}(t)}=\widehat{f}(-t)$ and $\overline{\widehat{g}(t)}=\widehat{g}(-t)$ for any $f,g\in {\mathcal{H}}_G$. Then, using Equation (7), we have$$\begin{array}{cc}\hfill \overline{{〈f,g〉}_{{\mathcal{H}}_G}}& =\overline{{\int }_{-\infty }^{\infty }\widehat{f}(t)\overline{\widehat{g}(t)}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt}={\int }_{-\infty }^{\infty }\overline{\widehat{f}(t)}\widehat{g}(t)exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\widehat{f}(-t)\widehat{g}(t)exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt={\int }_{-\infty }^{\infty }\widehat{f}(t)\widehat{g}(-t)exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\widehat{f}(t)\overline{\widehat{g}(t)}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt={〈f,g〉}_{{\mathcal{H}}_G}.\hfill \end{array}$$

Therefore, ${〈f,g〉}_{{\mathcal{H}}_G}\in \mathbb{R}$. $\square$

Proposition 8

If $f\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$, then $\overline{f}\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$.

Proof

From Proposition 5, $\widehat{\overline{f}}(t)=\overline{\widehat{f}(-t)}$ for $f\in L^2(\mathbb{R},\mathbb{C})$. Then, using Equation (7), we have$$\begin{array}{cc}\hfill {∥\overline{f}∥}_{{\mathcal{H}}_G(\mathbb{R},\mathbb{C})}^2& ={〈\overline{f},\overline{f}〉}_{{\mathcal{H}}_G(\mathbb{R},\mathbb{C})}\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{\left|\widehat{\overline{f}}(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt={\int }_{-\infty }^{\infty }{\left|\overline{\widehat{f}(-t)}\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{\left|\widehat{f}(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt={∥f∥}_{{\mathcal{H}}_G(\mathbb{R},\mathbb{C})}^2<\infty .\hfill \end{array}$$

Therefore, $\overline{f}\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$. $\square$

Here, we denote by $\mathrm{Re}$ and $\mathrm{Im}$ the real part and the imaginary part of a complex number, respectively. We also denote by $\text{Cl}(A)$ the closure of a subset A in a topological space.

Corollary 3

If $f\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$, then $\text{Re}(f),\text{Im}(f)\in {\mathcal{H}}_G$.

Proof

If $f\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$, then $\overline{f}\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$ by Proposition 8. Hence we see that$$\begin{array}{c}\hfill \text{Re}(f)=\frac{f+\overline{f}}{2}\in {\mathcal{H}}_G,\text{Im}(f)=\frac{f-\overline{f}}{2\sqrt{-1}}\in {\mathcal{H}}_G.\end{array}$$

This completes the proof. $\square$

Remark 3

If $f\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$, then there uniquely exist $f_1,f_2\in {\mathcal{H}}_G$ such that $f=f_1+\sqrt{-1}{f}_2$ by Corollary 3. This means that ${\mathcal{H}}_G(\mathbb{R},\mathbb{C})={\mathcal{H}}_G\oplus \sqrt{-1}{\mathcal{H}}_G$, where $\oplus$ denotes the direct sum.

Proposition 9

For any $f\in L^2(\mathbb{R},\mathbb{C})$ and for any $ϵ>0$, there exists $g\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$ such that ${\Vert f-g\Vert }_2<ϵ$. In other words, ${\mathcal{H}}_G(\mathbb{R},\mathbb{C})$ is dense in $L^2(\mathbb{R},\mathbb{C})$.

Proof

Let $C_0(\mathbb{R},\mathbb{C})$ denote the space of continuous complex-valued functions with compact support on $\mathbb{R}$. Let us define ${\widehat{\mathcal{H}}}_G(\mathbb{R},\mathbb{C})$ by$$\begin{array}{c}\hfill {\widehat{\mathcal{H}}}_G\left(\mathbb{R},\mathbb{C}\right):=\left\{\begin{array}{cc}h\in L^2(\mathbb{R},\mathbb{C})& {\int }_{-\infty }^{\infty }{\left|h(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt<\infty \end{array}\right\}.\end{array}$$

Note that ${\widehat{\mathcal{H}}}_G(\mathbb{R},\mathbb{C})$ coincides with the image of ${\mathcal{H}}_G(\mathbb{R},\mathbb{C})$ by the Fourier transform. Then, $C_0(\mathbb{R},\mathbb{C})\subset {\widehat{\mathcal{H}}}_G(\mathbb{R},\mathbb{C})\subset L^2(\mathbb{R},\mathbb{C})$ and $\text{Cl}(C_0(\mathbb{R},\mathbb{C}))=L^2(\mathbb{R},\mathbb{C})$. Hence $\text{Cl}({\widehat{\mathcal{H}}}_G(\mathbb{R},\mathbb{C}))=L^2(\mathbb{R},\mathbb{C})$. In other words, for any $f\in L^2(\mathbb{R},\mathbb{C})$ and for any $ϵ>0$, there exists $\widehat{g}\in {\widehat{\mathcal{H}}}_G(\mathbb{R},\mathbb{C})$ such that $\Vert \widehat{f}-\widehat{g}{\Vert }_2<ϵ$ because $\widehat{f}\in L^2(\mathbb{R},\mathbb{C})$, which implies that there exists $g\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$ such that ${\Vert f-g\Vert }_2<ϵ$. This completes the proof. $\square$

The following corollary has also been shown in Theorem 4.63 in Steinwart and Christmann (2008).

Corollary 4

$\text{Cl}({\mathcal{H}}_G)=L^2(\mathbb{R})$.

Proof

From Proposition 9, for any $f\in L^2(\mathbb{R})\subset L^2(\mathbb{R},\mathbb{C})$ and for any $ϵ>0$, there exists $g\in {\mathcal{H}}_G(\mathbb{R},\mathbb{C})$ such that ${\Vert f-g\Vert }_2<ϵ$. By Remark 3, there exist $g_1,g_2\in {\mathcal{H}}_G$ such that $g=g_1+\sqrt{-1}{g}_2$. Thus,$$\begin{array}{cc}\hfill {ϵ}^2& >{∥f-g∥}_2^2={\int }_{-\infty }^{\infty }{\left|f-g\right|}^{2}dx={\int }_{-\infty }^{\infty }{\left|(f-g_1)-\sqrt{-1}{g}_2\right|}^{2}dx\hfill \\ \hfill & \ge {\int }_{-\infty }^{\infty }{\left|f-g_1\right|}^{2}dx={∥f-g_1∥}_2^2.\hfill \end{array}$$

Therefore, ${∥f-g_1∥}_2<ϵ$. This completes the proof. $\square$

Definition 11

Let us define $r,r_n\in L^2(\mathbb{R})$ as $$\begin{array}{c}\hfill r(t):=\frac{1}{\left|t\right|}{1}_{(1,\infty )}(|t|),r_n(t):=\frac{1}{\left|t\right|}{1}_{(1,n)}(|t|),\end{array}$$

where $1_{(1,\infty )}$ and $1_{(1,n)}$ denote the indicator functions of the intervals $(1,\infty )$ and $(1,n)$, respectively. We also put $h_n:=\check{r_n}$ and $h:=\check{r}$. Note that ${lim}_{n\to \infty }{r}_n=r\in L^2(\mathbb{R})$, because$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{∥r_n-r∥}_2^2=2\underset{n\to \infty }{lim}{\int }_n^{\infty }\frac{1}{x^2}dx=0.\end{array}$$

Proposition 10

$h_n,h\in L^2(\mathbb{R})$.

Proof

It is obvious that $h_n,h\in L^2(\mathbb{R},\mathbb{C})$. Since $r_n\in L^1(\mathbb{R})\cap L^2(\mathbb{R})$, we see that$$\begin{array}{cc}\hfill \overline{h_n(x)}& =\overline{\check{r_n}(x)}=\overline{\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{r}_n(t)exp\left(\sqrt{-1}tx\right)dt}\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{r}_n(t)exp\left(-\sqrt{-1}tx\right)dt=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{r}_n(-t^{\prime })exp\left(\sqrt{-1}{t}^{\prime }x\right)d{t}^{\prime }\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{r}_n(t^{\prime })exp\left(\sqrt{-1}{t}^{\prime }x\right)d{t}^{\prime }=\check{r_n}(x)=h_n(x),\hfill \end{array}$$

where $t^{\prime }=-t$. Hence, $h_n\in L^2(\mathbb{R})$. On the other hand,$$\begin{array}{cc}\hfill h(x)& =\underset{n\to \infty }{lim}\frac{1}{\sqrt{2\pi }}{\int }_{-n}^{n}r(t)exp\left(\sqrt{-1}tx\right)dt\hfill \\ \hfill & =\underset{n\to \infty }{lim}\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{r}_n(t)exp\left(\sqrt{-1}tx\right)dt\hfill \\ \hfill & =\underset{n\to \infty }{lim}{h}_n(x).\hfill \end{array}$$

Therefore $h\in L^2(\mathbb{R})$. $\square$

Let us define $k_a(·):=\sqrt{2\pi }\sigma k_G(·,a)=exp\left(-\frac{{(·-a)}^2}{2{\sigma }^2}\right)\in {\mathcal{H}}_G$ for $a\in \mathbb{R}$. Now, we prove that $k_a\notin \text{Ran}(C_{\mathit{XX}})$ for any $a\in \mathbb{R}$. This implies that $C_{\mathit{XX}}$ is not surjective.

Proposition 11

For any $a\in \mathbb{R}$, $k_a\in {\mathcal{H}}_G\backslash \text{ran}(C_{\mathit{XX}})$.

Proof

Suppose that there exists $g\in {\mathcal{H}}_G$ such that $C_{\mathit{XX}}g=k_a$. Then, for any $f\in {\mathcal{H}}_G$,(12) $$\begin{array}{c}\hfill {〈k_a,f〉}_{{\mathcal{H}}_G}={〈C_{\mathit{XX}}g,f〉}_{{\mathcal{H}}_G}.\end{array}$$(12)

Let us put $k(·)=\sqrt{2\pi }\sigma k_G(·,0)=exp\left(-\frac{{(·-0)}^2}{2{\sigma }^2}\right)$. From Proposition 4, $\widehat{k}(t)=\sigma exp\left(-\frac{{\sigma }^2}{2}{t}^2\right)$. Then, using Equation (7) and Proposition 6, the left hand side of Equation (12) equals$$\begin{array}{cc}\hfill {\int }_{-\infty }^{\infty }{\widehat{k}}_a(t)\overline{\widehat{f}(t)}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt& ={\int }_{-\infty }^{\infty }exp\left(-\sqrt{-1}at\right)\widehat{k}(t)\overline{\widehat{f}(t)}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt\hfill \\ \hfill & =\sigma {\int }_{-\infty }^{\infty }exp\left(-\sqrt{-1}at\right)\overline{\widehat{f}(t)}dt.\hfill \end{array}$$

The right hand side of Equation (12) is equal to$$\begin{array}{cc}\hfill E\left[g(X)f(X)\right]& ={\int }_{-\infty }^{\infty }g(x)f(x)p(x)dx={〈gp,f〉}_{L^2(\mathbb{R})}.\hfill \end{array}$$

Thus, Equation (12) is equivalent to the following equation:(13) $$\begin{array}{c}\hfill {〈gp,f〉}_{L^2(\mathbb{R})}=\sigma {\int }_{-\infty }^{\infty }exp\left(-\sqrt{-1}at\right)\overline{\widehat{f}(t)}dt.\end{array}$$(13)

Let us define $h_{n,a}(x):=h_n(x-a)$ and $h_a(x)=h(x-a)$. Then $h_{n,a},h_a\in L^2(\mathbb{R})$. It is easy to see that $\Vert h_{n,a}-h_a{\Vert }_2=\Vert h_n{-h\Vert }_2={\Vert r_n-r\Vert }_2\to 0$ as $n\to \infty$. Hence ${\displaystyle \underset{n\to \infty }{lim}{h}_{n,a}=h_a}$ in $L^2(\mathbb{R})$. Since ${\widehat{h}}_{n,a}(t)=exp(-\sqrt{-1}at){\widehat{h}}_n(t)$ by Proposition 6, we have$$\begin{array}{cc}\hfill {\int }_{-\infty }^{\infty }{\left|{\widehat{h}}_{n,a}(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt& ={\int }_{-\infty }^{\infty }{\left|{\widehat{h}}_n(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt={\int }_{-\infty }^{\infty }{\left|r_n(t)\right|}^{2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt\hfill \\ \hfill & =2{\int }_1^n\frac{1}{t^2}exp\left(\frac{{\sigma }^2}{2}{t}^2\right)dt<\infty ,\hfill \end{array}$$

which indicates that $h_{n,a}\in {\mathcal{H}}_G$. Substituting $h_{n,a}$ for f, Equation (13) becomes(14) $$\begin{array}{c}\hfill {〈gp,h_{n,a}〉}_{L^2(\mathbb{R})}=\sigma {\int }_{-\infty }^{\infty }exp\left(-\sqrt{-1}at\right)\overline{{\widehat{h}}_{n,a}(t)}dt.\end{array}$$(14)

If n goes to infinity, the left hand side of Equation (14) becomes ${⟨gp,h_a⟩}_{L^2(\mathbb{R})}\in \mathbb{R}$. On the other hand, the right hand side of Equation (14) becomes$$\begin{array}{cc}\hfill \sigma {\int }_{-\infty }^{\infty }exp\left(-\sqrt{-1}at\right)\overline{exp(-\sqrt{-1}at){\widehat{h}}_n(t)}dt& =\sigma {\int }_{-\infty }^{\infty }\overline{{\widehat{h}}_n(t)}dt\hfill \\ \hfill & =\sigma {\int }_{-\infty }^{\infty }\overline{r_n(t)}dt\hfill \\ \hfill & =2\sigma {\int }_1^n\frac{1}{t}dt\to \infty (n\to \infty ).\hfill \end{array}$$

This is a contradiction. Therefore, there exists no $g\in {\mathcal{H}}_G$ such that $C_{\mathit{XX}}g=k_a$. This completes the proof. $\square$

7. Supplementary material

Supplementary material for this article can be accessed here http://dx.doi.org/10.1080/23311835.2018.1447220.

Additional information

Funding

Kazunori Nakamoto was partially supported by JSPS KAKENHI [grant numbers JP23540044, JP15K04814].

Notes on contributors

Hisashi Johno

Hisashi Johno is a PhD student at the Department of Mathematical Sciences, Faculty of Medicine, University of Yamanashi, Japan. His current research interests include probability theory and interpretable machine learning.

Kazunori Nakamoto

Kazunori Nakamoto is a professor of mathematics at Center for Medical Education and Sciences, Faculty of Medicine, University of Yamanashi, Japan. His main research interests include algebraic geometry, invariant theory, and the moduli of representations.

Tatsuhiko Saigo

Tatsuhiko Saigo is an associate professor of probability and statistics at Center for Medical Education and Sciences, Faculty of Medicine, University of Yamanashi, Japan. His research fields include probability theory, statistics, and applied mathematics.