Finding the strong defining hyperplanes of production possibility set with constant returns to scale using the linear independent vectors

Abstract

Production Possibility Set (PPS) is defined as the set of all inputs and outputs of a system in which inputs can produce outputs. In Data Envelopment Analysis (DEA), it is highly important to identify the defining hyperplanes and especially the strong defining hyperplanes of the empirical PPS. Although DEA models can determine the efficiency of a Decision Making Unit (DMU), but they cannot present efficient frontiers of PPS. In this paper, we propose a new method to determine all strong efficient (Pareto-efficient) DMUs and strong defining hyperplanes of the PPS with constant returns to scale including the Pareto-efficient DMUs. Furthermore, we apply the newly proposed method to find the normal vectors or gradient of the strong defining hyperplanes of the PPS including strong efficient DMUs which are under evaluation. Consequently, the equations of these hyperplanes are determined. To illustrate the applicability of the proposed method, some numerical examples are finally provided. Our method can be easily implemented using existing packages for operation research, such as GAMS.

Keywords:

• data envelopment analysis (DEA)
• decision making unit (DMU)
• production possibility set (PPS)
• defining hyperplane
• Pareto efficient
• normal vector

Public interest statement

In this paper, a method to evaluate DMUs and finding all Pareto-efficient DMUs and strong defining hyperplanes of the PPS has been introduced.

Some of the applications of strong defining hyperplanes are: marginal discussions, marginal rates, sensitivity analysis, returns to scale and the efficiency analysis of DMUs.

1. Introduction

Data Envelopment Analysis (DEA) is a non-parametric method which is used for measuring the relative efficiency of a set of Decision Making Units (DMUs). In order to measure the relative efficiency of DMUs, input-oriented or output-oriented CCR or BCC envelopment models can be used (Banker, Charens, & Cooper, 1984; Charnes, Cooper, & Rhodes, 1978). Of course, there are some other models in DEA by which the relative efficiency of the DMUs can be measured (Cooper, Li, Seiford, & Tone, 1999).

The main problem in standard models of DEA is the presence of weak efficient frontiers. These frontiers are identified by adopting zero weights for the input and output factors. Although due to the compensatory structure of these models, there would be many alternative optimal solutions and the zero weights might go unnoticed. Therefore, identification and determination of strong defining hyperplanes, or in other words, the hyperplanes with corresponding strong efficient frontiers become highly significant.

This issue was first raised by Charnes et al. (1978). Yu, Wei, Brockett, and Zhou (1996) analysed the structural properties of PPS efficiency frontiers in a generalized DEA model. By using their method, all DMUs on a hyperplane can be identified, so that an analysis on DEA hyperplanes may be offered (Yu et al., 1996). Jahanshahloo, Hosseinzadeh Lotfi, ZhianiRezai and Rezai Balf (2007) presented an algorithm for finding PPS strong defining hyperplanes. Although their method was based on pure mathematics, by using the hyperplanes identified in this method, all members or elements reference set of a DMU can be determined (Jahanshahloo et al., 2007). Another different method is introduced by Jahanshahloo, Shirzadi and Mirdehghan (2009). In their paper, a three-stage algorithm is introduced which using the solutions of additive model and multiplier form of BCC model, the strong efficient hyperplanes are identified (Jahanshahloo et al., 2009). Amirtaymouri and Korrostami (2012) found all linearly independent strong defining hyperplanes (LISDHs) of the PPS passing through a specific DMU. To do so, they defined corresponding to each efficient unit, a perturbed inefficient unit and by solving at most $m+s$ linear programs, identified the hyperplanes (Amirteimoori & Kordrostami, 2012). All of the studies mentioned above were conducted using radial models. There are also some studies which used non-radial models, especially Slack Based Measure (SBM) (Aparicio & Pastor, 2013; Hadi Vencheh, Jablonsky, & Esmaeilzadeh, 2015; Tone & Tsutsui, 2010).

In this paper, for each given DMU of $T_C$, the corresponding problem in the offered model is formed, and by solving it, the Pareto-efficient or nonPareto-efficient nature of the DMU under evaluation is determined. If the DMU under evaluation is Pareto-efficient, then the production possible set, $T_C$, strong defining hyperplanes passing through the origin which including the pareto-efficient DMU under evaluation can be identified. Also, the normal vectors and equations of these defining hyperplanes can be characterized.

2. CCR model and defining hyperplanes

Suppose we have n DMUs, where each $DM{U}_j$$(j=1,\dots ,n)$, produces the same s outputs $y_{\mathit{rj}}$$(r=1,\dots ,s)$, and using the same m inputs $x_{\mathit{ij}}$ (i=1,...,m). The PPS corresponding to these DMUs are defined as follows:(1) $$\begin{array}{c}\hfill T_C=\{(x,y)|x\ge \sum _{j=1}^n{\lambda }_j{x}_j,y\le \sum _{j=1}^n{\lambda }_j{y}_j,{\lambda }_j\ge 0,j=1,\dots ,n\}.\end{array}$$(1)

In fact, linear combinations of inputs and outputs form the frontier of PPS. These combinations are indeed the supporting (or defining) hyperplanes of the PPS. CCR model which first proposed by Charnes et al. (1978) is developed by Tc in the following format:(2) $$\begin{array}{cc}& min\theta \hfill \\ \hfill & s.t\hfill \\ \hfill & \theta x_{\mathit{ip}}-\sum _{j=1}^n{\lambda }_j{x}_{\mathit{ij}}\ge 0i=1,\dots ,m\hfill \\ \hfill & \sum _{j=1}^n{\lambda }_j{y}_{\mathit{rj}}\ge y_{\mathit{rp}}r=1,\dots ,s\hfill \\ \hfill & {\lambda }_j\ge 0j=1,\dots ,n\hfill \end{array}$$(2)

where $x_{\mathit{ip}}$ (i=1, ...,m) and $y_{\mathit{rp}}$ (r=1, ...,s) are the inputs and outputs of the unit under evaluation, respectively. This model is called the envelopment form of the CCR model. The corresponding dual model of (2(2) $$\begin{array}{cc}& min\theta \hfill \\ \hfill & s.t\hfill \\ \hfill & \theta x_{\mathit{ip}}-\sum _{j=1}^n{\lambda }_j{x}_{\mathit{ij}}\ge 0i=1,\dots ,m\hfill \\ \hfill & \sum _{j=1}^n{\lambda }_j{y}_{\mathit{rj}}\ge y_{\mathit{rp}}r=1,\dots ,s\hfill \\ \hfill & {\lambda }_j\ge 0j=1,\dots ,n\hfill \end{array}$$(2) ) is as follows:(3) $$\begin{array}{cc}& max\sum _{r=1}^s{u}_r{y}_{\mathit{rp}}\hfill \\ \hfill & s.t\hfill \\ \hfill & \sum _{i=1}^m{v}_i{x}_{\mathit{ip}}=1\hfill \\ \hfill & \sum _{r=1}^s{u}_r{y}_{\mathit{rj}}-\sum _{i=1}^m{v}_i{x}_{\mathit{ij}}\le 0j=1,\dots ,n\hfill \\ \hfill & u_r\ge 0,v_i\ge 0r=1,\dots ,s,i=1,\dots ,m\hfill \end{array}$$(3)

Optimal solutions of model (3) are corresponding to the coefficient of the supporting hyperplanes of the PPS. These hyperplanes are identified by the following equations:(4) $$\begin{array}{c}\hfill \sum _{r=1}^s{u}_r^{\ast }{y}_{\mathit{rj}}-\sum _{i=1}^m{v}_i^{\ast }{x}_{\mathit{ij}}=0,j=1,\dots ,n\end{array}$$(4)

where $v_i^{\ast }$ (i=1,..., m) and $u_r^{\ast }$ (r=1,..., s) are the optimal solutions of model (3). Suppose that $U^{{\ast }^T}=(u_1^{\ast },\dots ,u_s^{\ast })$ and $V^{{\ast }^T}=(v_1^{\ast },\dots ,v_m^{\ast })$. If ${\sum }_{r=1}^s{u}_r^{\ast }{y}_{\mathit{rp}}=U^{{\ast }^T}{Y}_p=1$ and the values for all coefficients are non-zero, then $DM{U}_p$ is called Strong Efficient or Pareto Efficient and a part of the strong efficiency frontier is made with these coefficients. These hyperplanes are called strong defining hyperplanes. If ${\sum }_{r=1}^s{u}_r^{\ast }{y}_{\mathit{rp}}=U^{{\ast }^T}{Y}_p=1$ and in some optimal solutions (3) some variables to be zero, then $DM{U}_p$ is called Weak Efficient or nonpareto Efficient. Weak efficiency occurs when the optimal objective of (3) is one and at least one coefficient of each optimal solution is zero. These weights identify the weakly efficient hyperplanes of the PPS. The efficient frontier is the set of all points (actual or virtual) with efficiency score equal to unity.

3. A model for determining defining hyperplanes

As mentioned in the previous section, the PPS corresponding to the CCR model is a set in the form of $T_c$. This set is a set with $m+s$ dimension. The defining hyperplanes of $T_c$ are the sets with a dimension of $m+s-1$. Therefore, if a DMU is lies on a face with $m+s-1$ dimension, then this DMU will be lie on one of the hyperplanes forming the frontier of the PPS. Equations for these hyperplanes can be obtained through solving model (3) and via (4). However, since Model (3) has alternative optimal solutions, without determining all optimal solutions, it is not possible to ensure that the hyperplane on which the DMU under evaluation is located is strong efficient.

Since the defining hyperplanes of $T_c$ are $m+s-1$ dimensional sets, we can find $m+s-1$ linearly independent vector of $T_c$ in such a way that every one of these vectors becomes orthogonal to normal vector of these hyperplanes. Suppose these vectors are in the form of ${[d_x^k,d_y^k]}^T$ in which $d_x^k$ is m-vector, $d_y^k$ is s-vector and ${[d_x^k,d_y^k]}^T$ is $(m+s)$-vector. If we consider the normal vector defining hyperplanes of $T_c$ as $(-{\mathit{V}}^{{\ast }^{\mathit{T}}},{\mathit{U}}^{{\ast }^{\mathit{T}}})$ which is obtained from solving model (3), then we must have :$$\begin{array}{c}\hfill (-{\mathit{V}}^{\mathbf{\ast }\mathit{T}},{\mathit{U}}^{\mathbf{\ast }\mathit{T}})\times \left(\begin{array}{c}{d}_x^k\\ d_y^k\end{array}\right)=0\end{array}$$

Suppose a DMU is located on a number defining hyperplanes of $T_c$. We know that on each of the defining hyperplanes, there are infinite numbers of vectors. From these infinite numbers of vectors, we select the vectors that along with the other selected vectors on the other hyperplanes binding to the DMU under evaluation form $m+s-1$ linearly independent vectors.

The aim of selecting the above-mentioned vectors is to find a direction for movement from the DMU under evaluation to these defining hyperplane in such a way that it is possible to stay on $T_c$. In order to locate such directions, the following model is offered:(5) $$\begin{array}{cc}& maxz=U^T{y}_p\hfill \\ \hfill & s.t\hfill \\ \hfill & \sum _{j=1}^n{\lambda }_j{x}_j\le x_p+{\epsilon }_k{d}_x^{k}k=1,\dots ,m+s-1(5-a)\hfill \\ \hfill & \sum _{j=1}^n{\lambda }_j{y}_j\ge y_p-{\epsilon }_k{d}_y^{k}k=1,\dots ,m+s-1(5-b)\hfill \\ \hfill & U^T{d}_y^k-V^T{d}_x^k=0k=1,\dots ,m+s-1(5-c)\hfill \\ \hfill & V^T{x}_p=1\hfill \\ \hfill & U^T{y}_j-V^T{x}_j\le 0j=1,\dots ,n\hfill \\ \hfill & U\ge 1_s·\epsilon \hfill \\ \hfill & V\ge 1_m·\epsilon \hfill \\ \hfill & {\lambda }_j\ge 0j=1,\dots ,n\hfill \end{array}$$(5)

where $\epsilon$ a non-Archimedean number and $1_m$ and $1_s$ are m-vector and s-vector respectively, with each component equal to one. ${\epsilon }_k>0(kϵ\{1,\dots ,m+s-1\})$ is a small number where we move from the DMU under investigation in the direction of vector ${(d_x^k,d_y^k)}^T={(d_{x_1}^k,\dots ,d_{x_m}^k,d_{y_1}^k,\dots ,d_{y_s}^k)}^T$ with a step length of ${\epsilon }_k$.

In model (5), constraints (5-a) and (5-b) ensure that the movement is in $T_c$. Constraints (5-c) are positioned in such a way that vectors ${(d_x^k,d_y^k)}^T$ are orthogonal to the normal vector of the hyperplane on which the $DM{U}_p$ under evaluation is located. In fact, constraints (5-c) can be as many as the number of the vectors on the mentioned hyperplane, but we will show later that these vectors have a special structure, and only $m+s-1$ linearly independent vectors are enough for solving model (5) as shown below:

Suppose that$$\begin{array}{c}\hfill D_{\mathit{ab}}^k=\left[\begin{array}{c}{d}_x^k\\ d_y^k\end{array}\right]\end{array}$$

Then according to constraints (5-c), it is easily possible to select $(m+s)$-component vectors ${\mathit{D}}_{\mathit{ab}}^k$ in the following manner:(6) $$\begin{array}{c}\hfill {\mathit{D}}_{\mathit{ab}}^k={\left(\begin{array}{c}0\\ ⋮\\ 1\\ ⋮\\ 0\\ \dots \dots \\ 0\\ ⋮\\ t_b^a\\ ⋮\\ 0\end{array}\right)}_{m+s}\end{array}$$(6)

where number 1 is the a-th $(\mathit{a}ϵ\{1,\dots ,m\}$ row and $t_b^a=\frac{v_a}{u_b}$ is the $(m+b)$-th $(bϵ\{1,\dots ,s\}$ row of ${\mathit{D}}_{\mathit{ab}}^k$ vector, and the value of the other components are zero. With this choice, the total of the possible cases for vector ${\mathit{D}}_{\mathit{ab}}^k$ will be equal to $m\times s$.

Now, it is enough from the $m\times s$ constructed vectors ${\mathit{D}}_{\mathit{ab}}^k$, we choose $m+s-1$ linearly independent vectors and set them in model (5). By solving it, the strong defining hyperplanes corresponding to $DM{U}_p$ is achieved.

By determining $d_x^k$ and $d_y^k$ vectors in the form of ${\mathit{D}}_{\mathit{ab}}^k$ in (6) and choosing $m+s-1$ linear independent vectors of it and by inserting the selected linear independent vectors in model (5), the constraint (5-c) will be a redundant constraint. Therefore, by inserting $m+s-1$ selected linearly independent vectors in model (5), the constraints (5-c) can be omitted and instead it constraints $t_b^a\times u_b-v_a=0$ contracted and solved the obtained model.

Theorem 1

From $m\times s$ vectors with $(m+s)$-components defined as (6), one can choose $m+s-1$ linearly independent vectors.

Proof

By using $m\times s$ vectors with $(m+s)$-components obtained from (6), matrix D where is an $(m+s)\times (m\times s)$ matrix, we form as follows :(7) $$\begin{array}{c}\hfill \mathit{D}={\left[\begin{array}{c}{D}_{11}^k{D}_{12}^k\cdots D_{1s}^k{D}_{21}^k\cdots {\mathit{D}}_{2s}^k\cdots D_{\mathit{ms}}^k\end{array}\right]}_{(m+s)\times (m\times s)}\end{array}$$(7)

By inserting(8) $$\begin{array}{c}\hfill t_b^a=\frac{v_a}{u_b}(a=1,\dots ,m,b=1,\dots ,s)\end{array}$$(8)

matrix D can be written in the following manner:(9) $$\begin{array}{c}\hfill \mathit{D}={\left[\begin{array}{cccccccccccccc}1& 1& \cdots & 1& 0& 0& \cdots & 0& \cdots \cdots & 0& 0& \cdots & 0& \\ 0& 0& \cdots & 0& 1& 1& \cdots & 1& \cdots \cdots & 0& 0& \cdots & 0& \\ 0& 0& \cdots & 0& 0& 0& \cdots & 0& \cdots \cdots & 0& 0& \cdots & 0& \\ ⋮& ⋮& \cdots & ⋮& ⋮& ⋮& \cdots & ⋮& \cdots \cdots & ⋮& ⋮& \cdots & ⋮& \\ 0& 0& \cdots & 0& 0& 0& \cdots & 0& \cdots \cdots & 1& 1& \cdots & 1& \\ \cdots & \cdots & \dots & \cdots & \cdots & \cdots & \dots & \cdots & \dots \dots & \cdots & \cdots & \dots & \cdots .& \\ \frac{v_1}{u_1}& 0& \cdots & 0& \frac{v_2}{u_1}& 0& \cdots & 0& \cdots \cdots & \frac{v_m}{u_1}& 0& \cdots & 0& \\ 0& \frac{v_1}{u_2}& \cdots & 0& 0& \frac{v_2}{u_2}& \cdots & 0& \cdots \cdots & 0& \frac{v_m}{u_2}& \cdots & 0& \\ ⋮& ⋮& \cdots & ⋮& ⋮& ⋮& \cdots & ⋮& \cdots \cdots & ⋮& ⋮& \cdots & ⋮& \\ 0& 0& \cdots & \frac{v_1}{u_s}& 0& 0& \cdots & \frac{v_2}{u_s}& \cdots \cdots & 0& 0& \cdots & \frac{v_m}{u_s}\end{array}\right]}_{(m+s)\times (m\times s)}\end{array}$$(9)

Now it is enough to show that:(10) $$\begin{array}{c}\hfill \text{Rank}(\mathit{D})=m+s-1\end{array}$$(10)

In order to prove (10), the following cases are considered.

Case 1: If $m=1$ and $s=1$, then matrix D is a $2\times 1$ matrix, and in this case, the accuracy of statement (10) is obvious.

Case 2: If ( $m=1$ and $s\ge 2$ ) or ( $s=1$ and $m\ge 2$ ) since in this case $m\times s=m+s-1$ as well as the number of rows in the resulting matrix D is equal to the number of columns plus one, then by omitting any row of matrix D, the determinant of the remaining matrix which is equal to $(m+s-1)\times (m+s-1)$ would not be equal to zero, and, as a result, Rank(D)=$m+s-1$, and so the statement (10) will be correct in this case as well.

Case 3: If $m=2$ and $s=2$, then Rank(D)=$m+s-1$, since if the i-th row of this matrix is considered to be $R_i$, then we will have:(11) $$\begin{array}{c}\hfill -\sum _{i=1}^2{v}_i{R}_i+\sum _{j=1}^2{u}_j{R}_{2+j}=0.\end{array}$$(11)

Therefore, the correctness of statement (10) is obvious.

Case 4: If $m>2$ and $s>2$, then since in this case $m+s<m\times s$ and$$\begin{array}{c}\hfill \text{Rank}(\mathit{D})\le min\{m+s,m\times s\}=m+s\end{array}$$

and(12) $$\begin{array}{c}\hfill -\sum _{i=1}^m{v}_i{R}_i+\sum _{j=1}^s{u}_j{R}_{m+j}=0.\end{array}$$(12)

Therefore, it is obvious that $\text{Rank}(\mathit{D})\ne m+s$, and as a result the rank of matrix D can be at last $m+s-1$. In order to prove Rank(D)=$m+s-1$, we construct a matrix $(m+s-1)\times (m+s-1)$ such as ${\mathit{D}}^{\prime }$ from matrix D in the following manner.

First consider the following matrix:$$\begin{array}{c}\hfill {\left[{\mathit{D}}_{11}^k{\mathit{D}}_{21}^k{\mathit{D}}_{31}^k\cdots {\mathit{D}}_{m1}^k{\mathit{D}}_{12}^k\cdots {\mathit{D}}_{1s}^k\right]}_{(m+s)\times (m+s-1)}\end{array}$$

and by omitting row $m+1$ from the above-mentioned matrix, the obtained matrix which is an $(m+s-1)\times (m+s-1)$ matrix is selected as matrix ${\mathit{D}}^{\prime }$. It is now enough to show that $|{\mathit{D}}^{\prime }|\ne 0$.

We have:$$\begin{array}{cc}\hfill |{\mathit{D}}^{\prime }|& =\frac{v_1^{s-1}}{u_2\cdots u_s}\times \left|\begin{array}{cc}{I}_m& 0\\ 0& I_{s-1}\end{array}\right|\hfill \\ \hfill |{\mathit{D}}^{\prime }|& =\frac{v_1^{s-1}}{u_2\cdots u_s}\times 1\hfill \end{array}$$

It is obvious that $|{\mathit{D}}^{\prime }|\ne 0$. (since, according to model (5), $U^{\ast }>0$, $V^{\ast }>0$), and it completes the proof.

Note that in proving the above-mentioned theorem, the choice of matrix ${\mathit{D}}^{\prime }$ from matrix D is not unique, and some other cases can be considered as well.

It should be mentioned that, we can choose $m+s-1$ linearly independent vectors out of the available $m+s$ component vectors of ${\mathit{Z}}_{\mathit{ab}}^k$ which are defined in the following manner:(13) $$\begin{array}{c}\hfill {\mathit{Z}}_{\mathit{ab}}^k={\left(\begin{array}{c}0\\ ⋮\\ l_b^a\\ ⋮\\ 0\\ \cdots \cdots \\ 0\\ ⋮\\ 1\\ ⋮\\ 0\end{array}\right)}_{m+s}\end{array}$$(13)

where 1 is placed in the $(m+b)$-th $(\mathit{b}ϵ\{1,\dots ,s\})$ row and $l_b^a=\frac{u_b}{v_a}$ is placed the a-th $(\mathit{a}ϵ\{1,\dots ,m\})$ row of the vector ${\mathit{Z}}_{\mathit{ab}}^k$, and all of the other components are zero.

By considering possible cases in choosing $m+s-1$ linearly independent vectors and putting them in the model (5), it can be normal vectors and equations all of PPS strong defining hyperplanes with constant returns to scale which including the strong efficient DMUs under evaluation, are determined.

4. Numerical examples

Example 4.1

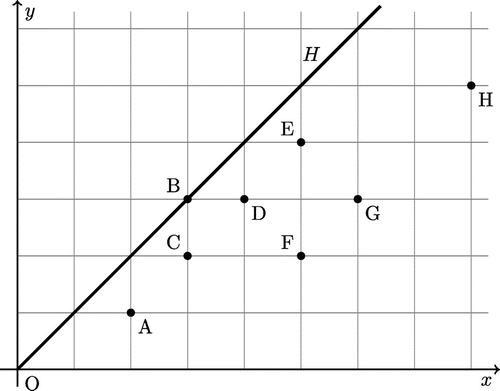
Consider a system of seven DMUs as shown in Figure 1. Data is given in Table 1 (see Cooper, Selford, & Tone, 2002).

 

Table 1. Data set for the numerical Example 4.1

	${\text{DMU}}_A$	${\text{DMU}}_B$	${\text{DMU}}_C$	${\text{DMU}}_D$	${\text{DMU}}_E$	${\text{DMU}}_F$	${\text{DMU}}_G$	${\text{DMU}}_F$
x	2	3	3	4	5	5	6	8
y	1	3	2	3	4	2	3	5

Figure 1. Numerical Example 4.1.

The resulting strong defining hyperplane by Cooper et al. (2002) is as follows.$$\begin{array}{c}\hfill H:y-x=0\end{array}$$

Since $m=1$ and $s=1$, So $m+s-1=1$. The linearly independent vector, ${\mathbf{Z}}_{11}^1$, is selected using (13) in the following manner:(14) $$\begin{array}{c}\hfill {\mathit{Z}}_{11}^1=\left(\begin{array}{c}{d}_{x_1}^1\\ d_{y_1}^1\end{array}\right)=\left(\begin{array}{c}\frac{u_1}{v_1}\hfill \\ 1\hfill \end{array}\right)\end{array}$$(14)

or supposing $l_1^1=\frac{u_1}{v_1}$, we have:(15) $$\begin{array}{c}\hfill {\mathit{Z}}_{\mathbf{11}}^{\mathbf{1}}=\left(\begin{array}{c}{l}_1^1\\ 1\end{array}\right).\end{array}$$(15)

By inserting ${\mathbf{Z}}_{11}^1$ in model (5), each of the DMUs in Table 1 is evaluated supposing $\epsilon =0.0001$ and ${\epsilon }_1=0.00001$. The obtained results are shown up to seven decimal digits in Table 2.

Table 2. The obtained results based on model (5): Data set for the numerical Example 4.1

Variables	${\text{DMU}}_A$	${\text{DMU}}_B$	${\text{DMU}}_C$	${\text{DMU}}_D$	${\text{DMU}}_E$	${\text{DMU}}_F$	${\text{DMU}}_G$	${\text{DMU}}_H$
z	0.5000000	1.0000000	0.6666666	0.7500000	0.8000000	0.4000000	0.5000000	0.6250000
$u_1$	0.5000000	0.3333333	0.3333333	0.2500000	0.2000000	0.2000000	0.1666667	0.1250000
$v_1$	0.5000000	0.3333333	0.3333333	0.2500000	0.2000000	0.2000000	0.1666667	0.1250000
$l_1^1$	1.0000000	1.0000000	1.0000000	1.0000000	1.0000000	1.0000000	1.0000000	1.0000000

The obtained results in Table 2 show that ${\text{DMU}}_B$ is Pareto-efficient and located on PPS strong defining hyperplane with constant returns to scales obtained from the seven DMUs of A, B, C, D, E, F, G and H. By examining at column ${\text{DMU}}_B$ in Table 2, we see that the obtained normal vector$$\begin{array}{c}\hfill (-v_1,u_1)=(-0.3333333,0.3333333)\end{array}$$

is the normal vector of defining hyperplane including ${\text{DMU}}_B$ and origin. Due to the obtained normal vector and considering (4), the equation of the strong defining hyperplane including Pareto efficient ${\text{DMU}}_B$ is in access. We have:$$\begin{array}{c}\hfill 0.3333333y-0.3333333x=0.\end{array}$$

and therefore the equation strong defining hyperplane can be written in the following manner: (The same strong defining hyperplane H is in Figure 1).$$\begin{array}{c}\hfill y-x=0.\end{array}$$

According to the obtained results in columns DMUs A, C, D, E, F, G and H, we observe that DMUs A, C, D, E, F, G and H are not Pareto-efficient or strong efficient.

As can be seen, the results of the proposed model is same as the Cooper et al. (2002).

Example 4.2

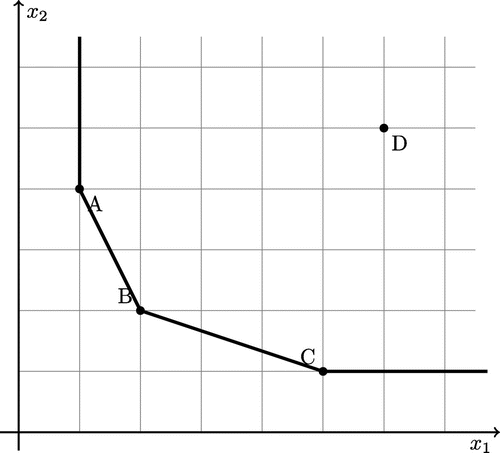
Consider a system of four DMUs as shown in Figure 2. Data is given in Table 3 (see Jahanshahloo et al., 2007).

 

Table 3. Data set for the numerical Example 4.2

	${\text{DMU}}_A$	${\text{DMU}}_B$	${\text{DMU}}_C$	${\text{DMU}}_D$
$x_1$	1	2	5	6
$x_2$	4	2	1	5
$y_1$	1	1	1	1

Figure 2. Numerical Example 4.2.

Solution: Since $m=2$ and $s=1$, then $m+s-1=2+1-1=2$. The two linearly independent vectors of $D_{11}^1$ and $D_{21}^2$ are selected using (6) in the following manner:(16) $$\begin{array}{c}\hfill {\mathit{D}}_{11}^1=\left(\begin{array}{c}{d}_{x_1}^1\\ d_{x_2}^1\\ d_{y_1}^1\end{array}\right)=\left(\begin{array}{c}1\hfill \\ 0\hfill \\ \frac{v_1}{u_1}\hfill \end{array}\right),{\mathit{D}}_{21}^2=\left(\begin{array}{c}{d}_{x_1}^2\\ d_{x_2}^2\\ d_{y_1}^2\end{array}\right)=\left(\begin{array}{c}0\hfill \\ 1\hfill \\ \frac{v_2}{u_1}\hfill \end{array}\right)\end{array}$$(16)

or supposing $t_1^a=\frac{v_a}{u_1}$ , $(a=1,2)$ , we have:(17) $$\begin{array}{c}\hfill {\mathit{D}}_{11}^1=\left(\begin{array}{c}1\\ 0\\ t_1^1\end{array}\right),{\mathit{D}}_{21}^2=\left(\begin{array}{c}0\\ 1\\ t_1^2\end{array}\right)\end{array}$$(17)

By inserting vectors $D_{11}^1$ and $D_{21}^2$ in model (5), each of the DMUs in Table 3 are evaluated supposing $\epsilon =0.00001$ and ${\epsilon }_1={\epsilon }_2=0.000001$ . The obtained results up to seven decimal digits are shown in Table 4.

Table 4. The obtained results based on model (5): Data set for the numerical Example 4.2

Variables	${\text{DMU}}_A$	${\text{DMU}}_B$	${\text{DMU}}_C$	${\text{DMU}}_D$
z	1.0000000	1.0000000	1.0000000	0.3809524
$v_1$	0.3333333	0.3333333	0.1250000	0.0476190
$v_2$	0.1666667	0.1666667	0.3750000	0.1428571
$u_1$	1.0000000	1.0000000	1.0000000	0.3809524
$t_1^1$	0.3333333	0.3333333	0.1250000	0.1250000
$t_1^2$	0.1666667	0.1666667	0.3750000	0.3750000

The obtained results in Table 4 show that ${\text{DMU}}_A$, ${\text{DMU}}_B$ and ${\text{DMU}}_C$ are pareto-efficient and are located on PPS defining hyperplanes with constant returns to scales obtained from the four DMUs of A, B, C and D. By looking at columns ${\text{DMU}}_A$ and ${\text{DMU}}_B$ in Table 4, we observe that the obtained normal vector$$\begin{array}{c}\hfill (-v_1,-v_2,u_1)=(-0.3333333,-0.1666667,1.0000000)\end{array}$$

is the normal vector of defining hyperplane including ${\text{DMU}}_A$, ${\text{DMU}}_B$ and origin. Due to obtained normal vector and considing (4), the equation of the strong defining hyperplane including pareto-efficient DMUs A , B and origin is in access. We have:$$\begin{array}{c}\hfill 1.0000000y-0.3333333x_1-0.16666677x_2=0,\end{array}$$

and therefore the equation strong defining hyperplane can be written in the following manner:$$\begin{array}{c}\hfill 6y-2x_1-x_2=0.\end{array}$$

Similarly, by considering the column ${\text{DMU}}_c$, the equation of the strong defining hyperplane includes pareto-efficient DMUs B, C and origin can be obtained as follows:$$\begin{array}{c}\hfill 8y-x_1-3x_2=0.\end{array}$$

According to the obtained results in column ${\text{DMU}}_D$, we observe that ${\text{DMU}}_D$ is not pareto-efficient.

5. Conclusion

This paper proposed a method to evaluate DMUs and find all Pareto-efficient DMUs and strong defining hyperplanes of the PPS with constant returns to scale including the Pareto-efficient DMUs. The proposed model uses the concept of the normal vectors of the hyperplanes instead of determining all optimal solutions for the multiplicative form of the CCR model and specifying positive weights. In the present paper, by only solving one problem for each DMU using model (5), the Pareto-efficient DMUs, as well as the normal vectors and equations strong defining hyperplanes of the PPS with constant returns to scale including the Pareto-efficient DMUs under evaluation, are determined. However, in the documented papers, for example in Jahanshahloo et al. (2009), just the strongly efficient hyperplanes are identified by offering a three-step algorithm and by solving the additive and multiplicative of the BCC form, or in another example such as Amirteimoori and Kordrostami (2012), by solving m + s linear programming problems, only the defining hyperplanes binding in a given DMU are determined.

Note that the model (5) is a non-linear model, and so one may modify it in such a way to be a linear model.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Nader Rafati-Maleki

Nader Rafati Maleki is currently a PhD student at Department of Mathematics, Research and Science Branch, Islamic Azad University, Tehran, Iran. His research interests include operation research and data envelopment analysis.

Mohsen Rostamy-Malkhalifeh

Mohsen Rostamy-Malkhalifeh is an associated professor of Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran. He has received his PhD in DEA from, Science and Research Branch, Islamic Azad University, Tehran, Iran. His researches includes DEA, decision making in industry and economic, supply chain and its scopes, application of DEA and supply chain in management.

F. Hosseinzadeh Lotfi

F. Hosseinzadeh Lotfi is a full Professor at the Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran. His research interests include operation research, data envelopment analysis, MCDM and fuzzy.