Do university students really need to be taught by the best instructors to learn?

Abstract

The present study sought to contribute to the discussion on linearity relationship between teaching and learning at university level. Although the basic assumption that students who are taught by effective instructors learn better is acknowledged, defining the effective instructor seems not so simple. This study attempted to (i) cluster instructors with respect to instructional practices rated by students, and (ii) identify different instructional profiles that may be associated with high learning, rather than just focusing on relationship between instructional practices and learning. Using student ratings from 625 courses in a university setting, subgroups were defined in terms of instructional practices via a segmentation approach. Then, distinct profiles showing high instructional effectiveness were extracted by investigating learning level differences as measured by the end-of-semester grades and self-reported learning levels. Results indicated that the students need not to be taught by the best instructors to reach high learning levels. Effective learning can also take place under lack of some aspects of instructional practices if other aspects receive higher ratings to compensate for the missing aspects.

Keywords:

• instructional profiles
• student learning
• student evaluation of teaching
• segmentation

View correction statement:

Corrigendum

Public Interest Statement

Many people assume that students learn better when they are taught by effective instructors. At all educational levels, including higher education, a linear relationship is expected between effective instruction and good learning. Although this seems logical, the validity of this assumption has not been made evident. Investigations as to what makes a teacher effective have been inconclusive. The central question around the current study is: Do students really need to be taught by the best instructors to learn? A part of the problem related to this investigation is that it may not be possible to define instructional characteristics that are valid for all instructors. There is no common agreement among educators and researchers of the meaning of the terms “instructional effectiveness” or “effective teacher”. Thus, instead of making a blanket statement regarding the qualities of an effective teacher, different profiles of instructors associated with high learning can be defined.

1. Introduction

Learning is one of the most significant outcomes at all levels of education whereas teaching is considered as one of the principal inputs in learning process. The relationship between learning and teaching has been a topic of interest even in the earlier literature (Hirst, 1973; Peters, 1967; Scheffler, 1960). In higher education sector, research has been the focus for a long time. Recently, institutions have started launching programmes to excel in quality of teaching and learning process. This study is intended to contribute to the discussion on the relationship between these two components.

Generally, a linear trend is assumed between teaching and learning at university level as well as other levels, that is, students who are taught by effective instructors are expected to learn better. An effective instructor is certainly one of the key elements influencing learning in higher education. However, despite the fact that the terms “instructional effectiveness” or “effective instructor” are commonly used, discussions as to what makes an instructor effective have been inconclusive. In the literature, effective instructors have been described mostly in terms of instructional practices. The first attempt to model instructional effectiveness was made by Carroll (1963) who proposed five components to explain the differences in student achievement: aptitude, opportunity to learn in school, perseverance, quality of instruction and ability to understand instruction. A large body of research, however, focused on instructional characteristics to explain effectiveness. For example, in their studies, Erdle, Murray, and Rushton (1985) and Murray, Rushton, and Paunonen (1990) found that variability in instructional effectiveness could be explained by instructor personality. In another earlier effort, Feldman (1989) identified thirty-one characteristics of effective instructors such as stimulation of interest in the course and its subject matter, availability and helpfulness. Since then, attempts to define effective instructor have been made. Among the other characteristics of effective instructors are the ability to effectively organize a course, create group interaction in class, balance the difficulty of assessment materials, explain course material clearly and concisely, find ways for students to answer their own questions, display personal interest in students, use time effectively, provide a positive learning environment and stimulating course materials as well as showing enthusiasm, and fairness in grading, assignments and workload/difficulty (Braskamp & Ory, 1994; Centra, 1993; Delaney, Johnson, Johnson, & Treslan, 2009; Marsh, 1984; Marsh & Bailey, 1993; Strong, Gargani, & Hacifazlioğlu, 2011). In their meta-analytic study, Abrami, d’Apollonia, and Rosenfield (2007) stated four factors mostly associated with instructional effectiveness: relevance of instruction, clarity of instruction, preparation and management style, and monitoring learning. Similarly, Murray (2007) supported these findings, reporting significant differences in the frequency of instructional practices between low- and high-rated instructors. Speaking expressively, showing interest in the subject, moving during lecturing, using humour and showing facial expression were five factors with the highest differences.

1.1. Relationship between Instructional Effectiveness and Learning

Although an effective instructor may show itself in different ways as stated above, student learning is probably the most common outcome of effective instruction. In one of the earliest efforts, Centra (1977) reported positive correlations between instructional practices measured by student ratings of teaching and learning (Marsh, 2007; Murray, 2007; Pascarella, Edison, Nora, Hagedorn, & Braxton, 1996). Feldman (1997) obtained significant correlations between student learning and different instructional practices such as instructor’s preparation, organization of course, clarity and being clear, following course objectives. Marks (2000) found positive relationships among several aspects of an effective instructor such as fairness in grading and student learning. Zohar and Dori (2003) provided evidence regarding the positive effect of instructor’s efforts to increase critical thinking skills on student learning. Similarly, Ainley (2006) suggested that the ability to stimulate student interest in class could boost student learning. Brint, Cantwell, and Hanneman (2008) pointed out the impact of active student participation on learning. Fairness of the assessment was also found to be an influential factor on learning by Hirschfeld and Brown (2009).

A simplistic view of the relationship between learning and effectiveness in instruction implies that good learning should be a result of being taught by an effective instructor. However, this is not always the case due to the complex relationship between learning and teaching as well as the difficulty of making a definition of effective instructor.

First, it should be acknowledged that instructional effectiveness is a multifaceted construct (Stehle, Spinath, & Kadmon, 2012). As stated by McKeachie (1997), “effective instructors come in all shapes and sizes” (p. 1218) and different definitions of effective instructors may include different aspects of instruction with varying weights. In other words, there might not be a common definition for all. Thus, a closer examination of linear relationship assumed between teaching and learning seems necessary.

The other problem with regard to making a clear definition of effective instructor is also related to assessment mechanism of learning. Actual grades are probably the mostly used indicator to assess student learning, while students’ perceived level of learning is another frequently used measure. However, a discussion over the relationship between these learning indicators and students’ actual learning is not conclusive. The relationship reported between actual grades and self-reported variables ranged between low and moderate (Cole & Gonyea, 2010; Pascarella, Seifert, & Blaich, 2010). Pollio and Beck (2000) found no relationship between students’ grades and learning levels based on self-reported variables. This finding is supported by Clayson (2009) who reported no relationship between these variables. On the other hand, he obtained another important result. There is a relationship between students’ perceived level of success and learning. This was explained by the fact that self-reported variables are less affected by grading leniency (Sailor, Worthen, & Shin, 1997). On the contrary, those who support the use of actual grades say that grades are a clear indicator of learning because they are not influenced by students’ inability to assess themselves (Grimes, 2002). Two learning indicators above have some deficits that made this study consider both of them.

1.2. Student ratings as an indicator of instructional effectiveness

Student ratings of teaching are considered as the main indicator of instructional effectiveness. Alderman, Towers, and Bannah (2012), Benton and Cashin (2012) and Donnon, Delver, and Beran (2010) provided evidence regarding the validity and reliability of student ratings. However, Benton, Duchon, and Pallett (2013) and Boring, Ottoboni, and Stark (2016) cautioned that although student ratings may be reliable, they might still be affected by instruction-irrelevant factors. Boring (2015) said that ratings given by students are mostly unrelated to instructional performance. Indeed, starting from Marsh’s study (1984), biases of student ratings have been studied extensively. For example, class size was reported as an influential factor on (Miles & House, 2015). Students in smaller classes tend to give higher scores for instructors. Grade level of the course was also reported to be affecting student ratings. Kalender (2011) and Donaldson, Flannery, and Ross-Gordon (1993) stated students at upper grade levels give higher scores to instructors. Peterson, Berenson, Misra, and Radosevich (2008) stated that instructors who teach at higher grade levels receive significantly higher scores. Similarly, Nargundkar and Shrikhande (2014) found that graduate level courses received higher scores than undergraduate level courses did. However, received or expected grades seem to be a factor, which is the most controversial relationship with student ratings. Greenwald and Gillmore (1997), Scherr and Scherr (1990) and Sailor et al. (1997) reported positive relationship between grades and ratings. More recent studies confirmed these findings (McPherson & Jewell, 2007; McPherson, Jewell, & Kim, 2009). Some researchers explain this relationship by the leniency hypothesis which states that instructors can buy ratings by relaxing grading criteria (Langbein, 2008; McPherson & Jewell, 2007). On the other hand, validity hypothesis explains the relationship between student ratings and grades as a positive outcome of good instruction (Marsh & Roche, 2000). Nevertheless, student ratings are still the most common way to assess instructional performance despite some validity-related problems (Dunn, Hooks, & Kohlbeck, 2016). Also, ratings can also be used to improve teaching in classes (Boysen, 2016).

1.3. Differentiating instructional profiles

Some findings related to the existence of student subgroups that can be defined under their populations led the researcher of this paper to think further about differentiating the definitions of instructional effectiveness. For example, Marsh and Hocevar (1991) showed that there are twenty-one student subgroups which could be defined based on academic disciplines and levels of instruction. Another study by Trivedi, Pardos, and Heffernan (2011) identified seven student segments which varied under whole body clustering data from Massachusetts Comprehensive Assessment System. Similarly, Wilson and Alloway (2013) focused on subgroups including indigenous, minority and lower socio-economic groups.

A limited number of studies were also found related to the profiles of instructional effectiveness in the literature. Murray (1983) found that some instructors with high effectiveness levels might not follow the expected pattern of instruction in class, indicating a possibility of different profiles leading to effective instruction. Marsh (1987) was the first who suggested multidimensional structure of teaching effectiveness. Later, Murray et al. (1990) found that an instructor’s characteristics might vary in different classes. Young and Shaw (1999) defined several profiles of effective instructors. Murray (2007) supported these findings, reporting significant differences in the frequency of instructional practices between low- and high-rated instructors. Speaking expressively, showing interest in the subject, moving during lecturing, using humour and showing facial expression were five factors with the highest differences. Although these studies did not link the instructional effectiveness to learning, they are still of importance in that they indicated that there might be nonlinear relationship between teaching and learning. In a recent study, Kalender (2014) reported similar results, identifying several profiles of effective instructions by segmenting the whole body of students in a university setting. However, Kalender’s study defined subgroups of students using instructor- and class-related variables, rather than instructional practices, which seemed somehow arbitrary clustering.

1.4. The present study

Despite the studies given above, the issue that whether different instructional profiles that lead to high student learning exists still persists. However, the answer to that question may give significant information in terms of the type of relationship between instruction and learning. Due to the existence of subgroups, defining several instructional profile segments rather than attempting to obtain one definition for instructional effectiveness may be a more appropriate approach. Thus, to seek an answer, this study attempted to (i) cluster instructors with respect to the instructional practices rated by students, and (ii) identify the different instructional profiles that may be associated with high learning, rather than just focusing on the relationship between instructional practices and learning. Thus, a segmentation method was employed to define the subgroups which may be hidden under larger sample. In this way, the relationships that cannot be detected by correlational studies conducted on entire bodies were expected to be defined. The results are expected to help determine effective instructional profiles which could be used to improve instruction and, in turn, learning.

2. Method

2.1. Data

The setting from which data were obtained is a non-profit university in the central region of Turkey. Language of instruction is English in the university which includes both Turkish and foreign instructors. Administration emphasises the importance of good quality instruction, and ratings provided by students are used in decision-making about instructors by the university administration.

The data set including student ratings and learning indicators has been obtained with official permission granted by the Ethics Committee of the university. Computer centre of the university removed any information that can be used to identify courses and/or instructor. In the data set, within the same course or classroom, there could be dependence among the students’ rating results which may create inflated Type I error rate in the statistical analyses. In order to avoid this problem, the means obtained in the item level for each classroom were used as the unit of analysis. A random sample of 625 classes with total 9,230 students was used in the data analysis. The total number of students enrolled in the courses is 20,621. Descriptive characteristics of the classes are as follows: 34.2% (n = 214) of the courses are freshmen, 24.8% (n = 155), sophomore; 20.3% (n = 125), junior; and 20.9% (n = 131), senior. Credits of the courses were two (n = 26), three (n = 454), four (n = 113) and five (n = 32) (M = 3.26, SD = 0.70). Lecture hours of the courses varied across two (n = 113), three (437) and four hours (n = 75) per week (M = 2.98, SD = 0.64). The number of students in the classes had a mean and a standard deviation of 32.99 and 19.26, respectively.

2.2. Effectiveness indicators

Students are given a rating form about instructional effectiveness at the end of semester. After the instructor leaves the class, a volunteer student takes the envelope including ratings forms and brings them to the class. Before distributing the forms, this student reads the directions of filling out the forms. It is emphasized that participation in the sessions is completely voluntarily. In addition, neither ID nor any other information that can be associated with the students is collected. The same student collects the forms, put them in the envelope again and deliver them at the administration office. Instructors are not allowed to see the forms. Student ratings are announced on the intranet of the university after grades are announced each semester.

The ratings are used to provide feedback for instructors also in the promotions of academic staff. The items in the forms were selected from a pool reflecting various aspects of instruction. The item pool included the items of various rating scales used before for the research purposes as well as for evaluating the instructional effectiveness by other higher education institutions. This scale has been used by the university for many years and, routine analyses by the rector’s office are carried out after each administration. Return rate was 72%. Mean number of forms filled out was 14.77 per class. No statistical procedure was applied to impute missing values since the rate of missing responses in forms was 0.2%.

The student ratings form comprised of seven 5-point Likert-type items (1:strongly disagree to 5:strongly agree) to elicit students’ opinions about instructors. There is also a separate section for writing opinions and/or suggestions about the course and instructor. Items are as follows: course objectives and expectations from students were clearly stated (expectations) (M = 3.61, SD = 0.44), interest was stimulated in the subject by instructor (interest) (M = 3.38, SD = 0.62), participation was promoted in class (participation) (M = 3.56, SD = 0.63), instructor helped develop higher-order thinking skills (thinking) (M = 3.40, SD = 0.59), mutual respect was held in class by instructor (respect) (M = 3.89, SD = 0.39), the instructor was on time and has not missed classes (timing) (M = 3.77, SD = 0.37) and exams, assignments, and projects required higher-order thinking abilities (exams) (M = 3.35, SD = 0.57) (Cronbach’s α = 0.944). As can be seen in the Introduction section, these practices are among the common indicators of instructional effectiveness. All ratings given by students on instructional practices were converted to z-scores so that they were put on the same scale.

2.3. Learning indicators

Two commonly used learning indicators were used: (i) the statement “I learned a lot in this course” and (ii) end-of-semester grades of students (CGPA). The former variable which was taken from the student rating form (a 5-point Likert-type item with a mean of 3.43 and a standard deviation of 0.56) is less objective and involves self-perceived information, while the latter is a more objective and direct way to quantify learning (with a mean of 2.40 out of 4.00 and a standard deviation of 0.57). The controversy discussed in the introduction section as to the relationship between these indicators and actual learning led the researcher to include both indicators in the present study. A significant moderate correlation was found between these two variables, r(623) = 0.43, p < 0.001, justifying the use of both indicators in this study. Self-reported learning scores were re-scaled to have a mean of zero and standard deviation of 0 to ensure that all items were on the same scale.

2.4. Segmentation approach

To define the subgroups, a methodology named Chi-squared Automatic Interaction Detection (CHAID), developed by Sonquist and Morgan (1964), was employed. The CHAID is a dependence method, and it provides a hierarchical tree model with predictor variables that create higher variation on target variable at higher levels of the tree. In this way, it maximizes differences between segments in terms of values of predictor variables with respect to a target variable. It also has some other unique advantages over traditional clustering approaches such as the ability to detect nonlinear relations and interactions between variables (Borden, 1995).

A typical CHAID proceeds as follows: the predictor variable that explains the largest portion of variation on target variables is determined, and the clusters defined based on different values of that predictor variable constitutes the first-level segmentation. The procedure goes on until a predefined number of clusters are reached or no predictor variables left providing a differentiation on target variable. The significance of differences between the clusters with respect to the mean of target variable for the whole body is evaluated using χ ² tests with Bonferroni correction procedure.

In this study, responses to the effectiveness indicators (expectations, interest, participation, etc.) were used as predictor variables in CHAID analyses. Similarly, the statement “I learned a lot in this course” and end-of-semester grades of students were the target variables in the analyses.

2.5. Procedure

As preliminary analyses, unidimensionality and normality were tested. Unidimensionality of the seven items was tested via conducting confirmatory factor analysis using covariance matrices via Lisrel (Jöreskog & Sorbom, 1999). Since χ ² test tends to be statistically significant with increasing sample size, several other fit indices were used to assess the goodness-of-fit. Acceptable values for a good data-model fit indices are below 0.05 for root mean square errors of approximation (RMSEA) and standardized root mean square residual (SRMR), and above 0.90 for Goodness-of-fit index (GFI), adjusted goodness-of-fit index (AGFI), comparative fit index (CFI) and non-normed fit index (NNFI) (Kline, 2005). Normality of the data sets was also checked. West, Finch, and Curran (1995) stated values less than 2 for skewness and less than 7 for kurtosis are enough to consider data normally distributed.

Terminal clusters (cluster with no sub-clusters) showing differences than the whole body in terms of learning (measured by actual grades and self-reported learning) were defined using student ratings given for seven items (expectations, interest, participation, thinking, respect, timing and exams) via two separate CHAID analyses. SPSS’s tree module was used, and SPSS’s default parameters were kept in CHAID analyses.

Having obtained trees, differences in learning levels between clusters and whole body were compared using one-sample t-tests. Clusters that had no significant mean differences were removed from the rest of the analyses. Likewise, another set of one-sample t-tests were employed to check the differences between the means of instructional practices and those of whole body (M = 0 for each instructional practices), and, again, clusters with instructional practices which provided no difference were removed. Then, clusters were categorized into separate learning groups based on means of learning differences via ANOVA.

3. Results

Based on the values of the fit indices, the trait under which the items could be groups can be labelled as a unidimensional trait, i.e. instructional effectiveness (RMSEA = 0.05 (90%CI = 0.03; 0.08), CFI = 0.98, NNFI = 0.97, SRMR = 0.01, GFI = 0.99, AGFI = 0.97). The range of skewness values changed between −1.66 and −1.12, while kurtosis values were between 0.835 and 3.99, indicating normality.

3.1. Segmentation based on Actual Grades

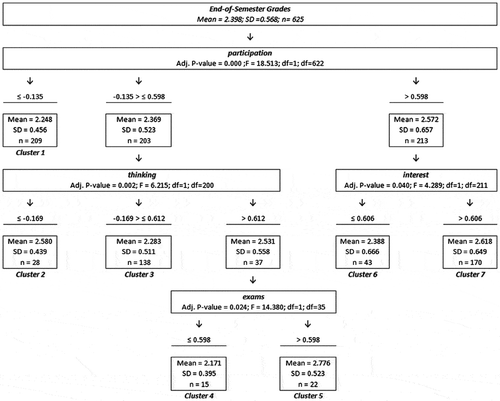
CHAID analysis based on the end-of-semester grades as the target variable produced the tree given in Figure 1. The tree, which was defined using student ratings given for thinking, interest, participation and exams, included seven terminal clusters at three levels. Mean learning levels can be seen in the boxes in the Figure 1, where mean student ratings are above the boxes. Clusters 1, 3, 4 and 6 had lower learning levels than the whole body which included all classes, whereas clusters 2, 5 and 7 had higher learning.

Figure 1. Tree produced with actual grades (clusters were numbered from left to right)

After defining clusters, series of one-sample t-tests were conducted to find out clusters constituted an significant instructional profile, compared to the mean learning level of whole group (M = 2.398). Results indicated that learning level of Cluster 6 was not statistically different than those of the whole group, t(42) = −0.121, p > 0.05. Thus, this cluster was excluded from the rest of the analyses. An additional group of one-sample t-tests were conducted to check the differences of means of instructional practices measures than grand mean (M = 0). Results revealed that all of the practices are significantly different than zero for all remaining six clusters (1, 2, 3, 4, 5 and 7).

Courses with ratings below −0.135 (inclusive) given for instructor’s ability to actively participate in the class (participation) for constituted Cluster 1. Courses with ratings between −0.135 (exclusive) and 0.598 (inclusive) for the active participation variable were again split into three clusters based on the ratings of instructors’ ability to develop students’ critical thinking skills (thinking). Courses received scores below −0.169 (inclusive) formed Cluster 2, while students who gave scores between −0.169 (exclusive) and 0.612 (inclusive) for critical thinking variable were grouped under Cluster 3. Dividing this cluster with the rating above 0.612 for thinking into two based on the ratings below (inclusive) and above 0.598 for the ability to develop assessment material of good quality (exams) created Clusters 4 and 5. Students who rated their instructors with scores above 0.598 for stimulating active participation were further divided into two including courses above 0.606 (exclusive) for stimulation of interest and formed Cluster 7.

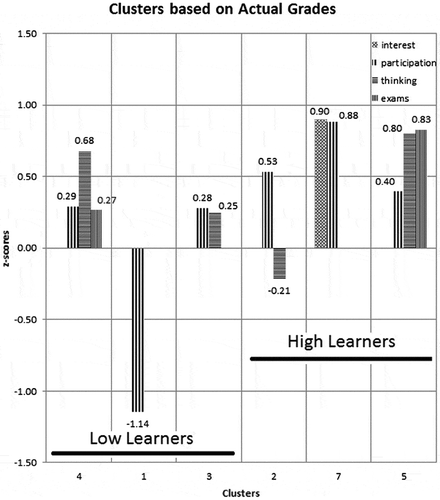
ANOVA conducted separately on clusters with respect to learning levels of clusters revealed that learning levels of the Clusters 1, 3 and 4 (with lower mean learning levels than the whole body) are not statistically different than each other (p > 0.05) and, similarly, the means of Clusters 2, 5 and 7 (with higher learning levels) were found not to have a statistically different mean differences between one another (p > 0.05) in this group of clusters. Based on that, two sets of clusters can be labelled as instructional profiles including low learners (Clusters 1, 3 and 4) and high learners (Clusters 2, 5 and 7), respectively (Figure 2).

Figure 2. Means of instructional practices based on actual grades

The investigation of clusters including high learners revealed that similar learning levels could be achieved via different instructional profiles including practices with different weights. For example, students who were in classes in which active participation was low (Cluster 5) reported that instructors developed their thinking skills, and assessment materials were of good quality. Cluster 7 included two practices with high scores. Cluster 2 indicated a different pattern of instructional practices that leads to high learning. In this pattern, lower ratings were observed for developing critical thinking skills, but higher ratings for active participation than other two clusters. This cluster still has a high learning level.

3.2. Self-reported learning

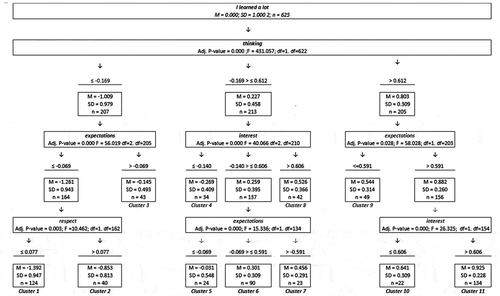
The tree which was produced as a result of the analysis is in Figure 3. A total number of 11 terminal clusters were defined using ratings given for thinking, expectations, interest and respect.

Figure 3. Tree produced with self-perceived learning (clusters were numbered from left to right)

One-sample t-tests conducted to determine if the mean learning levels of clusters which are not different than whole body (M = 0.00) revealed that mean learning levels of Cluster 3, t(42) = −1.933, p > 0.05, and Cluster 5, t(23) = −0.790, p > 0.05, had not significantly different mean than the whole body. Similarly, additional analyses showed that none of the measures of instructional practices were different than mean of zero for Cluster 4 (p > 0.05). Thus, three clusters were removed and the remaining eight clusters were used in the further analyses.

Clusters 1 and 2 included students who gave ratings below (inclusive) and above 0.077, respectively, for instructor’s respectful behaviour (respect). For these two clusters, student ratings given for clear expectations of instructor were lower than −0.069 (inclusive) and developing critical thinking skills below −0.169 (inclusive). Cluster 8 had relatively higher ratings for developing critical thinking (between −0.169 and 0.612 [inclusive]) and scores above 0.606 for sparking interest. Clusters 6 and 7 were defined using the same values for these two practices. Stating clear expectations was the third variable which defined these clusters. Students in Cluster 9 rated their instructors with scores above 0.612 for their ability to develop critical thinking and below −0.591 (inclusive) for clear expectations. Clusters 10 and 11 received ratings above 0.591 for stating expectations and 0.612 for developing critical thinking skills. Ratings below (inclusive) and above 0.606 for the generating interest in the class defined the clusters.

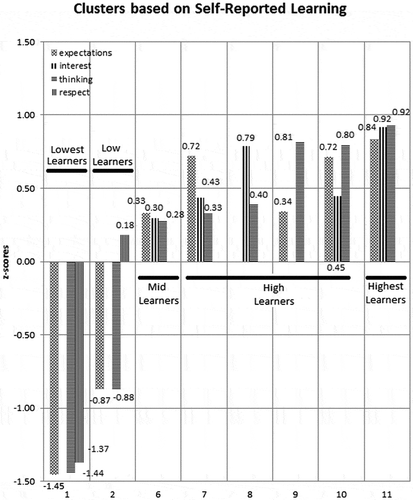
ANOVA indicated that Clusters 1 and 2 (low learners) were statistically different in terms of mean learning levels (p < 0.05). Cluster 1 had considerable lower learning level (M = −1.392) than Cluster 2 (M = −0.853). Similarly, analyses on high learners’ clusters revealed that Clusters 6 and 7 had a significant mean difference, as well as with the other clusters. Furthermore, Clusters 7, 8, 9 and 10 were also found not to be different from each other in mean learning level, but different from Cluster 6 and 11. Cluster 11 had significantly higher mean than all the others did. Therefore, five groups of clusters (1/2/6/7–10/11) were obtained. The groups were named as the lowest, low, mid, high and highest learners, respectively. Figure 4 shows the clusters and the means of instructional practices.

Figure 4. Means of instructional profiles based on self-reported learning

The highest learning seems to take place in classes in which instructor clearly states his or her expectation, stimulates interest and creates students’ thinking skills (Cluster 11). In other classes that were rated with relatively lower scores, students still achieve high learning levels (see Clusters 7–10). As in the previous tree, different instructional profiles leading to the similar learning levels with varying weights of instructional practices.

4. Discussion

The most significant outcome of the present study is nonlinear relationship between the quality of instructional practices, as perceived by students, and instructional effectiveness. CHAID analysis revealed several instructional profiles are associated with high learning. Analyses on actual grades-based tree revealed that classes in clusters with higher learning levels seemed, in general, to receive higher scores for instructional practices. However, a closer investigation of the clusters defined by actual grades indicated that high learning could take place in different ways in terms of instructional practices. Thus, no single definition of the effective instructor was reached, confirming McKeachie’s (1997) statement that an effective instructor can come with various shapes. For example, classes taught by an instructor who received student ratings around the mean for making students active participants in the class can reach high learning levels by receiving higher ratings for developing critical thinking skills of students or proving assessment materials of good quality (see Cluster 5). Similarly, lower ratings for developing thinking skill but higher ratings for active participation seem associated with high learning (see Cluster 2). The pattern which was observed for the tree based on self-reported learning indicator was similar: students learn better in classes in which effective instructors teach (see Cluster 11) (Cashin, 1995). Likewise, despite the fact that the highest learning takes place in classes rated by students with high ratings for many instructional practices, different profiles can be defined leading to relatively higher learning levels. Students in classes where they think that their critical thinking skills are not developed can still have a high learning thanks to the instructors who are able to create interest towards the subject (see Cluster 8). Similarly, instructors who receive average ratings for developing critical thinking skills/triggering interest may still achieve high learning by clearly stating expectations from students (see Cluster 7). Alternatively, in a class where students do not agree that expectations are clearly stated by instructor, but agree that interest was stimulated, can receive high learning (see Cluster 9).

Thus, a common result with regard to the relationship between learning and instructional profiles can be stated as follows: although instructors who are able to apply some instructional practices less can still hold the learning level of students high by compensating for the lack of these aspects through other aspects. The findings supported the idea that a simplistic view that good teaching creates good learning is a rather simplistic view and should not naively be accepted due to the multifaceted nature of teaching (Stehle et al., 2012). The findings also support the conclusions received by Young and Shaw (1999) and Kalender (2014) who suggested that the effectiveness of an instructor can be defined in several ways by weighting instructional practices differently.

Regarding instructional practices that defined the profiles of instructors, the ability to promote participation in class and to develop higher-order thinking was found to be the practices associated with high learning. Similar results were reported by Brint et al. (2008) and Pritchard and Potter (2011) for in-class participation, and by Braskamp and Ory (1994), Centra (1993), Marsh and Bailey (1993) and Marks (2000) for the development of students’ thinking skills. Likewise, Zohar and Dori (2003) obtained evidence regarding the positive relationship between efforts to increase students’ critical thinking skills and learning level. Ainley (2006) found that instructor’s ability to stimulate interest towards the subject has been found as influential on student learning.

It should be noted that instructional practices with no statistically significant correspondence with learning might still be influential on learning by creating a significant interaction. In this study, difference-based analyses, rather than correlational ones formed trees. Thus, instructional practices creating large differences between groups were favoured in the trees. This does not necessarily mean that excluded variables had no relationships with student learning. Due to the number of courses included in the present study the depth of tree was set to three. Accordingly, analyses revealed that five of the seven instructional practices had been associated with high learning: instructor’s ability to trigger interest in class, make students active participants, increase students’ thinking skills, state his or her expectations clearly from students and/or give exams of good quality. If higher levels of depths in segmentation were defined, other predictors might have been included in the trees. However, the predictor variables which were defined as significant as a result of CHAID analyses can be considered as more related to learning. Also, the investigation of the distinction between significance and relevance of instructional practices may provide significant information in depicting better pictures of instructional effectiveness.

Based on the results, it can be said that focusing on learner subgroups, rather than the whole body, may be more helpful due to the existence of distinct instructional profiles as shown by the findings of the present study, as well as by Marsh and Hocevar (1991) and Trivedi et al. (2011). However, it should be noted that scale invariance of students across different subgroups should be checked in order to make meaningful comparisons. Only if the invariance is shown to be held, all profiles could be evaluated at a common scale of student ratings (Kalender, 2015).

The results have also implications for instructors. First, instructors should acknowledge that learning may take place under different instructional profiles. They should be aware of the different needs of students and adapt themselves accordingly. For example, active participation may trigger learning for some students, while others need interest to be sparked. Also, an instructor may have some weakness in practices. As long as he or she tries to compensate for them with stronger practices, learning may occur. A similar result was also reported by Murray et al. (1990) who stated that instructors should tend to adapt themselves to different students and/or courses. It should be acknowledged that it is not an easy task for an instructor to be able to compensate for the lack of some instructional skills for low learners. For example, ability to develop higher-order thinking skills of students was not adequate to achieve high learning when the instructor was not able to create participation and to develop exams of good quality (see Cluster 4 in Figure 2).

Another point that should be noted that some students expecting/receiving lower grades may start to skip classes especially towards the end of the semester. Given student ratings are collected at the end of the semester, absent students with low grade expectations may constitute missing values and they could be considered as a potential source of selection bias in self-reported learning (Wolbring & Treischl, 2016). Similarly, students with lower expectations may wish to penalize instructors by giving the lower grades. Collecting student ratings at earlier stages of the courses may be helpful in lessening the bias due to learning levels. Implementing student ratings more than once in a semester may be a solution (Wolbring, 2012). There are some older studies reporting relationships between the ratings collected at the mid-semester and end of the semester (Costin, 1968). Similarly, Kohlan (1973) stated that students’ opinions become stable at earlier weeks.

Given that student ratings are widely used in decisions regarding instructors’ career, administrators should also consider the nonlinear relationship between instructional effectiveness and learning. As shown by Murray (1985) and gained support by Young and Shaw (1999) and Kalender (2014) in the literature as well as in this study, some instructors may deviate from expected pattern on instruction. This should not be considered as a problem as long as high learning measured by different criteria such as actual grades and self-reported learning occurs. Furthermore, administrators should not expect any pattern of instruction from instructors in classes, not give weights to some instructional practices and not penalize instructors who receive low scores for some practices as long as high learning is observed (Chan, Luk, & Zeng, 2014).

However, Golding and Adam (2016) and Houston, Meyer, and Paewai (2006) stated that administrators who rely on student ratings on decision-making have little research-based guidance on how to use those ratings. Evaluation centres in high education institutions may be established to help both for administrators and instructors in incorporating student ratings into decision-making and instructional improvement. These centres may provide assistance in interpreting results and a simplified summary. Also, administrators should aware that even if the ratings are low, learning can still be high. Student can lower the ratings when a course is made more difficult but the difficulty can be a productive one (Kornell & Hausman, 2016).

When student ratings are used by administrators, the bias due to the student learning levels can be corrected in the ratings. Statistical adjustment methods such as weighting for grades might be used to control for the effect of bias on student ratings. There are several adjustment formula based on different weighting approaches (Soh, 2014; Wolbring, 2012). These adjustments seem promising but the major use of student rating of instruction should be the improvement of educational practices rather than promotion. Whatever the purpose of using student rating is, alternative ways should also be considered (Chapman & Lindner, 2016; Hornstein, 2017; Oravec, 2015).

Corrigendum

This article was originally published with errors. This version has been corrected. Please see Corrigendum (https://doi.org/10.1080/2331186X.2017.1410308).

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Ilker Kalender

Dr Ilker Kalender is an assistant professor in Graduate School of Education, Bilkent University in Turkey. He has also worked as a consultant in national testing agency in Turkey. He teaches statistics and test development courses at graduate level and works in teacher training programme in the same university. Dr Kalender’s research agenda primarily focuses on student evaluations of teaching and computerized adaptive testing procedures.