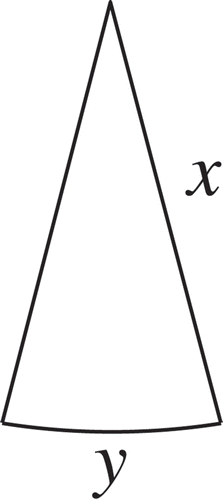Finding extrema without resorting to calculus

Abstract

The article is dedicated to solving extrema problems in teaching mathematics, without using calculus. We present and discuss a wide variety of mathematical extrema tasks where the extrema are obtained and find their solutions without resorting to differential. Particular attention is paid to the role of arithmetic and geometric means inequality in solving these problems.

Keywords:

• mathematical extrema problems
• calculus
• arithmetic and geometric mean inequality

Public Interest Statement

An effective educator needs to be able to help students to think outside the box of ordinary and stimulate their creativity and curiosity to explore the frontiers of unknown. Future teachers of mathematics, whether at school or college levels, are to be well rounded, knowledgeable, and be prepared with alternative avenues and methods in solving mathematical problems. One such topic is dealing with mathematical optimization problems using methods other than differential and integral calculus. One most effective such alternative method is a combination of classical geometrical arguments amalgamated with known arithmetic and algebraic inequalities such as arithmetic and geometric means inequalities. The application of the contents of the present article is multifacet. They are ready to be adopted in classroom presentations or can be used in training future teachers of mathematics. More importantly, the contents of this article are loaded with ideas and topics that can be used for graduate research dissertations

1. Introduction

The customary manner of dealing with tasks of finding the extrema is making use of differential calculus. But in quite a few tasks in various fields in mathematics, the extrema can be found without resorting to differential calculus.

It must be emphasized that even without command or skills in differential and integral calculus, one can obtain solutions through extensive knowledge in various subjects in mathematics, sophistication and unorthodox thinking, and sometimes by a simpler or shorter method. However, it should be noted that alternative methods of solution such as use of arithmetic and geometric means (AGM) suit only to a few particular cases, while calculus provides solution to most cases; but, the former method requires elementary geometrical methods while the latter requires precalculus, trigonometry and calculus as perquisites that most high school students may not have acquired when taking a geometry course. Moreover, the integration of different methods in problem-solving can give students a wider outlook to mathematics as a comprehensive discipline while creating connections between its different branches.

Successful development of reasoning and solution of diverse problems in mathematics depends very much on the teacher’s ability to create and elicit appropriate stimuli in the teaching and learning process, while accentuating the beauty of mathematics.

Solving a problem by a regular method usually leaves the bright and curious students indifferent and without any particular reaction. However, different solutions of the same problem may cause emotional enthusiasm. The special and the beautiful solution is unexpected, but tangible, and in most cases—simpler and shorter. The use of alternative methods highlights mathematics as a magical field of surprising solutions.

Mathematics educators agree that linking mathematical ideas by using more than one approach to solving the same problem (e.g. proving the same statement) is an essential element in the development of mathematical reasoning (National Council of Teachers of Mathematics, 2000; Polya, 1973; Schoenfeld, 1985). Problem-solving in different ways requires and develops mathematical knowledge (Polya, 1973), and encourages flexibility and creativity in the individual’s mathematical thinking (Krutetskii, 1976; Liekin & Lev, 2007; Oxman & Stupel, 2018; Silver, 1997; Stupel & Ben-Chaim, 2017; Tall, 2007).

In addition to the specific roles of proof in mathematics, we suggest that attempts to also prove a certain result (or solve a problem) using methods from several other different areas of mathematics (geometry, trigonometry, analytic geometry, vectors, complex numbers, etc.) are very important in developing deeper mathematical understanding, creativity, and appreciation of the value of argumentation and proof in learning different topics of mathematics.

All of the above is fully relevant to the extrema problems in mathematics.

2. Extrema problems in mathematics and mathematics education

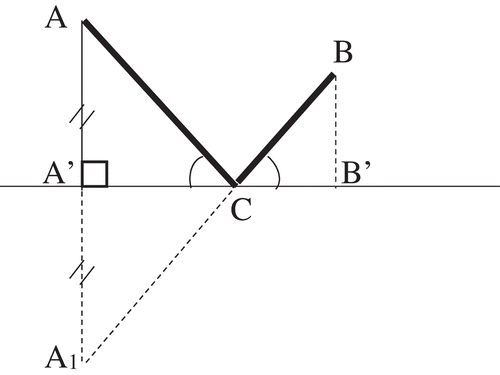
The history of extrema problem-solving is as old as the history of mathematics itself. The ancient Greek mathematicians (Archimedes, Euclid, and Heron) sought and found solutions to some of the extrema problems. One such problem is the well-known Heron’s problem (Heron of Alexandria, about 10AD–70AD, (Tikhomirov, 1990, p.4) that “Given two points A and B on one side of a line, find the point C on the line so that $\overline{AC}+\overline{CB}$ is minimal.”

The development of calculus during the 18th–20th centuries provided powerful and systematic methods for solving extrema problems. But there are a number of reasons as to why, in some cases such as Heron’s problem, it is better to seek extrema without using calculus.

1. The technical issue in using calculus.

For instance, for the Heron’s problem, (refer to Figure 1), using calculus one must find an appropriate function $f\left(x\right)=\sqrt{a^2+x^2}+\sqrt{b^2+{\left(c-x\right)}^2}$ ($A{A}^{\prime }=a,B{B}^{\prime }=b,A^{\prime }{B}^{\prime }=c,A^{\prime }C=x$) and consider

$f^{\prime }\left(x\right)=\frac{2x}{2\sqrt{a^2+x^2}}-\frac{2\left(c-x\right)}{2\sqrt{b^2+{\left(c-x\right)}^2}}=0\Rightarrow cos\mathrm{\angle }AC{A}^{\prime }=cos\mathrm{\angle }BC{B}^{\prime }\Rightarrow \mathrm{\angle }AC{A}^{\prime }=\mathrm{\angle }BC{B}^{\prime }.$

Then, we need to the increasing/decreasing argument to justify that the above angles $\mathrm{\angle }AC{A}^{\prime }=\mathrm{\angle }BC{B}^{\prime }$ are the only case where $\overline{AC}+\overline{CB}$ is minimal.

Figure 1. Heron’s problem

Clearly, this is a technically involved solution. Plus, those students who take geometry may have not yet taken calculus.

(2) A number of geometry extrema problems have several variables and using calculus requires the knowledge of partial derivatives, which usually goes beyond the school curriculum.

(3) Although calculus serves as a systematic and powerful technique, this rigorous instrument might hinder students’ ability to understand the behavior and constraints of the objective function (Dvir & Tabach, 2017).

From the point of view of posing the extrema problems to students, there are two types of problems. The first type is when students are given an answer to an extrema problem and they are asked to prove that this answer is correct. The second type is an extrema problem given to students and they are asked to find the correct answer. This is usually more challenging than the first type.

For example, if students are asked to find the point C in Heron’s problem mentioned above, for which $\overline{AC}+\overline{CB}$ is minimal, for many of them it turns out to be a difficult task. They assume that the point C should be the midpoint of the segment A’B’, where A’ and B’ are the respective projections of A and B on the given line (see Figure 1). On the other hand, if the students are asked to prove that $\overline{AC}+\overline{CB}$ is minimal when $\mathrm{\angle }AC{A}^{\prime }=\mathrm{\angle }BC{B}^{\prime },$ the problem turns out to be much simpler for students to prove.

The advantages of extreme problems without a given answer are many. For example, they stimulate the investigation activity of students plus that is what happens in a real-life situation when we face a problem but don’t know the answer. To make the life a little bit easier, nowadays we have powerful computerized tools (such as GeoGebra) that can help students to explore a variety of possibilities and situation by fixing or changing different parameters in the given problem (Dvir & Tabach, 2017; Oxman, Stupel, & Segal, 2016).

There are many various methods, other than calculus, for solving extrema problems such as mathematical induction, proof by contradiction, method of partial variation, methods based on tangency principle (in geometry), employing known inequalities and others (Andresku, Mushkarov, & Stoyanov, 2006; Niven, 1982; Su & Xiong, 2016). Many problems can be effectively solved by combining several of such methods. Not all of these methods are equally suitable for use in teaching mathematics at school or college, in terms of accessibility for students. One of the most elementary methods among them is the use of known inequalities. Among such inequalities, the AGM inequalities stand out since they allow the students to solve a wide class of extrema problems (see, for instance, (Anderson, 1994; Andresku et al., 2006; Askey, Matsuura, & Sword, 2015; Bullen, 2003; Katz, 1989; Niven, 1982; Su & Xiong, 2016).

3. AGM inequality

The Arithmetic Mean (AM) of n numbers a₁, a₂,…, a_n is equal to $\frac{a_1+a_2+\dots +a_n}{n}$. The Geometric Mean (GM) of n numbers a₁, a₂,…, a_n is equal to $\sqrt[n]{a_1\cdot a_2\cdot \dots \cdot a_n}$. The well-known inequality between AM and GM which is called The Arithmetic and Geometric Mean (AGM) inequality states that for all real non-negative real numbers a₁, a₂, …, a_n; $GM\le AM$, or in other words

$\sqrt[n]{a_1\cdot a_2\dots a_n}\le \frac{a_1+a_2+\dots +a_n}{n}.\left(\mathrm{3.1.1}\right)$

The equality holds in (3.1.1) if and only if $a_1=a_2=\dots =a_n$.

Almost all of our students with a college algebra background are able to prove the AGM inequality for n = 2, that is;

${\left(\sqrt{a_1}-\sqrt{a_2}\right)}^2=a_1-2\sqrt{a_1{a}_2}+a_2\ge 0\Rightarrow \sqrt{a_1\cdot a_2}\le \frac{a_1+a_2}{2}$

Students with more algebraic skills are challenged to test the AGM inequality for lower values of n and our brighter students are referred to research literatures such as Bullen (Bullen, 2003) for higher values of n.

It is the aim of this article to present solutions to various extrema problems with the help of employing AGM inequality. For the sake of applicability to a wide range of problems and various situations, most of the extrema problems are considered in their general cases. We also kept in mind the accessibility of the contents of this article to a wide range of our teacher education students as well as those who are majoring in mathematical sciences.

In the next four sections, we discuss extrema problems in plane and solid geometry, algebraic functions, trigonometric functions, and multivariate extremum problems.

4. Plane and solid geometry

Task 4.1

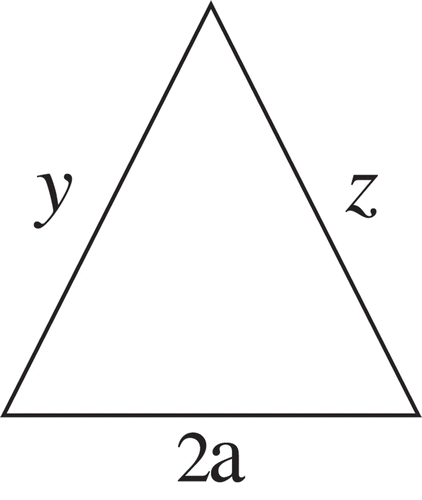
Prove that the largest area of a triangle whose perimeter is 2p and whose base is 2a is obtained for an isosceles triangle.

Proof

Let the sides of the triangle be 2a, y and z, as shown in Figure 2. From Heron’s formula for the area of a triangle, we have: $S=\sqrt{p(p-2a)(p-y)(p-z)}$.

Figure 2. The largest area of a triangle with given perimeter

By the AGM inequality for n = 2, we obtain:

$\sqrt{(p-y)(p-z)}\le \frac{(p-y)+(p-z)}{2}=\frac{2p-(y+z)}{2}=a.$

Therefore,

$S=\sqrt{p(p-2a)(p-y)(p-z)}=\left(\sqrt{(p-y)(p-z)}\right)\left(\sqrt{p(p-2a)}\right)\le a\left(\sqrt{p(p-2a)}\right).$

Since the equality in (*) is obtained only if $a_1=a_2=a_3=\dots =a_n$, the maximal area also will be obtained when y = z, that is $S_{max}=a\sqrt{p(p-2a)}$. This proves that the maximal area is obtained for an isosceles triangle.

Task 4.2

Find the radius of a sector with a given perimeter and with maximal area.

Solution

Denote the radius of the sector by x and the arc length of the sector by y (Figure 3).

The given perimeter of the sector is denoted by l and its area is denoted by S.

Then, $l=2x+y\Rightarrow y=l-2x$

Using the relation “angle α of the sector = y/x”, the area of the sector becomes $S=\frac{1}{2}\alpha x^2=\frac{1}{2}xy$.

We substitute l-2x for y to obtain $S=\frac{x\left(l-2x\right)}{2}=\frac{2x\left(l-2x\right)}{4}$.

Applying the AGM inequality for n = 2, we obtain $\sqrt{4S}=\sqrt{2x\left(l-2x\right)}\le$ $\frac{2x+\left(l-2x\right)}{2}=\frac{l}{2}$.

The equality will only hold if $l-2x=2x$; in other words, the maximal area of the sector is obtained when $x=l/4$ and it is equal to $l^2/16$.

Task 4.3

Figure 3. The maximal area of a sector

Find the minimal value of the ratio $\frac{p^2}{r^2}$, where p is the semi-perimeter of a triangle, r is its inradius.

Solution

Let S denote the area of a given triangle with sides a,b and c.According to Heron’s formula, the area of the triangle is given by$S=$ $\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}.$We also have S = pr . Then $\frac{S^2}{p}=\left(p-a\right)\left(p-b\right)\left(p-c\right).$Now, according to AGM inequality for n = 3 we obtain$\frac{S^2}{p}=\frac{p^2\cdot r^2}{p}\le {\left(\frac{\left(p-a\right)+\left(p-b\right)+\left(p-c\right)}{3}\right)}^3={\left(\frac{p}{3}\right)}^3=\frac{p^3}{27}\Rightarrow \frac{p^2}{r^2}$ $\ge 27$.

Since the equality holds only for a = b = c, we obtain that the minimal value of the ratio $\frac{p^2}{r^2}$ is 27 and it is obtained only for equilateral triangle.

Task 4.4

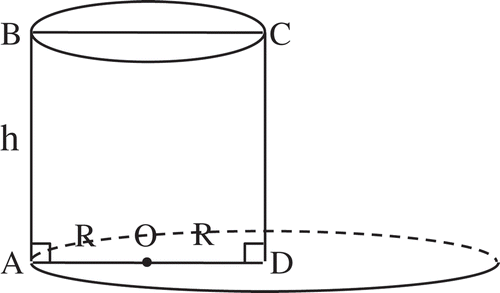
Among all the cylinders with axial incision ABCD with perimeter $2p$ find such one with the maximal volume (Figure 4).

Figure 4. The maximal volume of a cylinder

SolutionWe observe that

$4R+2h=2p$

or

$2\mathrm{R}+\mathrm{h}=\mathrm{p}\Rightarrow \frac{\mathrm{R}+\mathrm{R}+\mathrm{h}}{3}=\frac{\mathrm{p}}{3}.$

According to the AGM inequality for n = 3,

$\frac{\mathrm{p}}{3}\ge \sqrt[3]{{\mathrm{R}}^2\mathrm{h}}$

From this, it follows that $\mathrm{V}=\pi {\mathrm{R}}^2\mathrm{h}\le \frac{\pi {\mathrm{p}}^3}{27}$, i.e. the maximal volume of the cylinder is $V_{max}=\frac{\pi p^3}{27}$ and it is reached for $\mathrm{R}=\mathrm{h}=\frac{\mathrm{p}}{3}$.

5. Algebraic functions

Task 5.1

Find the minimal value of the sequence $a_n={\left(1+\frac{1}{n}\right)}^n$, n = 1, 2, ....

Solution

We prove that the sequences is strictly monotonic increasing, i.e. a_n+1≥ a_n for all natural n.

First we set

$a_n=\frac{\left(1+\frac{1}{n}\right)\cdot \left(1+\frac{1}{n}\right)\dots \left(1+\frac{1}{n}\right)\cdot 1}{\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{s}}$. Here, we have n + 1 multipliers which are not all equal ($1\ne 1+\frac{1}{n}$). Then from the AGM inequality, it follows the strict inequality $a_n<{\left(\frac{\left(1+\frac{1}{n}\right)n+1}{n+1}\right)}^{n+1}={\left(\frac{n+2}{n+1}\right)}^{n+1}={\left(1+\frac{1}{n+1}\right)}^{n+1}=a_{n+1}.$

So, the minimal value of the sequence is $a_1=2$.

Note that the proved inequality is usually used for the proof of existence of the number e as a limit of the sequence $a_n$, where $\to \mathrm{\infty }$.

Task 5.2

Find the minimal value of the function $\frac{1+x+x^2+\dots +x^{2n}}{x^n}$, x > 0, n = 0,1,2, ….

Solution

From the AGM inequality, it follows that $\frac{1+x+x^2+\dots +x^{2n}}{2n+1}$ $\ge \sqrt[2n+1]{1\cdot x\cdot x^2\dots x^{2n}}$.

This yields $\frac{1+x+x^2+\dots +x^{2n}}{2n+1}\ge \sqrt[{\hspace{0.17em}}^{2n+1\hspace{0.17em}}]{x^{1+2+\dots +2n}}=\sqrt[{\hspace{0.17em}}^{2n+1\hspace{0.17em}}]{x^{n\left(2n+1\right)}}=x^n.$Therefore$\frac{1+x+x^2+\dots +x^{2n}}{x^n}\ge 2\mathrm{n}+1.$

Task 5.3

Find the minimal value of the function: $y=\frac{(x+\mathrm{a})(x+\mathrm{b})}{x}$ where x is positive and a and b are fixed positive real numbers.

SolutionWe observe that

$y=\frac{(x+\mathrm{a})(x+\mathrm{b})}{x}=\frac{x^2+(\mathrm{a}+\mathrm{b})x+\mathrm{a}\mathrm{b}}{x}=x+\frac{\mathrm{a}\mathrm{b}}{x}+\mathrm{a}+\mathrm{b}.$

On the other hand, by AGM inequality for n = 2 we have $x+\frac{\mathrm{a}\mathrm{b}}{x}\ge 2\sqrt{x.\frac{\mathrm{a}\mathrm{b}}{x}=}2\sqrt{\mathrm{a}\mathrm{b}}$.

Hence$y=\frac{(x+\mathrm{a})(x+\mathrm{b})}{x}=x+\frac{ab}{x}+a+b\ge 2\sqrt{ab}+a+b={\left(\sqrt{a}+\sqrt{b}\right)}^2.$

The equality is obtained for $x=\frac{ab}{x}\Rightarrow x=\sqrt{ab}$.

Task 5.4

Find the maximal value of the function $y=x^{2n}(a-x^{2n})$ where x is real, a is a non-negative real number and n is a non-negative integer.

Solution

Obviously, the maximum occurs if the expression $a-x^{2n}$ is positive, i.e.$\left|x\right|<\sqrt[2n]{a}$.

Using the AGM inequality for n = 2, the maximum of y is

$y=x^{2n}(a-x^{2n})\le {\left[\frac{x^{2n}+(a-x^{2n})}{2}\right]}^2=\frac{a^2}{4}.$

This occurs when $x^{2n}=a-x^{2n}$ or if $\left|x\right|=\sqrt[2n]{\frac{a}{2}}$.

Task 5.5

Find the maximum of the function $y=\frac{x}{a{x}^2+b}$ for a, b > 0.

Solution

It is easy to show that the function obtains its maximum for x > 0.

From the AGM inequality for n = 2, one can obtain:

$\frac{a{x}^2+b}{2}\ge \sqrt{a{x}^{2}b}=x\sqrt{ab}.$

Therefore, for any x > 0, we have: $y=\frac{x}{a{x}^2+b}\le \frac{x}{2x\sqrt{ab}}=\frac{1}{2\sqrt{ab}}$.

The equality holds only if $a{x}^2+b=2x\sqrt{ab}$, or in other words $x_{max}=\sqrt{\frac{b}{a}}$, and the maximum of the function is $y_{max}=\frac{1}{2\sqrt{ab}}$.

6. Trigonometric functions

Task 6.1

Find the minimal value of the function $y={sin}^{2n}x+{cos}^{2n}x$ in the range $0\le x\le \frac{\pi }{2}$.

Solution

We denote ${sin}^{2}x=a$ and ${cos}^{2}x=b$.

By trigonometric identities, it is known that $\mathrm{a}+\mathrm{b}=1$, and therefore ${cos}^2\mathrm{x}=1-\mathrm{a}$.

$y=\mathrm{s}\mathrm{i}{\mathrm{n}}^{2\mathrm{n}}x+{cos}^{2\mathrm{n}}x={\mathrm{a}}^{\mathrm{n}}+b^{\mathrm{n}}={\mathrm{a}}^{\mathrm{n}}+{\left(1-a\right)}^n.$

On the other hand, by the AGM inequality for n = 2 we have ${\mathrm{a}}^{\mathrm{n}}+{\mathrm{b}}^{\mathrm{n}}\ge 2{\left(\sqrt{a(1-a)}\right)}^n$.

Therefore${\mathrm{a}}^{\mathrm{n}}+(1-\mathrm{a}{)}^n\ge 2{\left(\sqrt{a(1-a)}\right)}^n.$or$({\mathrm{a}}^{\mathrm{n}}-(1-a{)}^n{)}^2\ge 0.$

The equality is obtained only when $\mathrm{a}=1-\mathrm{a}$ or if $\mathrm{a}=\frac{1}{2}\Rightarrow sinx=\frac{\sqrt{2}}{2}.$Therefore${sin}^{2n}x+{cos}^{2n}x\ge \frac{1}{2^{n-1}}.$

Task 6.2

For $0\le {\alpha }_1,{\alpha }_2\le \frac{\pi }{2}$ prove that $si{n}^2\left(\frac{{\alpha }_1+{\alpha }_2}{2}\right)-$ $sin{\alpha }_1\cdot sin{\alpha }_2$ is never negative.

Solution

According to the AGM inequality for n = 2 we have $sin{\alpha }_1\cdot sin{\alpha }_2\le$ ${\left(\frac{sin{\alpha }_1+sin{\alpha }_2}{2}\right)}^2$and by trigonometric identities, we have $\frac{sin{\alpha }_1+sin{\alpha }_2}{2}$ = $sin\frac{{\alpha }_1+{\alpha }_2}{2}\cdot cos\frac{{\alpha }_1-{\alpha }_2}{2}$.

Also, $0\le cos\frac{{\alpha }_1-{\alpha }_2}{2}\le 1$ since $-\frac{\pi }{2}\le \frac{{\alpha }_1-{\alpha }_2}{2}\le \frac{\pi }{2}$. Therefore, $\frac{sin{\alpha }_1+sin{\alpha }_2}{2}\le sin\frac{{\alpha }_1+{\alpha }_2}{2}$.

This, in combination with the AGM inequality above, yields $sin{\alpha }_1\cdot sin{\alpha }_2\le si{n}^2\frac{{\alpha }_1+{\alpha }_2}{2}$.

Thus, the minimal value of $si{n}^2\left(\frac{{\alpha }_1+{\alpha }_2}{2}\right)-$ $sin{\alpha }_1\cdot sin{\alpha }_2$ is 0 and it is obtained if ${\alpha }_1={\alpha }_2$.

Task 6.3

For $a>0,a\ne 1$ find the maximal values of the function

$y=\sqrt{{cos}^{2}x+a{sin}^{2}x}+\sqrt{{sin}^{2}x+a{cos}^{2}x}$

Solution

Squaring the above equation and using the trigonometric identities, we obtain

$y^2=1+a+2\sqrt{({cos}^{2}x+a{sin}^{2}x)({sin}^{2}x+a{cos}^{2}x)}$

Now applying the AGM inequality for n = 2 yields

$y^2\le 1+a+({cos}^{2}x+{sin}^{2}x+a{sin}^{2}x+a{cos}^{2}x)=1+a+1+a=2(1+a)$

The equality occurs for${cos}^{2}x+a{sin}^{2}x={sin}^{2}x+a{cos}^{2}x$.

Therefore, $y_{max}=\sqrt{2(1+a)}$ is obtained for $x_{max}=\frac{\pi }{4}+\frac{\pi }{2}k$, where k is a whole number.

7. Multivariate extremum problems

Naturally, this type of problems is not included in the high school program of studies, but rather it is more suitable for a university framework. This type of problems may, however, be presented to outstanding high school students or those who are interested in mathematics as enrichment activities.

Task 7.1

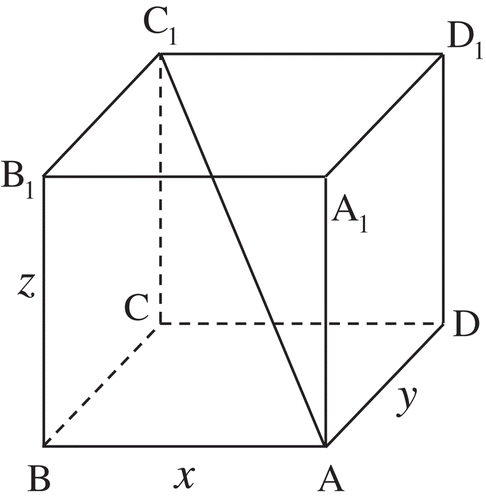
What is the value of the maximal surface area of a right rectangular prism with a diagonal a?

Solution

Let the width, length, and height of the right rectangular prism be x, y, and z, respectively (Figure 5).

Figure 5. The maximal surface area of a prism

The diagonal of the cuboid and its edges satisfy the relation $x^2+y^2+z^2=a^2$ (the spatial Pythagorean theorem). The value of the surface area S is: $S=2(xy+xz+yz)$.

From the AGM inequality for n = 2, one can write the following relations:

$xy=\sqrt{x^2\cdot y^2}\le \frac{x^2+y^2}{2}$

$xz=\sqrt{x^2\cdot z^2}\le \frac{x^2+z^2}{2}$

$yz=\sqrt{y^2\cdot z^2}\le \frac{y^2+z^2}{2}$

And, hence, using the formula for the surface area and by adding the aforementioned inequalities, we shall obtain:

$\mathrm{S}=2\left(xy+xz+yz\right)\le 2.\frac{2x^2+2y^2+2z^2}{2}=2{\mathrm{a}}^2$

The maximal area of $a^2$ shall be obtained when $x=y=z$, for a cube.

Task 7.2

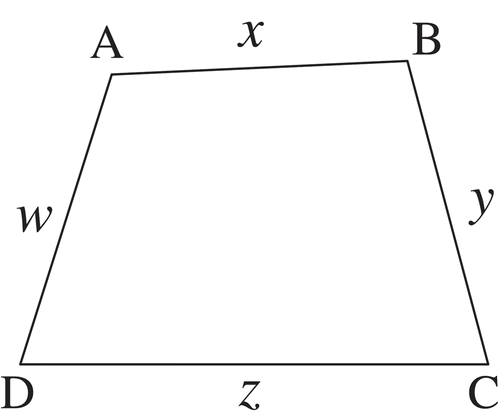
What is the maximal area of a quadrilateral with a given perimeter 2p?

We denote the sides of the quadrilateral by x, y, z, and w, as shown in Figure 6.

Solution

Given: $x+y+z+w=2\mathrm{p}$.

From the Brahmagupta formula for the area of a quadrilateral:

$S=\sqrt{\left(\mathrm{p}-x\right)\left(\mathrm{p}-y\right)\left(\mathrm{p}-z\right)\left(\mathrm{p}-w\right)-xyza{cos}^2\left(\mathrm{\angle }\mathrm{A}+\mathrm{\angle }\mathrm{C}\right)}$

The maximal area shall be when $cos\left(\mathrm{\angle }\mathrm{A}+\mathrm{\angle }\mathrm{C}\right)=0$, in other words when the quadrilateral ABCD is inscribable.

The maximal area shall be: $S=\sqrt{\left(\mathrm{p}-x\right)\left(\mathrm{p}-y\right)\left(\mathrm{p}-z\right)\left(\mathrm{p}-w\right)}$ for all the segments x, y, z, and w that describe an inscribable quadrilateral.

To obtain the quadrilateral with the maximal area, we must calculate the maximal value of the expression $\mathrm{F}=\left(\mathrm{p}-x\right)\left(\mathrm{p}-y\right)\left(\mathrm{p}-z\right)\left(\mathrm{p}-w\right)$ when it is known that $x+y+z+w=2\mathrm{p}$.

From the AGM inequality for n = 4:

$\mathrm{F}\le {\left[\frac{\left(\mathrm{p}-x\right)+\left(\mathrm{p}-y\right)+\left(\mathrm{p}-z\right)+\left(\mathrm{p}-w\right)}{4}\right]}^4={\left[\frac{4\mathrm{p}-2\mathrm{p}}{4}\right]}^4={\left[\frac{\mathrm{p}}{2}\right]}^4$

Therefore, the maximal area shall be ${\left[\frac{\mathrm{p}}{2}\right]}^4$, and it is obtained when $\mathrm{p}-\mathrm{x}=\mathrm{p}-\mathrm{y}=\mathrm{p}-\mathrm{z}=\mathrm{p}-\mathrm{w}$, in other words—when ABCD is a square.

Figure 6. The maximal area of a quadrilateral with given perimeter

Task 7.3

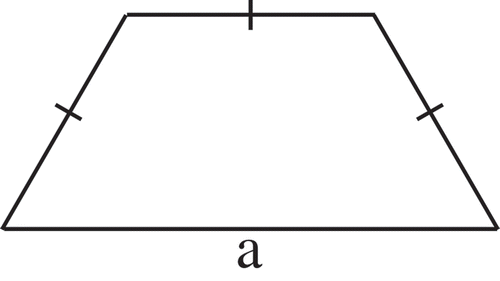
Identify the quadrilateral with a fixed side and a fixed parameter with the maximum area.

Solution

Let a be the given side and p be the perimeter of a given quadrilateral (See Figure 7).

We let x,y and z denote the other three sides of the quadrilateral. Therefore $x+y+z=\mathrm{p}-\mathrm{a}$.

From the Brahmagupta formula for the area of a quadrilateral we have$S=\sqrt{\left(\frac{\mathrm{p}}{2}-x\right)\left(\frac{\mathrm{p}}{2}-y\right)\left(\frac{\mathrm{p}}{2}-z\right)\left(\frac{\mathrm{p}}{2}-a\right)-xyza\cdot {cos}^2\left(\mathrm{\angle }A+\mathrm{\angle }C\right)}$.

Obviously, the maximum for S as given above is obtained if$cos(\mathrm{\angle }A+\mathrm{\angle }C)=0$, that is $S_{max}=\sqrt{\left(\frac{\mathrm{p}}{2}-x\right)\left(\frac{\mathrm{p}}{2}-y\right)\left(\frac{\mathrm{p}}{2}-z\right)\left(\frac{\mathrm{p}}{2}-a\right)}.$

We let $F=\left(\frac{\mathrm{P}}{2}-x\right)\left(\frac{\mathrm{p}}{2}-y\right)\left(\frac{\mathrm{P}}{2}-z\right).$

Figure 7. The maximal area of a quadrilateral with given perimeter and one of the sides

Now from the AGM inequality for n = 3 we obtain $F\le {\left(\frac{\frac{3p}{2}-\left(x+y+z\right)}{3}\right)}^3={\left(\frac{\frac{3p}{2}-\left(p-a\right)}{3}\right)}^3={\left(\frac{a+\frac{p}{2}}{3}\right)}^3.$

Therefore$S\le \sqrt{{\left(\frac{a+\frac{p}{2}}{3}\right)}^3\left(\frac{p}{2}-a\right)}=\frac{\sqrt{3}}{12}(p+2a)\sqrt{p^2-4a^2}.$

By the AGM inequality, the equality for the maximum of the area S occurs if$x=y=x=\frac{p-a}{3}.$

Remark

So far, we have considered using only the AGM inequality for solving the above given extremal problems. To further challenge our students, we introduced the Cauchy-Schwarz inequality${\left(a_1{b}_1+a_2{b}_2+\dots +a_n{b}_n\right)}^2\le \left({a_1}^2+{a_2}^2+\dots +{a_n}^2\right)\left({b_1}^2+{b_2}^2+\dots +{b_n}^2\right).$Then, our students were given the opportunity to apply the Cauchy-Schwarz inequality to the following multivariate extrema problem.

Task 7.4

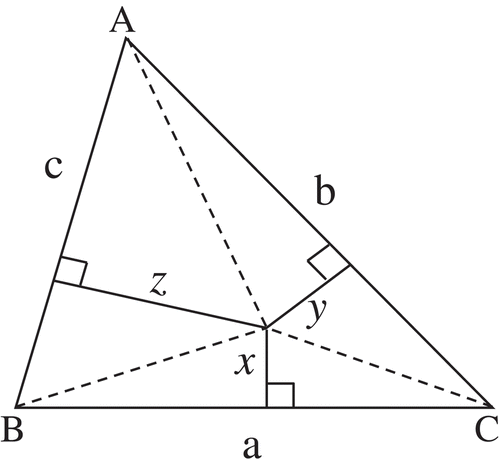
The triangle ABC with an arbitrary interior point O is given (See Figure 8). Let x, y and z be the distances of the given point O from the sides BC, CA and AB respectively. What is the minimal value of $x^2+y^2+z^2$?

Figure 8. The minimal value of the expression $x^2+y^2+z^2$

Solution

The area of the triangle ABC, based on the areas of the triangles BOC, COA and AOB, is

$S=\frac{1}{2}\left(BC\right)x+\frac{1}{2}\left(CA\right)y+\frac{1}{2}\left(AB\right)z=\frac{1}{2}\left(ax+by+cz\right).$

From the Cauchy-Schwarz inequality for n = 3, we obtain

$2S=\mathrm{a}x+\mathrm{b}y+\mathrm{c}z\le \left(\sqrt{x^2+y^2+z^2}\right)\left(\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2}\right).$

Therefore, the minimum value for $x^2+y^2+z^2$ is

${\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2\ge \frac{4{\mathrm{s}}^2}{{\mathrm{a}}^2+{\mathrm{b}}^2+{\mathrm{c}}^2}.$

For if the triangle was an equilateral triangle with sides a we get

${\mathrm{x}}^2+{\mathrm{y}}^2+{\mathrm{z}}^2\ge \frac{1}{4}{a}^2.$

8. Classroom experiment and conclusion

In the framework of a course in a combination of subjects taught to 32 pre-service teachers in mathematics who have completed a first course in calculus, we explained the two methods of finding extrema—with the help of AGM inequality and with the help of calculus. During the course of the semester (usually a 17-week long course), we gave our students the extrema problems discussed above and gave them the option of choosing the AGM inequality or calculus approach. Of course, no multivariate extrema problems were chosen since not all of the students were familiar with the multivariable calculus. Table 1 shows the number of students in each category of using the AGM inequality, using calculus, and could not find any solutions for the indicated extrema problems.

Table 1. Distribution of students' choice of methods for solving problems

Task	AGM inequality	Calculus	No solution
4.2	23	7	2
4.4	19	10	3
5.1	1	0	31
5.3	25	7	0
5.4	21	11	0
5.5	13	19	0
6.1	19	12	1
6.3	21	9	2

After the completion of each task, the class collectively discussed each student’s preferred strategy and the rationale for choosing it. The overwhelming response for choosing the AGM inequality method was the simplicity and elegance of this method. The main answer of those who used calculus was the ease of using a universal method and no need of any further exploration of the problem situation.

With over half a century of teaching experience among the authors of this article, it is our life-long teaching belief that using alternative methods in mathematics helps students to think outside the box of ordinary and stimulates their creativity as well as trigger their curiosity for further advancement of their mathematical knowledge.

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Victor Oxman

The authors are engaged in research to improve the methods of teaching mathematics and searching for new aspects and innovative methods of teaching classical areas of mathematics using the available state-of-the-art educational technologies. An important moment in this work is the use of connections between different parts of mathematics and enrich the “tool box” used by students in mathematics learning. We recognize the great importance of students’ skill development in problem-solving using a variety of methods and techniques from various fields of mathematics and this article is meant to exactly address this task.