The relationships between computational and mathematical thinking: A review study on tasks

Abstract

This review study synthesises the literature on how computational thinking (CT) and mathematical thinking (MT) are integrated into mathematics education research with a focus on tasks. A review of 28 relevant articles on the Web of Science Core Collection database indicated that (1) CT helps students develop and apply mathematical concepts and competence using software or programming; (2) MT helps students solve problems in CT, not necessarily including programming; (3) a reciprocal relationship between CT and MT embeds CT into mathematics learning, where CT is involved in problem-solving, and MT is developed to improve student performance on debugging or reflection; (4) tasks rarely involve creative thinking for creating computational artefacts in CT practices; and (5) tasks rarely involve critical thinking for constructing viable arguments and critiquing the reasoning of others in MT practices. Subsequently, features (including relationship, entry, and what to do) of tasks for integration between CT and MT are proposed.

Keywords:

• computational thinking
• mathematical thinking
• tasks
• systematic review
• cross-disciplinary

1. Introduction

The development of technology has changed our lives. As a result of technological development, computational thinking (CT), including decomposition, pattern recognition, abstraction, and algorithm design, has become a fundamental skill for learners in the 21st century (Hoyles & Noss, 2015; Wing, 2006). Papert (1980) noted that “computer languages that simultaneously provide a means of control over the computer and offer new and powerful descriptive languages for thinking will undoubtedly be carried into the general culture” (p. 98). In his view, computer languages are established to facilitate communication and thinking. This view is echoed in Berland and Wilensky’s (2015) definition of CT as “the ability to think with the computer-as-tool” (p. 630). However, Wing (2006) pointed out that CT uses computers as a thinking tool and a universal attitude and skillset. CT, according to her, accounts for “solving problems, designing systems, and understanding human behaviour, by drawing on the concepts fundamental to computer science” (p. 33).

Therefore, CT can be viewed as a tool and an object of learning, such as language for thinking and thinking skills for problem-solving and positive disposition. Some studies further recognise CT’s ability to help students think mathematically and learn mathematics efficiently (Kynigos & Grizioti, 2018). Using mathematical techniques, concepts, and processes for problem-solving is a form of mathematical thinking (MT; Henderson et al., 2001). MT contributes to problem-solving and conceptual understanding of CT, and CT, in turn, simplifies and performs abstraction by constructing and representing problems in mathematical ways (Rambally, 2016). Thus, there appears to be a reciprocal relationship between them.

Pérez (2018) highlighted the complementary relationship between CT and MT through the inward orientation of MT and outward orientation of CT. The inward orientation serves MT as the dominant epistemic frame with the real-world application of computer science functions to strengthen the understanding of mathematics, whereas the outward orientation emphasises CT as offering a powerful epistemic frame to foreground the relevance of mathematics across diverse disciplines. It implies two roles of CT for MT: development and application.

A common perspective is to view MT and CT as problem-solving (ISTE, 2011; Khalid, 2006). Although some researchers have identified CT as problem-solving using programming, to develop their CT, students do not necessarily need to develop programs (Kaufmann & Stenseth, 2020). Tasks requiring CT with and without the use of computers are categorised as plugged and unplugged tasks, respectively (Kostopolous et al., 2017). Accordingly, two perspectives on CT can be identified as problem-solving with and without programming. Analogically, the perspectives on MT are regarded as problem-solving focused on specific math content and those without such a focus.

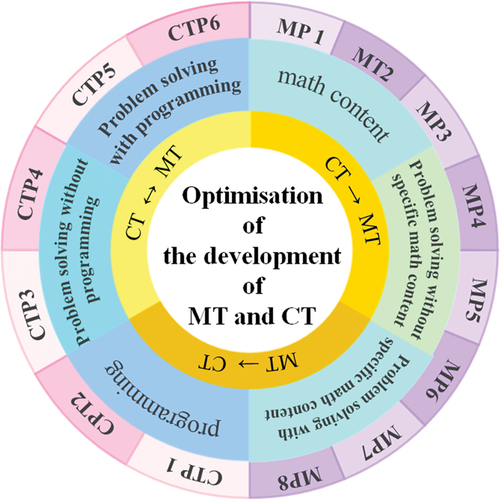
Literature indicates that tasks direct learners’ attention to aspects of content and structure, and influence their learning (Doyle, 1983, p. 161). Different learning tasks may require various types of MT in and with CT and lead to different cognitive outcomes through experiencing a variety of practices. The 2017 College Board highlighted six CT practices based on ideas about problem-solving and creativity in computer science curriculum frameworks. The components of CT practices include CTP1 (connecting computing), CTP2 (creating computational artefacts), CTP3 (abstracting), CTP4 (analysing problems and artefacts), CTP5 (communicating), and CTP6 (collaborating; College Board, 2017). Furthermore, the Common Core State Standards Initiative for Mathematics (CCSSI-M) listed eight mathematical practices for educators to help students develop mathematical competencies. The components of MT practices include MP1 (make sense of problems and persevere in solving them), MP2 (reason abstractly and quantitatively), MP3 (construct viable arguments and critique the reasoning of others), MP4 (model with mathematics), MP5 (use appropriate tools strategically), MP6 (attend to precision), MP7 (look for and make use of structure), and MP8 (look for and express regularity in repeated reasoning; Common Core State Standards Initiative (CCSSI), 2010).

In terms of the relationships between CT and MT and corresponding problem-solving perspectives and practices, the framework of this review study is presented in Figure 1. The inner circle depicts the relationships between MT and CT, including CT contributing to MT, MT contributing to CT, and a reciprocal relationship between the two. For problem-solving, the perspective on CT includes problem-solving with and without programming, and programming itself. The perspective on MT includes problem-solving focused on and not focused on specific math content, and focused on math content. The outermost circle includes six components of CT practices and eight of MT practices. Thus, this review study addresses the following questions:

1. Which relationship between MT and CT has been most emphasised?

2. Which perspective on CT and which component of CT practices in each relationship have been most emphasised?

3. Which perspective on MT and which component of MT practices in each type of relationship have been most emphasised?

Figure 1. Study framework.

Based on the review results, the characteristics of tasks and features of task design will be discussed.

2. Materials and methods

2.1. Resources

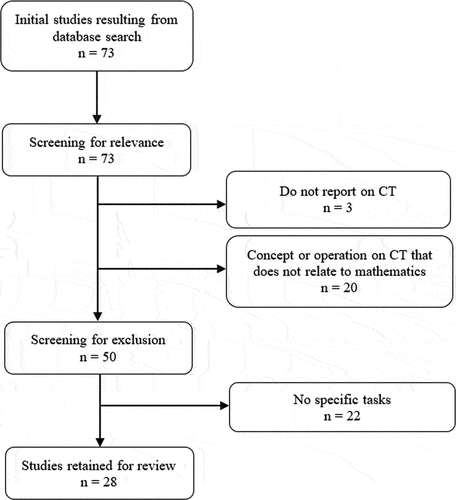
We used keywords for three categories: CT, MT, and Task, and Table 1 illustrates the search terms for these. Within the same category, we used the logic command “OR”, and between categories, we used “AND” in the Web of Science Core Collection database. The inclusion criteria were peer-reviewed articles written in English. The search yielded 71 (n = 71) articles on 23 March 2021. Based on the quality evaluation of mathematics education journals, 13 were identified (Törner & Arzarello, 2012; Williams & Leatham, 2017). However, four of the 13 journals are not included in the Web of Science Core Collection database: EURASIA Journal of Mathematics, Science and Technology Education (EURASIA); For the Learning of Mathematics (FLM); International Journal for Mathematics Teaching and Learning (IJMTL); and ZDM: International Journal on Mathematics Education (ZDM). For the period mentioned above, EURASIA, FLM, and ZDM were included in the Scopus database. We used the same keywords to investigate these three journals, and a total of four papers were identified. Duplicate articles (n = 2) were removed, and finally, a total of 73 (n = 73) articles were identified.

Table 1. Search terms for the three categories

Category	Search terms
CT	computational thinking, computational literacy, computational competence, computational proficiency, computational skill*, programming thinking, programming competence, programming literacy, programming proficiency, programming skill*, programmatic thinking, programmatic literacy, programmatic competence, programmatic proficiency, programmatic skill*
MT	mathematics, mathematical
Task	task*, activity*

Note: CT, computational thinking; MT, mathematical thinking

Figure 2 illustrates the literature-screening process. First, we excluded articles (n = 3) that did not report on CT. Next, concepts or operations on CT unrelated to mathematics (n = 20) were removed. Finally, studies that did not report specific tasks were excluded (n = 22).

Figure 2. Diagram of the screening process.

Six coders conducted the literature-screening process to confirm the retained articles. One coder read each of the 73 articles, and the other read 14–15 articles independently. Then, we examined the inter-rater reliability of each pair and calculated the average of the five inter-rater reliability values, which came to 86.4%. Then, the six coders discussed the articles to reach a consensus. Consequently, 28 articles comprising 78 tasks were finally included.

2.2. Analysis of units

Table 2 presents the number of tasks in each article; most studies include one task. Table 3 illustrates the educational level of tasks in each article; most studies focus on elementary students.

Table 2. The number of tasks in each article

Number of tasks	Article ID	Total articles
n = 1	No.1, No. 4, No. 6, No. 7, No. 9, No. 11, No. 13, No. 19, No. 21, No. 22, No. 24, No. 26	12 (43%)
n = 2	No.15, No. 17, No. 25	3 (11%)
n = 3	No.12, No. 14, No. 16, No. 18, No. 23, No. 28	6 (21%)
n = 4	No.2, No. 5, No. 8, No. 10	4 (14%)
n = 7	No.3	1 (4%)
n = 9	No.27	1 (4%)
n = 10	No.20	1 (4%)

Table 3. Level of tasks of each article

Articles Level	Article ID	No. of Tasks
Kindergarten N = 3 (4%)	No.13, No. 21, No. 25	#33, #58, #64
Elementary school N = 46 (59%)	No.1, No. 2, No. 3, No. 5, No. 6, No. 7, No. 10, No. 11, No. 12, No. 15, No. 16, No. 17, No. 18, No. 20, No. 24, No. 25, No. 26	#1, #2, #3, #4, #5, #6, #7, #9, #10, #11, #14, #15, #16, #17, #18, #19, #25, #26, #27, #28, #29, #30, #31, #37, #38, #39, #40, #41, #42, #43, #44, #45, #46, #48, #49, #50, #51, #52, #52, #54, #55, #56, #57, #63, #65, #66
High school N = 11 (14%)	No.3, No. 4, No. 9, No. 12, No. 23, No. 28	#8, #12, #13, #24, #32, #60, #61, #62, #76, #77, #78
College/university N = 13 (17%)	No.14, No. 19, No. 27	#34, #35, #36, #47, #67, #68, #69, #70, #71, #72, #73, #74, #75
School teacher N = 5 (6%)	No.8, No. 22	#20, #21, #22, #23, #59

2.3. Coding schemes

To answer the research questions, coding schemes for relationships, perspectives on CT and MT, and components of CT and MT practices were determined. The following coding schemes were used in the study.

2.3.1. Relationships

Pérez (2018) proposed two orientations of CT and MT. The outward orientation can be regarded as applying mathematics; for example, students programmed a parametric cube model that could be animated from a 2D cube net to a cube with dynamic manipulation. Students needed to know the dihedral angle and rotation in space, and they used these concepts for the role of parameters in procedural programming (Kynigos & Grizioti, 2018).

By contrast, inward orientation can be regarded as applying CT. For example, computer programs show a secant clicking along a curve, representing the gradient function of the curve. Computer programs allow teachers to demonstrate mathematical concepts and practices and allow students to explore them (Tall, 1986). In addition to the two orientations, Rambally (2016) pointed out the existence of a synergistic relationship between CT and MT. For example, students used Scratch to make a square. In solving this task, students’ understanding of mathematical patterns and structures was promoted based on their initial understanding of squares and through learning how to code. The task questions included: “Which mathematical concepts did you need to use to solve this problem?” and “How did you code your Scratch cat/robot to rotate 90 degrees?” The progress of problem-solving starts from applying MT (concept of squares) to CT, then returning to deepen the understanding of MT (rotation of the angle). Based on Pérez (2018) and Rambally (2016), the relationships between CT and MT were coded as CT contributes to MT (CT→MT), MT contributes to CT (MT→CT), and a reciprocal relationship between CT and MT (CT↔MT).

2.3.2. Perspectives on CT

Miller’s (2019) study on how MT can be promoted through coding activities is an example of problem-solving with programming. This study focused CT on recognising patterns, decomposing, abstracting, and creating algorithms in computer programming contexts to solve mathematical problems. Rosamond’s (2018) task of contextualising directed graph theory would be an example of problem-solving without programming. This study focused CT on the algorithmicising approach, which denotes “an approach to solving mathematical problems whereby one explicitly creates an algorithm that can be used to find a solution at hand” (Moala, 2021, p. 267). Further, Munõz et al.’s (2020) study on improving logical-mathematical skills through educational robotics is an example of programming. This study did not focus on problem-solving; instead, it aimed to improve logical-mathematical skills through writing programs.

2.3.3. Perspectives on MT

Lockwood and De Chenne (2020) study on how Python programming can facilitate student combinatorial reasoning is an example of problem-solving focused on specific math content. Nam et al.’s (2019) study on the effects of a card-coded robotics curriculum is an example of problem-solving without focus on specific math content. These researchers used a card-coded robotic curriculum and examined the effects of associated activities on kindergarteners’ sequencing and problem-solving skills. Moreover, Rosamond’s (2018) study on how unplugged activities can assist teachers in motivating and arousing students’ interest in informatics is an example of math content. In their study, they assigned participants an unplugged activity to demonstrate the mathematics underlying public-key cryptography.

2.3.4. Components of CT practices

Table 4 displays the six components (College Board, 2017) of CT practices and their expectations for students.

Table 4. Components of computational thinking practices (College Board, 2017)

Components of CT practices		Expectations for students
CTP1	Connecting computing	Identify impacts of computing. Describe connections between people and computing. Explain connections between computing concepts.
CTP2	Creating computational artefacts	Create a computational artefact with a practical, personal, or societal intent. Select appropriate techniques to develop a computational artefact. Use appropriate algorithmic and information management principles.
CTP3	Abstracting	Explain how data, information, or knowledge is represented for computational use. Explain how abstractions are used in computation or modelling. Identify abstractions. Describe modelling in a computational context.
CTP4	Analysing problems and artefacts	Evaluate a proposed solution to a problem. Locate and correct errors. Explain how an artefact functions. Justify the appropriateness and correctness of a solution, model, or artefact.
CTP5	Communicating	Explain the meaning of a result in context. Describe computation with accurate and precise language, notations, or visualisations. Summarise the purpose of a computational artefact.
CTP6	Collaborating	Collaborate with another student in solving a computational problem. Collaborate with another student in producing an artefact. Share the workload by providing individual contributions to an overall collaborative effort. Foster a constructive, collaborative climate by resolving conflicts and facilitating the contributions of a partner or team member. Exchange knowledge and feedback with a partner or team member. Review and revise their work as needed to create a high-quality artefact.

Note: CT, computational thinking

2.3.5. Components of CT (MT) practices

Table 5 displays the eight components of MT practices and their meanings.

Table 5. The components of mathematical thinking practices (Common Core State Standards Initiative (CCSSI), 2010)

CCSSI for the components of mathematics practices		The meaning of mathematics practices
MP1	Make sense of problems and persevere in solving them.	Students start by explaining to themselves the meaning of a problem and looking for entry points to its solution.
MP2	Reason abstractly and quantitatively.	Students make sense of quantities and their relationships in problem situations.
MP3	Construct viable arguments and critique the reasoning of others.	Students understand and use stated assumptions, definitions, and previously established results in constructing arguments.
MP4	Model with mathematics.	Students can apply their mathematical skills to solve problems arising in everyday life, society, and the workplace.
MP5	Use appropriate tools strategically.	Students consider the available tools when solving a mathematical problem.
MP6	Attend to precision.	Students try to communicate precisely with others.
MP7	Look for and make use of structure.	Students look closely to discern a pattern or structure.
MP8	Look for and express regularity in repeated reasoning.	Students notice if calculations are repeated and look for both general methods and shortcuts.

Note: CCSSI-M, Common Core State Standards Initiative for Mathematics

For example, Kopcha et al. (2021) used an educational robotics activity to explore CT embodiment. Two students controlled a robot using two-unit movements—one for turning and the other for moving forward—simulating the motion with their bodies. They established unit movements based on the distance-speed-time relationship to control the robot and multiplicative reasoning to manipulate forward unit movement. Thus, they analogised themselves to a robot and found a connection between themselves and computing, specifically, CTP1. Multiplicative reasoning and data representation for the computation were coded as CTP3; sensing quantities and reasoning quantitatively were coded as MP2. Describing computation using accurate language by communicating with each other to solve problems were coded CTP5, MP6, and CTP6.

2.4. Data analysis

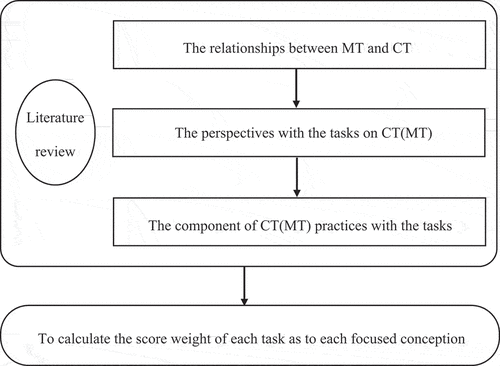
Based on the literature screening, 28 articles and 78 tasks were recognised. The data analysis comprised four steps (Figure 3). The first step was to identify the relationship between CT and MT to clarify whether CT contributes to MT, MT contributes to CT, or a reciprocal relationship exists between the two. The second step was analysing the perspectives on CT and MT. Each study was classified as problem-solving with (and without) programming, or programming itself. Additionally, each study was classified as problem-solving focused on (and without focus on) specific math content or focus on math content itself. The third step was analysing each task by identifying the components of CT (MT) practice. The coding categories included CTP1 to CTP6 and MP1 to MP8. The fourth step was calculating the score weight of each task, according to the count of coding categories, for each focused conception. Since each article included a different number of tasks, we defined the total score of each article as 1. The score weight of each task was calculated as 1 divided by the number of tasks in each article. The score weight of each practice of the same task was calculated as the score weight of each task divided by the number of practices for each task.

Figure 3. Research processes.

To ensure coding validity, the justification process was divided into three rounds. First, two authors reviewed one article comprising three tasks to clarify the meaning of coding schemes for the focused conceptions. Then, they independently coded seven articles, including 20 common tasks, and achieved an inter-rater reliability of 88.7%. In the event of a disagreement, discussions were held to achieve consensus. The first author independently coded 20 articles, including the remaining 55 tasks.

3. Results

This study analysed 78 tasks identified from 28 articles. The results of the study are given below.

3.1. Relationships between MT and CT

As illustrated in Table 6, the major relationship found in the tasks in the articles was the contribution of CT to MT (50.0%), followed by the contribution of MT to CT (39.3%), and only a few reciprocal relationships between CT and MT (10.7%). Regarding the contribution of CT to MT, CT is the core and promotes mathematical knowledge, concepts, and structures. For example, Lockwood and De Chenne (2020) used coding to facilitate mathematical learning in combinatorics. For the contribution of MT to CT, mathematics is the core and is explicitly required to solve problems and write programming codes. For example, students used mathematical concepts, such as odd and even numbers, to design computer programs (Milicic et al., 2020). For the reciprocal relationship between CT and MT, learning paths can be divided into two types: CT→MT→CT and MT→CT→MT. By infusing CT into the domain of mathematics, CT becomes the major thinking in students’ problem-solving. Reciprocally, MT may improve students’ debugging performance, such as by checking their incorrect answers. Students are required to solve problems within a block-based programming environment, where the CT tasks include the concepts of sequence, repetition, and conditional logic.

Table 6. The relationships between mathematical and computational thinking

Relationships	CT→MT N = 14 (50.0%)	MT→CT N = 11 (39.3%)	CT←→MT N = 3 (10.7%)
Article ID (N = 28)	No.1, No. 3, No. 4, No. 5, No. 11, No. 12, No. 13, No. 16, No. 20, No. 21, No. 24, No. 26, No. 27, No. 28	No.6, No. 7, No. 8, No. 10, No. 14, No. 15, No. 18, No. 19, No. 22, No. 23, No. 25	No.2, No. 9, No. 19

Note: CT, computational thinking; MT, mathematical thinking

3.2. Perspectives on CT and components of CT practices

3.2.1. Perspectives on CT

Table 7 illustrates the result of the perspectives on CT. Most of the perspectives comprise problem-solving with programming (60.7%), followed by problem-solving without programming (28.6%), and programming (10.7%). For the contribution of CT to MT, most perspectives on CT comprise problem-solving with programming (35.7%), indicating that CT promoted understanding and learning of mathematics more with programming, than without. Problem-solving with programming is considered an approach drawing upon CT. For example, Lockwood and De Chenne (2020) introduced some simple concepts in Python (for loops and particular conditional statements) for students to code. Students wrote computer programs to list sets of outcomes and received immediate feedback. Python programming helps students better understand and strengthen the relationship between counting processes and sets of outcomes, such as unrestricted repetition or no repetition.

Table 7. Perspectives on computational thinking

Relationships The perspectives on CT	CT→MT N = 14 (50.0%)	MT→CT N = 11 (39.3%)	CT←→MT N = 3 (10.7%)
Problem-solving without programming N = 8 (28.6%)	2 (7.1%)	6 (21.4%)	-
Problem-solving with programming N = 17 (60.7%)	10 (35.7%)	4 (14.3%)	3 (10.7%)
Programming N = 3 (10.7%)	2 (7.1%)	1 (3.6%)	-

Note: CT, computational thinking; MT, mathematical thinking

For the contribution of MT to CT, most CT perspectives comprised problem-solving without programming (21.4%), indicating that the process as a solution is more important than programming itself. Moala (2021) provided a contextualised graph theory unplugged task for 12th graders and university students, requiring them to create and explicitly articulate an algorithm. He indicated that the algorithmicising approach revolves around students’ mathematical activity on tasks and can enhance students’ CT.

For the reciprocal relationship between CT and MT, the perspective on CT only relates to problem-solving with programming. This implies that programming may be key to integrating CT and MT. For example, in a task by Ng and Cui (2021), Mr Cheng gave Claire $3, which doubled each subsequent weekend. Students had to design a device to display Claire’s deposits. Some coded the balance after n days in a geometric series, and others used different approaches. They found the mathematical rule to determine the next sequence term: t_n = 2t_n-1 + 3. Thus, CT strengthens learners’ understanding of mathematical concepts, which is explicitly required to write programming codes, and MT and CT are closely linked to the task.

3.2.2. Components of CT practices

Table 8 presents the components of CT practices. CTP3 (abstracting) (38.6%) was the major component, followed by CTP6 (collaborating) (24.1%), indicating that abstracting is the most common component for MT and CT combined.

Table 8. Components of computational thinking practices

Relationships Component of CT practices	CT→MT N = 14 (50.0%)	MT→CT N = 11 (39.3%)	CT←→MT N = 3 (10.7%)
CTP1 (7.7%)	3.5%	1.6%	2.6%
CTP2 (3.3%)	1.9%	0.7%	0.7%
CTP3 (38.6%)	22.0%	14.7%	1.9%
CTP4 (16.0%)	6.8%	7.7%	1.4%
CTP5 (13.0%)	4.6%	5.8%	2.6%
CTP6 (24.1%)	11.3%	8.8%	1.4%

Note: CT, computational thinking; MT, mathematical thinking

For the contribution of CT to MT, tasks involving CTP3 often provided CT environments where students had to explain how abstractions are used in computation or modelling, and develop an understanding of mathematical concepts by reflecting on CT practices. For example, as demonstrated by Miller (2019), students explored repeating patterns using Scratch, and found that a spirolateral moves one length and turns 90 degrees as a pattern. They used coding to develop their own generalised rules for the perimeter and promote their understanding of mathematical patterns and structures.

In terms of the contribution of MT to CT, tasks involving CTP3 often require mathematical skills to decompose complex problems using computational perspectives to solve them. They explain how data, information, or knowledge are represented, and this process may improve their CT. For example, students programmed and designed abstract models when they deconstructed 3D complex models into smaller parts or 2D shapes (e.g., cube to squares). Then, they used these smaller shapes to create other objects (e.g., a square pyramid; Kynigos & Grizioti, 2018).

For the reciprocal relationship between CT and MT, tasks involving CTP3 often embedded CT into mathematics learning, which reciprocally supports the abstract concepts in programming contexts. For example, when students used an angle card to make their turns and explained how to make turns using the card, they were required to create coding blocks for the path of an equilateral triangle as they performed on the floor grid or a piece of paper (Sung & Black, 2020). Tasks involving CTP1 (connecting computing) and CTP5 (communicating) were the most common components of CT practices for the reciprocal relationship between CT and MT. This may be due to the use of the perspective of a robot or virtual character in tasks. Further, students must describe algorithms using accurate language when interacting with a robot or writing programs. In addition to abstracting, CTP6 (collaborating) (19.1%) was the secondary component of CT practices for each type of relationship identified in the literature. This implies that collaboration is important for problem-solving.

3.3. Perspectives on MT and components of MT practices

3.3.1. Perspective on MT

Table 9 presents the perspectives on MT. Most perspectives on MT comprise the math content itself (46.4%), followed by problem-solving without specific math content (28.6%) and problem-solving with specific math content (25.0%). In terms of the contribution of CT to MT, most perspectives on MT were related to the math content itself (25.0%), indicating that the task design first considers mathematical concepts. For example, teachers first considered the mathematical content they intended to teach (e.g., fractions—identifying; geometry and measure—area, perimeter, and angles), and then the CT (including unplugged and plugged) that would support the teaching and learning of the specific content (Bouck & Yadav, 2020).

Table 9. Perspectives on mathematical thinking

Relationships The perspectives on MT	CT→MT N = 14 (50.0%)	MT→CT N = 11 (39.3%)	CT←→MT N = 3 (10.7%)
Problem-solving without specific math content N = 8 (28.6%)	4 (14.3%)	3 (10.7%)	1 (3.6%)
Problem-solving with specific math content N = 7 (25.0%)	3 (10.7%)	2 (7.1%)	2 (7.1%)
Math content N = 13 (46.4%)	7 (25.0%)	6 (21.4%)	-

Note: CT, computational thinking; MT, mathematical thinking

For the contribution of MT to CT, most perspectives on MT also comprised the math content itself (25.0%), indicating that embodied mathematical concepts guided CT. For example, students used decomposition to conceptualise a possibility for action. They used their hands and bodies to indicate moving forward one unit square while engaging in pattern recognition and algorithmic thinking simultaneously (Kjällander et al., 2021).

For the reciprocal relationship between CT and MT, there was no task focused on the math content, implying that problem-solving is a feasible approach to making CT and MT reciprocal. Tasks may provide learning environments designed to apply CT concepts in solving mathematical problems, and reflecting on thinking procedures affects performance in programming tasks. Tasks created problem-solving opportunities for students to demonstrate their mathematical understanding through CT activities and learn mathematics through CT experiences. For example, students learnt to calculate area and volume by calculating the volume of a real tower using its physical models created with Unifix cubes. The model and code developed by one student were hidden from another, and the second student followed the code to build the tower (Israel & Lash, 2020). The tasks provided the opportunity for another type of collaboration for problem-solving.

3.4. Components of MT practices

Table 10 presents the components of MT practices. MP6 (attend to precision) (23.8%) was the major component, followed by MP7 (look for and make use of structure) (19.3%). This may be because precision and unambiguous language can support students in communicating abstract and logical ideas. For the contribution of CT to MT, tasks involving MP6 often needed students to state the meaning of the program. The following task demonstrated both MP6 and MP7 simultaneously. The researcher presented an image of a spirolateral to the students and asked them to draw its shape using a specific repeating pattern (Miller, 2019), which allowed students to think abstractly and mathematically. Programming language helped students reason with mathematical concepts.

Table 10. Components of mathematical thinking practices

Relationships Component of MT practices	CT→MT N = 14 (50.0%)	MT→CT N = 11 (39.3%)	CT←→MT N = 3 (10.7%)
MTP1 (13.4%)	8.9%	3.6%	0.9%
MTP2 (14.6%)	3.0%	10.7%	0.9%
MTP3 (0.9%)	-	0.9%	-
MTP4 (11.6%)	7.1%	1.8%	2.7%
MTP5 (12.2%)	8.9%	2.1%	1.2%
MTP6 (23.8%)	8.9%	12.8%	2.1%
MTP7 (19.3%)	8.9%	7.4%	3.0%
MTP8 (4.2%)	4.2%	-	-

Note: CT, computational thinking; MT, mathematical thinking

For the contribution of MT to CT, tasks involving MP6 often required students to use mathematical language to discuss their reasoning with others. For example, students were asked to create an unplugged algorithm (the solution for a problem) for finding an optimal seating arrangement (i.e. the highest group happiness score) on a contextualised graph theory task (Moala, 2021). Thus, students applied mathematical concepts to formulate their problem-solving strategies.

For the reciprocal relationship between CT and MT, tasks involving MP6 often provided the chance to state the meaning of programming or communicate precisely to others through different task designs. MP7 (look for and make use of structure) and MP4 (model with mathematics) were the first and second most common components, respectively, of CT practices. Similarly, for the contribution of CT to MT, tasks involving MP4 often required students to use their mathematical skills to solve problems or describe a situation. Some tasks focused on space and shape and asked students to discern a pattern or a feature of the shapes. For example, students were asked to draw a shape that looks like a plus sign consisting of five squares of the same size using the Scratch program. Students needed to know the graph patterns and structures while coding and correct the errors, because the program does not demonstrate what is supposed to be done (Milicic et al., 2020). Some tasks focused on algebra and asked students to discern a structure such as the same amount, mathematics expressions, or algebraic expressions. For example, students developed a multiplication machine in Scratch and noticed the structure of number patterns to design a machine that multiplies two numbers by repeating addition, such as 17∙5 calculated as follows:

$17\cdot 1=17\cdot 0+17=0+17=17$

$17\cdot 2=17\cdot 1+17=17+17=34$

$17\cdot 3=17\cdot 2+17=34+17=51$

$17\cdot 4=17\cdot 3+17=51+17=68$

$17\cdot 5=17\cdot 4+17=68+17=85$

(Bråting & Kilhamn, 2021, p. 178).

4. Discussion and conclusion

4.1. Creative thinking for creating computational artefacts

Among the components of CT practices, this study found that CTP2 (creating computational artefacts) (3.0%) was rarely involved in the task of mathematical education for the learning and teaching of CT and MT. Creative thinking is one of the 21st-century skills included in the Programme for International Student Assessment (PISA) 2021 (Organisation for Co-operation and Development (OECD), 2019). Creative thinking results in original and effective solutions, and also benefits the way students learn. Some studies (Akcaoglu, 2014) have claimed that learning CT can help them develop their creativity and problem-solving skills. It would be beneficial to conduct creative task studies on mathematical education for the learning and teaching of CT and MT.

4.2. The need for MT3 and MP8 for systems thinking

Among the components of MT practices, there was little research demonstrating the use of MP3 (construct viable arguments and critique the reasoning of others) (1.1%) and MP8 (look for and express regularity in repeated reasoning) (3.2%) for task design. Solving problems in MP3 and MP8 may involve systems thinking, which is another of the 21st-century skills in PISA 2021 (Organisation for Co-operation and Development (OECD), 2019). The literature indicated that systems thinking potentially benefits teaching and learning (Mathews & Jones, 2008). For example, students who demonstrate systems thinking exhibit higher problem-solving skills, as they consider a wider range of factors and organise their responses more effectively (Jacobson, 2001). When students reason inductively about data, establish results in constructing arguments, and recognise and use counterexamples, they use critical thinking and reflection. These two thinking skills are also 21st-century skills (Organisation for Co-operation and Development (OECD), 2019). Therefore, it would be beneficial to design tasks in MP3 and MP8 on mathematical education for the learning and teaching of CT and MT.

4.3. Features of tasks for integration between CT and MT

As for each type of relationship between CT and MT, we highlight the entries and what to do in various tasks for the most common practices, as illustrated in Table 11.

Table 11. Features of tasks with integration between CT and MT

Relationship		Entry	What to do
Contribution of CT to MT		(1) Use of tools Software, e.g., Excel, spreadsheet, etc. Physical material, e.g., calculator, colour beads, etc.	To visualise mathematical concepts using tools (CTP3, MP5). To release calculation burden using tools (CTP4, MP5).
		(2) Programming, e.g., Scratch, Python, etc.	To interpret mathematical concepts by applying them to write programs (CTP3, MP1, MP6, MP7) To explore mathematical concepts through recognising patterns to write programs (CTP3, MP7)
Contribution of MT to CT		Math concepts or competencies, e.g., definitions, relationships, logical thinking, etc.	To solve problems with or without programming by applying mathematical concepts (CTP3, MP1, MP6, MP7) To learn procedural thinking for algorithm design by applying mathematical competencies to establish models (CTP3, MP4)
Reciprocal relationship between CT and MT	CT→MT→CT	Programming, e.g., Arduino, C++, etc.	To interpret mathematical concepts by applying them to write programs and test codes (CTP1, CTP3, CTP5, MP1, MP6, MP7) To explore mathematical concepts by testing others’ programs step by step and debugging the programs (CTP1, CTP3, CTP5, MP4, MP7)
	MT→CT→MT	Math problem	To solve mathematical problems with or without programming by applying mathematical concepts or competencies and reflecting the result (CTP3, CTP5, MP1, MP6, MP7)

Note: CT, computational thinking; MT, mathematical thinking

4.4. Contribution of CT to MT

Regarding the contribution of CT to MT, using tools (digital or physical) and programming are two main entries. Students are asked to visualise mathematical concepts using tools as one entry, which can also be used to release the calculation burden (Benakli et al., 2017; Bouck & Yadav, 2020). Programming is the second entry. Students are asked to interpret and explore mathematical concepts by applying their prior knowledge of CT, such as pattern recognition, decomposing, abstract, and creating algorithms in computer programming contexts. The entry is similar to Threlfall’s (1999) notion that the ability to discern patterns, that is, identifying the unit of repetition, is the precursor to generalising mathematics. As students engaged with CT tasks, they constructed and internalised their knowledge of mathematical concepts and symbolic understanding (Miller, 2019; Nam et al., 2019; Sung et al., 2017).

4.5. Contribution of MT to CT

For the contribution of MT to CT, applications of mathematical concepts or competences are the main entry. Students are asked to write programs by applying their prior knowledge of mathematical concepts, such as definitions (Kynigos & Grizioti, 2018; Moala, 2021; Rosamond, 2018), or to establish the model by applying their mathematical competences. This process can promote procedural thinking for algorithm design (Wilkerson & Fenwick, 2017). For example, students must create an algorithm to find an optimal seating arrangement on a contextualised graph theory task. This task can be interpreted as a problem of finding the maximum Hamiltonian path in the given network. Students use their mathematical competencies to create an algorithm to derive a solution for a problem, and the algorithmicising approach is a critical component of CT (Moala, 2021).

4.6. Reciprocal relationship between CT and MT

There are two types of learning paths: CT→MT→CT and MT→CT→MT. In the first path, programming is the entry. Students are asked to interpret and explore mathematical concepts by applying their prior CT knowledge in computer programming contexts and then applying mathematical concepts to test the code (Cui & Ng, 2021). Students must also test others’ programs step by step and debug them (Israel & Lash, 2020). In the second path, the mathematical problem is the main entry. Students are asked to write programs by applying their mathematical concepts or competencies to solve mathematical problems; consequently, their understanding of mathematical concepts is deepened and extended through explaining and reflecting on programming and programs (Sung & Black, 2020).

4.7. Why CT and MT are reciprocal

For problem-solving, CT and MT commonly concern the structure of a process involving symbolisation and the understanding of systematic representations (Bråting & Kilhamn, 2021). This may be one reason CT and MT can be reciprocal. Using tools, CT can benefit the transformations within or between semiotic representations, which are pivotal for mathematical thinking and working, according to Duval’s (2006) theory of semiotic representations. Additionally, programming languages, which does not involve vagueness and builds all communication on algorithmic processes, can deepen students’ understanding of mathematical concepts (Gazoni, 2018). By contrast, both horizontal and vertical mathematisation as part of problem-solving can benefit CT learning (Kallia et al., 2021). Another common feature of CT and MT is the application of algorithms and the development of algorithmic thinking (Kalelioglu et al., 2016; Lockwood et al., 2016; Stephens & Kadijevich, 2020). Algorithmic thinking can act as a bridge between processes and concepts or between operational and structural conceptions because of the symbol’s dual role as a process and concept (Tall et al., 2000). According to our review study, algorithms can be developed through testing and debugging codes, which can engender the ability to recover from mistakes effectively to improve CT and MT.

In addition to the above features, one entry to implement most of the tasks (e.g., Kynigos & Grizioti, 2018; Munõz et al., 2020; Pérez, 2018) is peer collaboration. This underlying feature is recognised as facilitating learning through the need for communication and implies the importance of social interactions for developing CT and MT.

5. Conclusion

This review study aimed to optimise the development of MT and CT. The result demonstrates that little research concerns the reciprocal relationship between CT and MT, and most of the tasks are related to the perspective on CT as problem-solving with programming and the perspective on MT as mathematical content. To make CT contribute to MT, mathematical concepts should be visualised by asking students to manipulate digital or physical tools, and interpret and explore mathematical concepts by writing programs. For example, students can embody mathematical concepts and generate procedures for drawing a square using Scratch (Miller, 2019). For MT to contribute to CT, procedural thinking for algorithm design should be learnt by asking students to apply mathematical concepts or competencies. For example, students are asked to break down the problem into smaller pieces by applying mathematical thinking to decompose complex 3D structures into 2D using Logo programming (Kynigos & Grizioti, 2018). For reciprocal relationships between CT and MT, there are two learning paths. The first path asks students to apply and explore mathematical concepts by asking students to test and debug codes in addition to writing programs (Cui & Ng, 2021). The second path asks students to solve mathematical problems using plugged tasks and reflect on the coherence between mathematical solutions and the codes (Sung & Black, 2020). The results also suggest that mathematics teachers need to learn more about writing programs to integrate MT with CT, which can deepen students’ learning of CT and MT.

For the components of CT practices, CTP3 (abstracting) was most frequently identified. This implies that abstraction—the “mental tool of computing”—is considered key to CT and MT. In CTP3, tasks can allow students to focus on the important information and filter out irrelevant and less useful information when solving problems. CTP2 (creating computational artefacts) was identified the least. Creative thinking is particularly necessary when students are challenged with problems where conventional techniques do not work. More efforts to design tasks involving CTP2 are needed to develop students’ CT and MT to creatively solve problems (College Board, 2017).

For the components of MT practices, MP6 (attend to precision) was identified as the most frequent practice. This might be because students are required to explain the meaning of programming or use mathematical language to discuss their work, and then, precise language is developed for effective communication and cooperation. MP3 (construct viable arguments and critique the reasoning of others) was rarely included in the tasks identified from the articles. The practice is related to test and debug codes, which were also less concerned in the literature. This indicates that researchers need to design tasks that require students to reflect on the coherence between solutions and codes, and construct mathematical arguments to explain why the codes are or are not effective.

The review results also suggest that the six components of CT practices and the eight components of MT practices are sufficient to classify the tasks concerning CT and MT. However, while principles for task design involving rich CT and MT practices require further investigation, this review study offers a comprehensive picture of the tasks that have been used to integrate CT and MT with different approaches and practices in the literature.

Acknowledgements

This work was supported by the Ministry of Science and Technology under Grant number 110-2511-H-003 −008 -MY3.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Ministry of Science and Technology, Taiwan [110-2511-H-003 −008 -MY3].