Analysis of senior high school students’ errors in solving trigonometry

Abstract

Students’ competence in solving trigonometry has been in doubt but little attention has been given in the area of research. An assessment of students’ answers to trigonometry problems is crucial to dealing with their conceptual challenges. This study employed a descriptive qualitative research design, with the goal of evaluating errors made by students when solving trigonometric problems. Ninety senior high school students were sampled for this purpose and the data collection instruments used were a Trigonometry Achievement Test (TAT) and a Semi-structured interview. The Trigonometry Achievement Test (TAT) was designed to identify the types of errors learners make when answering trigonometry problems. Data gathered from the (TAT) was analyzed and presented using descriptive statistics. In classifying students’ errors, Newman’s Error Hierarchy was utilized. A semi-structured interview was also conducted and aimed at identifying the root cause of students’ errors. Findings showed that a greater part of student errors relate to transformation, processing skills, and comprehension. Also, teachers’ methods of instruction, students’ carelessness, incorrect application of trigonometric identities and formulas, overgeneralization, and a lack of practice are the primary reasons for errors. Thus, trigonometry lessons should be taught by math teachers in a more hands-on and inductive manner as students are also advised to constantly practice solving trigonometry. Our study argues that assessment of students’ answers in solving trigonometry problems, recognizing the errors made and comprehending the reasons behind them will guide instructional strategies that will make trigonometry learning easier.

Keywords:

• Error analysis
• trigonometry
• Newman hierarchical model
• mathematical errors
• error types
• qualitative analysis

Subjects:

• Mathematics Education
• Study Skills
• Theory of Education
• Curriculum Studies
• International & Comparative Education
• Middle School Education
• Research Methods in Education
• Secondary Education
• Education – Social Sciences

Introduction

Mathematics as a subject is indispensable in our dispensation whereby there are many progressive advancements. An individual’s capability to improve oneself whether in technological advances or diverse areas in the future depends heavily on early mathematics competence (Geraniou & Misfeldt, 2023; Larbi et al., 2024). The academic world is not complete without mathematics. In view of this, we can say for human activities to advance, mathematics is essential. Many studies have revealed that indeed many students face challenges while learning mathematics (Irfan et al., 2020; Moschkovich, 2010). Oleson and Hora (2014) have indicated that learning difficulties can be influenced by the student’s history and culture, the instructor’s approach, and the materials used in the classroom; this demonstrates that students may face a range of difficulties while acquiring mathematical knowledge. There may exist distinctive dissimilar difficulties in learning mathematics since mathematics is a broad area with other branches as Algebra, Calculus, Statistics, etc. Because trigonometry integrates algebraic, geometric, and pictorial reasoning, it remains as being part of the most crucial subjects in High Schools’ mathematics curriculum. For students to succeed in calculus and other advanced mathematics, trigonometry is a crucial mathematics subject that needs to be mastered (Hanifah et al., 2020). Most junior high school [JHS] trigonometry textbooks typically start with the identification of the sides of right-angled triangles. Students are subsequently shown how to compute right angles using Pythagoras’ theorem and regular trigonometric ratios such as cosine, sine, and tangent. All these also have elements of Algebra and Geometry (Banson et al., 2022). Throughout high school, students are steadily introduced to more complex trigonometric concepts such as the sine and cosine rules, trigonometric identities, compound identities and their numerous applications in the real world which is seen in the concepts of bearing, and projectile motion as well as the angle of elevation and depression. In light of this, Weber (2008) argues that having a basic understanding of trigonometry can act as a crucial building block for calculus, as well as college-level mechanics, surveying, architecture and engineering courses.

According to Gur (2009), students perceive trigonometry to be more challenging and esoteric when compared to other math topics. Students face difficulties for the first time since it necessitates that they connect triangle diagrams with numerical connections and deal with the symbols utilized in these kinds of relationships. Therefore, it is important to help students perceive and comprehend why learning trigonometry is important (Gur, 2009), as this will enable students to appreciate and stimulate their interest in learning trigonometry.

A trigonometry problem is an inquiry into mathematics that pertains to trigonometry and that also demands students to read, understand, transform, process and encode. Trigonometric problems are sometimes posed as word problems. In some cases, learners are required to use multi-steps to deal with a task. Unfortunately, such logic is unfamiliar to many SHS students (Weber, 2008). According to studies, using multiple stages to solve a math word problem can increase the likelihood of making mistakes while determining the correct solutions (Dewanto et al., 2017). This explains why most students are reluctant to answer examination questions (both internal and external) on trigonometry problems. The West African Senior Secondary Certificate Examinations (WASSCE), which include word problems involving trigonometry, have long been a source of complaint for the West Africa Examination Council [WAEC], an examination body in West Africa. The examiner’s report for the WASSCE (2015, 2016) indicates that few students undertake word problem questions and those that do make mistakes. Agoestanto et al., in their study, reported that except for reading, students with low cognitive abilities frequently make all kinds of errors. Sulistyaningsih et al. (2021) study on students’ errors in solving trigonometry reported a total of 679 student errors according to the classification of Newman’s error theory as fluency (reading and comprehension) errors accounted for 22.98% of the errors, but mathematical processing errors (transformation, processing skills and encoding) accounted for 77.02% of the errors. Notwithstanding, Mensah (2017), reported in his study that process skills, transformation, and comprehension errors are the most common mistakes students make while applying formulas and right-angled triangles to solve trigonometrical ratios.

According to a study by Orhun (2002) on the challenges students encounter when applying trigonometry concepts to trigonometric–related problems, it was found that students could not fully comprehend the fundamental concepts of trigonometry and based on this they made mistakes. Students’ trigonometry knowledge is only briefly imparted via the teacher-active approach and memorization techniques, and this knowledge is not long-term maintained. This poses a problem for students progressing through the academic ladder and some even still face these difficulties and continue to make errors at the higher levels of education. In this study, we first elaborate on errors, error types and error analysis. These led to the generation of the research questions as guided by the issues raised.

Error and error types

Error is basically seen as something done incorrectly (Erdogan, 2005), in which the learner utilizes an improper form and loses the ability to obtain the right form for the task. According to Spooner (2002), an error is caused by carelessness, which frequently results from misinterpretation and a lack of knowledge. In the course of solving mathematical word problems, an error can be termed as the mistake students make which leads them to get wrong answers. Written or verbal errors are common when resolving mathematical problems (Zakaria & Maat, 2010). According to Arhin and Hokor (2021), instructors have the ability to exploit learners’ mistakes as a necessary skill (through reviewing prior knowledge) before introducing a new topic. According to Hodes et al. (2014), students make four different kinds of mistakes when attempting to solve mathematical issues. These mistakes are careless, conceptual, application, and procedural errors.

Error analysis

Error analysis is a critical study strategy for answering fundamental concerns about learning mathematics (Padmavathy, 2020). It is an excellent source of information regarding the processes and dynamics associated with figuring out mathematical solutions. Error analysis, according to Radatz (1980), is important in two ways. First, in terms of academic practice, as a means of diagnosing learning issues, defining standards for distinguishing mathematics instruction, as well as raising awareness and providing encouragement for individual student progress and understanding. Second, error analysis is an excellent place to begin studying the mathematical teaching-learning process. Analyzing student errors allows teachers to gain insight into their students’ ‘procedural and conceptual misunderstandings’ (Mercer & Sams, 2006). Understanding is essential in learning mathematics because without a sufficient understanding of the contents, the application of knowledge becomes challenging for students. Error analysis is one of the most important aspects of mathematics teaching and learning because research in mathematics education has shown that focusing on errors as evidence of mathematical thinking on the part of learners helps teachers understand learners’ thinking, transform the ways they interact with learners in the classroom situation, and revise their methods of instruction (Adler, 2005; Venkat & Adler, 2012). The Newman Error Analysis (NEA) model is a basic approach for measuring student errors (Prakitipong & Nakamura, 2006; Zakaria & Maat, 2010) and that is what this study implemented. Newman’s model is well organized and its proper implementation will serve as a standard measure of students’ error, thus desired and implemented in our research on students’ errors.

Numerous studies for example, Orhun’s (2015) and Thapa’s (2016) study on learning difficulties faced by students in learning and solving trigonometry focused on the challenges in trigonometry as a whole. A number of issues were being looked into at once in such circumstances. It might be challenging to identify important issues when so many contents are being considered at once. Special attention to trigonometry word problems and the use of an existing widely accepted framework like Newman’s model makes this inquiry exceptional and serves as a guide to explore students’ thinking, which has not been the case for most studies in mathematics education. As a result, this study is highly focused only on errors students make when solving trigonometry word problems. Therefore, this study sought to analyze high school students’ errors in solving trigonometry. This was specifically with the intention of uncovering the type and root causes of the errors students commit. The study looked at providing answers to the following questions.

1. What type of errors do students commit in solving trigonometry problems?

2. What are the causes of errors made by students in solving trigonometry problems?

Theoretical review

Theories and models are essential in research. In either case, theories and models are developed to explain, forecast, and comprehend a phenomenon. By offering instructions and fundamental assumptions, researchers are able to make profound findings when guided by theories and models. This indicates that when we are led by theories, predictions are possible.

Some studies note that students’ errors may be due to some causes and can even be explained by several models. For instance, Prakitipong and Nakamura (2006) explain that there are two things that prevent students from coming up with the right response: issues with language fluency and conceptual understanding, and issues with mathematical processing. Priyani and Ekawati (2018) also indicated that errors can be analyzed by grouping them into conceptual, operational and principal error. Based on these three levels, Priyani and Ekawati (2018) indicate that learners commit errors by not being able to apply mathematical concepts (conceptual errors) and their inability to make correct calculations also lead to operational error which in turn leads to principal error. Lai (2012) also notes that the error analysis model constitutes factual, procedural, or conceptual errors. These error models suggested by these authors all look at either two stages (Prakitipong & Nakamura, 2006) or three stages (Lai, 2012; Priyani & Ekawati, 2018). However, the Newman categorization looks at five errors and that forms a strong reason for its use in this study. It helps to visualize units of errors in solving trigonometric problems.

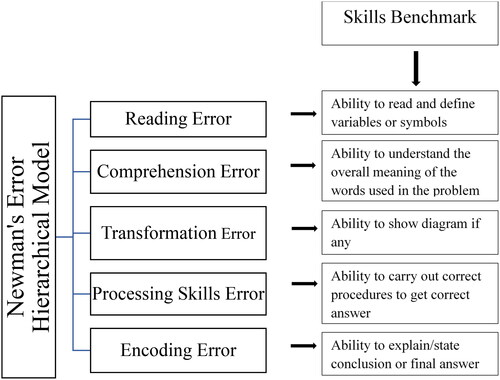
According to Saleh et al. (2017) the Newman Error Hierarchical Model has proven to be suitable for error identification and analysis based on students’ problem-solving capabilities. Also, for teachers of mathematics, this model of error analysis put forth by Newman (1977) has proven to be an effective model. The framework distinguishes between five different forms of errors: reading, comprehension, transformation, processing skills and encoding errors. This approach contains a hierarchy that divides error types based on the complexity of the students’ solutions to problems.

Newman (1977) has been used for analyzing mathematics topics like, Series and Sequence, solving linear and quadratic equations, algebra problems and others (Agustiani, 2021; Pedai et al., 2021; Saputri & Kamsurya, 2021). Wardhani and Argaswari (2022) also used the Newman model in analyzing students’ errors in solving trigonometry word problems. Thus, Newman’s model is an established and reliable framework as far as error analysis in mathematics is concerned. The categorization according to Newman (1977) suggests that the students must interpret what the question is asking before moving on to mathematical computation to arrive at the correct response. On the basis of the first breakdown point, the results of the written work provided by students in their test were examined in accordance with the type of error in the Newman Error Hierarchical Model. This model is shown in Figure 1.

Figure 1. Newman error hierarchical model. Developed by Researchers.

Figure 1 shows that Newman’s Error Hierarchical Model contains a hierarchy that classifies error kinds according to students’ proficiency levels in problem-solving. This hierarchy applies to mathematical issues whilst trying to solve a problem (Arhin & Hokor, 2021).

The five types of errors proposed by Newman (1977) that students commit in problem-solving as demonstrated in Figure 1 are explained as follows:

• Reading Errors: Reading error is concerned with the student’s inability to read keywords or symbols written in the mathematical problem.

• Comprehension Errors: Comprehension error occurs as a result of a student’s inability to understand the overall meaning of the words used in the mathematical problem and then as a result, the appropriate paths for problem-solving are not taken further.

• Transformation Errors: This type of error occurs as a result of students’ inability to transform the given question in a mathematically acceptable form and solve it or students’ inability to diagrammatically represent the information given in the mathematics problem.

• Process Skill Errors: Students commit this blunder because they are unfamiliar with or do not know the steps required to complete the operation to get the correct and accurate answer. Process skills error also refers to the mistake of computing mathematical tasks to obtain the proper result and identify the operation.

• Encoding Errors: These are the errors made by students in explaining the conclusion or their final answer. Students are able to answer problems correctly, but they are unable to communicate their solutions using appropriate notation that can be taken as a conclusion.

The above explanation of the Newman Error Hierarchical Model suggests that a student’s inability to pass a level will hinder his/her ability to reach the final level (Encoding).

Methods and materials

A descriptive qualitative design was used in this study. Ninety (90) students from the final year of a senior high school were selected. Also, three (3) teachers who are in the mathematics teaching field were purposively sampled for the interview. These teachers are very experienced and have taught the selected students mathematics since their entry into the school, thus they have prior knowledge on students’ academic strengths and weaknesses. Glass (2001) as well as Stronge and Hindman (2006) explain that experienced teachers do not only have mastery on content but also they have the skills of understanding students’ reasoning and abilities. Hence, participants were chosen on the basis of their judgement of the typicality or possession of particular components assessed in this study (Cohen et al., 2017). The ninety (90) students that were sampled for the study constituted 12.6% of the study’s population which is in line with the work of Gorard (2001) who asserted that it is appropriate to sample between 10% and 20% of the population. As a result, sampling ninety (90) students which represents (12.6%) percent of the population is within (10%–20%) which is enough for the study.

Two main instruments, that is Trigonometry Achievement Test (TAT) and a semi-structured interview based on Newman’s error hierarchical model were employed. The Trigonometry Achievement Test (TAT) was designed and conducted by researchers to identify the types of errors committed by the students and also to find out if the students will be able to apply the basic concepts in trigonometry to solve trigonometry word problem questions involving, simplifying and evaluating trigonometry expressions and equations, applications to right angled-triangle, angle of elevation and depression. The researchers intentionally made the test open-ended just to give students the opportunity to present their solutions so as to aid researchers in pinpointing the learners’ mistakes when solving trigonometric problems.

Also, the semi-structured interview was used. This was to find out respondents’ feelings, and opinions pertaining to the particular problem that showed in their performance on the worksheets. Also, through interviews, participants had the opportunity to express their views and share their reasons and possible causes of the errors committed.

Validity and reliability of the instrument

To establish the validity of the instrument, the researchers consulted two professionals and experts with long service in teaching mathematics and gave them some copies of the test items to verify the appropriateness and quality of the test items in terms of ambiguity and clarity. These two experts have taught mathematics for at least ten years and also serve as examiners for the West African Examination Council. The opinions and suggestions received from these experts after critically examining the test items revealed that the test items were suitable and relevant and as such could be used for the study and this process is supported (Piesie-Anto, 2012). Reliability is the degree to which an instrument produces stable and consistent results). Prior to the commencement of the study, test items were pilot-tested on ten (10) different students and the reliability of the test items was established by using the split-half method, this was carried out in order to determine the consistency of the test items specifically shown at (Appendix A), giving chance to researchers to redesign and anticipate potential issues that might arise while employing the test items (Lancaster et al., 2004). The total marks obtained by each student in odd questions and even questions were tabulated and the Spearman-Brown correlation coefficient formula was used to calculate the correlation coefficient with the help of Statistical Package for Social Sciences (SPSS) version 23. Results from the (SPSS) revealed that the value of the correlation coefficient is 0.802. According to Fraenkel and Wallen (2006), the correlation coefficient of 0.802 indicates that the reliability of the test instrument is very high and as such would be able to test or measure what it was designed for.

Data analysis

Data gathered through the trigonometry achievement test (TAT) was coded and analyzed using descriptive statistics. In an effort to comprehend, interpret and categorize the students’ errors in the process of answering trigonometry word problems, Newman’s Error Hierarchical Model, which is the conceptual framework served as the basis of analysis. Qualitative data gathered from the respondents through interviews was analyzed by employing a general inductive analysis strategy. Thomas (2006), explained inductive analysis as the approach in which an evaluator or researcher employs precise raw data interpretations to generate concepts, themes, or a model.

Findings

Students’ test data

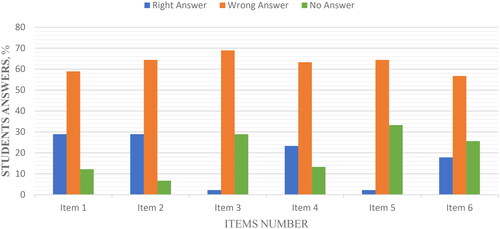
After students completed the test items and the scoring was completed, the results from their performance showed that the total number of questions that students correctly answered was 17.2%, followed by 62.8% of questions that they incorrectly answered and lastly, 20% of questions that they did not attempt to answer. Figure 2 shows the distribution of the student’s responses to each test question.

Figure 2. Students’ responses on each test item. Source: (Field data).

According to Figure 2, item test 1 was attempted by 87.7% (N = 79) of the students, but only 28.9% of the students answered the question correctly, while 58.9% answered incorrectly. 93.3% (N = 84) of the students attempted test item 2, but only 28.9% of them worked to come up with the correct response, leaving 64.4% of them unable to do so. Additionally, just 2.2% of 71.1% (N = 64) of the students who worked on test item 3 submitted the correct response, leaving 68.9% of the students unable to do so. Furthermore, only 23.3% of the 79 students who took test item 4 (out of a total of 86.7%, N = 78) provided the correct response, while 63.3% provided incorrect responses. Results from Figure 2 also indicated that only 66.6% (N = 60) of the students attempted test item 5, out of 66.6%, only 2.2% were able to solve and get the right answer with 64.4% of students having challenges in getting the right answer. Lastly, 74.4% (N = 67) of students attempted test item 6 and only 17.8% passed by getting the right answer, whereas 56.7% failed to get the right answer. Results from Figure 2 show that most students chose not to attempt test item 5. This shows that students believed question 5 to be the most challenging whiles, few students did not attempt test items 1 and 2.

The type of errors students committed in solving trigonometry problems

Students’ error types based on the test results were critically categorized and analyzed using Newman’s error analysis model. These are a reading error (RE), comprehension error (CE), transformation error (TE), processing skills error (PSE) and lastly encoding error (EE). Figure 3 below displays the percentage of error for each test item on various error categories based on Newman’s error model.

Figure 3. Percentage of error for each item examined based on Newman’s Error Model. Source: (Field data, 2024).

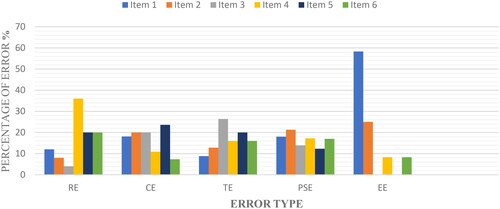
In total, students made 7.4%, 16.2%, 36.9%, 35.9% and 3.5% errors in reading error, comprehension error, transformation error, processing skills error and encoding error respectively.

From Figure 3, reading errors were 36%, comprehension errors 23.6%, transformation errors 26.4%, processing skills errors 21.3% and 58.3% encoding errors occurred when students answered test items 4, 5, 3, 2 and 1 respectively.

Analysis of causes of various error types committed by students

Reading error

The data gathered shows that most of the students made the most reading errors when they attempted Test Item 4. Major factors that can be a cause of this error type include a lack of students’ attention to details in the question, a lack of practice and misreading of questions by students. Figure 4 displays this type of error (reading error) exhibited by some of the students.

Figure 4. Examples of students’ work with reading errors. Source: (Field data, 2024).

From Figure 4 it could clearly be seen that students were able to draw and label the distance between the foot of the ladder and the wall as well as the length of the ladder but students made some reading errors and as a result, could not answer the question as appropriately demanded of them. In test item 4, the question demanded students to find the angle the ladder makes with the wall, but unfortunately, students calculated the angle the ladder makes with the ground due to misreading and their lack of paying attention to details in the question given. This was confirmed by an interview we had with some of the students.

• Rsc: So please tell me, can you read the question?

• Student #9: Yes, please

• Rsc: what do you think the question asked you to do, please?

• Student #9: Sir please, I think when you put a ladder on the ground to lean against something, the angle the ladder will form with the ground. I quite remember we solved one of this type of example in class and we calculated the angle I worked for in my solution so that’s how I understood it, please.

• Rsc: please, do now realize where you were at fault in answering test item 4 after showing your scripts to you?

• Student #9: Yes please, the angle I calculated was not what the question was demanding of me, I will try my best not to make that mistake again.

Most of our students here rely only on the few things they learn in class, even when you ask them to buy past question books and textbooks that they can use to practice more on what they learnt in class, they won’t and for that reason when a question is twisted small from what they learnt in class, then they start to fumble. Also, most have problems reading to understand mathematical statements.

Teacher #2

The interview reveals that the student could not interpret or define the terms used in the question well before attempting it. According to the student, they solved one example relating to test item 4 in the class so he thought it was the same as was given in item test 4. This means students do not really practice solving questions on trigonometry after the normal class they have with their teachers and as a result, are unable to notice the difference between what they solved in the class and what was given in item test 4. The student was therefore in a rush to answer the question, but unfortunately, provided a wrong answer.

Comprehension error

Most of the students were able to read the question but being able to decipher the question was a major challenge for them. Most of the students made comprehension errors when they answered Test Item 5. Students did not understand the overall meaning of the question as well as the term ‘angle of elevation’ as used in the question. Figure 5 depicts the occurrence of comprehension errors in students’ work.

Figure 5. Work produced by students that exhibits comprehension errors. Source: (Field data, 2024).

From Figure 5, it could clearly be observed that students didn’t understand the overall meaning of the question and the term angle of elevation used in the question and as a result, students couldn’t solve the problem to get the right answer. Students were confused on the concept an angle of elevation and depression. Students had challenges as to how to approach the given question. This could be a result of the student’s lack of understanding of basic concepts, misinterpretation of problem statements, inadequate problem-solving strategies and more importantly how the concepts of trigonometry were taught to students. The causes of this type of error (comprehension error) were revealed in the interview below;

• Rsc: So in your opinion which category will you place item test 5 whether being difficult, medium or easy?

• Student #34: Please Sir, it’s difficult and I always find it difficult to understand this kind of question in trigonometry that is questions pertaining to the angle of elevation and depression.

• Rsc: Please tell me, what do you think the question asks you to do?

• Student #34: Sir please, I don’t really know, I always get confused when I see these types of questions.

• Rsc: So what do you think are the factors that make it difficult for you to understand the concepts of trigonometry and its application?

• Student #34: Sir please it’s a whole lot

• Rsc: Please tell me what you know

• Student #34: Hmm Sir, our teacher was so fast when he was teaching us, he always solves the questions all by himself, when you ask him questions too he will tell you to see your friends after the class. Also when he comes to class he always pays attention to our colleagues who are good at mathematics, leaving us who are not good behind. With this, nothing even motivates me to learn mathematics. Mathematics is really difficult and it contains a lot of formulas and calculations, therefore I don’t like learning it because I know no matter how I try I won’t understand it.

Well, what I can say is that most students have challenges remembering and understanding trigonometry due to the negative perception they have about trigonometry as being so difficult to understand, most students do not take learning trigonometry seriously as they think it’s irrelevant and also difficult. Also, how my colleague teachers introduce the concepts of trigonometry to students is also a factor that causes the errors students commit

Teacher #3

From the interview above, the causes of students’ errors were a result of the negative perception they have about trigonometry as being difficult, also the strategies and methods employed by teachers while teaching the concepts of trigonometry are other factors that contribute to the comprehension errors committed by students. From the interview, we noticed that concepts of trigonometry were taught abstractly to students which made it difficult for most of the students to understand. With this, we can say comprehension errors might be a result of teachers not placing enough emphasis on teaching topics as they appear to be simplified (Mensah, 2017).

Transformation error

Transformation errors happen when students are unable to solve a given question by transforming it into a format that is acceptable mathematically or when students are unable to diagrammatically depict the data in a mathematical problem. This type of error mostly occurs when students can read and understand the question, but, are unable to transform the question into acceptable mathematical form as a result of their inability to remember and apply the appropriate trigonometry operation and incorrect usage of basic arithmetic operations. The causes of these errors include learning by rote, that is memorizing formulas rather than understanding the concept, and lack of constant practice which as a result leads to a lack of familiarity with the trigonometry identities and also confusion about different trigonometric identities and formulas. The data obtained from the study depicted that most errors committed by students were transformation errors and this happen when they attempted Test Item 3. An exhibition of student’s work involving the occurrence of transformation errors is captured (see Figure 6).

Figure 6. Exhibition of student’s work involving transformation errors. Source: (Field data, 2024).

From Figure 6, it could be noticed that students were not able to recall and apply the appropriate trigonometry identity and therefore could not solve to get the right answer to the question given. Due to this, students tried to use their own ways and identities which unfortunately was not appropriate and therefore provided a wrong answer to the problem. The interview below provided details on the reasons for this kind of error (transformation error).

• Rsc: Please do you really understand Test Item 3?

• Student #64: Yes, Sir

• Rsc: In that case, tell me, what did you use to solve the question, please?

• Student #64: Sir, please, I used compound angles identity

• Rsc: Great, so why is your answer wrong?

• Student #64: Sir, please, it is because I use the wrong trigonometry identity in solving the question.

• Rsc: Please, why did that happen so?

• Student #64: Sir please, I have this challenge of memorizing formulas, as you can see the formulas in trigonometry are many and even those that I’ve managed to memorize, I barely use them as I do not constantly practice solving trigonometry and that makes it difficult for me to recall. Also, our teacher didn’t solve many examples with us concerning this type of question.

Most of the students do not learn to acquire knowledge but rather grades and positions in class. Due to that students after having a class session with their teacher will never sit down to go over what they learnt in order to understand the concept well, instead most of them will wait until it’s exams and they will do what they call ‘chew and poor’ that is learning by rote, students as a result of having so many formulas in mind, therefore get confused as to which one they need to apply to solve a given question.

Teacher #1

According to the interview, it is clear that a large portion of the transformation errors that students made were due to their method (rote learning) of learning trigonometry concepts. Students also frequently struggle with trigonometric identities and formulas because they don’t regularly practice using the identities, properties, and formulas they have learned to solve trigonometry problems.

Processing skills error

The data gathered indicates that processing skills errors are the second most common error students make when solving trigonometry problems. Students made most processing skills errors when they attempted Item Test 2 and the cause of this error was as a result of overgeneralization of concepts. Overgeneralization occurs when students try to apply a familiar concept or rule without fully understanding its limitations or applicability in a specific context. Sometimes too the student knows the working process but, as a result of rushing to solve more questions, they end up using the arithmetic operation signs incorrectly thereby getting wrong answers. Below is an example of processing skills errors committed by students.

From Figure 7, it could be seen clearly that the student used the idea of expansion in algebraic expression not knowing that the concept is not applicable to Item Test 2 as far as trigonometry is concerned. One student also had the idea but unfortunately, used the arithmetic sign (+ and −) incorrectly and as a result provided a wrong answer. The root causes of processing skills errors were confirmed in the interview below

Figure 7. An exhibition of student’s work involving processing skills errors. Source: (Field data, 2024).

• Rsc: Please why is your answer 77.9?

• Student #81: Sir, I first expanded the bracket and went through the process to get that answer, please.

• Rsc: Great, so tell me is your answer right or wrong?

• Student #81: Sir please, it’s wrong

• Rsc: Why did you get a wrong answer, please?

• Student #81: Sir please it’s because I used the wrong procedure.

• Rsc: so why did you use that approach?

• Student #81: I used that approach because that is what we taught when we were learning expansion of algebraic expression and binomial expansion so I thought whenever anything is being multiplied by an expression in a bracket it means we should multiply the one outside through the one in the bracket. I did not know it is not applicable to question 2.

Students most of the time don’t take their time to answer questions, as they are always in a rush to answer more questions and as a result, they sometimes interchange the operational signs. The most common ones are the plus and minus and this happens when students are simplifying expressions and evaluating equations especially when one term or expression crosses an equal sign to either side

Teacher #3

From the interview above, we can then say most processing skills errors occur as a result of overgeneralization of concepts, incorrect use of the operational signs, students’ inability to go through the right process to obtain correct answers and carelessness.

Encoding error

This type of error (Encoding error) happens when students can successfully solve the problem but, are unable to describe the result in an acceptable notation that can be embraced as a conclusion. Students most times commit this type of error when they are asked to leave or correct their answer to a certain decimal place, surd form, a certain number of significant figures, etc. This type of error could be a result of a lack of attention to detail in a question, misinterpretation of instructions pertaining to a question and carelessness on the students’ side as they are always in a rush to answer questions. Most of the students made encoding errors when they attempted Test Item 1. Beneath shows evidence of a student work involving encoding errors.

Figure 8 shows that students were able to pass through the first four stages based on Newman’s Model but unfortunately as a result of not double-checking (looking back), carelessness and rushing they could not state their conclusion in a manner that can be accepted as an answer. The causes of the aforementioned error were confirmed in the interview we conducted below:

Figure 8. An exhibition of students’ work involving encoding error. Source: (Field data, 2024).

• Rsc: please do you really understand question number 1?

• Student #81: Yes pls

• Rsc: In your opinion, is Item Test 1 easy, medium or difficult?

• Student #81: Sir please, I will say it is easy

• Rsc: Is there anywhere in your calculation that you made a mistake?

• Student #81: No pls, I made no mistake.

• Rsc: So tell me, what do you think prevented you from getting the full mark for Item Test 1?

• Student #81: Sir pls, I made a mistake in stating the final answer.

• Student #81: Why did that happen, please?

• Rsc: Sir I saw it to be very easy so after solving it I didn’t consider taking my time to check the solutions and the answers as I was aiming to solve all the questions so there was this kind of pressure on me.

Most students after solving a question do not take their time to go through their solutions to see if indeed what they have gotten as the final answer is correct or not, this happens when students are in a rush to answer more questions and also most of do not pay attention to the instructions and details in the question. To even correct an answer to two or one decimal place is a problem for some students

Teacher #2

The interview conducted indeed confirmed that most encoding errors students commit are a result of not paying attention to details in questions, carelessness, lack of accuracy in their calculations and rushing to solve more questions.

Discussion

Errors committed by the students have been presented by the findings and out of the five types of errors committed by students according to Newman’s Error Model, the reading error was ranked at the fourth (4^th) position which indicates that most of them were able to read the questions. However, the students’ comprehension of the test items is at an extremely poor level. This means that students were unable to decipher the overall meaning of the test items and as a result could not provide the right answer as the questions demanded from them. The findings of this study agree with the findings of numerous researches. For example, according to research by (Clements & Ellerton, 1996; Singhatat, 1991), a significant number of errors occurred at the comprehension and transformation levels. Also, the results of this study support earlier findings of a study conducted by Mensah (2017), who in his study discovered that process skills errors, transformation errors, and comprehension errors are the most common mistakes students make when using formulas and right-angled triangles to solve trigonometric ratios. According to Newman (1977), when learners display a notion of not understanding the words in a question, it will surely lead to their inability to transform the question into mathematical equations or forms and this definitely causes wrong computations. Awantagusnik et al. (2021) note that learners are able to use more than a single representation (can also be transformation) to contextualize a problem and solve it but findings from this study reveal that some of these errors were committed because learners are not able to represent or transform trigonometry problems in a context that can be computed.

The findings of Norasiah (2002), who found that problematic students had challenges understanding the special terminology in mathematics and could not transform mathematical problems into mathematical form agree with those of this study regarding students’ failure to understand the questions. More so, the results of this study are consistent with an earlier study conducted by Orhun (2015) who in his study discovered that the students did not develop the concepts of trigonometry fully and that they made some mistakes. Additionally, the responses of some students to Test Item 2 shows that students were faced with problems such as $\mathrm{\text{tan}}(25+x),$ it could be seen from the responses of the students that, students as a result of overgeneralizing the concept of algebraic expression expanded $\mathrm{\text{tan}}(25+x)$ as $\mathrm{\text{tan}}25+\mathrm{\text{tanx}}.$ Trying to overgeneralize tasks of this nature led to improper computation and it depicts that the student committed a process skill error (Newman, 1977). This result is consistent with that of Skane and Graeber (1993), who assert that the distributive law is responsible for some of the errors students make when applying the concepts of algebra, logarithms, exponents, and trigonometry. Furthermore, they contend that for some students, traditional instruction is insufficient as a method of correcting distributive law mistakes. Interviews with students further showed that students fail to appreciate learning trigonometry; hence made some errors due to their negative perception of trigonometry, lack of motivation as the teacher only gave attention and focus only to the few students who are good at mathematics and the way and manner in which the concept of trigonometry is presented to them. As a result of this, students fail to practice more on what they have learnt as they also rely only on what they were taught in the class. Most of them also learnt the concepts of trigonometry by rote rather than meaningfully understanding the concepts, this means that students appear to understand the concept of trigonometry at the end of the unit, but struggle to retain it. As a result, students get stuck in the process of solving the problem when they forget or get confused with the appropriate identity or formula to use, because of this, students use their own ideas which ends them up in getting wrong answers.

Conclusions and recommendations

Conclusions can be drawn from the findings that a greater part (about 80%) of the student population had challenges in solving trigonometry problems and as a result, they made errors in the process of finding the solution to trigonometry problems. The test results indicated that these challenges including transformation, processing and comprehension that students encountered likely contributed to the errors they made. The interview conducted showed that the main causes of errors students commit include a lack of paying attention to details in questions, misreading and misinterpretation of questions, lack of practice, student’s negative attitude and perception towards trigonometry, carelessness, misapplication of formulas and identities in trigonometry, overgeneralization and lack of motivation.

The study recommends that mathematics teachers should make use of inductive teaching strategies which include, incorporating real-world applications, using manipulatives and also starting with specific examples or problems during the teaching and learning process before moving to generalization of formulas in order to make the teaching of trigonometry practical and more activity-oriented. Future research can therefore concentrate on the impact of incorporating technology into teaching and learning trigonometry, as well as investigating the role teachers play in preventing errors made by students when solving trigonometry, particularly trigonometry word problems.

Implications

Information from students revealed that abstract teaching methods might be a contributing factor to students’ difficulties and errors in solving trigonometry word problems. Perhaps, there could be other reasons. Findings from Zengin et al. (2012), reported a significant difference between the post-test results of students taught with GeoGebra and those without in trigonometry, as those taught with GeoGebra performed better than their counterparts taught without GeoGebra. Similarly, Reis (2010) and Tatar (2012) found a notable difference in the average scores of trigonometry achievement tests between the two groups, with the GeoGebra group showing a statistically significant advantage. It is therefore possible that practical teaching and strategic use of technology (eg GeoGebra) alongside other teaching methods in teaching trigonometry can help reduce the errors committed by students. It is therefore suggested for teachers to explore how GeoGebra can complement their existing curriculum.

Authors contributions

All authors were involved in the concept, design, collection of data, interpretation, writing, and critically revising the article. All authors approve the final version of the article.

Data availability and sharing policy

Data generated or analyzed during this study are available from the authors on request.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The authors received no financial support for the research and/or authorship of this article.

Notes on contributors

Benjamin Adu Obeng

Benjamin Adu Obeng (Doctor of Philosophy) is a lecturer and has long-term experience in teaching. He holds a PhD in mathematics education, Master’s and Bachelor’s degrees as well. His research focus is mathematics education and applied mathematics.

Gideon Mensah Banson

Gideon Mensah Banson holds a Master of Philosophy in Mathematics Education from Akenten Appiah-Menka University of Skills Training and Entrepreneurial Development, Kumasi-Ghana. He also holds a Bachelor’s degree from University University of Cape Coast, Ghana. His research interest encompasses mathematics educational issues, technology in education and curriculum and instructional development. He has great interest in teacherdevelopment and he is opened to research grants and consultations.

Ebenezer Owusu

Ebenezer Owusu holds a Bachelor of Science degree in Mathematics Education from the University of Education, Winneba. Currently, he serves as a teaching assistant at Akenten Appiah-Menka University of Skills Training and Entrepreneurial Development, Kumasi-Ghana. His research interests lie in the fields of Mathematics Education and Applied Mathematics, with a focus on exploring innovative methods and approaches to teaching and learning mathematics, as well as solving real-world problems using mathematical models and techniques.

Raphael Owusu

Raphael Owusu holds a Master of Philosophy in Mathematics Education from Akenten Appiah-Menka University of Skills Training and Entrepreneurial Development, Kumasi-Ghana. He also holds a Bachelor’s degree from University of Education Winneba in Ghana. He has experience in teaching and his research interest is mathematics education, technology in teaching and learning, teachers professional development and learning. He is available for research grants and contracts.

Appendix-A.

Trigonometry achievement test (TAT)

1. If sin(x) = $\frac{8}{17},$ find the value of $2\mathrm{\text{tan}}\hspace{0.17em}\left(x\right)+\mathrm{\text{cos}}(x).$

2. Given that $\mathrm{\text{tan}}(\mathrm{x}+25)°=5.145,$ where $0°\le x\le 90°,$ find to one decimal place the value of x.

3. Given that $\mathrm{\text{sin}}\mathrm{ }(5\mathrm{x}–28)°=\text{cos}(3\mathrm{x}–50)°,$ find the value of x where $0°<x<90°.$

4. A ladder 10 m long rests against a vertical wall so that the distance between the foot of the ladder and the wall is 4.5 m. Find the angle the ladder makes with the wall.

5. A pole 15 m stands on the same horizontal level with a tree. From the top of the pole, the angle of elevation of a bird on top of the tree is $36°.$ If the pole and the tree are 220 m apart, calculate the height of the tree.

6. A bird sits on top of a lamppost. The angle of depression from the bird to the feet of an observer standing away from the lamppost is $34°.$ The distance from the bird to the observer is 24 m. How tall is the lamppost?