Interpreting Kendall’s Tau and Tau-U for single-case experimental designs

Abstract

Tau (τ), a nonparametric rank order correlation statistic, has been applied to single-case experimental designs with promising results. Tau-U, a family of related coefficients, partitions variance associated with changes in trend and level. By examining within-phase trend and across-phase differences separately with Tau-U, single-case investigators may gain useful descriptive and inferential insights about their data. Heuristic data sets were used to explore Tau-U’s conceptual foundation, and 115 published single-case data sets were analyzed to demonstrate that Tau-U coefficients perform predictably when they are well understood. An understanding of Tau-U’s theoretical basis and unique limitations will help investigators select the appropriate statistical method to test their hypotheses and interpret their results appropriately. Limitations of Tau-U include as follows: vague or inconsistent Tau-U terminology in published single-case research; arithmetic problems that lead to unexpected and difficult-to-interpret results, especially when controlling for baseline trend; Tau-U methods are difficult to graph visually, and a comparison with visual raters found that several Tau-U effect size statistics are weakly correlated with visual analysis.

Keywords:

• effect size
• single-case
• single-subject
• Tau
• time series

PUBLIC INTEREST STATEMENT

Did the treatment work? All stakeholders, whether a medical or mental health service provider, educator, consultant, or patient, want to know if a treatment works. That is why using single-case experimental designs have become increasingly popular—they allow one to determine if a treatment benefitted a particular client or patient. The dilemma for researchers is that there are numerous ways to analyze data from a single-case experimental design. This article walks the reader through some of the issues related to single-case data analysis and illustrates one popular technique (Tau-U) for analyzing such data. It is hoped that this article will promote the informed use of Tau-U, assist researchers in the analysis of single-case data, and help them answer the question, “Did the treatment work?”

Competing Interests

The authors declare no competing interest.

Single-case experimental designs (SCEDs) provide investigators with research designs that have been described as “effective and powerful” (Shadish, Cook, & Campbell, 2002, p. 171) nonrandomized experimental designs (Shadish, Rindskopf, & Hedges, 2008). These designs are ideal when a meaningful control group is difficult or impossible to attain, a situation faced in many clinical scenarios. For instance, in studies of expensive treatment protocols or for certain disease conditions or pathologies, SCEDs play an important role because large numbers of subjects may not be achievable (Barnett et al., 2012). In other cases, SCEDs are useful when studying low incidence conditions (i.e., traumatic brain or spinal cord injuries) or complicated co-occurring conditions such as post-traumatic stress disorder, depression, substance abuse, and traumatic brain injuries. SCEDs are also valuable when validating treatment efficacy in underserved or understudied populations. Furthermore, there are times when a control condition may not be ethically appropriate because participants cannot be randomized and treatment cannot be withheld (Barnett et al., 2012). For these and other reasons, investigators increasingly consider using SCEDs (Kratochwill et al., 2013).

Although SCEDs have played an important role in the evidence-based practice movement (Byiers, Reichle, & Symons, 2012; Matson, Turygin, Beighley, & Matson, 2012), the need for a consensus on how to evaluate the quality of single-case studies has led to the development of various standards (Kratochwill et al., 2010; Tate, McDonald, Perdices, Togher, & Savage, 2008). While these standards are helpful in that they allow one to evaluate the methodological rigor of one’s design, there is still a need for consensus on the role and selection of statistical methods in single-case research (Smith, 2012). Traditionally, only visual analysis was used in the analysis of single-case data because statistical methods were viewed as unnecessary. Within this historical context, there has been considerable debate about the need for statistical analysis of single-case data (e.g., Baer, 1977; Huitema, 1986; Parsonson & Baer, 1986) and a number of studies documenting problems with the reliability of visual analysis (e.g., Brossart, Parker, Olson, & Mahadevan, 2006; DeProspero & Cohen, 1979; Harbst, Ottenbacher, & Harris, 1991; Park, Marascuilo, & Gaylord-Ross, 1990; Ximenes, Manolov, Solanas, & Quera, 2009). This led to recent efforts to improve the reliability of visual analysis using various training strategies (e.g., Fisher, Kelley, & Lomas, 2003; Hagopian, Fisher, Thompson, & Owen-DeSchryver, 1997; Kahng et al., 2010; Wolfe & Slocum, 2015). Most experts on single-case data analysis advocate for the use of both visual analysis and statistical analysis (e.g., Brossart, Meythaler, Parker, McNamara, & Elliott, 2008; Brossart, Vannest, Davis, & Patience, 2014; Shadish, Hedges, Horner, & Odom, 2015) because (a) statistical methods can only partially address issues related to clinical significance (although efforts to define clinical significance statistically have produced useful methods; e.g., Atkins, Bedics, McGlinchey, & Beauchaine, 2005), (b) visual analysis incorporates contextual factors that one typically cannot include in statistical models (although multilevel models may include covariates), and (c) visual analysis and statistical analysis should corroborate one another and when they do not, there is typically a problem in either the visual analysis or the statistical method (e.g., ITSACORR; Huitema, McKean, & Laraway, 2007; Parker & Brossart, 2003).

Even though there is no consensus on which statistical methods are optimal for analyzing data from SCEDs, there are important reasons for calculating statistical effect sizes for SCEDs. Parker and Hagan-Burke (2007b) note that effect sizes for single-case data have four distinct benefits: objectivity, precision, dependability, and general credibility. Numerous statistical methods have been proposed to analyze single-case data ranging from regression models (e.g., Brossart et al., 2008; Brossart, Parker, & Castillo, 2011; Faith, Allison, & Gorman, 1996; Parker & Brossart, 2003) to nonparametric methods (Parker, Vannest, & Davis, 2011b), to simulation, standardized mean difference, and multilevel methods (e.g., Borckardt et al., 2008; Shadish, Zuur, & Sullivan, 2014). Yet researchers have noted that so far, no single method has been identified that is clearly superior to other methods (Brossart et al., 2006; Campbell, 2004; Parker & Brossart, 2003; Parker et al., 2011b; Smith, 2012).

One family of nonparametric methods purported to perform well is based on Kendall’s $\tau$ (Brossart et al., 2014; Parker, Vannest, Davis, & Sauber, 2011b). While these “Tau-U” methods are flexible, proper implementation requires an understanding of what they do and how they perform when applied to “real-world” single-case data. In addition to providing a conceptual primer on rank correlation methods in single-case research, this paper examines the Tau-U coefficients in detail through a range of real and illustrative data sets. Tau-U’s performance on a sample of published single-case data sets is also compared to judgments made by trained visual raters. The goal is to provide the single-case researcher with an in-depth understanding of Kendall’s Tau and its Tau-U variants that have been proposed for single-case researchers.

1. Theoretical review of Tau

1.1. Kendall’s τ

Tau, denoted by the Greek letter τ, is a nonparametric rank correlation coefficient introduced by Kendall (1938). Like other correlation statistics (e.g., Pearson r), τ is arithmetically bound between −1 and +1, and its value characterizes the degree of agreement between two ordinal variables. As a rank correlation statistic, τ indicates how similarly two variables order a set of individuals or data points. A value of ${\tau }_{\left(X,Y\right)}$ = + 1.00 indicates that two variables, X and Y, order a set of data points in exactly the same way, with the same data point occupying the same rank position in both variables (as in Figure 1A). A value of ${\tau }_{\left(X,Y\right)}$ = −1.00 indicates that two variables order a set of data points in exactly the opposite way, with one data point occupying the first rank in one variable and the last rank in the other variable, etc. (as in Figure 1B). When ${\tau }_{(\mathrm{x},\mathrm{y})}$ = .00, there is no relationship in the way that the two variables rank order a set of data points (as in Figure 1C), i.e., the two variables are independent. Kendall (1976) described τ as a “coefficient of disarray” (p. 7), which is conceptually useful when one considers that the τ value of two variables approaches 0 as the disorder or independence between their compared ranks increases.

Figure 1. Heuristic examples for Tau and Tau-U analyses. Data series presented are hypothetical single-case AB designs with baseline phase followed by experimental phase.

To better understand τ and the Tau-U analyses, the interested reader may benefit from using any number of statistical software tools that calculate τ. Many statistical software packages offer Kendall Rank Correlation (KRC) modules that yield τ values, p values, and other metrics for statistical inference, meta-analysis, etc. Tarlow (2014) developed syntax for R (R Core Team, 2013) that calculates τ and Tau-U and graphs single-case data series.

1.2. τ in SCEDs: measuring trend

The trend of data in a time series may be analyzed as the τ rank correlation between the time (typically the x-axis values) and the observed score (y-axis values) of measured data points, e.g. ${\tau }_{(\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e},\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e})}$. The observed score is typically the measured dependent variable under study (e.g., depression rating, frequency of disruptive behaviors, cognitive performance measurement, etc.). Here the researcher is essentially asking, “Do time and score values order these data points in the same way?”

1.2.1. Pairwise comparisons

Whereas Spearman’s ρ is calculated with ordinary least squares, finding τ involves the pairwise comparison of all data points. To calculate τ for a time series, each observed score is compared to every future score. For example, in a series of 10 observations, the first score measured in time (the leftmost point on a visual plot) would be compared to the other 9 scores, because all 9 of the other scores occur after it. The second score would be compared to the eight scores that occur after it, but not the first one that precedes it, and so on. The last score would not be compared to any other scores, as no scores occur after it in time. Thus, the number of pairwise comparisons can be calculated as $n_{\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}}=n(n-1)/2$ where n is the number of observations in the series. A series of 10 scores would therefore have $n_{\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}}$ = 10(9)/2 = 45 pairwise comparisons.

1.2.2. The Kendall score (S)

Each pairwise comparison contributes additively to the Kendall score, S, which is used to calculate τ. A pairwise comparison of two scores is determined to be concordant, discordant, or tied. In a concordant pair, the two measured scores (y-axis values) increase with time, i.e., the score measured later in time is greater than the earlier score. Figure 1A shows a series where all pairs of scores are concordant, indicating that all measured scores increase in a time-forward fashion. In a discordant pair, the two measured scores decrease with time, i.e., the score measured later in time is less than the earlier score. Figure 1B shows a series where all pairs of scores are discordant, indicating that all measured scores decrease in a time-forward fashion. In a tied pair, both measured scores are equal, neither increasing nor decreasing over time.

To find the Kendall score, S, the number of discordant pairs is subtracted from the number of concordant pairs, and the number of tied pairs is disregarded ($S=n_{\mathrm{c}}-n_{\mathrm{d}}$). For the time series in Figure 1A, S = 45 − 0 = 45. Thus, the maximum possible S is equal to the number of pairwise comparisons and the minimum possible S is equal to the negative value of the number of pairwise comparisons.

1.2.3. Calculating τ from n_pairs and S

In data series with no ties, τ is calculated from S and n_pairs with the equation $\tau =S/n_{\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}}$. From this equation it is clear that τ is bound between −1 and +1, because S cannot exceed the positive or negative value of the number of pairwise comparisons. In Figure 1A, τ = 45/45 = 1.00, and in Figure 1B, τ = −45/45 = −1.00. In Figure 1C, there is almost no observed relationship between the rank orders of time and score, τ = 3/45 = .07; one could conclude from Figure 1C result that time and score are probably independent. To summarize, as agreement between two variables’ rank orders increases, Tau approaches +1. As disagreement between two variables’ rank orders increases, Tau approaches −1. And as disarray, or lack of agreement/disagreement between two variables’ rank orders increases, Tau approaches 0.

1.2.4. Calculating τ with ties

An alternative τ formula is substituted when there are ties in one or both variables of a data set (Kendall, 1976). When ties exist, the maximum possible value for S no longer equals the number of total pairwise comparisons between points. Thus, the absolute value of τ is attenuated when using the original formula because in the presence of ties $n_{\mathrm{c}}+n_{\mathrm{d}}<n_{\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}}$ and no configuration of tied data points can result in a +1 or −1 value. Consider the series in Figure 1D that includes several ties so that $\tau =n_{\mathrm{c}}+n_{\mathrm{d}}/n_{\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}}=33-0/45=.7$, even though there are no discordant pairs. The alternate τ formula proposed by Kendall uses a complex correction in the denominator to account for this attenuation. For the series in Figure 1D, the corrected formula yields τ = 33/38.5 = .9, which is a considerable increase from .7 and arguably a better representation of the data’s positive monotonic trend.

Most statistical software automatically corrects for ties when calculating τ, including the R syntax used in this study. Consider that τ is essentially calculated through a series of counting procedures—first, concordant and discordant pairs are counted, and second, the total number of pairs are counted. To correct for tied ranks, the number of ties must also be counted. In a time series, it is assumed that the values of the time variable X are untied, i.e., all Y scores were observed at different time points. However, observed Y scores may be tied at different X time values. To correct for tied values in Y, the number of scores in each set of ties is counted as t. For example, in Figure 1D series, there is one set of four scores tied at value Y = 4, so t = 4, and there is a second set of tied scores at Y = 7, with t = 4 as well. The correction variable T is calculated as

$T=\frac{1}{2}\sum _{t}t(t-1)$

To correct for ties, τ is then calculated as

$\tau =\frac{S}{\left(\sqrt{\frac{1}{2}n(n-1)}\right)\left(\sqrt{\frac{1}{2}n(n-1)-T}\right)}$

Note that when no ties exist, the equation above reduces to the original τ formula, $\tau =S/n_{\mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}}$. To apply the corrected version of τ to Figure 1D data, $T=1/2(4\times 3)+1/2(4\times 3)=12$ so that $\tau =33/\left(\sqrt{45}\times \sqrt{45-12}\right)=33/38.5=.9$.

1.3. Limitations of τ in SCEDs: trend or phase differences, but not both

Recall that ${\tau }_{(\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e},\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e})}$ characterizes the trend present in data. When the ranks of time and score data are correlated, the result answers the question, “How do my scores change over time?” Unfortunately, this is not strictly the question that most researchers want to answer. Single-case researchers typically use alternating baseline or control and treatment phases (e.g., AB or ABAB) to detect the effects of an intervention. While phases are implemented systematically over time, the researcher is not directly concerned with detecting change over time, but would rather know, “Do my scores change between phases?”

One way to answer this question is to instead calculate ${\tau }_{(\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e},\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e})}$, with a dummy code phase variable (0/1 for A/B designs), though more complex dummy coding strategies could be used for sophisticated multiphase designs (Huitema & McKean, 2000; Parker & Brossart, 2006). Conceptually, the phase variable serves as a time variable in which all phase A scores are tied at time X = 0, and all phase B scores are tied at time X = 1. This analysis more closely answers the question, “Do my scores change between phases?”, or, more accurately, “Is there a rank order association between phase and score?” In this analytic strategy, τ is essentially a Mann–Whitney U test of group independence (Kendall, 1976) and will yield identical p values to that test. Therefore, ${\tau }_{(\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e},\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e})}$ may be more desirable to the single-case researcher than ${\tau }_{(time,score)}$ and indeed this statistic, or the equivalent Mann–Whitney U, can be used for single-case research (Parker et al., 2011b). The weakness of this approach is that when a time variable is converted to a phase/dummy code variable, any information about trends within the data are lost. Investigators studying an individual’s change over time may want to better understand if trend is present and how it is impacted by the experimental treatment.

In the next section, we will review the Tau-U coefficients and demonstrate how Tau-U offers one possible solution to this problem. After reviewing the logic of this new statistic, we will refine previous work on the method and conceptualization of Tau-U (Parker et al., 2011b), pointing out its strengths and limitations, and we will use Tau-U to analyze a large sample of published time series data to explore empirical support for its use. We will also compare Tau-U results to judgments made by visual analysts to determine how well the Tau-U coefficients agree with visual analysis.

1.4. Tau-U: an analysis of phase differences

The Tau-U analysis allows the single-case researcher to examine treatment effects on both between-phase differences and within-phase trends. For single-case research with a baseline phase followed by an experimental/treatment phase (AB), there are three possible types of pairwise comparisons in a τ calculation: (1) a phase A score is compared with another phase A score, (2) a phase B score is compared with another phase B score, and (3) a phase A score is compared with a phase B score.

In an AB experimental design, the scores in phase A contain a different type of information than the scores in phase B; the information in phase A describes the dependent variable before treatment whereas the information in phase B describes the dependent variable after treatment is introduced. Similarly, the three types of pairwise score comparisons (A-to-A, B-to-B, and A-to-B) also contain different types of information.

To illustrate how different types of pairwise comparisons contribute different types of information to the total variance of τ, consider the “difference matrix” in Figure 2, where observed (y-axis) scores are arranged in chronological order along the horizontal edge of the matrix from left to right, and in chronological order along the vertical edge of the matrix from bottom to top. Figure 2A shows a difference matrix for the time series in Figure 1C, and Figure 2B shows a difference matrix for the time series in Figure 1E. Pairwise comparisons are then made in the corresponding cells of the matrix, with a “+” representing each pair where the later value is larger (a concordant pair), a “−” representing each pair where the later value is smaller (a discordant pair), and a “0” representing a tied pair. The Kendall score, S, may be calculated from this matrix by subtracting the number of “−” symbols from the number of “+” symbols. Kendall (1976) also showed that the variance of τ may be calculated from the difference matrix.

Figure 2. Dependent variable scores are arranged in chronological order along the horizontal edge of a matrix from left to right, and in chronological order along the vertical edge of the matrix from bottom to top. Pairwise comparisons are made in a time-forward fashion within the corresponding cells of the matrix, with a “+” representing a concordant pair, a “−” representing a discordant pair, and a “T” representing a tied pair. For Figure 2A, S = 3, n_pairs = 45, and τ = .7. For Figure 2B, S = 5, n_pairs = 45, and τ = 5/45 = .1. (A) Difference matrix for time series in Figure 1C. (B) Difference matrix for time series in Figure 1E.

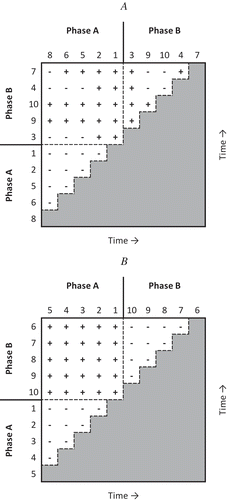
Parker et al. (2011b) pointed out that the τ difference matrix of single-case data may be partitioned to evaluate within-phase trend and between-phase differences. In Figure 2, the A-to-A pairs are grouped in the triangular area in the lower left corner of the matrix, the B-to-B pairs are grouped in the triangular area in the upper right corner of the matrix, and the A-to-B pairs are grouped in the rectangular area in the upper left corner of the matrix. Each type of pairwise score comparison, A-to-A, B-to-B, and A-to-B, contributes a unique type of information and each is located in a discrete area of the τ difference matrix.

For A-to-A comparisons, earlier scores are compared with later scores and counted as either concordant (increasing), discordant (decreasing), or tied; however, all comparisons of this type exist in Phase A only, before the introduction of the experimental treatment. Thus, A-to-A comparisons together characterize the trend within phase A. We can use $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{A}}=S_{\mathrm{A}}/n_{\mathrm{A}}$ to calculate the τ score for this discrete area of the difference matrix. Similarly, τ can be calculated for the trend within phase B using $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{B}}=S_{\mathrm{B}}/n_{\mathrm{B}}$. One way of thinking about the A-to-B pairwise comparisons is as a measure of overall concordance or discordance between phases: $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}=S_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}/n_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}$. Together, A-to-B pairwise comparisons describe the degree to which phase B is generally increasing (concordant), decreasing (discordant), or similar (tied) to phase A.

1.5. Interpreting Tau-U_{trend A}, Tau-U_{trend B}, and Tau-U_{A vs. B}

Tau-U was proposed (Parker et al., 2011b) as a family of τ coefficients that together illustrate the effects of treatment on within-phase trend and between-phase differences in single case research studies. The Tau-U coefficients are found by partitioning the difference matrix into these three regions and, in some cases, recombining them in various combinations to yield different τ values. $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{A}}$, $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{B}}$, and $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}$ are the first three coefficients in Tau-U, as well as the building blocks for the remaining three coefficients outlined by Parker, Vannest, Davis, et al. This method allows the researcher to consider both trend and phase effects in the same τ metric.

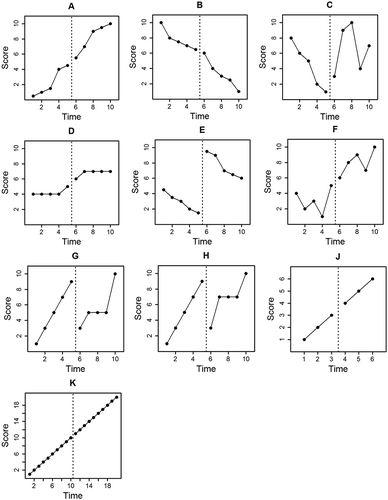
For example, consider the data set in Figure 1E. What effect size best characterizes the treatment that was implemented between phases? While there seems to have been an increase in level, a decreasing trend appears unaffected by treatment. We will use the first three coefficients in Tau-U ($\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{A}}$,$\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{B}}$, and $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}$) to demonstrate how a Tau-U analysis helps quantify these patterns. For Figure 1E data, $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{A}}=S_{\mathrm{A}}/n_{\mathrm{A}}=-10/10=-1.0$ and $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{B}}=S_{\mathrm{B}}/n_{\mathrm{B}}=$$-10/10=-1.0$. This makes logical sense: within each phase, there are 5 points and 10 pairwise comparisons; also, when points are compared to one another within each phase, all pairwise comparisons are discordant (decreasing) with time. Thus, according to Tau-U, there is a consistent downward trend of scores within both phase A and phase B. This statement agrees with a visual inspection of the data. One conclusion that might be inferred from $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{A}}$ and $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{B}}$ is that the experimental treatment had no effect on the downward trend of scores. In addition to studying the trends within each phase, we find that $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}=S_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}/n_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}=$$25/25=1.0$. In this case, for all 25 A–B pairwise comparisons, the phase B score was larger than the phase A score. This Tau-U coefficient shows that, overall, all phase B scores have increased over all phase A scores. This statement also agrees with visual analysis. So, with $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{A}}$, $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{B}}$, and $\mathrm{T}\mathrm{a}\mathrm{u}-{\mathrm{U}}_{\mathrm{A}\mathrm{v}\mathrm{s}.\mathrm{B}}$, one can describe quantitatively that, while the experimental treatment did not appear to affect the decreasing trend of scores, there was a large positive effect on the level of scores.

1.6. Tau-U: controlling for baseline trend

The inferential problem posed by baseline trend has been thoroughly discussed in single-case research literature, and many recognize the importance of accounting for baseline trend when evaluating SCEDs (Barlow & Hersen, 1984; Kazdin, 1978; Kratochwill et al., 2010; Tarlow, 2016a). However, there is little consensus on how best to address this problem. Ideally, investigators will identify outcome variables of interest that are stable (i.e., flat) during baseline phase measurement, but for many variables or research domains, this may not be feasible (Solomon, 2014). When there is evidence of baseline trend, as in Figure 1E data, many analytic strategies attempt to “control” or “correct” for the trend by (1) estimating the degree of baseline trend present and (2) adjusting baseline and treatment phase observations to remove the influence of baseline trend. Then an effect size is estimated from the “corrected” or “residualized” data that are assumed to demonstrate how the individual might have responded in the absence of baseline trend. This general strategy is used in parametric (Allison & Gorman, 1993; Faith et al., 1996; Huitema & McKean, 2000), nonparametric (White & Haring, 1980), and stochastic (Manolov & Solanas, 2008) baseline trend control methods.

The example data in Figure 1E illustrate the problem of baseline trend often encountered by single-case investigators. As discussed in the previous section, the three “building block” Tau-U coefficients (Tau-U_{trend A}, Tau-U_{trend B}, Tau-U_{A vs. B}) may be used to parse out within-phase trend from between-phase differences. Parker et al. (2011b) proposed three additional Tau-U coefficients that recombine the three building block statistics in different ways. One of those was a Tau-U coefficient that could be substituted for Tau-U_{A vs. B + trend B} when baseline trend control is necessary. For this new coefficient, the S value of Tau-U_{trend A} is subtracted from the numerator of Tau-U_{A vs. B + trend B} and its n value is added to the denominator: Tau-U_{A vs. B + trend B − trend A} = (S_{A vs. B} + S_B − S_A)/(n_{A vs. B} + n_B + n_A). Conceptually, the Tau-U_{A vs. B + trend B − trend A} calculation includes the information in Tau-U_{trend A}; however, the sign of the baseline trend component is reversed to control for its influence. For the series in Figure 1E, it is apparent how the S values for Phase A trend and Phase B trend are “cancelled out” in the numerator: Tau-U_{A vs. B + trend B − trend A} = [25 + (−10) − (−10)]/(25 + 10 + 10) = 25/45 = .6.

The Tau-U_{A vs. B + trend B} and Tau-U_{A vs. B + trend B − trend A} coefficients provide two different baseline trend control options, the former less extreme than the latter. While Tau-U_{A vs. B + trend B − trend A} does offer a stronger control method, it may distort effect size estimates when used inappropriately. For example, the data series in Figure 1F have a Tau-U_{trend A} = 0, Tau-U_{trend B} = .6, and Tau-U_{A vs. B} = 1. There is no reason to control for baseline trend because there is no evidence that such a trend exists (Tau-U_{trend A} = 0). For this data series, Tau-U_{A vs. B + trend B} = .9. However, if a researcher inappropriately applied a Tau-U baseline control, they would find that Tau-U_{A vs. B + trend B − trend A} = .7. Researchers (Parker et al., 2011b, 2011b) point out that the method of “monotonic trend correction” employed by Tau-U_{A vs. B + trend B − trend A} is less likely to distort results than other less conservative control methods (e.g., regression methods). However, it is clear that a thoughtless implementation of baseline control methods will lead researchers to draw erroneous conclusions about the effects of their experimental interventions.

In the event that researchers are uninterested in score trends in either baseline or experimental phase and wish only to characterize phase independence, as in a Tau-U_{A vs. B} or Mann–Whitney U test, they may still want to control for baseline trend on effect size measurement. In this case, we propose the combination of Tau-U_{A vs. B} and Tau-U_{trend A} in a manner similar to the one used by Parker et al. (2011b): Tau-U_{A vs. B − trend A} = (S_{A vs. B} − S_A)/(n_{A vs. B} + n_A). For the data series in Figure 1E, Tau-U_{A vs. B − trend A} = [25–(−10)]/(25 + 10) = 35/35 = 1.

How then should researchers resolve the question of baseline trend correction given the variety of options offered by the family of Tau-U coefficients? This is clearly an important concern in single-case data analysis with worrisome implications when neglected. We argue that baseline trend correction should only be conducted when there is both a theoretical and empirical rationale for its use. In terms of theoretical rationale, a researcher might make decisions about baseline trend correction on a case-by-case basis or for groups of cases depending on the experimental design. For example, the researcher may suspect that there is a Hawthorne effect because some participants have started filling out surveys which changed their behavior, but they have not yet received any treatment. In an equally plausible scenario, a researcher might decide against using any baseline trend correction if baseline trend is difficult to interpret given the type of data collected (e.g., if developmental processes are thought to contribute to baseline trend, “controlling for development” could be considered inappropriate). In terms of empirical rationale for baseline trend correction, the Tau-U family of coefficients provides a good indicator for making this decision. The p value for Tau-U_{trend A} is a reasonable gauge for the necessity of baseline trend correction: when there is a statistically significant Tau-U_{trend A} effect, the researcher may use a baseline trend corrected method; when Tau-U_{trend A} is not statistically significant, as is the case for the data series in Figure 1F, the researcher probably lacks the empirical support for baseline trend correction. Alternatively, Parker et al. (2011b) selected a trend level (Tau-U_{trend A}) of .4 noting that Tau-U_trend A = .4 represented the 75th percentile in their sample of published data sets that they examined. They only used baseline correction in those data sets where Tau ≥ .40 in phase A and in the Tau-U_{A vs. B} contrast.

1.7. Phase nonoverlap: what Tau-U tells us and what it does not

Parker et al. (2011b) suggest that Tau-U_{A vs. B} is a nonoverlap measure. Indeed, Parker, Vannest, Davis, et al. (2011b) refer to Tau-U_{A vs. B} as Tau_nonoverlap. We argue that this is an oversimplification that can be misleading. The data series in Figure 1G and 1H clarify this issue. For reference, Table 1 contains a summary of the statistics for the graphs in Figure 1. Note that for these series, the degree of phase nonoverlap may be considered equivalent. In both graph G and H, percent of nonoverlapping data (PND; Scruggs, Mastropieri, & Casto, 1987) = 20%, indicating that one out of the five experimental phase scores exceed all baseline phase scores. The only difference between the two series is the configuration of scores within the overlapping region. However, Tau-U_{A vs. B} is not the same for these series. For graph G, Tau_{A vs. B} = .1, and for graph H, Tau_{A vs. B} = .4. Clearly, the Tau-U_{A vs. B} coefficient is describing more than the nonoverlap of phases.

Table 1. Tau-U effect sizes and p values for graphs in Figure 1

Figure 1	Tau-Utrend A	Tau-Utrend B	Tau-UA vs. B	Tau-UA vs. B − trend A	Tau-UA vs. B + trend B	Tau-UA vs. B + trend B − trend A
Graph A	1.00 (.03)	1.00 (.03)	1.00 (.01)	.43 (.18)	1.00 (<.01)	.56 (.03)
Graph B	−1.00 (.03)	−1.00 (.03)	−1.00 (.01)	−.43 (.18)	−1.00 (<.01)	−.56 (.03)
Graph C	−1.00 (.03)	.20 (.81)	.44 (.30)	.60 (.05)	.37 (.25)	.51 (.05)
Graph D	0.40 (.29)	.40 (.29)	1.00 (<.01)	.60 (.03)	.83 (<.01)	.56 (.02)
Graph E	−1.00 (.03)	-1.00 (.03)	1.00 (.01)	1.00 (<.01)	.43 (.18)	.55 (.03)
Graph F	.00 (1.0)	.60 (.22)	1.00 (.01)	.71 (.02)	.89 (<.01)	.69 (<.01)
Graph G	1.00 (.03)	.70 (.10)	.12 (.83)	-0.20 (.43)	.29 (.37)	.00 (1.0)
Graph H	1.00 (.03)	.70 (.10)	.36 (.39)	-0.03 (.84)	.46 (.13)	.13 (.64)
Graph J	1.00 (1.0)	1.00 (1.0)	1.00 (.08)	.50 (.31)	1.00 (.03)	.69 (<.01)
Graph K	1.00 (<.01)	1.00 (<.01)	1.00 (<.01)	0.38 (.06)	1.00 (<.01)	.53 (<.01)

Note: The number in parentheses is the two-sided p-value.

It is helpful to consider that Tau-U_{A vs. B} is in many ways equivalent to the Mann–Whitney U test of group independence (Parker et al., 2011b). As noted above, when used for hypothesis testing, Tau-U_{A vs. B} yields p values identical to Mann–Whitney U for single-case data series (the p value is produced by Tau-U_{A vs. B} in addition to providing an estimate of effect size). The Mann–Whitney U test is analogous to a nonparametric t test; both infer whether two data sets are statistically different from each other. Most researchers would agree that if a t test were used to determine if two phases of a single-case data series were different (acknowledging that using a t-test for time series data would almost certainly violate the assumptions inherent to that statistic), the result of the t test would not tell the researcher about phase nonoverlap. Rather, the result would indicate if the two samples were different enough to reject a null hypothesis about their similarity. The Mann–Whitney U test and the Tau-U_{A vs. B} coefficient infer the same conclusion. To further clarify this point, consider the data series in Figure 1J and 1K. In both series, there is complete nonoverlap between phases. Yet Tau-U_{A vs. B} and Mann–Whitney U for graph J are not significant at the p < .05 level, whereas in graph K, Tau-U_{A vs. B} and Mann–Whitney U are significant at the p < .001 level.

In a sense, Tau-U_{A vs. B} can be thought of as an indirect indicator of phase nonoverlap, because it generally increases with magnitude as the scores being analyzed spread apart from one another and become less disordered (all Tau-U coefficients have this property). Tau-U_{A vs. B} is unique among the Tau-U coefficients in that it only considers pairwise comparisons of scores between phases. Therefore, Tau-U_{A vs. B} is unique in that Tau-U_{A vs. B} = 1 if (and only if) there is complete nonoverlap between phases. So, for the data series in Figure 1J and 1K, Tau-U_{A vs. B} = 1, although we demonstrated that their p values are not equivalent. Accurate conclusions made from Tau-U_{A vs. B} about phase nonoverlap can only be made in the extreme case where there is complete nonoverlap between phases. In all other cases, only broad assumptions about nonoverlap can be made from Tau-U_{A vs. B}, as the examination of Figure 1G and 1H showed. Tau-U_{A vs. B} is not a pure nonoverlap measure, because it conveys a more nuanced description of phase independence.

1.8. Theoretical limitations of Tau-U and recommendations

1.8.1. Discrepancies in published Tau-U articles

It is important to offer some clarifying commentary regarding the original theoretical development of Tau-U in Parker et al. (2011b) and Parker et al. (2011a), as well as the online Tau-U calculator developed by Vannest, Parker, and Gonen (2011) available at www.singlecaseresearch.org/calculators/tau-u. Both articles present Tau-U as a desirable effect size for single-case research, but they are in some ways inconsistent in terminology and method. Here we hope to clear up any confusion and identify some potential limitations of Tau-U not identified in those authors’ original works.

As made clear above and by Parker et al. (2011b), Tau-U is essentially a family of rank correlation indices which, although theoretically related, require different interpretations. Throughout this paper, we have tried to be very clear about identifying these indices with subscript notation (e.g., Tau-U_{A vs. B}). That said, in Parker, Vannest, Davis, et al., the authors use “Tau-U” to refer to Tau-U_{A vs. B + trend B}, “which combines nonoverlap between phases with trend from within the intervention phase” (p. 284), with the added option of baseline trend control, i.e., Tau-U_{A vs. B + trend B − trend A}. However, in Parker et al. (2011a), they use “Tau-U” to refer to Tau-U_{A vs. B − trend A}, which “extends Tau_novlap to control for undesirable positive baseline trend” (p. 313). The online calculator (Vannest, Parker, & Gonen, 2011) appears to use this second Tau-U method as well. These discrepancies are unfortunate, because vague language obscures the conceptual value of the Tau-U family of indices, which we have tried to develop in this paper. Another implication is for possible inconsistent reporting of Tau-U results in published research—it may be unclear to readers which “Tau-U” is being reported by authors.

1.8.2. Results may not be bounded between −1 and +1

There is a more serious concern raised by the Tau-U_{A vs. B − trend A} procedure in Parker et al. (2011a) and available to investigators on their online calculator (Vannest et al., 2011). To calculate Tau-U, they instruct the investigator to

score a specially-coded phase variable … for Phase A, input is a reverse time sequence and for Phase B, input is Phase B’s first time value, repeatedly. For our example, the phase coding is 6, 5, 4, 3, 2, 1/7, 7, 7, 7, 7, 7, 7. From the KRC analysis, the Tau output will not be accurate … Tau-U must be hand calculated as S/number of Pairs…. The KRC analysis yields S = 31, so Tau-U = S/number of Pairs = 31/42 = .74. (p. 313–314; emphasis added)

Little rationale is provided for the instruction to hand calculate Tau-U with a different denominator. What is not made clear is that this change in the Tau formula, by substituting a denominator that is a smaller value than the original Tau denominator, will (1) inflate the value of the Tau-U result and (2) give a coefficient no longer bounded between −1 and +1. For example, a Tau-U analysis of the time series [5, 4, 3, 2, 1/6, 7, 8, 9 10] with the suggested specially coded variable [5, 4, 3, 2, 1/6, 6, 6, 6, 6] gives S = 35 so that Tau = S/n_pairs = 35/25 = 1.4. This strange result was verified with the Tau-U online calculator (Vannest et al., 2011).

This result raises difficult questions about how to interpret a correlation coefficient not bounded between −1 and +1. Even more concerning is the reality that many investigators using the method in Parker et al. (2011a) or using the online calculator at www.singlecaseresearch.org/calculators/tau-u may not realize that their result is inflated unless it falls outside of the typical bounds of −1 and +1. Put another way, investigators may be interpreting their results as if they were bounded between −1 and +1 when in reality, they are not, leading them to conclude that their effect sizes are much larger than they are. For this reason, we recommend against the hand calculation method in Parker, Vannest, and Davis as well as the online calculator until these issues can be further resolved.

1.8.3. Tau-U baseline control cannot be visualized

Parker et al. (2011a) point out that their method of monotonic trend control cannot be graphically visualized; however, this is not explored as a significant limitation of the method. Given the strong historical ties between single-case research and visual analysis (see Brossart et al., 2006), the trade-off of statistical analysis for visual analysis may be unpalatable for some investigators. Furthermore, without being able to visualize baseline trend control, the method is something of a “black box” where one cannot easily interpret the effect of baseline trend control on observed data.

2. Study 1: empirical review of τ and Tau-U

2.1. Data collection and extraction

In order to develop empirical support for τ and Tau-U, we analyzed 115 single-case data sets from 40 previously published articles. The 115 data sets were retained from a larger pool of 209 published series after several exclusion criteria were considered. In order to be included in this study, data series were required to have at least two phases (one baseline/control phase and one experimental/treatment phase; i.e., an AB design). We also excluded data sets that did not meet the What Works Clearinghouse recommendation that single-case studies include at least five observations in each phase (Kratochwill et al., 2010). Of the 115 data sets retained for this study, the mean number of phase A observations was 9.97 (SD = 5.86), and the mean number of phase B observations was 12.77 (SD = 9.39). The 115 data series analyzed in this paper were published between 1993 and 2009 (2 unpublished dissertations were included), and they represent original research conducted in the fields of psychotherapy, education, neuropsychology, speech therapy, and sport psychology. We searched for single-case articles using PubMed and PsycINFO because we wanted to include articles from a wide range of studies and because PubMed is often not included in literature searches of single-case designs. While our literature search was not as comprehensive as the one conducted by Smith (2012), we were able to collect a wide range of studies not included in Smith’s review as well as earlier studies (e.g., Parker & Hagan-Burke, 2007a; Parker, Hagan-Burke, & Vannest, 2007; Parker & Vannest, 2009). We also focused on studies that had an AB design because Smith (2012) found that 69% of the single-case studies reviewed were multiple baseline or combined series designs, which are basically multiple AB experiments using multiple participants. Smith reported that other designs were used much less frequently: alternating/simultaneous designs (6%), changing criterion designs (4%), reversal designs (17%), and mixed designs (10%).

Time, score, and phase data were extracted from the selected studies using GetData Graph Digitizer (GetData Graph Digitizer, 2013), followed by randomly selecting 5% of the data sets for comparison to the corresponding original publication to confirm the overall accuracy of the data extraction methods. Tau-U coefficients and their corresponding p values were calculated using R syntax (Tarlow, 2014; Tarlow, 2016b).

2.2. Analytic approach

To verify the conceptual underpinning empirically, we developed four hypotheses which were then tested using real data. We compared the calculated τ and Tau-U effect sizes for our sample using two mutually supportive approaches. First, a nomothetic approach was used to test four hypotheses about the overall comparative performances of these effect sizes. These hypotheses represent broad generalizations about how the τ and Tau-U coefficients, on average, will compare to one another when calculated on the same sample of data sets. Hypotheses 1 and 2 make predictions about the absolute values, or magnitudes, of the effect size coefficients. Hypotheses 3 and 4 make predictions about the correlations between the effect size coefficients. PND was included as a comparison statistic to aid in addressing Hypothesis 4. These hypotheses are based on the theoretical information presented previously, i.e., they are generated from a priori theories about what these coefficients measure and how they perform. This kind of nomothetic information will help researchers and practitioners translate their theoretical understanding of τ and Tau-U into interpretation and evaluation of real-world single-case data sets. Then, an idiographic approach is used to examine specific, individual graphs. These data sets were selected because they yielded the most discrepant effect size coefficients. For each study in the ideographic review, we provide the AB graph along with a descriptive summary of the data set in terms of score independence between phases and score trend, followed by explanation of the discrepant effect sizes. These illustrations provide researchers and practitioners with real-life examples of individual data sets that can yield hugely discrepant effect sizes based on which effect size they choose to calculate. Used together, these two approaches allow one to better understand these effect sizes, how they work to measure treatment outcome, and for which data sets they are or are not appropriate.

2.3. Overall performance of τ and Tau-U coefficients (nomothetic approach)

2.3.1. Hypothesis 1. Tau-U_{A vs. B} will yield larger results than other Tau-U coefficients

In their review of 176 single-case data sets, Parker et al. (2011b) found that within-phase trends were generally smaller in magnitude than between-phase differences. It was therefore expected that Tau-U_{A vs. B} would yield the largest values of the Tau-U coefficients in this study, perhaps with a demonstrated ceiling effect. The expectation of a ceiling effect for Tau-U_{A vs. B} is also based in a theoretical understanding of the coefficient. When all data points in the B phase are greater than (or less than) all points in the A phase, i.e., there is total nonoverlap between phases, Tau-U_{A vs. B} will yield the result of ±1. It is expected that this “total nonoverlap” condition is more common in published single-case studies than graphs with perfectly increasing or decreasing within-phase monotonic trends, i.e., the conditions that would create ceiling effects in the other Tau-U coefficients.

2.3.2. Hypothesis 2. Tau-U_{A vs. B + trend B − trend A} will yield smaller results than other Tau-U coefficients

Including Tau-U_{trend A} is expected to control, or reduce, the effect size in most cases—indeed, attenuating the effect size by controlling trend is the intent of including phase A trend (with the direction reversed). An increase is expected only in cases where baseline trend occurs in the opposite direction of the expected treatment effect (e.g., disruptive behavior is increasing in frequency prior to behavioral therapy). In those cases, which were infrequent in our investigation, the reversal of the undesired trend increases the effect size. In the majority of cases where baseline trend is nonexistent or increasing in the direction of the treatment effect, subtracting Tau-U_{trend A} will attenuate the total effect size. This occurs even in the absence of trend because the denominator of the Tau-U equation increases by the number of pairs in the A phase analysis—or put another way, the variance of the statistic increases but the effect does not.

Parker et al. (2011b) found that adding the within-phase trend of the B phase similarly attenuated most of their calculated effect sizes, i.e., Tau-U_{A vs. B + trend B} tended to be smaller in magnitude than Tau-U_{A vs. B}. Parker et al. demonstrated that effect sizes were often reduced by adding the phase B trend because within-phase trends were relatively small when compared to cross-phase differences. Thus, by adding variance to the analysis (increasing the Tau-U denominator, as described above) without a substantial increase in the overall effect (weak or nonexistent phase B trend), Tau-U_{A vs. B + trend B} is relatively small in magnitude.

2.3.3. Hypothesis 3. Tau-U_{trend A} will be least associated with other Tau-U coefficients. However, Tau-U_{trend A} will be somewhat correlated with Tau-U_{trend B}

Preexisting baseline trend (i.e., Tau-U_{trend A}) is not expected to accurately predict treatment outcome. However, Tau-U_{trend A} is expected to be associated with Tau-U_{trend B} because baseline trend is thought to persist, to some degree, throughout the treatment phase (hence baseline trend correction).

2.3.4. Hypothesis 4. Of the Tau-U coefficients, Tau-U_{A vs. B} will have the strongest association with the PND

PND (Scruggs et al., 1987) is a widely used single-case statistic that describes the percentage of treatment phase data that exceeds the most extreme score in the baseline phase. Although it has considerable limitations (Allison & Gorman, 1993; Ma, 2006; Wolery, Busick, Reichow, & Barton, 2010), it has remained popular because of its simple calculation and straightforward interpretation as a measure of phase nonoverlap. As discussed previously, Tau-U_{A vs. B} is an indirect indicator of phase nonoverlap and is thus expected to correlate highly with PND.

3. Results

To test Hypotheses 1 and 2, we calculated the average absolute magnitudes for the Tau-U coefficients across the 115 sampled data sets. Table 2 indicates that, on average, the selection of a Tau-U coefficient can substantially impact the magnitude of the effect size results. These results are also presented in Figure 3 boxplot. Table 3 presents a correlation matrix of the Tau-U coefficients in order to test Hypothesis 3. For Hypothesis 4, PND values were calculated for the sample of 115 data sets and PND’s correlations with the Tau-U effect sizes are included in Table 3.

Table 2. Means and standard deviations for Tau-U effect sizes of 115 published single-case data sets

Effect size	M	SD
Tau-Utrend A	.50	.24
Tau-Utrend B	.32	.24
Tau-UA vs. B	.73	.27
Tau-UA vs. B − trend A	.51	.24
Tau-UA vs. B + trend B	.57	.28
Tau-UA vs. B + trend B − trend A	.43	.22

Note: Means and standard deviations are for the absolute values of effect sizes; absolute values were used to compare relative magnitude of measured effects regardless of the direction of change (e.g., decrease an undesirable variable or increase a desirable variable).

Table 3. Correlations of Tau-U and PND coefficients for 115 published single-case data sets

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Tau-Utrend A	1.00
Tau-Utrend B	.24	1.00
Tau-UA vs. B	.14	.60	1.00
Tau-UA vs. B − trend A	−.10	.54	.96	1.00
Tau-UA vs. B + trend B	.20	.76	.97	.90	1.00
Tau-UA vs. B + trend B − trend A	−.02	.73	.95	.96	.96	1.00
PND	.04	.35	.81	.61	.75	.66	1.00

Note: Correlations in bold were statistically significant at p < .05.

Figure 3. Boxplot for effect sizes of 115 published single-case data sets. Absolute values used to compare relative magnitude of measured effects.

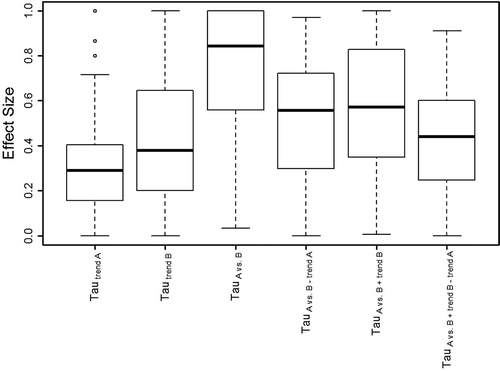
Hypothesis 1 stated that Tau-U_{A vs. B} will yield larger results on average than other Tau-U coefficients. As predicted, the average Tau-U_{A vs. B} effect size (.73) was considerably larger than the next largest average Tau-U effect size, Tau-U_{A vs. B + trend B} (.57). The boxplot in Figure 3 also illustrates the ceiling effect present in this coefficient, where over a quarter of graphs produced Tau-U_{A vs. B} = 1.00. This was the only Tau-U coefficient with a pronounced ceiling effect. However, there were a small number of data sets in other Tau-U coefficients that yielded larger effect sizes than Tau-U_{A vs. B}. These exceptions generally occurred when there was (1) a noticeable lack of any phase nonoverlap, and (2) a clear upward or downward trend within or across phases.

Hypothesis 2 stated that Tau-U_{A vs. B + trend B − trend A} will on average yield the smallest effect size results. Tau-U_{A vs. B + trend B − trend A} did have a relatively small average absolute value (.43) compared to the other Tau-U coefficients. However, the baseline trend coefficient Tau-U_{trend A} did have a smaller average effect size (.32) and the treatment phase trend coefficient Tau-U_{trend B} had the same average absolute value (.43). Interestingly, those results suggest that the average data set had some small-to-moderate monotonic trend in both baseline and treatment phases.

Hypothesis 3 stated that Tau-U_{trend A} will be least associated with the other Tau-U coefficients. However, Tau-U_{trend A} was expected to correlate slightly better with Tau-U_{trend B}. As predicted, baseline trend (Tau-U_{trend A}) correlated the least with other coefficients. The results in Table 3 strongly support theoretical explanations for why baseline trend is not expected to be an accurate predictor of treatment outcome. Still, as expected, Tau-U_{trend A} did correlate slightly better with Tau-U_{trend B} and other coefficients that consider Tau-U_{trend B} (i.e., Tau-U_{A vs. B + trend B}), though it did not correlate with Tau-U_{A vs. B − trend A} or Tau-U_{A vs. B + trend B − trend A} (this is expected, as the influence of Tau-U_{trend A} is removed in those coefficients).

Hypothesis 4 predicted that PND, a classic measure of phase nonoverlap, would correlate highly with Tau-U_{A vs. B}, an indirect measure of phase nonoverlap. Results support this hypothesis. As discussed above (in the example of Figure 1G and 1H), Tau-U_{A vs. B} could be more accurately interpreted as a measure not only of nonoverlap but also of overall between-phase difference. It should also be noted that Tau-U_{A vs. B} and PND had, overall, the largest magnitude effect sizes. While a measure that tends to yield large effect sizes may be attractive to an investigator, they may also discriminate relatively poorly among different treatments (e.g., ceiling effects). These two measures also do not account for baseline trend, which may explain their tendency to yield large results.

3.1. Performance of τ and Tau-U coefficients within individual datasets (idiographic approach)

For many of the data sets in our sample, the values for the various effect sizes were reasonably close. However, researchers and practitioners will benefit from understanding when (and why) major discrepancies occur among the various effect sizes, even when calculated for the same data set. This understanding will allow researchers and practitioners to be aware of situations in which they may infer drastically different treatment effects simply through the selection of one effect size coefficient over another. For this analysis, five effect size coefficients were compared and described for heuristic purposes:

• Tau-U_{A vs. B}, an effect size coefficient that considers the independence of scores between phases but not the trend of the scores.

• Tau-U_{A vs. B − trend A}, an effect size coefficient that simultaneously considers the independence of scores between phases while incorporating a monotonic baseline trend control method. This is the Tau-U method recommended in Parker et al. (2011b) and in their online calculator (Vannest et al., 2011).

• Tau-U_{A vs. B + trend B}, an effect size coefficient that simultaneously considers the independence of scores between phases with the phase B trend. This method, along with the baseline control method below, is the coefficient recommended in Parker et al. (2011b).

• Tau-U_{A vs. B + trend B − trend A}, an effect size coefficient that simultaneously considers the independence of scores between phases and the trend of phase B along with a monotonic baseline trend control.

• τ_{(TIME, SCORE)}, a coefficient that considers the cross-phase trend of scores but not the independence of scores between phases. This coefficient, like the within-phase trend coefficients Tau-U_{trend A} and Tau-U_{trend B}, would rarely be appropriate as experimental effect sizes per se, as they contain no information about phase differences. However, τ_{(TIME, SCORE)} is examined alongside the other Tau-U effect size coefficients because it illustrates useful lessons about the interpretation of single-case treatment effects.

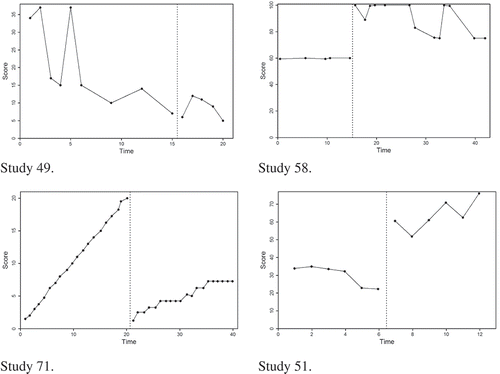
3.1.1. Study 49

The calculated τ_{(TIME, SCORE)} for Study 49’s data set (see Figure 4) is −.70 (a large negative effect). While still negative, the calculated Tau-U_{A vs. B − trend A} for this dataset is only −.14 (a small negative effect). Characteristically, this data set shows (1) a strong downward trend in phase A, (2) a continuation of this downward trend in phase B, and (3) some independence between phases.

Figure 4. Illustrative real-world data sets.

The τ_{(TIME, SCORE)} value in Study 49 is large (−.70) because, again, τ_{(TIME, SCORE)} only considers: “Do my scores change predictably over time?” Disregarding the phase distinction, the data collectively show a strong downward trend across phases (i.e., the scores change predictably over time), so τ_{(TIME, SCORE)} infers a strong effect. However, the Tau-U_{A vs. B − trend A} effect size is attenuated due to removing the strong baseline trend. In other words, Tau-U_{A vs. B − trend A} distinguishes between the phases and then removes the strong negative trend effect from the baseline.

Visual analysis of Study 49 in Figure 4 suggests that the overall downward treatment effect was more likely due to a preexisting (i.e., cross-phase) trend than an effect of the treatment itself. By using Tau-U_{A vs. B − trend A}, the researcher acknowledges the preexisting baseline trend and takes steps to “control” for this preexisting trend (by removing it) in an attempt to more fairly represent the actual effect brought on by the treatment itself.

3.1.2. Study 58

This study yielded some of the largest effect size discrepancies of the 115 sampled data sets. Characteristically, this data set shows (1) substantial independence of scores between phases (e.g., 100% nonoverlap), and (2) an erratic but overall downward trend in the B phase that undermines the desired treatment effect (Figure 4).

For three of the four discrepant comparisons, the cause of the discrepancy is the inability of Tau-U_{A vs. B} to account for any phase trend when there are strong trend issues within the data. The Tau-U_{A vs. B} value (1.00) suggests a perfect positive treatment effect. Recall that Tau-U_{A vs. B} considers the independence of scores between phases but not the trend of the scores. Because the data set has perfect phase nonoverlap, Tau-U_{A vs. B} is 1.00. However, the second characteristic of the data set (the erratic, but overall downward trend in phase B) strongly attenuates Tau-U_{A vs. B + trend B} (.23) and Tau-U_{A vs. B + trend B − trend A} (.19). Despite the large, clean “jump up” in scores when treatment begins, phase B data either remains flat or decreases substantially at times. Thus, the apparent “improvement” in the treatment phase is not only erratic and unreliable (i.e., showing high variability, especially compared to the stable baseline data) but is also apparently worsening over time. In other words, the B phase trend works against the positive treatment effect indicated by the independence of scores between phases (i.e., Tau-U_{A vs. B}). Both of these effect sizes account for these “problematic” phase B trend issues, making them strongly discrepant with perfect positive effect suggested by Tau-U_{A vs. B}.

Similarly, the Tau-U_{A vs. B − trend A} value suggests a large positive effect (.81), while the Tau-U_{A vs. B + trend B − trend A} value suggests only a small positive effect (.19). The only difference between the two coefficients is the inclusion of B phase trend. Similar to Tau-U_{A vs. B}, Tau-U_{A vs. B − trend A} does not account for the problematic phase B trend issues, so it remains quite large. In contrast, Tau-U_{A vs. B + trend B − trend A} does account for the phase B trend and is attenuated for the same reasons as described above. Incidentally, interested readers may wonder why Tau-U_{A vs. B − trend A} (.81), while still large, is noticeably attenuated from Tau-U_{A vs. B} (1.00), given that there is almost no phase A trend. Recall that subtracting S_A from the numerator has almost no effect, but adding n_A to the denominator reduces the Tau-U value (essentially, “adding a lot of variance but not a lot of effect”).

3.1.3. Study 71

Figure 4 displays the single largest absolute discrepancy out of all the effect size comparisons for all 115 data sets. For Study 71, τ_{(TIME, SCORE)} = .18 (a small positive cross-phase trend effect), while Tau-U_{A vs. B − trend A} = −.68 (a strong negative effect). The fact that two researchers could draw essentially opposite conclusions from the exact same data set underscores the importance of understanding what the different effect sizes actually measure and the careful selection of an effect size that is appropriate for answering one’s question. Characteristically, this data set shows (1) a sharp, nearly perfect upward phase A trend, (2) an immediate and dramatic drop in scores after the intervention begins (but no independence of scores between phases, i.e., no nonoverlap), and (3) a gradual upward phase B trend.

“Stable” baseline data allow one to confidently attribute any change in the magnitude or trend of scores to the treatment rather than any preexisting baseline trends. However, there are some dependent variables that have such strong inherent trend that researchers may simply wish to reduce, pause, or reverse the variable’s trend. Accomplishing this would be deemed an “effective” treatment. Visual analysis of Study 71 in Figure 4 suggests that the researchers were probably working with this kind of dependent variable and hoping for this kind of treatment effect. For example, perhaps the dependent variable was post-traumatic depressive symptoms. Given how rapidly the depressive symptoms were increasing, the researchers would probably have deemed any intervention that at least slowed down the increase in the subject’s depressive symptoms successful. In this case, the researchers clearly implemented a successful intervention. Not only was there an immediate and dramatic drop in depressive symptoms with the start of the intervention but the intervention also slowed down—and even stabilized for periods of time—the rapid increase in scores. Thus, a viewer of study 71’s AB graph would probably infer that the treatment had an important (negative) effect (i.e., a desired decrease in depressive symptoms).

In order to capture the dynamics of these data, an appropriate effect size coefficient to represent this effect would need to include a phase comparison and consider the extreme preexisting baseline trend. Tau-U_{A vs. B − trend A} does both, which is why it yields a reasonable effect size value for this study (−.68). Although the phase B upward trend undermines the researcher’s desired treatment effect, when compared to the phase A trend (which is why Tau-U_{A vs. B + trend B − trend A} is not appropriate), we can confidently say that there was a desired treatment effect (i.e., the scores did not increase as much as they had been increasing prior to treatment). Furthermore, the scores dropped immediately and dramatically with the onset of treatment. Tau-U_{A vs. B − trend A} accounts for these dynamics by controlling for (or removing, “flattening”) the phase A trend, yielding an effect size that is more consistent with visual analysis of the data.

3.1.4. Study 51

The data set in Figure 4 is characterized by total nonoverlap between phases, a downward phase A trend, and an upward phase B trend. Another way to conceptualize these features is to consider what the Tau analysis “difference matrix” (Figure 2) would look like for this data set: all A–B comparisons would be positive, and most of the B–B comparisons would be positive, but most of the A–A comparisons would be negative. As such, any effect size that takes into account only the two positive portions of the matrix (A–B and B–B) and ignores the negative portion of the matrix (A–A) would yield a large positive effect size. This is precisely what occurred with the Tau-U_{A vs. B + trend B} value (.92). Including a correction for the slope in phase A resulted in a small reduction in the Tau-U_{A vs. B + trend B − trend A} effect size (.91).

3.2. Study 2: the relationship between visual analysis and Tau-U

Parker et al. (2011b) pointed out that “validation by visual analysis is especially important with increasingly complex analyses” (p. 298). A supplementary study was conducted to determine how closely Tau-U results agree with the judgments of trained visual raters. Due to the historical ties between single-case experimental research and visual analysis, statistical methods of single-case data analysis would ideally agree with visual judges. While Tau-U methods have been well received by single-case researchers, there has until now been little investigation into the relationship between this family of coefficients and visual analysis.

3.3. Methods

3.3.1. Data selection

Thirty AB graphs were randomly selected for visual analysis from the 115 total data sets sampled in the larger study; this number was chosen based on examples of prior visual analysis research (Brossart et al., 2006; Matyas & Greenwood, 1990). Extracted data points were de-identified and digitally regraphed so as to make the 30 AB graphs as visually uniform as possible.

3.3.2. Training of visual raters

The problem of poor interrater reliability in the visual analysis of single-case experiments is well documented and is a major impetus for the development of standardized statistical effect size measures (Brossart et al., 2006; Harbst et al., 1991; Park et al., 1990). However, recent studies have shown that structured criteria and training may improve the accuracy of visual raters (Fisher et al., 2003; Kahng et al., 2010; Stewart, Carr, Brandt, & McHenry, 2007). However, it is noted that in most of these promising studies of visual analysis, judges responded to artificial AB graphs (usually generated with Monte Carlo methods) rather than published single-case graphs; this limitation warrants caution about the generalizability of those findings to “real-life” data analysis. Wolfe and Slocum (2015) developed computer-based training for single-case visual analysts (http://foxylearning.com/tutorials/va) that improved the performance of visual judges over a no-training control. Four raters completed this evidence-based training independently before completing the visual judgment tasks.

3.3.3. Visual judgment tasks

The four judges independently completed three visual analysis tasks. First, each judge rated the 30 AB graphs on a 5-point scale based on “how certain or convinced you are that the experimental intervention yielded an effect,” with 1 indicating “not at all certain” and 5 indicating “very certain.” Second, each judge independently ranked the 30 graphs from “least certain” of a treatment effect to “most certain,” essentially assigning a unique rank score of 1–30 to each AB graph. These two visual rating tasks were assigned to identify the task that yielded the best interrater reliability for use in further analyses (similar to Kahng et al., 2010). Finally, each judge independently rated “how certain or convinced you are that there is a non-zero slope (trend) in the baseline phase, either increasing or decreasing”, on a 5-point scale as in the first task.

3.4. Interrater reliability

Krippendorff’s α is a measure of agreement used in this study to estimate interrater reliability. On the rating task (1–5), the judges’ scores had an α = .70, 95% CI [.63, .77] and on the ranking task (1–30), their scores had an α = .86, 95% CI [.82, .90]. When judges were asked to visually rate baseline trend only, their scores had an α = .68, 95% CI [.60, .75]. Krippendorff (2004) suggested that α > .67 indicated acceptable agreement, with greater interpretability when α > .80. On all three tasks, the ratings had at least an acceptable level of interrater reliability between judges. However, we chose to retain the ranking scores from the second task for further analysis with Tau-U given the higher level of agreement between judges.

3.5. Agreement between Tau-U coefficients and visual analysis

Table 4 presents the Spearman correlations of the six Tau-U coefficients with the average ranking determined by the four trained visual raters. Table 5 presents the range of Tau-U values that fell within each quartile of visually ranked graphs; for example, the first quartile (Q1) corresponds to the quarter of the AB graphs determined by visual raters to have the least evidence of treatment effect, and so on. Ideally, there would be little overlap between the ranges of Tau-U values in each quartile of visually ranked graphs, (e.g., “all Tau values greater than .7 were in the fourth quartile”). However, this was not the case for most coefficients. For example, when the 30 graphs were divided into four quartiles based on visual judges’ average rankings, each quartile contained Tau-U_{A vs. B + trend B} values ranging from .4 to .9.

Table 4. Spearman correlations of Tau-U coefficients and average visual ratings for 30 single-case data sets

	Correlation with average visual rating (ρ)
Tau-Utrend A	−.40
Tau-Utrend B	−.16
Tau-UA vs. B	.39
Tau-UA vs. B − trend A	.66
Tau-UA vs. B + trend B	−.01
Tau-UA vs. B + trend B − trend A	.48

Note: Correlations in bold were statistically significant at p < .05.

Table 5. Quartiles of 30 visually rated graphs and their corresponding Tau-U effect size ranges

	Quartiles of graphs by visual ratings
	Q1	Q2	Q3	Q4
Tau-Utrend A	.20–.61	.20–.71	.07–.40	.00–.60
Tau-Utrend B	.10–.73	.11–.80	.00–.67	.01–79
Tau-UA vs. B	.26–.97	.40–1.00	.63–1.00	.61–1.00
Tau-UA vs. B − trend A	.22–.69	.17–.49	.33–.76	.43–.97
Tau-UA vs. B + trend B	.08–.93	.37–.91	.39–.90	.33–.90
Tau-UA vs. B + trend B − trend A	.18–.68	.21–.54	.08–.74	.26–.75

Note: The first quartile (Q1) corresponds to the quarter of the graphs determined by visual raters to have least evidence of a treatment effect, and the fourth quartile (Q4) corresponds to the quarter of the graphs determined by visual raters to have the most evidence of a treatment effect, etc. Q1 and Q4 had 7 graphs, while Q2 and Q3 had 8 graphs.

Overall, these results suggest a disappointingly low level of agreement between visual judges and the Tau-U statistical methods. These results are presented as tentative given the modest scope of this supplementary study; however, some summary points are offered:

3.5.1. Baseline trend negatively predicted visual judgments of effect size

Tau-U_{trend A} had a moderate negative correlation with visual judgments of effect, ρ = −.40. This may suggest that judges are in fact able to visually detect baseline trend in some graphs, and when they do, they are cautious about concluding the treatment was effective. This was confirmed by examining the rank correlation of Tau-U_{trend A} and the judges’ visual ratings of baseline trend, where ρ = .76, p < .01.

3.5.2. Visual ratings were most associated with Tau-U_{A vs. B − trend A}

Over half of the 30 randomly selected graphs (n = 16) contained baseline trend of Tau-U_{trend A} < .4, the criterion suggested by Parker et al. (2011b) for trend control. This would appear to suggest that baseline trend control is unnecessary for a majority of the graphs and that correcting baseline trend across all graphs would lead to disagreement with visual analysis. However, Tau-U_{A vs. B − trend A} predicted visual ratings better than any other Tau-U coefficient, ρ = .66. One might expect the “uncorrected” Tau-U_{A vs. B} to be a better predictor of visual ratings because of the relatively minor baseline trends present; however, Tau-U_{A vs. B} had only a moderate association with visual judges, ρ = .39. It is possible that this unexpected result is due to Tau-U_{A vs. B}’s ceiling effect, discussed above. Over a third (n = 11) of the sampled graphs had a Tau-U_{A vs. B} > .95, suggesting that there is less variance with which to differentiate effects or predict visual ratings.

3.5.3. Tau-U_{A vs. B + trend B} was a poor predictor of visual ratings

Parker et al. (2011b) promoted Tau-U_{A vs. B + trend B} as the most useful Tau-U coefficient due to its distribution (no ceiling effects) and statistical properties. The Tau-U_{A vs. B + trend B} coefficient most clearly embodies their ideal of “nonoverlap … with trend from the intervention phase” (p. 284). However, Tau-U_{A vs. B + trend B} was least associated with the judgments made by visual raters, demonstrating essentially 0 correlation, ρ = −.01. Added baseline trend control (Tau-U_{A vs. B + trend B − trend A}) strengthened this association, ρ = .48, suggesting that the absence of baseline trend is at least as important a predictor of visual ratings as phase independence and phase B trend.

4. Discussion

Single-case investigators who wish to incorporate statistical methods into their analyses have many options to choose from—and often little guidance in selecting an appropriate measure of effect. One advantage of the Tau-U family of effect size coefficients is its flexibility under a variety of experimental conditions. The goal of this paper was to demonstrate this flexibility and show that the Tau-U coefficients perform predictably when they are well understood. In a review of single-case research standards, Smith (2012) stated “analysts need to select an appropriate model for the research questions and data structure, being mindful of how modeling results can be influenced by extraneous factors” (p. 521). We concur with this recommendation, and have attempted to offer a theoretical and empirical exploration of Tau-U for investigators who wish to model and measure their single-case data statistically. It is hoped that the review has demonstrated the potential problems of assuming a particular effect size is appropriate for every single-case experiment and yet also provided enough direction to thoughtfully apply Tau-U in a way that fits with the unique characteristics of each study.

When selecting an effect size to represent a single-case treatment effect, one could reasonably begin by examining the “building block” Tau-U coefficients because each component contributes unique information about how the data set is characterized. Using these initial Tau-U coefficients with a visual examination of one’s graphs will help determine the proper effect size to report. For example, important information can be obtained from first simply comparing phase A trend with phase B trend. If Tau-U_{trend A} is large, a small or “less large” Tau-U_{trend B} would suggest that the treatment may have stopped or at least slowed down the data trend occurring prior to treatment (e.g., Study 71 in Figure 4).

The next step is to determine whether to control for phase A trend only (Tau-U_{A vs. B − trend A}), to include phase B trend only (Tau-U_{A vs. B + trend B}), or both (Tau-U_{A vs. B + trend B − trend A}). This requires careful consideration of the research question and what assumptions about the data the researcher is willing to make. In Study 58 (Figure 4), if the researcher cares only about the degree of “improvement” (in terms of how “spread out” the scores from phase A and phase B were), there may be justification in using Tau-U_{A vs. B − trend A}. However, if the researcher wants to be able to claim that the treatment improvement was both reliable and lasting, then phase B trend—which, unfortunately, is unstable, erratic, and even in opposition to the desired treatment effect—should be accounted for by using either Tau-U_{A vs. B + trend B} or Tau-U_{A vs. B + trend B − trend A}. Regardless of which decision a researcher makes in these cases, consideration must be made to the various data characteristics (phase independence, nonoverlap, phase A trend, phase B trend) and the intended research question(s) when selecting an effect size and reporting results.

Investigators may wish to test certain hypotheses about their own study, prior to calculating Tau-U coefficients, based on what they expect given the nature of the dependent variable and the intervention. For example, investigators may be able to generate hypotheses depending on whether the dependent variable is typically stable/slow-to-change or more volatile, stable specifically during baseline procedures, stable once the behavior is learned or subject to deterioration over time, limited in range or unlimited in how much change can occur, etc. Investigators may generate hypotheses depending on whether the intervention is expected to engender sudden or immediate changes versus more gradual trending changes; short-term changes or long-lasting effects; changes in score magnitude only, trend only, or both. Three basic hypotheses that could be formulated and later tested by calculating the Tau-U coefficients are as follows:

1. Due to the nature of the dependent variable and the intervention, we expect little to no immediacy in change (change at treatment onset), but treatment is expected to have strong trend changes. For example, there is substantial interest today in various diet and exercise weight loss intervention programs. Weight change is a gradual process, and attempting to achieve immediate weight loss overnight would require very unsafe practices. Thus, it would be nonsensical for a researcher to predict that a weight loss program would result in a sudden change at treatment onset. However, if the intervention program is successful, the researcher would expect to see consistent, gradual decrease in weight loss (i.e., Tau-U_{trend B}).

2. Due to the nature of the dependent variable and the intervention, we expect a large immediate change, but no trend changes. For example, research shows that stimulant medications can result in strong initial improvements for hyperactivity. However, once the behavior has improved, medication should not continue to “improve” behavior over time. Therefore, a researcher testing a new medication for hyperactivity would expect little Phase A trend and Phase B trend. Further, there is no reason to assume that medication should lead to infinitely increasing symptom improvement. The value in the medication is in its potential to “lower” a person’s hyperactivity and then maintain it.

3. Due to the nature of the dependent variable and the intervention, we expect a large, immediate change and strong trend changes. For example, an intervention that could achieve both a large immediate change at treatment onset and strong trend changes would be quite the ideal intervention. In behavioral sciences, interventions like this would be rare, yet desirable.

This confirmatory process of anticipating the variable–treatment interactions and treatment outcome is a valuable approach for investigators because it prompts them later to consider why unexpected results (if any) occurred. Investigators can use this information to justify their decision about which effect size is most appropriate in estimating treatment outcome.

Tau-U has several strengths over other approaches currently available. Tau-U can incorporate both level and monotonic trend. As a rank order correlation, Tau-U statistics have minimal distributional assumptions and are relatively robust to autocorrelation (Parker et al., 2011a; Tarlow, 2016a). Tau has demonstrated good statistical power (Parker et al., 2011b) although recent findings suggest that power may be a limitation (specifically when trying to determine if one should correct for baseline trend because power for baseline trend detection with Tau can be difficult with few baseline data points and/or a small baseline trend; Tarlow, 2016a). The flexibility of Tau-U allows for the thoughtful selection of an effect size that matches the nature of the variable studied and the expected treatment response.

4.1. Limitations

Tau-U’s most significant limitation is its weak association with visual analysis, both in theory and practice. There is no straightforward way to visualize its monotonic trend control procedure, and as a result, the use of Tau-U baseline trend correction is a kind of “black box” process that makes nuanced interpretation of effect size results difficult. Comparison with visual ratings demonstrated that many Tau-U effect size coefficients have poor agreement with visual analysis. One coefficient, Tau-U_{A vs. B − trend A}, showed moderate agreement with visual analysis, although the rationale for implementing baseline trend control is unclear for data sets with stable baselines. Single-case investigators would benefit from additional evaluation of monotonic trend control and the relationship between Tau-U and visual analysis.

Tau-U baseline correction is impacted by the ratio of baseline phase data points to the treatment phase data points (see Figure 1J and 1K). Specifically, Tarlow (2016a) reported that the effect of baseline correction increases with the length of both the baseline and treatment phase. Using a Theil–Sen regression method (Theil, 1950; Sen, 1968) to correct for baseline trend, Tarlow (2016a) found Tau-U_{A vs. B} performed well except with short baseline phases.

The theoretical review of Tau-U noted that authors and investigators should be clearer in specifying which Tau-U coefficients are being reported in their analyses, as the empirical review demonstrated how different Tau-U coefficients may produce dramatically different effect sizes for the same single-case time series. Arithmetic problems in the calculation of Tau-U baseline trend control—including in the web-based Tau-U calculator (Vannest et al., 2011)—should also be resolved, as calculation errors may lead to distorted or misleading results (such as effect sizes falling outside of conventional bounds).

Parker et al. (2011b) noted that complex SCEDs (e.g., ABAB) could be analyzed using meta-analytic methods. For example, multiple AB phase contrasts could be combined within or across individuals by weighting Tau-U effect sizes with their standard errors. A limitation of this paper is our focus on simple AB contrasts, as those designs make up a majority of single-case studies, typically as multiple baseline designs with multiple individuals (Smith, 2012). Investigators would benefit from additional research into the application of meta-analytic methods to nonparametric single-case effect size estimates, including Tau-U.

The authors would like to thank Kevin R. Tarlow for his assistance with manuscript preparation and developing R scripts for this project.

Additional information

Funding

The authors received no direct funding for this research. The open access publishing fees for this article have been covered by the Texas A&M University Open Access to Knowledge Fund (OAKFund), supported by the University Libraries and the Office of the Vice President for Research.

Notes on contributors

Daniel F. Brossart

Daniel Brossart is an associate professor at Texas A&M University in the Department of Educational Psychology. His research interests include intervention research and studying change.

Vanessa C. Laird

Vanessa Laird is a Postdoctoral Fellow at the Albany Medical Center.

Trey W. Armstrong

Trey Armstrong is a doctoral candidate at Texas A&M University.