Meter for what? Meter strength affects ordinal but not temporal learning

Abstract

Both dance and music performers must learn timing patterns (temporal learning, or “when”) along with series of different movements (ordinal learning, or “what”). It has been suggested that the organization of temporal events into regular beat cycles (meter strength) may enhance both temporal and ordinal learning, but empirical evidence is mixed and incomplete. In the present study, we examined meter-strength effects on the concurrent temporal and ordinal learning of sequences. Meter strength enhanced ordinal learning (“what”) when the concurrent temporal learning was incidental, but it had no effects on temporal learning itself (“when”). Our findings provide guidelines for dance and music teaching, as well as rhythm-based neurological rehabilitation.

Keywords:

• sequence learning
• dynamic attending theory
• meter

PUBLIC INTEREST STATEMENT

When we dance, we move to the meter of music. In a waltz, we count 1-2-3 and step heavier on count 1 – this is triple meter. In a march, we count 1-2 and raise the legs one at a time – this is double meter. Meter provides a frame for rhythm —the specific time pattern of events— and for the events proper, that is, what we hear embedded in rhythm: the notes, the words, etc. Meter can be more or less clear to the listener – this is meter strength. We examined if meter strength affects how we learn the rhythm itself, or if it has an impact on how we learn the contents that are embedded in it. We found that the latter was true. So, if we want to memorize words, dance steps, or musical notes embedded in rhythm, they should feel 1-2-3 or 1-2 as clearly as possible.

Competing Interest

The authors declare no competing interest.

1. Introduction

Both dance and music engage the learning of temporal patterns based on a regular time unit, known as the beat: dancers must know when to perform each move, and musicians must know when to produce each sound. Along with this temporal learning of beat-based patterns, dancers and musicians must also learn what do to with their bodies—which sequence of moves (e.g., arms up–arms down), which sequence of notes (e.g., high pitch–low pitch): this is known as ordinal learning. In the present study, we examined how temporal vs. ordinal learning are affected by the characteristics of temporal patterns, namely by meter.

Meter indicates high-order periodicities in temporal patterns (Fitch, 2013, 2016), based on groups of 2, 3, or 4 beats (double, triple, quadruple meter, respectively). When the perception of one of these high-order periodicities is maximized, we have strong meter. Strong meter may be defined by two features: the onset of a meter cycle (2, 3, 4 beats) is marked by the onset of an event (sounds, image in the sequence, Essens & Povel, 1985), and by intensity accents (see Silva, Petersson, & Castro, 2017). In contrast, there is weak meter when the onset of a meter cycle does not match the onset of an event (see Figure 1), and the perception of high-order periodicities is blurred. In between levels of strong and weak meter, we can also consider defined meter, where the onset of a meter cycle is filled with the onset of an event, but there are no intensity accents to highlight those meter-cycle onsets. Strong, weak, and defined meter types are different levels of meter strength.

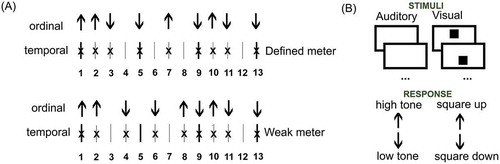
Figure 1. Sequences for serial recall. (A) The two temporal structures used in defined meter vs. weak-meter conditions (short vertical lines = beat onsets; crosses = sequence events). Arrows indicate an example of concurrent ordinal information. (B) Ordinal structures were random series of nine tones, high or low, in the auditory conditions, nine spatial positions, up or down, in the visual ones. In both cases, participants used the arrow up/down keys of the keyboard to reproduce the sequence

The investigation of meter-strength effects on sequence learning has been largely motivated by the Dynamic Attending Theory (DAT, Jones, 1976; Jones & Boltz, 1989; Large & Jones, 1999) and its development into the metric binding hypothesis (Jones, 2009). DAT posits that attention proceeds in cycles, and the match between these internal cycles and those of the outside world enhances temporal expectations. Matching one’s attention to the beat-level would give rise to an internal oscillator. Matching attention to both the beat- and the meter-level, as it happens in strong meter, would create two oscillators with nested periods (e.g., 600 ms for beat cycles and 2400 ms for meter cycles), which bind (therefore metric binding) and strengthen each other. This is why meter strength would reinforce expectations, enhance sequence processing, and foster learning.

Based on DAT, it has been claimed that meter strength facilitates both temporal (Jones 2009; Schultz, Stevens, Keller, & Tillmann, 2013) and ordinal learning (Selchenkova et al., 2014): In face of strong meter, one would be expected to learn better both “when” and “what”. To dancers and musicians, this would mean that strong meter would favor both the learning of rhythms and the learning of dance steps or music notes. But is it really so? What do empirical findings say about this?

Evidence concerning the effects of meter strength on temporal learning (learning “when”) is mixed. Discrimination between strong and weak meter is real (Vuust, Ostergaard, Pallesen, Bailey, & Roepstorff, 2009), and change detection under strong meter is facilitated compared to weak meter (Grube & Griffiths, 2009). When it comes to proper sequence-learning, Brandon and colleagues (Brandon, Terry, Stevens, & Tillmann, 2012) found that participants learn strong-meter patterns implicitly (i.e., without intention to learn and without awareness), but they did not compare strong with weak meter. Schultz and collaborators (Schultz et al., 2013) did such comparison, and they found that both weak- and strong-meter patterns lead to the same learning outcome. A previous study of ours (Silva et al., 2017) was consistent with the absence of meter-strength effects. We saw that temporal learning depended on the complexity of the combination of events (syllables, pitches)—the ordinal load of the sequence: participants learned sequences with a simple ordinal load (two tones, High and Low, mapped onto up/down arrow response keys), but not those with a complex one (four syllables, mapped onto up/down/left/right arrow response keys). Critically, changing the weak meter of complex-load sequences into strong meter did not facilitate temporal learning, neither when learning was incidental—i.e., when participants had no intention to learn temporal patterns, nor when it was intentional—when they had the intention do to so. This suggests that meter may be irrelevant to temporal learning, at least under a complex ordinal load.

Concerning meter effects on ordinal learning (learning “what”), at least one study has shown the advantage of strong-meter patterns over isochronous ones, when learning is incidental (Selchenkova et al., 2014). However, and to our knowledge, neither a direct comparison between meter-strength levels (e.g., weak vs. strong) has been done, nor intentional learning has been addressed.

The main goal of the present study was to investigate meter-strength effects on temporal vs. ordinal learning. We used the paradigm of our previous study on temporal learning (Silva et al., 2017). In this paradigm, participants are exposed to random ordinal information embedded in temporal patterns that remain constant across 50 trials. Participants are then asked either to recall ordinal information and nothing else (incidental temporal learning: “reproduce the sequence”), or to recall both ordinal and temporal information (intentional temporal learning: “reproduce the sequence with the right rhythm”). Thus, the paradigm allows us to examine not only incidental and intentional temporal learning but also intentional ordinal learning. This is what we did in the present study: On the one hand, we tested whether meter-strength effects on temporal learning—which were absent under complex ordinal load (Silva et al., 2017)—remain absent under simple ordinal load. On the other hand, we examined if intentional ordinal learning is enhanced by meter strength, just as incidental ordinal learning seems to be (Selchenkova et al., 2014). The design of the experiment is depicted in Table 1.

Table 1. Design of the experiment

Factors (between-subjects)
Meter strength	Weak meter				Defined meter
Temporal instruction	Incidental		Intentional		Incidental		Intentional
Modality	Auditory^a	Visual	Auditory^a	Visual	Auditory	Visual	Auditory	Visual
Eight groups matched for Age (years): M ±SD = 22 ± 4; F (7,120) = 2.07, p = .051) Schooling (years): M ±SD = 14 ± 1; F (7,120) = 1.44, p = .20) Sex: χ^2(7) = 10.24, p = .17 Musical experience (yes/no): χ^2 (7) = 0.29, p = 1
Effects on
Temporal learning	Basal learning Improvement
Ordinal learning	Basal learning

^a Data collected for Silva et al. (2017).

Our secondary goal was to determine whether meter-strength effects depend on modality (auditory vs. visual stimuli, Table 1). In addition to help defining the scope of meter-strength effects, this approach taps into the association vs. dissociation between beat and meter. Although beat and meter are often viewed as indissociable periodical phenomena that only differ in time scale (Nozaradan, Peretz, & Mouraux, 2012; Tierney & Kraus, 2014), evolutionary (Fitch, 2013) and neuroanatomical evidence (Thaut, Trimarchi, & Parsons, 2014) points to dissociation—meter may not be merely a “supra-beat”, or an extension of beat. Here is how we tested for the dissociation hypothesis: It is known that modality affects beat processing, in that beat-based auditory temporal patterns are easier to learn than visual ones (Pasinski, McAuley, & Snyder, 2016; Repp & Penel, 2002; Silva & Castro, 2016). In the present study, we checked whether these modality effects on beat processing existed (temporal learning of auditory vs. visual sequences), and then we looked at modality effects on meter processing (meter-strength effects across modalities). Finding out that modality has an effect on meter processing would support the association between beat and meter, while the reverse would indicate dissociation.

In sum, we wanted to (1) determine whether meter-strength affects temporal learning, ordinal learning, both or none, and (2) whether meter-strength effects differ across modalities. We predicted that (1) meter strength (weak vs. defined meter, see Table 1) would enhance ordinal, but not temporal learning, and that this would be independent from temporal instruction (incidental vs. intentional temporal learning, Table 1). Concerning (2) modality effects, our prediction was that modality would affect beat, but nor meter processing.

2. Methods

2.1. Participants

One-hundred and twenty-eight participants took part in the experiment, split into 8 groups with 16 participants each (see Table 1). The groups were formed according to meter strength (weak vs. defined), temporal instruction (incidental vs. intentional), and modality (auditory vs. visual), in a 2 x 2 × 2 between-subjects design (Table 1). Data for the two auditory weak-meter groups (incidental and intentional, 16 + 16 = 32) had been previously collected (Silva et al., 2017). The other six groups (auditory defined, visual weak, and visual defined—each divided into incidental and intentional learning, 3 × 2 = 6) were matched for age, schooling, sex, and musical experience with the auditory weak-meter ones (see Table 1). Since we were comparing new data (six groups) with previously collected data (two groups, Silva et al., 2017; see Table 1), a full within-subjects approach was impossible to get in the present study. Moreover, our previous comparison of incidental vs. intentional temporal learning in the auditory weak-meter conditions (Silva et al., 2017) was a between-subjects approach because there would be drawbacks if the same participants underwent intentional and incidental temporal instruction conditions. Therefore, our choice for the present study could not be other than a full between-subjects design.

None of the participants reported neurological, psychiatric, auditory, or visual problems, and none was taking medication. All provided informed consent, according to the Declaration of Helsinki.

2.2. Stimuli

Participants were given the same temporal sequence in all 50 trials of the serial recall task, but they were not informed that the sequence was constant. There were two target temporal sequences (Figure 1 A)—weak meter and defined meter, one per condition. Both sequences comprised the same nine events (four two-beat-length events, five one-beat-length events), ordered in different ways so as to comply with weak vs. defined meter requirements. The weak-meter sequence had event onsets not compatible with either double, triple, or quadruple meter. The defined meter sequence was compatible with both double and quadruple meter. We contrasted weak with defined meter—instead of weak with strong—because the visual modality does not have an obvious equivalent of auditory intensity accents, which characterize strong meter.

Ordinal sequences were random across trials (50 different sequences), and they were built from the combination of two events: In the auditory condition, there were two tones (high and low); in the visual one, two images of a square (square-up and square-down, Figure 1 B). The same 50 ordinal sequences (example sequence—up-up-down-up-up-down-up-up-down) were used in both modalities, either implemented with tones (up = high-tone, down = low-tone, auditory) or with spatial positions (square-up vs. square-down, visual).

In sum, we had 50 different ordinal (random) combinations and two different temporal patterns. These 50 combinations were presented to the four weak-meter groups (auditory incidental, auditory intentional, visual incidental, visual intentional) under the same weak-meter pattern, and to the four defined-meter groups under the defined-meter pattern.

2.3. Procedure

The procedure differed for the two levels of temporal instruction (incidental vs. intentional). In the incidental learning groups, participants were asked to reproduce the order in which sequence elements were presented, using the up/down arrow keys of the computer (high tone/low tone for auditory, square up/square down for visual, see Figure 1 B). For instance, in auditory conditions, they were told to “press the up and then the down arrow” in case they heard “a high and then a low tone”. In visual conditions, they should do the same if they saw “square up and then square down”. In the intentional learning group, they were given the same instruction as incidental learners regarding the order of elements, coupled with the indication to press the keys using the rhythm they heard, “as if they were playing a song in the piano”. Thus, under incidental learning, participants had no intention to learn the temporal pattern, but they were instructed to do so under intentional learning.

2.4. Statistical analysis

We measured the error of temporal responses (produced rhythms) relative to the target (constant) rhythm, and the ordinal accuracy of event series (series of high/low events and up/down events) relative to each of the 50 random combinations of events.

The accuracy of temporal performance was obtained by an error measure—the mean relative error (Karabanov & Ullén, 2008). The mean relative error of a sequence is the average deviation of the intervals produced by the subject in that sequence relative to the target intervals. Each of the eight target intervals was subtracted from the produced one, and the absolute value of the difference was divided by the target interval. The obtained value reflected the fraction of the target interval that was added or subtracted during performance (e.g., a value of 0.5 indicates that participants added or subtracted 50% of the original duration).

Ordinal accuracy was measured with the similarity score provided by the Needleman–Wunsch algorithm (Needleman & Wunsch, 1970) as implemented in Matlab (www.mathworks.com). The score qualifies the global alignment between two sequences, in our case, the alignment between the target series of events (high-low tones, up-down squares) and the ones produced by participants. Higher scores indicate increased similarity, hence increased response accuracy.

We used two measures to characterize temporal learning: learning as improvement (across trials) and basal learning (average performance in the experiment). Learning as improvement was indexed by block effects (5 blocks with 10 trials each) and its interactions with temporal instruction, modality or meter strength. Effects not involving block (temporal instruction, modality, meter strength) characterized basal performance (see Tables 2 and 3). For ordinal accuracy, we focused on basal learning. Since ordinal information was random and—unlike temporal learning, based on a single sequence—we did not expect any improvement across trials.

Table 2. Predictors of temporal error

	Temporal error
	B	CI	p
Fixed Parts
(Intercept)	0.39	0.30–0.48	<.001
IMPROVEMENT
Block	−0.02	−0.03–0.00	.008
Block x Temporal instruction	0.01	−0.01–0.03	.235
Block x Modality	0.01	−0.01–0.03	.467
Block x Meter strength	−0.00	−0.02–0.01	.662
BASAL PERFORMANCE
Temporal instruction	−0.12	−0.25–0.02	.086
Modality	0.24	0.10–0.37	<.001
Meter strength	0.13	−0.00–0.26	.055
Temporal instruction x Modality	0.02	−0.16–0.21	.798
Temporal instruction x Meter strength	−0.01	−0.19–0.18	.951
Modality x Meter strength	−0.13	−0.31–0.06	.176
Three- and four-way interactions			n.s.
Random Parts
σ^2	0.075
τ00, suball	0.027
Nsuball	128
ICCsuball	0.267
Observations	6331
R^2/Ω0^2	.342/.342

Table 3. Predictors of ordinal accuracy

	Ordinal accuracy
	B	CI	p
(Intercept)	17.36	15.94–18.77	<.001
IMPROVEMENT
Block	0.01	−0.24–0.26	.948
Block x Temporal instruction	0.19	−0.16–0.55	.289
Block x Modality	−0.23	−0.60–0.13	.212
Block x Meter strength	−0.08	−0.44–0.27	.647
BASAL PERFORMANCE
Temporal instruction	−2.23	−4.26—−0.20	.033
Modality	0.24	−1.79–2.28	.816
Meter strength	−2.13	−4.13—−0.13	.038
Instruction x Modality	1.43	−1.45–4.30	.332
Temporal instruction x Meter strength	3.38	0.53–6.23	.021
Modality x Meter strength	0.94	−1.91–3.80	.518
Three- and four-way interactions			n.s.
σ^2	25.712
τ00, suball	5.492
Nsuball	126
ICCsuball	0.176
Observations	6243
R^2/Ω0^2	.213/.212

We analyzed the effects of block, temporal instruction, modality, and meter strength on temporal and on ordinal learning using linear mixed-effects regression models (lmer function) as implemented in the lme4 package (see Bates et al., 2015) for R (R Core Team, 2013). The lmerTest package (Kuznetsova, Brockhoff, & Christensen, 2017) was used to obtain significance values. Block, temporal instruction, modality and meter strength entered the analysis as fixed factors (all main effects and interactions, see Tables 2,3), and participants as random intercepts. Random slopes were not included because the latter did not increase explanatory power. Please note that local effect size measures such as partial eta-squared do not apply to linear mixed effects models (Selya, Rose, Dierker, Hedeker, & Mermelstein, 2012), and R^2/Ω₀² measures may be used instead as whole-model effect sizes for the purpose of comparison and meta-analysis (Nakagawa & Schielzeth, 2013).

3. Results

3.1. Temporal performance

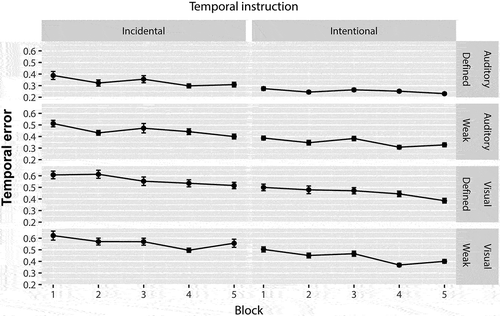
Participants improved their temporal performance across the 5 blocks of the serial recall task, showing a progressive decrease in temporal error (Figure 2). Despite this main effect of block (showing generalized learning as improvement under simple load), there were no significant interactions with temporal instruction, modality or—critically—with meter strength (Table 2). Thus, meter strength did not have any effect on temporal learning viewed as improvement, and this lack of effect was common to visual and auditory stimuli.

Figure 2. Mean temporal error across block (1–5), temporal instruction (incidental vs. intentional learning), modality (auditory vs. visual) and meter-strength levels (defined vs. weak). Vertical bars represent the standard error of the mean. Temporal performance improved across blocks regardless of temporal instruction, modality, or meter strength

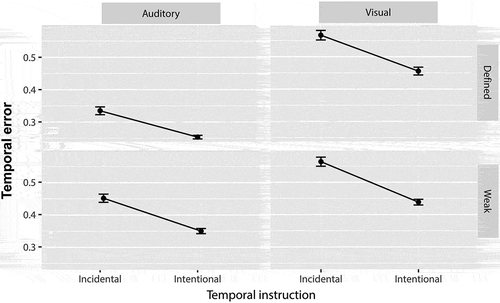
Basal temporal performance showed marginal effects of temporal instruction (marginally enhanced performance in Intentional conditions, Table 2, Figure 3), and no significant meter-strength effects. There were no significant interactions between meter strength and modality: Meter-strength effects on temporal performance were equivalent for visual and auditory stimuli, although—as predicted—basal temporal performance was enhanced in the auditory domain (modality effect, Table 2, Figure 3).

Figure 3. Mean temporal error across temporal instruction (incidental vs. intentional learning), meter strength (defined vs. weak) and modality. Vertical bars represent the standard error of the mean. There were no meter-strength effects. Modality had an effect on beat processing (main effect on temporal performance), but not on meter processing (no interaction with meter-strength effects)

3.2. Ordinal performance

As expected, given that ordinal information was random, participants’ ordinal accuracy (tones in the auditory condition, spatial positions in the visual one) did not improve across blocks (non-significant block effects or any interactions involving block, Table 3).

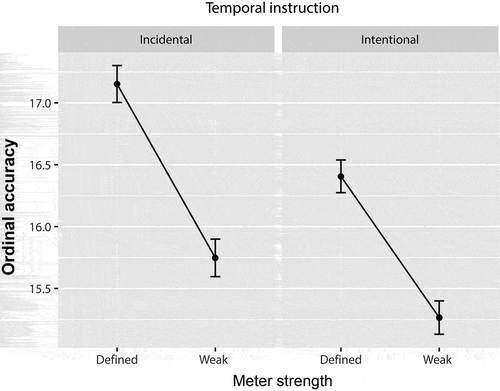
Basal ordinal performance (Figure 4) was enhanced by defined meter (meter-strength effect, Table 3). Meter strength interacted with temporal instruction (Table 3), such that defined meter significantly enhanced performance for incidental temporal learning (p = .029), while meter-strength effects were marginal in the intentional group (p = .063).

Figure 4. Mean ordinal accuracy across temporal instruction (incidental vs. intentional learning) and meter strength (defined vs. weak). Vertical bars represent the standard error of the mean. Meter strength enhanced ordinal learning

4. Discussion and conclusion

Our first goal was to clarify some aspects related to meter-strength effects on temporal learning vs. ordinal learning. Specifically, we tested whether meter-strength effects are absent in temporal learning (incidental and intentional) under simple ordinal load, and whether meter-strength effects can be found in intentional ordinal learning. Our results supported the two hypotheses, contributing to the idea that meter strength may influence the learning of “what” (ordinal) but not the learning of “when” (temporal).

The absence of meter-strength effects on incidental and intentional temporal learning under simple ordinal load extends our previous findings for complex load (Silva et al., 2017). The meter strength of temporal sequences seems to have no impact on temporal learning, whatever the associated ordinal content (complex or simple), and whatever the meaning assigned to learning (improvement or basal learning). From a theoretical viewpoint, this suggests that currently held predictions based on the Dynamic Attending Theory (Jones, 2009; Schultz et al., 2013) may not be entirely valid. From the viewpoint of applications to dance or music performance, this is consistent with the idea that weak-meter rhythms are not necessarily harder to learn (Schultz et al., 2013; Silva et al., 2017). This possibility should, of course, be taken with caution: Several types of cognitive differences among learners may play a role in temporal learning processes, and we did not control for these differences in our study.

Meter strength improved basal ordinal performance. Viewed in a dance or music context, this suggests that a new sequence of dance movements (e.g., arms up-turn around-arms up-leg up) or notes to be played (do-fa-do-mi) may be better apprehended if these movements/notes are presented in a metrically defined context than in a metrically weak one. This may be associated with a chunking mechanism, with ordinal events being grouped in regular-length macro-units (Lerdahl & Jackendoff, 1985) based on the (regular) metric frame of defined meter. The interaction we saw between meter strength and temporal instruction suggests that this will be more so if the learner’s attention and effort is not drawn to the metrically defined rhythm that is being used (incidental learning of temporal structure), and s/he focuses only on ordinal information. One possible explanation for the advantage of incidental learning may lie on the competition between types of intentional processing (temporal and ordinal): The meter-based chunking mechanism may operate either incidentally or intentionally, but the competition for resources is stronger in the latter case.

As expected (Pasinski et al., 2016; Repp & Penel, 2002; Silva & Castro, 2016), basal temporal performance was enhanced for auditory sequences compared to visual ones. In terms of applications, this suggests that dance teachers may benefit from saying out loud the timing of the movements, instead of just showing them. It also means that music teachers may not benefit from focusing the learner’s attention on finger movements (visual information) if their purpose is to foster rhythmic learning. Again, it is possible that these effects are modulated by individual differences among learners, which we did not control for, and thus these suggestions should be taken with caution. From a fundamental viewpoint, this is another piece of evidence that audition is more akin to beat-based time than vision.

This leads us to our second goal, which was knowing whether meter-strength effects on temporal learning differ across audition and vision. We found that they did not. Importantly, we found that audition outperformed vision in basal temporal learning, which indicates that modality affects beat, but not meter processing. On the one hand, this strengthens our main finding: Since we saw no meter-strength effects on temporal learning—neither in auditory sequences, nor in visual ones—the absence of these effects seems generalized. On the other hand, our findings speak in favor of the hypothesis of dissociation (Fitch, 2013; Thaut et al., 2014) between beat and meter: While beat processing depends on modality, meter processing does not seem to. Of course, since meter effects were null for both modalities, we can be facing a floor effect. Future studies could address this possibility.

One limitation of our study concerns sample size: Even though our main finding (meter-strength effects on ordinal learning) arose from comparing 64 participants (weak meter) with other 64 (defined meter), the group size in each of the 8 conditions (n = 16) was small, compromising the generalization of our results. Another limitation is that we only addressed intentional ordinal learning, which prevents us from doing direct comparisons with previous findings of meter effects on incidental learning (Selchenkova et al., 2014). Future studies could address both limitations, by increasing sample size, and contrasting intentional with incidental learning conditions. Finally, the way we measured temporal learning was limited: While ordinal learning was measured with and without the elicitation of concurrent temporal learning, temporal learning was always measured with concurrent ordinal learning. Therefore, our findings that meter strength has no effect on temporal learning remain restricted to circumstances in which ordinal learning coexists. Although learning “when” together with “what” (what we tested here) is probably the most common scenario in real-life, dance/music learning settings, the challenge of addressing temporal learning in the absence of simultaneous ordinal learning remains open.

The relevance of our main finding—that meter strength enhances ordinal but not temporal learning—goes beyond the domains of music and dance. There is an increasing awareness that the mind/brain system can be more efficient when it adjusts, or entrains to the periodical, beat-based events of the outside world. Neurological rehabilitation has capitalized on this idea to promote the use of rhythmic stimulation in clinical settings, such as the rehabilitation of gait in Parkinson’s Disease patients (Schaefer, 2014; Thaut, McIntosh, & Hoemberg, 2015), or the intervention on the reading deficits of dyslexic children (Bhide, Power, & Goswami, 2013; Degé, Kubicek, & Schwarzer, 2015). Although both scenarios employ beat-based temporal structures, they consider different learning targets—Parkinson’s Disease rehabilitation addresses temporal learning (gait rhythm), while dyslexia rehabilitation targets ordinal learning (speech sounds). Given that the level of meter strength can be controlled in rhythmic stimulation, the question is whether it matters to control for meter strength in any of the two scenarios. According to our findings, it should matter in dyslexia rehabilitation (meter for “what”), but not for the purpose of temporal learning (meter for “when”).

Cover Image

Source: The Authors.

Additional information

Funding

This work was supported by the Fundação para a Ciência e a Tecnologia [UID/PSI/00050/2013].

Notes on contributors

Susana Silva

Susana Silva is a post-doc fellow at the Neurocognition and Language Research Group (NCL) from the University of Porto. São Luís Castro is a Professor of Psychology at the University of Porto and NCL group leader. The group takes a neurocognitive approach to the study of cognitive processes, with a special focus on language and communication. These are investigated as complex neurocognitive systems that rely on domain-general processes (sequencing, segmentation, timing, vision), undergo structural and functional changes as a result of experience (normative development, learning), and are impaired in a number of developmental and acquired disorders. Susana Silva has been doing research on Timing and Implicit Learning.