Wave propagation in a rotating disc of polygonal cross-section immersed in an inviscid fluid

Abstract

In this paper, the wave propagation in a rotating disc of polygonal cross-section immersed in an inviscid fluid is studied using the Fourier expansion collocation method. The equations of motion are derived based on two-dimensional theory of elasticity under the assumption of plane strain-rotating disc of polygonal cross-sections composed of homogeneous isotropic material. The frequency equations are obtained by satisfying the boundary conditions along the irregular surface of the disc using Fourier expansion collocation method. The triangular, square, pentagonal and hexagonal cross-sectional discs are computed numerically for Copper material. Dispersion curves are drawn for non-dimensional wave number and relative frequency shift for longitudinal and flexural (symmetric and anti-symmetric) modes. This work may find applications in navigation and rotating gyroscope .

Keywords:

• wave propagation in disc
• vibration of thermal plate
• waves in cylinder
• disc immersed in fluid
• polygonal cross-section
• rotating gyroscope

Public Interest Statement

This article presents the propagation in a rotating disc of polygonal cross-section immersed in an inviscid fluid using the Fourier expansion collocation method. The computed non-dimensional wave number and relative frequency shift of triangular, square, pentagonal and hexagonal cross-sectional disc are plotted in the form of dispersion curves for Copper material. The results of this study are useful in construction and design of rotating gyroscope, and this method is straightforward. The numerical results for any other polygonal cross-section can be obtained directly for the same frequency equation by substituting geometric values of the boundary of any cross-section analytically or numerically with satisfactory convergence.

1. Introduction

The rotating disc of polygonal cross-section is the important structural component in construction of gyroscope to measure the angular velocity of a rotating body. The wave propagation in a disc contact with a fluid finds many applications in the field of structural acoustics, the acoustic microscopic wave interaction in geophysics, characterisation of material properties of thin metal wires, optical fibres and reinforcement filaments used in epoxy, metal and ceramic matrix composites and non-destructive evaluation of solid structures. The characteristics of wave propagation in rotating disc of polygonal cross-section immersed in fluid have a wide range of applications in the field of machinery, submarine structures, pressure vessel, chemical pipes and metallurgy.

The most general form of harmonic waves in a hollow cylinder of circular cross-section of infinite length has been analysed by Gazis (1959) in two parts. He has presented the frequency equation in part I and numerical results in part II in detailed form. Nagaya (1981, 1983a, 1983b) has discussed wave propagation in a thick-walled pipe, bar of polygonal plate and ring of arbitrary cross-section based on the two-dimensional theory of elasticity. The boundary conditions along both outer and inner free surface of the arbitrary cross-section are satisfied by means of Fourier expansion collocation method. Venkatesan and Ponnusamy (2002) have obtained frequency equation of the free vibration of a solid cylinder of arbitrary cross-section immersed in fluid using the Fourier expansion collocation method. The frequency equations are obtained for longitudinal and flexural vibrations, are studied numerically for elliptic and cardioidal cross-sectional cylinders, and are presented both in tabular and in graphical forms. Later, Ponnusamy (2011) studied the wave propagation in thermoelastic plate of arbitrary cross-sections using the Fourier expansion Collocations Method. Ponnusamy and Selvamani (2012, 2013) investigated the dispersion analysis of generalised magneto-thermo-elastic waves in a transversely isotropic cylindrical panel and wave propagation in magneto thermo elastic cylindrical panel, respectively, using Bessel functions. Yazdanpanah Moghadam, Tahani, and Naserian-Nik (2013) obtained an analytical solution of piezolaminated rectangular plate with arbitrary clamped/simply supported boundary conditions under thermo-electro-mechanical loadings.

Sinha, Plona, Sergio, and Chang (1992) have discussed the axisymmetric wave propagation in a cylindrical shell immersed in fluid, in two parts. In part I, the theoretical analysis of the wave propagating modes is discussed and in part II, the axisymmetric modes excluding tensional modes are obtained theoretically and experimentally and are compared. Berliner and Solecki (1996) have studied the wave propagation in fluid-loaded transversely isotropic cylinder. In that paper, part I consists of the analytical formulation of the frequency equation of the coupled system consisting of the cylinder with inner and outer fluid and part II gives the numerical results.

Loy and Lam (1995) discussed the vibration of rotating thin cylindrical panel using Love’s first approximation theory. Bhimaraddi (1984) developed a higher order theory for the free vibration analysis of circular cylindrical shell. Zhang (2002) investigated the parametric analysis of frequency of rotating laminated composite cylindrical shell using wave propagation approach. Body wave propagation in rotating thermoelastic media was investigated by Sharma and Grover (2009). The effect of rotation, magneto field, thermal relaxation time and pressure on the wave propagation in a generalised viscoelastic medium under the influence of time harmonic source is discussed by Abd-Alla and Bayones (2011). The propagation of waves in conducting piezoelectric solid is studied for the case when the entire medium rotates with a uniform angular velocity by Wauer (1999). Roychoudhuri and Mukhopadhyay (2000) studied the effect of rotation and relaxation times on plane waves in generalised thermo-viscoelasticity. Dragomir, Sinnott, Semercigil, and Turan (2014) studied the energy dissipation and critical speed of granular flow in a rotating cylinder and they found that the coefficient of friction has the greatest significance on the centrifuging speed. One-dimensional analysis for magneto-thermo-mechanical response in a functionally graded annular variable-thickness rotating disc was discussed by Bayat et al. (2014).

In this paper, the wave propagation in rotating disc of polygonal cross-section immersed in an invicid fluid is analysed. The boundary conditions along irregular surfaces have been satisfied by means of Fourier expansion collocation method. The frequency equations of longitudinal and flexural modes are analysed numerically for triangular, square, pentagonal and hexagonal cross-sections, and the computed non-dimensional wave number and relative frequency shift are plotted in graphs.

2. Formulation of the problem

We consider a homogeneous, isotropic rotating elastic disc of polygonal cross-section immersed in an inviscid fluid. The elastic medium is rotating uniformly with an angular velocity $\overrightarrow{\mathrm{\Omega }}=\mathrm{\Omega }\overrightarrow{n}$, where n is the unit vector in the direction of the axis of rotation. The system displacements and stresses are defined by the polar coordinates r and θ in an arbitrary point inside the disc and denote the displacements u_r in the direction of r and u_θ in the tangential direction θ. The in-plane vibration and displacements of rotating polygonal cross-sectional disc is obtained by assuming that there is no vibration and a displacement along the z axis in the cylindrical coordinate system $(r,\mathit{\theta },z)$. The two-dimensional stress equations of motion, strain–displacement relations in the absence of body forces for a linearly elastic medium are(1) $$\begin{array}{c}{\mathit{\sigma }}_{rr,r}+r^{-1}{\mathit{\sigma }}_{r\mathit{\theta },\mathit{\theta }}+r^{-1}\left({\mathit{\sigma }}_{rr}-{\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta }}\right)+\mathit{\rho }\left(\overrightarrow{\mathrm{\Omega }}\times (\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{u})+2\overrightarrow{\mathrm{\Omega }}\times {\overrightarrow{u}}_{,t}\right)=\mathit{\rho }{u}_{r,tt}\hfill \\ {\mathit{\sigma }}_{r\mathit{\theta },r}+r^{-1}{\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta },\mathit{\theta }}+2r^{-1}{\mathit{\sigma }}_{r\mathit{\theta }}=\mathit{\rho }{u}_{\mathit{\theta },tt}\hfill \end{array}$$(1)

where(2) $$\begin{array}{c}{\mathit{\sigma }}_{rr}=\mathit{\lambda }\left(e_{rr}+e_{\mathit{\theta }\mathit{\theta }}\right)+2\mathit{\mu }{e}_{rr}\hfill \\ {\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta }}=\mathit{\lambda }\left(e_{rr}+e_{\mathit{\theta }\mathit{\theta }}\right)+2\mathit{\mu }{e}_{\mathit{\theta }\mathit{\theta }}\hfill \\ {\mathit{\sigma }}_{r\mathit{\theta }}=2\mathit{\mu }{e}_{r\mathit{\theta }}\hfill \end{array}$$(2)

where ${\mathit{\sigma }}_{rr},{\mathit{\sigma }}_{\mathit{\theta }\mathit{\theta }},{\mathit{\sigma }}_{r\mathit{\theta }}$ are the stress components, $e_{rr},e_{\mathit{\theta }\mathit{\theta }},e_{r\mathit{\theta }}$ are the strain components, $\mathit{\rho }$ is the mass density, $\mathrm{\Omega }$ is the rotation, t is the time, $\mathit{\lambda }$ and $\mathit{\mu }$ are Lame’ constants. The displacement equation of motion has the additional terms with a time-dependent centripetal acceleration $\overrightarrow{\mathrm{\Omega }}\times (\overrightarrow{\mathrm{\Omega }}\times \overrightarrow{u})$ and $2\overrightarrow{\mathrm{\Omega }}\times {\overrightarrow{u}}_{,t}$ where, $\overrightarrow{u}=(u,0,0)$ is the displacement vector and $\overrightarrow{\mathrm{\Omega }}=(0,\mathrm{\Omega },0)$ is the angular velocity, the comma notation used in the subscript denotes the partial differentiation with respect to the variables.

The strain $e_{ij}$ related to the displacements are given by(3) $$e_{rr}=u_{r,r},e_{\mathit{\theta }\mathit{\theta }}=r^{-1}\left(u_r+u_{\mathit{\theta },\mathit{\theta }}\right),e_{r\mathit{\theta }}=u_{\mathit{\theta },r}-r^{-1}\left(u_{\mathit{\theta }}-u_{r,\mathit{\theta }}\right)$$(3)

in which $u_r$ and $u_{\mathit{\theta }}$ is the displacement components along radial and circumferential directions, respectively. The comma in the subscripts denotes the partial differentiation with respect to the variables.

Substituting the Equations 3 and 2 in Equation 1, the following displacement equations of motions are obtained as(4a) $$(\mathit{\lambda }+2\mathit{\mu })\left(u_{r,rr}+r^{-1}{u}_{r,r}-r^{-2}{u}_r\right)+\mathit{\mu }{r}^{-2}{u}_{r,\mathit{\theta }\mathit{\theta }}+r^{-1}(\mathit{\lambda }+\mathit{\mu })u_{\mathit{\theta },r\mathit{\theta }}+r^{-2}(\mathit{\lambda }+3\mathit{\mu })u_{\mathit{\theta },\mathit{\theta }}+\mathit{\rho }{\mathrm{\Omega }}^2{u}_r=\mathit{\rho }{u}_{r,tt}$$(4a) (4b) $$\mathit{\mu }\left({u_{\mathit{\theta }}}_{,rr}+r^{-1}{u}_{\mathit{\theta },r}-r^{-2}{u}_{\mathit{\theta }}\right)+r^{-2}(\mathit{\lambda }+2\mathit{\mu })u_{\mathit{\theta },\mathit{\theta }\mathit{\theta }}+r^{-2}(\mathit{\lambda }+3\mathit{\mu })u_{r,\mathit{\theta }}+r^{-1}(\mathit{\lambda }+\mathit{\mu })u_{r,r\mathit{\theta }}=\mathit{\rho }{u}_{\mathit{\theta },tt}$$(4b)

3. Solutions of solid medium

Equations 4a and 4b are coupled partial differential equation with two displacements components. To uncouple Equations 4a and 4b, we follow Mirsky (1965) by assuming the vibration and displacements along the axial direction z equal to zero. Hence, assuming the solutions of Equations 4a and 4b in the following form(5a) $$u_r(r,\mathit{\theta },z,t)=\sum _{n=0}^{\infty }{\mathit{\epsilon }}_n\left[\left({\mathit{\varphi }}_{n,r}+r^{-1}{\mathit{\psi }}_{n,\mathit{\theta }}\right)+\left({\overline{\mathit{\varphi }}}_{n,r}+r^{-1}{\overline{\mathit{\psi }}}_{n,\mathit{\theta }}\right)\right]e^{i\mathit{\omega }t}$$(5a) (5b) $$u_{\mathit{\theta }}(r,\mathit{\theta },z,t)=\sum _{n=0}^{\infty }{\mathit{\epsilon }}_n\left[\left(r^{-1}{\mathit{\varphi }}_{n,\mathit{\theta }}-{\mathit{\psi }}_{n,r}\right)+\left(r^{-1}{\overline{\mathit{\varphi }}}_{n,\mathit{\theta }}-{\overline{\mathit{\psi }}}_{n,r}\right)\right]e^{i\mathit{\omega }t}$$(5b)

where ${\mathit{\epsilon }}_n=\frac{1}{2}$ for n = 0, ${\mathit{\epsilon }}_n=1$ for $n\ge 1$, $i=\sqrt{-1}$, and $\mathit{\omega }$ is the angular frequency; ${\mathit{\varphi }}_n(r,\mathit{\theta })$, ${\mathit{\psi }}_n(r,\mathit{\theta })$, ${\overline{\mathit{\varphi }}}_n(r,\mathit{\theta })$ and ${\overline{\mathit{\psi }}}_n(r,\mathit{\theta })$ are the displacement potentials.

By introducing the dimensionless quantities $\overline{\mathit{\lambda }}=(\mathit{\lambda }/\mathit{\mu })$, $\mathit{\xi }=\sqrt{\mathit{\rho }{\mathit{\omega }}^2{a}^2/\mathit{\mu }}$, $\overline{z}=z/a$, $c^2={\mathrm{\Omega }}^2{\mathit{\xi }}^2/{\mathit{\omega }}^2$, ${\mathit{\omega }}^{\ast }=\mathit{\xi }/a\sqrt{\mathit{\mu }/\mathit{\rho }}$, $T=t\sqrt{\mathit{\mu }/\mathit{\rho }}/a$, $x=r/a$, $c^2$ is the rotational velocity, and substituting Equations 5a and 5b in Equations 4a and 4b, we obtain(6) $$\left[\left(2+\overline{\mathit{\lambda }}\right){\mathrm{\nabla }}^2+\left({\mathit{\xi }}^2+c^2\right)\right]{\mathit{\varphi }}_n=0$$(6)

and(7) $$\left[{\mathrm{\nabla }}^2+\left({\mathit{\xi }}^2+c^2\right)\right]{\mathit{\psi }}_n=0$$(7)

where ${\mathrm{\nabla }}^2\equiv {\mathit{\partial }}^2/\mathit{\partial }{x}^2+x^{-1}\mathit{\partial }/\mathit{\partial }x+x^{-2}{\mathit{\partial }}^2/\mathit{\partial }{\mathit{\theta }}^2$

From Equation 6, we obtain(8) $$\left({\mathrm{\nabla }}^2+{(\mathit{\alpha }a)}^2\right){\mathit{\varphi }}_n=0$$(8)

where ${\left(\mathit{\alpha }a\right)}^2=\left({\mathit{\xi }}^2+c^2\right)/\left(2+\overline{\mathit{\lambda }}\right)$. The solution of Equation 7 for symmetric mode is(9) $${\mathit{\varphi }}_n=A_1{J}_n\left({\mathit{\alpha }}_{1}ax\right)cosn\mathit{\theta }$$(9)

Similarly, the solution for the anti symmetric mode $\overline{{\mathit{\varphi }}_n}$ is obtained by replacing $cosn\mathit{\theta }$ by $sinn\mathit{\theta }$ in Equation 9.(10) $${\overline{\mathit{\varphi }}}_n={\overline{A}}_1{J}_n\left({\mathit{\alpha }}_{1}ax\right)sinn\mathit{\theta }$$(10)

where $J_n$ is the Bessel function of first kind, ${\left({\mathit{\alpha }}_{1}a\right)}^2$ are the roots of Equation 6. Solving Equation 7, we obtain(11) $${\mathit{\psi }}_n=A_2{J}_n\left({\mathit{\alpha }}_{2}ax\right)sinn\mathit{\theta }$$(11)

for symmetric mode and ${\overline{\mathit{\psi }}}_n$ is obtained from Equation 11 by replacing $sinn\mathit{\theta }$ by $cosn\mathit{\theta }$(12) $${\overline{\mathit{\psi }}}_n={\overline{A}}_2{J}_n\left({\mathit{\alpha }}_{2}ax\right)cosn\mathit{\theta }$$(12)

for the anti symmetric mode. Where ${\left({\mathit{\alpha }}_{2}a\right)}^2=({\mathit{\xi }}^2+c^2)$. If ${\left({\mathit{\alpha }}_{i}a\right)}^2<0$, i = 1, 2 then the Bessel function of first kind is to be replaced by the modified Bessel function of the first kind I_n.

4. Solution of fluid medium

In cylindrical coordinates, the acoustic pressure and radial displacement equation of motion for an in viscid fluid are of the form Achenbach (1973)(13) $$p^f=-B^f\left({u^f}_{,r}+r^{-1}\left(u^f+{v^f}_{,\mathit{\theta }}\right)\right)$$(13)

and(14) $$c^{-2}{u^f}_{,tt}={\mathrm{\Delta }}_{,r}$$(14)

respectively, where $(u^f,v^f)$ is the displacement vector, $B^f$ is the adiabatic bulk modulus, $c=\sqrt{B^f/{\mathit{\rho }}^f}$ is the acoustic phase velocity of the fluid in which ${\mathit{\rho }}^f$ is the density of the fluid and(15) $$\mathrm{\Delta }=\left({u^f}_{,r}+r^{-1}\left(u^f+{v^f}_{,\mathit{\theta }}\right)\right)$$(15)

substituting $u^f={{\mathit{\varphi }}^f}_{,r}$ and $v^f=r^{-1}{{\mathit{\varphi }}^f}_{,\mathit{\theta }}$ and seeking the solution of Equation 14 in the form(16) $${\mathit{\varphi }}^f(r,\mathit{\theta },t)=\sum _{n=0}^{\infty }{\mathit{\epsilon }}_n\left[{\mathit{\varphi }}_n^{f}cosn\mathit{\theta }+{{\overline{\mathit{\varphi }}}_n}^{f}sinn\mathit{\theta }\right]e^{i\mathit{\omega }t}$$(16)

where(17) $${\mathit{\varphi }}_n^f=A_3{J_n}^1\left({\mathit{\alpha }}_{3}ax\right)$$(17)

for inner fluid. In Equation 17, ${\left({\mathit{\alpha }}_{3}a\right)}^2={\mathit{\xi }}^2/\overline{{\mathit{\rho }}^f}\overline{B^f}$ in which $\overline{\mathit{\rho }}=\mathit{\rho }/{\mathit{\rho }}^f$, $\overline{B^f}=B^f/\mathit{\mu }$, $J_n^1$ is the Bessel function of the first kind and ${\overline{\mathit{\varphi }}}_n^f$ is as same as ${\mathit{\varphi }}_n^f$. If ${\left({\mathit{\alpha }}_{3}a\right)}^2<0$, the Bessel function of first kind is to be replaced by the modified Bessel function of second kind $K_n$.

By substituting the expression of the displacement vector in terms of ${\mathit{\varphi }}^f$ and Equations 17 in Equation 13, we could express the acoustic pressure of the disc as(18) $$p^f=\sum _{n=0}^{\infty }{\mathit{\epsilon }}_n{A}_3{\mathit{\xi }}^2\overline{\mathit{\rho }}{J}_n^1\left({\mathit{\alpha }}_{3}ax\right)cosn\mathit{\theta }{e}^{i\mathit{\omega }t}$$(18)

5. Boundary conditions and frequency equations

In this problem, the vibration of a polygonal cross-sectional rotating disc immersed in fluid is considered. Since the boundary is irregular, it is difficult to satisfy the boundary conditions both inner and outer surface of the disc directly. Hence, in the same lines of Nagaya (1983a, 1983b), the Fourier expansion collocation method is applied to satisfy the boundary conditions. Thus, the boundary conditions are obtained as(19) $${\left({\mathit{\sigma }}_{xx}+p^f\right)}_l={({\mathit{\sigma }}_{xy})}_l={(u-u^f)}_l=0$$(19)

where x is the coordinate normal to the boundary and y is the tangential coordinate to the boundary, ${\mathit{\sigma }}_{xx}$ is the normal stress, ${\mathit{\sigma }}_{xy}$ is the shearing stress and ( )_l represents the value at the lth segment of the boundary. The first and last conditions in Equation 19 are due to the continuity of the stresses and displacements of the disc and fluid on the curved surface. If the angle ${\mathit{\gamma }}_l$ between the normal to the segment and the reference axis is assumed to be constant, the transformed expression for the stresses are given by(20) $$\begin{array}{c}{\mathit{\sigma }}_{xx}=\mathit{\lambda }\left(u_{,r}+r^{-1}\left(u+v_{,\mathit{\theta }}\right)\right)+2\mathit{\mu }[u_{,r}{cos}^2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)+r^{-1}\left(u+v_{,\mathit{\theta }}\right){sin}^2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)+0.5\left(r^{-1}\left(v-u_{,\mathit{\theta }}\right)-v_{,r}\right)sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)]\hfill \\ {\mathit{\sigma }}_{xy}=\mathit{\mu }[u_{,r}-r^{-1}\left(v_{,\mathit{\theta }}+u\right)sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)+\left(r^{-1}\left(u_{,\mathit{\theta }}-v\right)+v_{,r}\right)sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)]\hfill \end{array}$$(20)

The boundary conditions in Equation 19 are transformed for rotating disc as(21) $$\begin{array}{c}\left[{(S_{xx})}_l+{\left({\overline{S}}_{xx}\right)}_l\right]e^{i\left(\mathit{\epsilon }\overline{z}+\mathrm{\Omega }T\right)}=0\hfill \\ \left[{(S_{xy})}_l+{\left({\overline{S}}_{xy}\right)}_l\right]e^{i\left(\mathit{\epsilon }\overline{z}+\mathrm{\Omega }T\right)}=0\hfill \\ \left[{(S_r)}_l+{\left({\overline{S}}_r\right)}_l\right]e^{i\left(\mathit{\epsilon }\overline{z}+\mathrm{\Omega }T\right)}=0\hfill \end{array}$$(21)

where(22) $$\begin{array}{c}{S}_{xx}=0.5\left(e_0^1{A}_{10}+e_0^2{A}_{20}\right)+\sum _{n=1}^{\infty }\left(e_n^1{A}_{1n}+e_n^2{A}_{2n}+e_n^3{A}_{3n}\right)\hfill \\ S_{xy}=0.5\left(f_0^1{A}_{10}+f_0^2{A}_{20}\right)+\sum _{n=1}^{\infty }\left(f_n^1{A}_{1n}+f_n^2{A}_{2n}+f_n^3{A}_{3n}\right)\hfill \\ S_t=0.5\left(g_0^1{A}_{10}+g_0^2{A}_{20}\right)+\sum _{n=1}^{\infty }\left(g_n^1{A}_{1n}+g_n^2{A}_{2n}+g_n^3{A}_{3n}\right)\hfill \end{array}$$(22) (23) $$\begin{array}{c}{\overline{S}}_{xx}=0.5\left({\overline{e}}_0^3{\overline{A}}_{30}\right)+\sum _{n=1}^{\infty }\left({\overline{e}}_n^1{\overline{A}}_{1n}+{\overline{e}}_n^2{\overline{A}}_{2n}+{\overline{e}}_n^3{\overline{A}}_{3n}\right)\hfill \\ {\overline{S}}_{xy}=0.5\left({\overline{f}}_0^3{\overline{A}}_{30}\right)+\sum _{n=1}^{\infty }\left({\overline{f}}_n^1{\overline{A}}_{1n}+{\overline{f}}_n^2{\overline{A}}_{2n}+{\overline{f}}_n^3{\overline{A}}_{3n}\right)\hfill \\ {\overline{S}}_t=0.5\left({\overline{g}}_0^3{\overline{A}}_{30}\right)+\sum _{n=1}^{\infty }\left({\overline{g}}_n^1{\overline{A}}_{1n}+{\overline{g}}_n^2{\overline{A}}_{2n}+{\overline{g}}_n^3{\overline{A}}_{3n}\right)\hfill \end{array}$$(23)

The coefficients for $e_n^i-{\overline{g}}_n^i$ are given in Appendix A.

Performing the Fourier series expansion to Equation 19 along the boundary, the boundary conditions along the surfaces are expanded in the form of double Fourier series. In the symmetric mode, the boundary conditions are obtained as(24) $$\begin{array}{c}\sum _{m=0}^{\infty }{\mathit{\epsilon }}_m\left[E_{m0}^1{A}_{10}+E_{m0}^2{A}_{20}+\sum _{n=1}^{\infty }\left(E_{mn}^1{A}_{1n}+E_{mn}^2{A}_{2n}+E_{mn}^3{A}_{3n}\right)\right]cosm\mathit{\theta }=0\hfill \\ \sum _{m=1}^{\infty }\left[F_{m0}^1{A}_{10}+F_{m0}^2{A}_{20}+\sum _{n=1}^{\infty }\left(F_{mn}^1{A}_{1n}+F_{mn}^2{A}_{2n}+F_{mn}^3{A}_{3n}\right)\right]sinm\mathit{\theta }=0\hfill \\ \sum _{m=0}^{\infty }{\mathit{\epsilon }}_m\left[G_{m0}^1{A}_{10}+G_{m0}^2{A}_{20}+\sum _{n=1}^{\infty }\left(G_{mn}^1{A}_{1n}+G_{mn}^2{A}_{2n}+G_{mn}^3{A}_{3n}\right)\right]cosm\mathit{\theta }=0\hfill \end{array}$$(24)

and for antisymmetric mode, the boundary conditions are expresses as(25) $$\begin{array}{c}\sum _{m=1}^{\infty }\left[{\overline{E}}_{m0}^3{\overline{A}}_{30}+\sum _{n=1}^{\infty }\left({\overline{E}}_{mn}^1{\overline{A}}_{1n}+{\overline{E}}_{mn}^2{\overline{A}}_{2n}+{\overline{E}}_{mn}^3{\overline{A}}_{3n}\right)\right]sinm\mathit{\theta }=0\hfill \\ \sum _{m=0}^{\infty }{\mathit{\epsilon }}_m\left[{\overline{F}}_{m0}^3{\overline{A}}_{30}+\sum _{n=1}^{\infty }\left({\overline{F}}_{mn}^1{\overline{A}}_{1n}+{\overline{F}}_{mn}^2{\overline{A}}_{2n}+{\overline{F}}_{mn}^3{\overline{A}}_{3n}\right)\right]cosm\mathit{\theta }=0\hfill \\ \sum _{m=1}^{\infty }\left[{\overline{G}}_{m0}^3{\overline{A}}_{30}+\sum _{n=1}^{\infty }\left({\overline{G}}_{mn}^1{\overline{A}}_{1n}+{\overline{G}}_{mn}^2{\overline{A}}_{2n}+{\overline{G}}_{mn}^3{\overline{A}}_{3n}\right)\right]sinm\mathit{\theta }=0\hfill \end{array}$$(25)

where(26) $$\begin{array}{c}{E}_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{i-1}}{\overset{{\mathit{\theta }}_i}{\int }}{e}_n^j\left(R_i,\mathit{\theta }\right)cosm\mathit{\theta }d\mathit{\theta }\hfill \\ F_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{l-1}}{\overset{{\mathit{\theta }}_l}{\int }}{f}_n^j\left(R_i,\mathit{\theta }\right)sinm\mathit{\theta }d\mathit{\theta }\hfill \\ G_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{i-1}}{\overset{{\mathit{\theta }}_i}{\int }}{g}_n^j\left(R_i,\mathit{\theta }\right)cosm\mathit{\theta }d\mathit{\theta }\hfill \end{array}$$(26) (27) $$\begin{array}{c}{\overline{E}}_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{i-1}}{\overset{{\mathit{\theta }}_i}{\int }}{\overline{e}}_n^j\left(R_i,\mathit{\theta }\right)sinm\mathit{\theta }d\mathit{\theta }\hfill \\ {\overline{F}}_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{l-1}}{\overset{{\mathit{\theta }}_l}{\int }}{\overline{f}}_n^j\left(R_i,\mathit{\theta }\right)cosm\mathit{\theta }d\mathit{\theta }\hfill \\ {\overline{G}}_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{i-1}}{\overset{{\mathit{\theta }}_i}{\int }}{\overline{g}}_n^j\left(R_i,\mathit{\theta }\right)sinm\mathit{\theta }d\mathit{\theta }\hfill \end{array}$$(27)

and where j = 1, 2, and 3, I is the number of segments, R_i is the coordinate r at the boundary and N is the number of truncation of the Fourier series. The frequency equations are obtained by truncating the series to N + 1 terms, and equating the determinant of the coefficients of the amplitude $A_{in}=0$ and ${\overline{A}}_{in}=0$, for symmetric and antisymmetric modes of vibrations. Thus, the frequency equation for the symmetric mode is obtained from Equation 24, by equating the determinant of the coefficient matrix of $A_{in}=0$. Therefore, we have(28) $$\left|\begin{array}{ccccccccccc}{E}_{00}^1& E_{00}^2& E_{01}^1& \cdots & E_{0N}^1& E_{01}^2& \cdots & E_{0N}^2& E_{01}^3& \cdots & E_{0N}^3\\ ⋮& ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮\\ E_{N0}^1& E_{N0}^2& E_{N1}^1& \cdots & E_{NN}^1& E_{N1}^2& \cdots & E_{NN}^2& E_{N1}^3& \cdots & E_{NN}^3\\ F_{00}^1& F_{00}^2& F_{01}^1& \cdots & F_{0N}^1& F_{01}^2& \cdots & F_{0N}^2& F_{01}^3& \cdots & F_{0N}^3\\ ⋮& ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮\\ F_{N0}^1& F_{N0}^2& F_{N1}^1& \cdots & F_{NN}^1& F_{N1}^2& \cdots & F_{NN}^2& F_{N1}^3& \cdots & F_{NN}^3\\ G_{00}^1& G_{00}^2& G_{01}^1& \cdots & G_{0N}^1& G_{01}^2& \cdots & G_{0N}^2& G_{01}^3& \cdots & G_{0N}^3\\ ⋮& ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮\\ G_{N0}^1& G_{N0}^2& G_{N1}^1& \cdots & G_{NN}^1& G_{N1}^2& \cdots & G_{NN}^2& g_{N1}^3& \cdots & G_{NN}^3\end{array}\right|=0$$(28)

Similarly, the frequency equation for antisymmetric mode is obtained from the Equation 25 by equating the determinant of the coefficient matrix of ${\overline{A}}_{in}$ to zero. Therefore, for the antisymmetric mode, the frequency equation obtained as(29) $$\left|\begin{array}{cccccccccc}{\overline{E}}_{10}^3& {\overline{E}}_{11}^1& \cdots & {\overline{E}}_{1N}^1& {\overline{E}}_{11}^2& \cdots & {\overline{E}}_{1N}^2& {\overline{E}}_{11}^3& \cdots & {\overline{E}}_{1N}^3\\ ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮\\ {\overline{E}}_{N0}^3& {\overline{E}}_{N1}^1& \cdots & {\overline{E}}_{NN}^1& {\overline{E}}_{N1}^2& \cdots & {\overline{E}}_{NN}^2& {\overline{E}}_{N1}^3& \cdots & {\overline{E}}_{NN}^3\\ {\overline{F}}_{10}^3& {\overline{F}}_{11}^1& \cdots & {\overline{F}}_{1N}^1& {\overline{F}}_{11}^2& \cdots & {\overline{F}}_{1N}^2& {\overline{F}}_{11}^3& \cdots & {\overline{F}}_{1N}^3\\ ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮\\ {\overline{F}}_{N0}^3& {\overline{F}}_{N1}^1& \cdots & {\overline{F}}_{NN}^1& {\overline{F}}_{N1}^2& \cdots & {\overline{F}}_{NN}^2& {\overline{F}}_{N1}^3& \cdots & {\overline{F}}_{NN}^3\\ {\overline{G}}_{10}^3& {\overline{G}}_{11}^1& \cdots & {\overline{G}}_{1N}^1& {\overline{G}}_{11}^2& \cdots & {\overline{G}}_{1N}^2& {\overline{G}}_{11}^3& \cdots & {\overline{G}}_{1N}^3\\ ⋮& ⋮& & ⋮& ⋮& & ⋮& ⋮& & ⋮\\ {\overline{G}}_{N0}^3& {\overline{G}}_{N1}^1& \cdots & {\overline{G}}_{NN}^1& {\overline{G}}_{N1}^2& \cdots & {\overline{G}}_{NN}^2& {\overline{G}}_{N1}^3& \cdots & {\overline{G}}_{NN}^3\end{array}\right|=0$$(29)

6. Polygonal cross-sectional disc with fluid and without rotation

The wave propagation in a polygonal cross-sectional disc is obtained by substituting the rotation speed $\mathrm{\Omega }=0$ in the corresponding equations and expressions in the previous section, the problem is reduced to wave propagation in polygonal cross-sectional disc immersed in fluid. Substituting Equations 2, 3 in Equation 1 along with $\mathrm{\Omega }=0$, we get the displacement equations as follows:(30a) $$\begin{array}{c}\left(\mathit{\lambda }+2\mathit{\mu }\right)\left(u_{r,rr}+r^{-1}{u}_{r,r}-r^{-2}{u}_r\right)+\mathit{\mu }{r}^{-2}{u}_{r,\mathit{\theta }\mathit{\theta }}+r^{-1}\left(\mathit{\lambda }+\mathit{\mu }\right)u_{\mathit{\theta },r\mathit{\theta }}\hfill \\ +r^{-2}\left(\mathit{\lambda }+3\mathit{\mu }\right)u_{\mathit{\theta },\mathit{\theta }}=\mathit{\rho }{u}_{r,tt}\hfill \end{array}$$(30a) (30b) $$\begin{array}{c}\mathit{\mu }\left(u_{\mathit{\theta },rr}+r^{-1}{u}_{\mathit{\theta },r}-r^{-2}{u}_{\mathit{\theta }}\right)+r^{-2}\left(\mathit{\lambda }+2\mathit{\mu }\right)u_{\mathit{\theta },\mathit{\theta }\mathit{\theta }}+r^{-2}\left(\mathit{\lambda }+3\mathit{\mu }\right)u_{r,\mathit{\theta }}\hfill \\ +r^{-1}\left(\mathit{\lambda }+\mathit{\mu }\right)u_{r,r\mathit{\theta }}=\mathit{\rho }{u}_{\mathit{\theta },tt}\hfill \end{array}$$(30b)

Equations 30a and 30b are coupled partial differential equation with two displacements components. To uncouple Equations 30a and 30b, use Equation 4 in Equations 30a and 30b, we obtain a differential equations of the form(31) $$\left[\left(2+\overline{\mathit{\lambda }}\right){\mathrm{\nabla }}^2+{\mathit{\xi }}^2\right]{\mathit{\varphi }}_n^{\prime }=0$$(31)

and(32) $$\left[{\mathrm{\nabla }}^2+{\mathit{\xi }}^2\right]{\mathit{\psi }}_n^{\prime }=0$$(32)

in which ${\mathrm{\nabla }}^2\equiv {\mathit{\partial }}^2/\mathit{\partial }{x}^2+x^{-1}\mathit{\partial }/\mathit{\partial }x+x^{-2}{\mathit{\partial }}^2/\mathit{\partial }{\mathit{\theta }}^2$

From Equation 6, we obtain(33) $$\left({\mathrm{\nabla }}^2+{(\mathit{\beta }a)}^2\right){\mathit{\varphi }}_n=0$$(33)

where ${\left(\mathit{\beta }a\right)}^2={\mathit{\xi }}^2/\left(2+\overline{\mathit{\lambda }}\right)\left(2+\overline{\mathit{\lambda }}\right)$. The solution of Equation 31 for symmetric mode is(34) $${\mathit{\varphi }}_n^{\prime }=A_1^{\prime }{J}_n\left({\mathit{\beta }}_{1}ax\right)cosn\mathit{\theta }$$(34)

Similarly the solution for the anti symmetric mode ${\overline{\mathit{\varphi }}}_n^{\prime }$ is obtained by replacing $cosn\mathit{\theta }$ by $sinn\mathit{\theta }$ in Equation 34.(35) $${\overline{\mathit{\varphi }}}_n^{\prime }={\overline{A}}_1^{\prime }{J}_n\left({\mathit{\beta }}_{1}ax\right)sinn\mathit{\theta }$$(35)

where $J_n$ is the Bessel function of first kind, ${\left({\mathit{\alpha }}_{1}a\right)}^2$ are the roots of Equation 6. Solving Equation 7, we obtain(36) $${\mathit{\psi }}_n^{\prime }=A_2^{\prime }{J}_n\left({\mathit{\beta }}_{2}ax\right)sinn\mathit{\theta }$$(36)

for symmetric mode and ${\overline{\mathit{\psi }}}_n^{\prime }$ is obtained from Equation 36 by replacing $sinn\mathit{\theta }$ by $cosn\mathit{\theta }$(37) $${\overline{\mathit{\psi }}}_n^{\prime }={\overline{A}}_2^{\prime }{J}_n\left({\mathit{\beta }}_{2}ax\right)cosn\mathit{\theta }$$(37)

for the antisymmetric mode. Where ${\left({\mathit{\beta }}_{2}a\right)}^2={\mathit{\xi }}^2$. If ${\left({\mathit{\beta }}_{i}a\right)}^2<0$, i = 1, 2 then the Bessel function of first kind is to be replaced by the modified Bessel function of the first kind I_n.

By applying the same procedure as discussed the previous sections, and using the boundary conditions given in Equation 19, we obtain the frequency equations for polygonal cross-sectional disc immersed in fluid as

(38) $$\left|\begin{array}{ccc}{b}_{11}& b_{12}& b_{13}\\ b_{21}& b_{22}& b_{23}\\ b_{31}& b_{32}& b_{33}\end{array}\right|=0$$(38)

where$$\begin{array}{c}{b}_{11}=2\left\{n\left(n-1\right)J_n\left({\mathit{\beta }}_{1}ax\right)+\left({\mathit{\beta }}_{1}ax\right)J_{n+1}\left({\mathit{\beta }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ -x^2\left\{{\left({\mathit{\beta }}_{1}a\right)}^2\left(\overline{\mathit{\lambda }}+2{cos}^2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)\right)\right\}{J}_n\left({\mathit{\beta }}_{1}ax\right)cosn\mathit{\theta }\hfill \end{array}$$$$\begin{array}{c}{b}_{12}=2n\left\{\left(n-1\right)J_n\left({\mathit{\beta }}_{2}ax\right)+\left({\mathit{\beta }}_{2}ax\right)J_{n+1}\left({\mathit{\beta }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ +2\left\{\left(n\left(n-1\right)-{\left({\mathit{\beta }}_{2}ax\right)}^2\right)J_n\left({\mathit{\beta }}_{2}ax\right)+\left({\mathit{\beta }}_{2}ax\right)J_{n+1}\left({\mathit{\beta }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \end{array}$$$$b_{13}={\mathit{\xi }}^2\overline{\mathit{\rho }}{J^1}_n\left({\mathit{\beta }}_{3}ax\right)cosn\mathit{\theta }$$$$\begin{array}{c}{b}_{21}=2\left\{n\left(n-1\right)-{\left({\mathit{\beta }}_{1}ax\right)}^2{J}_n\left({\mathit{\beta }}_{1}ax\right)+\left({\mathit{\beta }}_{1}ax\right)J_{n+1}\left({\mathit{\beta }}_{1}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ +2n\left\{\left({\mathit{\beta }}_{1}ax\right)J_{n+1}\left({\mathit{\beta }}_{1}ax\right)-\left(n-1\right)J_n\left({\mathit{\beta }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \end{array}$$$$\begin{array}{c}{b}_{22}=2n\left\{\left(n-1\right)J_n\left({\mathit{\beta }}_{2}ax\right)-\left({\mathit{\beta }}_{2}ax\right)J_{n+1}\left({\mathit{\beta }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ +2\left\{\left({\mathit{\beta }}_{2}ax\right)J_{n+1}\left({\mathit{\beta }}_{2}ax\right)-\left(n\left(n-1\right)-{\left({\mathit{\beta }}_{2}ax\right)}^2\right)J_n\left({\mathit{\beta }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \end{array}$$$$b_{33}=0$$$$b_{31}=\left\{n{J}_n\left({\mathit{\beta }}_{1}ax\right)-\left({\mathit{\beta }}_{1}ax\right)J_{n+1}\left({\mathit{\beta }}_{1}ax\right)\right\}cosn\mathit{\theta }$$$$b_{32}=n{J}_n\left({\mathit{\beta }}_{2}ax\right)cosn\mathit{\theta }$$(39) $$b_{33}=-\left[n{J^1}_n\left({\mathit{\beta }}_{3}ax\right)-\left({\mathit{\beta }}_{3}ax\right){J^1}_{n+1}\left({\mathit{\beta }}_{3}ax\right)\right]cosn\mathit{\theta }$$(39)

7. Polygonal cross-sectional disc without fluid and rotation

The free vibration of homogeneous isotropic disc of polygonal cross-section without fluid medium and without rotation can be recovered from the present analysis by omitting the fluid medium and setting $\mathrm{\Omega }=0$, along win the corresponding equations and solutions in the previous sections, then the problem of rotating disc of polygonal cross-section immersed in fluid is converted into a problem of a two-dimensional vibration analysis of polygonal cross-sectional disc. The frequency equations of an polygonal cross-sectional disc without fluid and rotation is obtained as

Stress-free (Unclamped edge), which leads to(40) $${\left({\mathit{\sigma }}_{xx}\right)}_i={\left({\mathit{\sigma }}_{xy}\right)}_i=0$$(40)

Rigidly fixed (Clamped edge), implies that(41) $${\left(u_r\right)}_i={\left(u_{\mathit{\theta }}\right)}_i=0$$(41)

By applying the same procedure as discussed in the previous section, the stresses are transformed for a disc without fluid and rotation is given as follows.$${\mathit{\sigma }}_{xx}^{\prime }=\mathit{\lambda }\left(u_{,r}+r^{-1}\left(u+v_{,\mathit{\theta }}\right)\right)+2\mathit{\mu }[u_{,r}{cos}^2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)+r^{-1}\left(u+v_{,\mathit{\theta }}\right){sin}^2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)+0.5\left(r^{-1}\left(v-u_{,\mathit{\theta }}\right)-v_{,r}\right)sin2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)]$$(42) $${\mathit{\sigma }}_{xy}^{\prime }=\mathit{\mu }[u_{,r}-r^{-1}\left(v_{,\mathit{\theta }}+u\right)sin2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)+\left(r^{-1}\left(u_{,\mathit{\theta }}-v\right)+v_{,r}\right)sin2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)]$$(42)

Substituting Equations 9–12 in Equation 40, the boundary conditions are transformed for stress-free disc as follows:$$\left[{\left(S_{xx}^{\prime }\right)}_i+{\left({\overline{S}}_{xx}^{\prime }\right)}_i\right]e^{i\mathrm{\Omega }{T}_a}=0$$(43) $$\left[{\left(S_{xy}^{\prime }\right)}_i+{\left({\overline{S}}_{xy}^{\prime }\right)}_i\right]e^{i\mathrm{\Omega }{T}_a}=0$$(43)

where(44) $$S_{xx}^{\prime }=0.5\left(k_0^1{P}_{10}\right)+\sum _{n=1}^{\infty }\left(k_n^1{P}_{1n}+k_n^2{P}_{2n}\right),S_{xy}^{\prime }=0.5\left(l_0^1{Q}_{10}\right)+\sum _{n=1}^{\infty }\left(l_n^1{Q}_{1n}+l_n^2{Q}_{2n}\right)$$(44) (45) $${\overline{S}}_{xx}=0.5\left({\overline{k}}_0^3{\overline{P}}_{30}\right)+\sum _{n=1}^{\infty }\left({\overline{k}}_n^1{\overline{P}}_{1n}+{\overline{k}}_n^2{\overline{P}}_{2n}\right),{\overline{S}}_{xy}^{\prime }=0.5\left({\overline{l}}_0^3{\overline{Q}}_{30}\right)+\sum _{n=1}^{\infty }\left({\overline{l}}_n^1{\overline{Q}}_{1n}+{\overline{l}}_n^2{\overline{A}}_{2n}\right)$$(45)

in which$$\begin{array}{c}{k}_n^1=2\left\{n\left(n-1\right)J_n\left({\mathit{\alpha }}_{1}ax\right)+\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)cosn\mathit{\theta }\hfill \\ -x^2\left\{{\left({\mathit{\alpha }}_{1}a\right)}^2\left(\overline{\mathit{\lambda }}+2{cos}^2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)\right)\right\}{J}_n\left({\mathit{\alpha }}_{1}ax\right)cosn\mathit{\theta }\hfill \end{array}$$$$\begin{array}{c}{k}_n^2=2n\left\{\left(n-1\right)J_n\left({\mathit{\alpha }}_{2}ax\right)+\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)cosn\mathit{\theta }\hfill \\ +2\left\{\left(n\left(n-1\right)-{\left({\mathit{\alpha }}_{2}ax\right)}^2\right)J_n\left({\mathit{\alpha }}_{2}ax\right)+\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)sinn\mathit{\theta }\hfill \end{array}$$$$\begin{array}{c}{l}_n^1=\left\{[2n\left(n-1\right)-{\left({\mathit{\alpha }}_{1}ax\right)}^2]J_n\left({\mathit{\alpha }}_{1}ax\right)+2\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)cosn\mathit{\theta }\hfill \\ +2n\left\{\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)-\left(n-1\right)J_n\left({\mathit{\alpha }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)sinn\mathit{\theta }\hfill \end{array}$$(46) $$\begin{array}{c}{l}_n^2=2n\left\{\left(n-1\right)J_n\left({\mathit{\alpha }}_{2}ax\right)-\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)cosn\mathit{\theta }\hfill \\ +2\left\{\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)-\left(n\left(n-1\right)-{\left({\mathit{\alpha }}_{2}ax\right)}^2\right)J_n\left({\mathit{\alpha }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)sinn\mathit{\theta }\hfill \end{array}$$(46)

The barred expressions for the antisymmetric case are obtained by replacing $cosn\mathit{\theta }$ by $sinn\mathit{\theta }$ and $sinn\mathit{\theta }$ by $cosn\mathit{\theta }$ in Equation 46. Performing the Fourier series expansion to Equation 40 and along the boundary, the boundary conditions along the surfaces are expanded in the form of double Fourier series. In the symmetric mode, the boundary conditions obtained as(47a) $$\sum _{m=0}^{\infty }{\mathit{\epsilon }}_m\left[{\widehat{K}}_{m0}^1{P}_{10}+\sum _{n=1}^{\infty }\left({\widehat{K}}_{mn}^1{P}_{1n}+{\widehat{K}}_{mn}^2{P}_{2n}\right)\right]cosm\mathit{\theta }=0$$(47a) (47b) $$\sum _{m=1}^{\infty }\left[{\widehat{L}}_{m0}^2{P}_{10}\sum _{n=1}^{\infty }\left({\widehat{L}}_{mn}^1{P}_{1n}+{\widehat{L}}_{mn}^2{P}_{2n}\right)\right]sinm\mathit{\theta }=0$$(47b)

where(48) $${\widehat{K}}_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{i-1}}{\overset{{\mathit{\theta }}_i}{\int }}{k}_n^j\left({\widehat{R}}_i,\mathit{\theta }\right)cosm\mathit{\theta }d\mathit{\theta },{\widehat{L}}_{mn}^j=\left(2{\mathit{\epsilon }}_n/\mathit{\pi }\right)\sum _{i=1}^I\underset{{\mathit{\theta }}_{l-1}}{\overset{{\mathit{\theta }}_l}{\int }}{l}_n^j\left({\widehat{R}}_i,\mathit{\theta }\right)sinm\mathit{\theta }d\mathit{\theta }$$(48)

where j = 1, 2 I the number of segments is, ${\widehat{R}}_i$ is the coordinate $\widehat{r}$ at the boundary, N is the number of truncation of the Fourier series. For the non-trivial solution of the systems of equations given in Equations 47a and 47b, the determinant of the coefficient matrix $P_{in}=0$ and these determinants give the frequencies of symmetric mode of vibration. Therefore, we have(49) $$\left|\begin{array}{ccccccc}{\widehat{K}}_{00}^1& {\widehat{K}}_{01}^1& \cdots & {\widehat{K}}_{0N}^1& {\widehat{K}}_{01}^2& \cdots & {\widehat{K}}_{0N}^2\\ ⋮& ⋮& & ⋮& ⋮& & ⋮\\ {\widehat{K}}_{N0}^1& {\widehat{K}}_{N1}^1& \cdots & {\widehat{K}}_{NN}^1& {\widehat{K}}_{N1}^2& \cdots & {\widehat{K}}_{NN}^2\\ {\widehat{L}}_{00}^1& {\widehat{L}}_{01}^1& \cdots & {\widehat{L}}_{0N}^1& {\widehat{L}}_{01}^2& \cdots & {\widehat{L}}_{0N}^2\\ ⋮& ⋮& & ⋮& ⋮& & ⋮\\ {\widehat{L}}_{N0}^1& {\widehat{L}}_{N1}^1& \cdots & {\widehat{L}}_{NN}^1& {\widehat{L}}_{N1}^2& \cdots & {\widehat{L}}_{NN}^2\end{array}\right|=0$$(49)

Similarly, the frequency equations for the antisymmetric mode are obtained by replacing $cosn\mathit{\theta }$ by $sin\mathit{\theta }$ and $sin\mathit{\theta }$ by $cosn\mathit{\theta }$ in the above corresponding equations.

8. Relative frequency shift

Relative frequency shift plays an important role in construction of rotating gyroscope, acoustic sensors and actuators. The frequency shift of the wave due to rotation is defined as $\mathrm{\Delta }\mathit{\omega }=\mathit{\omega }(\mathrm{\Omega })-\mathit{\omega }(0)$. $\mathrm{\Omega }$ being the angular rotation; the relative frequency shift is given by(50) $$R.F.S=\left|\frac{\mathrm{\Delta }\mathit{\omega }}{\mathit{\omega }}\right|=\left|\frac{\mathit{\omega }(\mathrm{\Omega })-\mathit{\omega }(0)}{\mathit{\omega }(0)}\right|$$(50)

where $\mathit{\omega }(0)$ is the frequency of the waves in the absence of rotation.

9. Numerical results and discussions

The frequency equations are obtained in symmetric and antisymmetric cases given in Equations 26 and 27 are analysed numerically for rotating disc of triangular, square, pentagonal and hexagonal cross-sections. 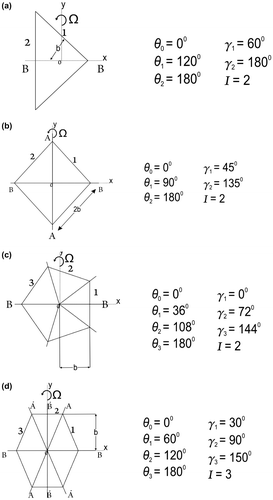The material properties used for the computation are as follows: for the solid the Poisson ratio $\mathit{\nu }=0.3$, density $\mathit{\rho }$ = 7,849 kg/m³ and the Young’s modulus E = 2.139 × 10¹¹ N/m² and for the fluid: the density ${\mathit{\rho }}^f$ = 1,000 Kg/m³ and the phase velocity c = 1,500 m/s. The geometric relations for the polygonal cross-section are taken from Equation 19 of Nagaya (1981) as$$R_i/b={\left[cos\left(\mathit{\theta }-{\mathit{\gamma }}_i\right)\right]}^{-1}$$

where b is the apothem and these relation is used directly for the calculation. The dimensionless frequency which are complex in nature, are computed by fixing the wave number for different thickness using Secant method for polygonal disc immersed in fluid. The polygonal cross-sectional disc in the range $\mathit{\theta }=0$ and $\mathit{\theta }=\mathit{\pi }$ is divided into many segments for convergence of frequency in such a way that the distance between any two segments is negligible. Integration is performed for each segment numerically by use of Gauss five point formula.

In Tables 1 and 2, a comparison is made for the frequency amongst triangular, square, pentagon and hexagon cross-sectional disc with fluid and without rotation for different aspect ratios. From these Tables it is clear that, as the vibration modes increases the non-dimensional frequencies are also increases in all the four cross-sectional discs and the non-dimensional frequency profiles exhibit high energy in hexagonal disc for increasing aspect ratio. Another spectrum of frequencies of triangular, square, pentagon and hexagon discs with the increasing aspect ratio in the absence of fluid medium and rotational speed is discussed in Tables 3 and 4. From Tables 3 and 4, it is observed that as the modes are increases the non-dimensional frequency also increases, whereas the values in the hexagonal modes are almost exponentially increasing with increasing aspect ratio. The amplitude of the all modes of vibrations exhibits high energy in the absence of fluid and rotational parameter (Figure 1).

Table 1. The non-dimensional frequency of triangular and square cross-sectional disc with fluid and without rotation for different aspect ratios

Mode	Triangle			Square
	a/b = 1.0	a/b = 1.5	a/b = 2.0	a/b = 1.0	a/b = 1.5	a/b = 2.0
S1	3.5251	3.6403	3.4426	3.2076	3.0775	3.2511
S2	4.8474	4.9872	4.8692	4.7112	4.8430	4.9522
S3	5.5647	5.6966	5.6625	5.4685	5.4844	5.8029
S4	6.2604	6.2625	6.3683	6.1122	6.1911	6.3618
S5	6.9675	6.9685	7.0676	6.8276	6.8976	7.0225

Table 2. The non-dimensional frequency of pentagon and hexagon cross-sectional disc with fluid and without rotation for different aspect ratios

Mode	Pentagon			Hexagon
	a/b = 1.0	a/b = 1.5	a/b = 2.0	a/b = 1.0	a/b = 1.5	a/b = 2.0
S1	4.2469	4.1053	4.2473	4.2469	4.2426	4.3841
S2	4.9545	4.9501	5.0964	4.9511	4.9497	5.0927
S3	5.6625	5.6556	5.8041	5.6624	5.6593	5.8041
S4	6.3693	6.2288	6.3712	6.3668	6.2257	6.5118
S5	7.0732	6.9290	7.2125	7.0680	6.9366	7.0704

Table 3. The non-dimensional frequency of triangular and square cross-sectional disc without fluid and without rotation for different aspect ratios

Mode	Triangle			Square
	a/b = 1.0	a/b = 1.5	a/b = 2.0	a/b = 1.0	a/b = 1.5	a/b = 2.0
A1	4.1440	4.1536	4.2475	4.0336	4.0978	4.2434
A2	4.8602	4.8621	4.9428	4.7134	4.8007	4.9526
A3	5.5753	5.5712	5.6615	5.4087	5.5055	5.6599
A4	6.2691	6.2785	6.3704	6.1590	6.2154	6.3711
A5	6.9696	6.9857	7.0715	6.8707	6.9220	7.0726

Table 4. The non-dimensional frequency of pentagon and hexagon cross-sectional disc without fluid and without rotation for different aspect ratios

Mode	Pentagon			Hexagon
	a/b = 1.0	a/b = 1.5	a/b = 2.0	a/b = 1.0	a/b = 1.5	a/b = 2.0
A1	4.2377	4.1785	4.3766	4.2480	4.2232	4.3144
A2	4.9598	4.8095	5.0695	4.9535	4.8513	5.2585
A3	5.6645	5.5171	5.8027	5.6723	5.5509	5.8042
A4	6.3672	6.2246	6.3815	6.5083	6.1846	6.5117
A5	7.0761	6.9380	7.2124	7.0833	7.0781	7.2201

Figure 1. Rotating disc of (a) Triangle (b) Square (c) Pentagon (d) Hexagonal cross-sections.

9.1. Triangular and pentagonal cross-sections

In triangular and pentagonal cross-sectional discs, the vibrational displacements are symmetrical about the x axis for the longitudinal mode and anti-symmetrical about the y axis for the flexural mode since the cross-section is symmetric about only one axis. Therefore, n and m are chosen as 0, 1, 2, 3, … in Equation 24 for longitudinal mode and n, m = 1, 2, 3, … in Equation 25 for the flexural mode.

9.2. Square and hexagonal cross-sections

In the case of longitudinal vibration of square and hexagonal cross-sectional disc, the displacements are symmetrical about both major and minor axes since both the cross-sections are symmetrical about both the axes. Therefore, the frequency equation is obtained by choosing both terms of n and m is chosen as 0, 2, 4, 6, … in Equation 24. During flexural motion, the displacements are antisymmetrical about the major axis and symmetrical about the minor axis. Hence, the frequency equation is obtained by choosing n, m = 1, 3, 5, … in Equation 25.

9.3. Dispersion curves

The notations used in the Figures namely, Lm, FSm and FASm denote the longitudinal, flexural symmetric and flexural antisymmetric modes of vibrations.

The non-dimensional wave number is calculated with increasing non-dimensional frequency for the longitudinal and flexural (symmetric and antisymmetric) modes of triangle, square, pentagon and hexagonal cross-sectional discs with different values of the rotational speed $\mathrm{\Omega }$ = 0.2, 0.4 in Figures 2^{Figure 3Figure 4}–5. From these curves, it can be seen that the frequencies are increases in all the three kinds of vibrational modes such as longitudinal and flexural (symmetric and antisymmetric) with increasing rotational speed of the disc. The flexural modes the frequency gets maximum in all the four cross-sectional discs. But, there is small oscillation and merging of curves in pentagon and hexagonal cross-section between $0\le \mathit{\xi }\le 0.6$ in Figures 4 and 5, it shows that there is energy transportation between the modes of vibrations by the damping effect of surrounding fluid and rotational speed.

Figure 2. Variation of non-dimensional wave number vs. non-dimensional frequency of rotating disc of triangular cross-section.

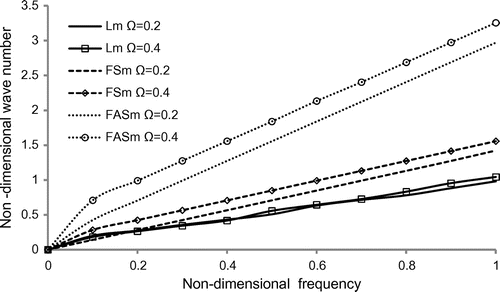
Figure 3. Variation of non-dimensional wave number vs. non-dimensional frequency of rotating disc of square cross-section.

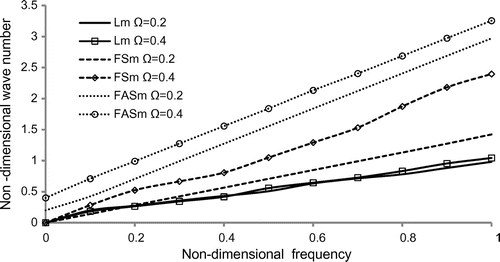
Figure 4. Variation of non-dimensional wave number vs. non-dimensional frequency of rotating disc of pentagonal cross-section.

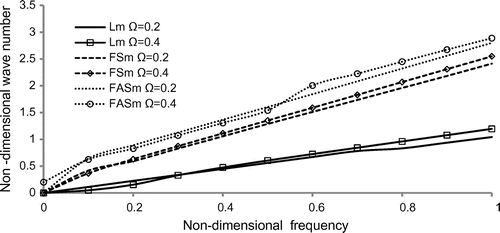
Figure 5. Variation of non-dimensional wave number vs. non-dimensional frequency of rotating disc of hexagonal cross-section.

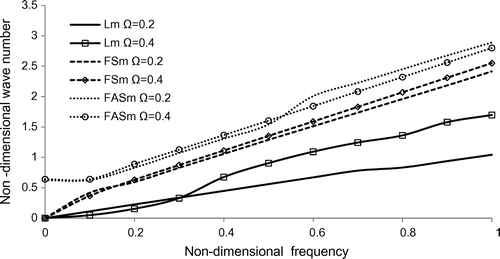
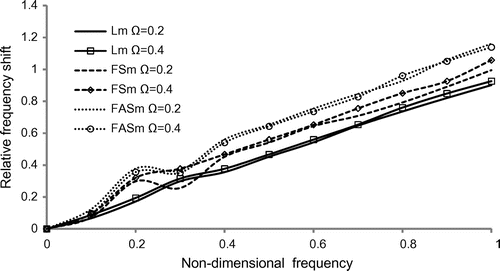
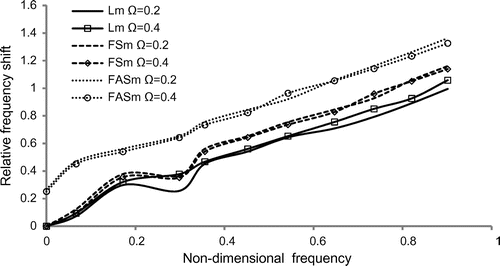
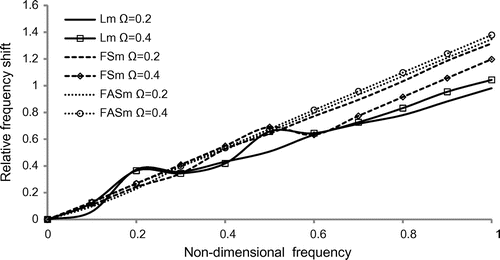
Figures 6^{Figure 7Figure 8}–9 reveals that the variation of relative frequency shift of triangle, square, pentagon and hexagonal cross-sectional discs with the non-dimensional frequency for the longitudinal and flexural (symmetric and antisymmetric) modes together with different rotational speed $\mathrm{\Omega }$ = 0.2, 0.4. From Figures 6 and 7, it is observed that, both in triangle and square cross-sections, the longitudinal and flexural (symmetric and antisymmetric) modes merges for $0\le \mathit{\xi }\le 0.2$ and begin starts increases monotonically. Also, in pentagon and hexagonal cross-sections in Figures 8 and 9, the relative frequency shift gets oscillating trend in the frequency range $0\le \mathit{\xi }\le 0.6$. The merging of curves between the vibrational modes shows that there is energy transportation between the modes of vibrations by the effect of fluid interaction and rotation. The relative frequency shift profile is highly dispersive in trend for pentagon and hexagonal cross-section than in triangle and square cross-section.

Figure 6. Variation of relative frequency shift vs. non-dimensional frequency of rotating disc of triangular cross-section.

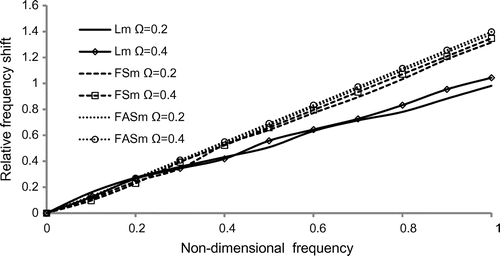
Figure 7. Variation of relative frequency shift vs. non-dimensional frequency of rotating disc of square cross-section.

Figure 8. Variation of relative frequency shift vs. non-dimensional frequency of rotating disc of pentagonal cross-section.

Figure 9. Variation of relative frequency shift vs. non-dimensional frequency of rotating disc of hexagonal cross-section.

10. Conclusions

In this paper, an analytical method for solving the wave propagation problem of rotating polygonal cross-sectional disc immersed in an inviscid fluid has been presented. The general frequency equation has been obtained using Fourier expansion collocation method. The frequency equations have been derived for the two cases:

1. Polygonal cross-sectional disc with fluid and without rotation

2. Polygonal cross-sectional disc without fluid and rotation

and are analysed numerically for different cross-sections. Numerical calculations for non-dimensional wave number and relative frequency shift have been carried out for triangular, square, pentagonal and hexagonal cross-sectional rotating disc immersed in fluid. From the dispersion curves it is observed that the non dimensional wave number and relative frequency shift are quite higher in all the cross-sections. The effect of rotation and fluid medium on the different cross-sectional discs is also observed to be significant and more in pentagon and hexagonal cross-sections. This method is straightforward and the numerical results for any other polygonal cross-section can be obtained directly for the same frequency equation by substituting geometric values of the boundary of any cross-section analytically or numerically with satisfactory convergence.

Cover image

Source: Author.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

R. Selvamani

R. Selvamani is working as an assistant professor in the department of Mathematics in Karunya University, Coimbatore, Tamilnadu, India. He has completed his PhD research from Bharathiar University, Coimbatore. He has published two books which are available in the amazon.com and has published a number of research papers in journals of national and international repute. His research area includes wave propagation in cylinder, panel, plate, composite cylinder and material with arbitrary cross-sections.

Appendix A

The equations for ${e^1}_n$ ~ ${\overline{g}}_n^3$ referred in Equation 22 are as follows:(A1) $$\begin{array}{c}{e^1}_n=2\left\{n\left(n-1\right)J_n\left({\mathit{\alpha }}_{1}ax\right)+\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ -x^2\left\{{\left({\mathit{\alpha }}_{1}a\right)}^2\left(\overline{\mathit{\lambda }}+2{cos}^2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)\right)\right\}{J}_n\left({\mathit{\alpha }}_{1}ax\right)cosn\mathit{\theta }\hfill \end{array}$$(A1) (A2) $$\begin{array}{c}{\overline{e}}_n^1=2\left\{n\left(n-1\right)J_n\left({\mathit{\alpha }}_{1}ax\right)+\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \\ -x^2\left\{{\left({\mathit{\alpha }}_{1}a\right)}^2\left(\overline{\mathit{\lambda }}+2{cos}^2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)\right)\right\}{J}_n\left(\mathit{\alpha }ax\right)sinn\mathit{\theta }\hfill \end{array}$$(A2) (A3) $$\begin{array}{c}{e^2}_n=2n\left\{\left(n-1\right)J_n\left({\mathit{\alpha }}_{2}ax\right)+\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ +2\left\{\left(n\left(n-1\right)-{\left({\mathit{\alpha }}_{2}ax\right)}^2\right)J_n\left({\mathit{\alpha }}_{2}ax\right)+\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \end{array}$$(A3) (A4) $$\begin{array}{c}{\overline{e}}_n^2=2n\left\{\left(n-1\right)J_n\left({\mathit{\alpha }}_{2}ax\right)+\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \\ -2\left\{\left(n\left(n-1\right)-{\left({\mathit{\alpha }}_{2}ax\right)}^2\right)J_n\left({\mathit{\alpha }}_{2}ax\right)+\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \end{array}$$(A4) (A5) $$e_n^3={\mathit{\xi }}^2\overline{\mathit{\rho }}{J^1}_n\left({\mathit{\alpha }}_{3}ax\right)cosn\mathit{\theta }$$(A5) (A6) $${\overline{e}}_n^3={\mathit{\xi }}^2\overline{\mathit{\rho }}{J^1}_n\left({\mathit{\alpha }}_{3}ax\right)sinn\mathit{\theta }$$(A6) (A7) $$\begin{array}{c}{f^1}_n=2\left\{n\left(n-1\right)-{\left({\mathit{\alpha }}_{1}ax\right)}^2{J}_n\left({\mathit{\alpha }}_{1}ax\right)+\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ +2n\left\{\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)-\left(n-1\right)J_n\left({\mathit{\alpha }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \end{array}$$(A7) (A8) $$\begin{array}{c}{\overline{f}}_n^1=2\left\{n\left(n-1\right)-{\left({\mathit{\alpha }}_{1}ax\right)}^2{J}_n\left({\mathit{\alpha }}_{1}ax\right)+\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \\ -2n\left\{\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)-\left(n-1\right)J_n\left({\mathit{\alpha }}_{1}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \end{array}$$(A8) (A9) $$\begin{array}{c}{f^3}_n=2n\left\{\left(n-1\right)J_n\left({\mathit{\alpha }}_{2}ax\right)-\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\hfill \\ +2\left\{\left(\mathit{\beta }ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)-\left(n\left(n-1\right)-{\left({\mathit{\alpha }}_{2}ax\right)}^2\right)J_n\left({\mathit{\alpha }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\hfill \end{array}$$(A9) (A10) $$\begin{array}{c}{\overline{f}}_n^3=2n\left\{\left(n-1\right)J_n\left({\mathit{\alpha }}_{2}ax\right)-\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)\right\}sin2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)sinn\mathit{\theta }\\ -2\left\{\left({\mathit{\alpha }}_{2}ax\right)J_{n+1}\left({\mathit{\alpha }}_{2}ax\right)-\left(n\left(n-1\right)-{\left({\mathit{\alpha }}_{2}ax\right)}^2\right)J_n\left({\mathit{\alpha }}_{2}ax\right)\right\}cos2\left(\mathit{\theta }-{\mathit{\gamma }}_l\right)cosn\mathit{\theta }\end{array}$$(A10) (A11) $${g^1}_n=\left\{n{J}_n\left({\mathit{\alpha }}_{1}ax\right)-\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}cosn\mathit{\theta }$$(A11) (A12) $${\overline{g}}_n^1=\left\{n{J}_n\left({\mathit{\alpha }}_{1}ax\right)-\left({\mathit{\alpha }}_{1}ax\right)J_{n+1}\left({\mathit{\alpha }}_{1}ax\right)\right\}sinn\mathit{\theta }$$(A12) (A13) $${g^2}_n=n{J}_n\left({\mathit{\alpha }}_{2}ax\right)cosn\mathit{\theta }$$(A13) (A14) $${\overline{g}}_n^2=n{J}_n\left({\mathit{\alpha }}_{2}ax\right)sinn\mathit{\theta }$$(A14) (A15) $${g^3}_n=-\left[n{J^1}_n\left({\mathit{\alpha }}_{3}ax\right)-\left({\mathit{\alpha }}_{3}ax\right){J^1}_{n+1}\left({\mathit{\alpha }}_{3}ax\right)\right]cosn\mathit{\theta }$$(A15) (A16) $${\overline{g}}_n^3=-\left[n{J^1}_n\left({\mathit{\alpha }}_{3}ax\right)-\left({\mathit{\alpha }}_{3}ax\right){J^1}_{n+1}\left({\mathit{\alpha }}_{3}ax\right)\right]sinn\mathit{\theta }$$(A16)