?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
In this paper, hybrid synchronization is investigated for n-scroll hyperchaotic Chua circuit using adaptive backstepping control. The theorem on hybrid synchronization for n-scroll hyperchaotic Chua circuit is established using Lyapunov stability theory. The backstepping scheme is recursive procedure that links the choice of Lyapunov function with the design of a controller and guarantees global stability performance of strict-feedback nonlinear systems. The backstepping control method is effective and convenient to hybrid synchronize the hyperchaotic systems which are mainly in this technique that gives the flexibility to construct a control law. Numerical simulations are also given to illustrate and validate the hybrid synchronization results derived in this paper.
Public Interest Statement
Chaos synchronization can be applied in the areas of physics, engineering and biological science. Synchronization has been widely explored in a variety of fields including physical chemical, and ecological systems, secure communications etc. Synchronization of chaotic systems is a phenomenon that may occur when two or more chaotic oscillators are coupled, or when a chaotic oscillator drives another chaotic oscillator. Because the butterfly effect which causes the exponential divergence of the trajectories of two identical chaotic systems started with nearly the same initial conditions, synchronizing two chaotic systems is seemingly a challenging problem. In most synchronization approaches, the master-slave or drive-response formalism is used. If a particular chaotic system is called the master or drive system and another chaotic system is called the slave or response system, then the idea of synchronization is to use the output of the master system to control the slave system so that the output of the response system tracks the output of the master system asymptotically.
1. Introduction
Synchronization in chaos refers to the tendency of two or more systems which are coupled together to undergo closely related motion, even when the motions are chaotic.
The synchronization for chaotic systems has been widespread to the scope (Alligood, Sauer, & Yorke, Citation1997; Fujisaka & Yamada, Citation1983; Pecora & Carroll, Citation1990), such as generalized synchronization (Harmov, Koronovskii, & Moskalenko, Citation2005a; Citationb; Wang & Zhu, Citation2006), anti-synchronization, phase synchronization (Ge & Chen, Citation2006; Tokuda, Kurths, Kiss, & Hudson, Citation2008; Zhao, Lai, Wang, & Gao, Citation2004), lag synchronization, projective synchronization (Qiang, Citation2007), and generalized projective synchronization (Jian-Ping & Chang-Pin, Citation2006; Li, Xu & Li, Citation2007).
The property of anti-synchronization establishes a predominating phenomenon in symmetrical oscillators, in which the state vectors have the same absolute values but opposite signs.
When synchronization and anti-synchronization coexist, simultaneously, in chaotic systems, then that synchronization is called hybrid synchronization.
A variety of schemes to ensure the control and synchronization of such systems have been demonstrated based on their potential applications in various fields including chaos generator design, secure communication (Chen, Citation1996; Kanter, Kopelowitz, Kestler, & Kinzel, Citation2008; Yang & Chua, Citation1999), physical systems (Chern & Otsuka, Citation2012; Lakshmanan & Murali, Citation1996; Moreno & Pacheco, Citation2004), chemical reaction (Coffman, McCormick, Noszticzius, & Simoyi, Citation1987; Han, Kerrer, & Kuramoto, Citation1995), ecological systems (Blasius & Huppert, Citation1999), information science (Bauer, Atay, & Jost, Citation2010; Ghosh, Banerjee, & Chowdhury, Citation2007; Kocarev & Parlitz, Citation1995), energy resource systems, ghostburster neurons (Wang, Chen & Deng, Citation2009), biaxial magnet models (Moukam Kakmeni, Nguenang, & Kofane, Citation2006), neuronal models (Che, Wang, Tsang, & Chen, Citation2010; Hindmarsh & Rose, Citation1984; Qi, Huang, Chen, Wang, & Shen, Citation2008), IR epidemic models with impulsive vaccination (Zeng, Sun, Li, & Sun, Citation2005), and predicting the influence of solar wind to celestial bodies (Junxa, Dianchen, & Tian, Citation2006; Suresh & Sundarapandian, Citation2012a).
So far a variety of impressive approaches have been proposed for the synchronization of the chaotic systems such as OGY method (Ott, Grebogi, & Yorke, Citation1990), sampled feedback synchronization method (Murali & Lakshmaman, Citation2003), time delay feedback method (Park & Kwon, Citation2003), adaptive design method (Lu, Wu & Han, Citation2004; Park, Citation2008; Park, Lee, & Kwon, Citation2007), sliding mode control method (Ya, Citation2004), active control method (Sundarapandian & Suresh, Citation2010). and backstepping control design (Suresh & Sundarapandian, Citation2012b; Wu & Lu, Citation2003; Yu & Zhang, Citation2006).
Recently, backstepping method has been developed and designed to control the chaotic systems. A common concept in the method is to synchronize the chaotic system. The backstepping method is based on the mathematical model of the examined system, introducing new variables into a form depending on the state variables, controlling parameters, and stabilizing functions. The difficult work of synchronizing the chaotic system is to remove nonlinearities which were done in the system and influencing the stability of state operation. The use of backstepping method creates an additional nonlinearity and eliminates undesirable nonlinearities from the system (Suresh & Sundarapandian, sundarhybrid12; Citation2013; Wang, Zhang, & Guo, Citation2010; Wang Citation2011a; Citationb).
The uncertainties are commonly in chaos synchronization and other control system problems. The uncertainties are one of the main factors in leading the adaptive-based synchronization. Adaptive control design is a direct aggregation of control methodology with some form of recursive system which identifies the system to determine the control of linear or nonlinear systems.
Adaptive control design is studied and analyzed in theory of unknown, but fixed parameter systems. The controller feedback gain could be depending on the system parameter.
2. Problem statement
Consider the chaotic system described by the dynamics(1)
(1)
where is the state of the system, in which the system (1) is considered as the master system; and
is the unknown parameter,
is the estimates as the parameter
.
The slave system is a chaotic system with the controller described by the dynamics
(2)
(2)
where is the input to the system with parameter estimator
, and
is the state of the slave system and
linear or nonlinear functions with input from systems (1) and (2).
If for all i, then the system (1) and (2) are called identical and otherwise they are nonidentical chaotic systems.
The hybrid synchronization error is defined as(3)
(3)
Then the synchronization error dynamics is obtained as(4)
(4)
The parameter estimation error is defined as
The hybrid synchronization problem basically requires the global asymptotically stability of the error dynamics (4), i.e.(5)
(5)
for all initial conditions
Backstepping design procedure is recursive and guarantee global stability performance of strict-feedback chaotic systems. By using the backstepping design, at the th step, the
th order subsystem is stabilized with respect to a Lyapunov function
by the virtual control
, and a control input function
Consider the global asymptotic stability of the system(6)
(6)
where is control input, which is the function of the error vector
and the state variables
As long as this feedback stabilizes, the system (6) will converge to zero as
, where
is regarded as a virtual controller.
For the design of is to stabilize the subsystem (6), the Lyapunov function is defined by
(7)
(7)
where are positive definite matrices.
The derivative of is
(8)
(8)
Suppose the derivative of is
(9)
(9)
where are positive definite matrices.
Then is a negative definite function.
Thus by Lyapunov stability theory, the error dynamics (6) is globally asymptotically stable.
The function is an estimative function when
is considered as a controller.
The error between and
is
(10)
(10)
Consider the subsystem given by
(11)
(11)
Let as a virtual controller in system (11).
Assume that when(12)
(12)
the system (11) is made globally asymptotically stable.
Consider the Lyapunov function defined by(13)
(13)
where are positive definite matrices.
Suppose the derivative of is
(14)
(14)
where are positive definite matrices.
Then is a negative definite function.
Thus by Lyapunov stability theory, the error dynamics (11) is globally asymptotically stable. The virtual controller and the state feedback input
make the system (11) asymptotically stable.
For the th state of the error dynamics, define the error variable
as
(15)
(15)
Considering the subsystem given by
(16)
(16)
Consider the Lyapunov function defined by(17)
(17)
where are positive definite matrices.
Suppose the derivative of is
(18)
(18)
where are positive definite matrices.
Then is a negative definite function on
Thus by Lyapunov stability theory (Hahn, Citation1967), the error dynamics (16) is globally asymptotically stable.
The virtual controller is(19)
(19)
and the state feedback input makes the system (11) globally asymptotically stable.
Hence, the state of master and slave systems are globally and asymptotically synchronized.
3. System description
Recently, theoretical design and hardware implementation of different kinds of chaotic oscillators have attracted increasing attention, aiming real-world applications of many chaos-based technologies and information systems.
The n-scroll hyperchaotic Chua circuit (Yu, Lu, & Chen, Citation2007) is given by the dynamics(20)
(20)
where is given by
(21)
(21)
The recursive positive switching points can be deduced as
(22)
(22)
and the values are obtained as
(23)
(23)
in which are the positive equilibrium points of
.
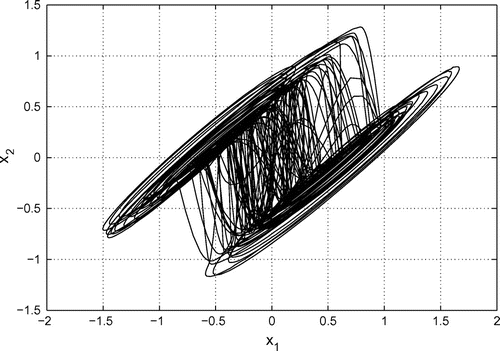
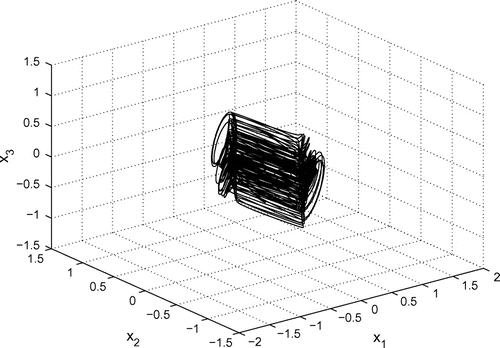
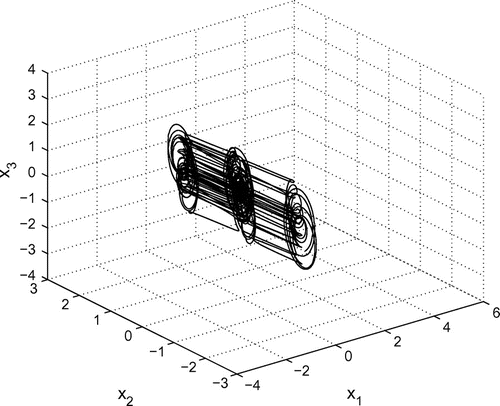
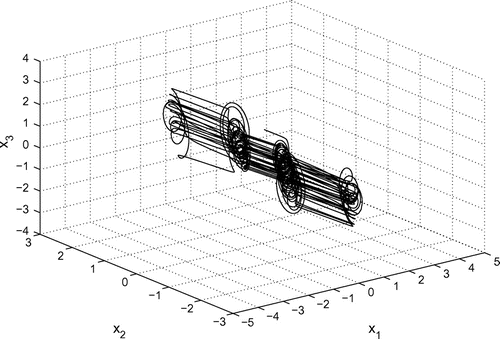
3.1. Case 1: 2-scroll hyperchaotic attractor
The parameters of the systems (20) are taken in the case of hyperchaotic case as
When , In Equation (20), the function
is given by
(24)
(24)
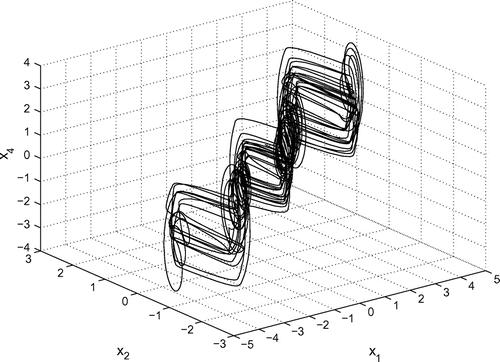
When the 2-scroll hyperchaotic attractor is generated. Figures – depict the 2-scroll hyperchaotic attractor.
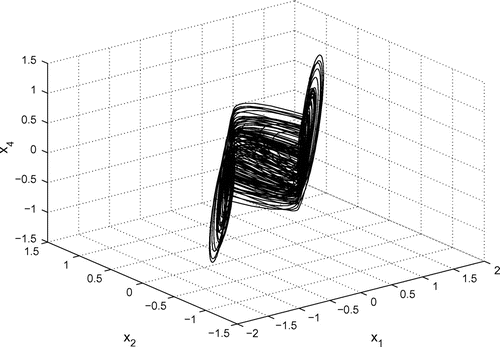
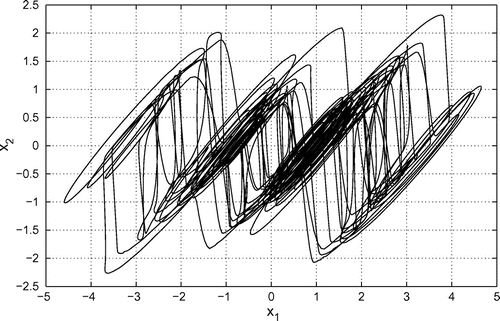
3.2. Case 2: 3-scroll hyperchaotic attractor
When , in Equation (20), the function
is given by
(25)
(25)
When the 3-scroll hyperchaotic attractor is generated. Figures – depict the 3-scroll hyperchaotic attractor.
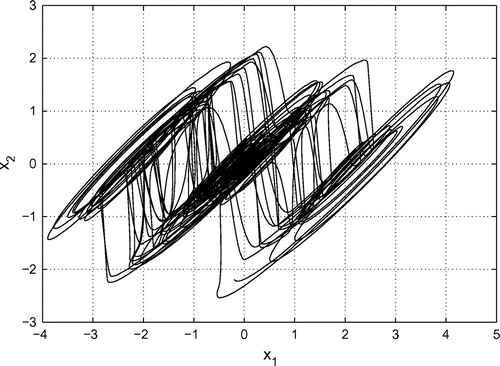
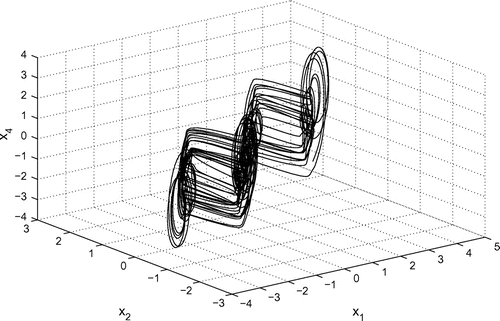
3.3. Case 3: 4-scroll hyperchaotic attractor
When , in Equation (20), the function
is given by
(26)
(26)
When the 4-scroll hyperchaotic attractor is generated.
Figures – depict the 4-scroll hyperchaotic attractor.
4. Hybrid Synchronization of n-scroll hyperchaotic Chua circuits via backstepping control with recursive feedback
In this section, the backstepping method with recursive feedback function is applied for the hybrid synchronization of identical hyperchaotic n-scroll Chua circuits (Yu et al., Citation2007).
The n-scroll hyperchaotic Chua circuit is taken as the master system, which is described by(27)
(27)
where is given by
(28)
(28)
where are state variables.
The n-scroll hyperchaotic Chua circuit is also taken as the slave system, which is described by(29)
(29)
where is given by
(30)
(30)
where are state variables.
The hybrid synchronization error is defined by(31)
(31)
The error dynamics is obtained as(32)
(32)
The modified error dynamics is defined by(33)
(33)
Now the objective is to find control law and for the parameter update law
for stabilizing the system (32) at the origin.
First consider the stability of the system(34)
(34)
where is regarded as virtual controller.
Consider the Lyapunov function defined by(35)
(35)
Let define the parameter estimation error as(36)
(36)
Differentiating the Equation (36)(37)
(37)
Differentiate along with the Equation (37)
(38)
(38)
Assume the controller .
If(39)
(39)
and the parameter update law is taken as
(40)
(40)
then(41)
(41)
which is a negative definite function. Hence, the system (34) is globally asymptotically stable.
The function is an estimative function when
is considered as a controller.
The error between and
is
(42)
(42)
Consider the subsystem given by
(43)
(43)
Let be a virtual controller in system (43).
Assume that when and the system (43) is made globally asymptotically stable.
Consider the Lyapunov function defined by(44)
(44)
Let us define the parameter estimation error as(45)
(45)
Differentiating the Equation (45), we get(46)
(46)
The derivative of is
(47)
(47)
Substituting for from (42) into (47) and simplifying, we get
(48)
(48)
Assume the virtual controller (49)
(49)
The parameter update law is
(50)
(50)
Then it follows that(51)
(51)
Thus, is a negative definite function and hence the system (43) is globally asymptotically stable.
Define the error variable and
as
(52)
(52)
Consider the subsystem given by
(53)
(53)
Let be a virtual controller in system (53).
Assume when it is equal to the system (53) is made globally asymptotically stable.
Consider the Lyapunov function defined by(54)
(54)
Let us define the parameter estimation error as(55)
(55)
The derivative of (55) is(56)
(56)
The derivative of is
(57)
(57)
i.e.(58)
(58)
Substituting for from (52) into (58) and simplifying, we get
(59)
(59)
Assume the virtual controller
choose(60)
(60)
The parameter update law is
(61)
(61)
Then it follows that(62)
(62)
Thus, is a negative definite function and hence the system (53) is globally asymptotically stable.
The error between and
is
(63)
(63)
Consider subsystem given by
(64)
(64)
Consider the Lyapunov function defined by(65)
(65)
Let define the parameter error as(66)
(66)
The derivative of is
(67)
(67)
The derivative of is
(68)
(68)
i.e.(69)
(69)
Choose the controller(70)
(70)
and the parameter update law is
(71)
(71)
Then(72)
(72)
Thus, is a negative definite function.
Thus, by Lyapunov stability theory (Hahn, Citation1967), the error dynamics (53) is globally asymptotically stable for all initial condition.
Thus, the states of master and slave systems are globally and asymptotically hybrid synchronized.
5. Theorem
The identical n-scroll hyperchaotic Chua’s circuit (27) and (29) are globally and asymptotically hybrid synchronized with the adaptive backstepping controls(73)
(73)
and with the parameter update laws(74)
(74)
6. Numerical simulation
For the numerical simulations, the fourth order Runge–Kutta method is used to solve the differential Equations (27) and (29) with the backstepping controls , and
given by (29).
6.1. Case 1: 2-scroll hyperchaotic attractor
The parameters of the systems (27) are taken in the case of hyperchaotic case as .
When the double scroll hyperchaotic attractor is generated.
The initial values of the master system (27) are chosen as and the initial values of the slave system (29) are chosen as
The initial values of the estimated parameters are
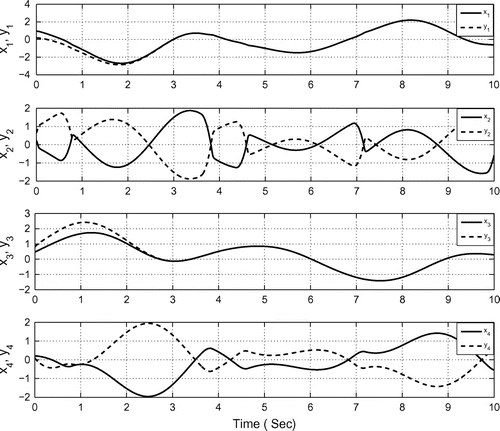
Figure depicts the hybrid synchronization of 2-scroll hyperchaotic Chua’s circuits (27) and (29).
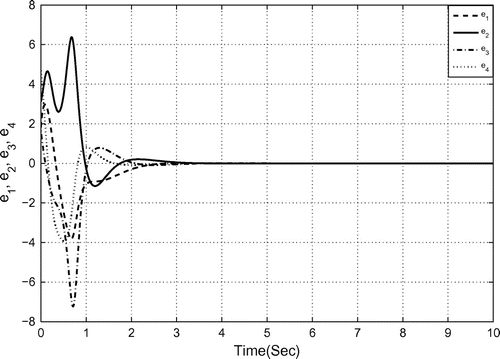
Figure 11. Hybrid synchronization error between 2-scroll hyperchaotic Chua’s circuits (27) and (29).
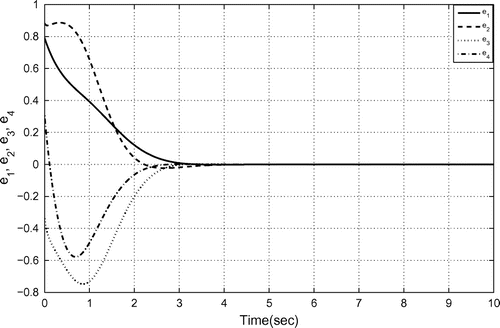
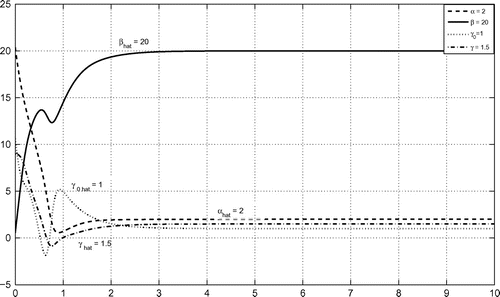
Figure 12. Parameter estimation of 2-scroll hyperchaotic Chua’s circuits (27) and (29). The estimated values of the parameters converge to system parameters
.
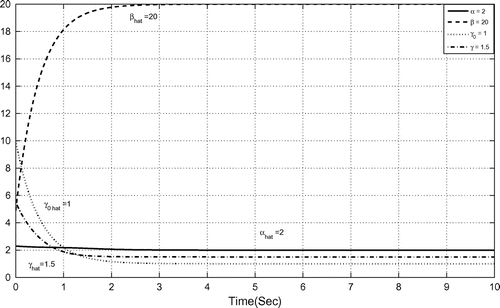
Figure depicts the hybrid synchronization error between 2-scroll hyperchaotic Chua’s circuits (27) and (29).
Figure depicts the parameter estimation of 2-scroll hyperchaotic Chua’s circuits (27) and (29).
The estimated values of the parameters converge to system parameters
6.2. Case 2: 3-scroll hyperchaotic attractor
When the 3-scroll hyperchaotic attractor is generated.
The initial values of the master system (27) are chosen as and the initial values of the slave system (29) are chosen as
The initial values of the estimated parameters are
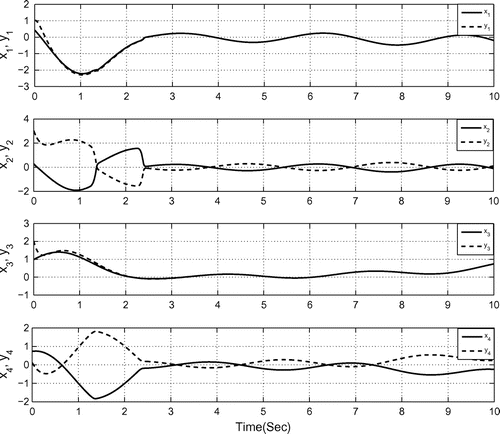
Figure depicts the hybrid synchronization of 3-scroll hyperchaotic Chua’s circuits (27) and (29).
Figure 14. Hybrid synchronization error between 3-scroll hyperchaotic Chua’s circuits (27) and (29).
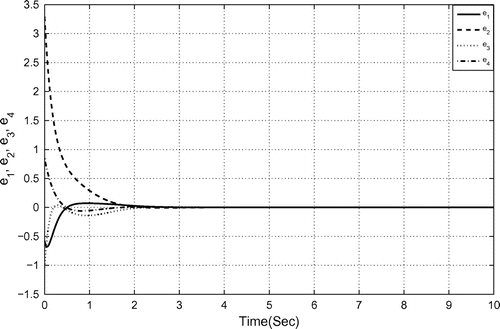
Figure 15. Parameter estimation of 3-scroll hyperchaotic Chua’s circuits (27) and (29). The estimated values of the parameters converge to system parameters
.
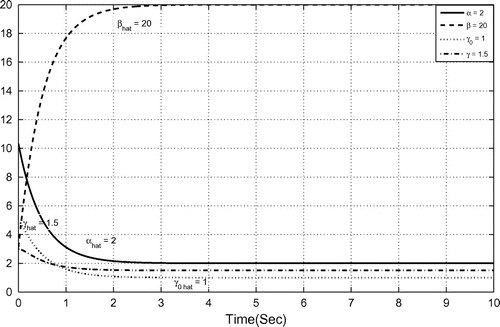
Figure depicts the hybrid synchronization error between 3-scroll hyperchaotic Chua’s circuits (27) and (29).
Figure depicts the parameter estimation of 3-scroll hyper chaotic Chua’s circuits (27) and (29).
The estimated values of the parameters converge to system parameters
6.3. Case 3: 4-scroll hyperchaotic attractor
When the 4-scroll hyperchaotic attractor is generated.
The initial values of the master system (27) are chosen as and the initial values of the slave system (29) are chosen as
The initial values of the estimated parameters are
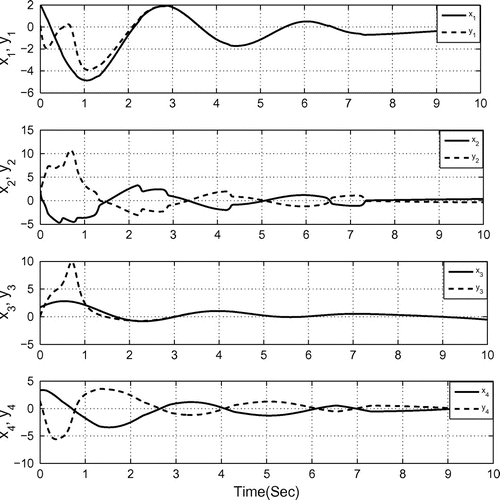
Figure depicts the hybrid synchronization of 4-scroll hyperchaotic Chua’s circuits (27) and (29).
Figure depicts the hybrid synchronization error between 4-scroll hyperchaotic Chua’s circuits (27) and (29).
Figure depicts the parameter estimation of 4-scroll hyperchaotic Chua’s circuits (27) and (29).
The estimated values of the parameters converge to system parameters
7. Conclusion
In this paper, the adaptive backstepping control method has been applied to achieve global chaos hybrid synchronization for a family of n-scroll hyperchaotic Chua circuits. The backstepping control is a systematic procedure for hybrid synchronizing hyperchaotic systems and there is no derivative in controller. The adaptive backstepping control design has been demonstrated to class of n-scroll hyperchaotic Chua circuits. Numerical simulations have been given to illustrate and validate the effectiveness of the proposed hybrid synchronization schemes of the chaotic circuit. The adaptive backstepping method is very effective and convenient to achieve global chaos hybrid synchronization.
Cover image
Source: Author.
Additional information
Funding
Notes on contributors
Suresh Rasappan
Suresh Rasappan obtained his PhD degree in Mathematics from Vel Tech Rangarajan Dr Sakunthala R & D Institute of Science and Technology, Chennai, Tamil Nadu, India in 2013, and MPhil degree in Mathematics from Bharathiar University, Coimbatore, Tamil Nadu, India in 2008. He is currently working as an associate professor in the Department of Mathematics, Vel Tech Dr RR & Dr SR Technical University, Chennai, India. He has published over 28 papers in international journals and book chapters. His research interest is differential equations.
References
- Alligood, K. T., Sauer, T., & Yorke, J. A. (1997). Chaos: An introduction to dynamical systems. Berlin: Springer-Verlag.
- Bauer, F., Atay, F. M., & Jost, J. (2010). Synchronized chaos in network of simple unit. Europhysics Letters, 89, 20002. doi:10.1209/0295-5075/89/20002
- Blasius, B., Huppert, A., & Stone, L. (1999). Complex dynamics and phase synchronization in spatially extended ecological system. Nature, 399, 354–359.
- Che, Y. Q., Wang, J., Tsang, K. M., & Chen, W. L. (2010). Unidirectional synchronization for Hindmarsh–Rose neurons via robust adaptive sliding mode control. Nonlinear Analysis: Real world Application, 11, 1096–1104.
- Chen, Y.-Y. (1996). Masking messages in chaos. Europhysics Letters, 34, 245–250.
- Coffman, K. G., McCormick, W. D., Noszticzius, Z., Simoyi, R. H., & Swinney, H. L. (1987). Universality, multiplicity and the effect of iron impurities in the Belousov–Zhabotinskii reaction. Journal of Chemical Physics, 86, 119–129.
- Fujisaka, H., & Yamada, T. (1983). Stability theory of synchronized motion in coupled-oscillator systems. Progress of Theoretical Physics, 69, 32–37.
- Ge, Z. M., & Chen, C. C. (2006). Projective synchronization of a new hyper chaotic Lorenz systems. Chaos, Solitons Fractals, 20, 639–647.
- Ghosh, D., Banerjee, S., & Chowdhury, A. R. (2007). Synchronization between variable time-delayed systems and cryptography. Europhysics Letters, 80, 30006. doi:10.1209/0295-5075/30006
- Hahn, W. (1967). The stability of motion. Berlin: Springer-Verlag.
- Han, S. K., Kerrer, C., & Kuramoto, Y. (1995). D-phasing and bursting in coupled neural oscillators. Physical Review Letters, 75, 3190–3193.
- Harmov, A. E., Koronovskii, A. A., & Moskalenko, O. I. (2005a). Generalized synchronization onset. Europhysics Letters, 72, 901–907.
- Harmov, A. E., Koronovskii, A. A., & Moskalenko, O. I. (2005b). Intermittent generalized synchronization in unidirectionally coupled chaotic oscillators. Europhysics Letters, 70, 169–174.
- Hindmarsh, J. L., & Rose, R. M. (1984). A model of neuronal bursting using 3-coupled First order differential equations. Proceedings of the Royal Society London B: Biological Sciences, 221, 81–102.
- Jian-Ping, Y., & Chang-Pin, L. (2006). Generalized projective synchronization for the chaotic Lorenz systems and the chaotic Chen system. Journal of Shanghai University, 10, 299–304.
- Kanter, I., Kopelowitz, E., Kestler, J., & Kinzel, W. (2008). Chaos synchronization with dynamics filter: Two-way is better than one way. Europhysics Letters, 83, 50005. doi:10.1009/0295-5075/50005
- Kocarev, L., & Parlitz, U. (1995). General approach for chaotic synchronization with application to communication. Physical Review Letters, 74, 5028–5030.
- Lakshmanan, M., & Murali, K. (1996). Chaos in nonlinear oscillators: Controlling and synchronization. Singapore: World Scientific.
- Li, R. H., Xu, W., & Li, S. (2007). Adaptive generalized projective synchronization in different chaotic systems based on parameter identifiction. Physics Letters A, 367, 119–206.
- Lih, J. S., Chern, J. L., & Otsuka, K. (2012). Joint time- frequency analysis of synchronized chaos. Europhysics Letters, 57, 810–816.
- Lu, J., Wu, X., & Han, X. (2004). Adaptive feedback synchronization of a unified chaotic system. Physics Letters A, 329, 327–333.
- Moreno, Y., & Pacheco, A. F. (2004). Synchronization of Kuramato oscillators in scale-free networks. Europhysics Letters, 68, 603–609.
- Moukam Kakmeni, F. M.; Nguenang, J. P., & Kofane, T. C. (2006). Chaos synchronization in bi-axial magnets modeled by bloch equation. Chaos, Solitons Fractals, 30, 690–699.
- Murali, K., & Lakshmaman, M. (2003). Secure communication using a compound signalmusing sampled-data feedback. Applied Mathematics and Mechanics, 11, 1309–1315.
- Ott, E., Grebogi, C., & Yorke, J. A. (1990). Controlling chaos. Physical Review Letters, 64, 1196–1199.
- Park, J. H. (2008). Adaptive control for modified projective synchronization of a four dimentional chaotic system with uncertain parameters. Journal of Computational and Applied Maths, 213, 288-293.
- Park, J. H., & Kwon, O. M. (2003). A novel criterion for delayed feedback control of time-delay chaotic systems. Chaos, Soliton Fractals, 17, 709–716.
- Park, J. H., Lee, S. M., & Kwon, O. M. (2007). Adaptive synchronization of Genesio-Tesi chaotic system. Physics Letters A, 371, 263–270.
- Pecora, L. M., & Carroll, T. L. (1990). Synchronization in chaotic systems. Physical Review Letters, 64, 821–824.
- Qi, G. X., Huang, H. B., Chen, L., Wang, H. J., & Shen, C. K. (2008). Fast synchronization in neuronal networks. Europhysics Letters, 83, 38003. doi:10.1209/0295-5075/82/38003
- Qiang, J. (2007). Phase synchronization of coupled chaotic multiple time scales systems. Physics Letters A, 370, 40–45.
- Sundarapandian, V., & Suresh, R. (2010). Global chaos synchronization for Rossler and Arneodo chaotic systems by nonlinear control. Far East Journal of Applied Mathematics, 44, 137–148.
- Suresh, R., & Sundarapandian, V. (2012a). Global chaos synchronization of WINDMI and Coullet chaotic systems by backstepping control. Far East Journal of Mathematical Sciences, 67, 265–287.
- Suresh, R., & Sundarapandian, V. (2012b). Hybrid synchronization of n-scroll Chua and Lur’e chaotic systems via backstepping control with novel feedback. Archives of Control Sciences, 22, 73–95.
- Suresh, R., & Sundarapandian, V. (2012c). Global chaos synchronization of hyperchaotic ChenLee system using backstepping contol via recursive feedback. In J.Mathew, P.Patra, D.K.Pradhan & A.J.Kuttyamma (Eds.), Lecture notes in computer science (Vol. 305, CCIS pp. 212). Berlin Heldelberg: Springer-Verlag.
- Suresh, R., & Sundarapandian, V. (2013). Global chaos synchronization of a family of n-scroll hyperchaotic Chua circuits using backstepping control with recursive feedback. Far East Journal of Mathematical Sciences, 73, 73–95.
- Tokuda, I. T., Kurths, J., Kiss, I. Z., & Hudson, J. L. (2008). Predicting phase synchronization of non-phase-coherent chaos. Europhysics Letters, 83.
- Wang, J., Chen, L., & Deng, B. (2009). Synchronization of ghostburster neurons in external electrical stimulation via H∞ variable universe fuzzy adaptive control. Chaos, Solitons Fractals, 39, 2076–2085.
- Wang, J., Dianchen, L., & Tian, L. (2006). Global synchronization for time delay WINDMI system. Chaos, Solitons and Fractals, 30, 629–635.
- Wang, Z., Zhang, W., & Guo, Y. (2010). Robust consensus for uncertain multi-agent systems on directed communication topologies. In IEEE International Conference on Decision and Control (p. 6317-6322). Atlanta, GA.
- Wang, Z., Zhang, W., & Guo, Y. (2011a). Adaptive output consensus tracking of a class of uncertain multi-agent systems. American Control Conference (pp. 3387–3392). San Francisco, CA.
- Wang, Z., Zhang, W., & Guo, Y. (2011b). Adaptive backstepping-based synchronization of networked uncertain Lagrangian systems. In American Control Conference (pp. 1057–1062). San Francisco, CA.
- Wang, Y. M., & Zhu, H. (2006). Generalized synchronization of continuous chaotic systems. Chaos Solitons Fractals, 27, 97–101.
- Wu, X., & Lu, J. (2003). Parameter identification and backstepping control of uncertain chaotic system. Chaos Soliton Fractals, 18, 721–729.
- Ya, H. T. (2004). Design of adaptive sliding mode controller for chaos synchronizationwith uncertainities. Chaos Soliton and Fractals, 22, 341–347.
- Yang, T., & Chua, L. O. (1999). Generalized synchronization of chaos via linear transformations. International Journal of Bifurcation Chaos, 9, 215–219.
- Yu, S., Lu, J., & Chen, G. (2007). A family of n-scroll hyperchaotic attractors and their realization. Physics Letters A, 364, 244–251.
- Yu, Y., & Zhang, S. C. (2006). Adaptive backstepping synchronization of uncertain chaotic systems. Chaos Soliton and Fractals, 27, 1369–1375.
- Zeng, G. Z., Chen, L. S., & Sun, L. H. (2005). Complexity of an SIR epidemic dynamics model with impulsive vaccination control. Chaos, Solitons and Fractals, 26, 495–505.
- Zhao, L., Lai, Y.-C., Wang, R., & Gao, J.-Y. (2004). Limits to chaotic phase synchronization. Europhysics Letters, 66, 324. doi:10.1209/epl/i2003-10220-2