Reliable terminal sliding mode control for uncertain high-order MIMO systems with actuator faults

Abstract

This paper considers the problem of terminal sliding mode control (TSMC) for uncertain MIMO systems in which the actuator faults may happen in any channel of actuators. By means of state transformation and exponent-logarithmic sliding surface method, a reliable TSMC is proposed such that both the finite-time stability of sliding mode dynamics and the reachability of sliding surface are ensured, despite actuator faults and parameter uncertainties. Finally, simulation results are provided to illustrate the effectiveness of the proposed controller.

Keywords:

• MIMO systems
• actuator faults
• terminal sliding mode control
• exponent-logarithmic terminal sliding mode

Public Interest Statement

Sliding mode control (SMC) is a useful and effective scheme to deal with parameter uncertainties and external disturbances for both linear and nonlinear systems. To tackle the problems of globally asymptotic stabilization, terminal sliding mode control scheme has been developed to achieve finite-time stabilization. It provides some superior properties such as fast, finite time convergence, and high static tracking precision.

In safety-critical systems, a minor fault of a single component can result in severe performance deterioration or may even produce catastrophic effects. To overcome this problem and realize finite time convergence, this paper introduces an exponent-logarithmic terminal sliding surface to improve the speed of response, and designs a reliable SMC approach to guarantee the stability of the overall closed-loop systems and finite time convergence of system states despite the presence of actuator faults.

1. Introduction

Sliding mode control (SMC) is a useful and effective scheme to deal with parameter uncertainties and external disturbances for both linear and nonlinear systems (Seshagiri & Khalil, 2002; Vicente & Gerd, 2001; Xu, Lee, & Pan, 2003). In general, the conventional sliding surface is the linear function of system states. Although the parameters in linear sliding surface can be adjusted to get faster convergence rate, the system states cannot usually reach the equilibrium points in finite time. To overcome this drawback, the terminal sliding mode control (TSMC) (Yu, Yu, & Man, 2000) was proposed and studied by many researchers, e.g. (Lin, 2006; Liu & Li, 2009; Tao, Taur, & Chan, 2004; Yu & Man, 2002; Zou, Kumar, Hou, & Liu, 2011) and the references therein.

Compared with the linear hyperplane-based SMC, TSMC provides some superior properties, such as fast, finite-time convergence, and high static tracking precision. For example, for second-order systems, a fast terminal sliding mode (FTSM) was proposed in Yu and Man (2002), which achieved better dynamic property by employing the FTSM concept in both reaching phase and sliding phase. In He, Liu, Liu, Liu, and Liu (2008), an exponential TSMC scheme was introduced into the learning algorithm to improve approximation ability for an unstable nonlinear system. Feng, Han, and Wang (2007) further considered the problem of high-order MIMO systems and proposed a hierarchical TSMC method. However, the TSMC method in Feng et al. (2007) only ensured that partial system states could be driven to zero in finite time and the rest converged to zero asymptotically. Wang, Yang, and Zhang (2007) then considered a new TSMC scheme which could drive all system states to equilibrium points in finite time, but its convergence performance was not so better compared to the one in second-order systems. Li, Ma, Zheng, and Geng (2014) presented a fast nonsingular integral TSMC which could avoid the singularity problem without any constraint, and provided faster responses by tuning the parameters. More recently, Hu, Jiang, Chen, and Liu (2014) developed an exponent-logarithmic terminal sliding surface for a special of SISO strict-feedback nonlinear systems, which could attain higher convergence performances. However, it is worthy of noting that the aforementioned works were made under the assumption that the actuator/sensor worked normally, i.e. there didn’t exist the faults of actuator/sensor.

As is well known, in safety-critical systems, a minor fault of a single component can result in severe performance deterioration or may even produce catastrophic effects. An effective way to maintain an acceptable stability/performance against undesired actuator/sensor failures is to utilize fault-tolerant control (FTC) strategies for the controlled systems (Bateman, Noura, & Ouladsine, 2011; Hu, 2010; Huo, Li, & Tong, 2012; Liu, Cao, & Shi, 2013). In the past decades, many reliable control methodologies have been applied, e.g. the coprime factorization approach (Vidyasagar & Viswanadham, 1985), the Hamilton–Jacobi based approach (Yang, Wang, & Soh, 2000), the linear matrix inequality based approach (Liao, Wang, & Yang, 2002), and so on. Moreover, the reliable SMC approach has been proposed (Chen, Niu, Zou, & Jia, 2013; Liang, Liaw, & Lee, 2000; Niu & Wang, 2009). Among them, Liang et al. (2000) first addressed the FTC design based on SMC, which did not require the solution of any Hamilton–Jacobi equation and could retain the advantages of conventional SMC designs Niu and Wang (2009) solved the problem of SMC with partial actuator degradation through adopting a model of actuator faults such that both normal operation and partial actuator degradation were covered. The results in Niu and Wang (2009) were further extended to the Markovian jumping systems in Chen et al. (2013). More recently, some interesting researches on FTC based on TSMC were made. For example, Xu and Liu (2014) studied the TSMC design based on the T–S fuzzy system models and presented both of the active and passive FTC schemes. Qu, Gao, Huang, Mei, and Zhai (2014) proposed a finite-time FTC scheme for the faulty UAV attitude control systems by utilizing a fault detection strategy, which ensured that the dynamic systems converge to a stable state in a finite-time in the case of actuator faulty. However, to the author’s best knowledge, the TSMC for high-order MIMO systems with actuator actuators has been not well addressed and remains still open. Moreover, the characteristic of TSMC structure also makes those existing works not to be simply extended to the present case.

Motivated by the above discussion, this paper considers the problem of TSMC for a class of uncertain high-order MIMO systems subject to actuator faults. Firstly, the model of actuator faults is presented, in which only the bounds of actuator faults are known. It should be pointed out that in the design of TSMC for uncertain high-order MIMO systems with actuator faults, one has to consider the realization of finite-time convergence for whole system states and the characteristic of actuator faults, which result in the aforementioned work that cannot be directly utilized in this paper. Hence, a state transformation is utilized and a high-order exponent-logarithmic sliding surface is designed, which can achieve the finite-time stability of sliding mode dynamics with shorter convergent time. And then, a reliable sliding mode controller is designed such that the system states can be driven onto the specified sliding surface in finite time. It is shown that the effect of actuator faults can be coped with by the present reliable TSMC method.

Notations: Throughout this work, || ⋅ ||denotes the Euclidean norm of a vector or the spectral of a matrix. ${\mathit{\lambda }}_{max}(·)$ denotes the maximum eigenvalue of a matrix. I represents an identity matrix of appropriate dimensions. ln ( ⋅ ) is a logarithmic function (base e). $\text{diag}(·)$ is a diagonal matrix. $\text{sgn}(·)$ is a sign function. Matrices, if not explicitly stated otherwise, are assumed to have compatible dimensions.

2. Problem statement

Consider a class of uncertain high-order MIMO systems(1) $$\dot{X}(t)=\left[A+\mathrm{\Delta }A(t)\right]X(t)+BU(t)+F(t)$$(1)

where X(t) ∊ Rⁿ are the system states, U(t) ∊ R^m are the control inputs, A and B are the known constant matrixes. Without loss of generality, it is assumed that the pair (A, B) is controllable and the matrix B has full column rank. ΔA(t) and F(t) represent the unknown parameter uncertainties and external disturbances, respectively, satisfying:

(2) $$\mathrm{\Delta }A(t)=B{N}_1(t),∥N_1(t)∥\le l_1$$(2)

(3) $$F(t)=B{N}_2(t),∥N_2(t)∥\le l_2$$(3)

where l₁and l₂ are known constants.

As discussed in the introduction, the actuator fault is usually inevitable in actual application. Hence, in this work, it is assumed that the actuator faults may happen and the control signal received by the system is U^F(t) satisfying:(4) $$U^F(t)=E(t)U(t)$$(4)

where $E(t)=\text{diag}[e_1(t),e_2(t),\dots ,e_m(t)]$ with faults factor $e_i(t)(i=1,2,\dots ,m)$ satisfying:(5) $$0<{\underline{e}}_i\le e_i(t)\le {\overline{e}}_i,{\underline{e}}_i\le 1,{\overline{e}}_i\ge 1i=1,2,\dots ,m$$(5)

In this work, it is assumed that both the lower and upper bounds of e_i(t) are known.

Define(6) $$e_{0i}=\frac{1}{2}({\underline{e}}_i+{\overline{e}}_i),r_i=\frac{{\overline{e}}_i+{\underline{e}}_i}{{\overline{e}}_i-{\underline{e}}_i},{\mathit{\delta }}_i(t)=\frac{e_i(t)-e_{0i}}{e_{0i}}$$(6)

and $E_0=\text{diag}[e_{01},e_{02},\dots ,e_{0m}]$, $R=\text{diag}[r_1,r_2,\dots ,r_m]$, $\mathit{\delta }(t)=\text{diag}[{\mathit{\delta }}_1(t),{\mathit{\delta }}_2(t),\dots ,{\mathit{\delta }}_m(t)]$. It is easily shown that $∥{\mathit{\delta }}_i(t)∥\le r_i<1\left(i=1,2,\dots ,m\right)$.

Then, the actuator faults model (4) can be written as:

(7) $$U^F(t)=E_0[I+\mathit{\delta }(t)]U(t),∥\mathit{\delta }(t)∥\le \Vert R\Vert <1$$(7)

Remark 1

It can be seen that the actuator faults model in (4)–(5) covers the normal operation case (as ${\underline{e}}_i=\overline{e}=1$) and partial faults case (as $0<{\underline{e}}_i<{\overline{e}}_i$), and each actuator may be a failure independently.

In the sequel, a lemma is given, which is useful for the development of the main results.

Lemma 1 (Yu, Yu, Shirinzadeh, & Man, 2005)

Assume that a continuous, positive-definite function V(t) satisfies the following differential inequality:(8) $$\dot{V}(t)\le -\mathit{\phi }{V}^{\mathit{\gamma }}(t)\forall t>0$$(8)

where $\mathit{\phi }>0,0<\mathit{\gamma }<1$ are constants. Then it can be found that V(t) which starts from V(0) can reach V = 0 in finite time. Moreover, the reaching time t_r is given by:(9) $$t_r=\frac{V^{1-\mathit{\gamma }}(0)}{\mathit{\phi }(1-\mathit{\gamma })}$$(9)

3. High-order exponent-logarithmic TSM design

3.1. State transformation

Firstly, a state transformation is made for the system model (1). Due to rank(B) = m, there exists an invertible matrix T satisfying $TB={\left[0B_2\right]}^T$, where B₂ ∊ R^m×m is full rank. Moreover, we have(10) $$\begin{array}{c}T(A+\mathrm{\Delta }A(t))T^{-1}=TA{T}^{-1}+TB{N}_1{T}^{-1}=\left[\begin{array}{cc}{A}_{11}\hfill & A_{12}\\ A_{21}\hfill & A_{22}\end{array}\right]+\left[\begin{array}{c}0\\ B_2{N}_1(t)T^{-1}\end{array}\right]\hfill \\ TF(t)=TB{N}_2(t)=\left[\begin{array}{c}0\\ B_2{N}_2(t)\end{array}\right]\hfill \end{array}$$(10)

where A₁₁ ∊ R^{(n−m)×(n−m)}, A₁₂ ∊ R^(n−m)×m,A₂₁ ∊ R^m×(n−m), A₁₁ ∊ R^{(n−m)×(n−m)}, A₂₂ ∊ R^m×m, B₂ ∊ R^m×m.

By means of the following state transformation:(11) $$Z(t)=TX(t)$$(11)

the system (1) can be transformed to the following form:(12b) $$\left\{\begin{array}{c}{\dot{Z}}_1(t)=A_{11}{Z}_1(t)+A_{12}{Z}_2(t)\text{(12a)}\hfill \\ {\dot{Z}}_2(t)=A_{21}{Z}_1(t)+A_{22}{Z}_2(t)+B_{2}U(t)+B_2{N}_1(t){\overline{T}}_1{Z}_1(t)+B_2{N}_1(t){\overline{T}}_2{Z}_2(t)+B_2{N}_2(t)\hfill \end{array}\right.$$(12b)

where Z₁(t) = [z₁, ⋯z_n−m]^T ∊ R^n−m, Z₂(t) = [z_n−m+1, ⋯z_n]^T ∊ R^m, $T^{-1}\stackrel{\mathrm{\Delta }}{=}[{\overline{T}}_1{\overline{T}}_2]$, ${\overline{T}}_1\in R^{n\times (n-m)}$, ${\overline{T}}_2\in R^{n\times m}$.

Note that Z(t) = TX(t), when Z(t) → 0, X(t) → 0. So the studied problem is equally transformed to the design of TSM surface and robust controller for system (12).

3.2. An exponent-logarithmic TSM

It is well known that the TSM has some superior properties, e.g. higher precision, faster convergence, etc. Hence, in this work, a new high-order exponent-logarithmic TSM is proposed as follows:

(13) $$S(t)=C_1{Z}_1(t)+C_2{Z}_2(t)+C_{3}G(t)+C_{4}H(t)=0$$(13)

where the vector functions G(t) and H(t) are given as:

(14) $$\left\{\begin{array}{c}G(t)={\left[(2e^{\left|z_1\right|}-1)ln(2-e^{-|z_1|})\text{sgn}(z_1),\dots ,(2e^{|z_{n-m}|}-1)ln(2-e^{-|z_{n-m}|})\text{sgn}(z_{n-m})\right]}^T\hfill \\ H(t)={\left[(2e^{|z_1|}-1){ln}^{q_1/p_1}(2-e^{-|z_1|})\text{sgn}(z_1),\dots ,(2e^{\left|z_{n-m}\right|}-1){ln}^{q_{n-m}/p_{n-m}}(2-e^{-|z_{n-m}|})\text{sgn}(z_{n-m})\right]}^T\hfill \end{array}\right.$$(14)

where $p_i,q_i,(i=1,\dots ,n-m)$ are positive odd integers satisfying q_i < p_i < 2q_i.

In (13), the matrices C₁ ∊ R^m×(n-m), C₂ ∊ R^m×m, C₃ ∊ R^m×(n-m) and C₄ ∊ R^m×(n-m) are chosen by the following expressions:(15) $$\left\{\begin{array}{c}{A}_{11}-A_{12}{C}_2^{-1}{C}_1=0\hfill \\ A_{12}{C}_2^{-1}{C}_3=\text{diag}({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_{n-m})\hfill \\ A_{12}{C}_2^{-1}{C}_4=\text{diag}({\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_{n-m})\hfill \end{array}\right.$$(15)

where α_i > 0, β_i > 0, (i = 1, …, n − m). The invertible matrix C₂ is usually chosen as an identity matrix for convenience. And then, the matrices C₁, C₃ and C₄ can be obtained as follows:

(16) $$\left\{\begin{array}{c}{C}_1=C_2{A}_{12}^{+}{A}_{11}\hfill \\ C_3=C_2{A}_{12}^{+}\text{diag}({\mathit{\alpha }}_1,\dots ,{\mathit{\alpha }}_{n-m})\hfill \\ C_4=C_2{A}_{12}^{+}\text{diag}({\mathit{\beta }}_1,\dots ,{\mathit{\beta }}_{n-m})\hfill \end{array}\right.$$(16)

where $A_{12}^{+}$ is the right inverse matrix of A₁₂ given as follows:

(17) $$A_{12}^{+}=A_{12}^T{(A_{12}^{}{A}_{12}^T)}^{-1}$$(17)

Apparently, the matrix A₁₂ should be full row rank for attaining (17).

According to the SMC theory, when the system states reach the sliding surface S = 0 and move along it, the sliding mode dynamics in S = 0 is a n−m order system. For S = 0, we obtain from (12a):

(18) $$Z_2=-C_2^{-1}(C_1{Z}_1+C_{3}G+C_{4}H)$$(18)

which substituted into system (12b) yields the reduced-order system as follows:(19) $${\dot{Z}}_1=(A_{11}-A_{12}{C}_2^{-1}{C}_1)Z_1-A_{12}{C}_2^{-1}{C}_{3}G-A_{12}{C}_2^{-1}{C}_{4}H$$(19)

In the following, we shall analyze the finite-time stability of sliding mode dynamics (19).

Theorem 1

Consider the uncertain high-order MIMO system (12). The exponent-logarithmic TSM is designed as (13) with the parameters satisfying (14 and 15). Then the sliding mode dynamics (19) on S = 0 is finite-time stable. That is, the state Z₁ of sliding mode dynamics will converge to the equilibrium points in finite time. Moreover, the states Z₂ will also converge to equilibrium points in finite time.

Proof

By means of the condition (15), it follows from (19) that(20) $${\dot{Z}}_1=\left[\begin{array}{c}-{\mathit{\alpha }}_1(2e^{|z_1|}-1)ln(2-e^{-|z_1|})\text{sgn}(z_1)-{\mathit{\beta }}_1(2e^{|z_1|}-1){ln}^{q_1/p_1}(2-e^{-|z_1|})\text{sgn}(z_1)\\ ⋮\\ -{\mathit{\alpha }}_{n-m}(2e^{\left|z_{n-m}\right|}-1)ln(2-e^{-\left|z_{n-m}\right|})\text{sgn}(z_{n-m})-{\mathit{\beta }}_{n-m}(2e^{\left|z_{n-m}\right|}-1){ln}^{q_{n-m}/p_{n-m}}(2-e^{-\left|z_{n-m}\right|})\text{sgn}(z_{n-m})\end{array}\right]$$(20)

which shows that all elements of Z₁ is independent. Thus, we can analyze every state variables $z_i(i=1,2,\dots ,n-m)$, respectively. To this end, choose the candidate Lyapunov function V₁ as follows(21) $$V_1=\frac{1}{2}{z}_i^2$$(21)

We have$${\dot{V}}_1=z_i{\dot{z}}_i=-{\mathit{\alpha }}_i(2e^{\left|z_i\right|}-1)ln(2-e^{-\left|z_i\right|})\left|z_i\right|-{\mathit{\beta }}_i(2e^{\left|z_i\right|}-1){ln}^{q_i/p_i}(2-e^{-\left|z_i\right|})\left|z_i\right|\le 0$$

which means that the state z_i is stable.

In the following, we shall analyze the finite-time convergence performance of state z_i. Firstly, it follows from the ith term in (20) that(22) $$-{\mathit{\beta }}_i=f{(z_i)}^{-q_i/p_i}\frac{\text{d}f(z_i)}{\text{d}t}+{\mathit{\alpha }}_{i}f{(z_i)}^{1-q_i/p_i}$$(22)

where $f(z_i)=ln(2-e^{-|z_i|})\text{sgn}(z_i)$. Define $y=f{(z_i)}^{1-q/p}$. We have:(23) $$\frac{\text{d}y}{\text{d}t}=(1-q_i/p_i)f{(z_i)}^{-q_i/p_i}\frac{\text{d}f(z_i)}{\text{d}t}$$(23)

And then, from (22) to (23), we can get:(24) $$-{\mathit{\beta }}_i\frac{p_i-q_i}{p_i}=\frac{\text{d}y}{\text{d}t}+{\mathit{\alpha }}_i\frac{p_i-q_i}{p_i}y$$(24)

By solving first-order linear differential equation (24), one obtains:(25) $$y=-\frac{{\mathit{\beta }}_i}{{\mathit{\alpha }}_i}+\frac{{\mathit{\beta }}_i}{{\mathit{\alpha }}_i}{e}^{-\frac{p_i-q_i}{p_i}{\mathit{\alpha }}_{i}t}+y(t_r)e^{-\frac{p_i-q_i}{p_i}{\mathit{\alpha }}_{i}t}$$(25)

where t_r denotes the instant when the system states arrive at the sliding surface S(t)=0 from any initial state. Define t_si as the instant when the state z_i converges to equilibrium point 0. Due to $f(z_i,t_{si})=0$ and $y(t_{si})=0$, we have from (25):(26) $$t_{si}=\frac{p_i}{{\mathit{\alpha }}_i(p_i-q_i)}ln\frac{{\mathit{\alpha }}_i{[ln(2-e^{-\left|z_i(t_r)\right|})\text{sgn}(z_i(t_r))]}^{(p_i-q_i)/p_i}+{\mathit{\beta }}_i}{{\mathit{\beta }}_i}$$(26)

From the above analysis, the state Z₁ is finite-time stable. That is, the state Z₁ of sliding mode dynamics will converge to the equilibrium points within a finite time $t_s=\underset{1\le i\le n-m}{max}(t_{si})$.

Furthermore, it is seen from (14) and (18) that the state vector Z₂ is fully determined by Z₁. Hence, when the states Z₁ reach equilibrium points in finite-time, the states Z₂ will also converge to equilibrium points in finite time.□

3.3. Reliable TSMC design

In the sequel, we shall design a reliable sliding mode controller U(t) to guarantee that the system states from any initial states Z(0) ≠ 0 are driven onto the sliding mode surface S = 0 in finite time.

In this work, the reliable SMC law is designed as:(27) $$U(t)=\left\{\begin{array}{cc}{U}_l+U_m,\hfill & S\ne 0\\ 0,\hfill & S=0\end{array}\right.$$(27)

with(28) $$\left\{\begin{array}{c}{U}_l=-{(C_2{B}_2{E}_0)}^{-1}[(C_1{A}_{11}+C_2{A}_{21}+C_3\tilde{G}{A}_{11}+C_4\tilde{H}{A}_{11})Z_1+(C_1{A}_{12}+C_2{A}_{22}+C_3\tilde{G}{A}_{12}+C_4\tilde{H}{A}_{12})Z_2]\hfill \\ U_m=-\frac{{(C_2{B}_2{E}_0)}^{T}S}{(1-{\mathit{\lambda }}_{max}(R))∥S^T{C}_2{B}_2{E}_0∥}[l_1∥E_0∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0∥∥{\overline{T}}_2∥∥Z_2∥+{\mathit{\lambda }}_{max}(R)∥U_l∥+l_2∥E_0∥+\mathit{\eta }]\hfill \end{array}\right.$$(28)

where η > 0 is a positive constant, $\tilde{G}=\text{diag}({\tilde{g}}_1,\dots ,{\tilde{g}}_{n-m})$ and $\tilde{H}=\text{diag}({\tilde{h}}_1,\dots ,{\tilde{h}}_{n-m})$ with(29) $$\left\{\begin{array}{c}{\tilde{g}}_i=\left[2e^{\left|z_i\right|}ln(2-e^{-\left|z_i\right|})+1\right]\text{sgn}(z_i),i=1,\dots ,n-m\hfill \\ {\tilde{h}}_i=\left[2e^{\left|z_i\right|}{ln}^{q_i/p_i}(2-e^{-\left|z_i\right|})+\frac{q_i}{p_i}{ln}^{q_i/p_i-1}(2-e^{-\left|z_i\right|})\right]\text{sgn}(z_i),i=1,\dots ,n-m\hfill \end{array}\right.$$(29)

Remark 2

The TSMC law (28 and 30) includes the matrix E₀ and the scalar ${\mathit{\lambda }}_{max}(R)$, which depend on ${\overline{e}}_i$ and ${\underline{e}}_i$, reflecting the effect of the faulty actuator. Hence, the present TSMC method can effectively deal with the effect of actuator faults.

Theorem 2

Consider the uncertain high-order MIMO system described by (12) with actuator faults as in (7). The reliable SMC law (28 and 29) can ensure that the system states are driven onto the sliding surface S = 0 in finite time.

Proof

Consider the following Lyapunov function candidate V₂:(30) $$V_2=\frac{1}{2}{S}^{T}S$$(30)

Taking the time derivative of V₂ yields:(31) $$\begin{array}{c}{\dot{V}}_2=S^T\dot{S}=S^T(C_1{\dot{Z}}_1+C_2{\dot{Z}}_2+C_3\tilde{G}{\dot{Z}}_1+C_4\tilde{H}{\dot{Z}}_1)\hfill \\ =S^T[C_1{A}_{11}{Z}_1+C_1{A}_{12}{Z}_2+C_2{A}_{21}{Z}_1+C_2{A}_{22}{Z}_2+C_2{B}_2{U}^F+C_2{B}_2{N}_1{\overline{T}}_1{Z}_1+C_2{B}_2{N}_1{\overline{T}}_2{Z}_2+C_2{B}_2{N}_2+C_3\tilde{G}{A}_{11}{Z}_1+C_3\tilde{G}{A}_{12}{Z}_2+C_4\tilde{H}{A}_{11}{Z}_1+C_4\tilde{H}{A}_{12}{Z}_2]\hfill \\ =S^T[(C_1{A}_{11}+C_2{A}_{21}+C_3\tilde{G}{A}_{11}+C_4\tilde{H}{A}_{11})Z_1+(C_1{A}_{12}+C_2{A}_{22}+C_3\tilde{G}{A}_{12}+C_4\tilde{H}{A}_{12})Z_2+C_2{B}_2{E}_{0}U+C_2{B}_2{E}_0\mathit{\delta }U+C_2{B}_2{N}_1{\overline{T}}_1{Z}_1+C_2{B}_2{N}_1{\overline{T}}_2{Z}_2+C_2{B}_2{N}_2]\hfill \end{array}$$(31)

By substituting the control law (28 and 29) into (31), one has:(32) $$\begin{array}{c}{\dot{V}}_2=S^T{C}_2{B}_2[E_0{U}_m+E_0\mathit{\delta }(U_l+U_m)+N_1{\overline{T}}_1{Z}_1+N_1{\overline{T}}_2{Z}_2+N_2]\hfill \\ =S^T{C}_2{B}_2{E}_0{U}_m+S^T{C}_2{B}_2{E}_0\mathit{\delta }{U}_m+S^T{C}_2{B}_2{E}_0[\mathit{\delta }{U}_l+E_0^{-1}{N}_1{\overline{T}}_1{Z}_1+E_0^{-1}{N}_1{\overline{T}}_2{Z}_2+E_0^{-1}{N}_2]\hfill \\ \le S^T{C}_2{B}_2{E}_0{U}_m+S^T{C}_2{B}_2{E}_0\mathit{\delta }{U}_m+∥S^T{C}_2{B}_2{E}_0∥[∥\mathit{\delta }∥∥U_l∥+l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥{\overline{T}}_2∥Z_2∥+l_2∥E_0^{-1}∥]\hfill \\ \le S^T{C}_2{B}_2{E}_0{U}_m+S^T{C}_2{B}_2{E}_0\mathit{\delta }{U}_m\hfill \\ +∥S^T{C}_2{B}_2{E}_0∥[∥{\mathit{\lambda }}_{max}(R)∥∥U_l∥+l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+l_2∥E_0^{-1}∥]\hfill \end{array}$$(32)

By means of U_m in (28), we further get:(33) $$\begin{array}{c}{\dot{V}}_2\le -∥S^T{C}_2{B}_2{E}_0∥\frac{1}{1-{\mathit{\lambda }}_{\text{max}}(R)}\hfill \\ \times [l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+∥{\mathit{\lambda }}_{\text{max}}(R)∥∥U_l∥+l_2∥E_0^{-1}∥+\mathit{\eta }]\hfill \\ +\frac{∥S^T{C}_2{B}_2{E}_0\mathit{\delta }{(C_2{B}_2{E}_0)}^{T}S∥}{∥S^T{C}_2{B}_2{E}_0∥}\frac{1}{1-{\mathit{\lambda }}_{\text{max}}(R)}\hfill \\ \times [l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥\overline{T}∥∥Z_2∥+∥{\mathit{\lambda }}_{\text{max}}(R)∥∥U_l∥+l_2∥E_0^{-1}∥+\mathit{\eta }]\hfill \\ +∥S^T{C}_2{B}_2{E}_0∥[∥{\mathit{\lambda }}_{\text{max}}(R)∥∥U_l∥+l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+l_2∥E_0^{-1}∥]\hfill \end{array}$$(33)

Note(34) $$∥S^T{C}_2{B}_2{E}_0\mathit{\delta }{(C_2{B}_2{E}_0)}^{T}S∥\le ∥{\mathit{\lambda }}_{max}(\mathit{\delta })∥∥S^T{C}_2{B}_2{E}_0{(C_2{B}_2{E}_0)}^{T}S∥\le {\mathit{\lambda }}_{max}(R)∥S^T{C}_2{B}_2{E}_0{(C_2{B}_2{E}_0)}^{T}S∥$$(34)

So, we have$$\begin{array}{c}{\dot{V}}_2\le -∥S^T{C}_2{B}_2{E}_0∥\frac{1}{1-{\mathit{\lambda }}_{max}(R)}\hfill \\ \times [l_1∥E_0^{-1}∥∥T_1^{-1}∥∥Z_1∥+l_1∥E_0^{-1}∥∥T_2^{-1}∥∥Z_2∥+∥{\mathit{\lambda }}_{max}(R)∥∥U_l∥+l_2∥E_0^{-1}∥+\mathit{\eta }]\hfill \\ +{\mathit{\lambda }}_{max}(R)∥S^T{C}_2{B}_2{E}_0∥\frac{1}{1-{\mathit{\lambda }}_{max}(R)}\hfill \\ \times [l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+∥{\mathit{\lambda }}_{max}(R)∥∥U_l∥+l_2∥E_0^{-1}∥+\mathit{\eta }]\hfill \\ +∥S^T{C}_2{B}_2{E}_0∥[∥{\mathit{\lambda }}_{max}(R)∥∥U_l∥+l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+l_2∥E_0^{-1}∥]\hfill \end{array}$$(35) $$\begin{array}{c}=-∥S^T{C}_2{B}_2{E}_0∥[l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+∥{\mathit{\lambda }}_{max}(R)∥∥U_l∥+l_2∥E_0^{-1}∥+\mathit{\eta }]\hfill \\ +∥S^T{C}_2{B}_2{E}_0∥[∥{\mathit{\lambda }}_{max}(R)∥∥U_l∥+l_1∥E_0^{-1}∥∥{\overline{T}}_1∥∥Z_1∥+l_1∥E_0^{-1}∥∥{\overline{T}}_2∥∥Z_2∥+l_2∥E_0^{-1}∥]\hfill \\ =-\mathit{\eta }∥S^T{C}_2{B}_2{E}_0∥\hfill \end{array}$$(35)

Furthermore, the expression (35) can be written as:(36) $${\dot{V}}_2\le -\mathit{\eta }∥S^T{C}_2{B}_2{E}_0∥\le -\mathit{\eta }∥C_2{B}_2{E}_0∥∥S∥=-\mathit{\eta }∥C_2{B}_2{E}_0∥{(2V)}^{1/2}=-\mathit{\phi }{V}^{\mathit{\gamma }}$$(36)

with $\mathit{\phi }=2^{1/2}\mathit{\eta }∥C_2{B}_2{E}_0∥>0$, γ = 1/2 < 1.

Thus, according to Lemma 1, it follows from (36) that the system (12) will reach the sliding mode S = 0 within a finite time t_r given by:

(39) $$t_r=\frac{V^{1-\mathit{\gamma }}(0)}{\mathit{\phi }(1-\mathit{\gamma })}$$(39)

□.

Remark 3

It is easily obtained from Theorem 1 and Theorem 2 that the system state Z₁(t) and Z₂(t) reach the equilibrium points in finite time t = t_s + t_r from any initial states. That implies that the system states X(t) will converge to the equilibrium points within finite time.

Remark 4

It can be seen from (13 to 15) and (27 to 29) that the proposed SMC method in this work involves some exponent and logarithmic computations. Besides, the state transformation (10) and the right inverse matrix (17) are required. Apparently, these computations don’t require any complex computing techniques and are simpler compared with some existing methods, e.g. linear matrix inequality.

Remark 5

It should be pointed out that the transformation matrix T needs to ensure that the block matrix A₁₂ is full row rank, which may bring some difficulty for the choice of matrix T.

Remark 6

It should be pointed out that although both this work and Wang (2014) are concerned with the uncertain MIMO-controlled systems, the former focuses on the problem of system states’ finite-time convergence with actuator faults, and the latter considered the adaptive tracking control problem under the assumption that the actuators work normally. This also results in the method in Wang (2014) that cannot be utilized to deal with the problem in the present work.

4. Simulation example

Consider the high-order MIMO system (1) with parameters as$$A=\left[\begin{array}{cccc}0\hfill & 0\hfill & 0& 1\\ 5\hfill & -5\hfill & -4& 1\\ -1\hfill & 1\hfill & 0& 0\\ -4\hfill & 0\hfill & 0& -5\end{array}\right],B=\left[\begin{array}{cc}0\hfill & 0\\ 4\hfill & 0\\ 0\hfill & 0\\ 0\hfill & 3\end{array}\right],F=\left[\begin{array}{c}0\hfill \\ 4.8sint\hfill \\ 0\hfill \\ 3.6cost\hfill \end{array}\right]$$$$\mathrm{\Delta }A=\left[\begin{array}{cccc}0\hfill & 0\hfill & 0& 0\\ 0.8sint\hfill & 1.6cost\hfill & 4sin2t& 1.6cos\frac{t}{2}\\ 0\hfill & 0\hfill & 0& 0\\ 1.2sint\hfill & 1.8cos2t\hfill & 0.6sint& 0.6cos\frac{t}{2}\end{array}\right]$$

And the boundaries of uncertainties and disturbances are given as $l_1=\sqrt{1.96}$ and $l_2=\sqrt{2.88}$. It is assumed that the actuator fault parameters ${\underline{e}}_1=0.8$, ${\overline{e}}_1=1.2$, ${\underline{e}}_2=0.6$, ${\overline{e}}_2=1.4$.

Define the state transformation as:$$Z=TX=\left[\begin{array}{cccc}0\hfill & 0\hfill & 1& 0\\ 1\hfill & 0\hfill & 0& 0\\ -1\hfill & 1\hfill & 0& 0\\ 0\hfill & 0\hfill & 0& 1\end{array}\right]X$$

we have

$A_{11}=\left[\begin{array}{cc}0\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right]$, $A_{12}=\left[\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right]$, $A_{21}=\left[\begin{array}{cc}-4\hfill & 0\hfill \\ 0\hfill & -4\hfill \end{array}\right]$, $A_{22}=\left[\begin{array}{cc}-5\hfill & 0\hfill \\ 0\hfill & -5\hfill \end{array}\right]$, $B_2=\left[\begin{array}{cc}4\hfill & 0\hfill \\ 0\hfill & 3\hfill \end{array}\right]$, ${\overline{T}}_1=\left[\begin{array}{cc}0\hfill & 1\\ 0\hfill & 1\\ 1\hfill & 0\\ 0\hfill & 0\end{array}\right]$, ${\overline{T}}_2=\left[\begin{array}{cc}0\hfill & 0\\ 1\hfill & 0\\ 0\hfill & 0\\ 0\hfill & 1\end{array}\right]$, $N_1=\left[\begin{array}{cccc}0.2sint\hfill & 0.4cost& sin2t& 0.4cos\frac{t}{2}\\ 0.4sint\hfill & 0.6cos2t& 0.2sint& 0.2cos\frac{t}{2}\end{array}\right]$, $N_2=\left[\begin{array}{c}1.2sint\hfill \\ 1.2cost\hfill \end{array}\right]$.

According to Theorem 1, the terminal sliding mode parameters are designed as follows:

$C_1=\left[\begin{array}{cc}0\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right]$, $C_2=\left[\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right]$, $C_3=\left[\begin{array}{cc}2\hfill & 0\hfill \\ 0\hfill & 2\hfill \end{array}\right]$, $C_4=\left[\begin{array}{cc}2\hfill & 0\hfill \\ 0\hfill & 2\hfill \end{array}\right]$, p₁ = p₂ = 11, q₁ = q₂ = 9.

In order to illustrate the performance of the proposed reliable SMC in this work, it is assumed that the actuator faults happen from 0.3 s with fault factors $e_1(t)=0.9$ and $e_2(t)=0.8$.

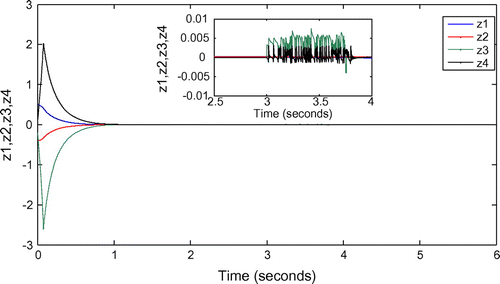
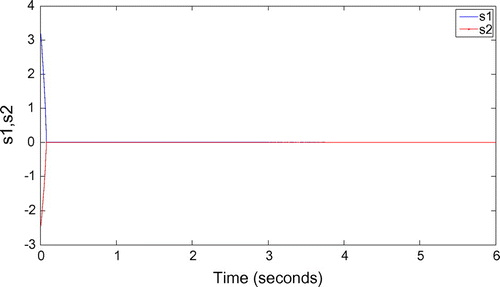
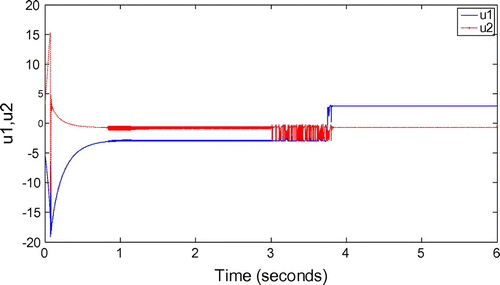
Simulation results are shown in Figures 1^{Figure 2}–3. It can be seen from Figure 1 that from 0 to 3 s (as actuator in fault free case), system states converge to the equilibrium points within finite time; after 3 s (as actuator in fault case), system states have a large-range change firstly, and then converge to the equilibrium points in finite time under the designed robust control.

Figure 1. The trajectories of system states z₁, z₂, z₃, z₄.

Figure 2. The trajectories of sliding variables s₁, s₂.

Figure 3. The control signals u₁, u₂.

5. Conclusion

In this work, the problem of TSMC for uncertain high-order MIMO systems subject to actuator faults has been considered. By means of exponent-logarithmic TSM technique, a reliable SMC law has been designed to attain the finite-time convergence of the closed-loop system, despite actuator faults. However, it should be pointed out that the underlying systems in this work only involve actuator faults. In practical applications, especially, in the network-based environment, there may exist time delay, packet dropouts, and quantization, which need to be further considered in future research, and some novel techniques may be required as in (Dong, Wang, Ding, & Gao, 2014, 2015; Dong, Wang, & Gao, 2013; Ding, Wang, Shen, & Dong, 2015).

Additional information

Funding

This work was supported by NNSF from China [grant number 61273073].

Notes on contributors

Jiaye Fu

Miss Jiaye Fu received the BE degree in electrical engineering and automation form East China University of Science and Technology , Shanghai, China, in 2013. From 2013, she has been pursuing her Master degree in control science and engineering in East China University of Science and Technology, Shanghai, China. Her research interests include sliding mode control, terminal sliding mode control, fault-tolerant control and their applications.