A comparative study of the Bees Algorithm as a tool for function optimisation

Abstract

The Bees Algorithm is a parameter optimisation method that mimics the foraging behaviour of honey bees. This paper presents an experimental study of the performance of the Bees Algorithm. Its strengths and weaknesses are analysed, and the most suitable parameterizations in relation to different optimisation tasks are revealed. The robustness of the optimisation results to reasonable modifications of the fitness landscape is studied for a large set of parameterizations. The Bees Algorithm is tested on 18 custom-made function minimisation benchmarks, and its performance compared to that of two state-of-the-art biologically inspired optimisation methods. Thanks to their two-dimensional nature, the proposed fitness landscapes are easy to visualise. Experimental evidence indicates also that they constitute a varied and challenging set of test cases, useful to reveal the specific abilities and biases of the search algorithms. In addition, the performance of the Bees Algorithm and the other two optimisation methods is tested on four real-world minimisation tasks from the literature. The results obtained on the benchmarks prove the effectiveness and robustness of the bees foraging metaphor, in particular on the most deceptive and high-dimensional fitness landscapes. They also confirm the ability of the Bees Algorithm to solve complex real-world optimisation tasks.

Keywords:

• optimisation
• Bees Algorithm
• swarm intelligence
• evolutionary algorithms
• optimisation benchmarks
• variable neighbourhood search

Public Interest Statement

This paper analyses the performance of the Bees Algorithm, a popular biologically inspired optimisation method. The Bees Algorithm is inspired by the foraging behaviour of honey bees, and can be used to solve a wide range of optimisation problems. The performance of the Bees Algorithm is based on a number of system parameters. This paper proves the effectiveness and efficiency of the Bees Algorithm, and its robustness to variations of the system parameters and optimisation landscape.

1. Introduction

Technological and scientific advances, and the globalisation of social and economic networks, produced increasingly large and complex systems. Optimisation, modelling and control of these systems often involve the tuning of several system parameters, in order to maximise the quality of products, reduce manufacturing times, reduce manufacturing costs, improve the reliability and accuracy of processes, increase the efficiency of logistic and telecommunication networks, and so forth. Classical system optimisation methods are based on the identification of the relationship between the variables and the desired quality measure. Unfortunately, due to the intrinsic complexity and non-linearity of real-world systems, such relationship is difficult to obtain. The identification task is often complicated by discontinuities and constraints on both state and input variables.

Swarm Intelligence (SI) (Bonabeau, Dorigo, & Theraulaz, 1999) includes many model-free innovative metaheuristics based on nature-inspired decentralised search processes, such as Ant Colony Optimisation (ACO) (Dorigo, Maniezzo, & Colorni, 1996), Particle Swarm Optimisation (PSO) (Kennedy & Eberhart, 1995), the Bees Algorithm (Pham et al., 2006), the Firefly algorithm (Yang & He, 2013), etc.

Wolpert and Macready (1997) proved that, on the whole set of all possible problems, all optimisation algorithms perform equally (No Free Lunch Theorem). Yet, on arbitrary subsets of problems, distinct procedures perform differently. That is, the success of a search approach on a given task depends on how well its operators and parameters match the features of the search space. Unfortunately, the amount of knowledge about the nature of the fitness landscape is often scarce of null. As a consequence, the choice and design of optimisation methods entail time-consuming trial and error.

In the design of an optimisation procedure, a deep understanding of the specific capabilities of the various approaches is of great help. Any known feature of the fitness landscape may already point to suitable choices of procedures, operators and configurations. Conversely, by trying a few algorithms or configurations, the designer may get important clues on the nature of the search space. Finally, understanding of the role and robustness of different parameters and operators might narrow down the design task to a restricted set of crucial choices.

One of the priorities in SI research is currently to characterise precisely the merits and shortcomings of the different algorithms. Benchmarking of optimisation methods is usually performed on a number of test functions which are commonly held as good standards (Adorio, 2005; Bersini, Dorigo, Langerman, Seront, & Gambardella, 1996; Karaboga & Basturk, 2008; Molga & Smutnicki, 2005). Although often challenging, these functions were not created systematically, and sometimes replicate similar problems.

This paper reports an experimental study on the performance of the Bees Algorithm. The study aims to highlight the specific abilities and limitations of this procedure, and investigate the effects of different parameterizations.

Thirty-two different combinations of learning parameters are tested. To study methodically and in detail the behaviour, strengths and limitations of the Bees Algorithm, 18 continuous function minimisation tasks with different features and degrees of complexity are designed. Even though not fully exhaustive in terms of possible fitness landscapes, the proposed set of test functions aims to constitute a first step toward a more analytical procedure for benchmarking optimisation methods. Four samples of the proposed benchmarks are modified to test the robustness of the performance of the different parameterizations.

To put in context the performance of the Bees Algorithm and the challenges posed by the test functions, two popular nature-inspired optimisation methods are tested on the proposed benchmarks, and their performance is compared to that of the Bees Algorithm. In order to demonstrate the effectiveness of the proposed algorithm on a real-world optimisation task, the Bees Algorithm and the two other procedures are also tested on four popular protein-folding benchmark problems.

2. The Bees Algorithm

The Bees algorithm does not make assumptions such as the continuity of the search space, and requires limited problem domain knowledge beyond the desired solution performance. Different versions of the Bees Algorithm have been used to solve various engineering problems, such as pattern classifier training (Pham & Darwish, 2010), dynamic control problems (Castellani, Pham, & Pham, 2012), machine shop scheduling (Packianather et al., 2014), robotic swarm coordination (Jevtic, Gazi, Andina, & Jamshidi, 2010), non-linear model identification (Fahmy, Kalyoncu, & Castellani, 2012) and control system tuning (Pham, Darwish, & Eldukhri, 2009).

This section presents the standard Bees Algorithm (Pham & Castellani, 2009), describing its biological motivation and the computational procedures.

2.1. Bees foraging process in nature

In a bee colony, part of the population explores randomly the area surrounding the hive in search of new flower patches rich in nectar or pollen (Tereshko & Loengarov, 2005). When they return to the nest, those scouts that found a rich food source communicate their finding to resting bees through a procedure known as the “waggle dance” (Seeley, 1996). The waggle dance encodes information on the location of the flower patch, and its quality rating (Camazine et al., 2003). The rating of a food source depends on its net energy yield, which compounds factors like its proximity to the nest, abundance, and energy concentration (i.e. sugar content) (Seeley, 1996). Using the information communicated through the waggle dance, a number of unemployed bees proceed to harvest the advertised food sources. When a recruited bee comes back to the hive, it may in turn waggle dance to guide other nest mates to the food source. Since the length of the waggle dance is determined by the quality rating of the flower patch, the most profitable food sources are more extensively advertised, and thus are visited by the largest number of foragers (Tereshko & Loengarov, 2005). In this way, the bee colony maximises the efficiency (i.e. energy yield) of the food-harvesting process.

2.2. The Bees Algorithm

Without loss of generality, it will be hereafter assumed that the optimisation problem entails the minimisation of a specified cost measure. A candidate solution to the problem is defined by a given number of parameters, and its cost is measured via an objective function (fitness function) of these parameters.

In the Bees Algorithm, each point in the solution space is thought of as a food source. When a “bee” visits a food source, it rates its quality via the fitness function. “Scout bees” are employed to sample the fitness landscape randomly, looking for unexplored areas of high fitness. In other words, new solutions are randomly created and evaluated. The visited sites are ranked, and “forager bees” are recruited to harvest (i.e. search further) the neighbourhood of the highest ranking locations. That is, new solutions similar to the current best finds are created and evaluated. The neighbourhood of a candidate solution is termed a “flower patch”. The Bees Algorithm explores the solution space, and samples the neighbourhood of the highest fitness points in search for the global fitness maximum (i.e. the solution that minimises the specified cost measure). Figure 1 shows the flowchart of the Bees Algorithm, whilst the main parameters of the algorithm are detailed in Table 1. The main steps of the algorithm are described below.

Figure 1. Flowchart of the Bees Algorithm.

Notes: Variables are italicised, routines are in bold.

Table 1. Bees Algorithm parameters

ns	Number of scout bees
ne	Number of elite sites
nb	Number of best sites
nre	Recruited bees for elite sites
nrb	Recruited bees for remaining best sites
ngh	Initial size of neighbourhood
stlim	Limit of stagnation cycles for site abandonment

2.3. Solutions encoding

Given a minimisation problem defined over the n-dimensional continuous solution space U = {x ∈ Rⁿ; min_i < x_i < max_i, i = 1, … , n}, each candidate solution is represented as an n-dimensional vector of decision variables x = {x₁, … , x_n}. The goal of the optimisation task is to find the solution that minimises the set cost function f(x):U → R.

2.4. Random initialisation

The number of scout bees is a fixed system parameter, henceforth denoted as ns. The algorithm starts scattering at random the scout bees across the search space. Each scout rates the fitness of the visited location (i.e. candidate solution) through the cost function. The procedure then enters the main loop, which consists of four phases.

2.5. Waggle dance

The recruitment procedure is implemented via a deterministic cut-off method.

The ns sites (i.e. solutions) visited by the scout bees are ranked in descending order of fitness (i.e. ascending order of cost measure). The first nb < ns locations (the best locations) are picked for neighbourhood search. Amongst these nb selected sites, the first ne ≤ nb elite (top-rated) sites are allocated nre foragers for local exploration. The remaining (nb − ne) sites picked for neighbourhood search are allocated nrb (nrb ≤ nre) foragers for local exploration.

The above recruitment mechanism assigns a larger number of bees to search the neighbourhood of the ne elite sites, which are considered the most promising regions of the solution space.

2.6. Local search

The neighbourhood search phase mimics the harvesting process carried out by forager bees in nature. For each of the nb selected sites, the spatial extent of the local search is delimited by an n-dimensional hyper-box of sides a₁, … , a_n centred on the location marked by the scout bee. The recruited foragers are randomly spread with uniform probability inside this hyper-box (flower patch). If one of the forager bees lands in a position of higher fitness than the scout bee, that forager is retained as the new scout bee. This bee becomes the dancer once back at the hive.

Two procedures named neighbourhood shrinking and site abandonment (Pham & Castellani, 2009) are called when local search fails to yield any fitness improvement within a flower patch. These two procedures aim to improve the search accuracy of the Bees Algorithm and avoid unnecessary computations.

2.7. Neighbourhood shrinking

The size a = {a₁, … , a_n} of the local neighbourhood of a selected site is initially set to a large value. For each variable a_i, it is set as follows:(1) $$\begin{array}{c}{a}_i(t)=ngh(t)\ast \left({max}_i-{min}_i\right)\hfill \\ ngh(\mathit{\tau })=1.0\hfill \end{array}$$(1)

where ngh(t) is a time-dependent variable, t is the tth cycle of the Bees Algorithm main loop, and τ is the cycle where the site is first selected for local search. If the local search yields higher points of fitness within a flower patch, the size of that patch is kept unchanged. Each time that local search does not bring any improvement in fitness, the extent of the flower patch is reduced according to the following empirical formula:(2) $$ngh(t+1)=0.8\ast ngh(t).$$(2)

At the level of the individual flower patches, the neighbourhood shrinking method acts in a way that is similar to the simulated annealing procedure (Zäpfel, Braune, & Bögl, 2010). The flower patches are initialised over a large area to foster the exploration of the search space. The size of the patches is then progressively reduced to make the search increasingly exploitative around the local optimum.

2.8. Site abandonment

Site abandonment is operated when the local search routine is not able anymore to find solutions of higher fitness than the scout within a flower patch. In this case, it is assumed that the local fitness peak has been reached, and the site is abandoned.

After each cycle of the local search procedure, the neighbourhood of those flower patches where the fitness stagnated is shrunk. If the fitness in a flower patch has stagnated for more than a predefined number (stlim) of consecutive cycles, the site is considered exhausted. In this case, the patch is abandoned and the scout bee is re-initialised to a new random point in the solution space. If the abandoned site corresponds to the best-so-far fitness value, its position is recorded. If no other solution of higher fitness is subsequently found, the recorded solution is taken as the final one.

2.9. Global search

In a bee colony, at any time a percentage of the population scouts the environment in search for new food sources. The Bees Algorithm mimics this exploration effort via random sampling of the solution space. That is, ns − nb scout bees are randomly scattered across the search space.

2.10. Population update

In the final phase of the main loop, the population of the bee colony is updated. The new population is formed out of two groups that combine respectively the products of the local and global search efforts. The first group is formed of nb scouts, each related to the centre (the best solution) of one of the high-fitness flower patches. The second group comprises ns − nb scouts, each consisting of a randomly generated solution.

2.11. Stopping criterion

The stopping criterion is set by the user. It can be either the location of a solution of fitness above a predefined threshold (e.g. in a minimisation problem, the cost f(x) of solution x is equal to f(x) ≤ threshold or the completion of a predefined number of learning cycles, or the elapsing of a pre-set computation time.

3. Related literature

The Bees Algorithm combines iterative neighbourhood search with random global search. The local search procedure in one flower patch is akin to the variable neighbourhood search (VNS) algorithm proposed by Mladenović and Hansen (1997). Each optimisation cycle is equivalent to a move to a new neighbourhood in VNS. Occasionally, the shrinking procedure reduces the size of the new neighbourhood. The main difference between the two algorithms is that the size of a flower patch is kept constant or reduced in the Bees Algorithm, whilst in the customary VNS routine is expanded. Moreover, flower patches are randomly sampled in the Bees Algorithm, whilst they are fully explored in VNS. The Bees Algorithm can be described as running nb VNS searches in parallel, and is thus akin to parallel VNS methods (Crainic, Gendreau, Hansen, & Mladenovic, 2004). The main difference between parallel VNS methods and the Bees Algorithm is in the exchange of information between the local search procedures. In the former, the result of the individual VNS procedures is shared at fixed time intervals, or at the end of the search. In the latter, no candidate solutions are exchanged between parallel searches. Instead, information on the progress of the local searches is shared through the waggle dance, and the amount of local exploitation is allocated accordingly. The differential recruitment method used in the Bees Algorithm represents the “social” aspect of the procedure, akin to the forager recruitment process in honey bees. Another difference in the two procedures concerns the way the local search is restarted once a neighbourhood has been explored. Whilst the Bees Algorithm uses the asynchronous site abandonment routine, parallel VNS methods synchronously restart the local searches once they have been all exhausted.

Amongst the various population-based metaheuristics, the Bees Algorithm shows some resemblance with (μ + λ)-evolutionary strategies (ES) (Fogel, 2000). In common with these procedures, the Bees Algorithm employs a deterministic selection method, and samples a number of points (offspring in ES terminology) in the neighbourhood of the selected solutions (parents in ES terminology). Like some kinds of ESs, the Bees Algorithm employs only selection and mutation to evolve the population. In contrast to ESs, the local exploitation effort is not fixed but allocated proportionally to the fitness of the parents. Also, competition for survival in the Bees Algorithm is decentralised at a local level amongst the scout and its recruits. In ESs, the whole parent population is pooled with the offspring in the replacement procedure, or is fully replaced by the offspring.

Compared to many popular SI algorithms, the Bees Algorithm does not exchange information through an interaction medium like pheromone in ACO or attraction forces in PSO. That is, the exploitation of the candidate solutions in the Bees Algorithm is set directly through the waggle dance, and not indirectly through a medium. Strictly speaking, due to the centralised apportionment of the sampling effort, the Bees Algorithm is not a true SI procedure.

Differently from customary evolutionary and swarm algorithms, the Bees Algorithm features the site abandonment procedure which prevents foragers from being trapped at a local fitness peak. Site abandonment is also useful to reinstate population diversity if several scouts converge on the same neighbourhood. A similar procedure is featured in some PSO versions like the multiswarm PSO proposed by Blackwell and Branke (2004). A consequence of the site abandonment procedure is that there is no population convergence in the Bees Algorithm.

In the field of bees-inspired optimisation, there are similarities between the Bees Algorithm and the Artificial Bee Colony (ABC) algorithm (Karaboga & Basturk, 2007). The two optimisation procedures can be visualised using the same flowchart. However, in ABC the waggle dance is simulated through the stochastic roulette wheel selection method (Fogel, 2000), instead of the deterministic cut-off procedure used in the Bees Algorithm. The most substantial difference between the Bees Algorithm and ABC is in how neighbourhood search is implemented. That is, ABC does not use mutation which is the local search operator in the Bees Algorithm. Instead, ABC uses the extrapolation crossover operator (Fogel, 2000).

For a more in-depth analysis of the differences and similarities between the Bees Algorithm and SI methods, the reader is referred to Pham and Castellani (2009, 2013).

4. Experimental setup

As previously mentioned, the performance of the Bees Algorithm is tested on 18 custom-made and 4 real-world continuous function minimisation benchmarks. An evolutionary algorithm (EA) (Fogel, 2000) and a PSO are used as terms of reference for the performance of the Bees Algorithm. All the optimisation problems entail the minimisation of a cost function F(x). Given a candidate solution x = {x₁, … , x_n}, the associated cost is calculated as follows:(3) $$F(x)=f(x)-\overline{f}$$(3)

where f(x) is the value of the benchmark function f at x, and $\overline{f}$ is the global minimum of f. The fitness of solution x is inversely proportional to its cost.

4.1. 2D function minimisation benchmarks

Pham and Castellani (2009) tested the Bees Algorithm and 3 other procedures on 12 popular minimisation benchmarks: Easom, Goldstein and Price, Martin and Gaddy, Schaffer, Schwefel, Ackley, Griewank, Hypersphere, Langermann, Rastrigin, Rosenbrock and Shekel. These functions are amongst the most widely used in the literature (Adorio, 2005; Bersini et al., 1996; Molga & Smutnicki, 2005), and have become de facto standards for the benchmarking of optimisation algorithms (Macnish, 2007). They will be called henceforth the customary functions.

Although some of the customary functions can be regarded as challenging tasks, they often repeat similar cases. In many instances, it is possible to obtain easily an indication of the approximate location of the optimum. This is the case in the four unimodal functions (Hypersphere, Martin and Gaddy, Easom and Rosenbrock), the Schaffer function (a high-frequency-damped sinusoid) and three functions characterised by an overall unimodal behaviour and local pockets added via a cosinusoidal “noise” component (Ackley, Griewank, Rastrigin). Moreover, optimisation methods that use averaging operators to exchange information amongst individuals (e.g. PSO and some EAs) are known to be biased toward the origin of the solution space (Monson & Seppi, 2005). These algorithms are best suited to functions where the minimum lies at or near the centre of the search space. This is the case of many of the customary functions.

Several of the customary functions share also a number of other features that might bias the benchmarking of optimisation methods, such as axial alignment of the peaks (Ackley, Griewank, Rastrigin, Schwefel), regular spacing of the peaks (Ackley, Griewank, Rastrigin, Schwefel), rotational symmetry of the function (Easom, Hypersphere, Schaffer) and linear separability of the function into a sum of independent one-variable functions (Hypersphere, Easom, Rastrigin, Ackley) (Macnish, 2007). Whilst rigid transformations of the fitness landscape can remove the biases caused by the location of the optimum and linear separability of the variables (Tang et al., 2009), other sources of bias (e.g. regular spacing of the peaks, rotational symmetry) are inherently related to the analytical formulation of the functions.

In order to provide a fairer and more thorough comparison of the Bees Algorithm, 18 test functions have been created. For ease of analysis and visualisation, all the proposed benchmarks are two-dimensional. All functions are defined within the interval [−100, 100], and map a fitness landscape defined within the continuous interval [0, 1] where zero is the value of the global minimum. The equations and fitness landscapes of the 18 benchmarks are given in the online electronic supplementary material (Online Appendix).

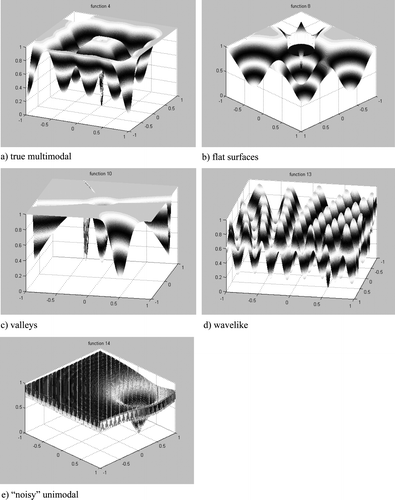
Function 1 maps two “holes” on opposite sides of the search space. It is designed to challenge algorithms that employ averaging search operators, since they are likely to produce several solutions in between the two poles of attraction.

Functions 2–6 are multimodal functions devised to test different biases in the search procedures. In the first three cases, the secondary minima are aligned on a regular grid, in the remaining two cases they are randomly arranged. In function 4 and 6 the global optimum lies at the centre of the search space, whilst in the other functions lies near the top-right corner of the search space. Finally, the peak is aligned with the grid of secondary minima in function 4, and is not in functions 2 and 3. Algorithms using procedures able to exploit regularities in the search space, such as the two-point crossover operator used in EAs (Fogel, 2000), are likely to be biased toward solutions aligned on grids. They should perform best on function 4, but also be more liable to get trapped in the secondary minima of functions 2 and 3. Search procedures biased toward the origin of the search space are expected to perform best on functions 4 and 6.

In functions 7 and 8, the global minimum lies in a hole characterised by a large flat step and a steep and narrow ending. The two functions are identical, with the exception that in the latter the minima are arranged on a grid. These two functions aim to test the ability of search algorithms to overcome flat surfaces. It should be noted that none of the customary functions includes this case.

Functions 9, 10 and 11 test the ability of the search algorithms to negotiate valleys. Function 9 is similar to function 2, it maps two valleys on opposite sides of the search space. Function 10 is characterised by two pairs of valleys of opposite slopes that create four narrow competing basins of attraction. The minimum is located near the borders of the search surface at the end of the narrowest valley. The four valleys join at the origin, where a further basin was placed to challenge origin-biased search algorithms. Function 11 is similar to the Rosenbrock function. However, in this case, the narrow parabolic valley is surrounded by a large flat surface. The valley is located in the half plane of positive x₁ values (x₁ > 0). The other half of the fitness landscape is covered by a sliding plane that makes the overall search surface extremely deceptive.

Function 12 combines two cosinusoidal functions. Each function depends on one of the two input variables, and its amplitude increases linearly with the associated variable. The global minimum is in a narrow hole that is added to one of the “pockets” of the search surface. Like many of the multi-pocketed customary functions, function 12 has an overall unimodal characteristic corresponding to a plane slanted toward the positive values of the two input variables. The optimum is located before the end of the plane, and therefore does not correspond to the minimum of the unimodal characteristic. Function 12 tests the capability of a search algorithm to explore and escape many local minima. Function 13 represents a more difficult optimisation task. In this case, the two sinusoidal oscillations that generate the mapping have constant amplitude and variable period. There is thus no regularity (i.e. fixed period) or general behaviour (i.e. slanted plane) that may help the search. Also in this case, the global minimum is in a narrow hole added to one of the pockets of the search surface.

Similarly to many of the customary functions, functions 14–18 are characterised by an overall unimodal fitness landscape and many local “potholes”. The local pockets of fitness are generated by a cosinusoidal high-frequency term. The minimum lies at the bottom of one of the potholes in the middle of the first quadrant. Functions 14, 15 and 16 differ for the magnitude of the cosinusoidal term, which is respectively 10, 25 and 40% of the magnitude of the unimodal term. Functions 17 and 18 differ from function 15 for the period of the oscillatory term, which is respectively 4 and ¼ times the period of the term of function 15.

The functions can be divided into five main groups, characterised respectively by two- and multimodal, flat, valley-like, wavelike and “noisy” unimodal fitness surfaces. To distinguish them from noisy unimodal functions, the first four groups of multi-modal functions will be henceforth referred as “true multi-modal”. For each class, a sample function is plotted in Figure 2. Table 2 summarises the main features of the 18 benchmarks.

Figure 2. Examples of proposed benchmarks.

Table 2. Main features of function benchmarks

Function	Two peaks	True multi-modal	Unimodal with potholes	Minima on a grid	Minimum at the origin	Valleys	Flat surface	Wavelike
1	x	x
2		x		x
3		x		x
4		x		x	x
5		x
6		x			x
7		x		x			x
8		x					x
9	x					x
10		x				x
11		x				x
12		x						x
13		x						x
14			x
15			x
16			x
17			x
18			x

4.2. Protein folding benchmarks

The protein folding problem consists of finding the minimal energy structure of a molecular cluster to find the configuration of a protein (Vavasis, 1994). The energy function of the molecular structure is defined by the following non-linear partially separable function:(4) $$f\left(x_1,\dots ,x_n\right)=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}r\left[\sqrt{\sum _{k=1}^3{\left(x_{ik}-x_{jk}\right)}^2}\right]$$(4)

where r(s) is the Lennard–Jones potential.(5) $$r(s)=s^{-12}-2·s^{-6}$$(5)

The vectors $x_l=\left\{x_{l1},x_{l2},x_{l3}\right\},l\in [1,n],l\in I^{+}$ correspond to the positions of n atoms in the 3D space, and are constrained as follows: $x_{lk}\in \left[-1,1\right],k\in \left\{1,2,3\right\}$. The overall function f is non-convex, and has an exponential number of local minima (Mongeau, Karsenty, Rouzé, & Hiriart-Urruty, 2000). The global minimum is known only for n ≤ 4 (Mongeau et al., 2000; Vavasis, 1994).

In this study, the four cases n = 3–6 are considered. They will be henceforth called pf3, pf4, pf5, and pf6. The solutions are encoded using 3⋅n long strings of real numbers, which are built chaining the 3D vectors of atom position coordinates x₁, … , x_n. The global minima for the four functions are given in Table 3, for n > 4, they are taken from the search results of Coleman, Shalloway, and Wu (1993).

Table 3. Global minima of protein folding problem

pf3	−3.0
pf4	−6.0
pf5	−9.1038F
pf6	−12.7120F

4.3. Performance measures

Each algorithm is tested 50 times with different random initialisations on each benchmark. Each time, the optimisation procedure is run until either it locates a solution ξ of fitness F(ξ) < 0.001, or the maximum number of learning cycles is reached. The learning speed S is measured as the number of solutions evaluated throughout the optimisation procedure. Whenever the site abandonment procedure of the Bees Algorithm requires the random re-initialisation of a new solution, the extra solution is counted in the computation of the speed S. The location error E of the final solution x_f is computed as in the equation below.(6) $$E=\left\{\begin{array}{cc}0\hfill & \text{if}F(x_f)\le 0.001\\ F\left(x_f\right)\hfill & \text{otherwise}\end{array}\right.$$(6)

The average location error μ_E and optimisation speed μ_S over the 50 independent learning trials are calculated for each parameter setting on each benchmark problem.

5. Experimental tests—2d benchmarks

This set of experiments is designed to evaluate the performance of the Bees Algorithm on the eighteen two-dimensional benchmarks. For each function, 32 different parameterizations of the algorithm are tested. They are shown in Table 4. In 16 cases, the optimisation procedure performs 102 function evaluations per learning cycle, and is run until the global minimum is located or 5,000 learning cycles have elapsed (see Section 4.3). In the remaining 16 cases, 51 function evaluations are performed per learning cycle, and the algorithm is run for a maximum of 10,000 learning cycles. These figures correspond to 100 (50) local search samples plus 2 (1) global search samples per evolution cycle, for a total of at most 510,000 fitness evaluations. The first strategy emphasises the role of the population size in the search process. It will be called henceforth “breadth-search” approach. The second strategy relies on the length of the evolution span, and will be called henceforth “depth-search” approach.

Table 4. Bees Algorithm parameterizations tested

No.	Population size	Learning cycles	stlim	ne	nre	nb	nrb	Random scouts
1	51	10,000	5	1	10	9	5	1
2	51	10,000	5	1	15	8	5	1
3	51	10,000	5	1	20	4	10	1
4	51	10,000	5	1	20	7	5	1
5	51	10,000	5	1	25	6	5	1
6	51	10,000	5	1	30	3	10	1
7	51	10,000	5	2	20	3	10	1
8	51	10,000	5	2	20	4	5	1
9	51	10,000	10	1	10	9	5	1
10	51	10,000	10	1	15	8	5	1
11	51	10,000	10	1	20	4	10	1
12	51	10,000	10	1	20	7	5	1
13	51	10,000	10	1	25	6	5	1
14	51	10,000	10	1	30	3	10	1
15	51	10,000	10	2	20	3	10	1
16	51	10,000	10	2	20	4	5	1
17	102	5,000	5	1	10	19	5	2
18	102	5,000	5	1	20	9	10	2
19	102	5,000	5	1	20	17	5	2
20	102	5,000	5	1	30	8	10	2
21	102	5,000	5	1	30	15	5	2
22	102	5,000	5	1	40	4	20	2
23	102	5,000	5	1	40	7	10	2
24	102	5,000	5	2	20	8	10	2
25	102	5,000	5	2	30	6	10	2
26	102	5,000	10	1	10	19	5	2
27	102	5,000	10	1	20	9	10	2
28	102	5,000	10	1	30	8	10	2
29	102	5,000	10	1	30	15	5	2
30	102	5,000	10	1	40	4	20	2
31	102	5,000	10	2	20	8	10	2
32	102	5,000	10	2	30	6	10	2

For each benchmark, the average location error and learning speed (Section 4.3), and the success rate (Section 4.3) achieved by the best performing Bees Algorithm configurations are reported in Table 5.

Table 5. Bees Algorithm—Minimisation results

Function	Population	Generations	stlim	ne	nre	nb	nrb	Success	Accuracy	Speed
1	51	10,000	10	1	10	9	5	50	0.0000	2,300
2	51	10,000	10	1	10	9	5	50	0.0000	7,659
3	51	10,000	10	1	10	9	5	50	0.0000	10,218
4	51	10,000	10	1	10	9	5	50	0.0000	7,162
5	51	10,000	10	1	10	9	5	50	0.0000	21,781
6	51	10,000	10	1	10	9	5	50	0.0000	18,782
7	102	5,000	10	1	30	15	5	50	0.0000	7,118
8	51	10,000	10	1	10	9	5	50	0.0000	5,300
9	51	10,000	10	1	20	7	5	50	0.0000	1,364
10	51	5,000	10	1	20	7	5	50	0.0000	31,599
11	51	5,000	10	1	10	9	5	3	0.0143	464,068
12	51	10,000	10	1	30	3	10	50	0.0000	2,747
13	102	5,000	10	1	30	15	5	50	0.0000	5,814
14	51	10,000	10	2	20	4	5	50	0.0000	5,776
15	51	10,000	10	2	20	3	10	50	0.0000	19,807
16	51	10,000	10	1	30	3	10	50	0.0000	53,837
17	51	10,000	10	2	20	4	5	50	0.0000	3,010
18	51	10,000	10	2	20	4	5	50	0.0000	13,934

5.1. Optimisation results

On the first eight true multimodal functions the best configurations of the Bees Algorithm correspond to fairly explorative strategies. They split the population amongst many selected nb sites without committing too many foragers on any location. The presence of a flat surface in functions 7 and 8 does not seem to affect much the optimisation speed, or require a substantially different search strategy.

In terms of optimisation speed, the Bees Algorithm appears to perform better on landscapes where the minima are aligned on a grid (3 and 4 vs. 5 and 6), and the global optimum is at the centre of the optimisation space (4 and 6 vs. 3 and 5). However, the differences in speed didn’t appear to be significant following a Mann–Whitney test.

On benchmarks 9 and 10 (valleys), the best-performing settings are still mainly explorative, even though less markedly than in the previous eight cases. A clearly explorative configuration excels on the highly deceptive function 11. This is likely due to the misleading nature of the fitness landscape, which makes it risky to commit a high number of foragers on a (few) location(s).

In function 12 the overall characteristic of the fitness surface is inclined (Section 4.1). Even though the global minimum does not correspond exactly with the end of the underlying slope, it lies in the same quadrant. This may help the search process, and make function 12 easier to optimise than function 13. This hypothesis might explain why a more exploitative configuration excels on function 12 than on function 13, and the Bees Algorithm performs better on the first benchmark than the second. Highly exploitative search strategies emerge also on the noisy unimodal functions (14–18).

In all the eighteen cases, the best configuration uses the high value for the stagnation limit. This feature balances the explorative search strategies used for many benchmarks, ensuring adequate exploitation of the search results.

Regarding the trade-off between the population size and number of optimisation cycles, depth-search appears the most suitable strategy for the Bees Algorithm. This is always the case except for function 7 (flat surface), and function 13 (wavelike).

The Bees Algorithm attains 100% success rate on all benchmarks, with the only exception of function 11.

6. Experimental tests—Robustness of performance

This set of experiments is designed to test the robustness of the performance of the Bees Algorithm configurations to alterations of the fitness surface. Four functions (4, 8, 10, 13) sampled from different landscape groups (see Figure 2) are slightly modified. In the case of functions 4, 8, and 10, the parameter k defining the value of the secondary minima (see electronic supplementary material) is changed from 0.25 to 0.3 (functions 4a, 8a, and 10a), and 0.2 (functions 4b, 8b, and 10b). This corresponds to raising (lowering) the depth of the local minima from 0.25 to 0.3 (0.2), whilst the value of the global minimum is kept fixed to 0. Similarly, functions 13a and 13b are created respectively increasing and decreasing the width k₁ (see electronic supplementary material) of the wavelike oscillations. Finally, functions 14 and 16 can be seen as variants of function 15 where the noise component is slightly modified.

For each of the eight modified fitness surfaces, 50 independent runs of the Bees Algorithm are executed. The significance of the differences between the distribution of the optimisation speeds obtained on the original and modified functions is analysed using Mann–Whitney U tests. The tests are run for a 0.05 (5%) level of significance. Table 6 reports, for each modified function, the p-value of the significance tests for each configuration. The total number of cases where the optimisation speeds obtained on the original functions differed in a statistically significant way from the optimisation speeds obtained on the modified functions is given at the bottom of the table. The shaded cells correspond to configurations that performed optimally on the original functions (i.e. their performance is not statistically distinguishable from the best reported in Table 5). The p-values in bold indicate configurations that performed optimally on the modified fitness landscapes.

Table 6. Robustness of optimisation results

Parameterization	Function
	4a	4b	8a	8b	10a	10b	13a	13b	14	16
1	0.250	0.266	0.004	0.009	0.442	0.145	0.063	0.967	0.000	0.005
2	0.612	0.357	0.871	0.003	0.948	0.454	0.200	0.127	0.000	0.005
3	0.506	0.266	0.931	0.068	0.021	0.654	0.934	0.136	0.000	0.000
4	0.398	0.450	0.011	0.000	1.000	0.059	0.108	0.556	0.000	0.000
5	0.241	0.027	0.000	0.264	0.677	0.471	0.022	0.839	0.000	0.000
6	0.959	0.085	0.888	0.361	0.605	0.213	0.915	0.278	0.000	0.000
7	0.099	0.329	0.014	0.396	0.203	0.182	0.266	0.402	0.000	0.001
8	0.145	0.165	0.828	0.374	0.136	0.091	0.031	0.764	0.000	0.000
9	0.008	0.347	0.003	0.725	0.764	0.994	0.804	0.432	0.000	0.000
10	0.598	0.506	0.359	0.869	0.669	0.480	0.446	0.002	0.000	0.000
11	0.574	0.920	0.749	0.863	0.574	0.408	0.012	0.015	0.000	0.000
12	0.551	0.161	0.664	0.001	0.099	0.524	0.379	0.890	0.000	0.000
13	0.546	0.281	0.063	0.245	0.010	0.572	0.617	0.009	0.000	0.000
14	0.817	0.013	0.311	0.456	0.986	0.738	0.967	0.381	0.000	0.147
15	0.049	0.506	0.634	0.000	0.657	0.959	0.836	0.153	0.000	0.000
16	0.151	0.275	0.374	0.622	0.809	0.772	0.785	0.004	0.000	0.000
17	0.184	0.702	0.177	0.393	0.159	0.615	0.248	0.166	0.000	0.011
18	0.586	0.085	0.001	0.510	0.336	0.817	0.078	0.416	0.000	0.004
19	0.040	0.087	0.537	0.014	0.484	0.446	0.622	0.037	0.000	0.000
20	0.940	0.090	0.028	0.956	0.196	0.642	0.301	0.896	0.000	0.000
21	0.953	0.476	0.517	0.008	0.975	0.150	0.199	0.068	0.000	0.000
22	0.385	0.008	0.486	0.041	0.833	0.203	0.546	0.264	0.000	0.001
23	0.208	0.920	0.000	0.208	0.989	0.780	0.469	0.336	0.000	0.000
24	0.667	0.054	0.067	0.012	0.161	0.823	0.270	0.973	0.000	0.006
25	0.501	0.956	0.343	0.372	0.450	0.370	0.682	0.422	0.000	0.000
26	0.233	0.023	0.057	0.521	0.025	0.637	0.348	0.117	0.000	0.001
27	0.488	0.298	0.570	0.123	0.004	0.095	0.164	0.027	0.000	0.000
28	0.588	0.287	0.556	0.016	0.608	0.270	0.644	0.465	0.000	0.000
29	0.839	0.005	0.820	0.191	0.754	0.929	0.603	0.404	0.000	0.000
30	0.200	0.815	0.245	0.057	0.245	0.677	0.480	0.190	0.000	0.018
31	0.442	0.418	0.002	0.131	0.556	0.210	0.410	0.081	0.000	0.000
32	0.136	0.493	0.697	0.001	0.177	0.588	0.937	0.034	0.000	0.000
Different	3	5	9	11	4	0	3	7	32	31

In most of the cases, the significance tests indicate that the optimisation speeds obtained by the 32 configurations on the modified functions are statistically indistinguishable from those obtained on the original functions. The only exceptions are functions 14 and 16. The set of configurations that perform optimally on the original and modified functions are also largely overlapping.

7. Experimental tests—Comparison with similar nature-inspired search methods

This set of experiments serves two purposes: to give terms of comparison to evaluate the performance of the Bees Algorithm, and test how challenging the proposed benchmarks are for different algorithms. It is important to emphasise that the results of the comparison cannot be used to support any claim regarding the absolute superiority of one optimisation procedure over any other (cf. the No Free Lunch Theorem). This study also does not intend compare the Bees Algorithm with the whole state-of-the-art in the literature. A comparison with every other continuous optimisation method would be impractical.

An EA and a PSO are chosen as control procedures. These two algorithms are amongst the best known and understood population-based metaheuristics. Hence, they are ideal terms of comparison to characterise the abilities of the Bees Algorithm, and evaluate the challenges that the test functions pose.

7.1. General settings

In order to test the algorithms on the same fitness landscape, the two control methods use the same representation scheme outlined in Section 2.3, and the fitness function described in Equation (3). The EA and PSO are also allocated the same sampling opportunities as the Bees Algorithm. Like in the case of the Bees Algorithm, the performance of the EA and PSO are optimised using 32 different combinations of system parameters and operators. The settings are divided into 16 depth-search (51 fitness evaluations repeated for a maximum of 10,000 learning cycles) and 16 breadth-search configurations (102 fitness evaluations repeated for a maximum of 5,000 learning cycles). Like the Bees Algorithm, the EA and PSO use general purpose operators and routines, and their configuration is optimised via a comparable number of trials (32 configurations each). This should ensure a fairly unbiased comparison of the three procedures.

7.2. Control algorithm I—EA

Two kinds of selection routines are tested: fitness ranking (Fogel, 2000) and an adaptive procedure recently introduced by Pham and Castellani (2010). Generational replacement (Fogel, 2000) is employed to update the population at the end of every evolution cycle.

Elitism (Fogel, 2000) is used to ensure that a copy of the fittest solution survives into the next generation. The population update strategy of the Bees Algorithm could be viewed as a form of local elitism, which preserves the best solution of every neighbourhood searched. However, elitism in EAs is usually applied at a global level, and thus is more likely to lead to loss of population diversity. For this reason, elitism is restricted only to the best fit solution.

The mutation operator picks at random a solution and slightly modifies the value of all its variables. The modification is sampled with uniform probability within an interval of width [−a, a]. The parameter a is encoded into the representation of the solutions x = {x₁, … , x_n, a}, and is adaptively tuned by the evolution process. The effect of mutation corresponds to the creation of a recruited bee in a flower patch of size a and centred on the mutant solution.

Four kinds of recombination (Fogel, 2000) operators are evaluated. In the first instance, genetic recombination is not used; mutation is the only genetic operator. In the second instance, the customary two-point recombination operator (hereafter called binary crossover) is used (Monson & Seppi, 2005). In the other two instances, the offspring are created from a weighted average of the parameters of the parent solutions. Given two solutions x = {x₁, … , x_n, a_x} and y = {y₁, … , y_n, a_y}, interpolation and extrapolation crossover create a new solution z = {z₁, … , z_n, a_z} as:(7) $$z_i=x_i·(1-random)+y_i·random(\text{interpolation crossover})$$(7) (8) $$z_i=x_i+random·(x_i-y_i)(\text{extrapolation crossover})$$(8)

where i = 1, … , n + 1, and random ∈ [0, 1] is a random number. The children generated using interpolation crossover lie inside a hyperbox delimited by the two parents (see Figure 3). The action of three crossover operators is shown in Figure 3. For each test function, the best-performing EA configuration is given in Table 7.

Figure 3. Action of the 3 EA crossover operators tested.

Note: The x and y circles represent the locations of the parent solutions.

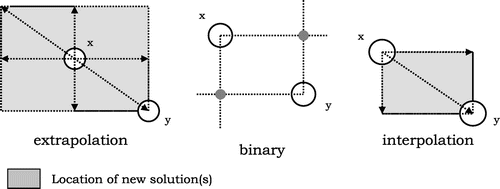
Table 7. EA learning parameters

Function	Population	Generations	Selection procedure	Crossover type	Crossover rate	Mutation rate	Mutation width
1	102	5,000	Adaptive	Extra	1	0.05	0.1
2	102	5,000	Adaptive	Extra	1	0.05	0.1
3	102	5,000	Adaptive	Extra	1	0.05	0.1
4	51	10,000	Adaptive	Inter	1	0.05	0.1
5	102	5,000	Adaptive	Extra	1	0.05	0.1
6	102	5,000	Adaptive	Extra	1	0.05	0.1
7	102	5,000	Adaptive	Extra	1	0.05	0.1
8	102	5,000	Adaptive	Extra	1	0.05	0.1
9	102	5,000	Adaptive	Extra	1	0.05	0.1
10	102	5,000	Adaptive	Extra	1	0.05	0.1
11	102	5,000	Adaptive	Binary	1	0.05	0.1
12	102	5,000	Adaptive	Binary	1	0.05	0.1
13	51	10,000	Adaptive	Extra	1	0.05	0.1
14	51	10,000	Adaptive	Inter	1	0.05	0.1
15	51	10,000	Adaptive	Inter	1	0.05	0.1
16	51	10,000	Adaptive	Inter	1	0.05	0.1
17	51	10,000	Ranking	Inter	0.75	0.25	0.05
18	51	10,000	Adaptive	Inter	1	0.05	0.1

7.3. Control algorithm II—PSO

PSO regards candidate solutions as particles that move across the fitness landscape. The procedure used in this study follows the PSO algorithm formulated by Kennedy and Eberhart (1995).

Each particle moves onto the solution space according to its velocity vector v. This vector is made up of three components modelling respectively the particle’s persistence (momentum), past experience (attraction toward the fittest location visited), and social interaction with its neighbours (attraction toward the fittest neighbour). The velocity and position of a particle are updated according to the equations proposed by Kennedy and Eberhart (1995).(9) $$\begin{array}{c}{x}_i(t+1)=x_i(t)+v_i(t+1)\hfill \\ i=1,\dots ,n\hfill \end{array}$$(9) (10) $$\begin{array}{c}{p}_i(t)=rando{m}_1·\left[pbest{(t)}_i-x{(t)}_i\right]\hfill \\ s_i(t)=rando{m}_2·\left[gbest{(t)}_i-x{(t)}_i\right]\hfill \\ v_i(t+1)=w(t)·v{(t)}_i+c_1·p_i(t)+c_2·s_i(t)\hfill \\ i=1,\dots ,n\hfill \end{array}$$(10)

where t is the tth PSO cycle, v = {v₁, … , v_n} is the velocity vector of particle x, c₁ and c₂ are pre-defined parameters, random₁ and random₂ are randomly sampled with uniform probability in the interval [0, 1], pbest(t) (personal best) is the vector of coordinates of the site of highest fitness found so far by the particle, and gbest(t) (global best) is the vector of coordinates of the site of highest fitness found so far by the social neighbours of the particle.

The weight w(t) is decayed as follows:(11) $$w(t)=w_{max}-\frac{w_{max}-w_{min}}{T}·t$$(11)

where w_max and w_min are predefined parameters, and T is the maximum allowed number of optimisation cycles.

All the components of the velocity vector are constrained within the interval [$-v_i^{max},v_i^{max}$](12) $$v_i^{max}=u·\frac{{max}_i-{min}_i}{2}$$(12)

where max_i and min_i are the upper and lower boundaries of variable i, and u is a system parameter. The learning parameters are set as recommended by Shi and Eberhart (1998).

The search efficiency of a PSO optimiser is by and large defined by the connectivity of the population (i.e. the number of social neighbours for each particle) and the maximum speed (v^max) of the particles. In this study, 16 combinations of v^max (obtained through u) and connectivity types are considered. Each combination is evaluated using the breadth-search and depth-search approach, for a total of 32 overall tests. For each test function, the best-performing PSO configuration is given in Table 8a. Table 8b refers to standard parameters that are not changed in the 32 PSO optimisation tests. A 102– (51–) neighbour connectivity corresponds to a fully connected population.

Table 8a. PSO learning parameters

Function	Population	Generations	Connectivity	Speed
1	102	5,000	10	0.01
2	102	5,000	102	0.01
3	102	5,000	20	0.005
4	51	10,000	20	0.01
5	102	5,000	2	0.01
6	102	5,000	20	0.01
7	102	5,000	2	0.1
8	102	5,000	2	0.1
9	102	5,000	2	0.1
10	102	5,000	2	0.005
11	102	5,000	20	0.01
12	102	5,000	20	0.1
13	102	5,000	2	0.05
14	51	10,000	20	0.01
15	51	10,000	102	0.01
16	51	10,000	102	0.01
17	51	10,000	102	0.05
18	51	10,000	20	0.01

Table 8b. Fixed PSO learning parameters

Parameter	Value
c1 (Shi & Eberhart, 1998)	2.0
c2 (Shi & Eberhart, 1998)	2.0
wmax (Shi & Eberhart, 1998)	0.9
wmin (Shi & Eberhart, 1998)	0.4

7.4. Results of comparison

For each function, Table 9 shows the median of the optimisation results attained by the three algorithms. The significance of the differences between the results obtained by the Bees Algorithm, and those achieved by the EA and PSO, was analysed via Mann–Whitney U-tests. The p-values are given in Table 9, highlighting in bold differences above the 5% level of significance.

Table 9. Comparison of optimisation procedures on proposed benchmarks

Function	Bees Algorithm			PSO					EA
	Success	Accuracy	Speed	Success	Accuracy	p (Accuracy)	Speed	p (Speed)	Success	Accuracy	p (Accuracy)	Speed	p (Speed)
1	50	0.0000	2,300	50	0.0000	–	3,111	0.0000	50	0.0000	–	4,029	0.0000
2	50	0.0000	7,659	23	0.2500	0.0000	510,000	0.1779	50	0.0000	–	1,9074	0.0000
3	50	0.0000	10,218	17	0.2442	0.0000	510,000	0.0001	50	0.0000	–	23,715	0.0001
4	50	0.0000	7,162	49	0.0007	0.0358	5,406	0.0027	46	0.0005	0.5556	765	0.0000
5	50	0.0000	2,1781	10	0.1580	0.0000	510,000	0.0000	50	0.0000	–	29,274	0.0231
6	50	0.0000	18,782	49	0.0005	0.9368	7,242	0.0005	50	0.0000	–	12,750	0.0445
7	50	0.0000	7,118	39	0.0006	0.0189	8,568	0.0745	50	0.0000	–	3,876	0.0000
8	50	0.0000	5,300	37	0.0006	0.0218	8,976	0.0003	50	0.0000	–	5,457	0.3683
9	50	0.0000	1,364	45	0.0002	0.9423	11,985	0.0000	50	0.0000	–	1,785	0.0486
10	50	0.0000	31,599	13	0.1927	0.0000	510,000	0.0000	49	0.0007	0.0013	4,1973	0.5327
11	3	0.0143	464,068	0	0.2000	0.0000	510,000	0.0000	1	0.2000	0.0000	510,000	0.0000
12	50	0.0000	2,747	50	0.0000	–	6,885	0.0000	50	0.0000	–	8,466	0.0000
13	50	0.0000	5,814	48	0.0005	0.6466	15,402	0.0000	50	0.0000	–	3,723	0.0016
14	50	0.0000	5,776	50	0.0000	–	5,636	0.8388	50	0.0000	–	3,749	0.0000
15	50	0.0000	19,807	50	0.0000	–	9,690	0.0055	50	0.0000	–	4,998	0.0000
16	50	0.0000	53,837	50	0.0000	–	18,437	0.0000	50	0.0000	–	12,291	0.0000
17	50	0.0000	3,010	50	0.0000	–	4,641	0.0603	50	0.0000	–	2,168	0.0000
18	50	0.0000	13,934	50	0.0000	–	10,710	0.1546	50	0.0000	–	5,916	0.0000

The benchmarks prove challenging for the PSO, which fails to reach full success rates in several cases. In five cases, the success rate obtained by the PSO was inferior to two-thirds. The origin-bias (Section 4.1) of the PSO’s velocity composition operator is clearly revealed by the large difference between the optimisation speeds attained on functions 4 and 6 (origin-centred) and the equivalent 3 and 5.

The EA achieves optimisation results comparable to those achieved by the Bees Algorithm. The origin bias of interpolation crossover is likely the reason for the very high optimisation speed on functions 4 and 6. Nearly all the best-performing EA configurations include the adaptive selection procedure. Extrapolation crossover excels in the majority of the cases. The success of extrapolation crossover is probably due to its large reach (Figure 2), which fosters the exploration of the search space. Interpolation crossover is instead more suitable to exploitative searches (Pham & Castellani, 2009), and for this reason excels on the noisy unimodal functions. The good performance of binary crossover on function 12 is likely due to the grid-like arrangement of the minima.

For each function, Table 10 reports the best-performing algorithm(s) versus the benchmarks features. The evaluation of the performance takes into consideration first the success rate, and successively accuracy and speed to break ties. If two or more algorithms attain the same success rate, and the differences in accuracy and speed are not statistically significant (Mann–Whitney U-test), they are considered to perform equally. Overall, the Bees Algorithm excels on true multi-modal functions, except for those characterised by flat surfaces where the EA performs best. The EA dominates the noisy unimodal functions.

Table 10. Summary of comparative tests on proposed benchmarks

Function	Two peaks	True multi-modal	Unimodal with potholes	Minima on a grid	Minimum at the origin	Valleys	Flat surface	Wavelike	Winner
1	x	x							BA
2		x		x					BA
3		x		x					BA
4		x		x	x				BA
5		x							BA
6		x			x				EA
7		x		x			x		EA
8		x					x		BA–EA
9	x					x			BA
10		x				x			BA
11		x				x			BA
12		x						x	BA
13		x						x	EA
14			x						EA
15			x						EA
16			x						EA
17			x						EA
18			x						EA

8. Experimental tests—Protein folding benchmarks

This set of experiments is designed to test the performance of the Bees Algorithm on a popular set of real-world test functions. The best-performing configurations for the Bees Algorithm, PSO and EA are given in Table 11.

Table 11. Protein folding benchmark problem—Parameter settings

(a) Bees Algorithm
Function	Population	Generations	stlim	ne	nre	nb	nrb
pf3	51	10,000	10	2	20	4	5
pf4	51	10,000	10	2	20	4	5
pf5	51	10,000	10	2	20	4	5
pf6	102	5,000	10	1	40	4	20
(b) PSO
Function	Population	Generations	Connectivity	Speed
pf3	51	10,000	51	0.01
pf4	51	10,000	51	0.01
pf5	51	10,000	51	0.005
pf6	102	5,000	2	0.1
(c) EA
Function	Population	Generations	Selection procedure	Crossover type	Crossover rate	Mutation rate	Mutation width
pf3	51	10,000	Ranking	Inter	0.75	0.25	0.05
pf4	51	10,000	Adaptive	2-point	1	0.05	0.1
pf5	51	10,000	Ranking	Inter	0.75	0.05	0.05
pf6	102	5,000	Ranking	Inter	0.75	0.05	0.05

The optimisation results are compared in Table 12. For each benchmark, the results obtained by the best-performing configurations are compared using same criteria (success rate, accuracy and speed) utilised in Table 10. The results of the best-performing algorithm are shaded in grey.

Table 12. Comparison of optimisation procedures on protein folding benchmarks

Function	Bees Algorithm			PSO					EA
	Success	Accuracy	Speed	Success	Accuracy	p (Accuracy)	Speed	p (Speed)	Success	Accuracy	p (Accuracy)	Speed	p (Speed)
pf3	50	0.0000	1,454	50	0.0000	–	4,845	0.0000	50	0.0000	–	1,275	0.0059
pf4	49	0.0007	2,346	47	0.0008	0.0015	17,876	0.0000	50	0.0000	–	71,961	0.0000
pf5	50	0.0000	3,188	50	0.0000	–	29,631	0.0000	50	0.0000	–	25,985	0.0000
pf6	48	0.0008	14,8642	18	0.4092	0.0000	510,000	0.0000	0	0.7158	0.0000	510,000	0.0000

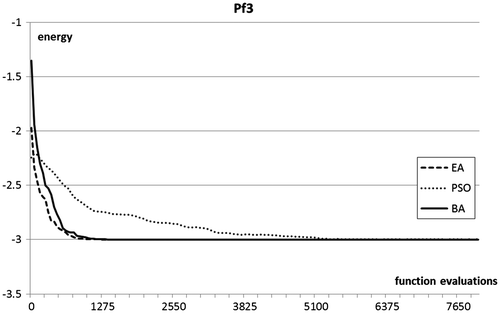
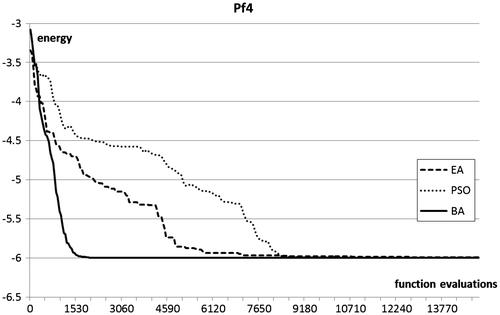
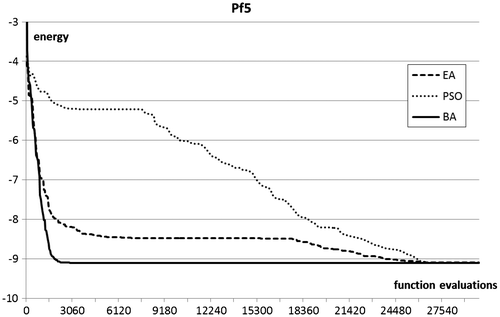
Figures 4–7 plot the evolution of the top fitness in the population during a sample run of the three optimisation procedures.

Figure 4. Optimisation plots for pf3 folding benchmarks.

Figure 5. Optimisation plots for pf4 folding benchmarks.

Figure 6. Optimisation plots for pf5 folding benchmarks.

Figure 7. Optimisation plots for pf6 folding benchmarks.

On this set of benchmarks, the Bees Algorithm benefits from mainly exploitative approaches, where all the foragers congregate on only four sites at a time. Also in this case, all the best parameterizations feature the highest value for the stagnation limit. Except for the highest dimensional pf6 benchmark, an exploitative search approach works best for the PSO. In this case, the use of full population connectivity (51) speeds up the convergence towards the fittest particle, and a low maximum speed reduces the exploration capability of the agents. The results confirm the importance of a high crossover rate for the performance of the EA, whilst fitness ranking and interpolation crossover work best in three cases out of four.

For all three algorithms, depth-search configurations excel on the first three functions, and breadth search on the last. The use of a large population probably helps the exploration of the large 18D pf6 space.

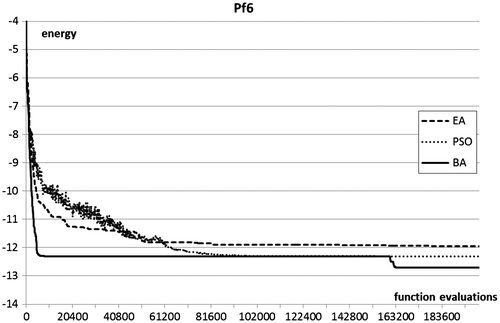
In terms of optimisation results, the Bees Algorithm excels on the two test functions of highest dimensionality, and obtains very competitive results in the other two. In particular, the Bees Algorithm is the only procedure that obtains nearly full success rate on the high-dimensional pf6 benchmark. Figure 7 shows that on this benchmark the performance of the EA stagnates after a certain number of generations, whilst the PSO maintains a slower but steady progress. The steepness of the optimisation curves (Figures 4–7) proves the ability of the Bees Algorithm to achieve fast progress on the protein folding benchmarks.

In general, the results obtained by the three algorithms compare well with the literature. For a reference, the reader may compare the results plotted in Figures 4–7 with those obtained by other six public domain optimisation methods plotted by Mongeau et al. (2000).

9. Discussion of results

The results of the tests on the two-dimensional benchmarks show that when the fitness landscape gives some information on the location of the optimum, the Bees Algorithm benefits most from exploitative search approaches. Otherwise, the winning strategy is to split the foragers and perform many parallel local searches. Overall, the Bees Algorithm benefitted most from a high stagnation limit and the use of the depth-search strategy.

Pham and Castellani (2009) reported the good performance of exploitative strategies characterised by a high stagnation limit, and focusing the search effort on a few selected sites. As mentioned in Section 4.1, the tests were performed on 12 popular benchmarks. Given that many of these functions are unimodal or give some indication on the location of the peak, the observations of Pham and Castellani (2009) are in good agreement with the results obtained on functions 12 and 14–18.

Functions 3–18 were used by Pham and Castellani (2013) to investigate specific abilities and biases of the Bees Algorithm, PSO, EA and ABC. Functions 1, 2, 4a, 4b, 8a, 8b, 10a,and 10b were purpose built for the specific tests described in this paper. The results of the comparison performed in Section 7 corroborate and complement the findings of the previous study (Pham & Castellani, 2013). In their earlier work, the authors (Pham & Castellani, 2013) focused on robust performance across the various groups of benchmarks (two- and multi-modal, flat, valley-like, etc.). In the present study (Section 7), they focused on top performance, and considered the best performing configuration for each algorithm on each individual benchmark. Other specific contributions of the present work are the study of the robustness of the Bees Algorithm to changes of parameterization (Section 6), and the comparison of the performance of the Bees Algorithm, PSO and EA on real-world test cases of varying dimensionality (Section 8).

The results confirm also that the proposed benchmarks constitute a set of varied and challenging functions for the study of optimisation algorithms. Fairly different configurations of the Bees Algorithm, PSO and EA are needed to solve optimally the test problems. The difference in the configurations can be often explained in term of the trade-off between exploration and exploitation needs, or known biases of the algorithms. Several benchmarks proved also difficult for the PSO. Even though the proposed study is limited to the particular implementations of the procedures used, and the restricted number of configurations tested, the results may point out some specific abilities of the Bees Algorithm.

It is important to emphasise that the features of the proposed benchmarks (arrangement of the peaks, position of the optimum, flat surfaces, unimodal with potholes, etc.) are independent of the dimensionality of the functions. That is, the experimental results presented in this paper are of general validity for any number of optimisation parameters. Thus, the proposed benchmarks allow the user to test the performance of different optimisation algorithms using simple and easy to visualise low-dimensional functions.

The comparison with the EA and PSO confirms the weaker performance of the Bees Algorithm (Karaboga & Basturk, 2008; Pham & Castellani, 2009) on noisy unimodal search surfaces (functions 14–18). On all the other benchmarks, the Bees Algorithm performs comparatively well.

The results highlight the advantages of the adaptive EA selection procedure used in this study. Thanks to its adoption, the performance of the EA compared much more favourably than in other studies to the performance of the PSO and Bees Algorithm (Karaboga & Basturk, 2008; Pham & Castellani, 2009).

Out of the three algorithms tested, the PSO is the only algorithm that does not use any feedback to adjust its behaviour according to the progress of the search, like the site abandonment procedure (Bees Algorithm) and the adaptive selection routine (EA). This might explain the inferior results obtained by the PSO on the benchmarks used in this study. Future work should include more complex PSO implementations such as multiswarm PSO (Blackwell & Branke, 2004), where a mechanism equivalent to site abandonment is used.

Even though it is not guaranteed that the EA and PSO are the most competitive algorithms on the proposed benchmarks, it is reasonable to assume that the best-performing configurations were fairly adapted to the test problems. Indeed, for every benchmark the best-performing algorithm was chosen out of 32 configurations including different operators and parameterizations. It is also important to point out that the proposed study did not aim to find the best-performing algorithm on the various test problems. The study compared the relative performances of the Bees Algorithm and two others in order to understand which algorithm and why works best. To make the study easily accessible to the widest audience, well-known and well-understood procedures such as EAs and PSO were chosen for the comparison.

Overall, the main factors affecting the performance of the algorithms and configurations tested were the complexity and deceptiveness of the search space. The effect of search biases resulting from the arrangement of the minima (e.g. on a grid) or the position of the global optimum were not statistically significant. In terms of location error and success rate the Bees Algorithm and EA performed comparably. The Bees Algorithm attained top accuracy (i.e. zero location error) in all 18 cases (Table 9) and the EA 15 times. The Bees Algorithm achieved 100% success rate on 17 benchmarks out of 18, the EA obtained full or close to 100% success rate on 17 benchmarks. These results suggest that, if speed is not paramount, the two algorithms can be considered to perform equivalently on this kind of functions.

The tests on the protein folding benchmarks confirm the competitiveness of the Bees Algorithm also on benchmarks of higher dimensionality. In particular, the Bees Algorithm outperforms the other two search procedures on the two highest dimensional functions, in terms of optimisation speed (pf5) and success rate (pf6). The results obtained by the Bees Algorithm on the protein folding functions are competitive also with those obtained by other algorithms in the literature.

10. Conclusions

Given a search problem, which optimisation algorithm should be chosen? How should the algorithm be configured? The optimisation literature offers a wide choice of procedures and operators, which are often tried on a common set of popular test functions. Unfortunately, the representativeness of this set of benchmarks is limited, allowing only a partial evaluation of the merits and drawbacks of the different methods.

This paper made two main contributions to the understanding of the behaviour of the Bees Algorithm: the first in the general field of benchmarking of population-based optimisation systems, and the second in the characterisation of the Bees Algorithm.

The first contribution consists of the eighteen new function minimisation benchmarks presented in Section 4. Although not exhaustive, the proposed set of functions offers a wide and varied choice of test cases. To the best of our knowledge, this is one of the few attempts in the literature to build a systematic collection of fitness landscapes.

All the 18 test functions are two-dimensional, and many of them present relatively straightforward fitness landscapes. This allows the user easily to visualise and understand the nature and the difficulty of the optimisation problem.

The 18 benchmarks were used to test the performance of the Bees Algorithm (Section 5), and compare it with that of an EA and a PSO (Section 7). Different algorithms excelled on different benchmarks, and each algorithm required different parameterizations to achieve top performance on the different benchmarks. Some of the benchmarks proved difficult to solve, particularly for the PSO. These results prove that, in spite of their simplicity, the proposed benchmarks represent a varied and challenging set of test problems.

As discussed in Section 9, the optimisation trials on the eighteen benchmarks highlighted the strengths and weaknesses of the Bees Algorithms in comparison to the EA and PSO. They also revealed the effects of different choices of parameterization on the search performance of the algorithms. These results represent the second contribution made by the present paper.

On the true multidimensional benchmarks, the main configuration issue for the Bees Algorithm concerns the allocation of foragers. A high stagnation limit, a moderate population size, and a long evolution time give optimal results across several kinds of fitness landscapes. The experimental results show also a substantial equivalence of the Bees Algorithm and EA in terms of success rate, search accuracy, and optimisation speed. However, the two algorithms excelled in complementary optimisation landscapes. Overall, the Bees Algorithm seems to work best when the search requires the exploration of large spaces, and landscapes composed of several basins of attraction. When the search problem requires overcoming many local potholes on a more regular fitness surface, the EA excelled.

The optimisation trials on the protein folding benchmarks added further evidence that the Bees Algorithm is able to achieve performances competitive with those of the EA, PSO and other state-of-the-art optimisers.

The experimental tests described in Section 6 proved that, given a fixed parameterization, the performance of the Bees Algorithm is robust to reasonable variations of the fitness surface. To the best of our knowledge, this is the first study of the tolerance of the Bees Algorithm to moderate variations of the fitness landscape.

Despite the great care taken in designing the benchmark functions, the results of this paper should not be taken as an indication of the absolute effectiveness of the optimisation methods tested (No Free Lunch Theorem (Wolpert & Macready, 1997)). The validity of the results is limited to the kind of benchmarks tested, the versions of the algorithms examined in the tests, and the kind of operators used.

The range of applicability of the Bees Algorithm to the field of engineering encompasses a large number of optimisation tasks. It comprises any problem amenable to being encoded via a fitness evaluation function, and allowing some sort of parametric representation of the solutions. Fields of application include mechanical components design (Pham, Ghanbarzadeh, Otri, & Koç, 2009), pattern classifier optimisation (Pham & Darwish, 2010), time-series modelling and prediction, control and identification of dynamic (Castellani et al., 2012) and nonlinear processes (Fahmy et al., 2012), optimisation of controllers (Pham et al., 2009), robotic swarm coordination (Jevtic et al., 2010), protein structure prediction (Jana, Sil, & Das, 2015), thermal engineering design (Zarea, Moradi Kashkooli, Mansuri Mehryan, Saffarian, & Namvar Beherghani, 2014), multimodal function optimisation (Zhou, Xie, Pham, Kamsani, & Castellani, 2015), chaos control in a rod-type plasma torch system (Gholipour, Khosravi, & Mojallali, 2015), feature selection (Packianather & Kapoor, 2015) and combinatorial optimisation problems such as PCB assembly optimisation (Pham, Otri, & Darwish, 2007), gene regulatory networks learning (Ruz & Goles, 2013) and machine job scheduling (Packianather et al., 2014).

In this study, we analysed only benchmarks constrained within convex continuous solution spaces. Further benchmarking work should include combinatorial optimisation problems, continuous problems including discontinuous or concave solution sets and problems characterised by mixed variables.

Notation
ABC	=	artificial bee colony
ACO	=	ant colony optimisation
EA	=	evolutionary algorithm
ES	=	evolutionary strategies
PSO	=	particle swarm optimisation
SI	=	swarm intelligence
VNS	=	variable neighbourhood search

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Duc Truong Pham

Duc Truong Pham has made wide-ranging contributions to the theory and practice of mechanical, manufacturing and systems engineering. His academic output includes over 500 technical papers and 15 books. He has supervised over 100 PhD theses to completion. He has won over of £30 M in research grants and contracts. He is the creator of the Bees Algorithm, a popular biologically inspired method for parameter optimisation. His is research interests include rapid manufacturing, micro manufacturing, automation, IT and intelligent systems.

Marco Castellani

Marco Castellani is lecturer at the School of Mechanical Engineering. He has done research for 20 years in a broad interdisciplinary area encompassing engineering, biology and computer science. He has worked on a wide range of application areas including motor control, remote sensing, pattern recognition, optimisation, systems modelling, natural language processing and ecological modelling. He has published over 40 research papers in scientific journals and international conferences.