A periodic review integrated inventory model for buyer’s unidentified protection interval demand distribution

Abstract

Nowadays, considering inflation observed in most societies, it is important to investigate on effect of this phenomenon on inventory/production decisions. Consequently, the paper aims to study the influence of inflationary condition on a specific periodic review integrated vendor–buyer inventory system in the presence of vendor’s imperfect manufacturing process. The lead time crashing cost is represented as a piecewise linear function of reduced lead time. In practice, the identification of the protection interval demand distribution of restricted data is a difficult task. As a result, this investigation assumes that the information about the protection interval demand for buyer is limited to its mean and standard deviation. Buyer’s ordering cost can be reduced through further investment. For the discussed model, an effective solution procedure is developed to determine optimal policy. Theorems on conditional convexity and concavity of objective cost function in the decision variables of the respective inflationary integrated inventory system are shown and proved. A numerical example is presented to illustrate the results of the proposed model.

Keywords:

• supply chain
• integrated vendor–buyer inventory model
• periodic review
• lead time
• ordering cost
• inflation
• nonlinear stochastic optimization, costing and pricing

Public Interest Statement

The inventory problem regarding integration between buyer and vendor has been received a lot of attention in recent years. Firms are appreciating that a more appropriate result is achieved over better coordination and cooperation of all parties involved a supply chain. Also, the significance of inflation and time value of money in inventory/production control systems is indisputable for modern decision-makers. Besides, lead time plays an important role in modern inventory management. In this paper, an integrated vendor–buyer periodic review inventory model under inflationary condition in the presence of vendor’s imperfect manufacturing system is developed.

1. Introduction

In many deterministic or stochastic inventory research papers, one facility (e.g. a buyer or a vendor) is assumed to minimize its own cost or maximize its own profit. This one-sided-optimal-strategy is not appropriate for global market. However, according to the just-in-time philosophy, many researchers concentrated on integration between buyer and vendor. Once they form a long-term strategic alliance, both facilities can cooperate and share information to achieve improved benefits.

The study of an integrated inventory model for vendor and buyer is pioneered by Goyal (1976). Subsequently, many researchers investigated this issue under various assumptions. For instance, Banerjee (1986) generalizes the model of Goyal (1976) by incorporating a finite vendor’s replenishment rate. Goyal (1988) extends Banerjee’s work by relaxing the lot-for-lot production policy for the vendor and assumes that the vendor’s lot size is an integral multiple of the buyer’s order quantity. Pan and Yang (2002) generalize Goyal (1988) by considering lead time as a decision variable and obtain a lower joint total expected cost and shorter lead time of integrated supply chain. Ouyang, Wu, and Ho (2004) extend Pan and Yang (2002) model considering reorder point as one of decision variable and shortages allowed. Chang, Ouyang, Wu, and Ho (2006) propose an integrated vendor–buyer cooperative inventory model in which lead time and ordering cost are controllable. They consider that buyer lead time can be reduced at an extra crashing cost C(L) which depends on the lead time length and ordering lot size. Lin (2009) presents an integrated vendor–buyer model with backorder price discount and ordering cost reduction. Shah (2015) proposes a manufacturer–retailer inventory model with deteriorating items and considers permissible delay in payment in the model. Alimardani, Rafiei, and Rabbani (2015) present an inventory model of two-layer supply chain including manufactures and retailers in a coordinated system environment.

In the inventory management literature, lead time and setup/ordering cost is treated as predetermined input parameters and therefore they are not subject to any control. Recently, based on modern production management, many research works in the inventory literature have been devoted to the study of changing some of the usual given parameters (setup/ordering cost, lead time, quality level, etc.) on the inventory system performances. This literature can be divided into two main categories: the first deals with lead time reduction, the second with setup/ordering cost reduction.

In the first category, if it is assumed that lead time can be decomposed into several components, such as setup time, process time, and queue time, it can be assumed that each component may be reduced at a C(L). One of first papers dealing with a lead time reduction policy in an inventory model is due to Liao and Shyu (1991). The authors assume that lead time can be decomposed into several components may be reduced to a given minimum duration. Under the assumption that the lot size is predetermined and demand is normally distributed, they calculate an optimal lead time and show that reducing lead time may result in lower expected total cost. Ben-Daya and Raouf (1994) extend this model by considering both lead time and order quantity as decision variables. The developed two models, one that used the lead time crashing cost-function proposed by Liao and Shyu (1991) and one that used an exponential C(L) function. Moon and Gallego (1994) assume unfavorable lead time demand (LTD) distribution and solved both continuous review and periodic review models with a mixture of backorders and lost sales using minimax distribution free approach. Ouyang, Yeh, and Wu (1996) introduce another extension and include shortages in the model. They assumed that a certain fraction of demand during stock out period is backordered and that remaining fraction results in lost sales. Later, Hariga and Ben-Daya (1999) extend Ouyang et al. (1996) study and presented both continuous review and periodic review inventory models in partial and perfect LTD distribution information environment in which reorder point treated as a variable. Chuang, Ouyang, and Chuang (2004) propose a periodic review inventory model with a mixture of backorders and lost sales by controlling lead time in order to reduce the inventory operating cost. Lee (2005) considers an inventory model involving variable lead time and they assumed that LTD follows a mixture of distribution. The previously mentioned studies, lead time C(L) is fixed and independent on ordering quantity. Pan, Hsiao, and Lee (2002) considered that lead time C(L) depends on ordering quantity and reduced lead time and proposed a solution procedure to solve the problem. Gholami-Qadikolaei and Mirzazadeh (2013) generalize minimax distribution free procedure for a constrained inventory problem with unknown LTD distribution.

Dealing with the second line of research, in some practical situations, ordering/setup cost can also be controlled and reduced through various efforts such as worker training, procedural changes, and specialized acquisition for the classical inventory/production model. The initial result in development of ordering/setup cost reduction model is that of Porteus (1985) who introduces a framework of the setup cost reduction in the classical economic order quantity (EOQ) and then, many authors such as Billington (1987), Kim and Hayya (1992), Paknejad, Nasri, and Afflsco (1995), Sarker and Coates (1997) explore more investigations in this area. Wu and Lin (2004) study on lead time and ordering cost reduction when the receiving quantity is different from the ordered quantity. Lee, Wu, and Lei (2007) consider an inventory model with backorder discount and ordering cost reduction including mixture of LTD distribution.

The effect of inflation and time value of money are vital in practical environment. Especially in developing countries with double-digit Gross National Product rates. The analysis of inventory systems under inflationary condition in the literature is carried out using two procedures. The first one determines optimal values of the control variables by minimizing the average annual cost, and the second one determines the optimal ordering policy by minimizing the discounted value of all future costs. Hadley (1964) shows that the detailed computations in the simplest case, corresponding to the familiar deterministic lot size model, the ordering quantities computed by minimizing the average annual cost and by minimizing the discounted cost do not differ significantly. Mirzazadeh (2011) extends the Hadely’s work by minimizing the inflation and time value of money under uncertain conditions, shortages, and the effects of deterioration. The above-mentioned system is formulated with two methods, which are derived under some assumptions that the objective of inventory management is to minimize the average annual cost and the discounted cost. These methods are compared to each other carefully. The results reveal that the mentioned methods (the average annual cost and the discounted cost) have a negligible different to each other. Besides, a number of papers have considered the effect of inflation on the inventory system since 1975. Buzacott (1975) and Misra (1975) develop an EOQ model with fixed inflation rate for all related costs. Bierman and Thomas (1977) propose an inventory model under inflationary condition that also incorporated the discount rate. Then, Misra (1979) extends an inventory model with different inflation rates for various related cost. Yang, Teng, and Chern (2001) develop different inventory models with time varying demand patterns under inflation. Moon, Giri, and Ko (2005) develop an inflation EOQ model for both ameliorating and deteriorating items assuming not only a constant length of each replenishment, but also, a constant fraction of shortage length with respect to the cycle length. Mirzazadeh, Seyyed Esfahani, and Fatemi Ghomi (2009) consider stochastic inflationary conditions with variable probability density functions over the time horizon and the demand rate is dependent to inflation rates. The developed model also implicates to a finite replenishment rate and finite time horizon with shortage. The objective is to minimize the expected present value of costs over the time horizon.

One of the assumptions of the inventory management literature is that the quality of the product in a lot is perfect. In practice, however, a received lot may contain some defective items. If there is a possibility that a lot contains defective items, the firm may issue a larger order than was originally planned so as to guarantee satisfaction of customer demand. Wu and Ouyang (2001) examine the effect of defective items on a mixture of backorders and lost sales inventory models and using the result of a basic theorem from renewal reward processes Ross (1996) they calculate expected annual cost. Ben-Daya and Noman (2008) propose integrated inventory models for inspection policies in which the number of defective units is beta-binomial random variable. Taheri-Tolgari, Mirzazadeh, and Jolai (2012) present a discounted cash-flow approach for an inventory model for imperfect item with considering inspection errors. They assume some produced items might not be perfect and first stage inspector of product quality control might make some inspection errors during separation of defective and perfect items.

In this investigation, the previous literature is extended by considering an integrated vendor–buyer periodic review inventory model under inflationary condition in the presence of vendor’s imperfect manufacturing system. The probability density function of demand during protection period (i.e. review period plus lead time) is unknown with given mean and variance. A minimax distribution-free procedure is applied in order to solve the proposed inventory system and a solution procedure is developed to determine optimal decision variables so that the joint expected annual cost of respective system is minimized. Finally, a numerical example is provided to illustrate the behavior of proposed model.

2. Notations and model assumptions

The following notations are employed throughout the paper.

T	=	length of a review period, decision variable
L	=	length of lead time, decision variable
A	=	buyer’s ordering cost per order at the time zero, decision variable
M	=	the number of production cycle, a positive integer (decision variable)
R	=	buyer’s reorder point
K	=	safety factor
δ	=	fraction of defective items in each deliver,0 ≤ δ ≤ 1
D	=	average demands per year for buyer
P	=	production rate per year for vendor
I	=	inflation rate per unit time, as a random variable
π	=	buyer’s stock out cost per unit short at the time zero
C pr	=	vendor’s production cost per unit at the time zero
C pu	=	buyer’s purchasing cost per unit at the time zero
h V	=	vendor’s holding cost per year per unit at the time zero
h b	=	buyer’s holding cost per year per unit at the time zero
A 0	=	buyer’s original ordering cost per order
L 0	=	maximum length of lead time
S	=	vendor’s setup cost per set up at the time zero
X	=	demand during protection period (T + L), which has a p. d. f, f T + L (x)with mean D (T + L) and variance σ 2 (T + L)
X +	=	maximum value of x and 0
E (·)	=	mathematical expectation

Further, the following assumptions will be utilized in this investigation:

(1)	There is single-vendor and single-buyer for a single product in this article and the inventory system deal with one type item.
(2)	The buyer orders a quantity DT and the vendor produces MDT, with a finite production rate P(P(1 − δ) > D) at one setup but ships in quantity DT to the buyer over M times.
(3)	Shortages are allowed and fully backlogged.
(4)	Inventory is periodic reviewed.
(5)	The target level of R units is equal to the sum of buyer expected demand during the production period, $D\left(T\left(1-\mathit{\delta }\right)+L\right)$, and safety stock, $k{\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}$, where k is safety factor.
(6)	X (i.e. demand during protection interval), I (i.e. inflation rate) are independent random variables.
(7)	Each arriving lot contains a fixed fraction of defective items, $0\le \mathit{\delta }\le 1$ and the number of defective items is δDT. When a lot is arrived in the buyer, all the items are inspected by buyer and all defective items are assumed to be found out and returned to the vendor at the same time.
(8)	Inspection is error free and inspection time is negligible.
(9)	Transportation cost from vendor to the buyer and buyer’s inspection cost are constant and independent of the ordering quantity. Therefore, the total transportation and inspection costs in the model are ignored.
(10)	We assume that the capital investment, I(A), in reducing buyer’s ordering cost is a logarithmic function of the ordering cost A. That is,

$$I\left(A\right)=bln\left(\frac{A_0}{A}\right)for0<A\le A_0$$

(11)	where 1/b is the fraction of the reduction in A per dollar increase in investment.
(12)	The lead time consists of m mutually independent components. The zth component has a minimum duration a z , the normal duration b z , and a crashing cost c z per unit time. Further, for convenience, we rearrange c z such that c 1 ≤ c 2 ≤ … ≤ c m .
(13)	If we let $L_0={\sum }_{j=1}^m{b}_j$ and L z be the length of lead time with components 1, 2, …, z crashed to their minimum duration, then L z can be expressed as $L_z={\sum }_{j=1}^m{b}_j-{\sum }_{j=1}^z\left(b_j-a_j\right),z=1,2,\dots ,m$; and the lead time C(L) per cycle for a given $L\in [L_z,L_{z-1}]$ is given by $C\left(L\right)=c_z\left(L_{z-1}-L\right)+{\sum }_{j=1}^{z-1}{c}_j\left(b_j-a_j\right)$.
(14)	The components of lead time are crashed one at a time starting with component 1 (because, it has a minimum unit C(L)) and then component 2 and so on.

3. Model formulation

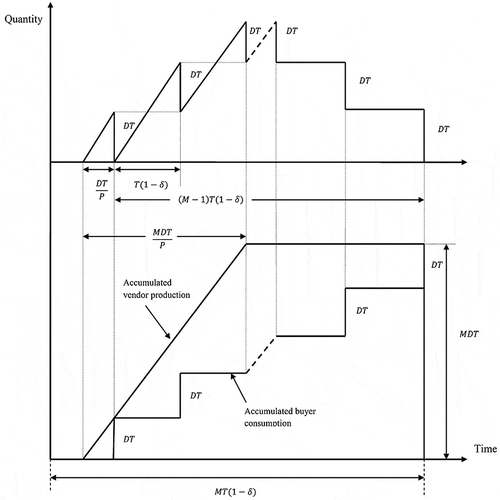
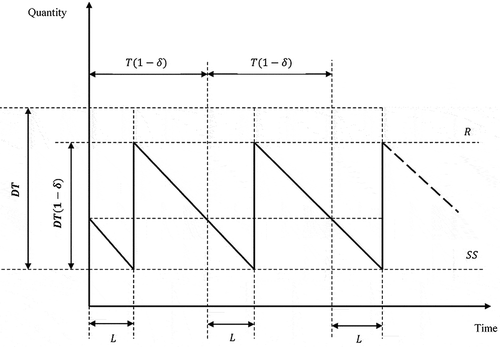
Consider a supply chain network with one vendor and one buyer. The vendor may be a manufacturer or a distributer and the buyer may be a downstream distributer or a retailer. The demand met by the buyer is probabilistic and the information about the probability distribution of the protection interval demand X is limited to its mean and standard deviation. Buyer’s ordering strategy is (T, R). Figures 1 and 2 show the inventory pattern for the buyer and the vendor and illustrate the common cycle coordinated inventory system proposed in this work.

Figure 1. Inventory level for the vendor

Figure 2. Inventory level for the buyer

3.1. Vendor’s expected annual cost

When the vendor produces the first DT units, he will deliver them to the buyer. After the first delivery and buyer’s inspection, the vendor will schedule successive deliveries every T(1 − δ) units of time until the inventory level falls to zero. Hence, total inventory for vendor is a random variable and can be expressed as follows:(1) $$\left[MDT\left(\frac{DT}{P}+\left(M-1\right)\left(T\left(1-\mathit{\delta }\right)\right)\right)-\frac{M^2{\left(DT\right)}^2}{2P}\right]-\left[D{T}^2\left(1-\mathit{\delta }\right)\left(1+2+\dots +\left(M-1\right)\right)\right]=\left[\frac{M{\left(DT\right)}^2}{P}-\frac{M^2{\left(DT\right)}^2}{2P}+\frac{M\left(M-1\right)D{T}^2\left(1-\mathit{\delta }\right)}{2}\right]$$(1)

Hence, dividing total inventory per cycle into vendor’s cycle time, $T_V=MT\left(1-\mathit{\delta }\right)$, average inventory level can be calculated as follows:(2) $$\left[\frac{M{\left(DT\right)}^2}{P}-\frac{M^2{\left(DT\right)}^2}{2P}+\frac{M\left(M-1\right)D{T}^2\left(1-\mathit{\delta }\right)}{2}\right]/MT\left(1-\mathit{\delta }\right)=\left[\frac{D^{2}T}{P\left(1-\mathit{\delta }\right)}\left(1-\frac{M}{2}\right)\right]+\frac{\left(M-1\right)DT}{2}$$(2)

The vendor’s total holding cost per year in the average annual cost method is dependent on the average inventory level. Thus, the buyer’s total holding cost per year with inflation can be computed as follows $\left(T_V=\frac{1}{n_V}=MT\left(1-\mathit{\delta }\right)\right)$:(3) $$\underset{0}{\overset{n_V{T}_V}{\int }}{h}_V\left[\left(\frac{D^{2}T}{P\left(1-\mathit{\delta }\right)}\left(1-\frac{M}{2}\right)\right)+\frac{\left(M-1\right)DT}{2}\right]\left(1+It\right)dt=h_V\left[\left(\frac{D^{2}T}{P\left(1-\mathit{\delta }\right)}\left(1-\frac{M}{2}\right)\right)+\frac{\left(M-1\right)DT}{2}\right]\left(1+\frac{I}{2}\right)$$(3)

Hence, the expected value of the holding cost per year with inflation (EHCWI _V ) for buyer is computed by:(4) $$\text{EHCWI}=h_V\left[\left(\frac{D^{2}T}{P\left(1-\mathit{\delta }\right)}\left(1-\frac{M}{2}\right)\right)+\frac{\left(M-1\right)DT}{2}\right]\left(1+\frac{E\left(I\right)}{2}\right)$$(4)

Also, according to computing the vendor’s inventory costs with inflation, this study assumes setup cost for vendor is paid at the beginning of the cycle. So, total setup cost per year with inflation can be calculated as follows $\left(T_V=\frac{1}{n_V}=MT\left(1-\mathit{\delta }\right)\right):$ (5) $$S+S\left(1+MT\left(1-\mathit{\delta }\right)I\right)+S\left(1+2MT\left(1-\mathit{\delta }\right)I\right)+\dots +S\left(1+\left(n-1\right)MT\left(1-\mathit{\delta }\right)I\right)=S\sum _{j=0}^{n_V-1}\left(1+MT\left(1-\mathit{\delta }\right)Ij\right)=S\left[n+MT\left(1-\mathit{\delta }\right)I\frac{n_V\left(n_V-1\right)}{2}\right]=S\left[\frac{1}{MT\left(1-\mathit{\delta }\right)}\left(1+\frac{I}{2}\right)-\frac{I}{2}\right]$$(5)

Thus, the expected value of setup cost per year for vendor (ESUCWI _V ) is obtained as follows:(6) $${\text{ESUCWI}}_V=S\left[\frac{1}{MT\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]$$(6)

Also, this study considers production cost is paid at the beginning of the vendor’s cycle. Hence, average production cost per unit is calculated as follows:(7) $$\frac{C_{pr}+C_{pr}\left(1+MT\left(1-\mathit{\delta }\right)I\right)+\cdots +C_{pr}\left(1+\left(n_V-1\right)MT\left(1-\mathit{\delta }\right)I\right)}{n_V}=\frac{C_{pr}}{n_V}\sum _{j=0}^{n_V-1}\left(1+MT\left(1-\mathit{\delta }\right)Ij\right)=\frac{C_{pr}}{n_V}\left[n_V+MT\left(1-\mathit{\delta }\right)I\frac{n_V\left(n_V-1\right)}{2}\right]=C_{pr}\left[1+\frac{I}{2}\left(1-T_V\left(1-\mathit{\delta }\right)\right)\right]$$(7)

Therefore, vendor’s total expected production cost per year with inflation is obtained as follows:(8) $${\text{EPCWI}}_V=\left(\frac{D{C}_{pr}}{1-\mathit{\delta }}\right)\left[1+\frac{E\left(I\right)}{2}\left(1-MT\left(1-\mathit{\delta }\right)\right)\right]$$(8)

Hence, the expected annual cost with inflation for vendor which is composed of holding cost, setup cost, and production cost is expressed as follows:(9) $${\text{EACWI}}_V\left(T,M\right)=h_V\left[\left(\frac{D^{2}T}{P\left(1-\mathit{\delta }\right)}\left(1-\frac{M}{2}\right)\right)+\frac{\left(M-1\right)DT}{2}\right]\left(1+\frac{E\left(I\right)}{2}\right)+S\left[\frac{1}{MT\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]+\left(\frac{D{C}_{pr}}{1-\mathit{\delta }}\right)\left[1+\frac{E\left(I\right)}{2}\left(1-MT\left(1-\mathit{\delta }\right)\right)\right]$$(9)

3.2. Buyer’s expected annual cost

In this subsection, the periodic review inventory model for buyer is considered. The inventory level of an item for buyer will be diminished due to the random demand. The buyer places an order with the amount of DT, which, DTδ items are defective. The amount of shortages per cycle is a random variable since X (i.e. demand during protection period) is a random variable and can be expressed by:(10) $${\left(X-r\right)}^{+}=\text{Max}\left(X-r,0\right)=\left\{\begin{array}{c}X-r,x\ge r\\ 0,x\le r\end{array}\right.$$(10)

Buyer’s shortage cost is assumed to pay at the end of protection interval. Therefore, buyer’s total shortages cost per year with inflation is a random variable and can be obtained as follows $\left(n_b=\frac{1}{T_b}=T\left(1-\mathit{\delta }\right)\right)$:(11) $$\mathit{\pi }{\left(X-R\right)}^{+}\left(1+LI\right)+\mathit{\pi }{\left(X-R\right)}^{+}\left(1+LI+T\left(1-\mathit{\delta }\right)I\right)+\mathit{\pi }{\left(X-R\right)}^{+}\left(1+LI+2T\left(1-\mathit{\delta }\right)I\right)+\dots +\mathit{\pi }{\left(X-R\right)}^{+}\left(1+LI+\left(n-1\right)T\left(1-\mathit{\delta }\right)I\right)=\mathit{\pi }{\left(X-R\right)}^{+}\sum _{j=0}^{n-1}\left(1+LI+T\left(1-\mathit{\delta }\right)Ij\right)=\mathit{\pi }{\left(X-R\right)}^{+}\left[n+nLI+T\left(1-\mathit{\delta }\right)I\frac{n\left(n-1\right)}{2}\right]=\mathit{\pi }{\left(X-R\right)}^{+}\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+LI+\frac{I}{2}\right)-\frac{I}{2}\right]$$(11)

Hence, by considering (I, X) as independent random variables, the buyer’s expected shortages cost per year with inflation (ESCWI _b ) is obtained by:(12) $${\text{ESCWI}}_b=\mathit{\pi }E{\left(X-r\right)}^{+}\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]$$(12)

The total holding cost per year with inflation for vendor can be obtained as follows:(13) $$\underset{0}{\overset{n_b{T}_b}{\int }}{h}_b\left[R-\frac{DT\left(1-\mathit{\delta }\right)}{2}-DL\right]\left(1+It\right)dt=h_b\left(1+\frac{I}{2}\right)\left[R-\frac{DT\left(1-\mathit{\delta }\right)}{2}-DL\right]$$(13)

Hence, by considering (I, X) as independent random variables, the buyer’s expected shortages cost per year with inflation (EHCWI _b ) is obtained by:(14) $${\text{EHCWI}}_b=h_b\left(1+\frac{E\left(I\right)}{2}\right)\left[R-\frac{DT\left(1-\mathit{\delta }\right)}{2}-DL\right]$$(14)

In this paper, we consider that the buyer’s ordering cost will be paid at the beginning of cycle. After some calculation and taking expected value, the buyer’s expected ordering cost per year with inflation can be calculated as follows:(15) $$\left(A+c_z\left(L_{z-1}-L\right)+\sum _{j=1}^{z-1}{c}_j\left(b_j-a_j\right)\right)\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]$$(15)

Besides, we consider that the buyer’s ordering cost can be reduced through capital investment. Hence, buyer’s expected ordering cost per year with inflation (EOCWI _b ) can be expressed as follows:(16) $${\text{EOCWI}}_b=\mathit{\theta }bln\left(\frac{A_0}{A}\right)+\left(A+c_z\left(L_{z-1}-L\right)+\sum _{j=1}^{z-1}{c}_j\left(b_j-a_j\right)\right)\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right],A\in \left(\left.0,A_0\right]\right.$$(16)

In addition, we assume that purchasing cost is paid at the time an order is received. Hence, after some calculations and taking expected value, the buyer’s expected purchasing cost per year with inflation (EPCWI _b ) can be expressed as follows:(17) $${\text{EPCWI}}_b=D{C}_{pu}\left[1+LE\left(I\right)+\frac{E\left(I\right)}{2}\left(1-T\left(1-\mathit{\delta }\right)\right)\right]$$(17)

Consequently, the expected annual cost with inflation for buyer can be obtained as follows:(18) $${\text{EACWI}}_b(T,A,L)=\mathit{\theta }bln\left(\frac{A_0}{A}\right)+\left(A+C_z(L_{z-1}-L)+\sum _{j=1}^{z-1}{c}_j(b_j-a_j)\right)\left[\frac{1}{T(1-\mathit{\delta })}\left(1+\frac{E(I)}{2}\right)-\frac{E(1)}{2}\right]+h_b\left(1+\frac{E(I)}{2}\right)\left[R-\frac{Dt(1-\mathit{\delta })}{2}-DL\right]+\mathit{\pi }E{(X-R)}^{+}\left[\frac{1}{T(1-\mathit{\delta })}\left(1+LE(I)+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+D{C}_{pu}\left[1+LE(I)+\frac{E(I)}{2}\left(1-T(1-\mathit{\delta })\right)\right],A\in (0,A_0],L\in \left[L_z,L_{z-1}\right],T\ge 0$$(18)

3.3. Joint expected annual cost and optimal solution

In this subsection, we consider the situation where vendor and buyer coordinate their production and inventory strategies to each other to determine their best policy for the periodic review inventory supply chain system. Therefore, the joint expected annual cost with inflation is given by:(19) $$\text{JEACWI}(T,A,L,M)={\text{EACWI}}_b(T,A,L)+{\text{EACWI}}_v(T,M)=\mathit{\theta }bln\left(\frac{A_0}{A}\right)+\left(A+C_z(L_{z-1}-L)+\sum _{j=1}^{z-1}{c}_j(b_j-a_j)\right)\left[\frac{1}{T(1-\mathit{\delta })}\left(1+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+h_b\left(1+\frac{E(I)}{2}\right)\left[R-\frac{Dt(1-\mathit{\delta })}{2}-DL\right]+\mathit{\pi }E{(X-R)}^{+}\left[\frac{1}{T(1-\mathit{\delta })}\left(1+LE(I)+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+D{C}_{pu}\left[1+LE(I)+\frac{E(I)}{2}\left(1-T(1-\mathit{\delta })\right)\right]+h_v\left[\left(\frac{D^{2}T}{P(1-\mathit{\delta })}\left(1-\frac{M}{2}\right)\right)+\frac{(M-1)DT}{2}\right]\left(1+\frac{E(I)}{2}\right)+S\left[\frac{1}{MT(1-\mathit{\delta })}\left(1+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+\left(\frac{D{C}_{pr}}{1-\mathit{\delta }}\right)\left[1+\frac{E(I)}{2}\left(1-MT(1-\mathit{\delta })\right)\right],A\in (0,A_0],L\in \left[L_z,L_{z-1}\right],T\ge 0,M>0\text{integer}$$(19)

In many practical situations, the probability distributional information of protection interval demand is often quite limited and thus, we cannot find the precise value of expected shortage, $E{\left(x-R\right)}^{+}$. Hence, in this situation, it is assumed that the protection interval demand, X, has given finite first two moments (thus, mean and variance are also given); i.e. the p. d. f. f _x of X belongs to the class $\mathcal{F}$ p. d. f. s with finite mean $D(T\left(1-\mathit{\delta }\right)+L)$ and standard deviation $\mathit{\sigma }\sqrt{T\left(1-\mathit{\delta }\right)+L}$. Now, we try to use the minimax distribution free procedure to solve the problem. The minimax distribution free approach for this problem is to find the “most unfavorable” p. d. f. f _x in $\mathcal{F}$ for each $\left(T,A,L,M\right)$ and then to minimize over $\left(T,A,L,M\right)$; therefore, the following problem is to solve:

$$\underset{T,A,M,L{f}_X\in \mathcal{F}}{\text{Min}}\text{Max}EAC\left(T,A,L,M\right)$$

For the above problem, the following proposition which is asserted by Gallego and Moon (1993) is applied to solve the problem:

Proposition 1. For any $f_x\in \mathcal{F}$

(20) $$E{\left(X-R\right)}^{+}\le \frac{1}{2}\left[\sqrt{{\mathit{\sigma }}^2\left(T\left(1-\mathit{\delta }\right)+L\right)+{\left[R-D\left(T\left(1-\mathit{\delta }\right)+L\right)\right]}^2}-\left[R-D\left(T\left(1-\mathit{\delta }\right)+L\right)\right]\right]=\frac{1}{2}\left({\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}\right)\left(\sqrt{1+k^2}-k\right)$$(20)

Moreover, the upper bound of the above equation is tight.

Because, $R=D\left(T\left(1-\mathit{\delta }\right)+L\right)+k{\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}$, and for any probability distribution of the protection interval demand X, the above inequality always holds. Then, from model (19) and inequality (20), the respective model is reduced to:(21) $$\text{JEACWI}(T,A,L,M)=\mathit{\theta }bln\left(\frac{A_0}{A}\right)+\left(A+C_z(L_{z-1}-L)+\sum _{j=1}^{z-1}{c}_j(b_j-a_j)\right)\left[\frac{1}{T(1-\mathit{\delta })}\left(1+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+h_b\left(1+\frac{E(I)}{2}\right)\left[\frac{DT(1-\mathit{\delta })}{2}+k{\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}\right]+\frac{\mathit{\pi }}{2}\left(\sqrt{1+k^2}-k\right){\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}\left[\frac{1}{T(1-\mathit{\delta })}\left(1+LE(I)+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+D{C}_{pu}\left[1+LE(I)+\frac{E(I)}{2}\left(1-T(1-\mathit{\delta })\right)\right]+h_v\left[\left(\frac{D^{2}T}{P(1-\mathit{\delta })}\left(1-\frac{M}{2}\right)\right)+\frac{(M-1)DT}{2}\right]\left(1+\frac{E(I)}{2}\right)+S\left[\frac{1}{MT(1-\mathit{\delta })}\left(1+\frac{E(I)}{2}\right)-\frac{E(I)}{2}\right]+\left(\frac{D{C}_{pr}}{1-\mathit{\delta }}\right)\left[1+\frac{E(I)}{2}\left(1-MT(1-\mathit{\delta })\right)\right],A\in (0,A_0],L\in \left[L_z,L_{z-1}\right],T\ge 0,M>0\text{integer}$$(21)

To solve the above nonlinear programming problem, this study temporarily ignores the constraint 0 ≤ A ≤ A ₀ and relaxes the integer requirement on M (the number of shipments from the vendor to the buyer during one production cycle). Taking the second partial derivative of $\text{JEACWI}\left(T,A,L,M\right)$with respect to M, we have:(22) $$\frac{{\mathit{\partial }}^2\text{JEACWI}\left(T,A,k,M\right)}{\mathit{\partial }{M}^2}=\frac{2S}{M{T}^3\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)\ge 0$$(22)

Therefore, $\text{JEACWI}\left(T,A,L,M\right)$ is convex in M, for fixed T, A, and L. Hence, the search for the shipment number, M*, is reduced to find a local minimum. Also, for fixed (T, A, M), JEACWI (T, A, L, M) is a concave function in $L\in [L_z,L_{z-1}]$, if 0 < L < α(L) (see Appendix 1 for detailed proof). Consequently, for fixed (T, A, M), the minimum joint expected annual cost with inflation occurs at the end of points of the interval$\left[L_z,L_{z-1}\right]$.

For fixed M and $L\in [L_z,L_{z-1}]$, taking the first partial derivatives of JEACWI (T, A, L, M) with respect to T and A and setting them to zero, we have:(23) $$\frac{\mathit{\partial }\text{JEACWI}}{\mathit{\partial }T}=-\frac{\left(A+c_z\left(L_{z-1}-L\right)+{\sum }_{j=1}^{z-1}{c}_j\left(b_j-a_j\right)+\frac{S}{M}\right)\left(1+\frac{E\left(I\right)}{2}\right)}{T^2\left(1-\mathit{\delta }\right)}+h_b\left(1+\frac{E\left(I\right)}{2}\right)\left[\frac{D\left(1-\mathit{\delta }\right)}{2}+\frac{k{\mathit{\sigma }}_D\left(1-\mathit{\delta }\right)}{2\sqrt{T\left(1-\mathit{\delta }\right)+L}}\right]+\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{4}\right)\frac{\left(\sqrt{1+k^2}-k\right)\left(1-\mathit{\delta }\right)}{\sqrt{T\left(1-\mathit{\delta }\right)+L}}\left[\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right)}-\frac{E\left(I\right)}{2}\right]-\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{2}\right)\sqrt{T\left(1-\mathit{\delta }\right)+L}\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^2\left(1-\mathit{\delta }\right)}\right]-\frac{D{C}_{pu}E\left(I\right)\left(1-\mathit{\delta }\right)}{2}-\frac{D{C}_{pr}E\left(I\right)M}{2}+h_V\left[\frac{D^{2}p\left(1-\frac{M}{2}\right)}{P\left(1-\mathit{\delta }\right)}+\frac{\left(M-1\right)D}{2}\right]\left(1+\frac{E\left(I\right)}{2}\right)=0$$(23) (24) $$\frac{\mathit{\partial }\text{JEACWI}}{\mathit{\partial }A}=-\frac{\mathit{\theta }b}{A}+\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]=0$$(24)

Solving Equation (24) for A, respectively, produces:(25) $$A=\frac{\mathit{\theta }b}{\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]}$$(25)

Hence, substituting Equation (25) into (23) and solving Equation (23), we have(26) $$\left(\frac{\mathit{\theta }b}{\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]}+c_z\left(L_{z-1}-L\right)+\sum _{j=1}^{z-1}{c}_j\left(b_j-a_j\right)+\frac{S}{M}\right)\left(1+\frac{E\left(I\right)}{2}\right)\left(\frac{1}{T^2\left(1-\mathit{\delta }\right)}\right)=h_b\left(1+\frac{E\left(I\right)}{2}\right)\left[\frac{D\left(1-\mathit{\delta }\right)}{2}+\frac{k{\mathit{\sigma }}_D\left(1-\mathit{\delta }\right)}{2\sqrt{T\left(1-\mathit{\delta }\right)+L}}\right]+\frac{1}{4}\frac{\left(\sqrt{1+k^2}-k\right)\left(\mathit{\pi }{\mathit{\sigma }}_D\right)\left(1-\mathit{\delta }\right)}{\sqrt{T\left(1-\mathit{\delta }\right)+L}}\left[\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right)}-\frac{E\left(I\right)}{2}\right]-\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{2}\right)\sqrt{T\left(1-\mathit{\delta }\right)+L}\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^2\left(1-\mathit{\delta }\right)}\right]-\frac{D{C}_{pu}E\left(I\right)\left(1-\mathit{\delta }\right)}{2}-\frac{D{C}_{pr}E\left(I\right)M}{2}+h_V\left[\frac{D^{2}p\left(1-\frac{M}{2}\right)}{\left(1-\mathit{\delta }\right)}+\frac{\left(M-1\right)D}{2}\right]\left(1+\frac{E\left(I\right)}{2}\right)$$(26)

Furthermore, by examining the Second-Order Sufficient Condition (SOSC), it can be verified that, for a given value of M and $L\in [L_z,L_{z-1}]$ JEACWI (T, A) is a convex function of (T, A), if 0 ≤ T ≤ ρ (T) (see Appendix 1 for detailed proof).

Theoretically, for given $M,\mathit{\theta },b,h_V,S,D,{\mathit{\sigma }}_D,\mathit{\pi },A,h_b,\mathit{\delta },p,C_{pr},C_{pu}$ and k (which depends on the allowable shortage probability, q, and the p. d. f. f _x of the protection interval demand, X), solving Equations (25) and (26), we can find optimal (T, A), and from model (21), we can get the minimum joint expected annual cost with inflation $\text{JEACWI}\left(T,A\right)$. However, in practice, since the p. d. f. f _x is unknown, even if the value of q is given, we cannot get the exact value of k. So, to find the value of k (safety factor), the following proposition is needed.

Proposition 2 (Chuang et al., 2004). Let X represents the protection interval demand which has a p. d. f. f _x with finite D (T + L) and standard deviation $\mathit{\sigma }\sqrt{T+L}$, then for any real number C > 0,

(27) $$P\left(X>C\right)\le \frac{{\mathit{\sigma }}^2\sqrt{T\left(1-\mathit{\delta }\right)+L}}{{\mathit{\sigma }}^2\sqrt{T\left(1-\mathit{\delta }\right)+L}+{\left[C-D\left(T\left(1-\mathit{\delta }\right)+L\right)\right]}^2}$$(27)

Since $R=D\left(T\left(1-\mathit{\delta }\right)+L\right)+k\mathit{\sigma }\sqrt{T\left(1-\mathit{\delta }\right)+L}$, if we consider R rather than C in the above inequality, we obtain:(28) $$P(X\ge R)\le \frac{1}{1+k^2}$$(28)

In this study, we assume that the allowable shortage probability, q, is given ($P\left(X>R\right)=q$); thus with considering the above inequality, we obtain $0\le k\le \sqrt{\left(\frac{1}{q}\right)-1}$. It is easy to verify that JEACWI (T, A, L, M) has a smooth curve for $k\in \left[0,\sqrt{\left(\frac{1}{q}\right)-1}\right]$. Therefore, we can follow the solution procedure below to obtain the suitable k and optimal T, A, L, and M.

Solution procedure

• For a given q, we divide the interval $\left[0,\sqrt{\left(\frac{1}{q}\right)-1}\right]$ into N equal subinterval, where N is large enough. And we let $k_0=0,k_N=\sqrt{\left(\frac{1}{q}\right)-1}$ and $k_j=k_{j-1}+\frac{\left(k_N-k_0\right)}{N},j=1,2,\dots ,N-1$.

• Set M = 1.

• For each L _z  = 0, 1, 2, …, n, perform Step 4–10.

• For a given $k_j\in \{k_0,k_1,\dots ,k_N\},j=1,2,\dots ,N$, we can use numerical search technique to compute T _j from Equation (26).

• Substituting $T_{z,k_j}$ into Equation (25) determines $A_{z,k_j}$.

• Check whether $A_{z,k_j}\le A_0$.

• If $A_{z,k_j}\le A_0,A_{z,k_j}$ is feasible, then go to Step 9.

• If $A_{z,k_j}>A_0,A_{z,k_j}$ is not feasible. Put $A_{z,k_j}=A_0$ and evaluate the corresponding values of $T_{k_j}$from Equation (26), then go to Step 10.

• Compute $\text{JEACWI}(T_{z,k_j},A_{z,k_j},L_z,M)$ from Equation (21).

• Find ${\text{Min}}_{k_j\in \{k_0,k_1,\dots ,k_N\}}\text{JEACWI}(T_{z,kj},A_{z,kj},L_z,M)=\text{JEACWI}(T^{k_{s(z)}},A^{k_{s(z)}},L_z,M)$.

• Find ${\text{Min}}_{z=0,1,2,\dots ,n}\text{JEACWI}(T^{k_{s(z)}},A^{k_{s(z)}},L_z,M)=\text{JEACWI}(T_M^{k_{s(z)}^M},A_M^{k_{s(z)}^M},L_M,M)$.

• Set M = M + 1, and repeat Steps 2–11 to get $\text{JEACWI}(T_M^{k_{s(z)}^M},A_M^{k_{s(z)}^M},L_M,M)$.

• If $\text{JEACWI}\left(T_M^{k_{s\left(z\right)}^M},A_M^{k_{s\left(z\right)}^M},L_M,M\right)\le \text{JEACW}(T_{M-1}^{k_{s\left(z\right)}^{M-1}},A_{M-1}^{k_{s\left(z\right)}^{M-1}},L_M,M-1)$, then go to Step 14, otherwise go to Step 12.

• Set $\left(T^{\ast },A^{\ast },M^{\ast },L^{\ast }\right)=(T_{M-1}^{k_{s\left(z\right)}^{M-1}},A_{M-1}^{k_{s\left(z\right)}^{M-1}},L_{M-1},M-1)$, then $\left(T^{\ast },A^{\ast },M^{\ast },L^{\ast }\right)$ is the optimal solution and $\text{JEACWI}(T^{\ast },A^{\ast },M^{\ast })$ is the minimum joint expected annual cost. The value of $k_s^{M^{\ast }}$ such that $\text{JEACWI}(T^{\ast },A^{\ast },M^{\ast })$ exists is the optimal safety factor and we denote it k*. Hence, the optimal target level is $R^{\ast }=D\left(T^{\ast }\left(1-\mathit{\delta }\right)+L^{\ast }\right)+k^{\ast }{\mathit{\sigma }}_D\sqrt{T^{\ast }\left(1-\mathit{\delta }\right)+L^{\ast }}$.

4. Numerical example

To illustrate the behavior of the model developed in this paper, we consider an inventory problem with the following data, which is analogous to those used in Chang et al. (2006), Pan and Yang (2002):

$$D=600unit/year,A_0=\mathrm{\$}200,h_b=\mathrm{\$}20,{\mathit{\sigma }}_D=15unit/year$$

$$\mathit{\pi }=\mathrm{\$}30,h_V=\mathrm{\$}15,S=\mathrm{\$}1000,b=2800,\mathit{\theta }=0.2,p=2000unit/year$$

Besides, we take $C_{pr}=\mathrm{\$}40,C_{pu}=\mathrm{\$}60$. Also defective rate is $\mathit{\delta }=0.1$ and 1 year = 336 days.

The lead time has three components with data shown in Table 1.The inflation rate has a normal distribution function. It is assumed that q = 0.2 ($k_0=0,k_N=2$). Let $k_j=k_{j-1}+\frac{\left(k_N-k_0\right)}{N},j=1,2,\dots ,N-1,N=200$. Applying proposed solution procedure yields the results shown in Table 2 for E (δ) =  0.00, 0.04, 0.08, 0.12, and 0.16. Further, a summary of optimal solutions for the first step of solution procedure are tabulated in Table 3. The associated results reveal that the larger inflation rate, the larger review period (T). Table 4 shows that optimal number of shipments is decreased when inflation rate becomes larger. Also, for instance, optimal values obtained in Table 4 are tabulated for different lead time and respective C(L).

Table 1. Lead time data

Lead time component z	Normal duration b z (days)	Minimum duration a z (days)	Unit crashing cost c z ($/day)
1	20	6	0.4
2	20	6	1.2
3	16	9	5.0

Table 2. The results of solution procedure (lead time in year)

E (i)	M	(T, A, k, L)	$\mathit{\rho }\left(T\right),\mathit{\alpha }(L)$	EOCWIb, EHCWIb, ESCWIb, EPCWIb	ESUCWIv, EHCWIv, EPCWIv	JEACWI
0.00	1	0.44, 200.00, 0.52, 0.1,250	3.39, concave	509.28, 2,535.75, 245.91, 36,000	2,477.07, 672.83, 26,666.67	69,107.54
	2	0.27, 138.25, 0.90, 0.1,667	1.89, concave	766.77, 1,655.78, 260.13, 36,000	2,025.27, 1,237.39, 26,666.67	68,609.04
	3	0.19, 100.34, 1.17, 0.1,667	1.35, concave	946.25, 1,282.09, 271.99, 36,000	1,860.32, 1,493.16, 26,666.67	68,520.50*
	4	0.15, 79.11, 1.38, 0.1,667	1.08, concave	1,079.32, 1,079.00, 284.97, 36,000	1,769.47, 1,648.31, 26,666.67	68,527.76
0.04	1	0.49, 200.00, 0.44, 0.0,833	3.40, 2.40	507.00, 2,812.92, 242.97, 36,520.65	2,279.71, 754.00, 26,963.44	70,080.73
	2	0.30, 151.66, 0.81, 0.0,833	1.76, 4.55	797.61, 1,831.23, 236.50, 36,642.16	1,836.13, 1,401.29, 26,906.91	69,651.87
	3	0.22, 110.50, 1.07, 0.0,833	1.25, 6.62	1,005.74, 1,402.37, 239.46, 36,695.65	1,675.89, 1,704.11, 26,879.22	69,602.47*
	4	0.17, 85.93, 1.29, 0.1,250	1.03, 11.90	1,069.50, 1,165.71, 265.89, 36,787.64	1,614.05, 1,857.03, 26,867.08	69,626.93
0.08	1	0.54, 200.00, 0.35, 0.0,833	3.56, 1.06	460.59, 3,158.28, 251.28, 36,970.57	2,071.01, 853.93, 27,207.83	70,973.53
	2	0.34, 168.56, 0.72, 0.0,833	1.83, 1.99	732.45, 2,064.85, 241.09, 37,236.14	1,647.04, 1,602.80, 27,075.77	70,600.16
	3	0.24, 122.00, 0.97, 0.0,833	1.28, 2.96	939.59, 1,571.29, 242.39, 37,356.54	1,503.31, 1,946.74, 27,014.53	70,574.41*
	4	0.19, 96.53, 1.17, 0.0,833	1.01, 3.84	1,097.87, 1,298.99, 246.54, 37,423.61	1,420.30, 2,160.28, 26,973.67	70,621.28
0.12	1	0.62, 200.00, 0.23, 0.0,625	3.88, 0.43	465.81, 3,663.86, 258.91, 37,205.42	1,809.71, 1,001.58, 27,359.57	71,764.89
	2	0.39, 191.11, 0.61, 0.0,833	1.92, 1.11	651.09, 2,383.39, 246.73, 37,754.31	1,435.12, 1,878.77, 27,132.31	71,481.75*
	3	0.28, 138.77, 0.86, 0.0,833	1.33, 1.69	856.93, 1,802.16, 245.64, 37,962.51	1,309.00, 2,279.84, 27,027.80	71,483.91
0.16	1	0.74, 200.00, 0.07, 0.0,625	4.37, 0.27	394.87, 4,355.36, 277.81, 37,312.97	1,534.09, 1,204.38, 27,372.57	72,452.09
	2	0.47, 200.00, 0.46, 0.0,625	2.14, 0.48	630.80, 2,869.68, 249.46, 38,010.92	1,185.34, 2,304.50, 26,979.15	72,229.89*
	3	0.35, 169.84, 0.68, 0.0,625	1.48, 0.73	840.76, 2,210.33, 243.27, 38,318.97	1,045.69, 2,878.21, 26,753.26	72,290.53

* Optimal value for each set of E(i).

Table 3. Summary of optimal results (lead time in year)

E (i)	T*	A*	L*	k*	m*	JEACWI*
0.00	0.19	100.34	0.1,667	1.17	3	68,520.50
0.04	0.22	110.50	0.0,833	1.07	3	69,602.47
0.08	0.24	122.00	0.0,833	0.97	3	70,574.41
0.12	0.39	191.11	0.0,833	0.61	2	71,481.75
0.16	0.47	200.00	0.0,625	0.46	2	72,229.89

Table 4. Optimal values in terms of different lead time (lead time in year)

E (i)	L z	C (L z )	(T z , A z , k z , M z )	$\mathit{\rho }\left(T_z\right),\mathit{\alpha }(L_z)$	JEACWI z
0.00	0.1,667	0	(0.19, 100.34, 1.17, 3)	1.35, concave	68,520.50*
	0.1,250	5.6	(0.19, 100.47, 1.17, 3)	1.28, concave	68,521.97
	0.0,833	22.4	(0.20, 101.91, 1.15, 3)	1.22, concave	68,583.27
	0.0,625	57.4	(0.20, 105.75, 1.12, 3)	1.25, concave	68,755.65
0.04	0.1,667	0	(0.21, 108.85, 1.09, 3)	1.37, 11.92	69,666.37
	0.1,250	5.6	(0.21, 108.97, 1.08, 3)	1.30, 9.44	69,606.76
	0.0,833	22.4	(0.22, 110.50, 1.07, 3)	1.25, 6.62	69,602.42*
	0.0,625	57.4	(0.23, 114.63, 1.04, 3)	1.28, 4.93	69,731.15
0.08	0.1,667	0	(0.24, 120.26, 0.99, 3)	1.40, 5.46	70,765.24
	0.1,250	5.6	(0.24, 120.36, 0.99, 3)	1.33, 4.27	70,644.76
	0.0,833	22.4	(0.25, 122.01, 0.97, 3)	1.28, 2.96	70,574.41*
	0.0,625	57.4	(0.25, 126.51, 0.94, 3)	1.32, 2.18	70,657.83
0.12	0.1,667	0	(0.39, 189.46, 0.62, 2)	2.05, 2.27	71,812.73
	0.1,250	5.6	(0.39, 189.46, 0.62, 2)	1.98, 1.69	71,631.08
	0.0,833	22.4	(0.39, 191.11, 0.61, 2)	1.92, 1.11	71,481.75*
	0.0,625	57.4	(0.40, 195.97, 0.59, 2)	1.97, 0.81	71,483.52
0.16	0.1,667	0	(0.46, 200.00, 0.49, 2)	2.18, 1.45	72,727.89
	0.1,250	5.6	(0.46, 200.00, 0.49, 2)	2.11, 1.05	72,485.85
	0.0,833	22.4	(0.46, 200.00, 0.49, 2)	2.08, 0.67	72,271.52
	0.0,625	57.4	(0.47, 200.00, 0.49, 2)	2.14, 0.48	72,229.89*

5. Conclusion

Nowadays, inflation is an observable phenomenon in most societies that its effect in determining optimal policies of inventory/production systems is a momentous concern for inventory managers. In economics, inflation is sustained increase in the general price level of goods and services in an economy over a period of time. When the general price level rises, each unit of currency buys fewer goods and services. Considering this important issue, the purpose of this paper is to examine the effect of inflationary condition on periodic review integrated inventory model under uncertainty for minimizing the length of review period for both buyer and vendor, buyer’s ordering cost, buyer’s lead time, and the number of lots in which the product is delivered from the vendor to the buyer in one production cycle.

In order to show how various parameters affect the optimal solution of the proposed inventory model, sensitivity analysis is performed. Keeping all other parameters fixed and varying a single parameter at a time, for the same set of values we study the results. Results of sensitivity analysis are shown in Table 5. Finally the main conclusions, one can draw from the sensitivity analysis, are as follows:

(1)	If the value of (θb) is increasing, for fixed lead time and number of shipment, then the optimal length of review period (T*), optimal ordering cost (A*), and the optimal joint expected annual cost with inflation (JEACWI*) are increasing simultaneously and the safety factor (k*) is decreasing. It implies that if the (b) is higher, then the length of review period (T*) and ordering cost (A*) should be increased and safety factor (k*) should be shortened to reduce expected annual cost (JEACWI*).
(2)	If the value of holding cost (h b ) is increasing, for fixed lead time and number of shipment, the optimal length of review period (T*), optimal ordering cost (A*), and the optimal safety factor (k*) are decreasing simultaneously and the optimal joint expected annual cost with inflation (JEACWI*) is increasing. It implies that if the holding cost is higher, then optimal length of review period (T*), optimal ordering cost (A*), and optimal safety factor (k*) should be decreased to reduce expected annual cost (JEACWI*).
(3)	Due to higher (π), resulting in increasing the joint expected annual cost with inflation (JEACWI*). Also optimal safety factor (k*) increases with an augment in (π).
(4)	A higher vendor’s holding cost, reduces the number of shipment. Also, as the most of the cost factors are higher, the joint expected annual cost with inflation (JEACWI*) increases automatically.

Table 5. Effect of changes in various parameters (lead time in year)

Parameter change (%)	−20%	−15%	−10%	−5%	+5%	+10%	+15%	+20%
$\frac{1}{\mathit{\delta }}$
T*	0.24	0.24	0.24	0.24	0.25	0.25	0.25	0.25
A*	94.83	101.49	108.23	115.08	129.02	136.14	143.35	150.68
k*	1.00	0.99	0.99	0.98	0.97	0.96	0.96	0.95
L*	4	4	4	4	4	4	4	4
M*	3	3	3	3	3	3	3	3
$\mathit{\rho }\left(T^{\ast }\right)$	1.27	1.27	1.27	1.28	1.28	1.28	1.29	1.29
$\mathit{\alpha }\left(L^{\ast }\right)$	3.06	3.03	3.01	2.98	2.93	2.91	2.88	2.86
JEACWI*	70,505.41	70,525.34	70,543.43	70,559.75	70,587.46	70,598.97	70,609.01	70,617.63
h b
T*	0.37	0.36	0.35	0.25	0.24	0.24	0.23	0.18
A*	185.02	180.27	175.82	124.10	120.01	118.11	116.29	97.72
k*	0.82	0.79	0.77	1.00	0.95	0.92	0.90	1.06
L*	4	4	4	4	4	4	4	4
M*	2	2	2	3	3	3	3	4
$\mathit{\rho }\left(T^{\ast }\right)$	1.88	1.86	1.85	1.29	1.27	1.27	1.26	0.99
$\mathit{\alpha }\left(L^{\ast }\right)$	2.01	2.01	2.00	2.96	2.95	2.95	2.94	3.82
JEACWI*	70,166.49	70,279.10	70,388.79	70,495.10	70,652.26	70,728.73	70,803.88	70,873.27
π
T*	0.24	0.24	0.24	0.24	0.24	0.24	0.24	0.24
A*	121.94	121.95	121.95	121.97	122.04	122.04	122.06	122.08
k*	0.80	0.84	0.89	0.93	1.02	1.05	1.09	1.13
L*	4	4	4	4	4	4	4	4
M*	3	3	3	3	3	3	3	3
$\mathit{\rho }\left(T^{\ast }\right)$	1.36	1.34	1.32	1.30	1.26	1.25	1.23	1.22
$\mathit{\alpha }\left(L^{\ast }\right)$	2.65	2.74	2.82	2.89	3.01	3.06	3.11	3.16
JEACWI*	75,522.68	70,536.28	70,549.41	70,562.10	70,586.35	70,597.97	70609.29	70,620.32
h v
T*	0.22	0.27	0.26	0.25	0.24	0.33	0.32	0.31
A*	109.45	132.15	128.51	125.14	119.11	163.07	158.83	156.13
k*	1.07	0.91	0.93	0.95	0.99	0.75	0.76	0.78
L*	4	4	4	4	4	4	4	4
M*	4	3	3	3	3	2	2	2
$\mathit{\rho }\left(T^{\ast }\right)$	1.04	1.31	1.30	1.29	1.27	1.81	1.79	1.79
$\mathit{\alpha }\left(L^{\ast }\right)$	3.35	2.69	2.78	2.87	3.04	2.08	2.14	2.19
JEACWI*	70,162.22	70,270.82	70,374.72	70,475.85	70,670.58	70,757.40	70,833.89	70,909.07

The proposed model can be extended in several directions. For instance we may assume the number of defective units is probabilistic and consider a random variable for it or assume sampling inspection, mixture of distributions, some inventory constraint in the developed model or optimizing model for continuous review policy instead of continuous review policy.

Acknowledgment

The authors gratefully acknowledge the constructive comments made by the anonymous referees on an earlier version of this article.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Hesamoddin Tahami

Hesamoddin Tahami received his BSc in Industrial Engineering at Khaje Nasir Toosi (KNTU) University in Tehran, Iran. He continued his education in Industrial Engineering and received his MSc degree from Kharazmi University in Tehran, Iran. His interest research areas are Production/Inventory Control, Supply and Operations Management, Fuzzy sets and its applications.

Abolfazl Mirzazadeh

Hesamoddin Tahami received his BSc in Industrial Engineering at Khaje Nasir Toosi (KNTU) University in Tehran, Iran. He continued his education in Industrial Engineering and received his MSc degree from Kharazmi University in Tehran, Iran. His interest research areas are Production/Inventory Control, Supply and Operations Management, Fuzzy sets and its applications.

Appendix 1

Theorem 1.

JEACWI (T, A, L, M) is concave function in $L\in \left[L_z,L_{z-1}\right]$, if 0 < L < α(L)

The first and second partial derivatives of JEACWI (T, A, L, M) with respect to L are (A.1) $$\frac{\mathit{\partial }\text{JEACWI}}{\mathit{\partial }L}=-c_z\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]+\frac{h_{b}k{\mathit{\sigma }}_D\left(1+\frac{E\left(I\right)}{2}\right)}{2\sqrt{T\left(1-\mathit{\delta }\right)+L}}+\frac{\mathit{\pi }{\mathit{\sigma }}_D\left(\sqrt{1+k^2}-k\right)}{4\sqrt{T\left(1-\mathit{\delta }\right)+L}}\left[\frac{1+LE\left(I\right)+\frac{E(I)}{2}}{T(1-\mathit{\delta })}-\frac{E(I)}{2}\right]+\frac{\mathit{\pi }{\mathit{\sigma }}_{D}E(I)\left(\sqrt{1+k^2}-k\right)\sqrt{T\left(1-\mathit{\delta }\right)+L}}{2T(1-\mathit{\delta })}+D{C}_{pu}E(I)$$(A.1) (A.2) $$\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{L}^2}=-\frac{h_b\left(1+\frac{E\left(I\right)}{2}\right)k{\mathit{\sigma }}_D}{4{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}-\frac{\mathit{\pi }{\mathit{\sigma }}_D\left(\sqrt{1+k^2}-k\right)}{8}\left[\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right){\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}-\frac{E\left(I\right)}{2{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]+\frac{\mathit{\pi }{\mathit{\sigma }}_D\left(\sqrt{1+k^2}-k\right)E\left(I\right)}{4T\left(1-\mathit{\delta }\right)\sqrt{T\left(1-\mathit{\delta }\right)+L}}$$(A.2)

If the above inequality (A.2) is smaller than zero, it can be written as(A.3) $$\mathit{\chi }\left(L\right)+\mathit{\epsilon }\left(L\right)>\mathit{\varrho }\left(L\right)+\mathit{\xi }\left(L\right)$$(A.3)

where(A.4) $$\mathit{\chi }\left(L\right)=\frac{h_b\left(1+\frac{E\left(I\right)}{2}\right)k{\mathit{\sigma }}_D}{4{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}$$(A.4) (A.5) $$\mathit{\epsilon }\left(L\right)=\frac{\mathit{\pi }{\mathit{\sigma }}_D\left(\sqrt{1+k^2}-k\right)}{8}\left[\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right){\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]$$(A.5) (A.6) $$\mathit{\varrho }\left(L\right)=\frac{\mathit{\pi }{\mathit{\sigma }}_D\left(\sqrt{1+k^2}-k\right)}{8}\left[\frac{E\left(I\right)}{2{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]$$(A.6) (A.7) $$\mathit{\xi }\left(L\right)=\frac{\mathit{\pi }{\mathit{\sigma }}_D\left(\sqrt{1+k^2}-k\right)E\left(I\right)}{2T\left(1-\mathit{\delta }\right)\sqrt{T\left(1-\mathit{\delta }\right)+L}}$$(A.7)

Since two sides of inequality are greater than zero, hence, the inequality (A.3) is transformed as(A.8) $$\frac{\mathit{\chi }\left(L\right)+\mathit{\epsilon }\left(L\right)}{\mathit{\varrho }\left(L\right)+\mathit{\xi }\left(L\right)}>1$$(A.8)

Since L is greater than zero, then inequality (A.8) is obtained as follows:(A.9) $$0<L<\frac{L\left[\mathit{\chi }\left(L\right)+\mathit{\epsilon }\left(L\right)\right]}{\mathit{\varrho }\left(L\right)+\mathit{\xi }\left(L\right)}=\mathit{\alpha }(L)$$(A.9)

Thus, the proof of Theorem 1 is completed.

Theorem 2.

JEACWI (T, A, L, M) is convex function in (T, A) for any $L\in \left[L_z,L_{z-1}\right]$ and M, if 0 < T < $\mathit{\rho }\left(T\right)$.

For a given value of M, we obtain the Hessian matrix H for objective function as follows:$$H=\left[\begin{array}{cc}\frac{{\mathit{\partial }}^2\text{JEACWI}\left(T,A\right)}{\mathit{\partial }{A}^2}& \frac{{\mathit{\partial }}^2\text{JEACWI}\left(T,A\right)}{\mathit{\partial }A\mathit{\partial }T}\\ \frac{{\mathit{\partial }}^2\text{JEACWI}\left(T,A\right)}{\mathit{\partial }T\mathit{\partial }A}& \frac{{\mathit{\partial }}^2\text{JEACWI}\left(T,A\right)}{\mathit{\partial }{T}^2}\end{array}\right]$$

where(A.10) $$\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{A}^2}=\frac{\mathit{\theta }b}{A^2}$$(A.10) (A.11) $$\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{T}^2}=\frac{2\left(A+c_z\left(L_{z-1}-L\right)+{\sum }_{j=1}^{z-1}{c}_j\left(b_j-a_j\right)+\frac{S}{M}\right)\left(1+\frac{E\left(I\right)}{2}\right)}{T^3\left(1-\mathit{\delta }\right)}-h_b\left(1+\frac{E\left(I\right)}{2}\right)\left[\frac{k{\mathit{\sigma }}_D^2{\left(1-\mathit{\delta }\right)}^2}{4{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]+\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{8}\right){\left(1-\mathit{\delta }\right)}^2\left[-\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right){\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}+\frac{E\left(I\right)}{2{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]-\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{2}\right)\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^2\sqrt{T\left(1-\mathit{\delta }\right)+L}}\right]+\left(\sqrt{1+k^2}-k\right)\mathit{\pi }{\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^3\left(1-\mathit{\delta }\right)}\right]$$(A.11) (A.12) $$\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }A\mathit{\partial }T}=\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }T\mathit{\partial }A}=-\frac{1}{T^2\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)$$(A.12)

Then, for fixed M and L, we proceed by evaluating the principal minor of H at point (T, A). From (A.10), the first minor of H denoted by $\left|H_{11}\right|$ is greater than zero:(A.13) $$\frac{{\mathit{\partial }}^{2}EACWI}{\mathit{\partial }{A}^2}=\frac{\mathit{\theta }b}{A^2}>0$$(A.13)

From (A.10) to (A.12) we obtain the second principal minor of H denoted $\left|H_{22}\right|$ as (A.14) $$\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{T}^2}\times \frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{A}^2}-{\left(\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }A\mathit{\partial }T}\right)}^2=\frac{\mathit{\theta }b}{A^2}\left\{\frac{2\left(A+c_z\left(L_{z-1}-L\right)+{\sum }_{j=1}^{z-1}{c}_j\left(b_j-a_j\right)+\frac{S}{M}\right)\left(1+\frac{E\left(I\right)}{2}\right)}{T^3\left(1-\mathit{\delta }\right)}-h_b\left(1+\frac{E\left(I\right)}{2}\right)\left[\frac{k{\mathit{\sigma }}_D^2{\left(1-\mathit{\delta }\right)}^2}{4{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]+\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{8}\right){\left(1-\mathit{\delta }\right)}^2\left[-\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right){\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}+\frac{E\left(I\right)}{2{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]-\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{2}\right)\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^2\sqrt{T\left(1-\mathit{\delta }\right)+L}}\right]+\left(\sqrt{1+k^2}-k\right)\mathit{\pi }{\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^3\left(1-\mathit{\delta }\right)}\right]\right\}-\frac{1}{T^4{\left(1-\mathit{\delta }\right)}^2}{\left(1+\frac{E\left(I\right)}{2}\right)}^2$$(A.14)

If the above inequality (A.14) is greater than zero, then obtained inequality can be written as follows, since $A=\frac{\mathit{\theta }b}{\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]}$ (A.15) $$\mathit{\eta }\left(T\right)+\mathit{\zeta }\left(T\right)+\mathit{\tau }\left(T\right)>\mathit{\omega }\left(T\right)+\mathit{\gamma }\left(T\right)+\mathit{\vartheta }\left(T\right)+\mathit{\psi }\left(T\right)$$(A.15)

where(A.16) $$\mathit{\eta }\left(T\right)=\frac{2\left(\frac{\mathit{\theta }b}{\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]}+c_z\left(L_{z-1}-L\right)+{\sum }_{j=1}^{z-1}{c}_j\left(b_j-a_j\right)+\frac{S}{M}\right)\left(1+\frac{E\left(I\right)}{2}\right)}{T^3\left(1-\mathit{\delta }\right)}$$(A.16) (A.17) $$\mathit{\zeta }\left(T\right)=\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{8}\right){\left(1-\mathit{\delta }\right)}^2\left[\frac{E\left(I\right)}{2{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]$$(A.17) (A.18) $$\mathit{\tau }\left(T\right)=\left(\sqrt{1+k^2}-k\right)\mathit{\pi }{\mathit{\sigma }}_D\sqrt{T\left(1-\mathit{\delta }\right)+L}\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^3\left(1-\mathit{\delta }\right)}\right]$$(A.18) (A.19) $$\mathit{\omega }\left(T\right)=h_b\left(1+\frac{E\left(I\right)}{2}\right)\left[\frac{k{\mathit{\sigma }}_D^2{\left(1-\mathit{\delta }\right)}^2}{4{\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]$$(A.19) (A.20) $$\mathit{\gamma }\left(T\right)=\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{2}\right)\left[\frac{\left(1+LE\left(I\right)+\frac{E\left(I\right)}{2}\right)}{T^2\sqrt{T\left(1-\mathit{\delta }\right)+L}}\right]$$(A.20) (A.21) $$\mathit{\vartheta }\left(T\right)=\left(\sqrt{1+k^2}-k\right)\left(\frac{\mathit{\pi }{\mathit{\sigma }}_D}{8}\right){\left(1-\mathit{\delta }\right)}^2\left[\frac{1+LE\left(I\right)+\frac{E\left(I\right)}{2}}{T\left(1-\mathit{\delta }\right){\left(T\left(1-\mathit{\delta }\right)+L\right)}^{\frac{3}{2}}}\right]$$(A.21) (A.22) $$\mathit{\psi }\left(T\right)=\frac{\mathit{\theta }b{\left(1+\frac{E\left(I\right)}{2}\right)}^2}{T^4{\left(1-\mathit{\delta }\right)}^2{\left[\frac{1}{T\left(1-\mathit{\delta }\right)}\left(1+\frac{E\left(I\right)}{2}\right)-\frac{E\left(I\right)}{2}\right]}^2}$$(A.22)

Since two sides are greater than zero, hence inequality (A.15) can be written as follows:(A.23) $$\frac{\mathit{\eta }\left(T\right)+\mathit{\zeta }\left(T\right)+\mathit{\tau }\left(T\right)}{\mathit{\omega }\left(T\right)+\mathit{\gamma }\left(T\right)+\mathit{\vartheta }\left(T\right)+\mathit{\psi }\left(T\right)}>1$$(A.23)

Since T > 0, multiply the two sides of the above inequality in T, the Equation (A.23) is transformed as follows:(A.24) $$\mathit{\rho }\left(T\right)=\frac{T\left[\mathit{\eta }\left(T\right)+\mathit{\zeta }\left(T\right)+\mathit{\tau }\left(T\right)\right]}{\mathit{\omega }\left(T\right)+\mathit{\gamma }\left(T\right)+\mathit{\vartheta }\left(T\right)+\mathit{\psi }\left(T\right)}>T$$(A.24)

$\left|H_{22}\right|=\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{T}^2}\times \frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }{A}^2}-{\left(\frac{{\mathit{\partial }}^2\text{JEACWI}}{\mathit{\partial }A\mathit{\partial }T}\right)}^2>0$, if $0<T<\mathit{\rho }\left(T\right)$.

Therefore, JEACWI (T, A, L, M) is convex function in (T, A) if, $0<T<\mathit{\rho }\left(T\right)$.

Thus, the proof of Theorem 2 is completed.