Non-permutation flow shop scheduling problem with preemption-dependent processing time

Abstract

In this paper, the non-permutation flow shop scheduling problem with preemption-dependent processing times is considered. A mixed integer programming formulation is proposed to tackle the problem. The optimization objective considered is the minimization of the total tardiness. The model is tested against random instances. The results allow us to identify the effect of some parameters such as coefficient of preemption-dependent processing time, number of preemptions and the selected machine for preemption on the total tardiness.

Keywords:

• preemption
• flow shop
• scheduling

Public Interest Statement

In this work, a preemption-dependent processing time is suggested for the non-permutation flow shop scheduling problem. A mathematical model is employed to minimize the total tardiness. The model is tested against random instances. The results allow us to conclude when the preemption-dependent processing time increases, the total tardiness may increase. Moreover, in 56% of experiments, the last machine is the best selected one for the problem. Furthermore, by increasing the number of preemptions, the total tardiness never increases.

1. Introduction

In order to employ full capacity of machines, it is essential to adjust the load so that it is evenly spread between them. In order to obtain an adjusted load, a job on one machine may need to be preempted and after that later restarted or resumed. Each preemption permits the schedule to divide a job in some parts. This may allow the objective function value to be improved.

The processing time of a job is considered as fixed in the classical scheduling problems with preemption; while in numerous real situations, due to the required time to prepare a machine or to be ready to process a job or preemptive job, the processing time of a job may be increased. In fact, in preemptive schedule, there is a time taken by the scheduler to suspend the running job, switch the context, and dispatch the new incoming job. Real world examples of the problem are the financial service area such as banking procedure and industrial applications such as melting the material in the furnace and processes that need jig and fixture. Therefore, a new assumption called preemption-dependent processing times is considered. Moreover, using the preemptions makes a schedule better responsiveness and scalability.

Consider different jobs to be handled on several machines. Suppose that each job has some operations, each operation needs a different machine, all jobs are processed in the same machine sequence, and the job sequence of each machine has to be identified to optimize an objective. This problem is known as the flow shop scheduling problem. When the same sequence of jobs for all machines is considered, the problem is called a permutation flow shop (Potts, Shmoys, & Williamson, 1991), and if the job sequences of the machines are different, the problem is termed as non-permutation flow shop.

Recently, the literature has grown up around the subject of preemptive scheduling problems. As clear examples see Dobrin and Fohler (2004), Klonowska, Lundberg, and Lennerstad (2009) and Ballestín, Valls, and Quintanilla (2009). There is a lack of considering setup time between preemptive operations in scheduling problems. However, as stated before, this paper suggests a new concept of preemption-dependent processing times. Considering this assumption leads us to more realistic problems.

The rest of the paper is organized as follows: in Section 2, the related works are discussed. In Section 3, a mixed integer programming formulation is presented for the problem. The computational results are given in Section 4. Finally, the conclusions are presented in Section 5.

2. Related works

2.1. Non-permutation flow shop scheduling problem

Historically, more than half a century has been passed since Johnson proposed his well-known algorithm for flow shop scheduling problem (Johnson, 1954). A considerable amount of literature has been published on the permutation flow shop since finding optimal non-permutation solutions is much more difficult than finding optimal permutation solution even for small-sized instances.

In comparison with permutation flow shop, there are few papers taking into account the non-permutation flow shop. According to Tandon, Cummings, and LeVan (1991) computational experiments, the average percentage improvement of makespan values of non-permutation over permutation schedule optimum is usually more than %1.5. Koulamas (1998) proposed a constructive heuristic to make non-permutation flow shop schedules for the makespan problem. Pugazhendhi, Thiagarajan, Rajendran, and Anantharaman (2003) suggested a heuristic to solve this problem with makespan and flow time. Liao, Liao, and Tseng (2006) compared the makespan, total tardiness, and total weighted tardiness of permutation and non-permutation flow shop. Lin and Ying (2009) developed a hybrid of simulated annealing and tabu search algorithms for this problem with the makespan objective. Vahedi-Nouri, Fattahi, and Ramezanian (2013) studied the non-permutation flow shop scheduling with the machine availability and learning effect constraints with respect to minimize the total flow time. Ramezanian (2014) considered machines availability constraints in a non-permutation flow shop scheduling problem to minimize the makespan. Xiao, Yuan, Zhang, and Konak (2015) researched on the non-permutation flow shop scheduling for a problem with order acceptance and weighted tardiness. Rossit, Tohmé, Frutos, Bard, and Broz (2016) proposed lot streaming in non-permutation flow shop problems to minimize the makespan. Cui, Lu, Zhou, Li, and Han (2016) investigated non-availability intervals in the non-permutation flow shop scheduling problems. They suggested two kinds of unavailability constraints that the jobs are non-resumable in both cases.

2.2. Preemptive scheduling problem

In preemptive scheduling problem, one can interrupt processes and resume them without any penalties. Obviously, there is flexibility in scheduling when jobs can be preemptively scheduled. Regularly, the preemptive schedules are dominant the non-preemptive one. Readers interested in this area can see researches of Agnetis, Billaut, Gawiejnowicz, Pacciarelli, and Soukhal (2014), Chen, Potts, and Woeginger (1999) and Cho and Sahni (1981). In the following, to show the importance of preemption in different types of scheduling problem, some papers for them are addressed.

McCormick and Pinedo (1995) studied the uniform parallel machines scheduling problem with preemption. They have considered the flow time and makespan objectives. Dobrin and Fohler (2004) suggested a method to reduce the number of preemptions in the fixed priority scheduling problems consisting of periods and offsets. Braun and Schmidt (2012) compared the makespan of preemptive and i-preemptive schedules where only a limited number of preemptions is permitted. Thekkilakattil, Pillai, Dobrin, and Punnekkat (2010) researched on a framework for eliminating preemptions in real-time systems, which does not need adjustments of job attributes. Jiang, Weng, and Hu (2012) proposed a simple method for parallel machines scheduling with a limited number of preemptions, which is according to the design and analysis of an algorithm for finding an instance in the worst case. Jiang, Hu, Weng, and Zhu (2014) studied the i-preemptive scheduling on parallel machines to maximize the minimum machine completion time. Thevenin, Zufferey, and Potvin (2016) proposed a new version of a parallel machine scheduling problem using concept of the graph colouring problem. In their model, preemption is allowed and considered incompatible jobs. Liaw (2016) studied the preemptive scheduling problems that jobs are processed on identical parallel machines to minimize total tardiness.

As can be concluded from the related works and to the best of our knowledge, in all researches, the processing time is not related to the preemption. Since, a setup time between preemptions of each job/operation is required, in this work, a new assumption called preemption-dependent processing time for the non-permutation flow shop scheduling problem is proposed.

3. Model formulation

The flow shop scheduling have several sequential stages with one machine for each stage. There are jobs, having each of different processing time. In the non-permutation flow shop each job sequence can be different through each of the machines. Moreover, the preemption strategy is allowed in this problem to minimize the total tardiness. Therefore, the processing time depends on the time taken by the scheduler to interrupt the running job, change the setting, and run the incoming job. As the aforementioned definition, this time plus processing time of the job is called preemption-dependent processing time.

The following assumptions are considered.

(1)	Each job can be processed at most on one machine at the same time.
(2)	Each machine can process only one job at a time.
(3)	Preemption is allowed; that is, the processing of an operation can be interrupted.
(4)	The preemption can be occurred just on a selected machine.
(5)	All jobs are independent and not busy for processing at time zero.
(6)	The machines are continuously available.

Below the problem is formulated as a mixed integer linear programming model. In this model. The sets, indices and parameters are given as follows.

N	=	Set of jobs
M	=	Set of machines
P	=	Set of allowable preemptions (show the maximum number of preemption for each operation)
i, i′	=	Index of jobs, i, i′ = 1,2,...|N|
k	=	Index of machines, k = 1,2,...|M|
p, p′	=	Index of allowable preemptions, p, p′ = 1,2,...|P|
$t_{ik}^0$	=	Without preemption processing time of job i on machine k
A k	=	Increasing coefficient of processing time of each job on machine k after each preemption
d i	=	Due date of job i
PM	=	Selected machine for preemption
M	=	A big number

The decision variables of the formulation are as follows.

T i	=	Tardiness of job i
C ikp	=	Non-negative continuous variable representing the completion time of job i on machine k in preemption p
t ikp	=	Preemption-dependent processing time of job i on machine k in preemption p
w ikp	=	Binary variable taking value 1 if preemption p of job i is occurred on processed on machine k, and 0 otherwise
Y ipi′p′k	=	Binary variable taking value 1 if preemption p of job i is processed before preemption p′ of job i′ on machine k, and 0 otherwise

The objective is to minimize the total tardiness. The proposed mathematical model for the problem can be formulated as follows.(1) $$min\sum _i{T}_i$$(1) (2) $$T_i\ge C_{i\left|M\right|1}-d_i\forall i,\left|M\right|\ne PM$$(2) (3) $$T_i\ge C_{i\left|M\right|p}-d_i\forall i,p,\left|M\right|=PM$$(3) (4) $$C_{iPM\left|P\right|}\le C_{i(k+1)1}-t_{i(k+1)1}\forall i,k\ne \left|M\right|$$(4) (5) $$C_{ik1}\le C_{i(k+1)1}-t_{i(k+1)1}\forall i,k\ne \left|M\right|,k\ne PM$$(5) (6) $$C_{iPMp}-t_{iPMp}\ge C_{i^{\prime }PM{p}^{\prime }}-M(2-w_{iPMp}-w_{i^{\prime }PM{p}^{\prime }})-M{y}_{ip{i}^{\prime }{p}^{\prime }PM}\forall i,p,i^{\prime },p^{\prime },i<i^{\prime }$$(6) (7) $$C_{i^{\prime }PM{p}^{\prime }}-t_{i^{\prime }PM{p}^{\prime }}\ge C_{iPMp}-M(2-w_{iPMp}-w_{i^{\prime }PM{p}^{\prime }})-M(1-y_{ip{i}^{\prime }{p}^{\prime }PM})\forall i,p,i^{\prime },p^{\prime },i<i^{\prime }$$(7) (8) $$C_{ik1}-t_{ik1}\ge C_{i^{\prime }k1}-M{y}_{i1i^{\prime }1k}\forall i,i^{\prime },k,i<i^{\prime }$$(8) (9) $$C_{i^{\prime }k1}-t_{i^{\prime }k1}\ge C_{ik1}-M(1-y_{i1i^{\prime }1k})\forall i,i^{\prime },k,i<i^{\prime }$$(9) (10) $$C_{i11}-t_{i11}\ge 0\forall i$$(10) (11) $$C_{iPMp}\le C_{iPM(p+1)}-t_{iPM(p+1)}\forall i,p\ne \left|P\right|$$(11) (12) $$t_{iPMp}\le M{w}_{iPMp}\forall i,p$$(12) (13) $$t_{ik1}\le M{w}_{ik1}\forall i,k\ne \left|M\right|$$(13) (14) $$w_{ik1}=1\forall i,k$$(14) (15) $$\sum _p{t}_{iPMp}=t_{iPM}^0+\sum _{p>1}{A}_{PM}{w}_{ikp}\forall i,p$$(15) (16) $$t_{ik1}=t_{ik}^0\forall i,k\ne \left|M\right|$$(16) (17) $$w_{iPMp}\ge w_{iPM(p+1)}\forall i,p,p\ne \left|P\right|$$(17) (18) $$T_i\ge 0\forall i,k$$(18) (19) $$t_{ikp}\ge 0\forall i,k,p$$(19) (20) $$w_{ikp}\in \left\{0,1\right\}\forall i,k,p$$(20) (21) $$y_{ip{i}^{\prime }{p}^{\prime }k}\in \left\{0,1\right\}\forall i,p,i^{\prime },p^{\prime },k$$(21)

In the above model, objective (1) minimizes the total tardiness. Constraints (2) and (3) define the tardiness of each job. Constraints (4) and (5) indicate that the completion time of each job on each machine must be less than the starting time of job before the first preemption on the next machine. Constraints (6) and (7) do not allow two jobs processed on the selected machine for preemption, simultaneously. Moreover, constraints (8) and (9) do not allow two jobs processed on the other machine, simultaneously. According to constraints (10), start time of each job on the first machine must be greater than or equal to zero. Constraints (11), (12) and (13) indicate the completion time of each job on each machine before each preemption should be less than the starting time of the job on the machine after preemption. Constraints (14) represent the first preemption is selected for all jobs on each machine. Constraints (15) calculate the preemption-dependent processing time for the selected machine for preemption. Constraints (16) determine the preemption-independent processing time for the other machine. Constraints (17) indicate when a preemption happened, next one can be occurred. Constraints (18)–(21) specify the variables domain.

4. Computational study

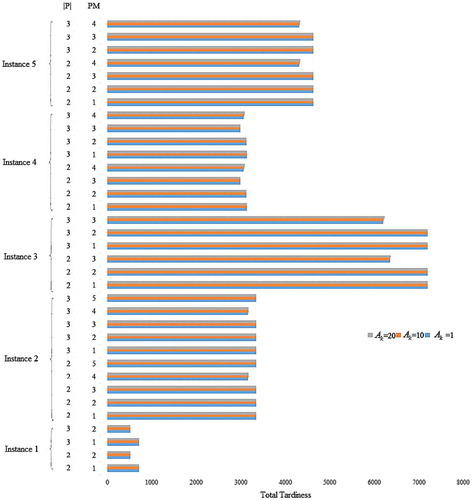
In order to check the performance of the proposed mathematical model, five instances are considered. The instances have been randomly generated with different combinations of the parameters. For each instance, |P|, PM and A _k have been changed. The computational results are demonstrated in Tables 1 and 2.

Table 1. Computational results obtained by mathematical model (part 1)

Instance number	|N|	|M|	|P|	PM	A k	Obj.	Instance number	|N|	|M|	|P|	PM	A k	Obj.
1	5	2	1	–	–	720	2	2	5	2	5	20	3,344
1	5	2	2	1	1	720	2	2	5	3	1	1	3,344
1	5	2	2	1	10	720	2	2	5	3	1	10	3,344
1	5	2	2	1	20	720	2	2	5	3	1	20	3,344
1	5	2	2	2	1	517	2	2	5	3	2	1	3,344
1	5	2	2	2	10	517	2	2	5	3	2	10	3,344
1	5	2	2	2	20	517	2	2	5	3	2	20	3,344
1	5	2	3	1	1	720	2	2	5	3	3	1	3,344
1	5	2	3	1	10	720	2	2	5	3	3	10	3,344
1	5	2	3	1	20	720	2	2	5	3	3	20	3,344
1	5	2	3	2	1	517	2	2	5	3	4	1	3,159
1	5	2	3	2	10	517	2	2	5	3	4	10	3,168
1	5	2	3	2	20	517	2	2	5	3	4	20	3,178
2	2	5	1	–	–	3,344	2	2	5	3	5	1	3,344
2	2	5	2	1	1	3,344	2	2	5	3	5	10	3,344
2	2	5	2	1	10	3,344	2	2	5	3	5	20	3,344
2	2	5	2	1	20	3,344	3	4	3	1	–	–	7,200
2	2	5	2	2	1	3,344	3	4	3	2	1	1	7,200
2	2	5	2	2	10	3,344	3	4	3	2	1	10	7,200
2	2	5	2	2	20	3,344	3	4	3	2	1	20	7,200
2	2	5	2	3	1	3,344	3	4	3	2	2	1	7,200
2	2	5	2	3	10	3,344	3	4	3	2	2	10	7,200
2	2	5	2	3	20	3,344	3	4	3	2	2	20	7,200
2	2	5	2	4	1	3,159	3	4	3	2	3	1	6,351
2	2	5	2	4	10	3,168	3	4	3	2	3	10	6,360
2	2	5	2	4	20	3,178	3	4	3	2	3	20	6,370
2	2	5	2	5	1	3,344	3	4	3	3	1	1	7,200
2	2	5	2	5	10	3,344	3	4	3	3	1	10	7,200

Table 2. Computational results obtained by mathematical model (part 2)

Instance number	|N|	|M|	|P|	PM	A k	Obj.	Instance number	|N|	|M|	|P|	PM	A k	Obj.
3	4	3	3	1	20	7,200	4	3	4	3	3	20	2,996
3	4	3	3	2	1	7,200	4	3	4	3	4	1	3,064
3	4	3	3	2	10	7,200	4	3	4	3	4	10	3,073
3	4	3	3	2	20	7,200	4	3	4	3	4	20	3,083
3	4	3	3	3	1	6,192	5	4	4	1	–	–	4,636
3	4	3	3	3	10	6,210	5	4	4	2	1	1	4,636
3	4	3	3	3	20	6,230	5	4	4	2	1	10	4,636
4	3	4	1	–	–	3,138	5	4	4	2	1	20	4,636
4	3	4	2	1	1	3,138	5	4	4	2	2	1	4,636
4	3	4	2	1	10	3,138	5	4	4	2	2	10	4,636
4	3	4	2	1	20	3,138	5	4	4	2	2	20	4,636
4	3	4	2	2	1	3,130	5	4	4	2	3	1	4,636
4	3	4	2	2	10	3,130	5	4	4	2	3	10	4,636
4	3	4	2	2	20	3,130	5	4	4	2	3	20	4,636
4	3	4	2	3	1	2,996	5	4	4	2	4	1	4,316
4	3	4	2	3	10	2,996	5	4	4	2	4	10	4,325
4	3	4	2	3	20	2,996	5	4	4	2	4	20	4,335
4	3	4	2	4	1	3,064	5	4	4	3	1	10	4,636
4	3	4	2	4	10	3,073	5	4	4	3	1	20	4,636
4	3	4	2	4	20	3,083	5	4	4	3	2	1	4,636
4	3	4	3	1	1	3,138	5	4	4	3	2	10	4,636
4	3	4	3	1	10	3,138	5	4	4	3	2	20	4,636
4	3	4	3	1	20	3,138	5	4	4	3	3	1	4,636
4	3	4	3	2	1	3,130	5	4	4	3	3	10	4,636
4	3	4	3	2	10	3,130	5	4	4	3	3	20	4,636
4	3	4	3	2	20	3,130	5	4	4	3	4	1	4,316
4	3	4	3	3	1	2,996	5	4	4	3	4	10	4,325
4	3	4	3	3	10	2,996	5	4	4	3	4	20	4,335

By analyzing these tables, as a common and logical result in preemptive scheduling problems, we conclude that the objective function value without preemption is not better than the preemptive one. Moreover, as another observation, larger A _k may lead to greater objective value. However, increasing of this coefficient does not effect on the objective function in some cases. In 22% of experiments, this coefficient effects on the total tardiness.

As another interesting observation, the best machine for preemption (PM) is |M| or |M|−1. In fact, in 56% of experiments, the last machine is the best selected machine for preemption, and in 44% of experiments, before the last machine (|M|) is the best selection.

Furthermore, by increasing in the value of |P|, the total tardiness never increases. In instance 3, with 4 jobs, 3 machines and the last machine selected for preemptions, when set of preemption increase from 2 to 3, the total tardiness decreases. In other cases, the objective function is not changed.

As it can be seen in Figure 1, when the selected machine for preemption is near to the last machine, the total tardiness will be less. Moreover, when the selected machine for preemption is near to the first machine, the total tardiness is near to the non-permutation case. Therefore, the selected machine affects the total tardiness.

Figure 1. Performances of five instances of formulation

5. Conclusions

In this paper, a mixed integer programming mathematical model for a realistic non-permutation flow shop scheduling problem is presented. In this problem, the job due dates and preemption-dependent processing times are considered to minimize the total tardiness. To the best of our knowledge, concept of preemption-dependent processing time has not been considered before in the literature.

In order to clearly identify the effect of several characteristics on the suggested mathematical model, some randomly instances have been solved and an analysis has been carried out. We conclude that the total tardiness without preemption is not less than the preemptive scheduling. Additionally, when the preemption-dependent processing time increases, the total tardiness may increase. Furthermore, in 56% of experiments, the last machine is the best selected one for the problem. Moreover, by increasing the number of preemptions, the total tardiness never increases.

Further research can be developing a solution method to for this problem. In addition, there is a number of assumptions in our problem. For example, it is assumed that the preemption should be occurred only on exactly one machine. More research is needed in order to further cover the gap between the theory and practice for the non-permutation flow shop scheduling problem. Moreover, as a new direction for future research, one can develop the formulation to more complex systems such as flexible flow shops, job shops and flexible job shops.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Mohsen Ziaee

Mohsen Ziaee accomplished his MSc in Industrial Engineering at University of Tehran, Tehran, Iran (1999–2001) and PhD in Industrial Engineering at Iran University of Science and Technology, Tehran, Iran (2003–2008). Currently, he is an assistant professor at Industrial Engineering Department, University of Bojnord, Bojnord, Iran. His research interests are production planning and scheduling, multi-criteria decision making, applied operations research, and artificial intelligence techniques.

Hossein Karimi

Hossein Karimi was born in 1987 in Kordkouy, which is a city in the north of Iran. He is assistant professor in Industrial Engineering at University of Bojnord. He received his PhD, MSc and BSc degree from K.N.T University of technology, Shahed University and University of Bojnord in 2015, 2011 and 2009, respectively. His main research interests focus on: facility location problem, mathematical programming and optimizations.