Iterative sliding window method for shorter number of operations in modular exponentiation and scalar multiplication

Abstract

Cryptography via public key cryptosystems (PKC) has been widely used for providing services such as confality, authentication, integrity and non-repudiation. Other than security, computational efficiency is another major issue of concern. And for PKC, it is largely controlled by either modular exponentiation or scalar multiplication operations such that found in RSA and elliptic curve cryptosystem (ECC), respectively. One approach to address this operational problem is via concept of addition chain (AC), in which the exhaustive single operation involving large integer is reduced into a sequence of operations consisting of simple multiplications or additions. Existing techniques manipulate the representation of integer into binary and m-ary prior performing the series of operations. This paper proposes an iterative variant of sliding window method (SWM) form of m-ary family, for shorter sequence of multiplications corresponding to the modular exponentiation. Thus, it is called an iterative SWM. Moreover, specific for ECC that imposes no extra resource for point negation, the paper proposes an iterative recoded SWM, operating on integers recoded using a modified non-adjacent form (NAF) for speeding up the scalar multiplication. The relative behaviour is also examined, of number of additions in scalar multiplications, with the integers hamming weight. The proposed iterative SWM methods reduce the number of operations by up to 6% than the standard SWM heuristic. They result to even shorter chains of operations than ones returned by many metaheuristic algorithms for the AC.

Keywords:

• addition chain
• modular exponentiation
• scalar multiplication
• sliding window method

Public Interest Statement

Data encryptions using public key cryptosystems (PKC) provide higher functionality services such as confidentiality, authentication, integrity and non-repudiation. However, the highly computational cost in the encryption process, involving modular exponentiation or scalar multiplication, made this optimisation strategy relevant. In both cases, very large size of integers (of up to 600 decimal digits) are being utilised as the keys. And, the key size determines that of the exponent or multiplier. One means of reducing the size of the computation is by transforming the process into series of simpler multiplications or additions.

In this paper, we proposed an iterative-based sliding window method (SWM) for improving the computational cost. Our proposed approach searches for optimal parameters for the SWM, corresponding to specific integer utilized as the exponent or multiplier. The experimental results demonstrate that our proposed method improves the solution quality, by reducing the computation size, up to 6

1. Introduction

In public key cryptosystems (PKC) (Diffie & Hellman, 1976; El-Gamal, 1985; Koblitz, 1987; Rivest, Adi, & Adleman, 1978), computations involving modular exponentiation and scalar multiplication found in the respective RSA (Rivest et al., 1978) and ECC (Koblitz, 1987; Miller, 1985) are the most expensive operations that determine the efficiencies of the algorithm, and on which the security of the systems also depends. For the applications to be computationally secured the size of the key, which is the exponent or multiplier, respectively, should be of at least 1,024 bits in multiplicative structure such as Diffie–Hellman (Diffie and Hellman, 1976) and RSA and 163 bits in additive structure of ECC.

One of the means of optimizing these operations without compromising the security effectiveness is by reducing an exhaustive operation of modular exponentiation to repeated squaring and multiplication and likewise scalar multiplication to repeated doubling and addition via the concept of addition chain (AC). Since modular exponentiation is an additive function of the exponent similar to that of multiplier from scalar multiplication, both operations are adoptable to the idea of AC. In other words, possible shortening of an AC for the exponent/multiplier by reducing the number of doubling and addition corresponds to that of either one of the two operations: thus should be understood as minimizing the number of multiplications in modular exponentiation or of additions in scalar multiplication.

The problem of finding optimal AC for an arbitrary integer, also known as addition chain problem (ACP), exists for long (Dellac, 1894; Scholz, 1937). Numerous theoretical studies on the problem can be found in Balega (1976), Brauer (1939), Downey, Leong, and Sethi (1981), Mignotte and Tall (2011), Thurber (1993) and Yao (1976). From experimentation perspective, exhaustive approaches have been applied (Clift, 2010; Hatem, 2011), as well as heuristics (Bos & Coster, 1990; Gelgi & Onus, 2006; Koç, 1995; Park, Park, & Cho, 1999; Thurber, 1999). Moreover, after Downey et al. (1981) proved that the generic case called addition sequence is an NP-complete problem, various metaheuristics have also been applied (Cruz-cortés, Rodríguez-Henríquez, & Coello, 2008; Domínguez-Isidro, Mezura-Montes, & Osorio-Hernández, 2015; Jose-Garcia, Romero-Monsivais, Hernandez-Morales, Rivera-Islas, & Torres-Jimenez, 2011; León-Javier, Cruz-Cortés, Moreno-Armendáriz, & Orantes-Jiménez, 2009, November; Nedjah & de Macedo Mourelle, 2006; Osorio-Hernández, Mezura-Montes, Cruz-Cortés, & Rodríguez-Henríquez, 2009, May).

For the purpose of simplicity, a generic integer e is used in this paper to represent the exponent or multiplier of either of the operations.

Definition 1.1

Given an integer e, the sequence $a_0=1,a_1=2,a_3,\dots ,a_r=e$, is said to be an AC for e if $\forall i\ge 1$, $a_i=a_j+a_k$, $i>j\ge k$. The length of the chain is r.

In the studies of AC by mean of heuristic approach, e is normally represented into an equivalent binary form, from which some form of manipulation is applied in the quest to produce the shortest possible chain.

Definition 1.2

The length of e (denoted as) n(e) is defined as the minimum number of bits to represent e in binary form $e={(e_{n-1}{e}_{n-2}\dots e_0)}_2$. n used to indicate the length of an arbitrary n-bit e.

Definition 1.3

The hamming weight (shorten as weight) of e denoted as H(e) is defined as the number of non-zero bits in the binary representation of e.

Using the binary form as found in many heuristic techniques, the total number of operations is counted to the number of doublings (squarings) and additions (multiplication) involved. In fact, the number of squarings is fixed to the bit-length n(e), and thus improvement can only be done on the number of multiplications which is proportionate to weight H(e).

Binary method (Knuth, 1998) has been the basic procedure for computing modular exponentiation as well as scalar multiplication. In the modular exponentiation, a sequence of squarings and optional multiplications are performed, depends upon the given digit value of the binary form for e that is 1 or 0, respectively. Similarly, a sequence of doublings and optional additions are performed in the scalar multiplication. For an n-bit e, represented in the binary form as $e=e_{n-1}{e}_{n-2}\dots e_0$, the method for the exponentiation $y=x^e$ follows in Algorithm 1.

In Algorithm 1, $n(e)-1$ number of squarings are performed in step 3, and a multiplication in step 5 corresponding to every non-zero bit encounter, less the most significant bit (MSB): $H(e)-1$. Thus, assuming multiplication and squaring are computationally equal, the number of multiplications (operations) $T_{bin}$ is(1) $$\begin{array}{c}\hfill T_{\text{bin}}(e)=n(e)+H(e)-2\end{array}$$(1)

Since there are n bits in e, each of which is equally likely to be 1 or 0, the asymptotic number of multiplications in Algorithm 1 is $n+n/2=3n/2$. The method is highly efficient in implementation due to its minimal book-keeping in the process (Knuth, 1998). However, it performs excessive number of multiplications than is necessary.

An m-ary (also known as or $2^k$-ary) method is an extension of the binary method. An n-bit e is padded (where necessary) with at most $k-1$ trail of 0s to form a multiple of k. It is then partitioned into $w=\lceil n/k\rceil$ blocks of fixed k-bit words: $m_i,i=w-1,\dots ,0,m_{w-1}$ being the most significant word (MSW). Thus, $0\le m_i=e_{ik+k-1}{e}_{ik+k-2}\dots e_{ik}={\sum }_{j=0}^{k-1}{2}^j{e}_{ik+j}<2^k$, and $e={\sum }_{i=0}^{w-1}{m}_i{2}^{ik}$. Initially, the values $x,x^2,\dots ,x^{2^k-1}$, corresponding to all possible value for $x^{m_i}$, are pre-computed. The algorithm proceed by scanning the most significant k bits $m_{w-1}$, raising the corresponding $x^{m_{w-1}}$ to the power of $2^k$ as the partial result. This is followed by subsequent scanning of the remaining $m_i,i=w-2,\dots ,0$, each time multiplying the partial result by $x^{m_i}$ and raising it to the power of $2^k$ as: $x^{2m_{w-1}},x^{4m_{w-1}},\dots ,x^{2^k{m}_{w-1}},x^{2^k{m}_{w-1}}cdot{x}^{m_{w-2}},x^{2(2^k{m}_{w-1}+m_{w-2})},\dots ,x^{(2^{n-k}{m}_{w-1}+2^{n-2k}{m}_{w-2}+\cdots +2^k{m}_1)}·x^{m_0}=x^e$. That is beginning from $x^{m_{w-1}}$, k-times squaring are performed followed by multiplying the partial result by the next $x^{m_i},i=w-2,\dots ,0$ until the last $x^{m_0}$ is multiplied by. The m-ary method has an average number of multiplications given by Koç (1995).(2) $$\begin{array}{c}\hfill T_m(n,k)=(2^k-2)+(\lceil n/k\rceil -1)k+(\lceil n/k\rceil -1)(1-2^k)\end{array}$$(2)

Depending on the k parameter, the method performs less number of multiplications than binary method. However, the pre-computations cost increases exponentially with an increase in the k size.

Note that when $m_i=0$ ($x^{m_i}=1$) the multiplication step is not necessary. Consequently, adaptive window methods are the enhancements of the m-ary that form partitions $m_i$ of arbitrary length of 0s. In the constant-length non-zero window (CLNW) version, in the partitioning process, the leading zeros in a given k-bit non-zero window (NW) partition $m_i\ne 0$ are carved out and concatenated with subsequent zeros encounter to form a zero window (ZW) $m_i=0$ partition. The ZW takes any arbitrary length until a non-zero bit is again encountered. Thus, only NWs are restricted to bit-lengths $n(m_i)\le k$, and for which list significant bit $(\mathit{LSB})=\mathit{MSB}=1$. As a result, the pre-computation stage involves computing only $x^2=x·x$ and odd values $x^3=x·x^2,x^5=x^3·x^2,\dots ,x^{2^k-1}=x^{2^k-3}·x^2$ at the cost of $2^{k-1}$ multiplications. Whereas, in the variable-length non-zero window (VLNW) version (Koç, 1995), the number of ZWs is further maximized by switching NW to ZW partition construction upon encounter of predetermined $0<q\le k-2$ consecutive zeros. Transition to the ZW-partition begins with the q zeros. Note, setting $q=k-1$ defaults to CLNW. Both methods are also known as SWM (refer to Koç, 1995; Park et al., 1999, for details).

Given an n-bit e, partitioned into $m_i$ windows of variable lengths such that $n(m_i\ne 0)\le k$, the number of multiplications in $y=x^e$ is determined as follows. Beginning from the MSB, let there be $p\le w$ number of NWs in the partition. On deferring until after the partitioning is completed and the largest NW ${max}_{0\le i<w}(m_i)$ (henceforth denoted as $max(m_i)$) is known, the pre-computation cost reduces to $(max(m_i)+1)/2$ multiplications. Beginning from MSW $m_{w-1}$, the exponentiation involves $n(e)-n(m_{w-1})$ squaring, and $p-1$ multiplications corresponding to remaining NWs. The generic procedure is presented as Algorithm 2.

Thus, the number of multiplications is given as follows:(3) $$\begin{array}{c}\hfill T(e)=(max(m_i)+1)/2+n(e)-n(m_{w-1})+p-1\end{array}$$(3)

On the average, $n(m_i\ne 0)$ are maximized, while their proportionate decimal values (determined by the weight) minimized with increase in the q value towards k; the reverse is the case for relatively smaller value. On the other hand, empirical result from sets of 16 to 2,048-bit es tested shows that delaying the pre-computation reduces the exponentiation cost by an average of three multiplications. Thus, given e, varying k and q while determining the corresponding p, $max(m_i)$ and $n(max(m_i))$ values, until those k and q that minimize Equation (3) are found, amounts to finding the optimal parameters for computing $y=x^e$ using SWM: that is it translates to finding the corresponding shortest number of multiplications in the computation. Note that only partitioning is required to determine the optimal parameters. This is the idea of the Iterative SWM.

This paper proposes finite iterative partitioning strategy to determine optimal SWM parameters for any given e, to achieve shortest chain of multiplications in computing modular exponentiation using the SWM. Additionally, the paper proposes an iterative version of the SWM on recoded e utilizing a modified NAF (Eğecioğlu & Koç, 1994): in which the increase in the NAF-length is controlled while achieving the same minimum weight. NAF is employed to reduce the cost of additions in scalar multiplication-based ECC. Furthermore the paper examined, utilizing empirical data, the relative increment in the number of additions in scalar multiplications with respect to H(e) in recoded es.

The rest of this paper is organized as follows: Section 2 detailed and analysed the proposed Iterative SWM algorithm; an experiment is then set up and carried out on the algorithm, and the result discussed at the end of the section; proposed recoded version of the iterative SWM is detailed and empirically examined in Section 3. Section 4 concludes the paper.

2. Iterative sliding window method (ISWM)

The proposed ISWM utilizes left-to-right version of the VLNW algorithm (Park et al., 1999). But in this case the partition size k is varied from an initial $k_0$ to a predetermined maximum value $k_{max}$. Similarly, the allowable consecutive zeros in a partition q is varied from $q_0>0$ to $q_{max}\le k-1$. At $q=k-1$ the algorithm is in CLNW mode (Koç, 1995). On every combination of $(k,q)$ parameter values, the algorithm partitions e and determines the number of multiplications T(e) according to Equation (3). It keeps track of the parameter values with the shortest T(e), and finally evaluates and returns the corresponding SWM. The ISWM is presented as Algorithm 3.

 

2.1. Algorithm analysis

Given n-bit e and $q\le k-1$, in Algorithm 3, the external loop executes at most $k_{max}$ times, in each of which the internal loop executes at most k times. Since $1\ge k\ge k_{max}$, the algorithm is bounded by $\frac{k_{max}(k_{max}-1)}{2}<\frac{k_{max}^2}{2}$ number of, mainly, partitioning due to steps 1 and 3. Empirical studies (as detailed shortly) shows that optimal k is bounded by $O(\text{lg}(n))$. Thus, the algorithm is bounded by $O({\text{lg}(n)}^2)$ partitionings. A complete SWM is executed once in step 11. The partitioning in step 1 is performed in a single pass, depending on the size of k. At worst $k=1$ and ith-bit$\ne (i+1)$th-bit, $i=n-1,\dots ,0$: whereby the n-bit e is partitioned into $w=n$ number of $m_i$, thus it is bounded by O(n).

In fact, for common $n\le 2048$ utilized in PKC, all optimal k value is bounded by $1\le k<8$ (Koç, 1995; Park et al., 1999): Thus, at most $\frac{7\times 6}{2}=21$ partitions are needed in the process.

The memory resource required in running the algorithm is the same as that of the standard left-to-right SWM: as since partitioning is part of the SWM. Estimated as memory units required for the pre-computed and final exponent, it is at worst $2^{k-1}+O(1)$ units.

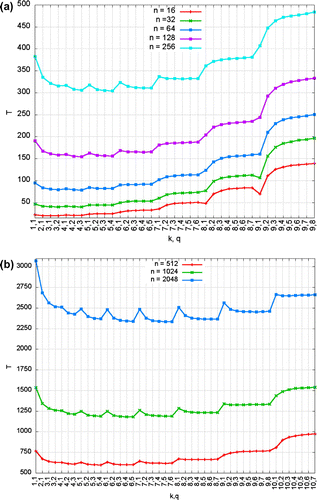
A preliminary experiment is conducted on the ISWM to estimate the bounds for the k and q, with view to optimizing the number of partitioning. Figure 1 shows the number of multiplications (T) as function of the $k,q$, corresponding to various sets of n.

Figure 1. ISWM respond with $k,q$ settings. (a) 16–256 bitse and (b) 512–2048 bitse.

As can be observed in Figure 1(a) and (b), and based on the empirical data collected during the experiment, the optimal T are (by 99.9%) within the $(k,q)$ parameters ranges as tabulated in Table 1.

Table 1. $k,q$ parameters ranges for optimal ISWM

n	k	q	Partitions
16–31	2–4	1–3	6
32–255	2–5	1–4	10
256–1,023	2–6	1–4	14
1,024–2,048	2–7	1–6	21

2.2. Experimental set-up and result discussions

2.2.1. Experiment setup

Koç (1995) reported theoretical optimal parameters for the standard right-to-left SWM. The same is reviewed by Park et al. (1999). The left-to-right method is more effective in terms of shorter number of multiplications (Park et al., 1999). However, there was no exclusive report on its optimal parameters. Therefore, an empirical analysis is carried out on the method to determine the corresponding values, for classes of integers mostly utilized in PKCs. The result is presented in Table 2.

Table 2. Optimal parameters for SWM

n	k	q
16, 32, 64	3	2
128, 256	4	3
512	5	4
1,024	6	5
2,048	7	6

In the subsequent experiment, the number of multiplications T and it relative behaviour with varying weight H(e) are investigated. Thus, random sample integers are generated, to ensure adequate representation for the e range covered, with the details as follows:

(1)	The integers are classified into 8 classes according to bit-lengths as $n=16,32,64,128,256,512,1,024,2,048$;
(2)	Each class is divided into 16 sub-classes: 1 to 16, such that class $i:i=1,\dots ,16$ has an average $H(e)=\frac{n}{32}(2i-1)$ randomly distributed in $\left[\frac{n}{16}(i-1)+1,\frac{n}{16}i\right]$;
(3)	1,000 sample, for each of the sub-class, is generated. And the corresponding numbers of multiplications are concurrently evaluated, applying binary method, SWM and our proposed ISWM, according to parameters in Tables 1 and 2, respectively; and
(4)	The results expressed as the average of the accumulated number of multiplications for the 16,000 ($1,000\times 16$) sample, generated from the sub-classes, as par each class, as the representative average for the class.

2.3. Result discussions for ISWM

To examine the effectiveness of the ISWM in shortening the number of multiplications, an experiment was conducted using the detailed set-up and the classes of integers in Section . The results are compared with ACs (corresponding to number of multiplications) due to SWM-metaheuristic hybrid methods in Cruz-cortés et al. (2008) and Domínguez-Isidro et al. (2015). This is presented in Table 3.

Table 3. Average T by various methods

n	${\text{Bin}}^{\text{a}}$	${\text{S-SWM}}^{\text{b}}$	${\text{AIS-SWM}}^{\text{c}}$	${\text{ACEP-SWM}}^{\text{d}}$	ISWM
16	23	22	–	–	20
32	47	41	–	–	39
64	94	80	–	–	78
128	191	156	152	154	154
256	383	308	304	304	303
512	767	602	604	604	599
1,024	1,535	1,186	1,196	1,190	1,180
2,048	3,070	2,344	–	–	2,332

${}^{\text{a}}$ Binary method; ${}^{\text{b}}$SWM based on (Park, Park, & Cho, 1999); ${}^{\text{c}}$in (Cruz-cortés, Rodríguez-Henríquez, & Coello, 2008); din (Domínguez-Isidro, Mezura-Montes, and Osorio-Hernández, 2015). Note: “$-$” indicates non-available result for the given algorithm

In all the entries in Table 3, ISWM performs better than the standard SWM. It reduces the length of multiplications on the average by at least 2 ($n=16$), and up to 12 ($n=2,048$). This reduction is very significant considering that it is on the average basis. On the other hand, AIS-SWM and ACEP-SWM perform better than both SWM and ISWM for 128-bit integers. However, as the integer size increases, the proposed ISWM outperforms both methods: indicating superior advantage of the SWM in handling large-sized integers such as the ones used in PKCs. Based on percentage deviation of ISWM from the standard SWM, the former gains 1% shorter number of multiplications than the latter.

It is interesting to note that SWM effectiveness in computing modular exponentiation with shorter number of multiplications is being underestimated at the expense of its implementation efficiency. In fact with proper choice of windows parameters, even the standard SWM is generally better than other reported heuristic/metaheuristics, for large integers (512–2,048 bits). When approached as proposed, ISWM is comparably better than the reported results in every respect. Therefore, this paper concludes that SWM is still the most effective method for computing modular exponentiation, while it is second to binary method in terms of efficiency.

3. Iterative recoded SWM (IRSWM)

ECC involves repeated point additions of the form $P+P+\cdots +P$ for some finite e times: referred to as scalar multiplication, and denoted as eP. The scalar multiplication is structurally similar to modular exponentiation, with the exception that squaring and multiplication are replaced by doubling and addition, respectively. The respective operations are accordingly interchanged in this section. The ECC has the advantage of achieving equivalent level of security with shorter key size than other standard PKCs such as RSA. For example, 233-bit key ECC provides security level equivalent to 2,048-bit key RSA (Dahshan, Kamal, & Rohiem, 2015; Win, Mister, Preneel, & Wiener, 1998). Additionally, the cost of inversion is negligible: for a point $P(x,y)$, $P{(x,y)}^{-1}=-P(x,y)=(x,-y)$. Therefore, introducing inversion in the computation process is proprietary to ECC with no extra cost.

The effect of the inversion in reducing the number of additions in eP can be demonstrated with n-bit es of the form $e=2^n-1$. They exhibit longest number of additions $2(n-1)$ on applying binary method to evaluate the corresponding $(2^n-1)P$. But by admitting inversion, the same method reduces the additions to $n+1$: consisting of n doublings and an inversion and addition, as $1P,2P,2^{2}P,2^{3}P,\dots ,2^{n}P,2^{n}P-1P$. In general, any k consecutive non-zero bits in binary form of e, $1\times 2^{n-1}+\cdots +0\times 2^{n-i}+\underline{1\times 2^{n-i-1}+1\times 2^{n-i-2}+\cdots +1\times 2^{n-i-k}}+\cdots (1\dots 0\underline{11\dots 1}\dots )$, can be recoded into $k+1$-bits as $1\times 2^{n-1}+\cdots +1\underline{\times 2^{n-i}+0\times 2^{n-i-1}+0\times 2^{n-i-2}+\cdots -1\times 2^{n-i-k}}+\cdots (1\dots \underline{10\dots -1}\dots )$. Therefore, signed recoding is introduced to reduce the number of additions that follows doubling due to the integer weight H(e). In this regard, balanced ternary $(-1,0,1)$ recoding (Knuth, 1998) is re-introduced to minimize the weight. Henceforth, $-1$ is denoted as $\overline{1}$ and recoded form for e as $\overline{e}$.

Various recoding methods exist, with NAF being canonical having the minimal non-zero bits density of n / 3 (Eğecioğlu & Koç, 1994; Reitwiesner, 1960; Morain & Olivos, 1990). A kNAF is a recoded equivalent of m-ary, capable of reducing the density asymptotically to $n/(k+1)$ (Okeya, Schmidt-Samoa, Spahn, & Takagi, 2004). Similarly, Laih and Kuo (1997) proposed an m-ary version of modified signed digit (MSD), having the same non-zero bits density as the kNAF. Another method similar to kNAF, but with the advantage of performing the conversion from the MSB, is mutual opposite form (MOF) (Okeya et al., 2004). The approach eliminates the need for two parses during the conversion, and an additional n-bit memory required in the process is reduced to 1 (or k-bit for kMOF). Basically, for an n-bit e (4) $$\begin{array}{c}\hfill \text{MOF}(e)=(e\ll 2)\ominus e\end{array}$$(4)

where all the operations in Equation (4) are bitwise.

Balasubramaniam and Karthikeyan (2007) introduced complementary recoding (CR): 1 + bitwise complement of e is bitwise-subtracted from $2^{n(e)+1}$ such that(5) $$\begin{array}{c}\hfill CR(e)=2^{n(e)}\ominus \overline{e}\ominus 1.\end{array}$$(5)

Note that, Equation (5) is equivalent to $2^{n(e)+2}-e$. However, CR is only effective in reducing the H(e) for an n-bit e, when $H(e)>n/2$: This is because and its ($n+1$)-bit CR-recoded $\overline{e}$ are related as$$H(\overline{e})=n(e)+1-H(e)$$.

Therefore, CR rather increases the non-zero bit density if $H(e)\le \frac{n(e)}{2}$. For example, consider $e={24066}_{10}={101111000000010}_2$ where $H(24066)=6$. $CR(24066)=10\overline{1}0000\overline{1}\overline{1}\overline{1}\overline{1}\overline{1}\overline{1}\overline{1}\overline{1}{0}_2$, $H(CR(24066))=10$. However, $NAF(24066)=10\overline{1}000\overline{1}000000010$, $H(NAF(24066))=3$.

NAF optimally reduces H(e), but at tines leads to additional bit to n(e) that could possibly be avoided (Saffar & Said, 2015). Integers with binary form $e=1011\dots$ have NAF-recoded form as $\overline{e}=10\overline{1}0(\overline{1}|0)\dots$ having $n(\overline{e})=n(e)+1$. But an equal non-zero bits density can be realized without the additional 1 bit increase, by suppressing the NAF conversion at the second MSB. For example, consider $e={93}_{10}={101110101}_2$ having $n(93)=9$ and $H(93)=6$. $\text{NAF}(93)=10\overline{1}00\overline{1}0101$, that is $n(NAF(93))=10$ and $H(NAF(93))=5$. On suppressing the conversion at the second MSB, ${93}_{10}$ is recoded as $1100\overline{1}0101$ with length and weight equal 9 and 5, respectively. As for suitable recoding for SWM heuristic, it is still an open problem (Win et al., 1998). Therefore, this paper proposes a modified NAF (mNAF) as a means of avoiding the additional bit increase where possible. The procedure is presented in Algorithm 4.

Table 4 presents average number of additions due to binary method, NAF and mNAF for sets of $10,16,32,\dots ,512$-bit integers.

Table 4. Effects of integer recoding on number of additions

n	Binary	NAF	mNAF
10	13.50 (5.5)	13.11 (4.11)	12.61 (4.11)
16	22.50 (8.5)	21.11 (6.11)	20.61 (6.11)
32	46.50 (16.50)	39.56 (8.56)	38.87 (8.56)
64	94.50 (32.50)	79.20 (16.20)	78.51 (16.20)
128	190.50 (64.50)	158.48 (31.48)	157.78 (31.48)
256	382.55 (128.55)	317.11 (62.11)	316.42 (62.11)
512	766.53 (256.53)	634.10 (123.10)	633.40 (123.10)

Note: Values in brackets show the average H(?e) for the respectiven-bit e sets.

As can be observed in Table 4, the NAF and mNAF recoding significantly reduce the number of additions, especially as the integer sizes become larger. On the other hand, the proposed mNAF exhibits shorter additions than the original NAF: this is due to its better performance in containing length $n(\overline{e})$ while equally reducing the weight $H(\overline{e})$ as the NAF.

Iterative recoded SWM (IRSWM) is similar to ISWM (Algorithm 3). Except that e is initially recoded using Algorithm 4; Squaring and multiplications in SWM are replaced with doublings and additions (or subtraction), thus called recoded SWM (RSWM); and, $max(m_i)$ is replaced with the largest absolute value $max(|m_i|)$. The procedure is presented in Algorithm 5.

The experimental set-up in Section is utilized to test the IRSWM. However, considering that the current scalars utilized in ECC are less than 512 bits, the experiment covers 512 bits only. Likewise, little variations where observed in the optimal window parameters for the SWM, when applied on recoded integers. Accordingly, the new values are presented in Table 5.

Table 5. Optimal parameters for RSWM

n	k	q
16	3	1
32, 64, 128	3	2
256, 512	5	4

Furthermore, preliminary experiment shows that CLNW ($q=k-1$) on the recoded integers results in shorter number of additions than VLNW. Thus, q is fixed, making Algorithm 5 even faster, as the number of iterations is always less than $k_{max}$.

Additionally, it is observed that level of the weight reduction due to the NAF and various other recoding methods (with the exception of CR) are subject to both the non-zero bits density and their distribution pattern: Two n-bit integers having the same weight exhibit different recoded density, depending on their respective pattern of the 1-bits distribution before recoding. The reduction is highly efficient when the initial 1 bits are clustered. For example, NAF for $e=11110011101111000$ is $1000\overline{1}01000\overline{1}000\overline{1}000$, having $H(\overline{e})=5$. On the other hand, NAF-recoding $e=11011011101101100$ with the same weight results to $100\overline{1}00\overline{1}000\overline{1}00\overline{1}0\overline{1}00$, having $H(\overline{e})=6$. As such empirical results for recoded sets of integers are highly subject to the non-zero bits distribution pattern of the set utilized. And, the resulting number of additions may not tally with theoretically expected ones, for example, asymptotic number of additions due to $NAF(n)=4n/3$, for an n-bit integer. In fact, tests on integers generated by various random generators yield different results, all of which having shorter number of additions than expected theoretical one. Therefore, the results presented in this section are only subjects to the set of random integer sets utilized.

3.1. Variation in number of additions with non-zero bit density

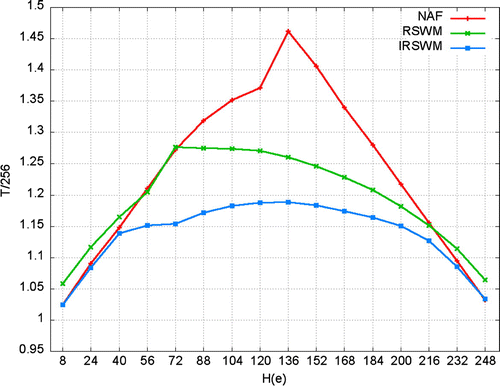
The relative behaviour is examined, of the corresponding number of additions with respect to the non-zero bit density. The test is carried out on NAF, IRSWM and the standard SWM applied on recoded integers, RSWM. A random set of 256-bit integers is utilized. The effect of bit-length is normalized by dividing the number of additions by n. The result is presented in Figure 2. It also shows relative reduction in the bit-density by the methods examined.

Figure 2. Variation in Number of Additions with H(e) for 256-bit e.

Note that from Figure 2, initially the number of additions in both NAF and IRSWM increases proportionately with the H(e). Fortunately, peak values are reached shortly after the weight reached n / 2. After which the length continue to decreases. RSWM also exhibits similar trend, except that the peak value is reached when $H(e)\approx n/3$. As for the relative efficiency in containing the density, IRSWM performed best among the three methods. In general, the trend shows that integers with about 1/3–2/3 non-zero bits density exhibit relatively larger number of additions even after recoded; the reverse is the case when the density is very sparse and as well when highly concentric.

3.2. Result discussions for IRSWM

In this section, the experimental results from IRSWM are compared with that of RSWM as well as recoded binary method. The proposed mNAF is utilized in the recoding. The result is presented in Table 6.

Table 6. Number of additions by various methods on recoded e

n	mNAF	RSWM	IRSWM
16	21	23	20
32	39	41	38
64	78	78	75
128	158	152	147
256	316	305	292
512	633	586	578

The result in Table 6 shows significant improvement on the number of additions returned by IRSWM over that of RSWM. It shows that iteratively searching for the optimal partitioning parameter values reduces the length, on average, by at least 2 ($n=16$) and up to 8 ($n=512$). As can be observed from both the Table 6 and Figure 2, IRSWM also significantly optimizes the length than the other methods examined when the integers bits densities are about half of the bit-length: which is the worst case scenario in terms of the number of additions. Overall estimate using percentage deviation shows that IRSWM improves on RSWM and SWM by 4 and 6%, respectively.

On general note: applying the IRSWM results in the shortest number of additions in ECC scalar multiplications. It is also expected that, for ECC applications in which the scalar can be chosen, the result presented may serve as a tool for much wiser and narrower selection for scalars whose number of additions is a lot lesser.

4. Conclusion and future works

This paper proposes iterative (recoded) SWM to achieve an even shorter number of operations in both modular exponentiation and scalar multiplication that are found in PKC. A modification to classic NAF algorithm is proposed, to contain the increase in integers bit-length after recoding. The relative responds is also explored, of the length of additions in computing scalar multiplications, with respect to hamming weight of the scalar. Empirical results show that the Iterative SWM optimize the number of operations by at least 1% over the SWM, and up to 6% when applied on recoded integer. With respect to relationship between the scalar multiplication and the hamming weight, recoded form of integers with original hamming weights below and above one-third of their corresponding length are more optimal for scalar multiplications than their counterparts. The paper concluded that iteratively finding the optimal window parameters while applying SWM effectively reduces the number of operation in the modular exponentiation and scalar multiplication. An even better performance is realized than the computationally much complex metaheuristic approaches at present.

Even as the proposed iterative SWM shortens the number of operations, there is still room for further optimization. It is expected that introducing simple but effective metaheuristic can further reduce operations towards (nearest) optimal.

Additional information

Funding

This research was partially supported by the Malaysian Ministry of Higher Education [grant number FRGS/1/2015/ICT03/UNISZA/02/1].

Notes on contributors

Adamu Muhammad Noma

Adamu Muhammad Noma received his Bachelor of Technology in Computer Science from Abubakar Tafawa Balewa University Bauchi Nigeria in 2006 and Master of Science in Computer Networking at the Universiti Putra Malaysia in 2014. He is a lecturer with Bauchi State University Gaudau, Nigeria, and is currently pursuing his Doctor of Philosophy in Computing Security at the Universiti Putra Malaysia. His area of research interest includes networks, security in distributed computing systems and optimization. In this research work, they propose a means of speeding up public key cryptosystems in an effort to ensure their seamless implementations in distributed and embedded systems, which are resources-constrained in terms of both computing and memory.

Abdullah Muhammed

Abdullah Muhammed received PhD in computer science from the University of Nottingham in 2014.He is a senior lecturer and HoD of the Department of Communication Technology and Networks, UPM. His research interests include cloud computing, mobile and wireless network, scheduling, heuristic and optimisation.

Zuriati Ahmad Zukarnain

Zuriati Ahmad Zukarnain is an associate professor at the same faculty. She received PhD from the University of Bradford. Her research interests include efficient multiparty QKD protocol for classical network and cloud; wireless and ad hoc networks load balancing; quantum processor unit for quantum computers, authentication time of IEEE 802.15.4 with multiple-key protocol, wireless networks intradomain mobility handling, efficiency and fairness for new AIMD algorithms and kernel model.

Muhammad Afendee Mohamed

Muhammad Afendee Mohamed received PhD in mathematical cryptography from UPM in 2011. Currently, he is a senior lecturer at this university and his research interests are in the domain of information security and mobile and wireless networking.