?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
Motivated by the conjecture that an interaction between scheduling and pre-scheduling phases in production planning may give certain benefits, we conduct a detailed study of the optimality conditions and dominance relations for a strongly NP-hard single-machine scheduling model when jobs have release and due-dates and the objective is to minimize maximum job lateness. By exploring the inherent structure of the problem, we establish the optimality conditions when the problem can be efficiently solved. We come to an NP-hard special case of the problem with only two possible job release times, that as we show allows stricter dominance rules and optimality conditions verifiable in polynomial time. The established properties give a potential of a beneficial interaction between scheduling and pre-scheduling phases in production planning, and also provide basic theoretical background for the construction of efficient heuristic and implicit enumerative algorithms.
Public Interest Statement
Scheduling problems are mathematical problems formalized for the solution of diverse practical real-life problems. They deal with a finite set of requests or jobs to be performed (or scheduled) on a finite (and limited) set of resources called machines or processors. The aim is to choose the order of processing the jobs on the machines so as to meet a given objective criterion. In this paper we study a scenario with a single machine when jobs have arrival and due dates: a job cannot be assigned to the machine before its arrival time, whereas it is desirable to complete it by its due date; if this is not possible, we wish to minimize the maximum job deviation from its due date (the so-called lateness). The problem is known to be intractable. Still, we derive conditions that lead to its optimal solution in polynomial time.
1. Introduction
The term scheduling refers to the assignment of a set of requests to the given set of resources over time with the objective to optimize a given objective criterion. The requests are called jobs or tasks and a resources are called machines or processors, whereas the aim is to choose the order of processing the jobs on the machines so as to meet a given objective criteria. Therefore, a scheduling problem is characterized by the three distinct components: the tasks or activities that one wishes to perform, the resources available for their implementation, and the aims or objectives that one wants to achieve (that identify the best solutions). Different characteristics of jobs and machines together with different optimality criteria originate a vast amount of the scheduling problems.
Scheduling is an important phase in production planning, that, in turn, constitutes part of a wider production cycle. Once a product is designated, its production process needs to be determined. Decisions that are taken at the earlier phases of production planning before the scheduling phase (such as allocation and distribution of resources, raw materials, time limits, etc.), determine a particular scheduling model that is to be solved, i.e. this scheduling model essentially depends on the decisions made at the earlier (pre-scheduling) stages of production planning. In practice, there is a little interaction between the scheduling stage and the earlier stages in production planning, in the sense that the earlier made decisions do not normally change depending on the (potential) outcomes at the scheduling stage, i.e. the scheduling model itself doesn’t change. However, such an interaction might be beneficial since two similar scheduling models may have drastically different complexity status and hence admit solution methods of different efficiency. Based on the simulation results for the originally selected scheduling model, the decisions taken at the earlier (pre-scheduling) stages may potentially be adjusted, which, in turn, may adjust the scheduling model itself. This is often difficult since the most of the arisen scheduling models turn out to be computationally intractable (NP-hard in formal terms), and hence the interaction becomes complicated because of a considerable amount of time needed to solve the corresponding scheduling problem for delivering a solution with the desired quality. Whereas a general solution method for the initially selected scheduling model may require inadmissible computational time, the instances of that model that occur in a given application may have specific characteristics or can be adjusted to satisfy some particular conditions and properties. To this end, the study of the inherent structure of the initially selected scheduling model and the optimality conditions for that model, i.e. the conditions when the model can be efficiently solved, is important.
In this paper, we carry out this kind of study for a single-machine scheduling model with n requests or jobs, where every request is released at an integer time moment, has a processing requirement on the machine, and a due-date that specifies a desirable time moment for its completion. A job completed behind its due-date is said to be late. The objective is to minimize the maximum lateness of any job, i.e. the difference between its completion time and due-date.
According to the conventional three-field notation introduced by Graham, Lawler, Lenstra, and Rinnooy Kan (Citation1979) the problem is abbreviated as : the first field indicates the machine (single-processor) environment, the second field specifies job parameters (
stands for the release time of job j), and in the third field the objective criterion is given (here
stands for the maximum job lateness, in the second field the processing time is omitted since it is an obligatory parameter for any scheduling problem). There is an equivalent formulation of the problem in which job due-dates are replaced by the delivery times, abbreviated
(
stands for the delivery times): once job completes on the machine, it needs to be delivered to the customer. Since the delivery is accomplished by an independent unit, it requires no machine time. The objective is then to minimize the maximum job full completion time that includes its delivery.
In Section 2 we show why these two versions are equivalent and give their detailed descriptions. Because of the equivalence, we shall refer to any of the two versions interchangeably. The problem is known to be strongly NP-hard (Garey & Johnson, Citation1979). There are exact implicit enumerative algorithms, see for instance, McMahon and Florian (Citation1975) and Carlier (Citation1982). An efficient heuristic method that is commonly used for problem was proposed long time ago by Jackson (Citation1955) for the version of the problem without release times, and then was extended by Schrage (Citation1971) for taking into account job release times. The extended Jackson’s heuristic (J-heuristic, for short) iteratively, at each scheduling time t (given by job release or completion time), among the jobs released by time t schedules one with the the largest delivery time (or smallest due-date). Since the number of scheduling times is O(n) and at each scheduling time search for a minimal/maximal element in an ordered list is accomplished, the time complexity of the heuristic is
. J-heuristic is sometimes referred to as EDD-heuristic (Earliest Due-Date) or alternatively, LDT-heuristic (Largest Delivery Time).
J-heuristic gives the worst-case approximation ratio of 2, i.e. it delivers a solution which is at most twice worse than an optimal one. There are polynomial time algorithms with a better approximation for problem . Potts (Citation1980) has proposed a modification of J-heuristic that repeatedly applies J-heuristic O(n) times and obtains an improved approximation ratio of 3/2. Hall and Shmoys (Citation1992) have expanded the later algorithm resulting in an improved approximation ratio of 4/3 by applying J-heuristic to the forward and backward versions of the problem simultaneously, and also proposed two polynomial approximation schemes (their algorithms allow partial order on the set of jobs). The idea of the usefulness of the simultaneous application of J-heuristic in forward and backward fashions was earlier exploited by Nowicki and Smutnicki (Citation1994). In a more recent work (Vakhania Perez, & Carballo, Citation2013), the magnitude
, no-more than the optimal objective value divided by the specially determined job processing time, is used to derive a more accurate worst-case approximation ratio of
for J-heuristic. The value of parameter
can be brutally determined in time
using an easily calculable lower bound on the optimal objective value instead of using the optimal objective value itself.
As to the special cases of our problem, if all job release times or delivery times are equal, J-heuristic (its original version) gives an optimal solution, and with integer release times and unit processing times, it also delivers an optimal solution. If job release times, processing times and delivery time are restricted in such way that each lies in the interval
, for some constant A and suitably large q, then the problem can also be solved in time
, see Hoogeveen (Citation1995). Garey, Johnson, Simons, and Tarjan (Citation1981) have proposed an
algorithm for the feasibility version with equal-length jobs (in the feasibility version job due-dates are replaced by deadlines and a schedule in which all jobs complete by their deadlines is looked for). Later in Vakhania (Citation2004) was proposed an
algorithm for the minimization version with two possible job processing times.
For other related criteria, in Vakhania (Citation2009) an algorithm that minimizes the number of late jobs with release times on a single-machine when job preemptions are allowed. Without preemptions, two polynomial-time algorithms for equal-length jobs on single machine and on a group of identical machines were proposed in Vakhania (Citation2013,Citation2012), respectively, with time complexities
and
, respectively.
Problem has been shown to be useful for the solution of the multiprocessor scheduling problems. For example, for the feasibility version with m identical machines and equal-length jobs, algorithms with the time complexities
and
were proposed in Simons (Citation1983) and Simons and Warmuth (Citation1989), respectively. In Vakhania (Citation2003) was proposed an
algorithm for the minimization version of the latter problem, where
is the maximal job delivery time and
is a parameter.
The problem is commonly used for the solution of more complex job-shop scheduling problems as well. A solution of the former problem gives a strong lower bound for job-shop scheduling problems. In the classical job-shop scheduling problem the preemptive version of J-heuristic applied for a specially derived single-machine problem immediately gives a lower bound, see, for example, Carlier (Citation1982), Carlier and Pinson (Citation1989) and Brinkkotter and Brucker (Citation2001) and more recent works of Gharbi and Labidi (Citation2010) and Della Croce and T’kindt (Citation2010). Carlier and Pinson (Citation1998) have used a straightforwardly generalized J-heuristic for the solution of the multiprocessor job-shop problem with identical machines. It can also be adopted for the case when parallel machines are unrelated, see Vakhania and Shchepin (Citation2002). J-heuristic can be useful for parallelizing the computations in scheduling job-shop Perregaard and Clausen (Citation1998), and also for the parallel batch scheduling problems with release times Condotta, Knust, and Shakhlevich (Citation2010).
Besides the above mentioned applications in multiprocessor, shop and batch scheduling problems, our problem has numerous immediate real-life applications in various production chains, CPU time sharing in operating systems (jobs being the processes to be executed by the processor), wireless sensor network transmission range distribution (where jobs are mobile devices with their corresponding ranges that can be modeled as release and due dates).
By exploring the inherent structural properties of the problem, here we derive new optimality conditions when practical special cases of our problem can be solved optimally in a low degree polynomial time. In particular, we provide explicit conditions that lead to an efficient solution of the problem by a mere application of J-heuristic. Then we study further useful structural properties of the J-schedules (ones created by J-heuristic) leading to the optimal solution of other versions of the problem with the same computational cost as that of J-heuristic. Finally, we focus on a special case of our problem with only two allowable job release times and
with
(abbreviated
or
). Although the latter problem remains NP-hard, it admits stricter dominance rules and optimality conditions leading to the corresponding polynomial-time verification procedures (and the reduction of the search space).
Employing the presented optimality and dominance conditions, a practitioner may simulate the scheduling phase under these conditions in real time (solving efficiently the scheduling problem under these conditions). Then it is verified whether the obtained solution also solves the original instance, i.e. if it is feasible for that instance. Otherwise, it might be possible to adopt the production process so that the optimality conditions are met. Carrying out this kind of simulation for a variety of arisen in a given production instances, a practitioner may adjust the pre-scheduling decisions and hence convert the initially determined scheduling model to another more restricted one admitting an efficient solution method. In this way, the production process might be adjusted to the optimality and dominance conditions resulting in a useful interaction between pre-scheduling and scheduling phases in production planning.
In the next subsection we give the basic concepts and some other preliminaries. In Section 3 we study efficiently identifiable conditions and cases when our generic problem can be solved in polynomial time. In Section 4 we show that the special case of the problem with only two allowable job due-dates remains NP-hard. Section 5 is devoted to the latter problem. In the first part of this section we give general properties for the polynomial time solution, whereas in Sections 5.1 and 5.2 we derive stricter dominance relations and other particular versions that can be efficiently solved. We give the final remarks in Section 6.
2. Basic concepts and definitions
Now we give a formal definition of our general scheduling problem. We have n jobs and single machine available at the time 0 . Each job j become available at its release time or head
, needs continuous processing time
on the machine, and needs an additional delivery time or tail
after the completion on the machine (note that
needs no machine time in our model). The heads and tails are non-negative integral numbers while a processing time is a positive integer. A feasible schedule S assigns to each job j a starting time
, such that
and
, for any job k included earlier in S; the first inequality says that a job cannot be started before its release time, and the second one reflects the restriction that the machine can handle only one job at the time. The completion time of job j,
; the full completion time of j in S,
. Our objective is to find an optimal schedule, i.e. a feasible schedule S with the minimal value of the maximal full job completion time
(called the makespan).
In an equivalent formulation , the delivery time
of every job j is replaced by the due-date
which is the desirable time for the completion of job j. Here the maximum job lateness
(the difference between the job completion time and its due-date) needs to be minimized.
Given an instance of , one can obtain an equivalent instance of
as follows. Take a suitably large constant K (no less than the maximum job delivery time) and define due-date of every job j as
. Vice-versa, given an instance of
, an equivalent instance of
can be obtained by defining job delivery times as
, where D is a suitably large constant (no less than the maximum job due date). It is straightforward to see that the pair of instances defined in this way are equivalent; i.e. whenever the makespan for the version
is minimized, the maximum job lateness in
is minimized, and vice-versa. We refer the reader to an early paper by Bratley, Florian, and Robillard (Citation1973) for more details.
Next, we give a more detailed description of J-heuristic. It distinguishes n scheduling times, the time moments at which a job is assigned to the machine. Initially, the earliest scheduling time is set to the minimum job release time. Among all jobs released by that time a job with the mini- mum due-date (the maximum delivery time, alternatively) is assigned to the machine (ties being broken by selecting a longest job). Iteratively, the next scheduling time is either the completion time of the latest assigned so far job to the machine or the minimum release time of a yet unassigned job, whichever is more (as no job can be started before the machine gets idle nether before its release time). And again, among all jobs released by this scheduling time a job with the minimum due-date (the maximum delivery time, alternatively) is assigned to the machine. Note that the heuristic creates no gap that can be avoided always scheduling an already released job once the machine becomes idle, whereas among yet unscheduled jobs released by each scheduling time it gives the priority to a most urgent one (i.e. one with the smallest due-date or alternatively the largest delivery time).
We will use for the initial J-schedule, i.e. one obtained by the application of Jackson’s heuristic (J-heuristic, for short) to the originally given problem instance, and
for an optimal schedule.
A J-schedule has a particular structure that enables us to deduce our conditions. Two basic classes of jobs in a J-schedule might be distinguished: the “urgent” (critical) and “non-urgent” (non-critical) ones. Critical jobs (that we call kernel jobs) are ones which may potentially realize the maximum value of the objective function in an optimal schedule (we call such jobs overflow jobs). In a J-schedule, the critical jobs form tight sequences that extend to limited time intervals. We call such sequences of critical jobs kernels. Then the non-critical jobs (that we call emerging jobs) are to be distributed within the remained intervals (in between the kernels) in some optimal fashion. Starting from Section 3, we derive conditions when this can be done in polynomial time. We need to introduce some preliminary definitions before we define formally the above mentioned notions.
A J-schedule may contain a gap, which is its maximal consecutive time interval in which the machine is idle. We assume that there occurs a 0-length gap whenever job i starts at its earliest possible starting time, i.e. its release time, immediately after the completion of job j; here
(
, respectively) denotes the starting (completion, respectively) time of job j.
A block in a J-schedule is its consecutive part consisting of the successively scheduled jobs without any gap in between preceded and succeeded by a (possibly a 0-length) gap. J-schedules have useful structural properties. The following basic definitions, taken from Vakhania (Citation2004), will help us to expose these properties.
Among all jobs in a J-schedule S, we distinguish the ones which full completion time realizes the maximum full completion time in S; the latest scheduled such job is called the overflow job in S. We denote the overflow job in S by o(S). The block critical of S, B(S) is the block containing o(S).
Job e is called an emerging job in schedule S if and
. The latest scheduled emerging job before the overflow job o(S) is called live and is denoted by l.
The kernel of S, K(S) is a sequence consisting of the jobs scheduled in schedule S between the live emerging job l(S) and the overflow job o(S), not including l(S) but including o(S) (note that the tail of any job K(S) is no less than of o(S)). Abusing slightly the terminology, we shall also use kernel for the corresponding set of jobs, and denote by r(K) the minimum job release time in kernel K.
It follows that every kernel is contained in some block in S, and the number of kernels in S equals to the number of the overflow jobs in it. Furthermore, since any kernel belongs to a single block, it may contain no gap. Note that if a J-schedule S has no emerging job then it will also have no kernel; then the overflow job in schedule S will not be part of any kernel. In general, we shall use for the set of all emerging jobs scheduled before kernel K(S) in schedule S.
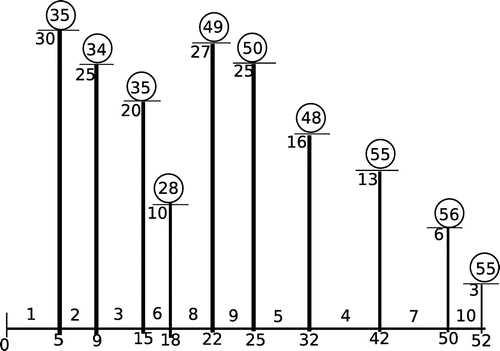
Figure illustrates the above introduced notions for an instance with 6 jobs below. Schedule consists of two blocks
y
. Block
is critical containing the overflow job 5 and kernel
. Job 4 is the only emerging job. There is a gap [16, 18] in
.
Figure 1. Schedule (the dashed line represents a gap, and vertical lines represent job delivery times).
If a J-schedule S is not optimal then there must exist an emerging job forcing the delay of the kernel jobs in K(S) and that of the overflow job o(S) which must be restarted earlier (see Lemma 2 a bit later). We denote the amount of this forced delay by .
Observation 1
In any feasible schedule, the jobs of kernel may be restarted earlier by at most
time units.
Proof
Immediately follows from the definition of and from the fact that no job of kernel
is released earlier than at time
.
In order to reduce the maximum job lateness () in S, we apply an emerging job e for K(S), that is, we reschedule e after K(S). Technically, we accomplish this into two steps: first we increase artificially the release time of e, assigning to it a magnitude, no less than the latest job release time in K(S); then we apply the J-heuristic to the modified in this way problem instance. Since now the release time of e is no less than that of any job of K(S), and
is less than any job tail from K(S), the J-heuristic will give priority to the jobs of K(S) and job e will be scheduled after all these jobs.
If we apply the live emerging job l, then it is easy to see that there will arise a gap before the jobs of kernel K(S) if no other emerging job scheduled in S behind kernel K(S) gets included before kernel K(S) taking the (earlier) position of job l. In general, while we apply any emerging job , we avoid such a scenario by increasing artificially the release time of any such an emerging job which may again push the jobs in kernel K(S) in the newly constructed schedule that we call a complementary to S schedule and denote by
.
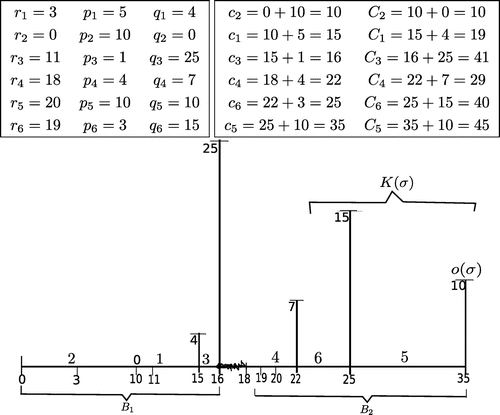
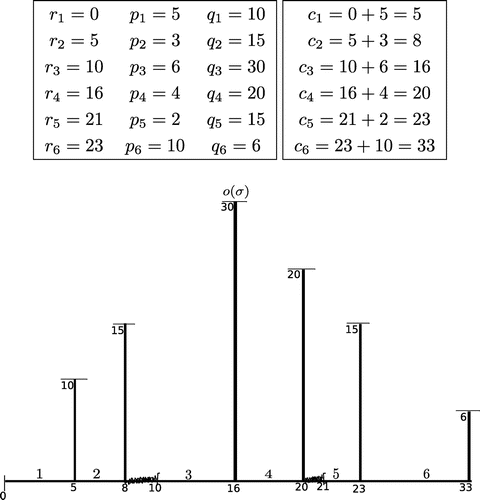
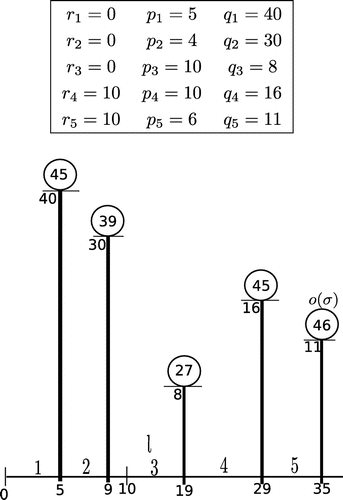
Below we illustrate the construction of schedule . The table specifies a problem instance with 9 jobs. Schedules
and
are illustrated in Figures and , respectively (the numbers within the circles stand for the full completion times of the corresponding jobs).
3. The cases and conditions for polynomial time solution of the problem
In this section we give conditions leading to the efficient solution of our generic problem. These conditions are derived as a consequence of the analysis of J-schedule immediately and hence provide an
time decision.
Lemma 1
If the overflow job is scheduled at its release time, then
is optimal.
Proof
If is scheduled at its release time
then its starting time
. Hence job
starts at its early starting time in
and ends at its minimum completion time. Therefore,
can not be rescheduled earlier in
, i.e. there is no scheduling
such that
and
is optimal.
If is not scheduled at its release time, then the starting time of
must be the completion time of some other job. Another case when schedule
is optimal, is when the tails of all the jobs scheduled in the critical block before
are greater than
:
Lemma 2
If the critical block does not contain an emerging job (equivalently, it has no kernel), then schedule
is optimal.
Proof
Assume that contains a critical block
which does not contain an emerging job, i.e. for all
scheduled before job
,
.
Suppose there is a non-empty sequence E of jobs in scheduled before
. If we reschedule some jobs of E after
the in the resultant schedule
at least one job e will be completed no earlier than at the moment
. But as e is not an emerging job,
and therefore the full completion time of e,
, will be no less than
. Then
. Therefore,
is optimal.
If set E is empty, then is scheduled in
at its release time, therefore by Lemma 1,
is optimal.
The case when has no kernel is quite similar.
The following two lemmas state earlier known results that we have mentioned in the introduction. Their proofs are presented for the sake of completeness of this presentation.
Lemma 3
If all release times (
) of jobs in
are equal to a constant r, then
is optimal.
Proof
As all jobs are released at the time r, then the J-heuristic in each iteration schedules the job j with largest tail. This gives us a schedule
, such that jobs are scheduled in non-increasing order. Then
cannot contain an emerging job and by Lemma 2,
is optimal.
Lemma 4
Let be a J-schedule with jobs
with integer release times
and unit processing times
. Then
is optimal.
Proof
Since the release time each job i is an integer number and its processing time is 1, during the execution of that job no other more urgent job may be released. Hence, at each scheduling time t, J-heuristic, among all the released by that time moment jobs, will include one with the largest tail. In addition, in
, every job is scheduled at its release time
or at the completion time of another job. If job
is scheduled at time
, then
is optimal by Lemma 1. If
is scheduled at the completion time of another job k so that job
was released before the completion time of that job, then
. Hence, there may exist no emerging job and
is optimal by Lemma 2.
Lemma 5
Let jobs in be ordered by a non-decreasing sequence of their release times. Then
is optimal if for any neighboring jobs
and
,
.
Proof
By the condition in the lemma, every job is scheduled in
in the interval
. So, the starting time of each job in
is
, i.e. each job
begins at its early starting time in
. This is true, in particular, for job
and therefore, by Lemma 1,
is optimal.
Figure illustrates schedule for an instance possessing the above indicated property.
For the given k job release times, , let
be the set of jobs released at the time
.
Theorem 1
For a given instance of problem , the initial J-schedule
is optimal if
.
Proof
By the condition, at any scheduling time behind release times , job
was released. Then by J-heuristic, for each job i scheduled in
before job
,
. Hence,
does not contain an emerging job and it is optimal by Lemma 2.
Assume K is any kernel which forms part of some J-schedule S (K can be a kernel of other J-schedule distinct from S). Then we will say that job is scheduled within kernel K if there is at least one job from that kernel scheduled before and after job e in schedule S.
Lemma 6
If job e is scheduled within kernel in schedule S then
.
Proof
First, it is easy to see that no job from kernel scheduled before job e can be the overflow job in schedule S. Neither job e can be the overflow job in S as it is succeeded by at least one kernel job
with
. Furthermore, no job k scheduled after kernel
can be the overflow job in schedule S as the right-shift of such a job in schedule S cannot be more than that of a more urgent kernel job.
It follows that only a job from kernel scheduled after job e may be the overflow job in schedule S. But because of the forced right-shift imposed by job e, the job j from kernel
scheduled the last in schedule S cannot complete earlier in schedule S than job
was completed in schedule
, i.e.
. At the same time, by the definition of kernel
job j is no less urgent than job
, i.e.
. Then
and hence
.
As a consequence of Lemmas 2 and 6 we get the following corollary:
Corollary 1
In any schedule better than , an emerging job is rescheduled behind kernel
.
4. The NP-hardness of 

From here on, we shall focus our attention on the special case of our problem with only 2 allowable job release times and tails. As we have seen earlier, J-heuristic delivers an optimal schedule whenever we have a single release time or a single tail (or due-date), i.e. the problems and
(
and
) are solvable in an almost linear time
(the general setting
being strongly NP-hard). Now we show that we arrive at an NP-hard problem by allowing two distinct release times or tails; i.e. the problem
is already NP-hard. For the convenience, let us consider the version with due-dates
.
Theorem 2
is NP-hard.
Proof
We use the reduction from an NP-hard SUBSET SUM problem for the feasibility version of , in which we wish to know if there exists a feasible schedule that meets all job due-dates (i.e. in which all jobs are completed no later than their due-dates). In SUBSET SUM problem we are given a finite set of integer numbers
and an integer number
.Footnote1 This decision problem gives a “yes” answer iff there exists a subset of C which sums up to B. Given an arbitrary instance of SUBSET SUM, we construct our scheduling instance with
jobs with the total length of
as follows.
We have n partition jobs released at time
with
,
and
, for
. Besides these partition jobs, we have another separator job I, released at time
with
,
and with the due-date
. Note that this transformation creating an instance of
is polynomial as the number of jobs is bounded by the polynomial in n, and all magnitudes can be represented in binary encoding in O(n) bits.
Now we prove that there exists a feasible schedule in which all jobs meet their due-dates iff there exists a solution to our SUBSET SUM problem. In one direction, suppose there is a solution to SUBSET SUM formed by the numbers in set . Let
be the set of the corresponding partition jobs in our scheduling instance. Then we construct a feasible schedule in which all jobs meet their due-dates as follows (see Figure ). We first schedule the partition jobs from set
in the interval
in a non-delay fashion (using for instance, Jackson’s heuristic). Then we schedule the separator job at time B completing it by its due-date
and then the rest of the partition jobs starting from time
again in a non-delay fashion by Jackson’s heuristic. Observe then that the latest scheduled job will be completed exactly at time
and all the jobs will meet their due-dates. Therefore, there exists a feasible schedule in which all jobs meet their due-dates whenever SUBSET SUM has a solution.
In the other direction, suppose there exists a feasible schedule S in which all jobs meet their due-dates. Then in that schedule, the separator job mist be scheduled in the interval , whereas the latest scheduled partition job must be completed by time
. But this may only be possible if the interval
in schedule S is completely filled in by the partition jobs, i.e. there must be a corresponding subset
of the partition jobs that fill in completely the interval
in schedule S (if this interval were not completely filled out in schedule S then the completion time of the latest scheduled partition job would be
plus the total length of the gap within the interval
and hence that job would not meet its due-date (seeas illustrated in Figure ). Now clearly, the processing times of the jobs in set
form the corresponding solution to SUBSET SUM.
5. Tractable special cases of problem 

In Section 4 we have shown that the version of our general problem with two job release times, i.e., the problem , is NP-hard. In this section we establish some useful properties of an optimal solution to this problem that can be verified in time
.
Assume that the sequence of jobs is enumerated so that the first m jobs of the sequence are ones released at time
and the next
jobs are ones released at time
(
). We let
and
stand for the set of jobs released at the time
and
, respectively.
Lemma 7
If then
is optimal.
Proof
Since , J-heuristic in the first m iterations will schedule all the jobs released at time
. As the jobs
,
are released simultaneously at the time
, they are scheduled optimally by Lemma 3.
By the condition in the Lemma, all jobs released at the time are completed by time
, and hence all the jobs in set
are available for scheduling at time
. Then again J-heuristic will schedule all these jobs optimally (Lemma 3).
Now clearly, by pasting together the two above partial schedules, we obtain a complete optimal schedule (as if there arises a gap between the two portions of that schedule then it is unavoidable).
Lemma 8
Let be such that for the first k jobs with the largest tails in schedule
the equality
holds. Then
is optimal.
Proof
We distinguish the following two cases based on the fact that for the first k jobs with the largest tails released at time ,
is satisfied:
Case 1: . In this case
and by Lemma 7, schedule
is optimal (with the equality being hold for any tow neighboring jobs).
Case 2: . Let
be the J-schedule for the first k jobs. Since all these jobs are released at the time
, they are scheduled optimally by Lemma 3. Further, since
, the earliest stating time of the jobs
is
. Hence by time
, all the remaining yet unscheduled
jobs become simultaneously available. Let
be the J-schedule for these jobs. Since all yet unscheduled jobs are available by time
,
is optimal by Lemma 3.
Now let be the J-schedule obtained joining the J-schedules
and
. Note that schedule
has no gap, hence it consists of a single block. By our construction, there exists no emerging job in schedule
, and it is optimal by Lemma 2.
Below we let i, , be the earliest arisen job from
during the construction of schedule
, such that
, and we let
be the largest tail among the tails of the jobs released at time
.
Lemma 9
If , then
is optimal.
Proof
As it is easily seen, because , schedule
contains no emerging job and hence is optimal by Lemma 2.
Due to Theorem 1, from now on, let us assume that and that
contains at least one emerging job (otherwise, schedule
is optimal by Lemma 2.
Observation 2
Proof
By the contradiction, suppose that kernel contains at least one job
. Then for all
scheduled before kernel
,
(by J-heuristic). As
is the job with smallest tail of kernel
(by the J-heuristic and the definition of kernel
),
and hence,
. Then schedule
may have no emerging job. We came to a contradiction proving our claim.
Observation 3
For problem ,
and for any emerging job
,
.
Proof
The first statement follows from the fact that the earliest scheduled job of kernel in schedule
belongs to set
which, in turn, follows from the J-heuristic. The second claim also follows from J-heuristic which schedules all jobs released at time
(in particular, the jobs from
) in the non-increasing order of their tails (in particular, up to time
before the jobs of kernel
), whereas job l is the latest scheduled one from set
in schedule
.
Observation 4
The kernel contains jobs with the largest tails from set
scheduled in the non-increasing order of their tails.
Proof
By Observation 3, . By definition the live emerging job, l is the last job scheduled before kernel
released at time
and the first job with completion time greater than or equal to
. There may exist no job of set
scheduled before job l in schedule
(job l starts strictly before time
). Then by J-heuristic, the first job of kernel
must be one with the largest tail from set
and the following jobs must be scheduled in the non-increasing order of their tails. Moreover, all these jobs pertain to set
by Observation 2.
Recall that, for a given J-schedule S, the complementary schedule always contains a gap before jobs of kernel K(S), i.e. the earliest scheduled job of K(S) starts at its release time in schedule
. In general, for any emerging job
, the complementary schedule
may contain a gap or not, depending on the length of that job (compared to that of job l). We will see this in more details later.
Observation 5
The order of the jobs scheduled after time , and before and after job e (particularly that of the jobs of
) is the same in both schedules
and
.
Proof
Note that since all jobs of kernel and the jobs scheduled after this kernel in
were released by time
, J-heuristic should have been scheduled these jobs in the non-increasing order of their tails in schedule
. Then J-heuristic will also schedule all the former jobs in the same order in schedule
, i.e. the jobs before job e and after that job (also released by time
), in particular, ones of kernel
will be included in the same order in both schedules.
Let now J[e] be the set of all jobs j scheduled after in
such that
. It follows that all jobs from set J[e] are scheduled immediately after kernel
and before job e in
.
Observation 6
.
Proof
First note that set J[e] has no job with the tail equal to . Besides,
and
, for every job
. Furthermore, by J-heuristic, for every job
scheduled in
before
,
, and for every job
scheduled after
,
, hence
as
and the Observation follows from the definition of set J[e].
Proposition 1
Without loss of generality, it might be assumed that all the jobs j with scheduled after kernel
in
are included behind job e in complementary schedule
.
Observation 7
In schedule , the jobs of kernel
and those of set J[e] are left-shifted by the same amount, whereas all jobs j with
are right-shifted also by the same amount.
Proof
Note that while constructing schedule , J-heuristic schedules all the jobs in the non-increasing order of their tails behind time
(as all of them are released by that time moment). While constructing schedule
, the same set of jobs plus job e are available behind time
. In particular, it is easy to see that if
, all jobs of kernel
and those from set J[e] will be left-shifted by
, and if
this left-shift will equal to
, whereas any j with
will be scheduled behind job e and will be right-shifted correspondingly.
Lemma 10
| (1) | If | ||||
| (2) | If | ||||
Proof
First note that is now
. By the definition of
, no job
with
scheduled after
in
will be scheduled before
in
. If
, in schedule
, the jobs of kernel
and of set J[e] will have the left-shift of length
(which is the maximum possible by Observation 1). Then
will have a gap of length
. If
, the jobs of kernel
and those of set J[e] will have a left-shift of length
, hence
will have no gap.
Due to Lemma 10 we define the gap in schedule
as follows:
for all .
Lemma 11
The full completion time of job e in ,
Proof
By the definition of the set J[e], job e will be scheduled in after all jobs of J[e] and before of all jobs i with
(see Proposition 1). By the Observation 1,
is the maximum possible left-shift for the jobs of
in
. The full completion time of job e in
will depend on the amount of this left-shift. Consider the following two cases. If
, then the jobs of
and those of set J[e] will be left-shifted by the amount
in schedule
. Recall that the last job of kernel
scheduled in
is
. Then,
Let , then
. Therefore
In this case, has a gap of length
.
If , then by the definition of set J[e] and the construction of schedule
, the jobs of kernel
and those of set J[e] will be left-shifted by amount
in schedule
. Therefore,
Note that in this case has no gap.
Consider the following inequality:(1)
(1)
Lemma 12
If and the inequality (1) for job
holds, then in
job e is scheduled before kernel
.
Proof
As ,
has a gap by Lemma 10 and kernel
starts at its early starting time
in schedule
. By inequality (1),
; hence,
. Then it follows that job e cannot be scheduled after kernel
in schedule
and the lemma is proved.
Theorem 3
If for every
and the inequality (1) is satisfied for job e, then
is optimal.
Proof
Recall that if schedule is not optimal, kernel
must be restarted earlier. This will be possible only if at least one job
is rescheduled after kernel
. Suppose
is a schedule with a better (smaller) makespan than schedule
. Then similarly, it is straightforward to verify that, by the condition of the Theorem, inequality (1) yields
for every
. Then by Lemma 12, schedule
must be optimal.
Let .
Lemma 13
If the inequality (1) is satisfied for job l, then in any job
is scheduled before kernel
.
Proof
. By Lemma 12, l is scheduled in before
. Let k be the last job scheduled of J[l] in
(recall that J[l] is the set of all jobs j scheduled after
in
such that
). By J-heuristic, job k has the tail less than the jobs of set J[l]. By the definition of the set J[l], without loss of generality we assume that the J-heuristic schedules job l after job k in
. In addition, the starting time of job l must be the completion time of job k in
, i.e.
(by Proposition 1 and because by J-heuristic, for any job i scheduled after of k in
,
and therefore
, by the definition of set J[l]).
It is easy to see that for all ,
(because
and by the definition of
). Besides, job k is scheduled after jobs of kernel
in
and job e can be scheduled before or after job k in
. We respectively distinguish the following two cases. If job e is scheduled in
after of job k, the starting time of job e in schedule
is equal to the starting time of job l in schedule
, i.e.
since for any job i scheduled after job l in
,
and
since
. As the inequality (1) is satisfied for l, it is also satisfied for job e because
and
. By Lemma 12, e is scheduled before
in
.
If job e is scheduled in before job k, the jobs scheduled after job e in schedule
(in particular the jobs of set J[l]) are right-shifted, therefore, the completion time of job k in
is greater than the completion time of job k in
. Also, because
, the completion time of job k in
is greater than or equal to the completion time of job l in
.
. As
,
and therefore
. Then job e cannot be scheduled after kernel
in schedule
since job l satisfies the inequality (1), hence
.
We have shown that job e cannot be scheduled after kernel in schedule
and Lemma is proved.
From here on, we denote by k be the job with the greatest full time completion in schedule among all the jobs scheduled after the jobs of set J[e]. As it can be easily seen, job k can be either from set
or
.
Observation 8
If the overflow job of schedule is scheduled after
, then it belongs to set
.
Proof
From Observation 5 the jobs scheduled behind time and before job e in schedule
have the same processing order as in schedule
. At the same time, by Observation 7 the jobs of kernel
and those from set J[e] have the same left-shift
in schedule
. Right after the latter jobs job e is included in schedule
(Proposition 1) and hence both, the processing order and the starting/completion times of the following jobs will remain unchanged. Now our claim follows from the definition of jobs
, e and k.
Lemma 14
Schedule is optimal if
and
.
Proof
Since , the jobs of kernel
are left-shifted in schedule
by the amount
. By definition of
and from the fact that all jobs of kernel
are released by time
, the earliest job from that kernel starts at its early starting time in
, i.e.
. By J-heuristic, for any job
,
. It follows that the completion time of job
in schedule
is the least possible and schedule
optimal.
Theorem 4
If job is scheduled before kernel
, then schedule
is optimal.
Proof
Since (Observation 2) and first job of
is the job with the largest tail in set
, all jobs scheduled before kernel
are in set
. Hence the overflow job
is in set
. By J-heuristic, all jobs scheduled before kernel
are scheduled in the non-increasing order of their tails (see also Lemma 3). Then there may exist no schedule
such that
and
is optimal.
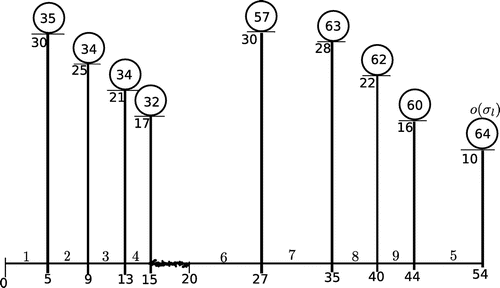
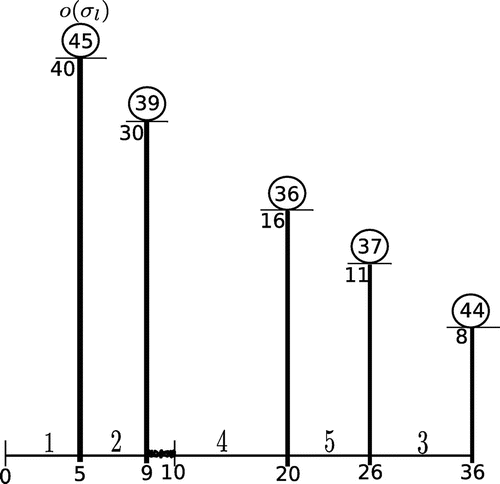
Below we illustrate the above Theorem using a problem instance of our problem with 5 jobs. Schedules and
are illustrated in Figures and , respectively (the numbers within the circles stand for the full completion times of the corresponding jobs).
Observation 9
If in schedule the overflow job
is scheduled before kernel
, then
.
Proof
Indeed, by the definition of an emerging job, all jobs from set have the tail smaller than that of the jobs in kernel
, whereas these jobs, except job e, are scheduled before the jobs of that kernel in schedule
. Then clearly, none of them (excluding job e) may be the overflow job in schedule
.
5.1. A few more properties for equal-length jobs in set 

In this section we consider another special case of our problem when all jobs released at time have the same processing time p. We abbreviate this problem as
(
denotes that all jobs released at the time
have processing time p).
Recall that the left-hand side in inequality (1) is the full completion time of job e in schedule (job k is defined as earlier). We define set
.
Lemma 15
The full completion time of job k in the schedule is:
Proof
Is analogous to that of Lemma 11.
Consider the following inequality:(2)
(2)
Lemma 16
For problem , in any schedule
there occurs a gap before kernel
. Moreover,
for every job
.
Proof
We have since
for all
. By Lemma 10, schedule
has a gap of length
and
for all
.
Lemma 17
If the full completion time of job k satisfies the inequality (2), then each job is scheduled before kernel
in
.
Proof
The inequality (2) implies that ; hence,
. As the full completion time of k in
is less than the full completion time of the overflow job
(otherwise, job k would be the overflow job in
) and
, job l cannot be scheduled after kernel
in schedule
. By Lemma 16,
for every emerging job e. Then the starting time of job k in schedule
is the same as that in
. Therefore
and
for each job
. It follows that no job
can be scheduled after kernel
in schedule
.
Theorem 5
For problem , schedule
is optimal, if:
| (1) | The inequality (1) is satisfied for job l in schedule | ||||
| (2) | The inequality (2) is satisfied for job k in schedule | ||||
Proof
For the first claim, by Lemma 13, any job is scheduled in
after kernel
. This implies that every job
satisfies the inequality (1) and by Theorem 3,
is optimal.
As to the second claim, by Lemma 17 every job must be scheduled before kernel
in
, hence
is optimal.
5.2. Short emerging jobs
In this subsection we study the case when the use of a short emerging job, i.e. one with processing time less than , leads us to useful optimality properties. Recall from Lemma 10 that for such a short job e schedule
has no gap. Throughout this subsection we let j be the job from set J[e] scheduled the last in schedule
, and, as earlier, k stands for the job with the maximum full completion time among the jobs scheduled behind the jobs of J[e] in schedule
.
Property 1
Let . If
then
, otherwise (
)
.
Proof
Suppose first . Consider the set of the emerging jobs from schedule
included in between job e and kernel
, the jobs of kernel
and ones from set J[e]. Note that these are the jobs which will be included before job e in schedule
. These jobs will be left-shifted by
time units in the latter schedule ( see Lemma 10). Since job j is one of these jobs, it will also be left-shifted by the same amount and job e will start immediately after after job j in schedule
(if there are jobs scheduled after kernel
with the tail equal to
, they will be included behind job e by Proposition 1). It follows that the completion time of job e in schedule
is equal to that of job j in schedule
. This completes the case
, and the other case
can be similarly seen.
Lemma 18
If , then
.
Proof
By Property 1, if
and
(by definition of set J[e]). Hence,
. But
and our claim follows. If now
, by Property 1,
and
(by definition of overflow job). Hence,
.
Observation 10
If , then
.
Proof
Since schedule has no gap (Lemma 10) all the emerging jobs scheduled between e and kernel
, the jobs of kernel
and ones from set J[e] will have the same left-shift of length
in schedule
. At the same time, all jobs scheduled after jobs of set J[e] in schedule
will have no shift in schedule
as job e will be included before them. Then the starting time of job k in both schedules
and
is the same and our claim follows.
Theorem 6
If , then
.
Proof
In schedule , either the overflow job
is scheduled before or behind kernel
. For the latter case, by Observation 8, the only potential overflow jobs in schedule
are jobs
, e and k. Since the jobs of kernel
have the left-shift of length
in schedule
,
and hence
. By Lemma 18,
and by Observation 10,
. But
and hence
. Thus the full completion time of jobs
, e and k in schedule
is no more than that in schedule
and the theorem holds for first second case above.
For the first case above (the overflow job is scheduled before kernel
), again
. Indeed, any job scheduled before kernel
in schedule
must have the full completion time no more than job
(by the definition of the overflow job) whereas the set of all jobs scheduled before kernel
in schedule
is the same as that in schedule
except that job e is rescheduled behind kernel
in schedule
.
Observation 11
If and
, then the overflow job in schedule
is:
| (1) | Job k if | ||||
| (2) | Job e if | ||||
| (3) | Job | ||||
Proof
Below we prove each of these cases using the fact that the overflow job in schedule is in set
(Observation 8).
| (1) | By the definition of the overflow job in | ||||
| (2) | From | ||||
| (3) | By the definition of the overflow job in | ||||
Observation 12
If and set
, then the overflow job in schedule
is:
| (1) | Job k if | ||||
| (2) | Job e if | ||||
| (3) | Job | ||||
Proof
Is analogous to that of Lemma 11.
Theorem 7
Schedule is optimal if
,
and
.
Proof
Schedule is better than schedule
due to Theorem 6. Moreover, we show that there may exist no better schedule than
. It suffices to consider potential rearrangements in which only the emerging jobs are involved (see Lemma 2). To this end, note first that
. In other words, the former kernel
need not be further left-shifted, whereas we show that job k cannot be further left-shifted. Indeed, let S be a schedule in which some emerging job(s) are rescheduled behind kernel
. Since
,
for any emerging job
(due to J-heuristic). Hence the J-heuristic will include any such emerging job before job k in schedule S. Let us consider the following two possibilities.
| (1) | If schedule S has no gap, then because of the above observations and due to the fact that the set of jobs scheduled before job k in both schedules | ||||
| (2) | If schedule S has a gap, then since in schedule S all the rescheduled emerging jobs are included before job k, the latter job will be right-shifted by the length of that gap. Then | ||||
Figure 10. Schedule has the makespan 59 and it is not optimal as
. Here inequality (1) is not satisfied for job l, job
is the overflow job in
.
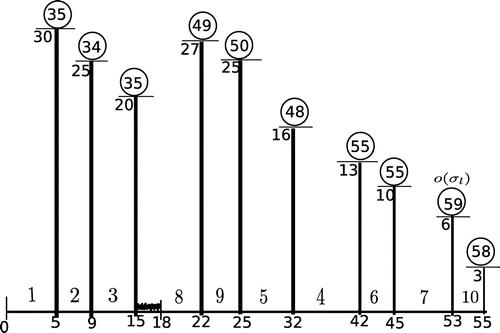
As we illustrate below with an instance of our problem, the above theorem cannot be extended to the case when and
, as then we are forced to solve the subset sum problem (see Section 4). Thus the problem bottleneck is reached when these conditions hold. The table below specifies our problem instance. In Figures and , illustrating schedule
and an optimal schedule, respectively, for that instance, the numbers within the circles are the full completion times of the corresponding jobs.
6. Conclusion
Based on the analysis of the J-schedules, we have established formal conditions when an optimal solution can be efficiently obtained. Our analysis yielded strict explicit relationships and polynomial time solution of these particular cases. We have conducted a similar study for an NP-hard spacial case of our generic problem with only two allowable job release times. Due to our conjecture of adaptive production planning, these results may stimulate the development of more efficient production planning allowing a beneficial interaction between scheduling and pre-scheduling phases for the scheduling models with release and delivery times, in particular.
Our study essentially relied on the partition of the whole scheduling horizon into two basic types of intervals containing urgent (kernel) and non-urgent (emerging) jobs, and extracting and treating the conflicts occurring between these two types of intervals. Such an analysis give some practical intuition on the general perspectives and potential conflicts that may occur while using simple heuristic rules for the solution of the problem at scheduling phase. Based on the derived dominance rules, one may assert when such conflicts may be efficiently resolved, and how. A practitioner may either choose to follow these rules for particular real-life instances or even modify some data that might be altered to avoid these conflicts and obtain an optimal solution for a modified instance, adjusting the production to the conditions and dominance rules. A practitioner may also choose to go deeper and expand the given optimality conditions and dominance relations into more complex heuristic methods depending on the nature of the problem instances that arise in his/her particular application.
For future work, it would be interesting to extend the presented results (limited to a single-machine environment) to more general scheduling models such as multiprocessor and shop scheduling.
Corrigendum
This article was originally published with errors. This version has been corrected. Please see Corrigendum (http://dx.doi.org/10.1080/23311916.2017.1336199).
Cover image
Source: Nodari Vakhania.
Additional information
Funding
Notes on contributors
Nodari Vakhania
Nodari Vakhania is a titular professor at the Centro de Investigacion en Ciencias, the State University of Morelos, Mexico and at the Institute of Computational Mathematics of the Georgian Academy of Sciences. He has received his PhD degree in mathematical cybernetics at the Russian Academy of Sciences in 1991, and the doctoral degree (habilitation) in mathematical cybernetics at the Georgian Academy of Sciences in 2004. His main research interests include design and analysis of algorithms, discrete optimization, computational complexity and scheduling theory. He has been interested in scheduling problems with job release times and due dates, and has developed novel efficient methods for their solution (so-called Blesscmore methods). The current work, carried our in collaboration with his PhD student Elisa Chinos, is part of this project.
Notes
Part of this work, in a preliminary form, was presented at the 4th Int. Conference on Mathematical, Computational and Statistical Sciences (MCSS 2016) and Int. Conference on Abstract and Applied Analysis (ABAPAN 2016)).
1 In this section n stands exclusively for the number of elements in SUBSET SUM; in the remained part, n denotes the number of jobs
References
- Bratley, P., Florian, M., & Robillard, P. (1973). On sequencing with earliest start times and due-dates with application to computing bounds for (n/m/G/Fmax) problem. Naval Research Logistics Quarterly., 20, 57–67.
- Brinkkotter, W., & Brucker, P. (2001). Solving open benchmark instances for the job-shop problem by parallel head-tail adjustments. Journal of Scheduling, 4, 53–64.
- Carlier, J. (1982). The one-machine sequencing problem. European Journal of Operational Research., 11, 42–47.
- Carlier, J., & Pinson, E. (1989). An algorithm for solving job shop problem. Management Science, 35, 164–176.
- Carlier, J., & Pinson, E. (1998). Jakson’s pseudo preemptive schedule for the Pm/ri,qi/Cmax problem. Annals of Operations Research, 83, 41–58.
- Condotta, A., Knust, S., & Shakhlevich, N. V. (2010). Parallel batch scheduling of equal-length jobs with release and due dates. Journal of Scheduling, 13, 463–477.
- Della Croce, F., & T’kindt, V. (2010). Improving the preemptive bound for the single machine dynamic maximum lateness problem. Operations Research Letters, 38, 589–591.
- Garey, M. R., & Johnson, D. S. (1979). Computers and intractability: A guide to the theory of NP-completeness. San Francisco, CA: Freeman.
- Garey, M. R., Johnson, D. S., Simons, B. B., & Tarjan, R. E. (1981). Scheduling unit-time tasks with arbitrary release times and deadlines. SIAM Journal on Computing, 10, 256–269.
- Gharbi, A., & Labidi, M. (2010). Jackson’s semi-preemptive scheduling on a single machine. Computers & Operations Research, 37, 2082–2088.
- Graham, R. L., Lawler, E. L., Lenstra, J. L., & Rinnooy Kan, A. H. G. (1979). Optimization and approximation in deterministic sequencing and scheduling: A servey. Annals of Discrete Mathematics, 5, 287–326.
- Hall, L. A., & Shmoys, D. B. (1992). Jackson’s rule for single-machine scheduling: Making a good heuristic better. Mathematics of Operations Research, 17, 22–35.
- Hoogeveen, J. A. (1995). Minimizing maximum promptness and maximum lateness on a single machine. Annals of Discrete Mathematics, 21, 100–114.
- Jackson, J. R. (1955). Schedulig a production line to minimize the maximum tardiness. Manegement Scince Research Project. Los Angeles: University of California.
- McMahon, G., & Florian, M. (1975). On scheduling with ready times and due dates to minimize maximum lateness. Operations Research, 23, 475–482.
- Nowicki, E., & Smutnicki, C. (1994). An approximation algorithm for a single-machine scheduling problem with release times and delivery times. Discrete Applied Mathematics, 48, 69–79.
- Perregaard, M., & Clausen, J. (1998). Parallel branch-and-bound methods for the job-shop scheduling problem. Annals of Operations Research, 83, 137–160.
- Potts, C. N. (1980). Analysis of a heuristic for one machine sequencing with release dates and delivery times. Operations Research, 28, 1436–1441.
- Schrage, L. (1971, March). Obtaining optimal solutions to resource constrained network scheduling problems. Unpublished manuscript.
- Simons, B. (1983). Multiprocessor scheduling of unit-time jobs with arbitrary release times and deadlines. SIAM Journal on Computing, 12, 294–299.
- Simons, B., & Warmuth, M. (1989). A fast algorithm for multiprocessor scheduling of unit-length jobs. SIAM Journal on Computing, 18, 690–710.
- Vakhania, N. (2003). A better algorithm for sequencing with release and delivery times on identical processors. Journal of Algorithms, 48, 273–293.
- Vakhania, N. (2004). Single-machine scheduling with release times and tails. Annals of Operations Research, 129, 253–271.
- Vakhania, N. (2009). Scheduling jobs with release times preemptively on a single machine to minimize the number of late jobs. Operations Research Letters, 37, 405–410.
- Vakhania, N. (2012). Branch less, cut more and minimize the number of late equal-length jobs on identical machines. Theoretical Computer Science, 465, 49–60.
- Vakhania, N. (2013). A study of single-machine scheduling problem to maximize throughput. Journal of Scheduling, 16, 395–403.
- Vakhania, N., & Shchepin, E. (2002). Concurrent operations can be parallelized in scheduling multiprocessor job shop. Journal of Scheduling, 5, 227–245.
- Vakhania, N., Perez, D., & Carballo, L. Theoretical expectation versus practical performance of Jackson’s heuristic. Mathematical Problems in Engineering, 2015, 10 pages. doi:10.1155/2015/484671

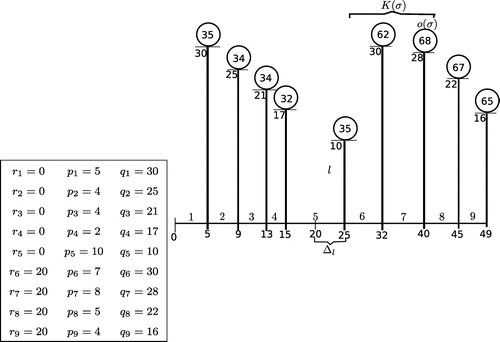
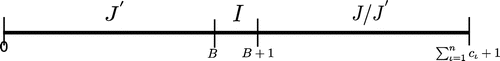
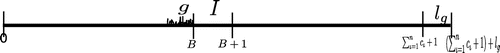
![Figure 9. Schedule σ, σ=57, with the live emerging job l=4 and o(σ)=9; J[l]=5,6 and k=7.](/cms/asset/871419f1-90b0-400c-a1fe-37ab67fd7436/oaen_a_1321175_f0009_b.gif)