Resource planning for just-in-time make-to-order environments: A scalable methodology using tabu search

Abstract

This paper develops a two-phase tabu search-based methodology for detailed resource planning in make-to-order production systems with multiple resources, unique routings, and varying job due dates. In the first phase rather than attempting to construct a good feasible plan from scratch, we define a novel approach to resource planning that computes an infeasible but optimal plan, uses it as the initial resource plan, and then makes the necessary modifications to the times of individual tasks to create a feasible finite-capacity plan. In the second phase we search for alternate finite-capacity plans that have decreased earliness, tardiness and lead time. To reduce earliness as well as tardiness, just-in-time philosophical elements are weaved into the construction of the initial solution, the neighborhood structure and the selection criteria. Computational experiments reveal that the tabu search-based methodology is more effective and reliable for resource planning than an exact approach using binary integer linear programming, which struggles to find a good solution in a reasonable amount of time even for trivially small instances. It also outperforms heuristic methods commonly used in practice for resource planning that sort jobs according to priority and load them onto resources one at a time.

Keywords:

• resource planning
• make-to-order
• MRP
• JIT
• tabu search

Public Interest Statement

In make-to-order manufacturing environments where demand is highly variable a resource planning algorithm is used to adjust the time that individual tasks are performed on resources so that capacity constraints are respected, due dates are met, and lead times are minimized. We develop a two-phase tabu search-based methodology for resource planning. Tabu search and other meta-heuristics are used to find solutions for complex, large-scale problems where exact optimal solutions cannot be computed. Our approach that is grounded in the concept that a better initial solution improves algorithm performance. The first phase of the algorithm begins with an ideal but infeasible solution and makes the minimum changes necessary to obtain a feasible solution. The second phase seeks to improve that solution by making incremental changes. To reduce both job earliness as well as tardiness, just-in-time philosophical elements are incorporated into the algorithms.

1. Introduction

Many manufacturers have shifted in recent years from a make-to-stock to a make-to-order production mode to better accommodate highly variable customer requirements, but this shift has made operational efficiency more challenging since the unique routings and variable due date tightnesses of jobs in a make-to-order system results in uneven resource loading. Detailed planning algorithms are needed in these environments to balance the load on individual resources over an intermediate horizon (e.g. 2–12 months) using a discrete-time representation of resource availability before scheduling is attempted over a shorter time horizon (e.g. 1–14 days) using a continuous-time representation of resource availability.

Unfortunately, despite their name, traditional techniques such as Material Requirements Planning and/or Capacity Requirements Planning do not actually perform planning, but only calculate requirements and furthermore do so with a fixed lead-time model. If the calculated requirements are infeasible, they do not create a feasible plan by making adjustments to the quantity being produced or the timing of production tasks. However, using a detailed model of the production system, a true resource planning algorithm can be created which first predicts when resources will be overloaded. Second, the algorithm can then seek to eliminate overloads by adjusting the time that tasks are performed on individual resources while respecting task precedence constraints and also attempting to meet individual job due dates and reduce job lead times and work in process (WIP). In this paper we develop such a methodology for resource planning.

In prior years many manufacturers have embraced the JIT philosophy, particularly at the operational level. According to JIT, a job should be processed and finished as close as possible to its due date, neither tardy nor early. In this paper we therefore define the ideal plan for a job to be that plan where each task is backward planned from the due date without allowances for queueing. This plan has zero earliness, zero tardiness, and minimal lead time and actually is very easy to compute. Unfortunately, multiple jobs cannot simultaneously follow their ideal plans due to resource capacity constraints. However, by superimposing all of the ideal plans for individual jobs a time-phased load profile for each resource can be constructed and overloads can be identified. Consequently, in this research rather than attempting to construct a good feasible plan from scratch, we compute what is an infeasible but optimal initial resource plan via superimposition of the various ideal plans and then make the minimal necessary modifications to the times of individual tasks in order to make the plan feasible.

To determine which tasks are pulled to earlier times or pushed to later times, we develop a two-phase tabu search-based methodology that weaves JIT philosophical elements into construction of the initial solution, the neighborhood structure and the selection criteria. Tabu search, an improvement-type heuristic algorithm, is often applied to solve complicated problems such as those faced by production systems since a good, if not optimal, solution often can be obtained within a reasonable time (Glover, 1986). When considering what moves to make (i.e. which tasks to push or pull and where to place them) the algorithm considers the deviation of the current plan from the ideal plan for each task on each job. Thus, the ideal plan for a job is not only used to construct the initial plan, but it also serves as a beacon to guide the tabu search algorithm when modifying the times of individual tasks.

The remainder of this paper is organized as follows. Section 2 reviews the related literature on resource planning, heuristic methods for job shop scheduling, and specific areas such as the earliness-tardiness problem. Section 3 defines a binary integer linear programming model for resource planning that can be used to obtain exact solutions for small instances. Section 4 describes our tabu search-based methodology for resource planning that can obtain solutions to realistically sized instances. Section 5 presents the results the computational evaluation, and Section 6 provides final conclusions.

2. Background and context

A large body of work exists on optimization approaches for aggregate planning. Aggregate planning uses a discrete representation of time and consolidates data on individual products and resources to reduce the size of the problem. An enormous body of literature also has been developed over the past century on optimization approaches for scheduling and sequencing, which use a continuous representation of time. Detailed resource planning falls in between aggregate planning and scheduling/sequencing. Such planning is concerned with balancing the load on individual resources over an intermediate horizon before scheduling is attempted. It is not so concerned with the exact sequence of tasks performed on a resource as it is with creating a feasible time-phased resource loading, which may require adding overtime capacity in some periods or completing some orders late, and predicting release dates that will balance resource capacity and job due date considerations. Obviously, scheduling will be more successful if the total workload being scheduled is feasible.

Very little literature exists on detailed resource planning (Chen, Moses, & Pulat, 2007; Hans, 2001; Tardif & Spearman, 1997; Wullink, Gademann, Hans, & van Harten, 2004; Wullink, Hans, & Harten, 2004). However, a variety of approaches have been studied to improve the performance of job shop scheduling, and these provide insights and techniques that can be adapted for use on planning problems. Since the job shop scheduling problem is NP-hard (Gary & Johnson, 1979; Logendran & Sonthinen, 1997), the computational effort grows exponentially as the problem size increases (Lawler, Lenstra, Rinnooy Kan, & Shmoys, 1989). Thus, exact solutions normally can be computed only for very tiny instances, and to obtain solutions for realistically sized instances heuristic algorithms are needed. Relevant heuristic methods for scheduling include priority rules, the shifting bottleneck method, and algorithms using local search techniques such as simulated annealing, genetic algorithms, ant colony optimization, particle swarm optimization, and tabu search.

Tabu search (Glover, 1989, 1990) has been successfully applied to many combinatorial optimization problems including job shop scheduling. Taillard (1989) first used tabu search to solve a job shop scheduling problem. Since then, numerous algorithms have been proposed and developed (Akhoondi & Lotfi, 2016; Armentano & Scrich, 2000; Barnes & Chambers, 1995; Dell’Amico & Trubian, 1993; Edwards, Sørensen, Bochtis, & Munkholm, 2015; Nowicki & Smutnicki, 1996; Zhang, Li, Guan, & Rao, 2007). Tabu search is an improvement algorithm that begins with an initial solution and generates a neighborhood of similar solutions. Each neighboring solution is evaluated, and the best of these is selected to begin the next iteration. This process is repeated until a stopping condition is met. To avoid stagnation at a local minimum, the algorithm stores recent solutions or solution attributes in a short-term memory list called the tabu list. These solutions or attributes are forbidden from selection from the neighborhood. Tabu status is removed after a certain number of iterations. Aspiration criteria allow the algorithm to override tabu status in an iteration. Most often, aspiration criteria simply allow the acceptance of a solution that is better than any previous solution.

Research on job shop scheduling most often uses an asymmetric penalty function for job lateness that considers job tardiness but not job earliness. The earliness-tardiness (ET) problem has been studied broadly in single machine environments (Baker & Scudder, 1990; Bauman & Józefowska, 2006; Lee & Kim, 1998; M’Hallah, 2007), and a few researchers have worked on problems with multiple resources. Project scheduling applications often consider both earliness and tardiness (Ballestín & Trautmann, 2008). Imanipour and Zegordi (2006) proposed tabu search to find the best routing of each job in the Flexible Job Shop problem, where tasks may be completed by more than one resource. Their searching scheme focused on assigning an alternative resource to each task and using a backward procedure to generate task schedules that minimize earliness and tardiness. Finke, Medeiros, and Traband (2007) used tabu search combined with the earliest due date dispatching rule to solve the ET scheduling problem with unequal due dates in a flow shop environment. Zhu, Ng, and Ong (2010) proposed a modified tabu search algorithm in a job shop problem with a JIT environment. They used forward and backward movement to generate a new schedule that minimized three costs: WIP holding cost, inventory holding cost and backorder cost.

Thus, although some research has considered both earliness and tardiness, relatively little research has focused on these metrics in complex job shop settings with multiple resources, variable routings, and varying job due dates. Our research explores whether incorporating the JIT philosophy into the main elements of a tabu search algorithm for resource planning can reduce both earliness and tardiness in realistic make-to-order production settings.

3. Mathematical programming model for resource planning

In this section we define a binary integer linear programming formulation for the job shop planning problem. The model provides a formal definition of the resource planning problem and can be used to obtain optimal solutions for small instances that can be compared to solutions obtained with the much more scalable tabu search-based methodology for resource planning that is described in Section 4.

A set of I jobs needs to be planned on a set of H resources in order to minimize a weighted cost function with costs for the earliness, tardiness, and lead time of each job. A variable number of tasks for each job is allowed, and each job follows a different routing. Since we are performing planning and not scheduling, a discrete-time model of capacity is used: on each resource the planning horizon is uniformly divided into intervals (time buckets), whose capacity can vary if desired. Each task is performed in a single bucket. To ensure that precedence constraints are respected, we do not allow consecutive tasks for a job to be processed in the same bucket.

Notation:
Xij	=	Bucket when task j of job i is planned
Lij	=	Latest desired start time of task j of job i
Pij	=	Processing time of task j of job i
Rij	=	Routing: index of resource that performs task j of job i
Ji	=	Number of tasks of job i
Si	=	Earliest feasible release time of job i
Di	=	Due date of job i
Fi	=	Finish time of job i (note that job i is tardy if Fi ≥ Di)
Bhk	=	Capacity of bucket k for resource h
$P_i^e$	=	Earliness penalty for job i
$P_i^t$	=	Tardiness penalty for job i
$P_i^l$	=	Lead time penalty for job i
$C_i^e$	=	Earliness cost of job i
$C_i^t$	=	Tardiness cost of job i
$C_i^l$	=	Lead time cost of job i
i	=	Index for set of jobs; i = 1 … I
j	=	Index for set of tasks required by a job; j = 1 … Ji
h	=	Index for set of resources; h = 1 … H
k	=	Index for set of buckets on each resource; k = 1 … K

Decision variable:
xijk	=	1 if task j of job i is planned in bucket k, 0 otherwise

Model:(1) $$\text{Minimize}\sum _{i=1}^I(C_i^e+C_i^t+C_i^l)$$(1)

subject to(2) $$\sum _{k=1}^{K}k{x}_{ilk}\ge S_{i}i=1\dots I$$(2) (3) $$\sum _{k=1}^{K}k{x}_{ijk}<\sum _{k=1}^{K}k{x}_{i(j+1)k}i=1\dots I,J=1\dots J_i-1$$(3) (4) $$\sum _{k=1}^K{x}_{ijk}\le 1i=1\dots I,J=1\dots J_i$$(4) (5) $$\sum _{i=1}^l\sum _{j=1}^{j_i}{x}_{ijk}{P}_{ij}\le B_{hk}\text{where}{R}_{ij}=h,h=1\dots H,k=1\dots K$$(5) (6) $$x_{ijk}\in \{0,1\}$$(6)

where(7) $$X_{ij}=\sum _{k=1}^{K}k{x}_{ijk}$$(7) (8) $$F_i=X_{iJi}$$(8) (9) $$C_i^e=\begin{array}{cc}((D_i-1)-F_i)(P_i^e)\hfill & \text{if}{F}_i<(D_i-1)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$(9) (10) $$C_i^t=\begin{array}{cc}(F_i-(D_i-1))(P_i^t)\hfill & \text{if}{F}_i<(D_i-1)\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$(10) (11) $$C_i^l=(F_i-X_{i1}+1)(P_i^l)$$(11)

Constraint (2) ensures that jobs are not planned on resources before they are available. Constraint (3) enforces task precedence constraints. Constraints (4) and (6) ensure each task is planned in only one bucket. Constraint (5) enforces resource capacity constraints. Equation (7) defines the planned time of each task of a job (note that X_i1 provides the planned release time of the job). Equation (8) defines the finish time of a job, which is used to calculate the various costs for each job. Equation (9) defines the earliness cost for a job, equation (10) defines the tardiness cost for a job, and Equation (11) defines the lead time cost for a job. By including lead time in the objective function (1), we are correspondingly reducing WIP (Little, 1961), which is an important objective of JIT systems.

4. Tabu search-based methodology for resource planning

This section defines our two-phase tabu search-based methodology for resource planning. Figure 1 provides an overview. The algorithm design is grounded in the concept that a better initial solution leads to better performance (Danna, Rothberg, & Le, 2004). Thus, rather than using a random initial plan our algorithm begins with an initial plan created by superimposing the ideal plan for all jobs, which is easily computed by performing infinite backward planning for each job (12).(12) $$X_{ij}=D_i-(J_i-j+1)i=1\dots I,j=1\dots J_i$$(12)

Figure 1. Methodology for resource planning.

The initial plan is optimal in the sense that it has zero earliness, zero tardiness, and minimal lead time, but it is not feasible due to violation of resource capacity constraints. Phase 1, the overload resolution algorithm (ORA), makes the minimal necessary adjustments to create a feasible finite-capacity plan. Phase 2, the Plan Improvement Algorithm (PIA), searches for alternate finite-capacity plans that have decreased earliness, tardiness and lead time.

Both phases of the methodology are guided by the following tabu search algorithm in which the initialization procedure, neighborhood structure and selection criteria incorporate JIT concepts to accelerate the search for a good solution.

4.1. Overload resolution algorithm

In the initial plan, some resources will be overloaded in certain time buckets (otherwise, the initial plan is both optimal and feasible and the algorithm can terminate). The ORA eliminates these overloads and creates a feasible resource plan by moving tasks from overloaded buckets to buckets that have sufficient available capacity. To do so, it first identifies the time bucket that has the maximum overload for any resource. For each task planned in that bucket a neighboring solution is then created by either pulling the task to an earlier bucket with sufficient available capacity or else by pushing the task to a later bucket (He, Yang, & Deal, 1993). Thus, the size of the neighborhood equals the number of tasks in the bucket.

4.1.1. Computing the neighboring solutions

In the initial plan, each task of a job was planned at the latest possible time given its due date. Thus, pulling a task earlier is preferable to pushing it later, since pushing will introduce tardiness. When a task is pulled (pushed), precedence constraints are checked for its predecessors (successors), and if necessary those tasks also are pulled (pushed). Consequently, although a neighboring solution is identified by the decision to pull or push a particular task in an overloaded bucket, other tasks planned on other resources may also have been pulled or pushed to complete the entire solution. To be able to pull a particular task capacity must be available in an earlier period not only for the task being pulled but also for its predecessor tasks.

Figure 2(a) provides a simple example to illustrate the procedure for computing a neighboring solution by pulling a task. Load graphs for three resources are shown where the dotted line represents the capacity of each resource and boxes indicate tasks planned on each resource. To eliminate the overload on resource M2, task 2 of the shaded job will be pulled from k = 4 to the next earlier bucket with availability, which is k = 3. This creates a precedence constraint violation so task 1 of the shaded job also is pulled to the next earlier bucket with availability. Figure 2(c) shows the result.

Figure 2. Pulling a task earlier and pushing a task later to create a feasible plan: (a) before pull, (b) before push and (c) after either pull or push.

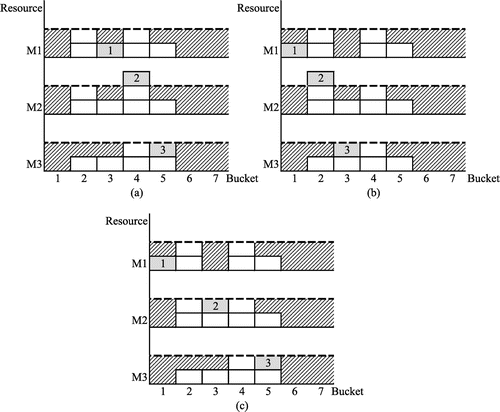
Figure 2(b) illustrates the procedure for computing a neighboring solution by pushing a task. Task 2 of the shaded job cannot be pulled earlier since that would require performing task 1 before the start of the planning horizon, and therefore task 2 is pushed to the next later bucket with availability. This creates a precedence constraint violation so task 3 of the shaded job also is pushed to the next later bucket with availability. Figure 2(c) shows the result.

4.1.2. Search strategy

Solution fitness is evaluated with a three-tiered hierarchy: maximum overload in a single bucket, total tardiness, and total lead time.

ORA selection criteria:

(1)	If (O′ < O*)
(2)	Else if (O′==O*) and (T′ < T*)
(3)	Else if (O′==O*) and (T′==T*) and (L′ < L*)

where O′, O* = maximum overload in the neighboring solution and best solution; T′, T* = total tardiness of the neighboring solution and best solution; L′, L* = total lead time of the neighboring solution and best solution.

After the best neighboring solution is found, the next step is to decide whether to accept it as the current best solution to the problem. Often, some attributes of the best neighboring solution will have been labeled tabu in a previous iteration. In that case aspiration criterion will accept the new solution if it is better than the best solution found so far.

The job and task from the best neighboring solution are stored in the tabu list to prevent revisiting the same solution. Iterations continue until one of three stopping conditions is met: no overloaded buckets remain in the solution, a preset number of stagnant iterations is reached, or a preset total number of iterations is reached. If the first stopping condition is satisfied, the PIA phase will begin. Otherwise, the resource planning procedure will terminate.

4.2. Plan improvement algorithm

The PIA phase begins with a feasible resource plan from the ORA, which potentially already is quite good but presumably contains both early and tardy jobs. ORA can be viewed as an algorithm whose purpose is to construct a good initial solution for PIA. Using the ideal plan as a beacon, the PIA pushes early jobs later and pulls tardy jobs earlier via task swapping and insertion methods so that job tardiness, earliness, and lead time are reduced while respecting capacity and precedence constraints.

We define the target job τ as the job that has maximum absolute lateness. The target task τ_j represents task j of job τ and is where we begin the search. A good neighborhood structure is important to efficiently explore new solutions, and several schemes have been proposed to generate neighborhoods (Dell’Amico & Trubian, 1993; James, 1997; Tsubakitani & Evans, 1992). Three main schemes are insert, swap, and a combination of insert and swap. James (1997) reviewed these three schemes in the context of a single machine early/tardy scheduling problem and concluded that the best scheme is the hybrid of insert and swap since it provides a variety of new solutions. Therefore, in the PIA both insert and swap methods are utilized to generate neighboring solutions. In the insert method τ_j is moved to a bucket with enough availability to accommodate the task, while in the swap method τ_j replaces another task, which must then be moved to a different bucket.

The search differs depending on whether the target job is tardy or early. If the target job is tardy (early) then the search will begin with the last (first) task on the routing and traverse backwards (forwards). To further focus the search, two parameters are calculated for each task: earliest allowed start time E_ij and latest desired start time L_ij. The E_ij is the earliest time that each task of a job can be processed irrespective of resource availability (13). The L_ij is the very latest time that each task of a job can be processed if it is to finish on time (14).(13) $$E_{ij}=S_i+j-1$$(13) (14) $$L_{ij}=(D_i-1)-(J_i-j)$$(14)

The search space constitutes the possible times at which τ_j can be planned and that potentially can improve the tardiness (earliness) of the target job τ:

Tardy τ: Between k = E_iJi and k = X_iJi – 1

Early τ: Between k = X_i1 + 1 and k = L_i1

We define a neighborhood point {ω_yz, k} to be a donor task ω_yz planned within bucket k on the same resource used by τ_j and thus that potentially can be swapped with τ_j. If τ is tardy (early), we consider each task where L_yz ≥ L_ij (L_yz ≤ L_ij) as a potential neighborhood point. We also consider every bucket that has sufficient available capacity to accommodate τ_j as a neighborhood point and in this case ω_yz is null. The neighborhood consists of solutions obtained from inserting or swapping τ_j with each of the neighborhood points. As was the case with the ORA, other tasks on the target job and the donor job may also need to be replanned to compute the entire solution.

The procedure to compute a solution for a single neighborhood point {ω_yz, k} is as follows:

Step 1: Replan the target task τ_j either by insertion or by swapping with ω_yz.

 (1) If τ was tardy: X_iJi = X_yz

 (2) If τ was early: X_i1 = X_yz

Step 2: Replan tasks on the donor job ω_y

 (1) If τ was tardy, find X_yz for task z to task J_y using finite forward planning.

 (2) If τ was early, find X_yz for task z to task 1 using finite backward planning or if that fails (due to insufficient capacity being available in some k ≥ E_yz for any z) then use finite forward planning.

Step 3: Replan other tasks τ_m on the target job τ

 (1) Traverse the routing backwards for a tardy job (m = J_i -1,…, 1) and forwards for an early job (m = 2,…, J_i).

 (2) Find X_im by using the insert method or else the swap method. For a task τ_m, the search space is defined as follows:

  Tardy τ: Between k = E_im and k = X_ij – (J_i – m)

  Early τ: Between k = X_ij + (m − 1) and k = L_im

   (i) Insert method: If the search space contains a bucket k with sufficient available capacity, set X_im = k. Go to task 4 of Step 3.

   (ii) Swap method: Swap with a donor task ρ_wx planned on the same resource as τ_m. Set X_im = X_wx.

   Tardy job: Select earliest ρ_wx in search space with L_wx ≥ L_im

   Early job: Select latest ρ_wx in search space with L_wx ≤ L_im

   (iii) If a feasible solution cannot be found, then {ω_yz, k} will no longer be considered as a neighborhood point.

 (3) Replan the donor job ρ_w using the procedure in Step 2.

 (4) Go to Step 4 if all tasks on the target job have been replanned. Otherwise, replan the next task on the target job.

Step 4: Evaluate the quality of the new solution.

The above procedure is repeated for all neighborhood points. To evaluate the fitness of neighboring solutions, a three-tiered hierarchy is used: total tardiness, total earliness, and total lead time. After selecting the best solution, the tabu list will be updated to include τ and ω_y.

PIA selection criteria:

(1)	If (T′ < T*)
(2)	Else if (T′==T*=) and (E′ < E*)
(3)	Else if (T′==T*) and (E′==E*) and (L′ < L*)

where E′, E* = total earliness of the neighboring solution and best solution.

To terminate the PIA, one of three stopping conditions must be met: a predefined number of sequential iterations without improvement of the objective value, a predefined computational time, or a predefined total number of iterations.

To illustrate the PIA, a simple example will be presented. The routings of four jobs are [M1, M2, M3], [M3, M2, M1], [M3, M1, M2], and [M1, M2, M3]. Each job has an earliest start date of 1 and a due date of 5. During the ORA phase an initial solution is generated by superimposing the ideal plans for each job. The load graphs for this initial solution are presented in Figure 3(a) in which the dotted line represents resource capacity and the digits in each box represent a job number followed by a task number. For simplicity only one task is performed in each time bucket in this example. From Figure 3(a) it can be seen that resource capacity is inadequate in k = 2 for M1 and M3, k = 3 for M2, and k = 4 for M3. The ORA pulls and pushes tasks to eliminate overloads. Figure 3(b) shows the output of the ORA.

Figure 3. Illustration of the ORA: (a) Initial solution using ideal plan, and (b) Feasible solution.

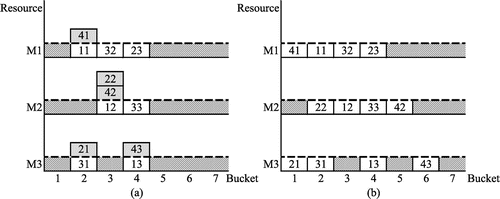
The PIA begins by computing the absolute lateness of each job and selecting the target job. From Figure 3(b), we select job 4 as the target job τ since it is tardy with absolute lateness = 2. To determine the neighborhood points we begin with the resource used on the last task of τ, which is M3. The search space is k = E₄₃ = 3 to the bucket preceding that of τ₃, which is k = 5. We determine neighborhood points in this search space for which L_yz ≥ (L₄₃ = 4). These are {ф, 3}, {ω₁₃, 4} and {ф, 5}. Figure 4 presents the solution for each neighborhood point. Below we illustrate how the solution is calculated for the neighborhood point {ω₁₃, 4}.

Figure 4. Illustration of the PIA for neighborhood point: (a) {ф, 3}, (b) {(1, 3), 4}, and (c) {ф, 5}.

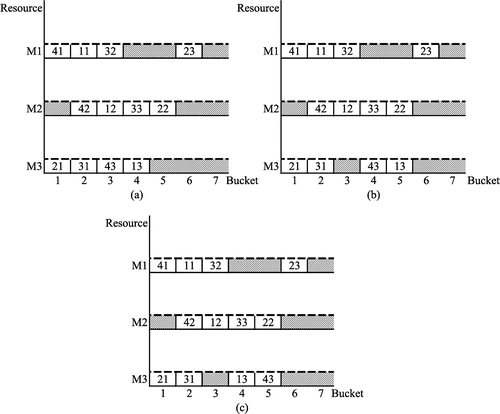
Step 1: Swap the target task τ₃ with the donor task ω_13. Thus, X₄₃ = 4.

Step 2: Replan affected tasks on ω₁, which in this case means to find X₁₃ using finite forward planning. We find X₁₃ = 5 and therefore the plan for ω₁ is {2, 3, 5}.

Step 3: Replan other tasks on the target job τ, which are τ₂ and τ₁.

 For task τ₂:

  (2) The search space is from k = 2 to k = 3. Consider the earliest task ρ₂₂ with X₂₂ = 2. Since L₂₂ ≥ L₄₂, the swap method is used to exchange τ₂ with ρ₂₂. Thus, X₄₂ = 2.

  (3) Replan ρ₂₂ and successor tasks using the procedure in Step 2. Thus, X₂₂ = 5 and X₂₃ = 6 and the plan for ρ₂ is {1, 5, 6}.

 For task τ₁:

  (2) The search space is from k = 1 to k = 1. Since X₄₁ = 1, we do not need to search for a new time. The new plan for τ is {1, 2, 4}

Step 4: For this neighborhood solution, T′ = 1 + 2 + 0 + 0 = 3, E′ = 0 + 0 + 0 + 0 = 0, and L′ = 4 + 6 + 3 + 4 = 17.

We repeat this procedure for the other neighborhood points. After evaluation we see that the first solution, {ф, 3}, is the best neighboring solution with T′ = 2, E′ = 1, and L′ = 15. It is not, however, better than the overall best solution, which is the initial solution, obtained from the ORA (T′ = 2, E′ = 0, and L′ = 16). The PIA will continue attempting to find a better solution until it meets one of the stopping criteria.

5. Computational evaluation

To evaluate the performance of the tabu search-based methodology for resource planning we conduct two sets of experiments. The first set compares the performance of ORA + PIA to that of an exact algorithm. Exact results provide an absolute benchmark for solution quality but only are obtainable for trivially small problem instances. The second set evaluates the efficacy of the methodology for larger problem instances that cannot be solved exactly.

Implementation of the algorithms is much more complex than it might appear from the description in Section 4. For example, the simple action of replanning a task requires a substantial amount of code that must be thoughtfully written in order to be fast and scalable (Moses, Gruenwald, & Dadachanji, 2008). The ORA and PIA are implemented in the Java language and experiments are run on a personal computer with a modest 1.73 GHz processor.

5.1. Generation of problem instances

Problem instances are generated by varying three parameters whose values are shown in Table 1: number of tasks on the routing, due date tightness, and bottleneck utilization. Each job follows a unique routing whose length varies according to uniform distribution, and processing times are variable. Four levels of due date tightness, which is the time allowance for processing a job, are considered for each routing length. Bottleneck utilization determines the amount of congestion in the system. Seven levels of loading per individual bucket on the bottleneck resource are evaluated. An important aspect of our approach to instance generation is that we vary the utilization of individual buckets on a resource. Doing so creates situations with uneven resource loading, which are realistic and are where resource planning algorithms are most beneficial. Solution quality is evaluated using a cost function where the costs of earliness, tardiness and lead time are 30 units/bucket, 50 units/bucket, and 20 units/bucket, respectively.

Table 1. Experimental parameters

Number of tasks (uniform distribution)	Due date tightness
3	3, [3, 6], [3, 9], [3, 12]
[3, 5]	5, [5, 10], [5, 15], [5, 20]
[3, 10]	10, [10, 15], [10, 20], [10, 25]
[3, 15]	15, [15, 20], [15, 25], [15, 30]
Utilization of single bucket on bottleneck (uniform distribution)	Overall bottleneck utilization
[25, 95%]	60%
[45, 95%]	70%
[65, 95%]	80%
[75, 95%]	85%
[85, 95%]	90%
[75, 110%]	92.50%
[55, 140%]	97.50%

5.2. Comparison with exact method for small problem instances

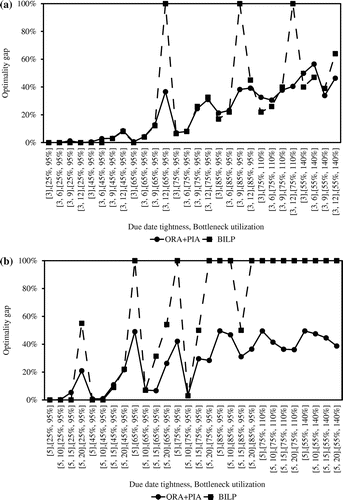
Table 2 compares the quality of solutions obtained from ORA + PIA to those obtained from the binary integer linear programming (BILP) optimization capabilities of IBM ILOG CPLEX 12. The maximum allowable computational time for both approaches is set to 1,800 s. It should be noted that the maximum computational time does not significantly constrain the BILP optimization procedure. If the optimal solution will be found, then it almost always is found within this time period. The optimality gap for the BILP method was set at 2%. Thus, ORA + PIA slightly outperformed BILP in three instances where utilization is U[25, 95%] because BILP terminated early before finding the exact optimum, but this is not significant.

Table 2. Solution quality for ORA + PIA and BILP methods

Bottleneck utilization	Routing length: 3 tasks				Routing length: 5 tasks
	Due date tightness	Total weighted cost			Duedate tightness	Total weighted cost
		ORA + PIA		BILP		ORA + PIA		BILP
[25, 95%]	[3]	15,560^*		15,600	[5]	25,300*		25,660
[45, 95%]		20,250		20,150		33,750		33,510
[65, 95%]		23,120		22,980		48,850*		18,280,200
[75, 95%]		28,070		25,539		45,700*		1,363,030
[85, 95%]		37,210		29,660		63,790*		3,080,300
[75, 110%]		52,270		35,280		69,260*		26,748,100
[55, 140%]		64,710		51,910		86,190*		44,502,000
[25, 95%]	[3, 6]	14,900*		15,050	[5, 10]	26,850		26,810
[45, 95%]		20,390		19,810		30,930		30,650
[65, 95%]		25,260		23,740		37,680		37,420
[75, 95%]		25,320		25,240		48,110		44,200
[85, 95%]		35,370		33,643		59,060*		585,390
[75, 110%]		42,110		35,800		55,460*		37,779,200
[55, 140%]		68,650		57,090		53,350*		558,410
[25, 95%]	[3, 9]	15,400		15,210	[5, 15]	36,660		34,690
[45, 95%]		18,870		18,410		36,470		35,720
[65, 95%]		26,430		25,220		50,130*		68,220
[75, 95%]		31,600*		33,600		58,500*		82,390
[85, 95%]		35,750*		46,990		62,420*		86,070
[75, 110%]		40,950*		43,390		70,920*		71,186,300
[55, 140%]		37,500*		43,200		101,100*		2,962,360
[25, 95%]	[3, 12]	16,880		16,440	[5, 20]	45,100*		75,240
[45, 95%]		22,120		20,630		40,400*		40,560
[65, 95%]		34,700*		41,230		56,840*		88,250
[75, 95%]		35,320*		37,129		63,350*		1,199,810
[85, 95%]		41,430*		47,540		74,410*		96,409,500
[75, 110%]		43,960*		514,940		83,050*		112,144,600
[55, 140%]		65,740*		90,760		82,260*		110,819,200

^* Total weighted cost of ORA + PIA solution is lower.

For routings with three tasks, the two approaches are comparable in quality, with BILP tending to outperform for extremely tight due dates and ORA + PIA outperforming for looser due dates where the number of feasible solutions is larger. For routings with five tasks, the lack of scalability of BILP becomes evident. In most instances both ORA + PIA and BILP run until the computational time limit is reached, and ORA + PIA have found a solution of either similar or much higher quality than BILP in the same amount of time, particularly as utilization approaches normal levels.

Figure 5 shows the optimality gap of the solutions obtained from ORA + PIA and BILP. As the routing length increases, as utilization approaches realistic levels, and as the due date tightness of jobs becomes more variable, the tabu search algorithms in ORA + PIA become a more effective and reliable methodology for resource planning. Even for what in practice are trivially small instances, BILP struggles to find a good solution in a reasonable amount of time. The problem is Strongly NP-Hard and thus the number of possible solutions grows exponentially with instance size. For example, in the case of routings with five tasks, ORA + PIA find higher quality solutions than BILP within the allowed computational time of 1,800 s for every instance when utilization is U[75, 95%] or above.

Figure 5. Optimality gap of ORA + PIA and BILP for routing length: (a) 3 and (b) 5.

5.3. Extended results for larger problem instances

The second set of experiments evaluates the efficacy of ORA + PIA for larger problem instances that cannot be solved in a reasonable time with an exact method.

5.3.1. Performance of ORA + PIA on large problem instances

The computational time required by the ORA to solve instances with up to 15 tasks on the routing for each job are shown in Table 3. As the routing length increases replanning a single task impacts a larger number of other tasks due to precedence constraints, and computational times increase. Bottleneck utilization also has a large effect on solution time, since higher congestion in the system requires the algorithm to replan more tasks to compute a feasible solution.

Table 3. ORA computational time (seconds)

Number of tasks	Due date tightness	Bottleneck utilization
		[25, 95%]	[45, 95%]	[65, 95%]	[75, 95%]	[85, 95%]	[75, 110%]	[55, 140%]
[3, 5]	[5]	8	11	76	141	128	131	181
	[5, 10]	16	84	84	138	231	249	275
	[5, 15]	12	131	124	234	231	288	330
	[5, 20]	59	182	277	298	314	373	568
[3, 10]	[10]	101	123	437	750	788	1,228	984
	[10, 15]	124	286	530	898	1,008	1,279	1,427
	[10, 20]	134	733	1,191	1,369	1,567	1,917	2,630
	[10, 15]	371	817	1,255	1,477	1,932	1,934	2,955
[3, 15]	[15]	485	825	2,861	3,904	6,358	5,713	6,590
	[15, 20]	885	1,019	2,934	3,543	5,537	5,529	8,539
	[15, 25]	715	1,863	5,168	6,697	7,691	6,947	10,232
	[15, 30]	767	3,081	5,525	6,677	9,702	9,873	11,263

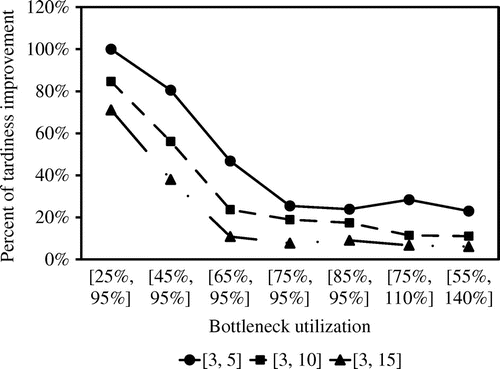
Figure 6 shows the percent that tardiness is reduced by the PIA after receiving a solution from the ORA for different levels of congestion and routing lengths. The PIA performs well at low utilizations. At higher utilization levels the opportunities to complete orders before their due dates are more limited and therefore improvement percentages are lower.

Figure 6. Effect of bottleneck utilization and routing length on the PIA performance.

5.3.2. Performance of ORA + PIA versus other heuristic methods

One family of methods for resource planning sorts jobs according to priority and loads them onto resources one at a time. We compare our approach to methods of this type because they are commonly used in practice and do not have overly burdensome implementation requirements. We compare ORA + PIA to two implementations of this method: finite forward loading (FFL) and finite backward loading (FBL). With FFL, jobs are sorted by arrival time and then loaded onto resources using a finite forward planning method. With FBL, jobs are sorted by earliest due date and then loaded onto resources using a finite backward planning method. Figure 7 shows the total weighted cost of each method for different levels of congestion and routing lengths. ORA + PIA outperforms the FFL and FBL methods in all instances and has an average of 49% lower expected total weighted cost than FFL and 59% lower than the FBL.

Figure 7. Solution quality of ORA + PIA, FFL and FBL for routing length: (a) [3, 5], (b) [3, 10] and (c) [3, 15].

6. Conclusion

In make-to-order environments where demand is highly variable a resource planning algorithm is used to adjust the time that individual tasks are performed on resources so that capacity constraints are respected, due dates are met, and lead times are minimized. This research develops a two-phase tabu search-based methodology for resource planning. Phase 1, the ORA, makes the minimal necessary adjustments to the initial plan to create a feasible finite-capacity plan. One of the key features of OIA is how it is initialized. Rather than using a random feasible plan as the initial solution, we define an ideal solution that would be optimal if capacity constraints did not exist and use it as the initial solution. OIA then modifies the solution to be capacity-feasible. Phase 2, the PIA, begins with the good, feasible solution obtained by ORA and searches for alternate finite-capacity plans with better performance. To guide the search by PIA a neighborhood structure is defined based on the JIT philosophy in which jobs are attempted to be processed and finished as close as possible to their due dates (neither tardy nor early). An appealing characteristic of our methodology is that it automatically identifies capacity constraints. It does not require assumptions about the number or location of bottlenecks and it accommodates dynamic bottlenecks, which are a natural occurrence make-to-order systems.

We take unusual care to create realistic instances for empirical evaluation. For instance, we vary the utilization of individual buckets on a resource so that the resource loading is uneven, as it would be in practice. Computational results show that as the routing length increases, as utilization approaches realistic levels, and as the due date tightness of jobs becomes more variable, the tabu search algorithms in ORA + PIA become a more effective and reliable methodology for resource planning than an exact method (binary integer linear programming), which struggles to find a good solution in a reasonable amount of time even for trivially small instances. ORA + PIA also outperform heuristic methods commonly used in practice for resource planning that sort jobs according to priority and load them onto resources one at a time.

Implementation of the algorithms requires many thousands of lines of code that must be thoughtfully written in order to be fast and scalable. Each neighboring solution must be identified and constructed efficiently, using data such as resource capacity, resource loading, job routings, task times, and task precedence relationships. Substantial calculations are required to compute each neighboring solution, especially since changing the time a task is performed on the resource being replanned not only affects tasks on that resource but also affects the timing of related tasks on other resources. To improve scalability and performance, further research could be performed to develop data structures and procedural primitives that are customized for resource planning problems.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Scott A. Moses

Scott A. Moses is an Associate Professor in the School of Industrial & Systems Engineering at the University of Oklahoma. His research activity focuses on scalable algorithms for real-time order promising and for high-speed tactical-level planning of production tasks and material flow in large discrete systems. Emphasis in research is given to computationally oriented approaches that have the flexibility and scalability needed to yield solutions meaningful to industry. His teaching interests also include factory physics and engineering economics. He received his PhD degree in industrial engineering from Purdue University and holds an MS degree in industrial engineering and a BS degree in mechanical engineering, both from Oklahoma State University.

Wassama Sangplung

Wassama Sangplung is a Lecturer at King Mongkut’s University of Technology Thonburi in Bangkok. She received her PhD in industrial engineering from the University of Oklahoma. Her interests are in supply chain management, production planning and business process management.