An application of Kernel estimation method to the demand in two-stage inventory model

Abstract

This paper proposes an improvement in the form of modeling the demand in models of stochastic inventories. For these purposes, it is proposed to occupy the Kernel estimation method to the demand per unit of time and demand during the lead time to generate input scenarios for a stochastic programming in two-stage, in a model of continuous review with shortage. An application of this methodology considers the obtaining of this scenarios from the modeling of actual data of demand of inputs of food service. The possibility of working directly with the densities and accumulated probabilities of demand in an empirical and more realistic way with regard to the data available, improve the task for the decision makers of the operations management.

Keywords:

• continuous review
• generation scenarios
• Kernel estimation method
• stochastic programming in two-stages

Public Interest Statement

This paper deals with an application in inventory models to perform sourcing, which considers the Kernel estimation method to obtain the probability density of the demand per unit time of products. We propose its use in a continuous review inventory model under a two stage stochastic programming framework.

The advantage of the use of this proposal is that the Kernel estimation is not limited by distributional assumptions about the demand per unit time of products, allowing a modeling closer to the empirical data of this variable, which causes a reduction of purchase lots, determination of reorder points, expected shortages and more accurate total costs. The proposal also includes a way of working when the supplier’s lead time is random.

1. Introduction

Supply system and the inventories policy reduce the vulnerability of the supply chain management in enterprises, which is achieved by optimizing inventory levels to meet the demand of products of the companies satisfying customers. This optimization is realize considering the variance of the demand data (Hillier & Lieberman, 2005). In this context, stochastic inventory models consider the demand for products as a random variable (RV) described by a continuous or discrete distribution. These models optimize total costs (TC) of inventory, which have three components: (a) a cost that is independent of the lot size, (b) a cost that depends on the quantity of products in the lot, and (c) a cost of shortage due to unsatisfied demand (Gjerdrum, Samsatli, Shah, & Papageorgiou, 2005). Once the inventory model indicators have been defined and distributional assumptions for demand per unit time (DPUT) and for demand during lead-time (LT), in short LTD, have been established, the expected value of the objective function based on the TC of the inventory must be optimized (Namit & Chen, 1999).

The probabilistic treatment of LTD is facilitated when the LT is constant. Otherwise, different distributions have been assumed directly for this RV or the sum of DPUT that conforms it (Rojas & Leiva, 2016).

Kernel density estimation is a non-parametric method for estimating a density function from a random sample of data (Pillonetto, Dinuzzo, Chen, De Nicolao, & Ljung, 2014). According to Wang, Wang, and Chung (2014), the Kernel estimation method has the advantage of being applicable to large databases, obtaining an approximation to the true PDF of the random data of excellent quality, which allows to obtain a more precise forecast for the RV . This feature makes it very useful for use in inventory models and modelling of the supply chain (Zhu, Ma, & Zhang, 2014). Then by this method it is possible obtain an descriptive structure that can must be inserted in the mentioned objective cost function of a inventory model, to find optimal cost by stochastic programming (SP) (Rojas & Leiva, 2016; Wanke & Leiva, 2015). The way to insert a RV into a objective function or constraints of a SP is by generating scenarios that best represent a finite number of this variable (Shapiro, Dentcheva, & Ruszczynski, 2014). Classically it is possible to segment the SP into two stages, where a first decision is made prior to the realization of the RV, and other second stage decisions can be made once the realization of the RVs is revealed (Birge & Louveaux, 2011).

The objective of this paper is to propose a way to improve the accuracy of a continuous review inventory models with shortage with a single supplier, by use of Kernel density estimation to randon DPUT and LTD in SP in two-stage. The paper is organized as follows: Section 2 reviews a background built on SP of inventory models of continuous review, Section 3 illustrates the proposal with a actual data and Section 4 provides a discussion and conclusions of the results obtained in this research, as well as their limitations and future research.

2. Background

2.1. Stochastic programming of inventory models of continuous review

As its name suggests, SP is a mathematical programming problem (linear, nonlinear, integer, between others) which contains in its formulation some stochastic element that is unknown, but that can be estimated from its probability distribution (Shapiro et al., 2014). The types of models appearing on SP are motivated primarily by problems with decisions kind here and now, or previous decisions under uncertain future, where decisions can be based on a priori information, existing or perceived, on future situations (Birges & Louveaux, 2011). This leads to the main idea that the decisions of a stochastic problem can be separated into two stages, where first stage decision is made before the uncertainty is revealed; and two stage decision is made after the uncertainty is revealed (Shapiro et al., 2014). This decisions of the first stage does not depend on the scenario that occurs really in the future.

In SP the decisions of first stage are those that determine the quality of the solution of the problem (Escudero, Garín, Merino, & Pérez, 2009).

To enter the randomness in stochastic optimization problems the generation of various scenarios is required. In real-life application this scenarios is considered finite. The scenarios represent a realization of RVs and are diagramed in a tree. Each scenario has a weight, that represents the likelihood assigned to this scenarios by the decisor. A common approach to generate scenarios is based on estimating an unknown distribution and matching its moments with moments of a discrete scenario model. By having actual data for the realization of an RV it is possible to estimate the probability density using a non-parametric estimation of Kernel (Rao, 2014). Once the empirical distribution is estimated, it is possible to simulate this distribution at each stage in parallel. The problem of finding valuable scenario approximations can be viewed as the problem of optimally approximating a given distribution with some distance function such as a cluster analysis (Gülpinar, Rustem, & Settergren, 2004).

A problem of multiple products commonly occurring in inventory policies is to decide what optimal quantities of products must be ordered simultaneously from a same supplier (Hillier & Lieberman, 2005). Continuous review policies provide solutions to problems of inventory management in many real-world situations. Inventory models of continuous review are known as $(Q,r)$ models, which are often used for inventory supply planning. This model is based on the economic order quantity or lot size and reorder point, denoted by Q and r, respectively (Rojas, Leiva, Wanke, & Marchant, 2015). Indicators Q and r must be determined to minimize the TC of the inventory management. Such a TC is function of the holding, ordering and shortage costs (Hillier & Lieberman, 2005). When calculating the reorder point for a fixed service level, the LTD distribution and its corresponding probability density function (PDF) must be used. When the LTD distribution is unknown, this PDF can be approximated by any suitable approach. We employ a simultaneous approach to optimize Q and r (Silver, Pyke, & Peterson, 1998; Wanke, Ebwank, Leiva, & Rojas, 2016). Then, as has been suggested for two-stage SP can be consider minimize the expected value of the objective function based on the TC of inventory of a continuous review policy, generating scenarios for the DPUT not IID on the time, by means of a density Kernel estimation. SP can be used to solve this optimization problem using the differential evolution (DE) algorithm, which belongs to the family of genetic algorithms, emulating the natural process of choice in evolutionary way (Price, Storn, & Lampinen, 2006; Rojas & Leiva, 2016; Thangaraj, Pant, Bouvry, & Abraham, 2010; Wanke & Leiva, 2015).

2.1.1. Continuous review model with inventory shortage in two stage

2.1.1.1. Modeling of demand during lead-time

Let $Y_t$ be the observed demand in period $t,t=1,\dots ,T$ with $\text{E}(Y_t)={\mathit{\mu }}_t$ and variance $\text{Var}(Y_t)$. Let S be the LTD for the product, which is the random sum given by(1) $$\begin{array}{c}\hfill S=\sum _{t=1}^L{Y}_t,\end{array}$$(1)

where L be lead time over which the estimation are desired, which has mean $\text{E}(L)={\mathit{\mu }}_L$ and variance $\text{Var}(L)={\mathit{\sigma }}_L^2$. Our goal is to estimate the entire distribution of the sum of the demands over the lead time, called LTD, furthermore, L is independent from each element of the sequence of independent identically distributed RVs $\{Y_1,\dots ,Y_L,L\in \mathbb{N}\}$, which have mean $\text{E}(\{Y_1,\dots ,Y_L\})={\mathit{\mu }}_S$ and variance $\text{Var}(\{Y_1,\dots ,Y_L\})={\mathit{\sigma }}_S^2$. Assume that orders do not cross (Hayya, Bagchi, Kim, & Sun, 2008).

Based on actual sequence of DPUT, we can define a Kernel estimate of the unknown PDF $f_{Y_t}(·)$ by(2) $$\begin{array}{c}\hfill {\widehat{f}}_{Y_t}(y_t)=\frac{1}{Th}\sum _{i=1}^{T}K\left(\frac{y_t-y}{h}\right),y>0,\end{array}$$(2)

where $K(·)$ is a kernel function satisfying ${\int }_0^{\infty }K(s)\text{d}s=1$, h a smoothing parameter (or bandwidth) and y the point at which the PDF is estimated. The Gaussian kernel with support in $\mathbb{R}$ is often assumed for $K(·)$ given in 2.

When LT denoted by L is a RV, it is necessary to consider a probabilistic distribution of easy estimation to model the LTD PDF as a sum of the DPUT during the LT. In this regard, Wanke et al. (2016) considered the triangular distribution (TRI) for the LT, because of the ease of interpretation of its parameters for decision makers. This justification is also valid in our case. In the case of variable LT, we can consider triangular (TRI) distribution for LT and Kernel distribution for DPUT. In this case, we can make a Kernel estimation for the PDF of the LTD, which generally does not have a closed form in these conditions.

Then, let L be a continuous RV following a TRI distribution with parameters $a,b,c\in \mathbb{R}$, where a and b are the minimum and maximum values of L, respectively, and c is the mode of the distribution. This is denoted by $L\sim \text{TRI}(a,b,c)$. Then, the PDF, cumulated distribution function (CDF) and QF of L are, respectively, given by$$\begin{array}{cc}& f_L(l)=\frac{\text{d}{F}_L(l)}{\text{d}l}=\left\{\begin{array}{cc}\frac{2(l-a)}{(b-a)(c-a)},& \text{if}a\le l\le c;\hfill \\ \frac{2(b-l)}{(b-a)(b-c)},& \text{if}c\le l\le b;\hfill \\ 0,& \text{otherwise};\hfill \end{array}\right.\hfill \\ \hfill & F_L(l)=\text{P}(L\le l)=\underset{0}{\overset{l}{\int }}{f}_L(v)\text{d}v=\left\{\begin{array}{cc}0,& \text{if}l<a;\hfill \\ \frac{(c-a)}{(c-b)}\frac{{(l-a)}^2}{{(c-a)}^2},& \text{if}a\le l\le c;\hfill \\ 1-\frac{(b-c)}{(b-a)}\frac{{(b-l)}^2}{{(b-c)}^2},& \text{if}c\le l\le b;\hfill \\ 1,& \text{if}l>b;\hfill \end{array}\right.\hfill \\ \hfill & l(q)=F_L^{-1}(q)=\left\{\begin{array}{cc}a+\sqrt{q(c-a)(b-a)},& \text{if}0\le q\le (c-a)/(b-a);\hfill \\ b-\sqrt{(1-q)(b-c)(b-a)},& \text{if}(c-a)/(b-a)\le q\le 1.\hfill \end{array}\right.\hfill \end{array}$$

The mean and variance of $L\sim \text{TRI}(a,b,c)$ are, respectively, given by$${\mathit{\mu }}_L=\text{E}(L)=\frac{a+b+c}{3}\text{and}{\mathit{\sigma }}_L^2=\text{Var}(L)=\frac{{(b-a)}^2}{18}\left(1-\frac{(c-a)(b-c)}{{(b-a)}^2}\right).$$

By fixing minimum, maximum and mode values for the RVs LT with TRI distributions, DPUT with Kernel distribution given in 3 and the expression given in (1), we are able to compute a sequence $\{s_1,\dots ,s_n\}$ of n LTD observations (data). Then, based on this sequence, we can define a kernel estimate of the unknown PDF $f_S(·)$ by(3) $$\begin{array}{c}\hfill {\widehat{f}}_S(s)=\frac{1}{nh}\sum _{i=1}^{n}K\left(\frac{s_i-s}{h}\right),s>0,\end{array}$$(3)

where $K(·)$ is a kernel function satisfying ${\int }_0^{\infty }K(s)ds=1$, h a smoothing parameter (or bandwidth) and s the point at which the PDF is estimated. The Gaussian kernel with support in $\mathbb{R}$ is often assumed for $K(·)$ given in 2. However, we are modeling demand data with support in [a, b]. Thus, instead of the Gaussian kernel, it seems more natural to estimate the unknown PDF with a TRI kernel by using 4(4) $$\begin{array}{c}\hfill {\widehat{f}}_S(s)=\frac{1}{n}\sum _{i=1}^n{K}_{h,s}(s_i),\end{array}$$(4) (4) $$\begin{array}{c}\hfill {\widehat{f}}_S(s)=\frac{1}{n}\sum _{i=1}^n{K}_{h,s}(s_i),\end{array}$$(4)

where $K_{h,s}$ is a TRI kernel of parameters h (bandwidth) and s (point at which the PDF is estimated); see details in Marchant, Bertin, Leiva, and Saulo (2013).

Let S be the LTD for the item, which is the random sum given by 1 with PDF $f_S(·)$ defined in 4, CDF and quantile function (QF) $s(q)=F_S^{-1}(q)$, for $0<q<1$ obtained only by numeric integration. The expectation and variance of S are, respectively, expressed as(5) $$\begin{array}{c}\hfill \text{E}(S)=\text{E}(L)\text{E}(Y_t)={\mathit{\mu }}_L{\mathit{\mu }}_t,t=1,\dots ,L\end{array}$$(5)

and(6) $$\begin{array}{c}\hfill \text{Var}(S)=\text{Var}(L){\text{E}}^2(Y_t)+\text{E}(L)\text{Var}(Y_t)={\mathit{\sigma }}_L^2{\mathit{\mu }}_t^2+{\mathit{\mu }}_L\text{Var}(Y_t).\end{array}$$(6)

Note that, in general, the LT and DPUT can be modeled by any discrete or continuous distribution. However, if LT is constant $\text{Var}(S)={\mathit{\mu }}_L\text{Var}(Y_t)$.

2.1.1.2. Use of DPUT and LTD in inventory management models

The expected annual total cost of inventory assuming shortage is expressed as a sum of (i) the holding cost per product unit per year, denoted by ${\text{C}}_{\text{h}}$, multiplied by the expected quantity in stock of product units; (ii) the ordering cost, denoted by ${\text{C}}_{\text{o}}$, multiplied by the number of orders per year, and (iii) the penalty cost whenever there are stock-outs, denoted by ${\text{C}}_{\text{p}}$, i.e. the penalty cost per shortage product unit per year multiplied by the number of orders per year and by the expected quantity of shortage product units per year. We are assuming a business has demand 365 days a year. Thus, for the $(Q,r)$ model, the expected total cost per year is(7) $$\begin{array}{c}\hfill {\text{C}}_{\text{T}}=G(Q,r)=\left(\frac{Q}{2}+r-\text{E}(S)\right){\text{C}}_{\text{h}}+\frac{365{\mathit{\mu }}_t}{Q}{\text{C}}_{vo}+S(r)\frac{365{\mathit{\mu }}_t}{Q}{\text{C}}_{\text{p}},\end{array}$$(7)

where ${\mathit{\mu }}_t$ and $\text{E}(S)$ are defined in (5) (Hadley & Whitin, 1963; Johnson & Montgomery, 1974; Silver et al., 1998). On the one hand, note that ${\mathit{\mu }}_t$ is multiplied by 365, because the total cost given in (7) is defined on an annual basis and ${\mathit{\mu }}_t$ on a daily basis. On the other hand, $\text{E}(S)$ is not altered, because its scope is verified within each safety inventory cycle. Q and r are decision variables of quantity to order and reorder point, respectively to the model EOQ with shortage. In addition, in (7), S(r) is the expected shortage per cycle given by(8) $$\begin{array}{c}\hfill S(r)=\underset{r}{\overset{s_{max}}{\int }}(s-r)f_S(s)\text{d}s,\end{array}$$(8)

where $s_{max}$ is the maximum value of the LTD and, as also mentioned, $f_S(·)$ is the LTD PDF. Following to Nahmias (2001), the solve of 7 requires an iterative process where an initial solution of $Q=\sqrt{\frac{2C_o{\mathit{\mu }}_t}{C_h}}$, then it is possible to obtain the complement of the CDF $F_s(r)$ or probability of stock break, as$$1-F_s(r)=\frac{Q{C}_h}{{\mathit{\mu }}_t{C}_p},$$

and therefore(9) $$\begin{array}{c}\hfill r=F_s^{-1}\left(1-\frac{Q{C}_h}{{\mathit{\mu }}_t{C}_p}\right),\end{array}$$(9)

then with this value of r we can obtain S(r) given in 8. Finally, it is possible to obtain,(10) $$\begin{array}{c}\hfill Q=\sqrt{\frac{2{\mathit{\mu }}_t(C_o+S(r))}{C_h}}.\end{array}$$(10)

Iterating 9 and 10 until reaching values that do not vary with respect to a minimum threshold, it is possible to obtain solutions that minimize 7.

In this proposal the TC to miminize is expressed as a general SP in two-stage. TC is a function of Q as a decision variable of first stage more a weighted sum in each scenario $\mathit{\omega }\in \mathrm{\Omega }$ for a decision variable of second stage (often called recourse), computable when of the RV of DPUT is revealed. In this case, the decision variable of second stage is the security factor, denoted by k, which serves to establish a reordering point. Thus, for the $z(Q,k(\mathit{\omega }))$ model in two stage, the annual total cost to minimized is expressed as$$minz(Q,r(\mathit{\omega }))=\underset{Q\ge 0}{min}{c}^{T}Q+\mathbb{F}(Q,\mathit{\omega })\text{s.t}AQ\le B,$$

where$$\mathbb{F}(Q,\mathit{\omega })=\mathbb{E}(F(Q,\mathit{\omega }))=\sum _{\mathrm{\Omega }}{p}^{\mathit{\omega }}\underset{r(\mathit{\omega })\in \mathbb{R}}{min}{q}^{T}r(\mathit{\omega })\text{s.t}T(\mathit{\omega })Q+W(\mathit{\omega })r(\mathit{\omega })=j(\mathit{\omega })$$

where

matrix $c^T=\left[\begin{array}{cc}h/2\hfill & Y_t(\mathit{\omega })o\hfill \end{array}\right],$

matrix $Q=\left[\begin{array}{c}Q\\ Q^{-1}\end{array}\right],$

where $Y_t(\mathit{\omega })$ can be calculated from selected scenarios $\mathit{\omega }$ gives parameters of PDF to each time t from model 2, the constraint $AQ\le B$, represented a budget constraint such that A is the unitary cost of the item, and B is the maximum annual budget available for the item. For second stage,

matrix $q^T=\left[\begin{array}{cc}r(\mathit{\omega })-\text{E}(S)\hfill & b/\sqrt{\frac{2(o+bS(r(\mathit{\omega })))}{h{Y}_t(\mathit{\omega })}}\hfill \end{array}\right],$

because $\frac{Y_t}{Q}=\frac{1}{\sqrt{\frac{2(o+bS(r(\mathit{\omega })))}{h{Y}_t(\mathit{\omega })}}}$

matrix $k(\mathit{\omega })=\left[\begin{array}{c}r(\mathit{\omega })\\ S(r(\mathit{\omega }))\end{array}\right],$

matrix $W=\left[\begin{array}{cc}\text{Var}(S)& 0\end{array}\right],$

matrix $j(\mathit{\omega })=\left[\begin{array}{cc}r(\mathit{\omega })& 0\end{array}\right],$

where $r(\mathit{\omega })$ correspond to reorder point that depends on the realization of the LTD in scenario $\mathit{\omega }\in \mathrm{\Omega }$ ($y_t(\mathit{\omega })$), and finally

matrix $T(\mathit{\omega })=\left[\begin{array}{cc}\frac{\mathbb{E}(L)}{\sqrt{\frac{2(o+bS(r(\mathit{\omega })))}{h{y}_t(\mathit{\omega })}}}& 0\end{array}\right].$

Then $F(Q,\mathit{\omega })$ is differentiable with respect to Q for $\mathit{\omega }$ continue or discrete, if recourse structure is complete, that is if the system $W(\mathit{\omega })r(\mathit{\omega })=\mathit{\chi }$ and $r(\mathit{\omega })\in \mathbb{R}$ has a solution for every $\mathit{\chi }$. In other words, the positive hull of $W(\mathit{\omega })$ is equal to the corresponding vector space. Also second stage problem is not unbounded. Because the second stage is a linear programming problem, its dual problem can be written in the form (Birge & Louveaux, 2011):$$\underset{\mathit{\pi }}{max}{\mathit{\pi }}^T(j(\mathit{\omega })-T(\mathit{\omega })Q)\text{s.t}W{(\mathit{\omega })}^T\mathit{\pi }\le q,$$

then if we consider the function $s_q(\mathit{\chi }):=\{q^{T}r(\mathit{\omega })\text{s.t}W(\mathit{\omega })k(\mathit{\omega })=\mathit{\chi },r(\mathit{\omega })\in \mathbb{R}\}$, then $F(Q,\mathit{\omega })=s_q(j(\mathit{\omega })-T(\mathit{\omega })Q)$. Suppose that for given $Q=Q_0$ and $\mathit{\omega }\in \mathrm{\Omega }$, the value $F(Q_0,\mathit{\omega })$ is finite. Then $F(·,\mathit{\omega })$ is subdifferentiable at $Q_0$ and$$\mathit{\partial }F(Q_0,\mathit{\omega })=-T{(\mathit{\omega })}^T\mathcal{D}(Q_0,\mathit{\omega }),$$

where $\mathcal{D}(Q_0,\mathit{\omega })=\text{arg}{max}_{\mathit{\pi }\in \mathrm{\Pi }(f)}{\mathit{\pi }}^T(\mathit{\omega })(j(\mathit{\omega })-T(\mathit{\omega })Q)$, is the set of optimal solutions of the dual problem. Therefore, $F(Q,\mathit{\omega })$ is differentiable, if the dual problem has a solution. Let $\mathit{\chi }=T(\mathit{\omega })(Q,\mathit{\omega })$, and $\mathit{\partial }\mathit{\vartheta }(\mathit{\chi },\mathit{\omega })=\mathcal{D}(\mathit{\chi },\mathit{\omega })$, further, that functions $c(·)$ and $T{(\mathit{\omega })}_{\mathit{\omega }}(·)$ are differentiable, and $0\in \text{int}\{T\mathit{\omega }(Q)+\mathrm{\nabla }T\mathit{\omega }(x){\mathbb{R}}^l-\text{dom}\mathit{\vartheta }(·,\mathit{\omega })\},$ then$${\mathrm{\nabla }}_{Q}F(Q,\mathit{\omega })=\mathit{\partial }F(Q,\mathit{\omega })=\mathrm{\nabla }T\mathit{\omega }{(x)}^T\mathcal{D}(\mathit{\chi },\mathit{\omega })$$, for more details see Shapiro et al. (2014 (chap.2)).

To solve this problem of two stages is possible to use the L-Shaped algorithm (see Birge & Louveaux, 2011).

2.1.2. Generation of scenarios of SP in two-stage

We deal a procedure based on simulation given a Kernel PDF IID of DPUT and LTD (Gülpinar et al., 2004). The input to the cost optimization problem is constructed through a tree of scenarios, where the nodes represent a possible value for the RV with certain levels of probabilities in their ramifications. This construction is can carry out considering randomized clustering of quantiles of PDF. Then one give quantile of Kernel PDF IID of DPUT and LTD is designated as the centroid to establish a node, and their probability of ocurrence is given by their PDF.

3. Application

Below, we show how inventory management of products can be planned within companies by using the background proposed in Section 2 and the computational framework developed for this.

3.1. Computational framework

R is a non-commercial and open source software for statistics and graphs, which can be obtained at no cost from http://www.r-project.org. The statistical software R is being currently very popular in the international scientific community. For a use of this software in inventory models, see Rojas et al. (2015). Some R packages related to statistical distributions that may be useful in inventory models are available at http://CRAN.R-project.org. The expected value and other moments of monthly demand products is calculated by using generalized additive models for localization, scale and shape (GAMLSS) implemented in the R software by the packages gamlss.util() for data analysis. The SP of inventory models is performed by the packaged DEoptim() of the same software.

3.2. The data set

To validate the proposed methodology, we use real-world monthly demand data for an assortment of foods service inputs, which it has extracted an example of one daily demand of input. The inputs are shipped from the warehouse of a food service and delivered to make menus that are available to the public, located at the city of Concon, Chile, for a study of supply policy.

3.3. Data analysis

Table 1 show descriptive statistics of monthly DPUTs of a illustrative product with mean, SD, interquartile range (IQR), percentile 0, 25, 75, 100 and sample size (n).

Table 1. Descriptive statistics of monthly DPUTs of illustrative product

mean	SD	IQR	0%	25%	50%	75%	100%	n
2,699.083	322.7705	438.25	2,115	2,477.25	2,647	2,915.5	3,331	500

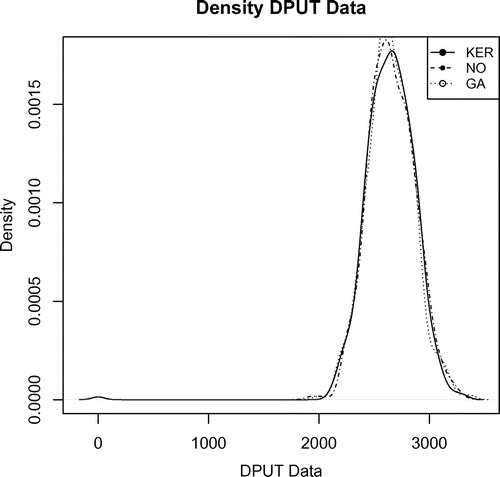
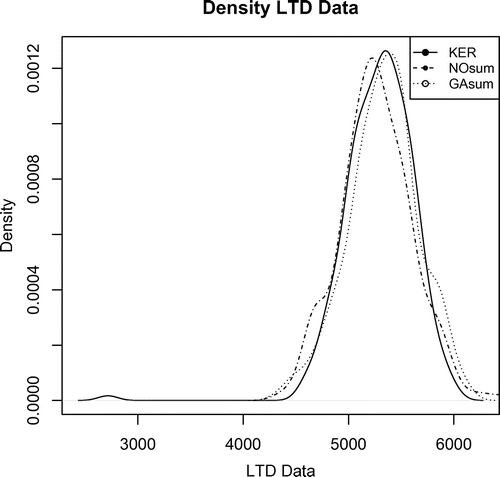
To compare the behavior of the proposed SP considering PDF Kernel estimation of the DPUT and LTD, we compare their performance with other distributions used in inventory models. These correspond to the Normal (NO) and Gamma (GA) distributions for the DPUT, and their sum, used as LTD model distributions, which we called Normal sum (NOsum) and Gamma sum (GAsum). Under a GAMLSS approach to modeling the mean of a probability distribution, and using the fitDist command of the gamlss package, we estimate the parameters of the following distributions to model the DPUT (Table ) and the LTD (Table 3), respectively. These estimates allow us to study the adequacy of these distributions in the modeling of DPUT and LTD, as well as to obtain results in the performance of the continuous revision inventory model formulated in 7.

Table 2. Modeling of DPUT

Distribution	PDF	CDF	Parameters
NO	$\mathit{\varphi }\left(\frac{y_t-{\mathit{\mu }}_t}{{\mathit{\sigma }}_{\text{NO}}}\right)\frac{1}{{\mathit{\sigma }}_{\text{NO}}}$	$\mathrm{\Phi }\left(\frac{y_t-{\mathit{\mu }}_t}{{\mathit{\sigma }}_{\text{NO}}}\right)$	${\mathit{\mu }}_t\in \mathbb{R},{\mathit{\sigma }}_{\text{NO}}>0$
GA	$\frac{y_t^{\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2}-1}}{\mathrm{\Gamma }\left(\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2}\right){\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_t^{\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2}}}$$exp\left(-\frac{y_t}{{\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_t}\right)$	$\frac{1}{\mathrm{\Gamma }\left(\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2}\right)}\mathit{\gamma }\left(\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2},y_t/{\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_t\right)$	${\mathit{\mu }}_t>0,{\mathit{\sigma }}_{\text{GA}}>0$

Table 3. Modeling of LTD

Distribution	PDF	CDF	Parameters
NOsum	$(\mathit{\varphi }\left(\frac{s-{\mathit{\mu }}_t{\mathit{\mu }}_k}{{\mathit{\sigma }}_{\text{NO}}\sqrt{(}{\mathit{\mu }}_k)}\right)\frac{1}{{\mathit{\sigma }}_{\text{NO}}\sqrt{(}{\mathit{\mu }}_k)}$	$\mathrm{\Phi }\left(\frac{s-{\mathit{\mu }}_t{\mathit{\mu }}_k}{{\mathit{\sigma }}_{\text{NO}}\sqrt{(}{\mathit{\mu }}_k)}\right)$	${\mathit{\mu }}_t{\mathit{\mu }}_k\in \mathbb{R},{\mathit{\sigma }}_{NO}\sqrt{(}{\mathit{\mu }}_k)>0$, ${\mathit{\mu }}_k\geqq 2$
GAsum	$\frac{s^{\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_k}-1}}{\mathrm{\Gamma }\left(\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_k}\right){\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_k{({\mathit{\mu }}_k{\mathit{\mu }}_t)}^{\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_k}}}$$exp\left(-\frac{s}{{\mathit{\sigma }}_{GA}^2{\mathit{\mu }}_t}\right)$	$\frac{1}{\mathrm{\Gamma }\left(\frac{1}{{\mathit{\sigma }}_{GA}^2}{\mathit{\mu }}_k\right)}\mathit{\gamma }\left(\frac{1}{{\mathit{\sigma }}_{\text{GA}}^2}{\mathit{\mu }}_k,s/{\mathit{\sigma }}_{\text{GA}}^2{\mathit{\mu }}_k{\mathit{\mu }}_t{\mathit{\mu }}_k\right)$	${\mathit{\mu }}_t{\mathit{\mu }}_k>0,{\mathit{\sigma }}_{\text{GA}}{\mathit{\mu }}_k>0$, ${\mathit{\mu }}_k\geqq 2$

Figures 1 and 2 show the modelling of NO and GA distributions to respect to Kernel estimation to DPUT, and NO sum and GA sum respecto to Kernel estimation to LTD.

Figure 1. Comparison of DPUT density modeling.

Figure 2. Comparison of LTD density modeling.

The two-stage SP considers find a lot size of purchase (Q) as decision variable of the first stage, before the realization of the DPUT. In the second stage, are considered twelve scenarios ($\mathit{\omega }$) of DPUT with PDF Kernel estimates for a single time, to compare with twelve scenarios NO IID and GA IID to realization of the centiles 95 and 5% of the DPUTs ($Y_{t_{95}}$ and $Y_{t_5}$) and their probabilities are generated by simulation in parallel according to Gülpinar et al. (2004). We compared outcomes of SP to inventory model with continuous review with shortage in two stage in Table 4. The parameters employed for this programming are TRI mean of lead time of 2 days (${\mathit{\mu }}_L$) and TRI standard deviation of lead time of 1.35 days (${\mathit{\sigma }}_L$), holding cost of 0.42 USD$/year*unit, shortage cost of 0.33 USD$/shortage unit, and order cost of 0.86 USD$/order. In each of the scenarios should find the reorder point (r) that optimizes the TC function. Note that the results of total costs (TCs), quantities to order (Q), reorder point (r) and expected shortage per cycle (S(r)) are more accurate when the PDF of the DPUTs is fits with a PDF Kernel estimation.

Table 4. Effect of modeling of DPUTs with PDF Kernel estimation, NO IID and GA IID on SP of continuous review with shortage in two stages

NO scenario	${\mathit{\omega }}^1$	${\mathit{\omega }}^2$	${\mathit{\omega }}^3$	${\mathit{\omega }}^4$	${\mathit{\omega }}^5$	${\mathit{\omega }}^6$	${\mathit{\omega }}^7$	${\mathit{\omega }}^8$	${\mathit{\omega }}^9$	${\mathit{\omega }}^{10}$	${\mathit{\omega }}^{11}$	${\mathit{\omega }}^{12}$
$Y_{t_{95}}$ (unit/month)	3,045	3,426	2,838	3,321	3,636	4,133	3,527	4,518	3,194	3,856	3,981	3,743
Weight (%)	8.1	12.5	4.9	12.3	10.9	3.3	11.4	0.3	11.9	7.0	6.1	11.3
$Q_{95}$ (unit)	1,721
$r_{95}$ (without unit)	1.75	1.54	1.88	1.59	1.44	1.24	1.49	1.12	1.66	1.35	1.30	1.39
$S(r_{95})$(unit shortage/cycle)	733	651	786	671	613	539	632	493	698	578	560	596
$T{C}_{95}$ (USD/year)	415.73
$Y_{t_5}$ (unit/month)	1,469	1,850	1,262	1,745	2,060	2,557	1,950	2,942	1,618	2,280	2,405	2,166
Weight (%)	8.1	12.5	4.9	12.3	10.9	3.3	11.4	0.3	11.9	7.0	6.1	11.3
$Q_5$ (unit)	507
$r_5$ (without unit)	1.16	0.86	1.39	0.93	0.74	0.50	0.80	0.36	1.03	0.62	0.57	0.68
$S(r_5)$ (unit shortage/cycle)	509	404	593	428	362	291	383	253	462	327	310	344
$T{C}_5$ (USD/year)	230.81
GA scenario	${\mathit{\omega }}^1$	${\mathit{\omega }}^2$	${\mathit{\omega }}^3$	${\mathit{\omega }}^4$	${\mathit{\omega }}^5$	${\mathit{\omega }}^6$	${\mathit{\omega }}^7$	${\mathit{\omega }}^8$	${\mathit{\omega }}^9$	${\mathit{\omega }}^{10}$	${\mathit{\omega }}^{11}$	${\mathit{\omega }}^{12}$
$Y_{t_{95}}$ (unit/month)	3,458	3,562	2,444	3,923	4,325	4,890	3,127	5,180	2,994	4,021	4,567	3,256
Weight (%)	8.1	12.5	4.9	12.3	10.9	3.3	11.4	0.3	11.9	7.0	6.1	11.3
$Q_{95}$ (unit)	1,932
$r_{95}$ (without unit)	2.57	2.84	1.12	1.34	2.01	0.98	2.01	0.91	1.86	1.52	1.67	1.87
$S(r_{95})$ (unit shortage/cycle)	753	676	805	694	637	544	636	497	721	602	582	615
$T{C}_{95}$ (USD/year)	444.92
$Y_{t_5}$ (unit/month)	1,507	1,872	1,285	1,766	2,083	2,570	1,973	2,965	1,641	2,303	2,428	2,189
Weight (%)	8.1	12.5	4.9	12.3	10.9	3.3	11.4	0.3	11.9	7.0	6.1	11.3
$Q_5$ (unit)	531
$r_5$ (without unit)	1.11	1.06	1.09	0.74	0.52	0.37	0.68	0.22	0.93	0.42	0.44	0.55
$S(r_5)$ (unit shortage/cycle)	520	421	614	443	373	303	400	275	489	351	331	376
$T{C}_5$ (USD/year)	233.21
PDF Kernel estimation scenario	${\mathit{\omega }}^1$	${\mathit{\omega }}^2$	${\mathit{\omega }}^3$	${\mathit{\omega }}^4$	${\mathit{\omega }}^5$	${\mathit{\omega }}^6$	${\mathit{\omega }}^7$	${\mathit{\omega }}^8$	${\mathit{\omega }}^9$	${\mathit{\omega }}^{10}$	${\mathit{\omega }}^{11}$	${\mathit{\omega }}^{12}$
$Y_{t_{95}}$ (unit/month)	2,990	2,970	3,047	2,907	2,885	2,858	2,856	2,862	2,848	2,900	3,103	2,924
Weight (%)	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3
$Q_{95}$ (unit)	1,443
$r_{95}$ (without unit)	2.51	2.53	2.47	2.59	2.61	2.63	2.63	2.63	2.64	2.59	2.42	2.57
$S(r_{95})$ (unit shortage/cycle)	525	528	515	540	544	549	549	548	551	541	505	536
$T{C}_{95}$ (USD/year)	347.44
$Y_{t_5}$ (unit/month)	2,198	2,178	2,256	2,115	2,094	2,066	2,064	2,071	2,056	2,108	2,312	2,132
Weight (%)	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3	8.3
$Q_5$ (unit)	1,077
$r_5$ (without unit)	1.89	1.91	1.84	1.97	1.99	2.02	2.02	2.01	2.03	1.98	1.80	1.95
$S(k_5)$(unit shortage/cycle)	397	400	387	412	417	422	423	421	424	414	377	409
$T{C}_5$ (USD/year)	258.3

4. Discussion, conclusions, limitations and future research

The approach of modeling the DPUT and LTD using a PDF Kernel estimation is novel and results in a performance of higher precision inventory models. That is to say, this approach leads to lower total costs, quantities to be requested from the supplier and possible shortages that can be caused by facing a random demand. The use of SP allows to take advantage of a generation of scenarios that acts as a replica of the possible input elements for the demand, where these become more adjusted to the reality when occupying the Kernel estimation of the PDF of DPUT and LTD. At present, the software available for data analysis implements this type of estimation facilitating this task for the decision makers of the area. This allows the possibility of working directly with the accumulated densities and probabilities of demand in an empirical and more realistic way with regard to the data available.

A current limitation of the proposed methodology is found in samples of intermittent demand data, because the PDF Kernel estimation does not consider these values as part of its estimation. In this respect the zero-inflated or zero-adjusted approach could be considered to deal with this type of demand data, where it is possible to construct mix distributions for the PDF Kernel estimation as well as in the empirical CDF of this type of data. This opens a field of investigation of sourcing operations when facing this type of scenarios.

Additional information

Funding

This research was partially funded by “Grants-CONICYT” of the National Commission for Scientific and Technological Research (CONICYT) government of Chile and Founding CIDI UV-4.

Notes on contributors

Fernando Rojas

Fernando Rojas is Chemical-pharmaceutical of University of Valparaiso, Chile; Master in Management Science at the University Adolfo Iba˜nez, Chile, and PhD of Management Science candidate at the same university. Currently serves as an adjunct professor at the School of Nutrition and Dietetics, that belongs to the Faculty of Pharmacy, University of Valparaiso, Chile, and is research associated to the Micro-Bio Innovation Center from the same school. His research interests is operations research linked to optimal supply decisions, especially in the area of food service.