A branch-and-bound method to minimize the makespan in a permutation flow shop with blocking and setup times

Abstract

This work addresses the minimization of the makespan criterion for the permutation flow shop problem with blocking, sequence and machine dependent setup times, which is a problem that has not been studied in previous works. Many papers considered the problem with an unlimited buffer or with the setup time embedded in the processing time of the job. However, considering an unlimited buffer may not represent reality in many industries. Additionally, separating the setup time from the processing time allows greater flexibility for production scheduling, thus allowing better time usage and a reduction in the makespan. Two structural properties of the problem are presented: an upper bound for the machine idle time and a lower bound for the machine blocking time. Using these properties, four lower bounds for the makespan are proposed (LB_TN1, LB_TN2, LB_TN3 and LB_TN4). Each of the lower bounds was used in a branch-and-bound algorithm and then compared to each other using a database containing 540 problems. A MILP model is also presented and compared with the best of the branch-and-bound models using a second database that consists of 80 different problems. Computational tests are presented, and the comparisons indicate that the proposed lower bounds are promising.

Keywords:

• flow shop
• blocking
• zero buffer
• setup times
• makespan
• lower bound
• branch–and-bound
• MILP

Public Interest Statement

With the advance of the Toyota production system and the lean manufacturing the study of optimization methods to guarantee the best usage of all resources of the system is becoming more and more important. However, optimization methods are not often explored in industries, one of the reasons for that is that the ideal environment assumed in theoretical problems are not sufficiently similar to those found in real industries. This paper considers a very common problem found in industries, which is a production line with limited space for buffering in process material and setup times between products, a problem that was never studied before in any other work. In this paper some optimization methods are proposed for the problem and they are compared between then, showing that the presented methods are very promising.

1. Introduction

This paper studies the scheduling problem in a permutation flow shop with zero buffer and sequence and machine dependent setup environment, a problem that has not yet been explored in the literature. In the problem, there are n jobs that must be processed by m machines, and all jobs must be processed in all machines in the same flow. The permutation constraint indicates that the process sequence of the jobs must be the same for all machines. In this paper, the setup time is separated from the process time (i.e. anticipatory setup), allowing a machine to be prepared to initiate the process of a job before the previous machine has finished the process of this job. That is, whenever a machine is not processing any job, it is possible to prepare the machine for the upcoming job in advance, regardless of whether the upcoming job is still being processed by previous machines. This ensures a better flexibility for the scheduling but is only possible if the processed part is not necessary for the setup. The setup time depends on the sequence of the jobs and the machine. In other words, there is a different setup time for each pair of jobs in each machine. In an environment with blocking, there are limited buffers in between the machines; in this paper, we consider a zero buffer constraint. In other words, if machine k finishes the processing of job j and machine k + 1 is not able to receive the job (because it is still processing job j − 1 or is still being set up), the job remains in machine k, thereby blocking it. In this case, machine k is unable to receive the next job of the sequence.

With the advancement of the Toyota production system and lean manufacturing, the buffer size between work stations is becoming increasingly limited. Therefore, studying the limited buffer constraint is becoming more important (Ronconi, 2005). The flow shop problem with zero buffer can be used to model any flow shop problem with a limited buffer because a unit capacity buffer can be represented by a machine with zero processing time for all jobs (McCormick, Pinedo, Shenker, & Wolf, 1989).

The flow shop with zero buffer and dependent setup time is an underexplored problem. Therefore, a bibliographic review of the flow shop with a blocking problem is presented first. This bibliographic review considers the few works that examine a flow shop with blocking and sequence dependent setup time problem, both with the objective of minimizing the makespan.

Among the most important and pioneering works is that of Gilmore and Gomory (1964). The authors solved the one- and two-machine problems by using a one state-variable with 0(N²) simple steps. Reddi and Ramamoorthy (1972) showed that the traditional flow shop problem with only two machines (two work stations) and the blocking constraint can be transformed into a special case of the travelling salesman problem.

Papadimitriou and Kanellakis (1980) proved that the problem with a limited buffer of only one unit between machines is NP-HARD. Hall and Sriskandarajah (1996), based on the results obtained by Papadimitriou and Kanellakis (1980), showed that the traditional flow shop with three work stations and a blocking problem is strongly NP-complete. In the same paper, the authors related the main works developed in the literature.

McCormick et al. (1989) presented a heuristic method denominated Profile Fitting (PF), in which jobs are scheduled in such a way that the idle and blocking times of the machines are minimized.

Leisten (1990) presented two heuristic methods for permutation and non-permutation flow shop problems with limited buffers. The performance measures of the methods used were the maximum use of the buffers and the minimum blocking times. The computational experiments showed that the adaptation of the traditional Nawaz-Enscore-Ham (NEH) created by Nawaz, Enscore, and Ham (1983), which was originally developed for the unlimited buffer problem, had better performance than did the proposed methods.

Ronconi (2004) addressed the zero buffer problem with the objective of minimizing the makespan. A constructive heuristic method that uses specific characteristics of the problem is presented. The new method, combined with some of the best methods in the literature, was compared to the adapted version of the NEH and presented better results.

Pan and Wang (2012) considered the flow shop with blocking problem, with the objective of minimizing the makespan. Initially, the authors presented two constructive heuristic methods, named Weighted Profile Fitting (wPF) and (PW), both of which were based on the Profile Fitting (PF) procedure presented by McCormick et al. (1989). They proposed three II phase heuristics (according to Framinan, Gupta, & Leisten, 2004 classification), named PF-NEH, wPF-NEH and PW-NEH, by combining the previous methods with the classic NEH. Finally, using a local search (LS) method based on job insertion, three III phase heuristics (according to Framinan et al., 2004 classification) were developed: PF-NED/LS, wPF-NEH/LS and PW-NEH/LS. The proposed methods were evaluated and compared with other existing methods using the database provided by Taillard (1993). The experiments showed that the proposed methods outperformed all other methods previously presented in the literature. In addition, the III phase methods significantly improved the results obtained by the constructive methods. The computational tests provided better solutions for 17 large problems from the database.

Ronconi and Armentano (2001) presented branch-and-bound algorithms for the flow shop with blocking problem. It proposed a lower bound for the departure time of the jobs. Thereafter, lower bounds for the total tardiness and makespan were developed.

Pranzo (2004) showed that the Batch scheduling in a two-machine flow shop with limited buffer and sequence independent setup times and removal times can be formulated as a special case of the TSP. It can be solved in polynomial time, depending on the batch size.

Subsequently, Ronconi (2005) presented a branch-and-bound algorithm that used new lower bounds, which advantageously used the nature and structure of the blocking problem. The new method outperformed the method proposed by Ronconi and Armentano (2001) that was adapted for the problem.

Moslehi and Khorasanian (2013) proposed two mixed integer linear programming (MILP), an initial upper bound generator and some lower bounds and dominance rules to be used in a branch-and-bound algorithm to minimize the total completion time in a permutation flow shop problem with zero buffer. The MILP models had some trouble with solving instances with sizes (n, m) equal to (16, 10), (18, 7), and (18, 10). The branch-and-bound model was able to solve 30 of the 120 instances from the Taillard (1993) database.

Chen, Zhou, Li, and Xu (2014) studied a two-stage flow shop problem with batch processing machines, arbitrary release dates and zero buffer, with the objective of minimizing the makespan. A MILP model for the problem was proposed, as was a Hybrid Discrete Differential Evolution (HDDE) algorithm. The proposed algorithm HDDE was compared to the MILP model, a Hybrid Simulated Annealing (HSA) and a Hybrid Genetic Algorithm (HGA). The HDDE algorithm outperformed the other methods in terms of solution quality, robustness, and computational time.

The first work to address the flow shop problem with limited buffer and sequence and machine dependent setup found in the literature is that by Norman (1999). The evaluation criterion used in this work was the minimum makespan. A Tabu search and two adapted constructive heuristics methods (NEH and PF) were presented to solve the problem. A greedy improvement procedure was added to the constructive heuristics. Overall, 900 problems were generated to evaluate the proposed methods, which had varying setup times, buffer sizes and numbers of jobs and machines.

Maleki-Darounkolaei, Modiri, Tavakkoli-Moghaddam, and Seyyedi (2012) developed a MILP model and a Simulated Annealing (SA) for the flow shop problem with three work stations, a sequence-dependent setup time only in the first stage and a blocking time between each stage, with two objectives: to minimize the makespan and the flow time. Problems with more than nine jobs were not solved due to the elevated computational time.

It is important to note that even though two works addressed the problem of blocking with sequence-dependent setup times, no work was found in the literature that considered the zero buffer among with the sequence and machine dependent setup time in all machines. Therefore, there are no existing methods to solve this problem. In this paper, a branch-and-bound (B&B) algorithm is presented to minimize the makespan in a permutation flow shop environment with zero buffer and sequence and machine dependent setup, with m machines and n jobs. An upper bound for the idle time of the machines and a lower bound and the blocking time of the machines are presented in this work. Then, four lower bounds for the makespan, based on these structural properties of the problem, are presented. The efficiency of the branch-and-bound and of the lower bounds for the makespan are tested using several problems that vary in number of jobs and machines. A MILP model is then presented for the problem, and its efficiency is compared with the efficiency of the best of the lower bound models.

This paper is structured as follows. The calculus used to calculate the makespan is presented in Section 2. Two structural properties of the problem (an upper bound for the machine idle time and a lower bound for the blocking time) are presented in Section 3. The branch-and-bound algorithm and the four lower bounds for the makespan are presented in Section 4. The MILP model for the problem is presented in Section 5. The computational tests for the lower bound models and their results are presented in Section 6. The computational tests for the MILP and the best lower bound models and their results are presented in Section 7. Finally, conclusions are presented in Section 8.

2. Makespan calculus

In this section, we describe how to calculate the makespan in a permutation flow shop environment with blocking and sequence and machine dependent setup time. Let $\mathit{\sigma }=\left\{1,2,\dots i,j,\dots m\right\}$ be an arbitrary sequence of jobs, $k=\left\{1,2,\dots ,m\right\}$ be the sequence of available machines, i be the job that directly precedes job j in the sequence, P_jk be the processing time of the jth job in sequence in machine k, S_ijk be the setup time of machine k between the ith and jth jobs in the sequence, S_01k be the setup time of machine k before processing the first job in the sequence, R_jk be the completion time of the setup of machine k to the jth job in the sequence, and C_jk be the departure time of the jth job in the sequence in machine k. The makespan is then calculated by the following:(1) $$R_{1k}=S_{01k}\left(k=1,\dots ,m\right)$$(1) (2) $$C_{j1}=\text{max}\left(R_{j2},R_{j1}+P_{j1}\right)\left(j=1,\dots ,n\right)$$(2) (3) $$C_{jk}=\text{max}\left(R_{j,k+1},C_{j,k-1}+P_{jk}\right)(j=1,\dots ,n);(k=2,\dots ,m-1)$$(3) (4) $$C_{jm}=C_{j,m-1}+P_{jm}\left(j=1,\dots ,n\right)$$(4) (5) $$R_{jk}=C_{i,k}+S_{ijk}\left(j=2,\dots ,n\right);\left(k=1,\dots ,m\right)$$(5)

Initially, the setup completion times of the machines for the first job in the sequence are calculated by Equation (1). Next, the departure times of the first job in all machines are calculated by Equations (2), (3), and (4). Then, Equation (5) is used to calculate the setup completion time of all machines for the following job. Equations (2), (3), and (4) are used again to calculate the departure times of the following job in all machines. The makespan (C_max) is equal to the departure time of the last job in sequence in the last machine. In other words, C_max = C_nm.

3. An important structural property of the problem

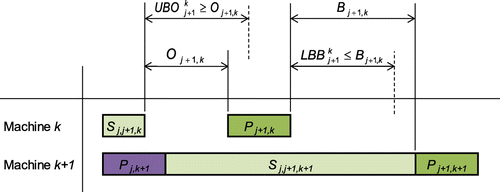
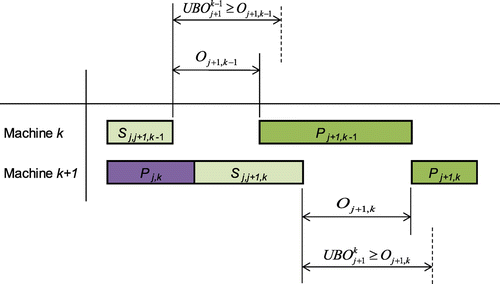
In the permutation flow shop problem with blocking and sequence and machine dependent setup time with n > 2 and m > 2, let B_j+1,k be the blocking time between the successive processes of the (j + 1)th job in the sequence in machines k and k + 1. Therefore, for any j, ${\text{LBB}}_{j+1}^k$ is a lower bound for B_j+1,k, given by(6) $$LB{B}_{j+1}^k=max\left(0,\left(P_{j,k+1}+S_{j,j+1,k+1}\right)-\left(UB{O}_{j+1}^k+S_{j,j+1,k}+P_{j+1,k}\right)\right)$$(6) (7) $$\text{with}LB{B}_{j+1}^m=0$$(7)

where $UB{O}_{j+1}^k$ is an upper bound for O_j+1,k. In other words, the gap between the completion time of the setup for the (j + 1)-th job in the sequence and its start time in machine k is given by(8) $$UB{O}_{j+1}^k=max\left(0,\left(UB{O}_{j+1}^{k-1}+S_{j,j+1,k-1}+P_{j+1,k-1}\right)-\left(P_{jk}+S_{j,j+1,k}\right)\right)$$(8) (9) $$\text{with}UB{O}_{j+1}^1=0$$(9)

The properties LBB and UBO are illustrated in Figures 1 and 2, respectively.

Figure 1. Property ${\text{LBB}}_{j+1}^k$.

Figure 2 Property ${\text{UBO}}_{j+1}^k$.

4. The branch-and-bound algorithm

The branch-and-bound algorithm (B&B) replaces the original problem for a set of sub problems. According to Ignall and Schrage (1965), the original problem is rewritten in a solution tree, in which each node represents a lower bound of the objective function. The B&B algorithm used was proposed by Kim (1995), and each node represents the partial sequence of the final result. This partial sequence is named |PS|, and the set of jobs that are not part of that partial sequence is named |NPS|.

When a node is branched, one or more partial sequences (nodes) are created by adding up a new job from |NPS| to the partial sequence associated with the branched node. A lower bound is calculated for the makespan for each node that was created. The selection of the node to be branched was used by Ronconi (2005) and is made by the depth first rule, where the node with the highest number of jobs in the partial sequence is selected. In case of a tie, the node with the lowest lower bound for the makespan is selected. The node selection rule was selected because of the successful application of the rule in the permutation flow shop with blocking problem by Ronconi (2005). The pseudo code of the algorithm is presented below.

B&B algorithm

 1. Initiation (creating root node)

  UB → Initial Upper Bound (calculated with any solution method);

  $\left|PS\right|=\left\{\mathrm{\varnothing }\right\}$;

  $\left|NPS\right|=\left\{1,2,3,\dots ,n\right\}$;

  Nodes = 0 (number of nodes that will be branched);

 2. First level branching step

  For Node = 1:n do;

  ${\left|PS\right|}_{Node}=\left\{j\right\}$;

  ${\left|NPS\right|}_{Node}=\left|NPS\right|-{\left|PS\right|}_{Node}$;

  LB_Node = Lower Bound for ${\left|PS\right|}_{Node}$;

  If LB_Node < UB;

  Nodes = Nodes + 1;

  End if;

  End for;

 3. Other levels branching step

  While Nodes > 0 do;

  Nodes = 0;

  For Node = 1:Nodes do;

  For $j\in \left|NP{S}_{Node}\right|$ do;

  ${\left|PS\right|}_{Node}={\left|PS\right|}_{Node}+\left\{j\right\}$;

  $\left|NP{S}_{Node}\right|=\left|NP{S}_{Node}\right|-\left\{j\right\}$;

  LB_Node =  Lower Bound for ${\left|PS\right|}_{Node}$;

  If LB_Node < UB;

  If Level < n;

  Nodes = Nodes + 1;

  Else;

  LB_Node = UB;

  End if;

  End if;

  End for;

  End while;

4.1. Lower bound for the makespan

Considering a partial sequence |PS|, the lower bound for the makespan is the minimum value of the departure time of the last job from $\left|\text{NPS}\right|$ in the last machine (m). Four lower bounds for the makespan were developed for the Fm|prmu, S_ijk, block|C_max problem, considering the lower bound for the blocking (${\text{LBB}}_{ij}^k$). Let PS be the last job in the partial sequence and $\left|NPS\right|$ be the set of jobs that are not part of the partial sequence. Let S_S_i,j,k be the sum of the minimum setup times of the jobs that are not part of the partial sequence in machine k, and let S_LBB_i,j,k be the sum of the minimum lower bound for the blocking time of the jobs that are not part of the partial sequence in machine k. S_S_i,j,k and S_LBB_i,j,k are given by Equations (10) and (11).(10) $${S\_S}_{i,j,k}=\sum _{i\in \left|NPS\right|\cup PS}\left(min\left(S_{i,\left|NPS\right|,k}\right)\right)-max\left(min\left(S_{\left|NPS\right|,\left|NPS\right|,k}\right)\right)$$(10) (11) $$S\_LB{B}_{i,j,k}=\sum _{i\in \left|NPS\right|{\cup }^{}PS}\left(min\left(LB{B}_{i,\left|NPS\right|}^k\right)\right)-max\left(min\left(LB{B}_{\left|NPS\right|,\left|NPS\right|}^k\right)\right)\forall k=1,\dots ,m-1$$(11)

The first part of Equation (10) sums the minimum setup times for all jobs that are not part of the partial sequence. The second part of the equation removes the setup time of the last job in the sequence from S_S_i,j,k, as the last job of the sequence is going to be determined in the lower bound equation. A similar method is used to calculate the value of S_LBB_i,j,k in Equation (11). Both S_Sn_i,j,k and S_LBBn_i,j,k are used to calculate LB_TN1, LB_TN2, and LB_TN4.

Let LW be the processing time summed by the value of the lower bound of the blocking time of the last job in the sequence. The last job in the sequence is the one with the smallest value for the sum of the processing times and the lower bound of the blocking. In other words,(12) $$LW(k)=\text{min}\left(\sum _{q=k+1}^m\left({\text{P}}_{\left|\text{NPS}\right|,\text{q}}\right)+min\left(\sum _{q=k+1}^m\left({\text{LBB}}_{\left|\text{NPS}\right|,|\text{NPS}|}^{\text{q}}\right)\right)\right)\forall k=1,\dots ,m-1$$(12)

The last job in the sequence is removed from $\left|NPS\right|$, and the new set of jobs is named $\left|NPSn\right|$. With this new set, it is possible to calculate S_Sn_i,j,k, which is the sum of the minimum setup times of the jobs that are not part of the partial sequence and are not the last job in the sequence in machine k. S_LBBn_i,j,k is the sum of the minimum lower bound for the blocking time of the jobs that are not part of the partial sequence or the last job in the sequence in machine k. We use the following equations:(13) $$S\_S{n}_{i,j,k}=\sum _{i\in |NPSn|{\cup }^{}PS}\left(min\left(S_{i,\left|NPS\right|,k}\right)\right)-max\left(min\left(S_{\left|NPSn\right|,\left|NPS\right|,k}\right)\right)\forall k=1,\dots ,m-1$$(13)

(14) $$S\_LBB{n}_{i,j,k}=\sum _{i\in |NPSn|{\cup }^{}PS}\left(min\left(LB{B}_{i,|NPS|}^k\right)\right)-max\left(min\left(LB{B}_{|NPSn|,|NPS|}^k\right)\right)\forall k=1,\dots ,m-1$$(14)

The first part of Equation (13) sums the minimum setup times for all jobs that are not part of the partial sequence. The second part of the equation removes the setup time of the last job in the sequence from S_Sn_i,j,k, as the last job of the sequence is already identified by LW(k). A similar method is used to calculate the value of S_LBBn_i,j,k in Equation (14). Both S_Sn_i,j,k and S_LBBn_i,j,k are used only to calculate LB_TN3.

The lower bounds were named LB_TN1, LB_TN2, LB_TN3 and LB_TN4 and are obtained by the following equations:(15) $$L{B}_{TN1}\left(k\right)=C_{\text{PS},k}+S\_S_{i,j,k}+\sum _{h\in \left|NPS\right|}\left(P_{hk}\right)+\text{S}\_{\text{LBB}}_{i,j}^k+mi{n}_{g\in \left|NPS\right|}\left(\sum _{q=k+1}^m\left(P_{g,q}+min\left(LB{B}_{g,g}^q\right)\right)\right)\forall k=1,\dots ,m-1$$(15)

(16) $$L{B}_{TN1}\left(m\right)=C_{\text{PS},m}+S\_S_{i,j,m}+\sum _{h\in \left|NPS\right|}\left(P_{hm}\right)$$(16) (17) $$L{B}_{TN1}=ma{x}_{1\le k\le m}\left(L{B}_{TN1}\left(k\right)\right)$$(17) (18) $$L{B}_{TN2}\left(k\right)=C_{PS,k}+S\_S_{i,j,k}+\sum _{h\in \left|NPS\right|}\left(P_{hk}\right)+\text{S}\_{\text{LBB}}_{i,j}^k+mi{n}_{g\in \left|NPS\right|}\left(\sum _{q=k+1}^m\left(P_{g,q}\right)+\text{min}\left(\sum _{q=k+1}^m\left(LB{B}_{g,g}^q\right)\right)\right)\forall k=1,\dots ,m-1$$(18)

(19) $$L{B}_{TN2}\left(m\right)=C_{\text{PS},m}+S\_S_{i,j,m}+\sum _{h\in \left|NPS\right|}\left(P_{hm}\right)$$(19) (20) $$L{B}_{TN2}=ma{x}_{1\le k\le m}\left(L{B}_{TN2}\left(k\right)\right)$$(20) (21) $$L{B}_{TN3}\left(k\right)=C_{\text{PS},k}+S\_S{n}_{i,j,k}+\sum _{h\in \left|NPS\right|}\left(P_{hk}\right)+\text{S}\_{\text{LBBn}}_{i,j}^k+LW\forall k=1,\dots ,m-1$$(21)

(22) $$L{B}_{TN3}\left(m\right)=C_{\text{PS},m}+S\_S_{i,j,m}+\sum _{h\in \left|NPS\right|}\left(P_{hm}\right)$$(22) (23) $$L{B}_{TN3}=ma{x}_{1\le k\le m}\left(L{B}_{TN3}\left(k\right)\right)$$(23) (24) $$L{B}_{TN4}\left(k\right)=C_{PS,k}+S\_S_{i,j,k}+\sum _{h\in \left|NPS\right|}\left(P_{hk}\right)+\text{S}\_{\text{LBB}}_{i,j}^k+\sum _{q=k+1}^m\left(mi{n}_{g\in \left|NPS\right|}\left(P_{g,q}\right)+mi{n}_{g\in \left|NPS\right|}\left(LB{B}_{g,g}^q\right)\right)\forall k=1,\dots ,m-1$$(24)

(25) $$L{B}_{TN4}\left(m\right)=C_{\text{PS},m}+S\_S_{i,j,m}+\sum _{h\in \left|NPS\right|}\left(P_{hm}\right)$$(25) (26) $$L{B}_{TN4}=ma{x}_{1\le k\le m}\left(L{B}_{TN4}\left(k\right)\right)$$(26)

The first part of Equations (15), (18), (21), and (24) sum the departure time of the last job in the partial sequence (CP_S,k), the sum of the setup times of all jobs in $\left|NPS\right|$ (S_S_i,j,k), the sum of the processing times of all jobs in $\left|NPS\right|$ ($\sum _{h\in \left|NPS\right|}\left(P_{hk}\right)$), and the sum of the lower bound for the blocking times of all jobs in $\left|NPS\right|$ ($\text{S}\_{\text{LBB}}_{i,j}^k$), respectively. The second part of the equations tries to identify the last job in the sequence and sum the processing times and lower bound for the blocking times in all subsequent machines.

In Equation (15), the last job in the sequence is the job with the minimum sum of the processing times and the minimum values of the lower bound for the blocking times in all further machines. In Equation (18), the last job in the sequence is the job that has the minimum value for the sum of all processing times in the subsequent machines added to the minimum value of the sum of the lower bound for the blocking times in all subsequent machines. In Equation (21), the last job in the sequence is job LW, as calculated by Equation (12). Finally, in Equation (24), the departure time of the last job in the sequence is calculated by summing the minimum value of the processing time, added by the value of the minimum lower bound for the blocking time in all subsequent machines.

In Equations (16), (19), (22), and (25), the departure time is calculated by summing the departure time of the last job in the partial sequence (CP_S,k), the sum of the setup times of all jobs in $\left|NPS\right|$ (S_S_i,j,k), and the sum of the processing times of all jobs in $\left|NPS\right|$ ($\sum _{h\in \left|NPS\right|}\left(P_{hk}\right)$). The lower bound for the blocking is not considered in these equations because there is no blocking in the last machine.

Equations (17), (20), (23), and (26) determine that the lower bound for that partial sequence is equal to the maximum value of the lower bounds of all machines for that partial sequence.

5. MILP model

Mixed Integer Linear Programming (MILP) models can be used to find the optimum solution for small and medium problems. With the advances in computation, the number of studies in this field has grown considerably (Ronconi & Birgin, 2012). However, the use of MILP models to optimize scheduling problems in permutation flow shop with blocking environment is not yet widely reported due to the high computational time.

In this paper, a MILP model is presented for the problem. The model is named TNZBS1, and the notations used for it are as follows:

n Number of jobs;

m Number of machines;

P_jk Processing time of job j in machine k;

S_ijk Setup time of machine k between the departure time of job i and the starting time of job j;

R_σk Completion time of the setup of machine k to the σth job in the sequence;

C_σk Departure time of the σth job in the sequence at machine k;

x_jσ  $\left\{\begin{array}{cc}1\hfill & \text{If job}j\text{is the}\mathit{\sigma }\text{th job in the sequence}\hfill \\ 0\hfill & \text{otherwise;}\hfill \end{array}\right.$

y_ijσ $\left\{\begin{array}{cc}1\hfill & \text{If job}i\text{directly precedes job}j,\text{which is the}\mathit{\sigma }\text{th job in the sequence}\hfill \\ 0\hfill & \text{otherwise;}\hfill \end{array}\right.$

5.1. Model TNZBS1

(27) $$\text{Minimize:}{C}_{max}=C_{nm}$$(27) (28) $$\sum _{j=1}^n{x}_{j\mathit{\sigma }}=1\forall \mathit{\sigma }=1,\dots ,n$$(28) (29) $$\sum _{\mathit{\sigma }=1}^n{x}_{j\mathit{\sigma }}=1\forall j=1,\dots ,n$$(29) (30) $$y_{ij\mathit{\sigma }}\ge x_{j\mathit{\sigma }}+x_{i,\mathit{\sigma }-1}-1\forall i=1,\dots ,n;j=1,\dots ,n;\mathit{\sigma }=1,\dots ,n;i\ne j$$(30) (31) $$\sum _{i=1}^n\sum _{j=1}^n{y}_{ij\mathit{\sigma }}=1\forall \mathit{\sigma }=2,\dots ,n$$(31) (32) $$\sum _{i=1}^n\sum _{j=1}^n{y}_{ij1}=0$$(32) (33) $$R_{1k}=\sum _{i=1}^n\sum _{j=1}{S}_{ijk}\ast x_{j1}\forall k=1,\dots ,m$$(33) (34) $$R_{\mathit{\sigma }k}=C_{\mathit{\sigma }-1,k}+\sum _{i=1}^n\sum _{j\ne i}{S}_{ijk}\ast y_{ij\mathit{\sigma }}\forall \mathit{\sigma }=2,\dots ,n;k=1,\dots ,m$$(34) (35) $$C_{\mathit{\sigma }k}\ge R_{\mathit{\sigma },k+1}\forall \mathit{\sigma }=1,\dots ,n;k=1,\dots ,m-1$$(35) (36) $$C_{\mathit{\sigma }1}\ge R_{\mathit{\sigma }1}+\sum _{j=1}^n{P}_{j1}\ast x_{j\mathit{\sigma }}\forall \mathit{\sigma }=1,\dots ,n$$(36) (37) $$C_{\mathit{\sigma }k}\ge C_{\mathit{\sigma },k-1}+\sum _{j=1}^n{P}_{jk}\ast x_{j\mathit{\sigma }}\forall \mathit{\sigma }=1,\dots ,n;k=2,\dots ,m$$(37) (38) $$C_{\mathit{\sigma }k},R_{\mathit{\sigma }k}\ge 0\text{and integer}\forall \mathit{\sigma }=1,\dots ,n;k=1,\dots ,m$$(38)

(39) $$x_{j\mathit{\sigma }},y_{ij\mathit{\sigma }}\in \left\{0,1\right\}\forall i=1,\dots ,n;j=1,\dots ,n;\mathit{\sigma }=1,\dots ,n$$(39)

Constraints (28) and (29) guarantee that each job will be allocated to exactly one position in the sequence and that each position in the sequence has exactly one job associated with it. Constraints (31) and (30) ensure that each job will have exactly one job that precedes it in the sequence. From constraint (30), if job j is not the σ-th job in the sequence and job i is not the (σ − 1)-th job in the sequence, y_ijσ will be greater than or equal to −1. If job j is the σ-th job in the sequence and job i does not directly precede job j in the sequence, y_ijσ will be greater than or equal to zero. Finally, if job j is the σ-th job in the sequence and job i directly precedes job j in the sequence, y_ijσ will be greater than or equal to one. Constraint (31) grants that only one y_ijσ will be equal to one for each position (σ) of the sequence. Constraint (32) guarantees that no job will precede the first job in the sequence. Constraints (33) and (34) are used to calculate the completion time of the setup of the machines. Constraint (33) is applied just to the first job in the sequence, whose completion time of the setup depends only of the release date (represented by S_jjk). In contrast, constraint (34) is the general formula for the completion time of the setup of the machines. In other words, the departure time of the (σ − 1)-th job in the sequence summed to the setup time of machine k between the processing of the (σ − 1)-th and σ-th jobs in the sequence. Constraints (35–37) are used to calculate the departure time of the jobs in the machines, considering the possibility of blocking. Constraint (35) is applied to all jobs in all machines except the last one and is used to verify the occurrence of blocking. If C_σk > R_σ,k+1, then blocks have not occurred in the machine, and constraints (36) or (37) will determine the value of C_σk. If C_σk = R_σ,k+1, then blocking has occurred, and its value is greater than zero. Constraint (36) is applied to all the jobs only in the first machine, where because there is no idle time, the starting time of the processing of all jobs is equal to the completion time of the setup of the machine. For all other machines, constraint (37) is applied, which determines the starting time of the processing of all jobs as equal to its departure time in the preceding machine.

6. Computational results for the branch-and-bound algorithms

The B&B algorithm was applied to 540 problems. Processing time data were proposed by Ronconi (2005). The problems vary in the number of jobs and machines and are classified into 27 different classes, each with 20 problems. In this database, the processing times are uniformly distributed between 1 and 99. The database provided by Ronconi (2005) does not include setup times. Therefore, the setup times for the machines were generated for these tests using the same method, where the values were uniformly distributed between 1 and 99. By doing so, it is possible that the setup time might be lower than, equal to, or higher than the processing time without a very large discrepancy in the values. Much lower values of setup times might generate problems where there is no blocking, and much higher values of the setup time might impose too many blocking occurrences. All lower bounds and branch-and-bound algorithms were written in C language. The experiments were performed on an Intel® core i7 3610QM with 2.3 GHz, 8 Gb DDR3 RAM and the Windows 7 operating system. The initial solution for the problems was calculated using the NEH algorithm adapted to the problem. The computational time for each problem was limited to 3,600 s.

To compare each class of problems, the mean computational time in seconds and the mean number of nodes were calculated. Table 1 presents the obtained results of the problems that were solved within the established computational time, using the four lower bounds.

Table 1. Performance of the branch-and-bound algorithms

Size		B&BTN1		B&BTN2		B&BTN3		B&BTN4
n	m	CPU time (sec)	Number of nodes	CPU time (sec)	Number of nodes	CPU time (sec)	Number of nodes	CPU time (sec)	Number of nodes
10	2	6.48	41,633.85	5.91	41,633.85	17.25	50,223.30	6.49	41,633.85
10	3	22.51	104,918.90	20.00	104,918.90	76.23	127,231.35	23.47	109,484.15
10	4	52.24	194,619.30	45.29	193,334.70	202.77	235,896.20	58.66	218,670.85
10	5	64.81	202,104.35	54.93	199,743.05	265.87	249,201.45	74.72	232,867.15
10	7	127.87	302,099.05	105.80	295,858.65	574.30	387,785.70	161.24	380,684.20
10	10	164.93	284,526.60	129.95	270,314.60	691.52	330,139.70	198.64	344,718.40
12	2	91.21	572,712.55	83.32	572,712.55	229.24	659,327.55	91.11	572,712.55
12	3*	423.18	1,903,380.06	376.59	1,903,380.06	1439.92	2,345,772.67	456.63	2,056,967.72
12	4*	727.54	2,648,836.14	629.66	2,618,464.14	2800.96	3,205,695.29	898.19	3,248,940.57
12	5*	785.60	2,389,311.00	660.51	2,337,803.00	2793.43	2,568,676.33	870.45	2,651,519.67
14	2*	594.16	3,890,057.80	542.23	3,890,057.80	1559.40	4,683,547.90	594.78	3,890,057.80
Mean		278.23	1,139,473	241.29	1,129,838	968.2627	1,349,409	312.2164	1,249,842

Note: Bold values are the minimum value of each category of problems.

* Mean computational time and mean number of nodes of the problems that were solved by all the lower bounds within the computational time of 3,600 s.

The classes of problems that are not shown in the table are those in which one or more lower bounds could not solve any of the problems within the computational time of 3,600 s. Therefore, the mean computational time and the mean number of nodes were not calculated for these classes. From Table 1, the best lower bound was LB_TN2, which solved all the problems while using fewer nodes and a shorter computational time.

After 3,600 s, the program stops and records the best result obtained so far. Therefore, to compare the methods, the mean relative deviation of the makespan and the number of unsolved problems for each class of problems were also computed for each lower bounds used. Table 2 shows the mean relative deviation of the makespan and the number of unsolved problems for each class of problems using each of the four proposed lower bounds.

Table 2. Mean relative deviation of the makespan and number of unsolved problems by the branch-and-bound algorithm

size		B&BTN1		B&BTN2		B&BTN3		B&BTN4
n	m	Mean relative deviation of the makespan	Number of unsolved problems	Mean relative deviation of the makespan	Number of unsolved problems	Mean relative deviation of the makespan	Number of unsolved problems	Mean relative deviation of the makespan	Number of unsolved problems
10	2	0.000%	0	0.000%	0	0.000%	0	0.000%	0
10	3	0.000%	0	0.000%	0	0.000%	0	0.000%	0
10	4	0.000%	0	0.000%	0	0.000%	0	0.000%	0
10	5	0.000%	0	0.000%	0	0.000%	0	0.000%	0
10	7	0.000%	0	0.000%	0	0.000%	0	0.000%	0
10	10	0.000%	0	0.000%	0	0.000%	0	0.000%	0
12	2	0.000%	0	0.000%	0	0.000%	0	0.000%	0
12	3	0.000%	0	0.000%	0	0.000%	2	0.000%	0
12	4	0.000%	0	0.000%	0	0.192%	13	0.000%	1
12	5	0.000%	4	0.000%	1	0.192%	17	0.000%	5
12	7	0.000%	8	0.000%	4	0.958%	20	0.000%	14
12	10	0.003%	17	0.003%	15	0.875%	20	0.395%	17
14	2	0.032%	5	0.032%	4	0.160%	10	0.032%	5
14	3	0.004%	18	0.004%	16	0.551%	20	0.004%	18
14	4	0.415%	20	0.242%	20	0.978%	20	0.444%	20
14	5	0.859%	20	0.735%	20	1.628%	20	0.855%	20
14	7	0.255%	20	0.191%	20	0.998%	20	1.009%	20
14	10	0.790%	20	0.542%	20	1.376%	20	1.276%	20
16	2	0.382%	16	0.220%	16	0.760%	20	0.382%	16
16	3	0.777%	20	0.773%	20	1.111%	20	0.921%	20
16	4	0.815%	20	0.729%	20	1.761%	20	1.470%	20
18	2	0.721%	20	0.721%	20	1.036%	20	0.721%	20
18	3	0.484%	20	0.484%	20	1.023%	20	0.272%	20
18	4	1.153%	20	1.090%	20	1.372%	20	1.061%	20
20	2	0.378%	20	0.378%	20	1.196%	20	0.378%	20
20	3	1.194%	20	1.167%	20	1.325%	20	0.805%	20
20	4	1.113%	20	1.095%	20	1.284%	20	1.361%	20
Total		9.375%	308	8.406%	296	18.776%	362	11.386%	316
Mean		0.347%	11.407	0.311%	10.963	0.695%	13.407	0.422%	11.704

Note: Bold values are the minimum value of each category of problems.

Each class of problems has 20 different problems, for a total of 540 problems. Having 20 unsolved problems in a class of problems means that the branch-and-bound algorithm using that lower bound was not able to find the optimal solution within the stated computational time for any of the problems in that class.

In Table 2, a mean relative deviation of the makespan of 0% means that that particular lower bound was able to achieve the best makespan in all 20 problems among all lower bounds compared in that specific class of problem. After 3,600 s, the branch-and-bound algorithm stopped running, and the best result obtained so far was taken as the best result obtained by that particular lower bound for that problem. A smaller value of the relative deviation of the makespan means that that particular lower bound was able to achieve the best (or close to best) makespan for most of the problems among all lower bounds that were compared in that specific class of problems.

As shown in Table 2, the lower bound LB_TN2 again gave the best results for most of the classes of problems. However, it can be noticed that the performance of the lower bound LB_TN4 improves as the number of jobs increases. A bigger problem database may be used to analyze the lower bound performances.

7. Computational results for the MILP model and the branch-and-bound algorithm

Due to the elevated computational time, the MILP model is recommended for small or medium sized classes of problems. Therefore, a new database was generated for these tests that was composed of 80 problems, which were classified into eight different classes of problems. Each class of problems varied in the number of jobs and machines, and each had 10 different problems. The processing and setup times were uniformly distributed between 1 and 99, as was made for the branch-and-bound tests. The MILP algorithm was programmed in GAMS software and solved using CPLEX 12. The lower bound used for the comparison was the LB_TN2, as it presented the best results for the problem. The branch-and-bound algorithm was again written in C language. The computational experiments were performed on a 2.3 GHz Inter® core i7 3610QM with 8 Gb DDR3 RAM memory and the Windows 7 operating system. The computational time was limited to 3,600 s to solve each problem using each of the models.

For comparison, we calculated the mean computational time (CPU time) in seconds. As the computational time was limited to 3,600 s, some models were unable to obtain the optimum result for some of the problems. Therefore, the mean relative deviation of the obtained results (makespan) and the number of unsolved problems were also calculated. The obtained results for the problems are presented in Table 3.

Table 3. Computational time and mean relative deviation of the makespan and number of unsolved problems by the branch-and-bound algorithm and the MILP model

Size		CPU Time (sec)		Number of unsolved problems		Mean relative deviation of the makespan
n	m	B&B	MILP	B&B	MILP	B&B	MILP
5	3	0.054609	0.1455	0	0	0.0000%	0.0000%
10	3	61.31284	213.107	0	0	0.0000%	0.0000%
10	7	249.5021	477.674	0	0	0.0000%	0.0000%
10	10	271.4882	453.3423	0	0	0.0000%	0.0000%
15	3	3600.002	3,600.022	10	10	0.3514%	0.8025%
15	7	3600.003	3,600.026	10	10	0.9361%	0.6603%
15	10	3600.003	3,600.054	10	10	1.5787%	0.3962%
20	3	3600.002	3,600.043	10	10	0.0000%	2.9399%
Total		14,982.37	15,544.41	40	40	2.8661%	4.7989%
Mean		1872.796	1943.052	5	5	0.3583%	0.5999%

Note: The minimum value of the mean relative deviation of the makespan of each category are presented in bold.

Each class of problems has 10 different problems, for a total of 80 problems. Having 10 unsolved problems in a class of problems means that the method was not able to find the optimal solution within the stated computational time for any of the problems in that class.

From Table 3, the B&B algorithm outperformed the MILP model in terms of both the computational time and the mean relative deviation of the makespan. However, for problems with 15 jobs and 7 and 10 machines, the MILP model presented better values for the mean relative deviation of the makespan. This indicates that the model converges to better results more quickly for problems with more machines. However, only a test with a bigger problem database could ensure that finding.

8. Conclusions

This paper considered a permutation flow shop problem with blocking and sequence and machine dependent setup times. Many papers considered the problem with an unlimited buffer (Ignall & Schrage, 1965; Nawaz et al., 1983) or the setup time embedded in the processing time of the job (Hall & Sriskandarajah, 1996; Leisten, 1990; McCormick et al., 1989; Pan & Wang, 2012; Papadimitriou & Kanellakis, 1980; Ronconi, 2004, 2005; Ronconi & Armentano, 2001; Ronconi & Birgin, 2012). Separating the setup time from the processing time allows greater flexibility for the production scheduling, thus allowing a better use of time and a reduction in the makespan. Only two works considered blocking and sequence-dependent setup times (Maleki-Darounkolaei et al., 2012; Norman, 1999). However, none considered the sequence and machine-dependent setup time and the zero buffer constraints in the same problem. Therefore, there are no existing methods to solve this problem.

Four lower bounds for the makespan that explore a structural property of the problem were proposed and demonstrated in this paper. The four lower bounds were then used in a branch-and-bound algorithm, and computational tests were performed. The numerical experiments indicate that the best lower bound was the LB_TN2, followed by LB_TN1, LB_TN4, and LB_TN3. In 100% of the studied problems, the lower bound LB_TN2 allowed the branch-and-bound to reach the optimum result for the problem by using fewer nodes than the other algorithms used, and it had a 75.08% smaller mean computational time compared to the less effective lower bound (LB_TN3). The lower bound LB_TN2 was also the one that solved most of the problems within the proposed limit computational time among all proposed lower bounds (18.23% fewer unsolved problems than the lower bound LB_TN3). For the problems in which the optimum result was not achieved within the computational time of 3,600 s, it was also the lower bound that obtained the best results (observed by the mean relative deviation of the makespan). However, it is important to note that the performance of the lower bound LB_TN4 improved as the number of jobs increased (as observed by the mean relative deviation of the makespan of the bigger classes). Therefore, a larger problem database may be used to validate that finding.

A MILP model was also proposed for the problem. The best lower bound (LB_TN2) was compared with the presented MILP model. A new database consisting of 80 problems that varied in the numbers of jobs and machines was created for this comparison. The number of unsolved problems was the same for both methods. However, the computational time required for the branch-and-bound algorithm to solve the problem was 3.616% shorter (50.893% if only problems in which “CPU time” was less than 3,600 s) than the computational time required for the MILP model. Additionally, the problems that were not solved within the computational time of 3,600 s had better results when solved by the branch-and-bound algorithm (on average, 40.275% lower than the results obtained by the MILP model). These results show the consistency of the proposed lower bounds for the branch-and-bound algorithm.

It is also important to notice (from Table 3) that the performance of the MILP model tends to improve relative to the branch-and-bound algorithm as the number of machines increases. However, the branch-and-bound model tends to improve in relation to the MILP model as the number of jobs increases. For a more accurate result, a larger database is required.

For future works, we propose developing a dominance rule for the branch-and-bound algorithm to reduce the number of nodes. Additionally, the use of heuristics other than NEH, such as MM (Ronconi, 2004), PF, or wPF (Pan & Wang, 2012), can be studied and adapted to the problem as an initial solution for the branch-and-bound. Some other MILP models can be studied and evaluated for their performance.

Funding

The authors acknowledge the partial research support of Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) – Brazil (projects 448161/2014-1, 308047/2014-1).

Additional information

Notes on contributors

Mauricio Iwama Takano

Mauricio Iwama Takano is an Assistant Professor in the Mechanical Engineering Department, Federal Technological University – Paraná, Brazil. He holds a PhD in Production Engineering at School of Engineering of São Carlos in the University of São Paulo, Brazil. His research interests include integrated process planning and scheduling, flexible job-shop scheduling and intelligent algorithm.

Marcelo Seido Nagano

Marcelo Seido Nagano is an Associate Professor at the School of Engineering of São Carlos in the University of São Paulo, Brazil, where is currently hold the position of Head of the Operations Research Group of the Production Engineering Department. Along with your teaching duties, your research interests refer to decision systems and models in industry and services, including a range of decisions related to the design and optimization of processes, production and planning and scheduling, as well as Knowledge Management and Innovation Management as a supporting infrastructure. In these areas, is carried out several research projects and produced a number of refereed publications.