Event-triggered non-cooperative distributed predictive control for dynamically coupled large-scale systems

Abstract

This paper proposes a strategy of event-triggered distributed predictive control (DPC) for large-scale systems with dynamic couplings. The event-triggering condition which only involves local information of the subsystems has been derived based on the input to state stability theory. In the propose scheme, all subsystems optimize with decoupled cost functions and constraints only when the event-triggering conditions are satisfied. The dynamic couplings as well as disturbance can be handled through a robustness constraint in the local optimization. In addition, a dual-mode control scheme is adopted to further save computation resources. Several sufficient conditions are developed to ensure the recursive feasibility and close-loop stability of event-triggered DPC. Finally, the effectiveness of the proposed approach is illustrated via four-tuck systems.

Keywords:

• large-scale systems
• distributed predictive control
• event-triggered control

Public Interest Statement

A class of complex large-scale system where each subsystem couples with some other subsystems is more and more common in the process control. Distributed predictive control (DPC) is an appropriate control method for controlling such large-scale systems due to its ability to handle the computational complexity, uncertainties, and hard constrains.

But the DPC method under time-triggered mechanism creates unnecessary waste of resources which is always limited in large-scale systems. To overcome this issue, this paper designs an event-triggered DPC strategy for large-scale systems with coupled dynamics to guarantee the robustness of the system under disturbance as well as reduce the complexity and resources of the systems.

1. Introduction

With the development of information science and technology, a class of complex large-scale control system where each subsystem interacts with some other subsystems by their states and/or inputs has recently become an active research area in control theory, such as chemical systems, transportation systems, and smart grid systems (Real, Arce, & Bordons, 2014; Zhang & Liu, 2014; Zhang, Zhang, & Wang, 2013).

Distributed predictive control (DPC) is usually the most appropriate control method for controlling such large-scale systems and becomes more popular due to its ability to handle the uncertainties and hard constrains in the various practical applications of the process industry (Mayne, 2014; Zou, Lam, Niu, & Li, 2015). For weakly dynamic coupled systems, a robust DPC strategy has been studied in Liu and Shi (2014). Dynamic couplings are handled using a robust constraint and each subsystem solves the local optimization problem in a completely decoupled way to reduce computational complexity. A distributed tube model predictive control method was studied in Trodden and Maestre (2017) for weakly coupled systems, and subsystems optimize the control inputs as well as the sizes of the state and input constraint sets which leads to minimal mutual disturbance set. For strong dynamic couplings, a DPC strategy for a large-scale system has been designed in Li, Zheng, and Lin (2015). Dynamic couplings are considered into optimization problem by exchanging the information between subsystems and the impact region of a subsystem is redefined according to the coordination strategy. In Conte, Jones, Morari, and Zeilinger (2016), a DPC strategy based on a separable terminal cost function, combined with novel time-varying local terminal sets is proposed to overcome the influence of strong dynamic couplings between subsystems.

However, the above-mentioned DPC algorithms are all under the time-triggered mechanism. This creates unnecessary waste of resources if the system performance meets the requirements. Thus, event-triggered mechanism is widely used in Zou, Wang, and Jia (2016) and Li, Fu, and Du (2016) and the main idea of it is to reduce the system triggered frequency by introducing certain conditions, that is, the control tasks are performed only when the event-triggered conditions are satisfied. In Wang, Zou, and Niu (2015) and Yin, Yue, and Hu (2016), event-triggered DPC strategies are considered for network control systems (NCS). The event-triggered condition associated with the deviation between actual state and predictive state is given in advance in Yin et al. (2016), while the event-triggered conditions are derived based on the input to state stability (ISS) theory in Wang et al. (2015). The event-triggering mechanism is used to reduce the number of states transmissions of the feedback channel of the NCS and to reduce the network resource consumption in the case of limited network. For multi-agent systems, event-triggered DPC methods are studied in Hashimoto, Adachi, and Dimarogonas (2015) and Zou, Su, and Niu (2016). In Hashimoto et al. (2015), the event-triggered condition only involves local information of the subsystem is given and the system’s computational and communication resources are effectively reduced. An additional constraint is constructed to ensure local stability of subsystems. In order to guarantee the global stability, an event-triggering condition with the information received from neighboring subsystems is derived for linear systems in Zou et al. (2016) and a constraint relevant to the triggered instant is imposed for stability of overall system. However, to the authors’ best knowledge, the research of event-triggered DPC is now mostly for dynamically independent subsystem and scarce works focus on the design of event-triggered DPC strategy for dynamically coupled subsystem. Compared with the methods for decoupled dynamics systems, couplings between subsystems for dynamics coupled systems are real-time rather than known in advance, which makes each subsystem must consider the information of other subsystems and the global performance of the systems when judging the event-triggered conditions. The existence of dynamic couplings increases the difficulty of the recursive feasibility of predictive control optimization problem and close-loop stability under the event-triggered mechanism. Therefore, how to design an event-triggered DPC with considering coupling dynamics between subsystems is still a challenge, which motivates this work.

In this work, we propose an event-triggered robust DPC approach for a large-scale system coupled via system dynamics. The main contributions of this paper can be summarized as follows: (1) The optimization problem based on event-triggering instant is constructed and a constraint which handles effectiveness of dynamic couplings and disturbances is introduced in the optimization to guarantee the robustness of systems. Each subsystem works in a totally decoupled way to reduce the complexity of problem; (2) The event-triggered conditions which related to the prediction error between current actual state and predicted state are derived based on ISS and sufficient conditions to guarantee the recursive feasibility of DPC optimization problem and stability of closed-loop system can be derived; (3) The proposed event-triggered robust DPC strategy can effectively reduce the number of solving optimization problems. In addition, the dual-mode control is taken into account in the proposed algorithm to further reduce system resource consumption.

The organization of this paper is as follows. Section 2 introduces the modeling and formulates the event-triggered DPC optimization problem for each subsystem. In Section 3, event-triggering conditions are derived and then the event-triggered dual-mode DPC algorithm is proposed. Furthermore, the sufficient conditions to ensure recursive feasibility and closed-loop stability are established. Section 4 provides a simulation example to verify the effectiveness of the proposed approach. Finally, the conclusion is drawn in Section 5.

Notation: Throughout this paper, ${\mathbb{R}}^n$ denotes the real n dimensional Euclidean space; diag$\{\cdots \}$ stands for a block-diagonal matrix; $\mathbb{N}$ is the collection of all natural numbers; $I_{n\times n}$ denotes the identity matrix with $n\times n$ dimension; The superscript T denotes the matrix transposition; Given a positive definite matrix Q and a column vector $x={\left[x_1,\dots ,x_n\right]}^T$, ${\Vert x\Vert }_{\infty }=max\left(\left|x_1\right|,\dots ,\left|x_n\right|\right)$ is the infinity norm of x; $\Vert x\Vert =\sqrt{x^{T}x}$ and ${\Vert x\Vert }_Q=\sqrt{x^{T}Qx}$ stand for the Euclidean norm and Q-weighted norm of x, respectively; $\overline{\lambda }(Q)$ and $\underline{\lambda }(Q)$ are the maximum eigenvalue and minimum eigenvalue of Q, respectively; ${max}_i[\cdots ],{max}_{i,j}[\cdots ]$ denotes the maximum element, subscripts indicate the range of elements; $Card\{\cdots \}$ denotes the number of elements of the set.

2. Problem formulation

We consider a large-scale system consisting of $\mathbb{M}$ linear subsystems, where the model of each subsystem ${\mathcal{S}}_i(i=1,\dots ,M)$ is described as:(1) $$\begin{array}{c}\hfill x_i(k+1)=A_{\mathit{ii}}{x}_i(k)+B_i{u}_i(k)+\sum _{j\in {\mathcal{N}}_i}{A}_{\mathit{ij}}{x}_j(k)+w_i(k),\end{array}$$(1)

where for each $l=1,\dots ,N-1$, $x_i(k)\in X_i\subset {\mathbb{R}}^{n_i}$ and $u_i(k)\in U_i\subset {\mathbb{R}}^{m_i}$ are the local states and control inputs, respectively; $X_i$ and $U_i$, are the constraints of the state and control input. $A_{\mathit{ii}}$ and $B_i$ denote local constant matrices, if $A_{\mathit{ij}}\ne 0$, then ${\mathcal{S}}_i(i=1,\dots ,M)$ and ${\mathcal{S}}_j(j=1,\dots ,M)$ are neighbors for each other. The external disturbance $w_i(k)$ is assumed to be bounded by $\Vert w_i(k)\Vert \le \rho$. The nominal decoupled dynamics of subsystem ${\mathcal{S}}_i$ are(2) $$\begin{array}{c}\hfill x_i(k+1)=A_{\mathit{ii}}{x}_i(k)+B_i{u}_i(k),\end{array}$$(2)

The overall system can be described by the following model:(3) $$\begin{array}{c}\hfill x(k+1)=Ax(k)+Bu(k)+w(k),\end{array}$$(3)

where $x(k)={[x_1^T(k),\dots ,x_M^T(k)]}^T$ and $u(k)={[u_1^T(k),\dots ,u_M^T(k)]}^T$. $A=$$\left[\begin{array}{c}{A}_{11},\dots ,A_{1M}\\ A_{21},\dots ,A_{2M}\\ \dots \\ A_{M1},\dots ,A_{\mathit{MM}}\end{array}\right]$, $B=$ diag$\{B_1,\dots ,B_M\}$.

Assumption 1

For each subsystem, there exists a decoupled static feedback $u_i(k)=K_i{x}_i(k)$ such that $A_{\mathit{di}}=A_{\mathit{ii}}+B_{\mathit{ii}}{K}_i$ is Shur stable.

Figure 1. Diagram of event-triggered DPC.

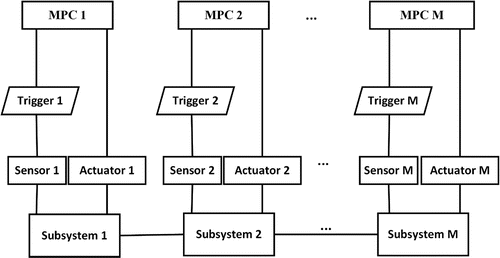
The structure of event-triggered DPC, as illustrated in Figure 1, is composed of many interacting subsystems, each of which is controlled by a model predictive controller. An event trigger is constructed between the sensor and controller for each subsystem to reduce system communication and computation resources.

Problem 1

For the system (1), define the time $k_d(d\in \mathbb{N})$ as the d-th triggering instant and let $k_0=0$. The DPC optimization problem of agent ${\mathcal{S}}_i$ to be solved at time $k_d$ is given as follows:(4) $$\begin{array}{c}\hfill \underset{u_i(k_d+l|k_d)}{min}{J}_i(k_d)=\sum _{l=0}^{N-1}\left[\Vert x_i(k_d+l|k_d){\Vert }_{Q_i}^2+\Vert u_i(k_d+l|k_d){\Vert }_{R_i}^2+{\Vert x_i(k_d+N|k_d)\Vert }_{P_i}^2\right],\end{array}$$(4)

subject to:(5) $$\begin{array}{cc}& x_i(k_d+l+1|k_d)=A_i{x}_i(k_d+l|k_d)+B_i{u}_i(k_d+l|k_d),\hfill \end{array}$$(5) (6) $$\begin{array}{cc}& \Vert x_i(k_d+l|k_d){\Vert }_{P_i}\le \frac{N{\alpha }_i{\epsilon }_i}{l},l=1,\dots ,N-1,\hfill \end{array}$$(6) (7) $$\begin{array}{cc}& u_i(k_d+l|k_d)\in U_i,l=0,\dots ,N-1,\hfill \end{array}$$(7) (8) $$\begin{array}{cc}& x_i(k_d|k_d)=x_i(k_d),\hfill \end{array}$$(8)

where ${\widehat{x}}_i(k_d+l|k_d)$ and ${\widehat{u}}_i(k_d+l|k_d)$ are the estimated state and control input for subsystem ${\mathcal{S}}_i$ based on the measurement at time $k_d$, respectively; $Q_i$ and $R_i$ are given positive definite weighting matrices; ${\mathcal{N}}_i$ denotes the set of indices of ${\mathcal{S}}_i$’s neighbors. ${\epsilon }_i$ is a positive constant that characterizes the positively invariant set ${\mathrm{\Omega }}_i$, that is ${\mathrm{\Omega }}_i=\left[x_i\in {\mathbb{R}}^{n_i}:{\Vert x_i\Vert }_{P_i}\le {\epsilon }_i\right]$. ${\alpha }_i$ is a shrinking factor that will be designed later and $P_i$ is the terminal weighting matrix which is chosen to satisfy the equation in Zou et al. (2016):(9) $$\begin{array}{c}\hfill A_{\mathit{di}}^T{P}_i{A}_{\mathit{di}}-P_i=-{\tilde{Q}}_i,\end{array}$$(9)

where ${\tilde{Q}}_i=Q_i+K_i^T{R}_i{K}_i$.

Denote $P=\text{diag}\{P_1,\dots ,P_M\}$, $Q=\text{diag}\{Q_1,\dots ,Q_M\}$, $\tilde{Q}=\text{diag}\{{\tilde{Q}}_1,\dots ,{\tilde{Q}}_M\}$, $R=\text{diag}\{R_1,\dots ,R_M\}$, $A_d=\text{diag}\{A_{d1},\dots ,A_{\mathit{dM}}\}$, $K=\text{diag}\{K_1,\dots ,K_M\}$, We have(10) $$\begin{array}{c}\hfill A_d^{T}P{A}_d-P=-\tilde{Q},\end{array}$$(10)

In addition, the terminal weighting matrix P for overall system should satisfy another inequality because of the coupled dynamics.

Assumption 2

(Zou et al., 2016) The matrix $A_o=A_c-A_d$ quantifies how strengthen the coupling is among subsystems, where $A_c=A+KB$. Then P satisfies:(11) $$\begin{array}{c}\hfill A_o^{T}P{A}_o+A_o^{T}P{A}_d+A_d^{T}P{A}_o<\frac{\tilde{Q}}{2},\end{array}$$(11)

Lemma 1

(Zou et al., 2016) Under Assumptions 1 and 2, with a positive scalar $\epsilon$, the set ${\mathrm{\Omega }}_{\epsilon }=\left[x\in {\mathbb{R}}^n:{\Vert x\Vert }_P\le \epsilon \right]$ is a positive invariant set for the closed-loop system $x(k+1)=A_{c}x(k)$.

The main task of this paper is to design an event-triggered DPC strategy for large systems with coupled dynamics to guarantee the robustness of the system under disturbance as well as reduce the complexity and resources of the systems.

3. Event-triggered DPC

In this section, we derive the event-triggering condition for each subsystem to reduce system resources efficiently firstly. Then, the recursive feasibility of Problem 1 and the sufficient conditions for ensuring the ISS of closed-loop system are given.

3.1. Event-triggering condition

In the framework of event-triggered DPC, states are transmitted to solve the Problem 1 only when event-triggering conditions are satisfied. In the interval of two consecutive triggering instants, a candidate control sequence based on the optimal control sequence of last triggering instant is applied. Assume that Problem 1 is solved at time $k_d$, define the next triggering instant as $k_{d+1}$. Then we can construct the following candidate control sequence ${\overline{u}}_i(k_d+l|k_d+m)$ based on $u_i^{\ast }(k_d+l|k_d)$ in $k_d+m\in (k_d,k_{d+1}](1\le m\le N-1)$ as follows:(12) $$\begin{array}{c}\hfill {\overline{u}}_i(k_d+l|k_d+m)=\left\{\begin{array}{cc}{u}_i^{\ast }(k_d+l|k_d),\hfill & l=m,\dots ,N-1,\hfill \\ K_i{\overline{x}}_i(k_d+l|k_d+m),\hfill & l=N,\dots ,m+N-1,\hfill \end{array}\right.\end{array}$$(12)

where ${\overline{x}}_i(k_d+l|k_d+m)$ is predicted state at time $k_d+l$ based on the control sequence in (12). In the following, we consider the difference between ${\overline{J}}_i(k_d+m)$ and ${\overline{J}}_i(k_d+m-1)$.(13) $$\begin{array}{cc}& \mathrm{\Delta }{J}_i(k_d+m)\hfill \\ \hfill & ={\overline{J}}_i(k_d+m)-\left\{\sum _{l=m}^{N-1}\left[\Vert x_i^{\ast }(k_d+l|k_d){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+l|k_d)\Vert }_{R_i}^2\right]+{\Vert x_i^{\ast }(k_d+N|k_d)\Vert }_{P_i}^2\right\}\hfill \\ \hfill & -{\overline{J}}_i(k_d+m-1)+\left\{\sum _{l=m}^{N-1}\left[\Vert x_i^{\ast }(k_d+l|k_d){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+l|k_d)\Vert }_{R_i}^2\right]+{\Vert x_i^{\ast }(k_d+N|k_d)\Vert }_{P_i}^2\right\}\hfill \\ \hfill & \le -\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2-{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2+{\mathrm{\Gamma }}_1^i(k_d+m)+{\mathrm{\Gamma }}_2^i(k_d+m)\hfill \\ \hfill & +{\mathrm{\Gamma }}_3^i(k_d+m),\hfill \end{array}$$(13)

where$$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_1^i(k_d+m)& =\sum _{l=m}^{N-1}\left[\Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{Q_i}^2-{\Vert x_i^{\ast }(k_d+l|k_d)\Vert }_{Q_i}^2\right],\hfill \\ \hfill {\mathrm{\Gamma }}_2^i(k_d+m)& =\Vert {\overline{x}}_i(k_d+m+N|k_d+m){\Vert }_{P_i}^2-{\Vert x_i^{\ast }(k_d+N|k_d)\Vert }_{P_i}^2\hfill \\ \hfill & +\sum _{l=N}^{m+N-1}{\Vert {\overline{x}}_i(k_d+l|k_d+m)\Vert }_{{\tilde{Q}}_i}^2({\tilde{Q}}_i=Q_i+K_i^T{R}_i{K}_i),\hfill \\ \hfill {\mathrm{\Gamma }}_3^i(k_d+m)& =\sum _{l=m}^{N-1}\left[\Vert x_i^{\ast }(k_d+l|k_d){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+l|k_d)\Vert }_{R_i}^2\right]+{\Vert x_i^{\ast }(k_d+N|k_d)\Vert }_{P_i}^2\hfill \\ \hfill & -\sum _{l=m}^{m+N-2}\left[\Vert {\overline{x}}_i(k_d+l|k_d+m-1){\Vert }_{Q_i}^2+{\Vert {\overline{u}}_i(k_d+l|k_d+m-1)\Vert }_{R_i}^2\right]\hfill \\ \hfill & -\Vert {\overline{x}}_i(k_d+m+N-1|k_d+m-1){\Vert }_{P_i}^2.\hfill \end{array}$$

Note that ${\overline{u}}_i(k_d+l|k_d+m)=u_i^{\ast }(k_d+l|k_d)(l=m,\dots ,N-1)$. We have(14) $$\begin{array}{c}\hfill \Vert {\overline{x}}_i(k_d+l|k_d+m)-x_i^{\ast }(k_d+l|k_d)\Vert \le \Vert A_{\mathit{ii}}{\Vert }^{l-m}{e}_i(k_d+m),\end{array}$$(14)

where $e_i(k_i^d+m)$ is the norm of difference between current actual state and predicted state computed at last triggering instant, that is, $e_i(k_d+m)=\Vert x_i(k_d+m)-x_i^{\ast }(k_d+m|k_d)\Vert$. By means of (14) and triangle inequality, the expression ${\mathrm{\Gamma }}_1^i(k_d+m)$ is rewritten as(15) $$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_1^i(k_d+m)& \le \frac{2\overline{\lambda }(Q_i)}{\sqrt{\underline{\lambda }(P_i)}}\sum _{l=m}^{N-1}\Vert x_i^{\ast }(k_d+l|k_d){\Vert }_{P_i}·\Vert {\overline{x}}_i(k_d+l|k_d+m)-x_i^{\ast }(k_d+l|k_d)\Vert \hfill \\ \hfill & +\overline{\lambda }(Q_i)\sum _{l=m}^{N-1}{\Vert {\overline{x}}_i(k_d+l|k_d+m)-x_i^{\ast }(k_d+l|k_d)\Vert }^2\hfill \\ \hfill & \le \frac{2\overline{\lambda }(Q_i)N{\alpha }_i{\epsilon }_i}{\sqrt{\underline{\lambda }(P_i)}}\sum _{l=m}^{N-1}\frac{\Vert A_{\mathit{ii}}{\Vert }^{l-m}}{l}{e}_i(k_d+m)+\overline{\lambda }(Q_i)\sum _{l=m}^{N-1}{\Vert A_{\mathit{ii}}\Vert }^{2(l-m)}{e}_i^2(k_d+m).\hfill \end{array}$$(15)

Let ${\mathrm{\Gamma }}_2^i(k_d+m)$ subtract and add the expression ${\sum }_{l=N}^{m+N-1}{\Vert {\overline{x}}_i(k_d+l|k_d+m)\Vert }_{P_i}^2$, then the following inequality is derived:(16) $$\begin{array}{cc}& {\mathrm{\Gamma }}_2^i(k_d+m)-\sum _{l=N}^{m+N-1}\Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{P_i}^2+\sum _{l=N}^{m+N-1}{\Vert {\overline{x}}_i(k_d+l|k_d+m)\Vert }_{P_i}^2\hfill \\ \hfill & \le -\Vert x_i^{\ast }(k_d+N|k_d){\Vert }_{P_i}^2+\sum _{l=N}^{m+N-2}\Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{{\overline{Q}}_i}^2-\sum _{l=N}^{m+N-2}{\Vert {\overline{x}}_i(k_d+l|k_d+m)\Vert }_{P_i}^2\hfill \\ \hfill & +\sum _{l=N}^{m+N-1}{\Vert {\overline{x}}_i(k_d+l|k_d+m)\Vert }_{P_i}^2\hfill \\ \hfill & \le \Vert {\overline{x}}_i(k_d+N|k_d+m){\Vert }_{P_i}^2-{\Vert x_i^{\ast }(k_d+N|k_d)\Vert }_{P_i}^2\hfill \\ \hfill & \le 2\sqrt{\overline{\lambda }(P_i)}{\alpha }_i{\epsilon }_i\Vert A_{\mathit{ii}}{\Vert }^{N-m}{e}_i(k_d+m)+\overline{\lambda }(P_i){\Vert A_{\mathit{ii}}\Vert }^{2(N-m)}{e}_i^2(k_d+m).\hfill \end{array}$$(16)

Substituting (15)–(16) into (13), it follows that(17) $$\begin{array}{cc}\hfill \mathrm{\Delta }{J}_i(k_d+m)& \le -\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2-{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2+{\mathrm{\Gamma }}_3^i(k_d+m)\hfill \\ \hfill & +{\mathrm{\Pi }}_1^i(k_d+m)e_i^2(k_d+m)+{\mathrm{\Pi }}_2^i(k_d+m)e_i(k_d+m),\hfill \end{array}$$(17)

where$$\begin{array}{cc}& {\mathrm{\Pi }}_1^i(k_d+m)=\overline{\lambda }(Q_i)\sum _{l=m}^{N-1}\Vert A_{\mathit{ii}}{\Vert }^{2(l-m)}+\overline{\lambda }(P_i){\Vert A_{\mathit{ii}}\Vert }^{2(N-m)},\hfill \\ \hfill & {\mathrm{\Pi }}_2^i(k_d+m)=\frac{2\overline{\lambda }(Q_i)N{\alpha }_i{\epsilon }_{\mathit{ii}}}{\sqrt{\underline{\lambda }(P_i)}}\sum _{l=m}^{N-1}\frac{\Vert A_{\mathit{ii}}{\Vert }^{l-m}}{l}+2\sqrt{\overline{\lambda }(P_i)}{\alpha }_i{\epsilon }_i{\Vert A_{\mathit{ii}}\Vert }^{N-m}.\hfill \end{array}$$

If the following relationship holds with parameter $0<{\sigma }_i<1$,(18) $$\begin{array}{cc}& {\mathrm{\Pi }}_1^i(k_d+m)e_i^2(k_d+m)+{\mathrm{\Pi }}_2^i(k_d+m)e_i(k_d+m)\hfill \\ \hfill & \le {\sigma }_i\left[\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2-{\mathrm{\Gamma }}_3^i(k_d+m)\right],\hfill \end{array}$$(18)

Then $\mathrm{\Delta }{J}_i(k_d+m)\le ({\sigma }_i-1)\left[\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2-{\mathrm{\Gamma }}_3^i(k_d+m)\right]<0$ the event-triggering condition is derived as follows:(19) $$\begin{array}{cc}& {\mathrm{\Pi }}_1^i(k_d+m)e_i^2(k_d+m)+{\mathrm{\Pi }}_2^i(k_d+m)e_i(k_d+m)\hfill \\ \hfill & >{\sigma }_i\left[\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2-{\mathrm{\Gamma }}_3^i(k_d+m)\right],\hfill \end{array}$$(19)

Remark 1

Taking into account of the practical situation, if the subsystem is not triggered within the prediction horizon N, Problem 1 will be solved at time $k_d+N$. Hence, the event-triggering condition is restated as:(20) $$\begin{array}{cc}& {\mathrm{\Pi }}_1^i(k_d+m)e_i^2(k_d+m)+{\mathrm{\Pi }}_2^i(k_d+m)e_i(k_d+m)\hfill \\ \hfill & >{\sigma }_i\left[\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2-{\mathrm{\Gamma }}_3^i(k_d+m)\right]\hfill \\ \hfill & ork=k_d+N\hfill \end{array}$$(20)

Remark 2

It is important to select the parameter ${\sigma }_i$ appropriately, because it is related to the resource utilization. As ${\sigma }_i$ closes to 1, the consumption of computation resource becomes less. Specially, event-triggered DPC degrades to time-triggered DPC when ${\sigma }_i=0$.

Remark 3

we can see the items ${\mathrm{\Pi }}_1^i,{\mathrm{\Pi }}_2^i,{\mathrm{\Gamma }}_3^i$ are independent of the current status $x_i(k_d+m)$ recording to (16), (21), (22) and event-triggered condition (24) does not contain any information of other subsystem. Therefore, each subsystem can quickly determine the event-triggered conditions according to their own current status.

The DPC signal is generated by the nominal decoupled subsystem dynamics in (2) as the predictive model. However, the actual state trajectories differ from the predicted state trajectories because of the coupling among the subsystems and the external disturbances. Lemma 2 will establish a bound on these deviations.

Lemma 2

For each subsystem ${\mathcal{S}}_i$, the deviation of its actual state trajectories from the predicted state trajectories is upper bounded by(21) $$\begin{array}{c}\hfill e_i(k_d+m)=\Vert x_i(k_d+m)-x_i^{\ast }(k_d+m|k_d)\Vert \le M\left\{\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^m-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\right\}\end{array}$$(21)

Each subsystem has in the symmetric super-graph which encodes the topology of the inter-subsystem couplings. $\overline{N_i}\ge {max}_i\text{Card}[N_i]$, $\overline{A}={max}_{i,j}[A_{\mathit{ij}}]$, $\overline{\alpha }={max}_i[{\alpha }_i]$, $\overline{\epsilon }={max}_i[{\epsilon }_i]$, $\overline{\gamma }={max}_i[\frac{1}{\sqrt{\overline{\lambda }(P_i)}}]$.

Proof

According to the system model (1), the prediction model (2) and symmetrical topology of the system, we have(22) $$\begin{array}{cc}& \sum _{i=1}^M(e_i(k_d+m))=\sum _{i=1}^M\{\Vert x_i(k_d+m)-x_i^{\ast }(k_d+m|k_d)\Vert \}\hfill \\ \hfill & =\sum _{i=1}^M\{\Vert A_{\mathit{ii}}{x}_i(k_d+m-1)+B_i{u}_i(k_d+m-1)+\sum _{j\in {\mathcal{N}}_i}{A}_{\mathit{ij}}{x}_j(k_d+m-1)+w_i(k)\hfill \\ \hfill & -A_{\mathit{ii}}{x}_i(k_d+m-1|k_d)-B_i{u}_i(k_d+m-1|k_d)\Vert \}\hfill \\ \hfill & =\sum _{i=1}^M\{\Vert A_{\mathit{ii}}{x}_i(k_d+m-1)-A_{\mathit{ii}}{x}_i(k_d+m-1|k_d)\Vert \hfill \\ \hfill & +\sum _{j\in {\mathcal{N}}_i}\Vert A_{\mathit{ij}}{x}_j(k_d+m-1)-A_{\mathit{ij}}{x}_j(k_d+m-1|k_d)\Vert +\Vert w_i(k)\Vert \}\hfill \\ \hfill & \le \sum _{i=1}^M\{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert \Vert x_i(k_d+m-1)-x_i^{\ast }(k_d+m-1|k_d)\Vert +(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\}\hfill \\ \hfill & \le M\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^m-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\hfill \end{array}$$(22)

This completes the proof. $\square$

In order to reduce the amount of information transmission, the dual-mode predictive control scheme is employed in this paper. The state feedback control law is applied at each sampling time when agent ${\mathcal{S}}_i$ enters its invariant set. In the sequel, the event-triggered dual-mode DPC algorithm is proposed.

Step 1	At time $k=0$: Step 1.1 If $x_i(0)\in {\mathrm{\Omega }}_i$, the state feedback control law $u_i(0)=K_i{x}_i(0)$ is applied. Else, go to Step 1.2. Step 1.2 Problem 1 is solved based on $x_i(0)$ to yield the optimal control sequence $u_i^{\ast }(0|0),\cdots ,u_i^{\ast }(N-1|0)$, and the first control input $u_i^{\ast }(0|0)$ is applied to ${\mathcal{S}}_i$.
Step 2	At time $k>0$: Step 2.1 If $x_i(k)\in {\mathrm{\Omega }}_i$, the state feedback control law $u_i(k)=K_i{x}_i(k)$ is applied. Else, go to Step 2.2. Step 2.2 If dynamic event-triggering condition is satisfied, the triggering instant is updated by $k_d=k$. Problem 1 is solved based on $x_i(k_d)$ to yield the optimal control sequence $u_i^{\ast }(k_d|k_d),\dots ,u_i^{\ast }(k_d+N-1|k_d)$, and the first control input $u_i^{\ast }(k_d|k_d)$ is applied to ${\mathcal{S}}_i$. Otherwise, go to Step 2.3. Step 2.3 Problem 1 is not solved and control sequence (12) is applied.
Step 3	Set $k=k+1$, return to Step 2.

3.2. Recursive feasibility and closed-loop stability

Based on the above discussion, we know that event-triggered DPC is different from traditional time-triggered DPC which only implemented when the event-triggered condition is satisfied. Accordingly, it is necessary to reconsider the recursive feasibility. The main results and sufficient conditions for recursive feasibility of Problem 1 are given as follows:

Theorem 1

For agent ${\mathcal{S}}_i$ in (1), if the upper bound of disturbance $\rho$ and constant ${\alpha }_i$ satisfy the following inequalities:(23) $$\begin{array}{cc}& \rho \le \frac{(\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1)(1-{\alpha }_i){\epsilon }_i}{M\sqrt{\overline{\lambda }(P_i)}\Vert A_{\mathit{ii}}\Vert (\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}{\Vert }^{N-1}-1)}-\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma },\hfill \end{array}$$(23) (24) $$\begin{array}{cc}& max\left\{\sqrt{1-\frac{\underline{\lambda }({\overline{Q}}_i)}{\overline{\lambda }(P_i)}},1-\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^{N-1}-1}{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^{N-1}-1+(N+1)\Vert A_{\mathit{ii}}{\Vert }^{N-2}(\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1)}\right\}\le {\alpha }_i,\hfill \end{array}$$(24)

Then Problem 1 is recursively feasible.

Proof

Suppose that Problem 1 is solved at time $k_d$. Problem 1 turns out to be feasible at time $k_d+m$ if the constraints (6) and (7) are satisfied under control sequence (12).

(i)

$\Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{P_i}\le \frac{N{\alpha }_i{\epsilon }_i}{l-m}(l=m+1,\dots ,m+N)$. First, according to (14) and (21), we have (25) $$\begin{array}{c}\hfill \Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{P_i}-\Vert x_i^{\ast }(k_d+l|k_d){\Vert }_{P_i}\le M\sqrt{\overline{\lambda }(P_i)}{\Vert A_{\mathit{ii}}\Vert }^{l-m}\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^m-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho ).\end{array}$$(25) Let $l=N$ in (25) and condition (23), we can get $\Vert {\overline{x}}_i(k_d+N|k_d+m){\Vert }_{P_i}\le {\epsilon }_i$, which implies ${\overline{x}}_i(k_d+l|k_i^d+m)\in {\varphi }_i$ with $N+1\le l\le m+N$. Thus, we have (26) $$\begin{array}{cc}& \Vert {\overline{x}}_i(k_d+N+1|k_d+m){\Vert }_{P_i}^2-{\Vert {\overline{x}}_i(k_d+N|k_d+m)\Vert }_{P_i}^2\hfill \\ \hfill & \le -\Vert {\overline{x}}_i(k_d+N|k_d+m){\Vert }_{{\tilde{Q}}_i}^2,\hfill \\ \hfill & ⋮\hfill \\ \hfill & \Vert {\overline{x}}_i(k_d+m+N|k_d+m){\Vert }_{P_i}^2-{\Vert {\overline{x}}_i(k_d+m+N-1|k_d+m)\Vert }_{P_i}^2\hfill \\ \hfill & \le -\Vert {\overline{x}}_i(k_d+m+N-1|k_d+m){\Vert }_{{\tilde{Q}}_i}^2.\hfill \end{array}$$(26) Adding all the inequalities in (26) and using condition (24), we have (27) $$\begin{array}{cc}\hfill \Vert {\overline{x}}_i(k_d+m+N|k_d+m){\Vert }_{P_i}^2& \le \Vert {\overline{x}}_i(k_d+N|k_d+m){\Vert }_{P_i}^2-{\Vert {\overline{x}}_i(k_d+N|k_d+m)\Vert }_{{\tilde{Q}}_i}^2\hfill \\ \hfill & \le \left[1-\frac{\underline{\lambda }({\tilde{Q}}_i)}{\overline{\lambda }(P_i)}\right]{({\epsilon }_i)}^2\le {({\alpha }_i{\epsilon }_i)}^2.\hfill \end{array}$$(27) To make $\Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{P_i}\le \frac{N{\alpha }_i{\epsilon }_i}{l-m}(l=m+1,\dots ,m+N-1)$ hold, that we need to prove $M\sqrt{\overline{\lambda }(P_i)}{\Vert A_{\mathit{ii}}\Vert }^{l-m}\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^m-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\le \frac{mN{\alpha }_i{\epsilon }_i}{l(l-m)}$. With condition (23), we have $M\sqrt{\overline{\lambda }(P_i)}\Vert A_{\mathit{ii}}{\Vert }^{l-m}\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^m-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\le {\Vert A_{\mathit{ii}}\Vert }^{N-2}\frac{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^{N-1}-1}(1-{\alpha }_i){\epsilon }_i$. Noting $l\le m+N-1$ and $m\ge 1$, it is obtained that $\frac{mN{\alpha }_i{\epsilon }_i}{l(l-m)}\ge \frac{{\alpha }_i{\epsilon }_i}{N-1}$. Furthermore, by condition (24), we can get $\Vert A_{\mathit{ii}}{\Vert }^{N-2}\frac{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^{N-1}-1}(1-{\alpha }_i){\epsilon }_i\le \frac{{\alpha }_i{\epsilon }_i}{N-1}$. Therefore, we have $\Vert {\overline{x}}_i(k_d+l|k_d+m){\Vert }_{P_i}\le \frac{N{\alpha }_i{\epsilon }_i}{l-m}(l=m+1,\dots ,m+N)$.

(ii)

${\overline{u}}_i(k_d+l|k_d+m)\in U_i(l=m,\dots ,m+N-1)$. It follows from (12) that ${\overline{u}}_i(k_d+l|k_d+m)=u_i^{\ast }(k_d+l|k_d)\in U_i(l=m,\dots ,N-1)$. Since ${\overline{x}}_i(k_d+l|k_d+m)\in {\varphi }_i(l=N,\dots ,m+N-1)$, we have ${\overline{u}}_i(k_d+l|k_d+m)=K_i{\overline{x}}_i(k_d+l|k_d+m)\in U_i(l=N,\dots ,m+N-1)$. From the above, we can conclude that ${\overline{u}}_i(k_d+l|k_d+m)\in U_i(l=m,\dots ,m+N-1)$.

$\square$

This complete the proof and Problem 1 turns out to be feasible under event-triggered DPC. In the following, the main results for closed-loop stability are given.

Theorem 2

Subsystem ${\mathcal{S}}_i$ will enter its disturbance invariant set ${\mathrm{\Omega }}_i=\{x_i\in {\mathbb{R}}^{n_i}:\Vert x_i{\Vert }_{P_i}^2\le {({\mu }_i{\epsilon }_i)}^2\}(0<{\mu }_i<1)$ in finite time under the event-triggered DPC if the upper bound of disturbance $\rho$, constants $\alpha$, $\mu$ and $\nu$ satisfy the following inequalities:(28) $$\begin{array}{cc}& \frac{\underline{\lambda }(Q_i)}{\overline{\lambda }(P_i)}{\epsilon }_i^2-{\widehat{\mathrm{\Gamma }}}_3^i>0\hfill \end{array}$$(28) (29) $$\begin{array}{cc}& \rho \le \sqrt{\frac{\mathrm{\Gamma }}{\mathrm{\Lambda }}}\mu \epsilon \hfill \end{array}$$(29) (30) $$\begin{array}{cc}& \frac{\left[\underline{\lambda }(\overline{Q})-\overline{\lambda }(P)\right]\underline{\lambda }(P)}{\overline{\lambda }(P)}<\nu <\frac{\underline{\lambda }(\overline{Q})\underline{\lambda }(P)}{\overline{\lambda }(P)}\hfill \end{array}$$(30)

where$$\begin{array}{c}\hfill \mathrm{\Gamma }=\frac{\underline{\lambda }(\overline{Q})}{2\overline{\lambda }(P)}-\frac{\nu }{\underline{\lambda }(P)}\mathrm{\Lambda }=\overline{\lambda }(P)+\frac{\Vert (A_c^{T}P{\Vert }^2}{\nu }.\end{array}$$

where$$\begin{array}{cc}\hfill {\widehat{\mathrm{\Gamma }}}_3^i& ={\left[\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^{N-2}-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\right]}^2·\left[\overline{\lambda }(Q_i)\sum _{l=2}^{N-1}{M}^2\Vert A_{\mathit{ii}}{\Vert }^{2(l-1)}+\overline{\lambda }(P_i)M^2{\Vert A_{\mathit{ii}}\Vert }^{2(N-1)}\right]\hfill \\ \hfill & +2N{\alpha }_i{\epsilon }_i\frac{\Vert A_{\mathit{ii}}{+\overline{N_i}\overline{A}\Vert }^{N-2}-1}{\Vert A_{\mathit{ii}}+\overline{N_i}\overline{A}\Vert -1}(\overline{N_i}\overline{A}N\overline{\alpha }\overline{\epsilon }\overline{\gamma }+\rho )\left[\frac{\overline{\lambda }(Q_i)}{\sqrt{\underline{\lambda }(P_i)}}\sum _{l=2}^{N-1}\frac{M\Vert A_{\mathit{ii}}{\Vert }^{l-1}}{l-1}\right.\hfill \\ \hfill & \left.+\frac{M\Vert A_{\mathit{ii}}{\Vert }^{N-1}}{2}\sqrt{\overline{\lambda }(P_i)}\right],\hfill \end{array}$$

Proof

Due to ET-DPC Algorithm employed in this paper, the proof of Theorem 2 involves two parts. Firstly, we show that agent ${\mathcal{S}}_i$ will converge to its invariant set ${\mathrm{\Omega }}_i$ under event-triggered DPC. The item $\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2-{\mathrm{\Gamma }}_3^i(k_d+m)\ge 0$ is necessary to ensure the convergence of ${\mathcal{S}}_i$. In the following, we give some relevant conditions to ensure this inequality holds. Since $x_i(k_d+m-1)\notin {\phi }_i$, we can get(31) $$\begin{array}{c}\hfill {\left[\Vert x_i(k_d+m-1){\Vert }_{Q_i}\right]}^2\ge \frac{\underline{\lambda }(Q_i)}{\overline{\lambda }(P_i)}{\left[\Vert x_i(k_d+m-1){\Vert }_{P_i}\right]}^2\ge \frac{\underline{\lambda }(Q_i)}{\overline{\lambda }(P_i)}{\epsilon }_i^2\end{array}$$(31)

In addition, we have(32) $$\begin{array}{cc}\hfill {\mathrm{\Gamma }}_3^i(k_d+m)& \le \sum _{l=m}^{N-1}\left[\Vert x_i^{\ast }(k_d+l|k_d){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+l|k_d)\Vert }_{R_i}^2\right]+{\Vert x_i^{\ast }(k_d+N|k_d)\Vert }_{P_i}^2\hfill \\ \hfill & -\Vert {\overline{x}}_i(k_d+m+N-1|k_d+m-1){\Vert }_{P_i}^2\le \widehat{{\mathrm{\Gamma }}_3^i}.\hfill \end{array}$$(32)

By means of the condition (28), we can obtain $\Vert x_i(k_d+m-1){\Vert }_{Q_i}^2+{\Vert u_i^{\ast }(k_d+m-1|k_d)\Vert }_{R_i}^2-{\mathrm{\Gamma }}_3^i(k_d+m)\ge \frac{\underline{\lambda }(Q_i)}{\overline{\lambda }(P_i)}{\epsilon }_i^2-{\widehat{\mathrm{\Gamma }}}_3^i\ge 0$. Thence, if the event-triggering condition (21) is not satisfied, we have $\mathrm{\Delta }{J}_i(k)<0$. Otherwise, $\mathrm{\Delta }{J}_i(k)\le -{\mathrm{\Gamma }}_3^i(k_d+m)<0$. In general, we can conclude that subsystem ${\mathcal{S}}_i$ will converge to its invariant set ${\mathrm{\Omega }}_i$.

Next, the closed-loop stability of overall system under state feedback control law K is analyzed. Suppose that $x(k_t)\in {\mathrm{\Omega }}_{\epsilon }$, the difference of Lyapunov function is given by(33) $$\begin{array}{cc}\hfill V(k+1)-V(k)& \le -\frac{1}{2}{\Vert x(k)\Vert }_{\overline{Q}}^2+{\Vert w(k)\Vert }_P^2+2x^T(k){(A+BK)}^{T}Pw(k)\hfill \\ \hfill & \le -{\mathrm{\Gamma }\Vert x(k)\Vert }_P^2+\mathrm{\Lambda }{\overline{w}}^2.\hfill \end{array}$$(33)

From condition (29), the expression (33) is rewritten as(34) $$\begin{array}{c}\hfill V(k+1)-V(k)\le \mathrm{\Gamma }\left[-{\Vert x(k)\Vert }_P^2+{(\mu \epsilon )}^2\right].\end{array}$$(34)

Assume that there doesn’t exist a time $k\ge k_t$ such that $x(k)\in \phi$. In other words, for all $k\ge k_t$, there must be a constant $ϵ>0$ such that(35) $$\begin{array}{c}\hfill {\Vert x(k)\Vert }_P^2\ge {(\mu \epsilon )}^2+ϵ.\end{array}$$(35)

By means of (35), the expression (34) is modified as $V(k+1)-V(k)\le -\mathrm{\Gamma }ϵ$. Thus, we have(36) $$\begin{array}{cc}& V(k_t+1)-V(k_t)\le -\mathrm{\Gamma }ϵ,\hfill \\ \hfill & ⋮\hfill \\ \hfill & V(k)-V(k-1)\le -\mathrm{\Gamma }ϵ.\hfill \end{array}$$(36)

Adding all the inequalities in (36), one obtains $V(k)\le {\epsilon }^2-(k-k_t)\mathrm{\Gamma }ϵ$. Let ${\overline{k}}_t=inf\left\{k\in \mathbb{N}:k\ge k_t+\frac{{\epsilon }^2-{(\mu \epsilon )}^2}{\mathrm{\Gamma }ϵ}\right\}$, then we have $\Vert x({\overline{k}}_t){\Vert }_P^2\le {(\mu \epsilon )}^2$, which contradicts with (35). This implies that there exists a time ${\overline{k}}_t\ge k_t$ such that $x({\overline{k}}_t)\in \phi$. With condition (30), we can get $0<\mathrm{\Gamma }<1$. Hence, it can be seen $\Vert x({\overline{k}}_t+1){\Vert }_P^2\le {\Vert x({\overline{k}}_t)\Vert }_P^2+\mathrm{\Gamma }\left[-\Vert x({\overline{k}}_t){\Vert }_P^2+{(\mu \epsilon )}^2\right]\le {(\mu \epsilon )}^2$, which shows that ${\mathrm{\Omega }}_{\epsilon }$ is a global disturbance invariant set. Therefore, overall system will enter its disturbance invariant set ${\mathrm{\Omega }}_{\epsilon }$ in finite time. $\square$

4. Simulation

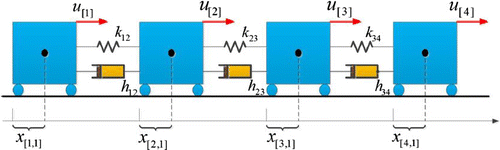
We consider four-truck systems which are shown in Figure 2, each truck is modeled as follows:(37) $$\begin{array}{cc}\hfill \left[\begin{array}{c}\dot{r_i}\hfill \\ \dot{{\nu }_i}\hfill \end{array}\right]& =\left[\begin{array}{cc}0\hfill & 1\hfill \\ -\frac{1}{m_i}\sum _{j\in {\mathcal{N}}_i}{k}_{\mathit{ij}}\hfill & -\frac{1}{m_i}\sum _{j\in {\mathcal{N}}_i}{h}_{\mathit{ij}}\hfill \end{array}\right]\left[\begin{array}{c}{r}_i\hfill \\ {\nu }_i\hfill \end{array}\right]+\left[\begin{array}{c}0\hfill \\ 100\hfill \end{array}\right]u_i\hfill \\ \hfill & +\sum _{j\in {\mathcal{N}}_i}\left[\begin{array}{cc}0\hfill & 1\hfill \\ \frac{1}{10m_i}\sum _{j\in {\mathcal{N}}_i}{k}_{\mathit{ij}}\hfill & \frac{1}{10m_i}\sum _{j\in {\mathcal{N}}_i}{h}_{\mathit{ij}}\hfill \end{array}\right]\left[\begin{array}{c}{r}_i\hfill \\ {\nu }_i\hfill \end{array}\right]+wi\hfill \end{array}$$(37)

Figure 2. A four-truck system.

where $r_i$ is the displacement of truck i from an equilibrium position and ${\nu }_i$ is its velocity and $u_i$ is the control input. The mass of the four trucks are chosen as $m_1=3\text{kg}$, $m_2=2\text{kg}$, $m_3=3\text{kg}$, $m_4=6\text{kg}$, and they are coupled via a spring k and damper h which chosen as $k_{12}=0.5{\text{Nm}}^{-1}$, $k_{23}=0.75{\text{Nm}}^{-1}$, $k_{34}=1{\text{Nm}}^{-1}$, $h_{12}=0.2{\text{Nm}}^{-1}{\text{s}}^{-1}$, $h_{23}=0.25{\text{Nm}}^{-1}{\text{s}}^{-1}$, $h_{34}=0.3{\text{Nm}}^{-1}{\text{s}}^{-1}$. The parameters in Problem 1 are chosen as $N=25,Q_i=I_{2\times 2},R_i=100$ and the constraints of states are $\Vert r_i{(k)\Vert }_{\infty }\le 4$, $\Vert {\nu }_i{(k)\Vert }_{\infty }\le 1$ and control inputs are $\Vert u_i{(k)\Vert }_{\infty }\le 1$ for i = 1, 2, 3, $\Vert u_i{(k)\Vert }_{\infty }\le 2$ for i=4. The initial conditions for four subsystems are $x_1(0)={[\begin{array}{c}1.8,0\end{array}]}^T$, $x_2(0)={[\begin{array}{c}-0.5,0\end{array}]}^T$ , $x_3(0)={[\begin{array}{c}1,0\end{array}]}^T$ and $x_4(0)={[\begin{array}{c}-1,0\end{array}]}^T$.

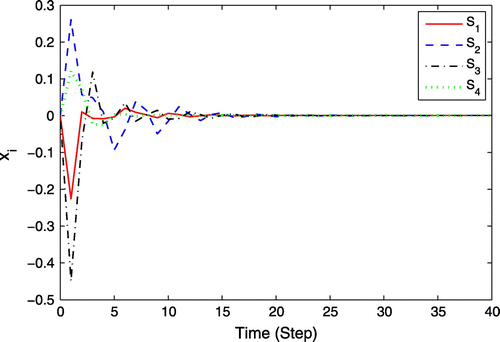
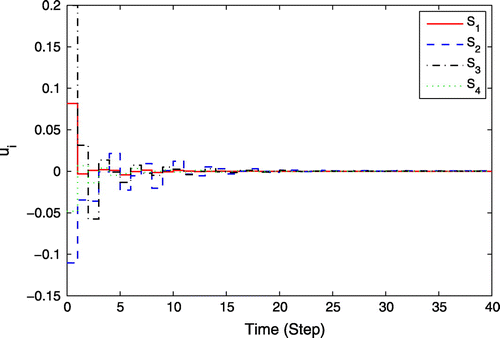
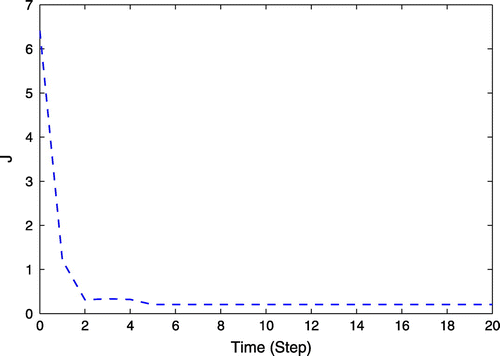
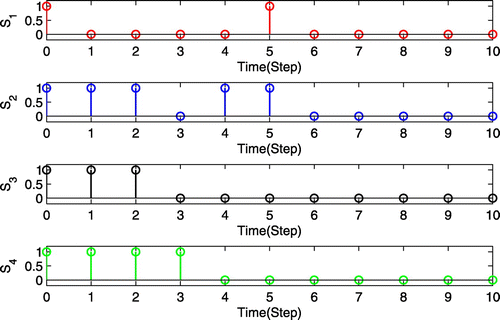
By executing the strategy mentioned above with the designed parameters, the simulation results are shown as follows. Figures 3 and 4 depict the trajectories of states and control inputs, it can be seen that the proposed event-triggered DPC algorithm drives the states of trucks to the origin despite the dynamic couplings among them and the control inputs can satisfy the constraints. From the result in Figure 5, it shows the trajectories of J(k) under event-triggered DPC indicates the convergence of the overall system under the proposed event-triggered DPC framework. The triggering instants for four subsystems are depicted in Figure 6, by which it can be seen that all four subsystems solve the optimization aperiodically. Compared with time-triggered mechanism, S1, S2, S3, S4 reduce the number of triggers about 81, 54, 72, and 63%, respectively. Therefore, the problem of online computation of predictive control itself and the complexity problem brought by large-scale systems are effectively solved.

Figure 3. States of four agents.

Figure 4. Control inputs of four agents.

Figure 5. Trajectories of J(k) under event-triggered DPC.

Figure 6. Triggering instants for four agents.

5. Conclusion

This work has proposed an event-triggered distributed robust model predictive control for a class of constrained linear discrete-time system with coupled dynamics and bounded disturbances. The event-triggering condition has been derived based on a deviation between actual state and predictive state by ISS theory. It should be pointed out that the proposed strategy, which also works in a decoupled way can not only simplify the whole problem but also reduce the online computation. The dual-mode control strategy is adopted to further saving computation resources. The sufficient conditions for ensuring the feasibility and stability are developed. The four-truck system is applied to demonstrate the effectiveness of the method. Communication between subsystems and coordination strategies will be further considered in the future research to get better overall performance and some network issues such as time delay, packet loss, etc. need to be taken into account in design of algorithm.

Additional information

Funding

This work is supported by National Nature Science Foundation of China [grant numbers 61773162, 61374107, 61673174].

Notes on contributors

Fenglin Yuan

Fenglin Yuan is a postgraduate in school of information science and technology, East China University of Science and Technology. she received her BSc degree from Nanjing University of Technology in 2015. Her research interests include predictive control, event-triggered control, distributed control systems.

Yuanyuan Zou

Yuanyuan Zou is an associated professor in department of automation, Shanghai Jiao Tong University. She received her BSc degree and MSc degree from Ludong University in 2002 and 2005, respectively, and her PhD degree from Shanghai Jiao Tong University in 2009. Her research interests include predictive control, network-based control systems and distributed control systems, smart grid.

Yugang Niu

Yugang Niu is currently a professor in school of information science and technology, East China University of Science and Technology. He received his BSc degree from Hebei Normal University in 1986, and his MSc degree and PhD degree from Nanjing University in 1992. His research interests include stochastic systems, sliding mode control, wireless sensor network, congestion control, smart grid.