Computational modeling of consistent observation of asynchronous distributed computation on N–manifold

Abstract

The present-day distributed computing systems are asynchronous in nature, and they cover heterogeneous nodes as well as networks having geographic distribution scale. These distributed systems are prone to unpredictable network partitioning, communication delay, and node failures. The realizations of consistent observation in such systems are challenging. The traditional models of distributed computation are not fully adequate to incorporate characteristics arising in the new paradigm. Alternatively, the homology and topology based distributed computing models are formulated to gain a new perspective. This paper proposes a computational model of consistent observation of asynchronous distributed computation on N-manifold. The proposed model offers control of granularity of fineness of observation of computation to varying degree. The discrete geometric simulations of computational structures on 3-manifold offer different analytical insights. The extracted lattice chains of distributed computation on manifold illustrate execution dynamics of the system under consideration.

Keywords:

• Distributed computing
• manifold
• lattice
• consistent observation
• sequence
• Hausdorff

PUBLIC INTEREST STATEMENT

The fault detection and analysis of observable distributed computing systems are central to system design. The manifold structural model of observable distributed computing systems would benefit the system designers to carry out fault modeling and analysis in a deterministic system. This paper proposes the analytical formulation of model of observable distributed computation on N-manifold. The analytical model incorporates the varying granularity of observation of computation.

1. Introduction

The modern applications of distributed computing systems are pervasive encompassing traditional cluster or grid systems, cloud computing systems, and mobile distributed systems (Akinwunmi, Olajubu, & Aderounmu, 2016; Babaoglu & Marzullo, 1993; Ranga, Dave, & Verma, 2016). The large-scale distributed computing systems are difficult to deploy maintaining stability and consistency without employing any monitor. The observation of distributed computation is an important factor in ensuring stability of computation (Fidge, 1996; Parlangeli & Notarstefano, 2012). Furthermore, correctness of distributed computation can be determined by incorporating consistency detection mechanism in a sequence of observations of computation (Babaoglu & Marzullo, 1993; Goldberg, Gopal, Lowry, & Strom, 1991). In large-scale mobile distributed systems involving wireless sensor networks, the network partitioning is unpredictable, and it results in random failures of distributed computation on aggregated data. Thus, the applications of monitor to enhance observability and consistency of distributed computation are required in order to generate stable output. The traditional models of distributed computations are constructed by using elements of graph theory and computational logic based formalisms (Garg, Agarwal, & Ogale, 2014; Schwarz & Mattern, 1994). However, a relatively new approach to model distributed computing systems is to employ concepts of algebraic topology and homology (Bauer, Kerber, & Reininghaus, 2014; Conde & Rajsbaum, 2012; Goubault, 2003). The topological models of distributed computing offer analytical insight to complex systems in new perspectives. The topological and homological models help in analyzing distributed systems having large event space, which results in formation of very large space of combinatorial executions. The manifold is a multidimensional space, which can be represented in geometric forms having certain characteristics. The construction of models of consistent observability of asynchronous distributed systems on a manifold would offer analytical insight to the sequences of executions represented as snapshots. Moreover, granularity of fineness of observation can be controlled in such asynchronous systems appropriately.

1.1. Motivation

The consistent observation of sequence of computation in a distributed system is critical to determine correctness of execution (Babaoglu & Marzullo, 1993). The determination of ordering of events in a distributed system is difficult due to enlarged combinatorial execution space of computation. As a result, the observability of distributed systems becomes difficult (Fidge, 1996). The recovery of distributed computation is often required if a fault is detected in the execution sequence. The mechanism of restoring consistent states in a large-scale distributed system involves persistent logging of multiple checkpoints for recovery (Goldberg et al., 1991). However, this mechanism enhances space complexity to a large extent if the combinatorial execution state space is large. Furthermore, determining correct combinatorial execution checkpoint is computationally expensive in a distributed system having a large state space. The realization of monitor of distributed computation is not trivial due to the existence of causal relations between any two pair of events (Schwarz & Mattern, 1994).

The formal modeling of computing systems enables to gain an analytical insight to the complex systems, which facilitates robust designs. For example, a formal specification of dependability of computation in large-scale pervasive systems is constructed (Ayara & Najjar, 2008). The stable predicate detection in distributed computation having infinite run is formulated by restricting the run within finite graph model (Garg et al., 2014). However, constraining the infinite computation on finite structure may invite oscillatory execution pattern incorporating indeterminate convergence. A comparatively new approach to model distributed computing systems involves elements of algebraic topology, lattice theory, and homological algebra offering new insights (Bagchi, 2018; Bauer et al., 2014; Conde & Rajsbaum, 2012; Herlihy & Rajsbaum, 1999). This paper proposes a formal model of consistent observation of a distributed computation on N-manifold. The proposed model does not impose any condition of finiteness of computation. The variable filter function can control the granularity of observation of states in a sequence of computation while maintaining consistency conditions. The main contributions of this paper are as follows.

• Construction of a formal model of observation of asynchronous distributed computing on N-manifold structure

• Integrating filtering method to generate consistent observation of distributed computation

• Incorporation of variability of filter to prepare consistent observation of computation with varying granularity

• Evaluation of resulting manifold structure of distributed computation in 3-D and lattice chain embedding on it

The rest of the paper is organized as follows. Section 2 presents related work. Section 3 describes preliminary concepts. Sections 4 and 5 present construction of distributed computing on N-manifold structure and formulation of consistent observation model, respectively. Section 6 presents analytical properties. Section 7 and 8 describe computational evaluation results and application aspects, respectively. Finally, section 9 concludes the paper.

2. Related work

In general, the formulation of analytical model of distributed computing is performed by using modular graph structures and relational algebraic operators (Rhode, Presicce, Simeoni, & Taentzer, 1999; Sitohang, 2002). The observations of a distributed computation in multiple phases are required in order to determine the controllability of the system. In theory of distributed computing, consistent observation of sequences of computation is a critical factor (Babaoglu & Marzullo, 1993). In general, observability of a distributed system is hard to realize due to combinatorial arrival order of events (Fidge, 1996). A distributed computation can be modeled as a cyclic graph, where nodes represent distributed processes and edges represent networks between processes. The graph structures can be dynamic, and hybrid distributed systems are modeled by using dynamic graphs structures (Kuhn, Lynch, & Oshman, 2010). It is proposed that number theoretic approaches can be successfully applied to determine observability and reachability of paths as well as cycles in an arbitrary graph (Parlangeli & Notarstefano, 2012). Furthermore, the unsolvable systems can be recognized by Eigen analysis. The main challenge of this model is that, detection of a prime number is necessary to realize observability of cycles in the graph, which is computationally expensive. This is because the prime number detection is computationally hard.

The debugging of distributed computation requires rollback recovery in the presence of faults. Researchers have proposed a rollback and reply mechanism to realize restoration of consistent global states in a distributed system (Goldberg et al., 1991). The design requires records of persistent logs and stable checkpoints, which enhances space complexity to a large extent if the combinatorial execution state space is large. Moreover, the determination of causal relationship between events in the event space of a distributed computing is necessary in order to implement computation monitor (Schwarz & Mattern, 1994). The topological models of distributed computing offer an analytical insight to the complex systems. In recent times, distributed computing systems are modeled by employing combinatorial topological structures (Armstrong, 1983; Edelsbrunner & Harer, 2010; Herlihy & Rajsbaum, 1999). The shared memory based distributed computing model is formulated by employing algebraic topology (Conde & Rajsbaum, 2012). The conceptual framework of persistent homology is utilized in modeling distributed computation (Bauer et al., 2014; Zomorodian & Carlsson, 2005). The homotopy theory and topological spaces are employed in modeling the mutual exclusion as well as its complexity in concurrent computing systems (Carson & Reynolds, 1987; Fajstrup, Rauben, & Goubault, 2006; Goubault, 2003; Gunawardena, 1994). However, the homotopy theory needs adaptation while formulating distributed systems due to directional property of homotopy theory.

3. Preliminary concepts

Let $X$ be a point set and ${\tau }_x\subseteq \mathrm{\Omega }(X)$ where $\mathrm{\Omega }(X)$ is a power set of $X$. If the 1-D space represented by $X$ is Euclidean, then the space can be metrized to generate a metric space $(X,d_X)$ by equipping it with a real-valued function, $d_X:X^2\to [0,+\mathrm{\infty })$. The resulting space $(X,d_X)$ is a 1-D finite metric space having size $n=\left|X\right|$ if following axioms are maintained:

(1) $\begin{array}{c}n\in (1,+\mathrm{\infty }),\\ \mathrm{\forall }a,b,c\in X,d_X(a,b)=d_X(b,a),\\ [a=b]\iff [d_X(a,b)=0],\\ d_X(a,c)\le d_X(a,b)+d_X(b,c)\end{array}$(1)

If ${\tau }_x$ represents a topology on $X$, then the resulting topological space induced in the metric space is $(X,d_X,{\tau }_x)$, where $\mathrm{\forall }{A}_i\in {\tau }_x,(A_i,d_X)$ constructs metric subspace. The metric space having topological structure $(X,d_X,{\tau }_x)$ maintains following properties:

(2) $\begin{array}{c}m\in Z^{+},m\in (1,+\mathrm{\infty }),\\ \left\{\varphi ,X\right\}\subset {\tau }_x,\\ [\left\{A_i,A_k\right\}\subset {\tau }_x]\Rightarrow [\left\{A_i\cup A_k\right\}\subset {\tau }_x],\\ \mathrm{\forall }{A}_i\in {\tau }_x,\underset{i=1}{\overset{m}{\cap }}{A}_i\in {\tau }_x\end{array}$(2)

The properties of generalized topological space state that the space is closed under arbitrary union as well as intersection operations. However, the intersection operation should be finite. Let, $N\in Z^{+}\mathrm{\setminus }\left\{1\right\},f_i:B_i\to {\mathrm{\Re }}^N$ be the homeomorphic and invertible function operated on the topological space $B_i\subseteq X$. If $X$ is Hausdorff, then the resulting structure $(B_i,f_i)$ is called a chart on N-manifold (Lee, 2013). If $(B_i\subset X,f_i)$ and $(B_k\subset X,f_k)$ are two charts on N-manifold, then a transition map can be constructed as,

(3) $\begin{array}{c}{B}_i\cap B_k=V,V\ne \varphi ,\\ f_{k\circ }{f_i}^{-1}:f_i(V)\to f_k(V)\end{array}$(3)

The charts $(B_i\subset X,f_i)$ and $(B_k\subset X,f_k)$ are smoothly compatible if $V=\varphi$. An N-manifold is called $C^{\mathrm{\infty }}$- class if the following property is maintained by it,

(4) $\begin{array}{c}r\in {\mathrm{\Re }}^N,\\ -\mathrm{\infty }<\underset{u\to +\mathrm{\infty }}{lim}{D}^u(f_{k\circ }{f_i}^{-1}){|}_r<+\mathrm{\infty }\end{array}$(4)

It can be possible that, an N-manifold is smooth to a degree $v<+\mathrm{\infty }$. Thus, different classes of manifolds can be formed depending on respective natures.

4. Distributed computing on N–manifold

Let $P=\left\{p_i:i\in Z^{+}\wedge i\le N\right\}$ be a set of distributed processes and $Z_0^{+}=Z^{+}\cup \left\{0\right\}$. The set of events local to a distributed process $p_i\in P$ is denoted by $E_i$, where $\varphi \in E_i$. Let $E_P$ be N-dimensional given by $E_P=E_1\times E_2\times ...\times E_N$. If $\mathrm{\forall }{p}_i\in P,C:E_i\to Z_0^{+}$ is a local bijection within individual distributed processes, then $C(T_E)\subset Z_0^{+}$, where $T_E=\underset{i=1}{\overset{N}{\cup }}{E}_i$ and $C(\varphi )=0$. Let, $C_P:E_P\to C(T_E{)}^N$ be such that,

(5) $\mathrm{\forall }\beta \in E_P:C_P(\beta )\in (Z_0^{+}{)}^N$(5)

If $\mathrm{\forall }{p}_i\in P,h_i:E_i\to C_P(E_P)$ is invertible, then a N-manifold $M_N$ is given as,

(6) $\begin{array}{c}{H}_P=\left\{h_i:\mathrm{\forall }{p}_i\in P\right\},\\ M_N=(T_E,H_P)\end{array}$(6)

In the proposed model of distributed computation on N-manifold, the underlying manifold structure is not differentiable due to discrete nature of computing space represented by $T_E$.

4.1. Hausdorff property of computing space

The distributed computing space can be metrized to form metric space by equipping it with a suitable function (Bagchi, 2018). Let a discrete metric $d_S:T_E^2\to [0,+\mathrm{\infty })$ be defined on distributed computing space $T_E$ as,

(7) $\begin{array}{c}\mathrm{\forall }a,b\in T_E,\\ [a=b]\iff [d_S(a,b)=0],\\ [a\ne b]\iff [d_S(a,b)=1]\end{array}$(7)

The resulting computing space $(T_E,d_S)$ is Hausdorff because the following axiom is maintained by it,

(8) $\begin{array}{c}\mathrm{\exists }\epsilon \in (0,1),a\ne b:\\ B_{\epsilon }(a)=\{x:x\in T_E\wedge d_S(a,x)<\epsilon \},\\ B_{\epsilon }(a)\cap B_{\epsilon }(b)=\varphi \end{array}$(8)

This validates that the distributed computing space $T_E$ is metrizable Hausdorff space, which can be mapped on an N-manifold.

4.2. Locally Euclidean space of computation

The set of events local to individual distributed processes can be counted by employing locally applicable monotone logical clock function defined over respective intervals as,

(9) $\begin{array}{c}\mathrm{\forall }{p}_i\in P,\mathrm{\exists }{I}_i\subset Z_0^{+}:\\ C(E_i)\subseteq I_i\end{array}$(9)

The logical clock function $C(.)$ is a local bijection. Hence, the local event spaces of distributed processes can be converted into respective metric spaces $(E_i,d_E)$ if it is equipped with a function, $\mathrm{\forall }A\subset T_E,d_E:A^2\to [0,+\mathrm{\infty })$. This leads to the restriction to local formulation as, $\mathrm{\forall }{p}_i\in P,A\subseteq E_i,d_E:A^2\to [0,+\mathrm{\infty })$. The resulting metrization function is defined as,

(10) $\begin{array}{c}\mathrm{\forall }\left\{a,b\right\}\subset E_i,\mathrm{\exists }x\mathrm{\exists }y\in I_i:\\ x=C(a),y=C(b),\\ d_E(a,b)=\left|x-y\right|\end{array}$(10)

This indicates that $(E_i,d_E)$ is a Euclidean metric space of the asynchronous distributed computation under consideration.

5. Computation observation on manifold

The observability of distributed computation is an important parameter in order to determine stability of systems and to measure control dynamics. The observability of a distributed system enables implementation of consistency detection in execution sequence as well as fault recognition. If a distributed system is designed with possibility of faults other than Fail-Stop mode, then consistent observation of distributed computation is required to ensure error-free execution. This section presents the model of consistent observation of distributed computation on N-manifold having varying granularity of observations.

5.1. The ε_k-fine cut of computation

Given a distributed computation on $M_N$, the computation is not consistent everywhere on $M_N$. The consistency of a computation can be verified by considering computational cuts on $M_N$ preserving snapshot of execution status of distributed processes. A set of N-dimensional cuts on $M_N$ is given by ${\mathrm{\Lambda }}_C\subset \underset{i=1}{\overset{N}{\cup }}{h}_i(E_i)$. The ${\epsilon }_k$-cut of ${\mathrm{\Lambda }}_C$ is a restriction on taking snapshots of execution on $M_N$ preserving consistency of observation of distributed computation. The ${\epsilon }_k$-cut (${\mathrm{\Lambda }}_k$) is defined by following axioms for ${\epsilon }_k,k\in Z^{+}$,

(11) $\begin{array}{c}{\mathrm{\Lambda }}_k\subset {\mathrm{\Lambda }}_C:\\ {\epsilon }_k\in (0,+\mathrm{\infty }),x_i=C(a_i\in E_i),\\ {\mathrm{\Lambda }}_k=\left\{(x_1,x_2,...,x_N):x_i\in Z_0^{+}\wedge d_E(a_i,a_k\in E_k)\le {\epsilon }_k\right\}\end{array}$(11)

Evidently, $\mathrm{\forall }{\epsilon }_k>0$, the ${\mathrm{\Lambda }}_k$ may not provide meaningful information about execution states of computation. This is due to the fact that, a widely dispersed cut on $M_N$ for a sufficiently large ${\epsilon }_k$ would violate consistency of observation of computation considering varying execution states of a group of processes in asynchronous distributed computing systems. If $S_{\epsilon }=\left\{{\epsilon }_k:k\subset Z^{+}\right\}$ represents a set of choices to generate ${\epsilon }_k$-cut on $M_N$, then an acceptable value to perform consistent observation in finite form is given by

(12) ${\epsilon }_d=inf(S_{\epsilon })$(12)

Thus, the finest possible observation ${\mathrm{\Lambda }}_d$ of an asynchronous distributed computation can be performed by maintaining the following axioms,

(13) $\begin{array}{c}{\mathrm{\Lambda }}_d\subset {\mathrm{\Lambda }}_k:\\ {\epsilon }_d=1,\\ {\mathrm{\Lambda }}_d=\left\{(x_1,x_2,...,x_N):x_i\in Z_0^{+}\wedge d_E(a_i,a_k\in E_k)\le {\epsilon }_d\right\}\end{array}$(13)

The coarse grained observation can be performed by considering ${\epsilon }_e=sup(S_{\epsilon })$ and $d_E(a_i,a_k\in E_k)\le {\epsilon }_e$. Hence, the variation of fineness of observation of asynchronous distributed computation can be performed on N-manifold.

5.2. Consistency and filter model

The manifold $M_N$ generated by distributed computing is not consistent everywhere within the space. Thus, an arbitrary function sequence on N-manifold of asynchronous distributed computation, given by $F_N=(h_i{)}_{i=1}^{i=N}$, may not be computationally consistent everywhere. The consistency can be maintained by employing a filter function on the N-manifold. Let all possible cuts of execution on N-manifold be given by ${\mathrm{\Lambda }}_M=\underset{\mathrm{\forall }{\epsilon }_k\in S_{\epsilon }}{\cup }{\mathrm{\Lambda }}_k$. A predicate $\mathrm{\Gamma }(\beta )\in \left\{0,1\right\}$ determines consistency of cut $\beta \in E_P$ by evaluating the predicate in corresponding event space given as,

(14) $E_{\mathrm{\Gamma }}=\left\{\beta :C_P(\beta )\in {\mathrm{\Lambda }}_M\right\}$(14)

Any generalized and arbitrary cuts of distributed computation are not observably consistent. Hence, a filter is required to generate consistent cuts out of a set of cuts of computation. Let us assume that $\mathrm{\Gamma }(\beta )=1$ signifies consistent cut on N-manifold. Let a function be given as,

(15) $A\subset (Z_0^{+}{)}^N,B\subseteq A,g:A\to B\cup \left\{\varphi \right\},\left[g(a\in A)=g(b\in B)\right]\Rightarrow \left[a=b\right]$(15)

The function $g(.)$ is a filter function on cuts on execution manifold if it satisfies the following axioms,

(16) $\begin{array}{c}A\subseteq {\mathrm{\Lambda }}_M,\mathrm{\forall }\beta \in E_{\mathrm{\Gamma }}:\\ [\mathrm{\Gamma }(\beta )=1]\Rightarrow [(g_{\circ }{C}_P)(\beta )\in B],\\ [\mathrm{\Gamma }(\beta )=0]\Rightarrow [(g_{\circ }{C}_P)(\beta )\notin B]\end{array}$(16)

The filter function $g(.)$ checks the validity of stable predicate while filtering out inconsistent cuts on manifold. The granularity of observable consistent cuts is determined by restricting the variations of clocks within cuts having finite limits. This indicates the non-commutative composition, $\mathrm{\forall }{h}_i\in H_P,g_{\circ }{h}_i(.)$, can be further restricted to generate a set of consistent observation on N-manifold at appropriate granularity having ${\epsilon }_k$-fineness by maintaining following conditions,

(17) $\begin{array}{c}{B}_k\subset B:\\ \mathrm{\exists }{\epsilon }_k\in S_{\epsilon },\\ [(g_{\circ }{C}_P)(\beta )\in B_k]\Rightarrow [(g_{\circ }{C}_P)(\beta )\in {\mathrm{\Lambda }}_k]\end{array}$(17)

In another view, it can be considered as an additional refinement to control the granularity of observation of computation.

5.3. Lattice embedding on N-manifold

Let the ${\epsilon }_k$-fine and consistent snapshot of observation of a distributed computation on $M_N$ be $B_k$. Let a partial ordering relation $<\subset B_k^2$ be constructed on $M_N$ maintaining lattice properties. If $L\subseteq B_k$, then a lattice chain $(L,<)$ can be formed by maintaining the following condition,

(18) $\mathrm{\forall }{l}_x,l_y\in L:[(l_x,l_y)\in <]\oplus [(l_y,l_x)\in <]$(18)

It is important to note that $(L,<)$ is an execution lattice chain in N-manifold. Evidently, an execution lattice chain represents a consistent sequence of observations of asynchronous distributed computation on the respective manifold.

6. Analytical properties

6.1 Theorem: The space (X, d_X) is not Hausdorff, where $\mathit{X}=\bigcup _{i=1}^{N}C\left(E_i\right)$ and ${\mathit{d}}_{\mathit{X}}\left(\mathit{x}\mathbf{\in }\mathit{X}\mathbf{,}\mathit{y}\mathbf{\in }\mathit{X}\right)\mathbf{=}$ $\left|\mathit{x}\mathbf{-}\mathit{y}\right|$.

Proof: Let $A\subset T_E$ such that $\mathrm{\exists }a\in E_i,\mathrm{\exists }b\in E_k,\left\{a,b\right\}\subset A$. However, there is no globally consistent clock in any distributed systems and $C(T_E)\subset Z_0^{+}$. Thus, the following axioms can be satisfied by a distributed computing system,

(19) $\begin{array}{c}C(E_i)\cap C(E_k)=D,\\ D\ne \varphi ,\\ [C(a)\in D\wedge C(b)\in D]\iff [d_X(C(a),C(b))=0]\end{array}$(19)

Hence, $\mathrm{\exists }\epsilon >0$ such that, if $B_{\epsilon }(C(a))=\{x:d_X(C(a),x)<\epsilon \}$ and $B_{\epsilon }(C(b))=\{y:d_X(C(b),y)<\epsilon \}$, then the following axiom is satisfied,

(20) $\begin{array}{c}a\ne b,\\ B_{\epsilon }(C(a))\cap B_{\epsilon }(C(b))\ne \varphi \end{array}$(20)

Hence, the space $(X,d_X)$ is not Hausdorff under local logical clock.

6.2 Theorem: If $C\left(E_i\right)\subseteq I_i$ and $I_i\cap I_k=\varphi$ for $i\ne k$, then (X, d_X) is Hausdorff.

Proof: As before, let be $X=\underset{i=1}{\overset{N}{\cup }}C(E_i)$ in a distributed computing system. However, for any two intervals $I_i\cap I_k=\varphi$ in the system if $i\ne k$. Moreover, any distributed computing system maintains following axiom due to monotone property of logical clock,

(21) $\begin{array}{c}\mathrm{\forall }{p}_i\in P:\\ [\left\{a,b\right\}\subset E_i\wedge \left\{C(a),C(b)\right\}\subset I_i]\Rightarrow [C(a)\ne C(b)]\end{array}$(21)

Hence, the global computation in the respective distributed system will maintain the following property,

(22) $\mathrm{\forall }x,\mathrm{\forall }y\in X,d_X(x,y)>0$(22)

Thus, $(X,d_X)$ is a metric space. As every metric space is Hausdorff, hence $(X,d_X)$ is Hausdorff.

7. Computational evaluation

The computational evaluation is performed through simulation considering 3-manifold ($M_3$), which is made up of execution event spaces of three distributed processes. The simulation is performed through Discrete Computational Geometry (DCG) modeling technique considering 3-D shapes. The shapes are constructed based on sets containing discrete data points using mesh topology. The data grid lines are spaced in equal distribution (50:50) to maintain topological mesh without any skew. The metric (norm) is fixed to constant positive integer value that equals to 02 while constructing the grid lines. The distributed computational structures represented as manifold shapes are simulated by considering four different network communication models. The simulation considers a closed group of three processes representing a distributed system on 3-manifold. The group communication models between processes considered in experimentation are: (1) unreliable cyclic unicast in monotone (UCU), (2) reliable cyclic unicast (RCU), (3) unreliable cyclic broadcast (UCB), and (4) reliable cyclic broadcast (RCB). The execution spaces of distributed processes are consisting of local event spaces of individual processes mapped under monotone logical clock function in positive integer range including origin ($Z^{+}\cup \left\{0\right\}$). 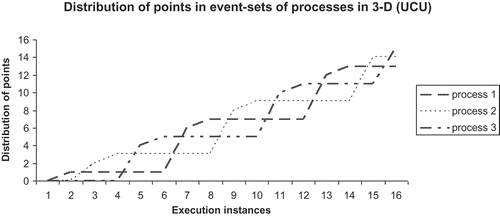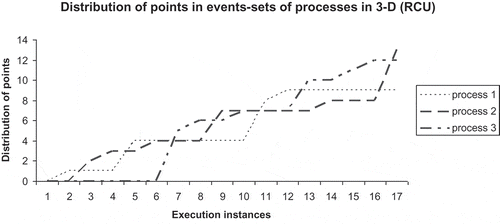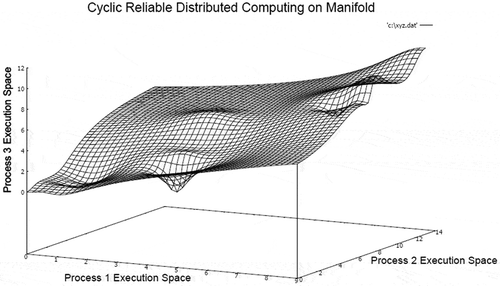The $M_3$ manifold structure is constructed by following the consistent execution sequences. The sets of inconsistent sequences of distributed computation are discarded by applying filter function. The snapshots of distribution profiles of points in sets in 3-D in UCU mode and RCU mode are illustrated in Figures 1 and 2, respectively.

Figure 1. Distribution profile of points in 3-D in UCU mode.

Figure 2. Distribution profile of points in 3-D in RCU mode.

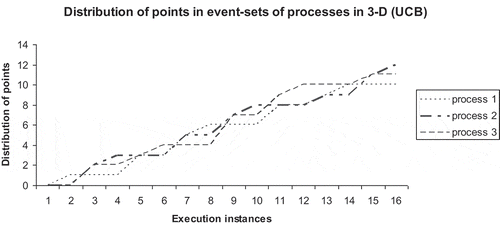
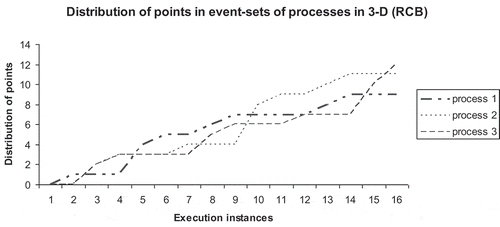
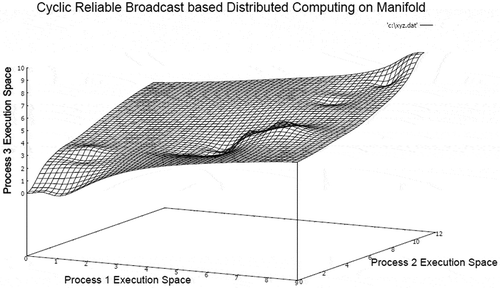
The corresponding snapshots of distribution profiles of points in sets in UCB and RCB modes are presented in Figures 3 and 4, respectively.

Figure 3. Distribution profile of points in 3-D in UCB mode.

Figure 4. Distribution profile of points in 3-D in RCB mode.

The detailed description about resulting manifold structures and embedded lattice chains are presented below considering reliable and unreliable communication models. The process execution spaces on 3-D axes in manifold structures represent execution events-spaces of distributed processes, which are dynamic in nature having combinatorial forms.

7.1. Experiment I: unreliable network communication

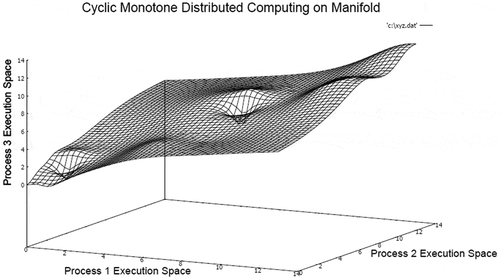
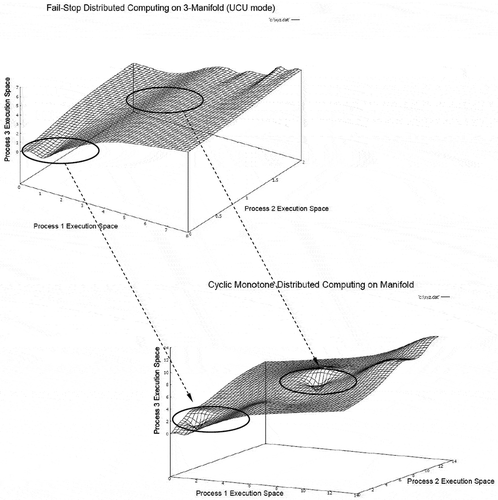
The 3-manifold structure of distributed computation for UCU communication model is presented in Figure 5. In this case, the group of processes synchronizes computation involving a shared variable by using unreliable unicasts in repeated cycles between a pair of processes in the group.

Figure 5. Distributed computing manifold using cyclic unreliable unicast.

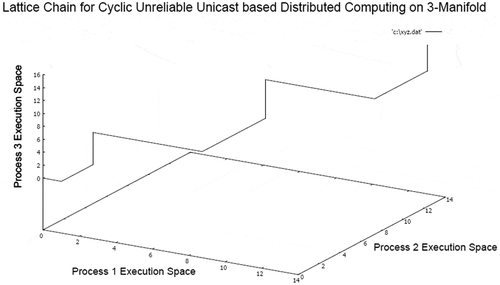
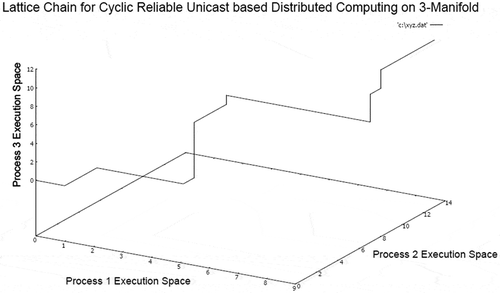
The 3-manifold structure illustrates existence of multiple local supremum and infimum points. However, a global supremum and infimum can be computed representing global state of computation. The majority of surface areas are relatively smoother during computation indicating finite bound in computation. In this model of computation, the overall message complexity is minimum in stable network condition because the communication is cyclic unicast and no acknowledgment is transacted between processes. The corresponding embedded lattice chain on 3-manifold representing a consistent distributed computing sequence is presented in Figure 6.

Figure 6. Execution lattice chain on 3-manifold for unreliable unicast based computing.

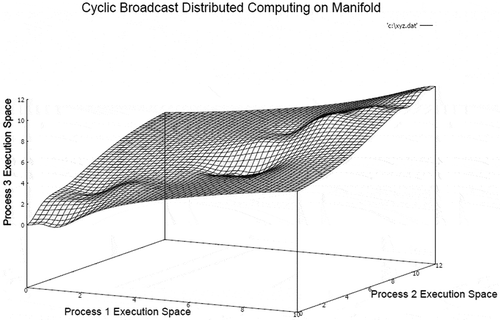
The lattice chain illustrates the presence of an apparently periodic structure, which is inline to the cyclic nature of synchronization between processes in the closed group. In the next experiment step, the unicast communication model is converted to broadcast network communication model (UCB) in the closed group. The resulting 3-manifold structure generated by distributed computation is presented in Figure 7.

Figure 7. Distributed computing manifold using cyclic unreliable broadcast.

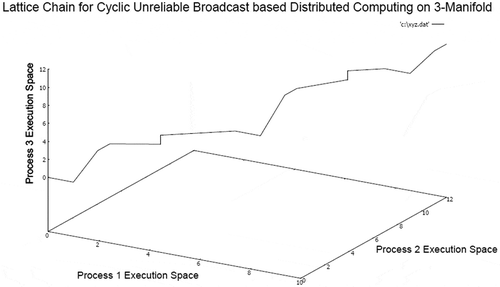
In this case, the processes in a closed group perform broadcasts in cycles without considering reliability of messages. It is considered in simulation that no two messages can be simultaneously sent or received by any process at a single time instant. The 3-manifold structure illustrates that distance between different local supremum and infimum points are reduced if the network is relatively stable. The overall smoothness of the surface is maintained in the majority of places with localized convex and concave deformations depending on the nature of process states. The corresponding embedded lattice chain of consistent distributed computing sequence is presented in Figure 8.

Figure 8. Execution lattice chain on 3-manifold for unreliable broadcast based computing.

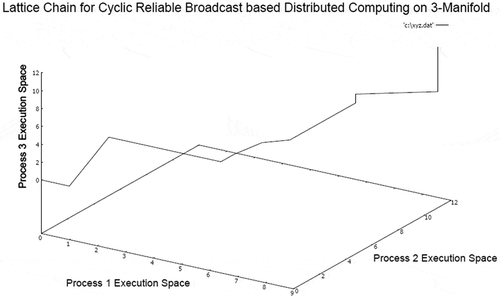
The lattice chain embedded on 3-manifold of UCB model represents that apparent periodicity of computation exists with relative dispersion. The dispersion effect is due to the time dilation required for completing a broadcast in a closed group.

7.2. Experiment II: reliable network communication

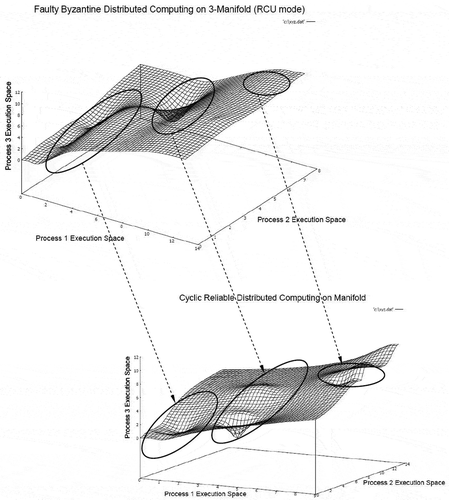
In this experimental set, the unreliable network communication models are changed by incorporating reliability in communication. The simulation model implements First-In-First-Out (FIFO) model of network communication. In the first experimentation, the UCU model is converted into RCU by incorporating reliability in the FIFO network communication. The resulting 3-manifold structure generated by distributed computation is presented in Figure 9.

Figure 9. Distributed computing manifold using cyclic reliable unicast.

In this case, the number of local supremum and infimum points are reduced, and surface appears to be relatively uniform locally (but not strictly uniform globally). The overall smoothness of the surface is moderately enhanced as compared to unreliable systems. The reason is that transitions are highly synchronized in reliable systems having bidirectional communication. The overall message complexity is higher in this 3-manifold as compared to unreliable unicast model. The corresponding embedded lattice chain of consistent distributed computing is presented in Figure 10.

Figure 10. Execution lattice chain on 3-manifold for reliable unicast based computing.

Evidently, the apparent presence of any periodicity is reduced, and the computation proceeds in phases. There are several discrete transitions between phases of distributed computation. The reason is that the cyclic synchronization forms several closed-loop graphs in RCU model of distributed computation. The 3-manifold structure generated by RCB model of network communication is presented in Figure 11.

Figure 11. Distributed computing manifold using cyclic reliable broadcast.

In this case, the processes in the closed group perform synchronization by using reliable broadcast in repeated cycles. However, no two messages can be simultaneously sent or received by any process at a single time instant, which is inline to real-life implementation of data communication. The global smoothness of the surface is further enhanced due to complete synchronization between every process in the system with reliable communications. The message complexity is highest in this case. The surface of RCB 3-manifold appears to be locally uniform covering a larger section indicating communication reliability and complete covering of the group of processes in each cycle. The corresponding lattice chain embedded on RCB 3-manifold is presented in Figure 12.

Figure 12. Execution lattice chain on 3-manifold for reliable broadcast based computing.

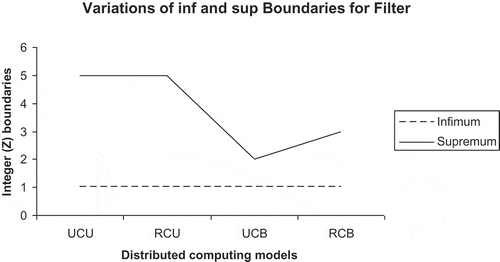
The lattice chain of RCB communication based distributed computation illustrates reduced frequency of discrete transitions in the sequence of consistent computation. This signifies the existence of highest reliability of data and distributed synchronization in a process group. The dynamics of controlled filter values for generating consistent execution sequence of distributed computation is presented in Figure 13.

Figure 13. Variations for infimum/supremum of fineness boundaries of observation filter.

The infimum of filter is kept fixed at lowest value (unity), and the supremum is varied while maintaining consistency of observation of distributed computation.

8. Application aspects—faults detection in computation

The modern approaches to analyze distributed computation employ various geometric analysis techniques. These techniques effectively result in shape analysis in order to detect consistency of computation in structural forms. For example, the simplicial complexes and topological models of distributed computation form a set of dynamic graph like shapes, which helps in determining consistency of computation (Conde & Rajsbaum, 2012; Herlihy & Rajsbaum, 1999). The manifold is a geometric structure, and its application helps in determining consistency of observation of distributed computation in N-dimensional space. The manifold structure employed in this paper facilitates computational shape analysis in order to detect inconsistency in observable distributed computation. The two main faults that occur in a distributed computation are: Fail-Stop fault and Byzantine fault. The faults are simulated by distribution of points in events space of processes with skews. In case of Fail-Stop fault, the points are clustered within event space of a faulty process. However, in case of Byzantine fault, the points are distributed arbitrarily within a sub-space of topological execution space of faulty process having nonconvergent nature. The application of manifold structure to detect fail-stop fault in distributed computing (UCU mode) is illustrated in Figure 14.

Figure 14. Deformation in distributed computing manifold due to fail-stop fault.

The first (top) surface of Figure 14 represents distributed computing having fail-stop fault within execution space of process 2. The local deformations are indicated on the surfaces representing fail-stop and regular computations in UCU mode. The manifold of a faulty distributed computation appears to be smoother with respect to regular manifold structure due to partial blocking of global execution space eliminating transitions. The deformation on manifold due to Byzantine fault in process 2 execution space in RCU mode of computation is illustrated in Figure 15.

Figure 15. Detecting Byzantine fault in distributed computing manifold (RCU mode).

The Byzantine fault induces a highly localized distortion in a bounded region. The distortion is severe due to Byzantine nature of fault in computation enhancing unpredictability. The manifold outside this region of deformation appears to be relatively smoother than regular distributed computation. This is due to the partial blocking of other processes due to existence of a Byzantine (faulty) process in the system. These examples illustrate the application of manifold model of distributed computation to monitor a system by detecting the existence of different types of failures of computation in a deterministic system. It would help the distributed systems designers to formulate and analyze possible fault models a priori along with detection of locality of faults in a system.

9. Conclusions

The observation of an asynchronous distributed computation is required in order to maintain stability in an execution sequence. The consistency of computation is evaluated for generating correct output of computation and to detect faults. The consistent observation of large-scale asynchronous distributed systems is challenging due to enlarged events space. The construction of computational model on manifold structure helps in gaining analytical insights to complex systems. The formulation proposed in this paper offers a model and analysis of consistent observation of asynchronous distributed computation on N-manifold. The fineness of consistent observation can be controlled by employing filter. The simulations of resulting structures offer better understanding of the dynamics of the computation in view of analysis.

Additional information

Funding

The author received no direct funding for this research.

Notes on contributors

Susmit Bagchi

Susmit Bagchi has received BSc (Honors) in 1993 from Calcutta University, B.E. in Electronics Engineering in 1997 from Nagpur University, M.E. in Electronics and Telecommunication Engineering in 1999 from Bengal Engineering and Science University (presently IIEST). He obtained PhD (Engineering) in Information Technology in 2008 from IIEST. Currently, he is Associate Professor in Department of Aerospace and Software Engineering (Informatics), Gyeongsang National University, Jinju, South Korea. His research interests are in Distributed Computing and Systems.