An improved particle swarm optimization based on the reinforcement of the population initialization phase by scrambled Halton sequence

Abstract

The use of meta-heuristic methods for solving nonlinear engineering and optimization problems is one of the paramount topics that attracted the attention of the researchers. Particle swarm optimization (PSO) is an optimization algorithm which has inspired by birds flocking. However, like other methods, PSO has some disadvantages such as problems in finding the best global minimum or trapping in the local minima in some special problems. In some works, the initial particles are randomly set using uniform or Gaussian distributions. These particles sometimes fail to cover the search space completely. The main goal of this paper is to improve the mechanism of the initial population production stage in the first step to cover the feasible space properly. So, with the help of the scrambled Halton sequence and producing quasi-random numbers, the initial population has been generated in a mathematical way without making a lot of change in the original PSO algorithm and its structure. These particles cover the search space more efficiently. This new hybrid algorithm is named the Halton-PSO in this research. The results show that Halton-PSO improves the ability and efficiency of PSO. The performance and ability of the proposed Halton-PSO algorithm have been examined by 11 benchmark functions and 7 different nonlinear engineering problems. Both of the optimization results of test functions and the real problems demonstrate that the Halton-PSO method is more successful than the original PSO and the PSO family algorithms and the other methods for distinguishing the global best minimum.

Keywords:

• Particle swarm optimization (PSO)
• scrambled Halton sequence
• Halton-PSO
• Benchmark function optimization
• engineering problem optimization

PUBLIC INTEREST STATEMENT

In this work a very popular and common optimization method named PSO is modified. Optimization methods are widely used in many topics e.g. engineering, financial problems and etc. The main purpose is to find the minimum of a goal function. Particle Swarm Optimization is one the most famous algorithm to find the best solution in different cases. So, it is significant to improve the performance of it. In this paper we used quasi-random numbers (scrambled Halton sequence) to heighten the capability of PSO and modified it.

1. Introduction

In recent years, various optimization algorithms had been used to solve engineering problems and provide optimal solutions to them. In contrary to classical algorithms, the new optimization techniques are implemented to evaluate the non-differentiable and non-continues optimization problems. Most of the meta-heuristic methods have been acquired by inspecting and studying the behavior of the mammals live in nature (Eberhart et al., 2001; Yang, 2010a).

The exploration and exploitation capabilities are two major features that make the meta-heuristic algorithms powerful to find the global optimum. In fact, the exploration phase of an algorithm helps to search for the feasible space for new results and finding the global optimum. On the other hand, in the exploitation phase, for choosing the best solution, the algorithm searches the neighborhood of the highest quality solution. So, the balance of these two phases is very important, and an efficient algorithm provides a good exploration phase in the inception of the process and a good exploitation ability in the final stages (Yang, 2010b).

One of the well-known meta-heuristic optimization algorithms is the particle swarm optimization (PSO), and it is based on principles such as population, the intelligent particles, and motion. This algorithm implements the social behavior of animals such as fish and bird flocks (Kennedy & Eberhart, 1995). By using the comprehensive of swarm intelligence, this method makes up new solutions. Since this algorithm has a few adjustable parameters, its implementation is very convenient. These characteristics have attracted researchers from various fields of science to use this algorithms in their studies such as harmonic elimination problem in PWM inverter (R. N. Ray et al., 2009), oil industry (Assareh et al., 2010), artificial neural networks (Chau, 2007), optimization of reservoir operation (SaberChenari et al., 2016), social networks (Rui et al., 2017), power system stability (Khadanga & Satapathy, 2015) and etc. However, the PSO has two main problems: 1) some of the particles walk into a local minimum trap and cannot find new solutions, and 2) the best solution is converged in the very first steps of the optimization procedure. Overcoming these difficulties involves many researchers from all over the world and many types of PSO had been introduced. Some of these researches are teaching-learning-based optimization (Shi & Eberhart, 1998a), self-organizing hierarchical PSO with time-varying acceleration coefficients (Ratnaweera et al., 2004), adaptive acceleration coefficients (Zjyu & Dingxue, 2009), PSO with asymmetric time-varying acceleration coefficients (Bao & Mao, 2009), a mathematical model of diverse particles groups called autonomous groups (Mirjalili et al., 2014a), time-varying accelerator coefficient (Cui et al., 2008) and combination of PSO, convergence and divergence operators for problems (Mahmoodabadi et al., 2012).

On the other hand, some of the researchers used the ability of other optimization methods to amplify the exploration and exploitation phases of the PSO method. For instance, PSO and Ant Colony Algorithm (PS-ACO) (Shuang et al., 2011), GA and PSO hybrid (Gray, 2016; Premalatha et al., 2009), gravitational search method with PSO (Mirjalili & Mohd Hashim, 2010), PSO-dragonfly method (Sree Ranjini & Murugan, 2017), PSO and multi-crossover of GA and Bee Colony mechanism (HEPSO) (Mahmoodabadi et al., 2014), PSO with Quantum behavior (IQS-QPSO) (Amini et al., 2019) and PSO with sine cosine algorithm and Levy flight (PSOSCALF) (Nezamivand Chegini et al., 2018) are some of these investigations.

The original PSO in the initialization step scatters the particles randomly. It is expected that by improving the initialization, the final results of PSO would be more exact. A number of researchers have tried to use other methods to improve the searching strategy in PSO. Song et al. (2007) used tent-map chaotic PSO (TCPSO) to avoid trapping to local minima and improve the searching performance of standard PSO. Dong et al. (2012) proposed an evolutionary circle detection method based on opposition-based learning (OBL) that was employed in the Chaotic Hybrid Algorithm (CHA) for the population initialization step. An improved PSO algorithm combined with the piecewise linear chaotic map (PWLCPSO) is proposed by Xiang et al. (2007).

There are various ordinary Monte Carlo methods that employ random numbers. Quasi-Monte Carlo is one of them produced highly uniform quasi-random numbers in the structure of Monte Carlo pseudorandom numbers. These methods are widely applied in many subjects especially in multidimensional domains (Niederreiter, 1992; Spanier & Maize, 1994). Halton sequence is one of the renowned low-discrepancy sequences and used in many Quasi-Monte Carlo applications. So, the Halton sequence could employ random numbers that have a mathematical structure and this strengthens the exploration phase and covers the search space by a logical method. Ganesha et al. (2016) applied optimal Halton sequences to only for 4 benchmark functions with PSO to understand and obtained some results and data to make a comparison between Halton sequences family. They did not apply this method to any engineering problems.

In this paper, Halton-PSO introduced to improve the operation of the original PSO algorithm. This method is based on a combination of the Halton sequence and the PSO algorithm. In this algorithm, the initial particles are produced by the scrambled Halton sequence. This proposed method examined by 11 different benchmark functions and 7 different nonlinear engineering problems. The Halton-PSO has placed 1^th in ranking among other benchmark functions and performs well in reaching the best solutions. The Halton-PSO has increased the capability of PSO in exploration phase and covers the search space very well. On the other hand, proposing a mathematical method instead of using a random number make the Halton-PSO stronger and more reliable. After that, the main spirit of PSO is still untouched and the simplicity of this method is preserved.

The rest of this paper is organized as follows: Section 2 provides a brief review of the PSO method. In Section 3, the Halton sequence and scrambled Halton sequence introduced. Section 4 introduces a combination of PSO with the scrambled Halton sequence. The benchmark functions, results of the proposed method and comparison of this algorithm with the other meta-heuristic algorithms are shown in Section 5. Section 6 shows the capability of Halton-PSO in solving engineering problems. Finally, Section 7 concludes the current study.

2. The particle swarm optimization

The PSO method is originated from simulating the social attribute of the population of birds. After data simulation, the researchers presented their optimization method in 1995 (Eberhart & Kennedy, 1995).

The population is defined as the following set:

(1) $\mathit{S}=\left\{x_1,x_2,\dots x_N\right\}$(1)

where N is the number of the particle (candidate solution). The position vector for each particle is defined as follows:

(2) $x_i={\left(x_{i1},x_{i2},\dots ,x_{in}\right)}^TϵA,i=1,2,\dots ,N$(2)

It is assumed that objective function f(x) is available for all particles of $A$ so that each particle has a unique function value $f_i=f\left(x_i\right)$. Also, all particles of the search space are frequently moving. These movements can be defined with the help of velocity definition in the following form:

(3) $v_i={\left(v_{i1},v_{i2},\dots ,v_{in}\right)}^T,i=1,2,\dots ,N$(3)

where $T$ represents the number of repetitions. The position of the particle and its velocity are indicated as $x_i\left(t\right)$ and $v_i\left(t\right)$, respectively.

The PSO memorizes the positions of particles as $P=\left\{p_1,p_2,\dots ,p_N\right\}$. $P$ explains the best position that every particle has ever met.

The positions are in the form of $p_i={\left(p_{i1},p_{i2},\dots ,p_{in}\right)}^{T}A,i=1,2,\dots ,N$ and $p_i\left(t\right)=ar{g}_{t}min{f}_i\left(t\right)$that $t$ is the number of repetitions.

The aim of the algorithm is to approximate the global optimum that has been observed by all particles during the run. Consider $g$ as the index of best position with the lowest amount of objective function in $p$, in a certain number of repetition $t$, the formula is as below:

(4) $p_g\left(t\right)=ar{g}_{i}minf\left(p_i\left(t\right)\right)$(4)

The velocity and position updating equations in the PSO technique are as follows:

(5) $v_{ij}\left(t+1\right)=\mathrm{w}{v}_{ij}\left(t\right)+c_1{R}_1\left(p_{ij}\left(t\right)-x_{ij}\left(t\right)\right)+c_2{R}_2\left(p_{gj}-x_{ij}\left(t\right)\right)$(5)

(6) $x_{ij}\left(t+1\right)=x_{ij}\left(t\right)+v_{ij}\left(t+1\right)i=1,2,\dots ,N,j=1,2,\dots ,n$(6)

where $t$ in the above equations represents the number of repetitions, $R_1$and $R_2$ are random values with the uniform distribution in the interval of [0,1], and $c_1$and $c_2$are weighting factors which $c_1$is the personal learning factor and $c_2$is the social learning factor.

It should be noted that the next version of this equation is affected by each of $c_1$ and $c_2$factors individually (Shi & Eberhart, 1998b). Inertia weight factor $w$ is embedded in order to consider the effect of velocity $v_{ij}\left(t\right)$during the run of the algorithm. Therefore, it is desirable that the value of $w$ to be decreased by time. In general, the linear reduction of factor $w$ is calculated as follows (Sun et al., 2011):

(7) $w\left(t\right)=w_{up}-\left(w_{up}-w_{low}\right)\frac{t}{T_{max}}$(7)

where $t$ represents the number of repetitions, $w_{up}$ and $w_{low}$ are upper and lower limits of $w$ factor and $T_{max}$ is the total number of repetitions. The weight factor in the convergence of particles plays a vital role. This factor adjusts the contrast between the capability of the population in local search and global search (Parsopoulos, 2010).

In this paper, Equations (8(8) $c_1\left(t\right)=c_{1min}+\left(\frac{t_{max}-t}{t_{max}}\right)+\left(c_{1max}-c_{1min}\right)$(8) ) and (9(9) $c_2\left(t\right)=c_{2max}+\left(\frac{t_{max}-t}{t_{max}}\right)+(c_{2min}-c_{2min}$(9) ) show that $c_1$ and $c_2$ linearly have been changed (Amini et al., 2019):

(8) $c_1\left(t\right)=c_{1min}+\left(\frac{t_{max}-t}{t_{max}}\right)+\left(c_{1max}-c_{1min}\right)$(8)

(9) $c_2\left(t\right)=c_{2max}+\left(\frac{t_{max}-t}{t_{max}}\right)+(c_{2min}-c_{2min}$(9)

where $c_{1min}$ and $c_{1max}$ are the minimum and maximum values of the personal learning factor, and $c_{2min}$ and $c_{2max}$ are the minimum and maximum values of the social learning factor.

3. Halton sequence

The Halton number sequence is created by Van der Corput sequences. In the production of this sequence, every nonnegative integer $g$ can be written uniquely using a prime base $r$ as follows:

(10) $g=\sum _{l=0}^L{b}_l\left(g\right)r^l$(10)

where $0\le b_l\left(g\right)\le r$. Then for the r-ray expansion in the Equation (10)(10) $g=\sum _{l=0}^L{b}_l\left(g\right)r^l$(10) , the function ${\phi }_r\left(g\right):\mathbb{N}\to \left[0,1\right)$ defined as follows:

(11) $r=\sum _{l=0}^L{b}_l\left(g\right)r^{-l-1},g\in \mathbb{N}$(11)

The Equation (11)(11) $r=\sum _{l=0}^L{b}_l\left(g\right)r^{-l-1},g\in \mathbb{N}$(11) is called radical inverse function base $r$. The obtained sequence ${\phi }_{r,N}\left(g\right)=\left\{{\phi }_r\left(g\right):g=0,1,2,\dots ,N\right\}$ is known as Van der Corput sequence. Halton extended this definition and generated a set of points in s-dimensional space as follows:

(12) $\phi \left(g\right)=\left({\phi }_{r1}\left(g\right),{\phi }_{r2}\left(g\right),\dots ,{\phi }_{rs}\left(g\right)\right)in{\left[0,1\right)}^s$(12)

where $r1,r2,\dots ,rs$ are $S$ distinct prime numbers (Fasshauer, 2007).

3.1. The scrambled Halton sequence

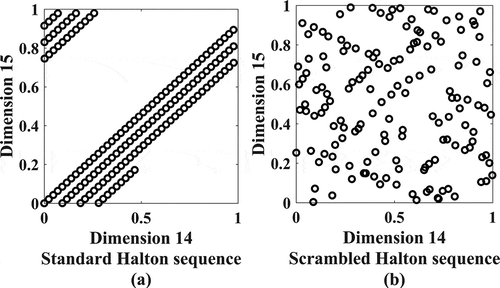
The main problem of the standard Halton sequence as discussed is when the number of dimensions increased a strong correlation occurred. It is caused by the cycle of size the prime number $r$. So in conditions which two big prime-based sequences with large dimensions coupled, the result for this S-dimensional cube is looked as located on parallel straight lines. As an example, the 14^th dimension exposes number 43 and the 15^th dimension which exposes prime number 47 include 43 and 47 rising numbers, respectively. This produces a correlation between these two numbers coordinates of the sequence. This is shown in Figure 1(a). The results for Halton Sequence in large dimensions are lost their unification as shown.

Figure 1. One hundred and fifty draws of standard and scrambled Halton sequences

Several methods have been proposed to improve the unification of the standard Halton sequence with large dimensions. The main approach is scrambled the cycles of length number $r$ to split the correlations among the coordinates of the standard Halton sequence. This is achieved by the combination of the coefficients $b_l$ in the radical inverse function of Equation (10)(10) $g=\sum _{l=0}^L{b}_l\left(g\right)r^l$(10) . The consequence of scrambled Halton sequence is proposed as:

(13) ${\phi }_r\left(g\right)=\sum _{l=0}^L{\sigma }_r(b_l\left(g\right))r^{-l-1}$(13)

where ${\sigma }_r$ is the operator of the combination on the numbers of the expansion $b_l\left(g\right)$ (the standard Halton sequence is the unique example of the scrambled Halton sequence with no scrambling of the numbers $b_l\left(g\right))$. Many researchers (Braaten & Weller, 1979; Hellekalek, 1984,; Kocis & Whiten, 1997) have proposed the variety of methods for achieving the combination of the coefficients $b_l$ in Equation (13)(13) ${\phi }_r\left(g\right)=\sum _{l=0}^L{\sigma }_r(b_l\left(g\right))r^{-l-1}$(13) . The algorithm adopted in the current study corresponds to that of Kocis & Whiten (1997). Figure 1 exposes the unification covering of the scrambled Halton sequence relative to the standard Halton sequence.

4. Proposed method: Halton-PSO

The first and one of the most essential steps which should be considered at the beginning of the PSO is how to scatter particles in search space. It is very important that initial particles cover the search space properly and if any mistakes take place in this step, the whole method will not efficiently work. To prevent this issue, the researchers proposed the different approaches in the initial step of the optimization process for covering the search space based on the specification of a cost function (Eberhart et al., 2001; Kennedy & Eberhart, 1995). To develop PSO, most of the researchers concentrate to change and improve the main structure of PSO and its coefficient such as $c_1,c_2\mathrm{a}\mathrm{n}\mathrm{d}w$. Thus, the initialization of PSO has not been investigated like other sections of the algorithm.

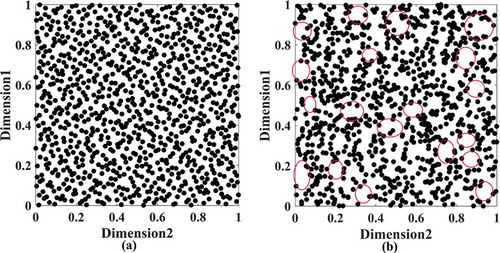
Some of the previous studies commonly consider the initial points without any specific method and usually, randomly (Kennedy & Eberhart, 1995). So, it has seen there is a great potential to investigate in the step of the PSO initialization. This could be considered to implement new mathematical methods and algorithms to improve the initialization at the beginning of PSO. In this paper, the scrambled Halton sequence has been used to produce diverse solutions and increase the exploration capability of PSO in the beginning steps of the optimization process. This statistic sequence helps PSO to generate initial particles, which are more reliable than random points. For better understanding, Figure 2 is drawn to demonstrate the effect of the Halton sequence in generating the initial population. This figure obviously illustrates the search space covering with 1000 particles in the initialization of the PSO algorithm with the use of the Halton sequence in the Halton-PSO, and a random function already utilized in previous researches. In Figure 2(b), there are several areas that are not covered with particles and shown by circles. These areas are covered as shown in Figure 2(a) properly. It is clear that the feasible space is searched by Halton-PSO to find the best solution very well. The simplicity of PSO encourages the scientist to apply it to a wide range of benchmark functions and engineering problems. The Halton sequence managed a part of this algorithm and do not impose any complicated statement or equation on PSO. So, the main characteristics of PSO still are untouched. On the other hand, the Halton-PSO establishes a general perspective on the effectiveness of initial points and makes it easy to compare and analyses the results of each method. According to the theory of the scrambled Halton sequence discussed in Section 3, it is revealed that this method faces no problem when the dimensions of a problem are increased.

The Halton-PSO can be described by following pseudo-code:

Generate an initial population with the scrambled Halton sequence (instead of using random numbers) for better covering of feasible space at the beginning of the PSO.

Repeat

For i = 1 to population size do

if $\mathit{f}\left({\mathit{x}}_i\right)$ < $\mathit{f}\left({\mathit{p}}_i\right)$ then ${\mathit{p}}_i={\mathit{x}}_i$;

${\mathit{p}}_g$ = arg min ($\mathit{f}\left({\mathit{p}}_i\right)$);

For j = 1 to D do

Velocity update with Equation (1)(1) $\mathit{S}=\left\{x_1,x_2,\dots x_N\right\}$(1) ;

Position update with Equation (2)(2) $x_i={\left(x_{i1},x_{i2},\dots ,x_{in}\right)}^TϵA,i=1,2,\dots ,N$(2) ;

End//end for loop j

End//end for loop i

Until the termination criterion is met

5. Results and discussion

In this section, the Halton-PSO technique is applied for solving the different benchmark functions. The results of the Halton-PSO have been compared with other algorithms.

Figure 2. Producing 1000 initial particles with (a) Halton-PSO and (b) Randomly

5.1. Parameter setting of Halton-PSO

The adjustable parameters of the Halton-PSO are set according to Table 1.

Table 1. Parameter settings for Halton-PSO

Parameter	C1 min	C2 min	C1max	C2max	Wlow	wup	npop	MaxIt
value	0.5	0.5	2.5	2.5	0.4	0.9	50	500

5.2. Benchmark functions

In this section, 11 benchmark formula for each function is presented (Mirjalili & Lewis, 2016). In Table 2, for each benchmark function utilized in this study, the mathematical formula, range of decision variables and the minimum value are reported. In the first part of Table 2, F1 to F5 functions are related to the unimodal test functions. These functions have only one global optimum point and are excellent to test the convergence rate and the exploitation capability of an optimization algorithm. On the other hand, F6 to F11 test functions are multimodal benchmark functions. They have different local minima solutions in addition to the global optimum point. These functions are ideal for evaluating the exploration because they have multi-local minimum solutions that could test algorithms (Mirjalili & Lewis, 2016).

Table 2. The benchmark functions

Function	$\mathit{d}im$	$\left[{\mathit{X}}_{min},{\mathit{X}}_{max}\right]$	${\mathit{f}}_{min}$
${\mathrm{F}}_1\left(\mathrm{x}\right)=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}^2$	30	[−100,100]	0
${\mathrm{F}}_2\left(\mathrm{x}\right)=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left(\sum _{\mathrm{j}-1}^{\mathrm{i}}{\mathrm{x}}_{\mathrm{j}}\right)}^2$	30	[−100,100]	0
${\mathrm{F}}_3\left(\mathrm{x}\right)=\mathrm{m}\mathrm{a}{\mathrm{x}}_{\mathrm{i}}\left\{\left|{\mathrm{x}}_{\mathrm{i}}\right|,1\le \mathrm{i}\le \mathrm{n}\right\}$	30	[−100,100]	0
${\mathrm{F}}_4\left(\mathrm{x}\right)=\sum _{\mathrm{i}}^{\mathrm{n}-1}\left[100{\left({\mathrm{x}}_{\mathrm{i}+1}-{\mathrm{x}}_{\mathrm{i}}^2\right)}^2+{\left({\mathrm{x}}_{\mathrm{i}}-1\right)}^2\right]$	30	[−30,30]	0
${\mathrm{F}}_5\left(\mathrm{x}\right)=\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left(\left[{\mathrm{x}}_{\mathrm{i}}+0.5\right]\right)}^2$	30	[−100,100]	0
${\mathrm{F}}_6\left(\mathrm{x}\right)=\frac{\pi }{\mathrm{n}}\left\{10sin\left(\pi {\mathrm{y}}_1\right)+\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-1\right)}^2\left[1+10\mathrm{s}\mathrm{i}{\mathrm{n}}^2\left(\pi {\mathrm{y}}_{\mathrm{i}}\right)\right]+{\left({\mathrm{y}}_{\mathrm{n}}-1\right)}^2\right\}+\sum _{\mathrm{i}=1}^{\mathrm{n}}\mathrm{u}\left({\mathrm{x}}_{\mathrm{i}},10,100,4\right)$${\mathrm{y}}_{\mathrm{i}}=1+\frac{{\mathrm{x}}_{\mathrm{i}}+1}{4}\mathrm{u}\left({\mathrm{x}}_{\mathrm{i}},\mathrm{a},\mathrm{k},\mathrm{m}\right)=\left\{\begin{array}{c}k{\left({\mathrm{x}}_{\mathrm{i}}-\mathrm{a}\right)}^{\mathrm{m}},{\mathrm{x}}_{\mathrm{i}}>a\\ 0,-a<{\mathrm{x}}_{\mathrm{i}}<a\\ k{\left(-{\mathrm{x}}_{\mathrm{i}}-\mathrm{a}\right)}^{\mathrm{m}},{\mathrm{x}}_{\mathrm{i}}<-a\end{array}\right.$	30	[−50,50]	0
${\mathrm{F}}_7\left(\mathrm{x}\right)=\sum _{\mathrm{i}=1}^{11}{\left[{\mathrm{a}}_{\mathrm{i}}-\frac{{\mathrm{x}}_1\left({\mathrm{b}}_1^2+{\mathrm{b}}_1{\mathrm{x}}_2\right)}{{\mathrm{b}}_1^2+{\mathrm{b}}_1{\mathrm{x}}_3+{\mathrm{x}}_4}\right]}^2$	4	[−5,5]	0.00030
${\mathrm{F}}_8\left(\mathrm{x}\right)={\left({\mathrm{x}}_2-\frac{5.1}{4{\pi }^2}{\mathrm{x}}_1^2+\frac{5}{\pi }{\mathrm{x}}_1-6\right)}^2+10\left(1-\frac{1}{8\pi }\right)\mathrm{c}\mathrm{o}\mathrm{s}{\mathrm{x}}_1+10$	2	[−5,5]	0.398
${\mathrm{F}}_9\left(\mathrm{x}\right)=\left[1+{\left({\mathrm{x}}_1+{\mathrm{x}}_2+1\right)}^2\left(19-14{\mathrm{x}}_1+3{\mathrm{x}}_1^2-14{\mathrm{x}}_2+6{\mathrm{x}}_1{\mathrm{x}}_2+3{\mathrm{x}}_2^2\right)\right]\times$$[30+{\left(2{\mathrm{x}}_1-3{\mathrm{x}}_2\right)}^2\times \left(18-32{\mathrm{x}}_1+12{\mathrm{x}}_1^2+48{\mathrm{x}}_2-36{\mathrm{x}}_1{\mathrm{x}}_2+27{\mathrm{x}}_2^2\right)$	2	[−2,2]	3
${\mathrm{F}}_{10}\left(\mathrm{x}\right)=-\sum _{\mathrm{i}=1}^7[\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right)(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}{)}^{\mathrm{T}}+{\mathrm{c}}_{\mathrm{i}}{]}^{-1}$	4	[0,10]	−10.4028
${\mathrm{F}}_{11}\left(\mathrm{x}\right)=-\sum _{\mathrm{i}=1}^7[\left(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}\right)(\mathrm{X}-{\mathrm{a}}_{\mathrm{i}}{)}^{\mathrm{T}}+{\mathrm{c}}_{\mathrm{i}}{]}^{-1}$	4	[0, 10]	−10.5363

5.3. Comparison results of Halton-PSO with the PSO Families and the other optimization algorithms

In this section, the results of the Halton-PSO algorithm are compared with other different versions of the PSO algorithm and the other methods. To achieve this purpose, the various functions introduced in Table 2 are used. The PSO family algorithms and the other metaheuristic algorithms that their results are presented in this paper are PSO (Kennedy & Eberhart, 1995), HPSO-TVAC (Ratnaweera et al., 2004), HEPSO (Mahmoodabadi et al., 2014), WOA (Mirjalili & Lewis, 2016), DA (Mirjalili, 2016), SCA (Mirjalili, 2016), GA (Coello, 2000), ALO (Mirjalili, 2015a), MFO (Mirjalili, 2015b), and MVO (Mirjalili et al., 2016). Because of stochastic nature in meta-heuristic algorithms, their results might be suspicious for only one run. So, for comprising each algorithm, each benchmark functions presented in Table 2 used for 30 independent runs and the results are shown in Table 3. The results are reported in Table 3 by statistical characteristics such as mean and standard deviation to compare easily these algorithms with each other.

Table 3. Comparison results of Halton-PSO with PSO families and other optimization algorithms

F		GA	DA	SCA	ALO	FA	MFO	MVO	PSO	HPSO-TVAC	HEPSO	Halton-PSO
F1	Mean	0.633	1.88E+03	3.5881	1.20E-04	2.12E+04	2.33E+03	0.73132	1.44E-08	5.19E-07	16.26772	1.05E-13
	Std.dev.	0.257	2.70E+03	7.0558	5.47E-05	3.55E+03	4.30E+03	0.16252	3.08E-08	2.19E-06	10.01293	2.60E-13
F2	Mean	3.91E+03	1.79E+04	6.20E+03	1.92E+03	2.78E+04	1.93E+04	87.65831	71.66699	2.35E+02	7.42E+03	60.42624
	Std.dev.	1.63E+03	1.08E+04	4.28E+03	9.38E+02	7.76E+03	1.29E+04	40.76549	45.59262	1.77E+02	3.88E+03	66.73438
F3	Mean	4.80456	34.17868	26.86848	12.5792	52.9671	58.69915	1.24477	1.188414	5.09682	23.95145	0.89557
	Std.dev.	1.23984	15.3078	9.70965	3.99733	4.98726	9.39231	0.49953	0.54926	1.39444	7.7146	0.63896
F4	Mean	2.22E+02	5.44E+05	2.15E+04	2.05E+02	2.73E+04	2.68E+06	2.84E+02	35.10321	74.05163	2.38E+03	0.00064
	Std.dev.	1.67E+02	5.61E+05	5.01E+04	4.26E+02	2.08E+04	1.46E+07	4.48E+02	22.1809	48.59594	1.85E+03	4.74E-04
F5	Mean	0.55122	1.99E+03	17.69731	9.99E-05	2.14E+04	1.34E+03	0.68486	1.39E-08	1.69E-07	21.55405	3.78E-13
	Std.dev.	0.2678	2.95E+03	34.6597	5.98E-05	3.63E+03	3.46E+03	0.18549	1.95E-08	3.97E-07	9.33263	1.23E-12
F6	Mean	0.00239	3.35E+05	1.51E+04	10.5912	9.55E+03	5.34522	1.44471	0.0691	0.19379	0.47856	0.03456
	Std.dev.	0.0034	1.54E+06	8.17E+04	5.06278	1.96E+04	4.32243	1.1173	0.11333	0.36667	0.22623	0.06851
F7	Mean	0.00162	0.00249	9.81E-04	0.0042	0.00256	0.00107	0.00406	0.00184	4.15E-04	6.40E-04	0.00064
	Std.dev.	0.00136	0.00362	3.41E-04	0.01221	0.00605	3.60E-04	0.00741	0.00505	3.04E-04	2.80E-04	4.74E-04
F8	Mean	0.39788	0.39788	0.39887	0.39788	0.39788	0.39788	0.39788	0.39788	0.39788	0.39788	0.39789
	Std.dev.	7.02E-07	1.91E-09	0.00104	1.28E-14	1.58E-12	0	7.21E-08	0	3.24E-16	6.59E-13	0
F9	Mean	3	2.99999	3.00003	3	3	2.99999	3	2.99999	2.99999	3	3
	Std.dev.	4.94E-05	4.33E-15	4.39E-05	1.86E-13	4.50E-11	1.56E-15	1.50E-06	7.00E-16	3.06E-15	5.15E-11	9.79E-16
F10	Mean	−8.06141	−8.91052	−4.0216	−7.30542	−5.3993	−8.91931	−8.58003	−6.88146	−8.2024	−10.3997	−10.40294
	Std.dev.	3.39594	2.54882	1.74729	3.24345	3.20939	2.77874	2.89763	3.65169	3.23277	0.01728	8.08E-16
F11	Mean	−8.24148	−8.19558	−4.55529	−7.63839	−5.06227	10.00826	−8.23796	−6.84098	−9.35303	−10.5364	−10.08968
	Std.dev.	3.57812	2.72152	1.21606	3.66626	3.68293	2.01056	3.15534	3.79229	2.72218	5.85E-07	1.70

In this paper, by comparing the results of the benchmark functions, the capability of each algorithm to evaluate the solutions in the search space has been revealed. The results of the algorithms presented in Table 3. The Halton-PSO is ranked 1 in F1, F2, F3, F5, F8, F9, and F10 functions. PSO ranked 1 in F4, GA in F6, HPSO-TVAC in F7 and HEPSO in F11. It is noticeable that in those benchmark functions which the Halton-PSO could not rank in the first place, it achieved to reach the 2nd position which is satisfaction. Therefore, by inspecting the results presented in Table 3, it is concluded that the Halton-PSO method is more efficacious than the other methods to find the best solution in the benchmark functions.

Performance ranking of the algorithms (i.e. the mean best values), as shown in Table 4, provides a specific opportunity to compare the algorithms. It is obvious that Halton-PSO reaches 15 in total rank and places on the top of the algorithms among other methods. The second position is taken by PSO and HPSO-TVAC algorithms with the total rank of 45. By inspecting the Table 4, it is clear that the total rank of other algorithms are at least triple in number and this shows the efficiency of the Halton-PSO.

Table 4. Ranking of the algorithmic performances

Algorithms	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	Total rank	Final rank
GA	5	6	4	5	5	1	6	10	6	7	4	73	5
DA	9	9	9	10	10	11	8	8	10	4	6	94	7
SCA	7	7	8	8	7	10	4	11	11	11	10	94	7
ALO	4	5	6	4	4	8	11	5	2	8	7	64	4
FA	11	11	10	9	11	9	9	7	3	10	9	99	8
MFO	10	10	11	11	9	7	5	2	8	3	11	87	6
MVO	6	3	3	6	6	6	10	9	5	5	5	64	4
PSO	2	2	2	1	2	3	7	2	7	9	8	45	2
HPSO-TVAC	3	4	5	3	3	4	1	4	9	6	3	45	2
HEPSO	8	8	7	7	8	5	3	6	4	2	1	59	3
Halton-PSO	1	1	1	2	1	2	2	1	1	1	2	15	1

5.3.1. Analysis of convergence behaviour

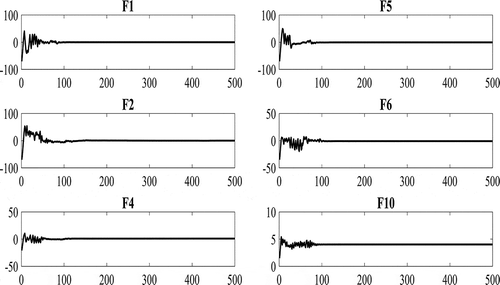
In the first steps of the optimization procedure, the particles should explore the entire design space to produce different solutions and then smoothly converge to the near best solution (Nezamivand Chegini et al., 2018). This has been done to guarantee the capability of the method to search and find the global optimum. To inspect this behavior in the Halton-PSO algorithm in all optimization stages, the variations of the first dimension of the first particle are shown in Figure 3. These fluctuations are exposed to F1, F2, F4, F5, F6, and F10 functions. From Figure 3, it is clear that in the first steps of the method, there are severe variations and then these variations are decreased. In fact, this particle searches the design space for a solution in the initial stages of the optimization process and then converges around the best solution in the final steps.

Figure 3. The trajectory of the first particle in the first dimension

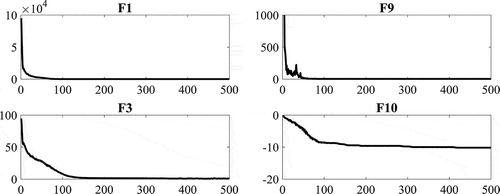
Since it is not possible to judge the improvement of the position of all particles in the optimization process by examining the behavior of a particular particle, therefore, it is necessary to study the behavior of all particles during the optimization procedure (Nezamivand Chegini et al., 2018). To reach this goal, the average fitness of all solutions is shown in Figure 4. The results are evaluated for F1, F3, F9, and F10 functions.

As shown in Figure 4, in early steps, a good exploration behavior is occurred by particles and after that variations are gradually decreased, and finally, exploitation behavior occurs and the average fitness has a very few changes.

Figure 4. The average fitness of all particles during the optimization process

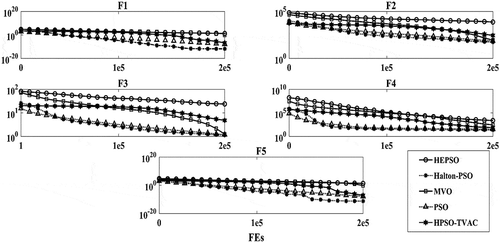
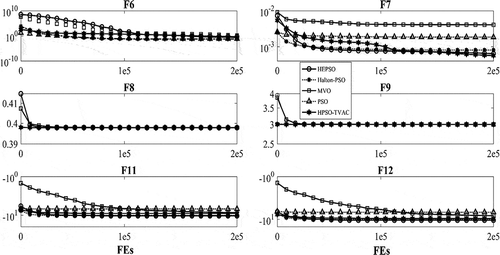
After investigating the behavior of all particles in the Halton-PSO, now the convergence rate of the Halton-PSO is investigated. The average fitness of best solutions during the optimization process for the benchmark functions is illustrated in Figures 5 and 6. These two figures demonstrate the rate of convergence for the most 5 highest ranked algorithms according to Table 4.

In Figure 5, the results are illustrated for convergence curves of the unimodal test functions. In F1, F2, F3, and F5, as the Halton-PSO algorithm ranked first among other algorithms, it improves the solutions continuously and converges to the best solution in the last stages. The rate of convergence of other methods progresses slowly. The Halton-PSO method reaches the optimal solution for F1 to F5 at 18000, 85000, 40000, 50000, and 175000 FEs (Function Evaluations), respectively. It also shows the power of exploitation of the proposed method in the last steps. Also, in these functions, the Halton-PSO has a smooth convergence rate which is very good and shows the ability of this method in the convergence. In fact, the Halton-PSO initial particles search the feasible space in the first of the process very well and this helps this algorithm to convergence better than other methods. In the F4, as the PSO method ranked first, it reaches the best rate of convergence among other methods while the Halton-PSO track the same rate and is very close to the PSO after near 50000 FEs.

In Figure 6, the convergence curves of 6 multimodal functions are presented. As it shows, the convergence curves of the responses obtained by the five algorithms for F8 and F9 are very similar. In the F6 and F7, the solutions of Halton-PSO smoothly converge to the best solution. In the F8 and F9, all of the methods are converged to the solution with approximately a similar rate and the Halton-PSO is also ranked as the first one. In the last two functions, HEPSO and the Halton-PSO show the best convergence rate among the other methods. Also, the Halton-PSO acquires the best optimal results in F6 to F12 at 20000, 30000, 40000, 30000, 40000, and 45000 FEs, respectively.

From Figures 5 and 6, it is obviously clear that the algorithms HEPSO, MVO, PSO, HPSO-TVAC, and the Halton-PSO could reach the global minimum as mentioned in Table 4. Also, it is seen that in the cases where the Halton-PSO placed the first rank among the other methods, it has also a good and satisfied convergence rate. Finally, the proposed algorithm reaches the best solution and determine it in most test functions.

Figure 5. The convergence curve for the unimodal test functions based on the number of function evaluations (FEs)

Figure 6. The convergence curve for the multimodal test functions based on the number of function evaluations (FEs)

6. Halton-PSO for classical engineering problems

The real engineering problems are common approaches for evaluating a meta-heuristic algorithm. Contrary to benchmark functions, most of the engineering problems solutions are unknown. Furthermore, real engineering problems have many various constraints (e.g. equality and inequality constraints). So, the proposed algorithm should be evaluated by constrained problems.

In this section, 7 real nonlinear engineering problems are shown to test the Halton-PSO technique: a gear train design, a pressure vessel design problem, a compression/tension spring, minimization of vertical deflection of an I-Beam, a speed reducer design, a truss design problem with three-bar and a welded beam design problem.

There are various penalty functions that could be used for solving these problems (Coello Coello, 2002). Since the main goal of this paper is not to search for a type of penalty functions, the minimalistic penalty function (the death penalty) has been used. The amount of computation of this approach compared to other penalty functions is very low and the establishment is very simple to evaluate the real constrained optimization problems (Coello Coello, 2002).

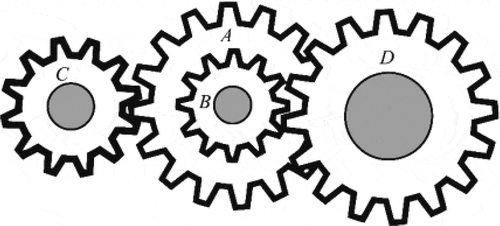
6.1. Gear train design problem

The gear train problem is one of the most well-known unconstrained engineering optimization problems in mechanics. The main goal of this issue is to minimize the ratio of gear as shown in Figure 5. The schematic of this problem has been exposed in Figure 7.

Figure 7. Gear train design problem

The n_A, n_B, n_C and n_D parameters are the tooth numbers of gears which are the design variables of this engineering optimization problem (Gandomi, 2014; Sandgren, 1990). The mathematical formula for this problem is provided in Table A1 in Appendix.

The gear train design is clearly a discrete problem. After evaluating the problem variables, they are round to the nearest integer number and then the objective function has been calculated. Table 5 provides the results of the Halton-PSO algorithm and the other methods in detail. The results are compared with CS (Gandomi et al., 2013), ALO (Mirjalili, 2015a), MFO (Mirjalili, 2015b), MVO (Mirjalili et al., 2016), ISA (Gandomi, 2014), MBA (Sadollah et al., 2013), GA (Coello, 2000), ABC (Sharma et al., 2012), and ALM (Kannan & Kramer, 1994). The term NA means that the values of the design variables are not available. From this table, it is clear that the results of optimal gear ratio obtained by the Halton-PSO algorithm are similar to the other algorithms (CS (Gandomi et al., 2013), ALO (Mirjalili, 2015a), MFO (Mirjalili, 2015b), MVO (Mirjalili et al., 2016), ISA (Gandomi, 2014), and MBA (Sadollah et al., 2013). These results show the efficiency of the Halton-PSO algorithm for solving the engineering discrete problems.

Table 5. Comparison result of the gear train design problem (NA means not available)

Algorithm		ALM	ABC	GA	MBA	ISA	MVO	MFO	ALO	CS	Halton-PSO
Optimal values for variables	$n_A$	33	19	33	43	NA	43	43	49	43	49
	$n_B$	15	16	14	16	NA	16	19	19	16	16
	$n_C$	13	44	17	19	NA	19	16	16	19	19
	$n_D$	41	49	50	19	NA	49	49	43	49	43
Optimal gear ratio		2.1469e-8	2.78e-11	1.362e-9	2.7009e-12	2.7009e-12	2.7009e-12	2.7009e-12	2.7009e-12	2.7009e-12	2.7009e-12

6.2. Pressure vessel design

Minimization of the construction cost of pressure vessel design is the main goal of this engineering problem. These costs include materials, shaping and welding, and associate with geometric parameters of the pressure vessel. So, to reach the minimum cost for design, calculation of the optimal values of the geometric parameters (as shown in Figure 8) is necessary. The formulation of these problems is provided in Table A1 in Appendix (Mirjalili & Lewis, 2016).

Figure 8. Pressure vessel design problem

Table 6 provides the results of Halton-PSO method and the other algorithms (GSA (Mirjalili & Lewis, 2016), WOA (Mirjalili & Lewis, 2016), MFO (Mirjalili, 2015b), MVO (Mirjalili et al., 2016), PSO (He & Wang, 2007), GA (Coello, 2000), ES (Mezura-Montes & Coello Coello, 2008), DE (Li et al., 2007), and ACO (Kaveh & Talatahari, 2010)) for this engineering problem. The efficiency of Halton-PSO is clearly revealed in this problem by providing the best solution among the other algorithms and is able to calculate the best design with the lowest cost.

Table 6. Comparison result for pressure vessel design problem

Algorithm		ACO	DE	ES	GA	PSO	MVO	MFO	WOA	GSA	Halton-PSO
Optimal values for variables	$T_s$	0.8125	0.8125	0.8125	0.9375	0.8125	0.8125	0.8125	0.8125	85388359	0.1930
	$T_h$	0.4375	0.4375	0.4375	0.5	0.4375	0.4375	0.4375	0.4375	0.625	0.0004
	$R$	42.103	42.098	42.098	48.329	42.0912	42.0907	42.0984	2.09826	58.988659	64.7668
	$L$	176.57	176.63	176.64	112.679	176.746	176.738	176.636	176.638	84454202	11.9886
Optimal cost		6059.0	6059.7	6059.7	6410.38	6061.07	6060.80	6059.71	6059.74	85388359	3137.3

6.3. Tension/compression spring design

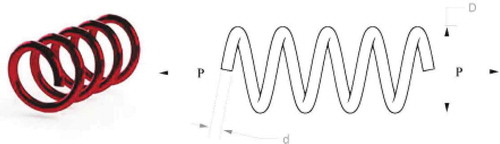
Tension/compression spring is the next engineering problem for evaluating by various algorithms. With four different nonlinear constraints, evaluating the best optimal design parameters to minimize the construction cost of a tension/compression spring is required. Wire diameter (d), mean diameter of spring (D), the number of active coils (N) are parameters that should be calculated. These parameters are shown in Figure 9. The mathematical formulation of this problem with its constraints is shown in Table A1 in Appendix (Mirjalili & Lewis, 2016).

Figure 9. Schematic of the tension/compression spring

This engineering problem was optimized by various optimization algorithms such as GSA (Mirjalili & Lewis, 2016), WOA (Mirjalili & Lewis, 2016), MFO (Mirjalili, 2015b), GWO (Mirjalili et al., 2014b), PSO (He & Wang, 2007), GA (Coello, 2000), ES (Mezura-Montes & Coello Coello, 2008), DE (Li et al., 2007) and RO (Kaveh & Khayatazad, 2012). Table 7 provides the best result for each method in detail. From this table, it is obvious that the Halton-PSO provides the best solution among other algorithms.

Table 7. Comparison result for pressure vessel design problem

Algorithm		RO	DE	ES	GA	PSO	GWO	MFO	WOA	GSA	Halton-PSO
Optimal values for variables	$D$	0.0513	0.0516	0.0519	0.05148	0.05172	0.05169	0.05100	0.05120	0.050276	0.0537
	$D$	0.3490	0.3547	0.3639	0.35166	0.35764	0.35673	0.36410	0.34521	0.323680	0.4058
	$N$	11.762	11.410	10.890	11.6322	11.2445	11.2888	10.8684	12.0040	13.525410	8.9027
Optimum weight		0.0126	0.0126	0.0126	0.01270	0.01267	0.01266	0.01266	0.01267	0.0127022	0.0126981

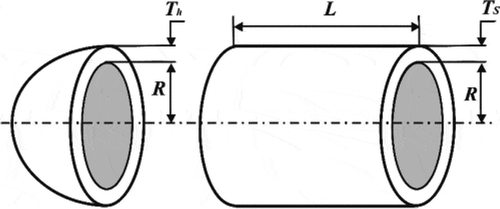
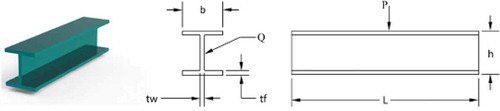
6.4. Minimization of vertical deflection of an I-Beam

Minimization of vertical deflection of an I-Beam is another engineering problem that can appear the capability of Halton-PSO in such cases. This problem has shown in Figure 10. Finding the optimal geometric parameters related to the cross-section of I-beam shaped is required. Length (b), height (h) and thicknesses $t_w$ and $t_f$ are the design parameters in this problem. These parameters should be evaluated to reach the cross-section of the beam smaller or equal to 300$c{m}^2$. The formulation of this problem is presented in Table A1 in Appendix (Mirjalili, 2015b).

Figure 10. I–beam design problem

This engineering problem was optimized by Halton-PSO and various meta-heuristic optimization algorithms such as CS (Gandomi et al., 2013), MFO (Mirjalili, 2015b), ARSM and IARSM (Wang, 2003), and SOS (Cheng & Prayogo, 2014). Table 8 provides the results of this problem for each algorithm. From Table 8, it is considered that the best results achieved by the Halton-PSO and the MFO.

Table 8. Comparison results for I-beam design problem

Algorithm		SOS	IARSM	ARSM	MFO	CS	Halton-PSO
Optimal values for variables	$b$	50	48.42	37.05	50	50	50
	$h$	80	79.99	80	80	80	80
	$t_w$	0.9	0.9	1.71	1.7647	0.9	1.7647
	$t_f$	2.32179	2.4	2.31	5	2.321675	5
Optimal cost		0.0130741	0.131	0.0157	0.0066259	0.0130747	0.0066

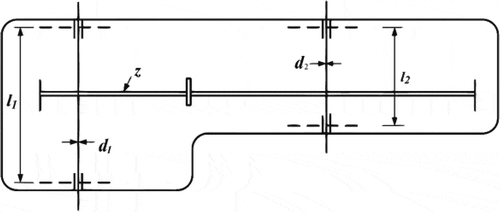
6.5. Speed reducer design

Speed reducer design is the next engineering problem that evaluated by Halton-PSO and the other meta-heuristic algorithms. Figure 11 shows a schematic of the problem. The building cost of the speed reducer is the objective function in this problem. Face weight (b), a module of teeth (m), number of teeth on pinion (z), the length of shaft 1 between bearings ($l_1$), the length of shaft 2 between bearings (l2) are the design parameters that are required to optimize. Nonlinear inequalities and equalities and the objective function are mathematically formulated and introduced in Table A1 in Appendix (Mirjalili et al., 2016).

Figure 11. Schematic of the speed reducer

Table 9 reports the results of this engineering problem by using the Halton-PSO algorithm and various optimization techniques (CS (Gandomi et al., 2013), TAS (Kuang et al., 1998), SBS (Akhtar et al., 2002; T Ray & Saini 2001; Montes et al., 2003). Table 9 shows that Halton-PSO by far has obtained the best optimal cost in comparison with other meta-heuristic methods. On the other hand, results that TAS and Ray and Saini evaluated are violated the constraints and are infeasible. So, CS and SBS are ranked second and third, respectively.

Table 9. Comparison results for speed reducer design

Algorithm		Montes and Coello	Ray and Saini	SBS	TAS	CS	Halton-PSO
Optimal values for variables	$b$	3.506163	3.514185	3.506122	3.6	3.5015	3.5
	$M$	0.700831	0.700005	0.700006	0.7	0.7	0.7
	$Z$	17	17	17	17	17	17
	$l_1$	7.460181	7.497343	7.549126	7.3	7.6050	7.3
	$l_2$	7.962143	7.8346	7.85933	7.8	7.8181	7.8
	$d_1$	3.3629	2.9018	3.365576	3.4	3.3520	2.9
	$d_2$	5.3090	5.0022	5.289773	5	5.2875	5.2865
Optimal cost		3025.005	2732.9006 (Infeasible)	3008.08	2876.117623 (Infeasible)	3000.9810	1909.9

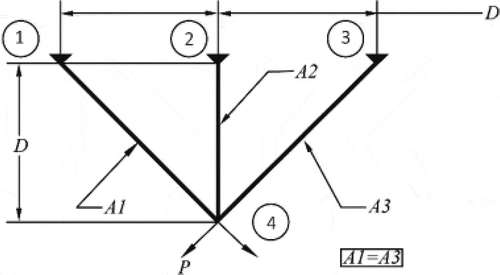
6.6. Truss design problem with three-bar

Another engineering problem that has been solved by the Halton-PSO is the truss design problem with three-bar. Minimization of the truss-weight without exceeding the deformation, buckling and tension constraints is required. In other words, determination of optimal values for a cross-section of $A_1$ and $A_2$ without violating the constraints is suitable. Figure 12 shows the parameters. The mathematical formulation of this engineering problem is given in Table A1 in Appendix.

Figure 12. The three-bar truss design problem

Many researchers have implemented many optimization algorithms to evaluate this problem (Gandomi et al., 2013; Liu et al., 2010; Mirjalili, 2015a, 2015b; Sadollah et al., 2013; Mirjalili et al., 2016; Tsai, 2005; Zhang et al., 2008). Table 10 has shown the capability of Halton-PSO and other meta-heuristic algorithms (CS (Gandomi et al., 2013), ALO (Mirjalili, 2015a), MFO (Mirjalili, 2015b), MVO (Mirjalili et al., 2016), MBA (Sadollah et al., 2013), DEDS (Zhang et al., 2008), Tsa (Tsai, 2005), and PSO-DE (Liu et al., 2010)) to evaluate the results of optimum cost of this engineering problem. Table 10 shows that the Halton-PSO and some of the other methods such as ALO (Mirjalili, 2015a), MVO (Mirjalili et al., 2016), DEDS (Zhang et al., 2008), and PSO-DE (Liu et al., 2010) are very close. This reveals the ability of Halton-PSO to resolve non-linear constrained problems.

Table 10. Comparison results of the three-bar truss design problem

Algorithm		PSO-DE	Tsa	DEDS	MBA	MVO	MFO	ALO	CS	Halton-PSO
Optimal values for variables	$A_1$	0.788675	0.788	0.7886	0.7885	0.78860	0.78824	0.78866	0.78867	0.7887
	$A_2$	0.40824	0.408	0.4082	0.4085	0.40845	0.40946	0.40828	0.40902	0.4083
Optimum cost		263.8958	263.68	263.89	263.89	263.895	263.985	263.895	263.971	263.8958

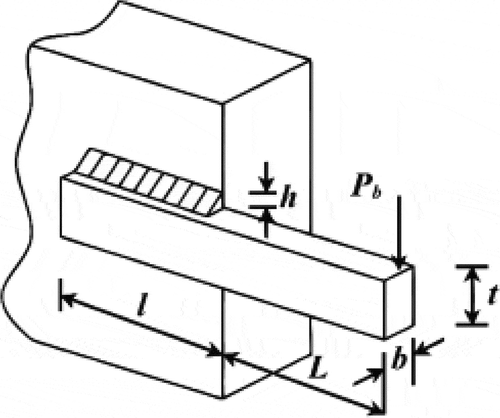
6.7. Welded beam design problem

The last engineering problem of this section is the welded beam design problem as shown in Figure 13. Shear stress ($\tau$), bending stress ($\sigma$), buckling load on the beam ($P_c$) and end deflection of the beam ($\delta$) are the constraints governing this problem. Weld thickness (h), the clamped bar length (L), the bar height (T) and the bar thickness (b) are four parameters of this problem. This nonlinear engineering optimization problem is mathematically formulated and shown in Table A1 in Appendix (Mirjalili & Lewis, 2016).

Figure 13. Schematic of welded beam design

Table 11 shows the results of this engineering problem obtained by the Halton-PSO and the other optimization methods such as WOA (Mirjalili & Lewis, 2016), GSA (Mirjalili & Lewis, 2016), MFO (Mirjalili, 2015b), MVO (Mirjalili et al., 2016), GWO (Mirjalili, Mirjalili $1., 2014b), RO (Kaveh & Khayatazad, 2012), GA (Coello, 2000), Random (Ragsdell & Phillips, 1976), and CPSO (Krohling & Dos Santos Coelho, 2006). The best optimal cost is evaluated by the Halton-PSO and does not violate any of the constraints. MFO and GWO are ranked second and third algorithms, respectively.

Table 11. Comparison of results for the welded beam design problem

Algorithm		CPSO	Random	GA	RO	GWO	MVO	MFO	GSA	WOA	Halton-PSO
Optimal	$H$	0.202369	0.4575	0.2489	0.20368	0.2056	0.2054	0.2057	0.1821	0.2053	0.1445
Values	$L$	3.544214	4.7313	6.1730	3.52846	3.4783	3.4731	3.4703	3.8569	3.4842	2.8365
For	$T$	9.048210	5.0853	8.1789	9.00423	9.0368	9.0445	9.0364	10	9.0374	9.0361
Variables	$b$	0.205723	0.6600	0.2533	0.20724	0.2057	0.2056	0.2057	0.2023	0.2062	0.2058
Optimal cost		1.73148	4.1185	2.4331	1.73534	1.7262	1.7264	1.7245	1.8799	1.7304	1.5714

7. Conclusion

Researchers select the initial particles of PSO randomly. This random selection fails to cover the search space as well as required. So, the exploration of the PSO algorithm needs to be better. To solve this issue, the Halton-PSO is proposed in this paper. This method is the combination of the Halton sequence and the original PSO. Then, the Halton-PSO performance compared with some of the different renowned PSO family algorithms. To reach this goal, 11 benchmark functions were used. Analyzing the convergence behavior of the test functions shows that the proposed algorithm is more successful than the other optimization algorithms in most of these functions. Therefore, the exploration problem faced in PSO is improved. On the other hand, the results of the Halton-PSO algorithm showed that this method provides a high-quality solution in design engineering problems with unknown search space. In fact, the capability of this method is proved for solving real constrained engineering problems with various characteristics and conditions.

The main purpose of this paper was to strengthen the initial population production phase in PSO optimization. On the other hand, applying the Halton sequence cannot solve the problems of early convergence and trapping into the local optimum. In fact, these problems can be overcome by enhancing the exploration phase in the early stages and the exploitation phase at the end of the optimization process. The balance between the exploration and exploitation phases during the optimization process is dependent on the velocity and position equations of the PSO algorithm. Combining the Halton sequence with position update equations to prevent early convergence can be recommended as future work.

Additional information

Funding

The authors received no direct funding for this Research.

Notes on contributors

Pouriya Amini Digehsara

This paper is a part of a greater project about signal processing, optimization methods, data mining and fault detection which is undergoing at University of Guilan. This new algorithm will be used for the future work as a section for the optimization part.

Appendix

Table A1. Engineering problems mathematical formulation and details

Problem	Decision Variables	Cost Function	Constraints	Variables Range
Gear Train Design Problem	$\vec{\mathrm{x}}=\left[{\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3,{\mathrm{x}}_4\right]=\left[{\mathrm{n}}_{\mathrm{A}},{\mathrm{n}}_{\mathrm{B}},{\mathrm{n}}_{\mathrm{C}},{\mathrm{n}}_{\mathrm{D}}\right]$	$\mathrm{f}\left(\vec{x}\right)={\left(\frac{1}{6.931}-\frac{x_3{x}_2}{x_1{x}_4}\right)}^2$	-	$12\le {\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3,{\mathrm{x}}_4\le 60$
Pressure Vessel Design	$\vec{x}=\left[x_1,x_2,x_3,x_4\right]=\left[T_s,T_h,R,L\right]$	$\mathrm{f}\left(\vec{\mathrm{x}}\right)=19.84{x_1}^2{x}_3+3.1661{x_1}^2{x}_4+1.7781x_2{x_3}^2+0.6224x_1{x}_3{x}_4$	$g_1\left(\vec{\mathrm{x}}\right)=-x_1+0.0193x_3\le 0$$g_2\left(\vec{\mathrm{x}}\right)=-x_3+0.00954x_3\le 0$$g_3\left(\vec{\mathrm{x}}\right)=-\pi {x_3}^2{x}_4-\frac{4}{3}\pi {x_3}^3+1296000\le 0$$g_4\left(\vec{\mathrm{x}}\right)=x_4-240\le 0$	$0\le x_1,x_2\le 99$$10\le x_3,x_4\le 200$
Tension/Compression Spring Design	$\vec{x}=\left[x_1,x_2,x_3\right]=\left[d,D,N\right]$	$\mathrm{f}\left(\vec{\mathrm{x}}\right)=\left(x_3+2\right)x_2{x}_1^2$	$g_1\left(\vec{\mathrm{x}}\right)=1-\frac{{x_2}^3{x}_3}{71785x_1^4}\le 0$$g_2\left(\vec{\mathrm{x}}\right)=\frac{4{x_2}^3-x_1{x}_2}{125666\left(x_2{x}_1^3-x_1^4\right)}+\frac{1}{5108x_1^2}\le 0$$g_3\left(\vec{\mathrm{x}}\right)=1-\frac{140.45x_1}{{x_2}^2{x}_3}\le 0$$g_4\left(\vec{\mathrm{x}}\right)=\frac{x_1+x_2}{1.5}\le 0$	$0.05\le x_1\le 2$$0.25\le x_2\le 1.3$$2\le x_3\le 15$
Vertical Deflection of an I-Beam	$\vec{x}=\left[x_1,x_2,x_3,x_4\right]=\left[b,h,t_w,t_f\right]$	$\mathrm{f}\left(\vec{x}\right)=\frac{5000}{\frac{t_w{\left(h-2t_f\right)}^3}{12}+\frac{b{t}_f^3}{6}+2b{t}_f{\left(\frac{h-t_f}{2}\right)}^2}$	$g_1\left(\vec{\mathrm{x}}\right)=2b{t}_w+t_w\left(h-2t_f\right)\le 0$	$10\le x_1\le 50$$10\le x_2\le 80$$0.9\le x_3,x_4\le 5$
Speed Reducer Design	$\vec{x}=\left[x_1,x_2,x_3,x_4,x_5,x_6,x_7\right]=\left[b,m,z,l_1,l_2,d_1,d_2\right]$	$\mathrm{f}\left(\vec{x}\right)=0.7854x_1{x}_2^2\left(3.3333x_3^2+14.9334x_3-43.0934\right)-1.508b\left(x_6^2+x_7^2\right)+7.477\left(x_6^3+x_7^3\right)+0.7854(x_4{x}_6^2+x_5{x}_7^2$	$g_1\left(\vec{\mathrm{x}}\right)=\frac{27}{x_1{x}_2^2{x}_3}-1\le 0$$g_2\left(\vec{\mathrm{x}}\right)=\frac{397.5}{x_1{x}_2^2{x}_3^2}-1\le 0$$g_3\left(\vec{\mathrm{x}}\right)=\frac{1.93}{x_2{x}_3{x}_4^3{x}_6^4}-1\le 0$$g_4\left(\vec{\mathrm{x}}\right)=\frac{1.93}{x_2{x}_3{x}_5^3{x}_7^4}-1\le 0$$g_5\left(\vec{\mathrm{x}}\right)=\frac{\sqrt{{\left(\frac{745x_4}{x_2{x}_3}\right)}^2+1.69\times {10}^6}}{110x_6^3}-1\le 0$$g_6\left(\vec{\mathrm{x}}\right)=\frac{\sqrt{{\left(\frac{745x_6}{x_2{x}_3}\right)}^2+157.5\times {10}^6}}{85x_7^3}-1\le 0$$g_7\left(\vec{\mathrm{x}}\right)=\frac{x_2{x}_3}{40}-1\le 0$$g_8\left(\vec{\mathrm{x}}\right)=\frac{5x_2}{x_1-1}-1\le 0$$g_9\left(\vec{\mathrm{x}}\right)=\frac{x_1}{12x_2}-1\le 0$	$2.6\le x_1\le 3.6$$0.7\le x_2\le 0.8$$17\le x_3\le 28$$7.3\le x_4\le 8.3$$7.8\le x_5\le 8.3$$2.9\le x_6\le 3.9$$5\le x_7\le 5.5$
Truss Design Problem with Three-Bar*	$\vec{x}=\left[x_1,x_2\right]=\left[A_1,A_2\right]$	$\mathrm{f}\left(\vec{x}\right)=\left(2\sqrt{2}{x}_1+x_2\right)l$	$g_1\left(\vec{\mathrm{x}}\right)=\frac{2\sqrt{2}{x}_1+x_2}{\sqrt{2}{x}_1^2+2x_1{x}_2}P-\sigma \le 0$$g_2\left(\vec{\mathrm{x}}\right)=\frac{x_2}{\sqrt{2}{x}_1^2+2x_1{x}_2}P-\sigma \le 0$$g_3\left(\vec{\mathrm{x}}\right)=\frac{1}{2\sqrt{2}{x}_2+x_1}P-\sigma \le 0$	$0.05\le x_1,x_2\le 2$
Welded Beam Design**	$\vec{x}=\left[x_1,x_2,x_3,x_4\right]=\left[h,L,T,b\right]$	$\mathrm{f}\left(\vec{x}\right)=1.10471x_1^2{x}_2+0.04811x_3{x}_4\left(14+x_2\right)$	$g_1\left(\vec{\mathrm{x}}\right)=\tau \left(\vec{\mathrm{x}}\right)-{\tau }_{max}\le 0$$g_2\left(\vec{\mathrm{x}}\right)=\sigma \left(\vec{\mathrm{x}}\right)-{\sigma }_{max}\le 0$$g_3\left(\vec{\mathrm{x}}\right)=\delta \left(\vec{\mathrm{x}}\right)-{\delta }_{max}\le 0$$g_4\left(\vec{\mathrm{x}}\right)=x_1-x_4\le 0$$g_5\left(\vec{\mathrm{x}}\right)=P-P_c\left(\vec{\mathrm{x}}\right)\le 0$$g_6\left(\vec{\mathrm{x}}\right)=\frac{1}{8}-x_1\le 0$$g_7\left(\vec{\mathrm{x}}\right)=1.10471x_1^2+0.04811x_3{x}_4\left(14+x_2\right)-5\le 0$	$0.1\le x_1,x_4\le 2$$0.1\le x_2,x_3\le 10$

$\ast l=100cm,P=2\frac{KN}{c{m}^2},\sigma =2\frac{KN}{c{m}^2}$

$\ast \ast \tau \left(\vec{\mathrm{x}}\right)=\sqrt{{\left({\tau }^{\prime }\right)}^2+2{\tau }^{\prime }{\tau }^{{ }^{\prime \prime }\frac{x_2}{2R}}+{\left({\tau }^{\prime \prime }\right)}^2},{\tau }^{\prime }=\frac{P}{\sqrt{2}{x}_1{x}_2},{\tau }^{\prime \prime }=\frac{MR}{J},M=P\left(L+\frac{x_2}{2}\right),$

$R=\sqrt{\frac{x_2^2}{4}+{\left(\frac{x_1+x_3}{2}\right)}^2},J=2\left\{\sqrt{2}{x}_1{x}_2\left[\frac{x_2^2}{4}+{\left(\frac{x_1+x_2}{2}\right)}^2\right]\right\},$

$\sigma \left(\vec{\mathrm{x}}\right)=\frac{6PL}{x_4{x}_3^2},\delta \left(\vec{\mathrm{x}}\right)=\frac{6P{L}^3}{E{x}_3^2{x}_4},P_c\left(\vec{\mathrm{x}}\right)=\frac{4.013E\sqrt{\frac{x_3^2{x}_4^6}{36}}}{L^2}\left(1-\frac{x_3}{2L}\sqrt{\frac{E}{4G}}\right)$

$P=6000lb,L=14in,{\delta }_{max}=0.25in,E=30\times {10}^{6}psi,G=12\times {10}^{6}psi,{\tau }_{max}=13600psi,{\sigma }_{max}=30000psi$