Determination of the optimal shape of matrix elements partitioning on three abstract heterogeneous processors

Abstract

The paper presents the results of a study done to find the optimal shapes of matrix element partitioning on three abstract heterogeneous processors when performing multiplication operations. An abstract processor model allows applying the research results in systems with different heterogeneous architectures. To determine the optimal partitioning shape, the work uses non-rectangular candidate shapes identified by Ashley DeFlumere in her work as a result of applying the technology of redistribution of matrix elements between the processors «push»: Square Corner, Rectangle Corner, Square Rectangle, Block Rectangle, L-Rectangle, Traditional 1D Rectangular. The optimality of shapes is determined for four classes of matrix multiplication algorithms: Serial Communication with Barrier (SCB), Parallel Communication with Barrier (PCB), Serial Communication with Bulk Overlap (SCO) and Parallel Communication with Overlap (PCO). The Hockney model was used to evaluate the communication complexity of algorithms. Mathematical models of the algorithm execution time were introduced in the paper for each considered candidate shape in all algorithms. Based on the developed mathematical models, software was developed that allows to select the form of elements partitioning between processors, depending on the ratio of their speeds and latency of the transmission medium.

Keywords:

• parallel computing
• parallel matrix multiplication
• data partitioning
• heterogeneous parallel systems
• hockney model
• serial communication with barrier
• parallel communication with barrier
• serial communication with overlap
• parallel communication with overlap

PUBLIC INTEREST STATEMENT

The paper presents the results of a study done to find the optimal shapes of matrix element partitioning on three abstract heterogeneous processors when performing multiplication operations. An abstract processor model allows applying the research results in systems with different heterogeneous architectures. To determine the optimal partitioning shape, the work uses non-rectangular candidate shapes identified by Ashley DeFlumere as a result of applying the technology of redistribution of matrix elements between the processors «push»: Square Corner, Rectangle Corner, Square Rectangle, Block Rectangle, L-Rectangle, Traditional 1D Rectangular. The optimality of shapes is determined for four classes of matrix multiplication algorithms: Serial Communication with Barrier, Parallel Communication with Barrier, Serial Communication with Bulk Overlap and Parallel Communication with Overlap. The Hockney model was used to evaluate the communication complexity of algorithms. Mathematical models of the algorithm execution time were introduced in the paper for each considered candidate shape in all algorithms.

1. Introduction

The amount of processed information and the complexity of computational tasks grow every year. In this regard, the field of parallel data processing research became more and more popular all over the world.

Parallel multiplication of matrices is one of the most popular tasks in various fields of scientific knowledge. In particular, such tasks may include work with connectivity matrices and correspondences in information, engineering and transport networks that control the main information about objects and flows movement continuity and at the same time has significant length and dynamic elements.

According to the state of the Top500 list as of November 2019, the maximum computing speed of 200 petaflops was reached by the Summit supercomputer developed by IBM for Oak Ridge National Laboratory. Summit is used in astrophysics, cancer research and systems biology; it consists of 4,608 servers (crosspoints) and 2 397 824 cores.

If at the initial stage of development of high-performance computing, the top lines of the rating were mainly occupied by supercomputers built on identical elements, now we can trace a steady trend towards greater efficiency of heterogeneous cluster solutions.

While the models and methods of distributing computing resources when multiplying matrices on homogeneous systems are studied well enough, the search for optimal solutions for heterogeneous systems is still being studied.

The partitioning of matrix elements among computational elements when performing linear algebra operations is performed for the purpose of reducing the total computation time.

At the first stages of scientific research in this area, rectangular data partitioning shapes were defined and studied in detail (Beaumont et al., 2001; Clarke et al., 2012; Lastovetsky, 2007). Later works (DeFlumere, 2014; DeFlumere & Lastovetsky, 2014) showed that non-rectangular shapes of matrix elements partitioning can also be optimal for certain ratios of the computational power of processors. But these works did not take into account the difference in the latency of data transmission networks among computing elements.

The objective of this study is to determine the optimal shapes for matrix partitioning in heterogeneous systems with different latencies between computational elements. A mathematical model is built for four classes of algorithms for parallel matrix multiplication:

• Serial Communication with Barrier (SCB);

• Parallel Communication with Barrier (PCB);

• Serial Communication with Overlap (SCO);

• Parallel Communication with Overlap (PCO).

To construct a mathematical model of computation, the notion of an “abstract processor”, considered in work (Zhong et al., 2011, 2012), is used. Earlier, DeFlumere & Lastovetsky (2014) proved that the model of an abstract processor that is mainly based on the volume of communications and calculations, which accurately forecasts the experimental performance of many processors and even entire clusters for matrix calculations.

The work was done as part of research on the project АР05133699 “Research and development of innovative telecommunication technologies using modern cyber-technical means for the city’s intelligent transport system” of the Institute of ICT of the MES RK.

2. Materials and research methods

For constructing model studies, several assumptions were done:

• square source matrices A, B and the resulting matrix Сwith dimension N × N of its elements are used;

• matrix multiplication operation is simulated on three abstract heterogeneous processors with fully connected topology;

• computing power of abstract processors P, R and S is determined by the ratio P_r:R_r: S_r, where P is the most powerful processor, and S_r = 1. The total processing power of the three-processor system will be equal to T = P_r + R_r + S_r;

• matrix elements are divided among the processors in proportion to their computing power;

• transmission network latency is ${\beta }_1$ between the processors P and S, ${\beta }_2$ between the processors P and R, ${\beta }_3$ between processors S and R;

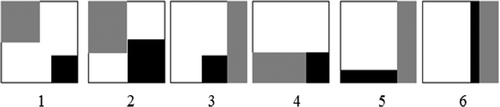
• optimality is evaluated for the following candidate shapes Square Corner (SC), Rectangle Corner (RC), Square Rectangle (SR), Block Rectangle (BR), L-Rectangle (LR), Traditional 1D Rectangular (TR) (DeFlumere, 2014, p. 77) (Figure 1).

The communication complexity of the considered algorithms is estimated using the Hockney model:

(1) $T_{comm}=\alpha +\beta M,$(1)

where $\alpha$—latency or message delay, measured in seconds;

$\beta$—bandwidth or time to transmit an element, measured in seconds;

$M$–message size or number of elements to send.

Figure 1. Candidate shapes defined as potentially optimal for three-processor systems.

2.1. Finding of the optimal data partitioning for the serial communication with barrier algorithm

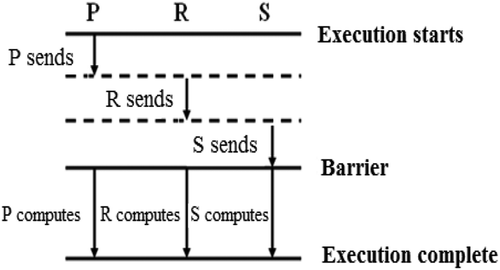
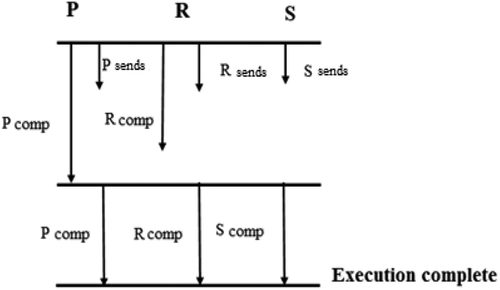
The Serial Communication with Barrier algorithm (SCB) is a simple matrix multiplication algorithm in which all data are sent consistently by the processors, and calculations begin only after all processors have completed data transfer and are running in parallel (Figure 2).

The execution time of the algorithm includes the communication time between processors and the time required to perform the calculations:

(2) $T_{exe}=V\beta +\mathrm{m}\mathrm{a}\mathrm{x}\left(c_{P_1},c_{P_2},\dots ,c_{P_p}\right),$(2)

where $V$—total number of communications;

$c_{P_x}$- the time required by the processor X to calculate the assigned part of the matrix C.

Because the area of the matrix and the number of elements allocated to each processor are proportional to its computing power, the parameter $c_{P_x}$ will be the same for all candidate forms considered and may not be taken into account when comparing the execution time of the algorithm.

Figure 2. The serial communication with barrier algorithm for three-processor systems.

The next step is to define the communication time $T_{comm}$ for each considered form according to the formula (2).

Square Corner:

$T_{comm}=2sN{\beta }_1+2rN{\beta }_2$

Square Rectangle:

$T_{comm}=\left(2N-r\right)s{\beta }_1+\left(N^2-s^2\right){\beta }_2++\left(r+s\right)s{\beta }_3$

where $r$–side of the square, intended for processor $R$;

$s$—side of the square, intended for processor $S$.

Block Rectangle:

$T_{comm}=\frac{{\beta }_1{N}^2}{T}\left(P_r-\frac{P_r{R}_r}{T-P_r}+1\right)+\frac{{\beta }_2{N}^2}{T}\left(P_r-\frac{P_r}{T-P_r}+R_r\right)+\frac{{\beta }_3{N}^2}{T}\left(1+R_r\right)$

L-Rectangle:

$T_{comm}=\frac{{\beta }_1{N}^2}{T}\left(P_r+1\right)+\frac{{\beta }_2{N}^2}{T}\left(P_r+R_r\left(1-\frac{1}{T-R_r}\right)\right)+\frac{{\beta }_3{N}^2}{T}\left(1+\frac{R_r}{T-R_r}\right)$

Traditional 1D Rectangular:

$T_{comm}=\frac{{\beta }_1{N}^2}{T}\left(P_r+1\right)+\frac{{\beta }_2{N}^2}{T}\left(P_r+R_r\right)+\frac{{\beta }_3{N}^2}{T}\left(1+R_r\right)$

For the Rectangle Corner shape, the optimal size of R and S will be the combined width of N; that cannot be true, however, based on the classification of candidate forms (DeFlumere & Lastovetsky, 2014, p.78). Alternatively, we can establish that ${\mathrm{R}}_{\mathrm{w}}+{\mathrm{S}}_{\mathrm{w}}=\left(\mathrm{N}-1\right)$. Then,

Rectangle Corner:

$T_{comm}=\left(\left(R_h+S_h\right)\left(S_w+1\right)+N\left(N-R_h-1\right)\right){\beta }_1+\left(\left(R_h+S_h\right)\left(R_w+1\right)+N\left(N-S_h-1\right)\right){\beta }_2+\left(\left(R_w+S_w\right)\left(S_h+R_h-N\right)\right){\beta }_3$

where $R_h$, $R_w$—height and width of the rectangle, intended for processor $R$;

$S_h,S_w$—height and width of the rectangle, intended for processor $S$.

To facilitate the analysis of the mathematical model, we get rid of the coefficient ${\beta }_3$, having obtained the ratio of the throughputs between the computational elements $\frac{{\beta }_1}{{\beta }_3},\frac{{\beta }_2}{{\beta }_3}$. Thus, we get four variables.

2.2. Finding of optimal data partitioning for parallel communication with the barrier algorithm

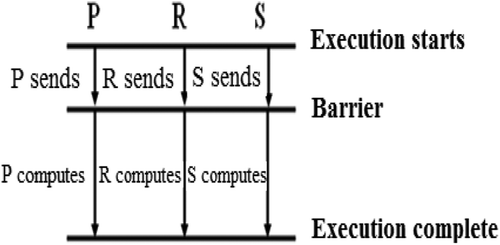
The algorithm of Parallel Communication with Barrier (PCB) assumes that the transfer of data between the processors is carried out in parallel, and that only after the communication is completely completed will the processors begin to perform parallel calculations (Figure 3).

Figure 3. The parallel communication with barrier algorithm for three-processor systems.

Evaluation of the execution time of the algorithm is performed using the formula:

(3) $T_{exe}=\mathrm{m}\mathrm{a}\mathrm{x}\left(V_{P_1},V_{P_2},\dots ,V_{P_p}\right)\beta +\mathrm{m}\mathrm{a}\mathrm{x}\left(c_{P_1},c_{P_2},\dots ,c_{P_p}\right),$(3)

where $V_{P_x}$- the amount of data to be transferred by the processor X.

Similar to the SCB algorithm, the parameter $c_{P_x}$ may not be taken into account in the formulas; the optimality of the forms will be determined based on the communication time ${\mathrm{T}}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{m}}$.

Square Corner:

$T_{comm}=max\left(2s{\beta }_1\left(N-s\right)+2r{\beta }_2\left(N-r\right),2s^2{\beta }_1,2r^2{\beta }_2\right)$

Square Rectangle:

$T_{comm}=max\left(\left(2sN-2s^2-sr\right){\beta }_1+\left(N^2-Nr-s^2\right){\beta }_2,Nr{\beta }_2+sr{\beta }_3,2s^2{\beta }_1+s^2{\beta }_3\right)$

Block Rectangle:

$T_{comm}=\mathrm{m}\mathrm{a}\mathrm{x}\left(\frac{{\beta }_1{N}^2{P}_r}{T}\left(1-\frac{R_r}{T-P_r}\right)+\frac{{\beta }_2{N}^2{P}_r}{T}\left(1-\frac{1}{T-P_r}\right),\frac{N^2}{T}{\beta }_1+\frac{N^2}{T}{\beta }_3,\frac{R_r{N}^2}{T}{\beta }_2+\frac{R_r{N}^2}{T}{\beta }_3\right)$

L-Rectangle:

$T_{comm}=max(\frac{N^2{P}_r}{T}{\beta }_1+\frac{N^2{P}_r}{T}{\beta }_2,\frac{N^2{R}_r}{T}{\beta }_2\left(1-\frac{1}{T-R_r}\right)+\frac{N^2{R}_r}{T\left(T-R_r\right)}{\beta }_3$, $\frac{N^2}{T}{\beta }_1+\frac{N^2}{T}{\beta }_3)$

Traditional 1D Rectangular:

$T_{comm}=max(\frac{N^2{P}_r}{T}{\beta }_1+\frac{N^2{P}_r}{T}{\beta }_2,\frac{N^2{R}_r}{T}{\beta }_2+\frac{N^2{R}_r}{T}{\beta }_3$, $\frac{N^2}{T}{\beta }_1+\frac{N^2}{T}{\beta }_3)$

Rectangle Corner:

$\begin{array}{rl}& T_{comm}=max(2S_w{S}_h{\beta }_1+S_w\left(S_h+R_h-N\right){\beta }_3,2R_w{R}_h{\beta }_2+R_w\left(S_h+R_h-N\right){\beta }_3,(N\left(N-R_h-1\right)\\ & -S_w{S}_h+S_w{R}_h+S_h+R_h){\beta }_1+\left(N\left(N-S_h-1\right)-R_w{R}_h+R_w{S}_h+S_h+R_h\right){\beta }_2)\end{array}$

2.3. Finding of the optimal data partitioning for the serial communication with overlap algorithm

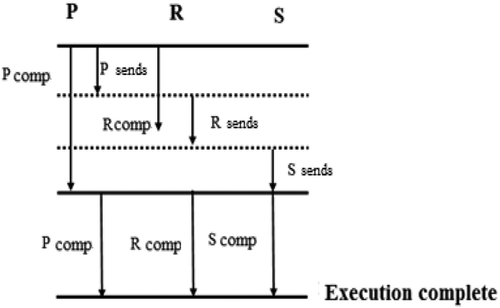
In the algorithm of the Serial Communication with Overlap (SCO), all data are transmitted by processor serially, and in parallelelementsnot engaged in the exchange are calculated.

The rest part of the operations is done only after completion of communication and overlap of computations (Figure 4).

The algorithm execution time is calculated by the formula:

(4) $T_{exe}=\mathrm{m}\mathrm{a}\mathrm{x}\left(max\left(V\beta ,O_{P_1}\right)+c_{P_1},max\left(V\beta ,O_{P_2}\right)+c_{P_2},\dots ,\mathrm{m}\mathrm{a}\mathrm{x}\left(V\beta ,O_{P_p}\right)+c_{P_p}\right),$(4)

where $O_{p_x}$ is time spent by processor X for computing elements that do not require communication;

$C_{p_x}$ is time spent by processor X for computing the rest elements.

Figure 4. The serial communication with overlap algorithm for three-processor systems.

Let us determine the execution time of the algorithm $T_{exe}$ for each shape considered according to formula (4).

Algorithm execution time for the shape of Square Corner is determined as follows:

$T_{com}=2SN+2$

$O_p=\frac{N\cdot {\left(N-r-s\right)}^2}{S_p}$

$Tex{e}_1=T_{comm}+C_p=2SN{\beta }_1+2rN{\beta }_2+\frac{2N}{S_p}\left(Nr-r^2-\frac{r^2}{\sqrt{R_r}}+\frac{N_r}{\sqrt{R_r}}-\frac{r^2}{R_r}\right)$

$Tex{e}_2=O_p+C_p=\frac{N}{S_P}\left(N^2-\frac{r^2}{R_r}-r^2\right)$

$Tex{e}_3=T_{comm}+C_R=2SN{\beta }_1+2rN{\beta }_2+r^2\cdot \frac{N}{S_r}$

Algorithm execution time for the shape of Square Rectangle equals to:

$Texe=T_{com}+max\left(C_P,C_R,C_S\right)$

$Texe=\left(2N-r\right)S{\beta }_1+\left(N^2-S^2\right){\beta }_2+\left(r+S\right)S{\beta }_3+max\left(\frac{P_r{N}^3}{T{S}_p},\frac{R_r{N}^3}{T{S}_r},\frac{N^3}{T{S}_s}\right)$

Since matrix elements are distributed among the processors proportionally to their computational power, $\frac{P_r{N}^3}{T{S}_p},\frac{R_r{N}^3}{T{S}_r}\mathrm{a}\mathrm{n}\mathrm{d}\frac{N^3}{T{S}_s}$ values will have the same value for all partitioning shapes, and in the rest formulas, it will be indicated as $C_P,C_R,C_s$, respectively.

Algorithm execution time for the shape of Block Rectangle equals to:

$Texe=T_{com}+max\left(C_p,C_R,C_s\right)$

$Texe=\frac{{\beta }_1{N}^2}{T}\left(P_r-\frac{P_r{R}_r}{T-P_r}+1\right)+\frac{{\beta }_2{N}^2}{T}\left(P_r-\frac{P_r}{T-P_r}\right)+\frac{{\beta }_3{N}^2}{T}\left(1+R_2\right)+max\left(C_P,C_R,C_s\right)$

Algorithm execution time for the shape of L-Rectangle is determined as:

$Texe=T_{com}+max\left(C_P,C_R,C_S\right)$

$Texe=\frac{{\beta }_1{N}^2}{T}\left(P_r+1\right)+\frac{{\beta }_2{N}^2}{T}(R_r+R_r\cdot \left(1-\frac{1}{T-R_r}\right)+\frac{{\beta }_3{N}^2}{T}\left(1+\frac{R_r}{\left(T-R_r\right)}\right)+\mathrm{m}\mathrm{a}\mathrm{x}\left(C_P,C_R,C_S\right)$

Algorithm execution time for the shape of Traditional 1D Rectangular is presented as follows:

$Texe=T_{comm}+max\left(C_{P_1},C_{P_2},C_{P_3}\right)$

$Texe=\frac{{\beta }_1{N}^2}{T}\left(P_r+1\right)+\frac{{\beta }_2{N}^2}{T}\left(P_r+R_2\right)+\frac{{\beta }_3{N}^2}{T}\left(1+R_r\right)+\mathrm{m}\mathrm{a}\mathrm{x}\left(C_{P_1},C_{P_2},C_{P_3}\right)$

For the shape of Rectangle Corner, R and S optimal size is a combined width N, which cannot be true based on the classification of candidate shapes (DeFlumere, 2014, p.78). As alternative, let us state that ${\mathrm{R}}_{\mathrm{w}}+{\mathrm{S}}_{\mathrm{w}}=\left(\mathrm{N}-1\right)$. Then,

$Texe=\left(\left(R_h+S_h\right)\left(S_w+1\right)+N\left(N-R_h-1\right)\right)\cdot {\beta }_1+\left(\left(R_h+S_h\right)\cdot \left(R_w+1\right)+N\left(N-S_h-1\right)\right)\cdot {\beta }_2+\left(\left(S_h+R_W\right)\left(S_h+R_h-N\right)\right)\cdot {\beta }_3+\mathrm{m}\mathrm{a}\mathrm{x}\left(C_{P_1},C_{P_2},C_{P_3}\right)$

To simplify the analysis of obtained mathematical model, let us get rid of ${\beta }_3$ coefficient having received the ratio of bandwidths between computational elements $\frac{{\beta }_1}{{\beta }_3},\frac{{\beta }_2}{{\beta }_3}$. Thus, we get four variables.

2.4. Finding of the optimal data partitioning for the parallel communication with barrier algorithm

Algorithm of Parallel Communication with Overlap (PCO) completes all communications in parallel and simultaneously calculates any sections of the C matrix that do not require interprocessor communication. As soon as the operation data are completed, the rest computations are done (Figure 5).

Figure 5. The parallel communication with overlap algorithm for three-processor systems.

Evaluation of the execution time of the algorithm is performed using the formula:

(5) $T_{exe}=\mathrm{m}\mathrm{a}\mathrm{x}\left(max\left(T_{comm},O_{P_1}\right)+c_{P_1},max\left(T_{comm},O_{P_2}\right)+c_{P_2},\dots ,\mathrm{m}\mathrm{a}\mathrm{x}\left(T_{comm},O_{P_p}\right)+c_{P_p}\right),$(5)

where $T_{comm}$ is equal to the communication time for the algorithm of the parallel communication with barrier PCB;

$O_{P_x}$ is time spent by the processor $X$ for computing the elements that do not require communication;

$c_{P_x}$ is time spent by the processor $X$ for computing the rest elements.

Let us construct computation models for each candidate shape according to the formula 5.

Square Corner:

$Tex{e}_1\left(T_{comm}+C_P\right)=max\left[2r\left(N-r\right)\cdot {\beta }_2+\left(2S\left(N-S\right)\right)\cdot {\beta }_1\right],2r^2\cdot {\beta }_2,2S^2\cdot {\beta }_1)+\frac{2r\left(N-r\right)+2S\left(N-r-S\right)}{\frac{S_P}{N}}$

$Tex{e}_2=\left(O_P+C_P\right)=\frac{N^2-r^2-s^2}{\frac{S_P}{N}}$

$Tex{e}_3\left(T_{comm}+C_R\right)=max\left(\left[2r\left(N-r\right)\cdot {\beta }_2+2S\left(N\cdot S\right)\cdot {\beta }_1\right],2r^2{\beta }_2,2S^2{\beta }_1\right)+\frac{r^2}{\frac{S_r}{N}}$

Square Rectangle:

$Tex{e}_1=\left(N^2-Nr-S^2\right){\beta }_2+\left(2SN-2S^2-Sr\right)\cdot {\beta }_1+C_P$

$Tex{e}_2=Nr\cdot {\beta }_2+Sr\cdot {\beta }_3+C_r$

$Tex{e}_3=S^2\cdot {\beta }_3+2S^2\cdot {\beta }_1+C_c$

Block Rectangle:

$Tex{e}_1=\frac{P_r{N}^2\cdot {\beta }_1}{T}\left(1-\frac{R_r}{T-P_r}\right)+\frac{P_r{N}^2{\beta }_2}{T}\left(1-\frac{1}{T-P_r}\right)+C_p$

$Tex{e}_2=\frac{N^2}{T}\cdot {\beta }_1+\frac{N^2}{T}\cdot {\beta }_3+C_S$

$Tex{e}_3=\frac{R_r{N}^2}{T}\cdot {\beta }_2+\frac{R_r{N}^2}{T}\cdot {\beta }_3+C_R$

L-Rectangle:

$Tex{e}_1=\frac{P_r{N}^2}{T}\cdot {\beta }_1+\frac{P_r{N}^2}{T}\cdot {\beta }_2+C_P$

$Tex{e}_2=\frac{R_r{N}^2}{T}\cdot {\beta }_2\cdot \left(1-\frac{1}{T-R_r}\right)+\frac{R_r{N}^2}{T\left(T-R_r\right)}\cdot {\beta }_3+C_R$

$Tex{e}_3=\frac{N^2}{T}\cdot {\beta }_1+\frac{N^2}{T}\cdot {\beta }_3+C_S$

For the shapes of Traditional 1D Rectangular and Rectangle Corner, to evaluate the total duration of execution, only time of communication between the elements is needed.

Traditional 1D Rectangular:

$T_{comm1}=\frac{P_r{N}^2}{T}\cdot {\beta }_1+\frac{P_r{N}^2}{T}\cdot {\beta }_2$

$T_{comm2}=\frac{R_r{N}^2}{T}\cdot {\beta }_2+\frac{R_r{N}^2}{T}\cdot {\beta }_3$

$T_{comm3}=\frac{N^2}{T}\cdot {\beta }_1+\frac{N^2}{T}\cdot {\beta }_3$

Rectangle Corner:

$T_{comm2}=2S_w{S}_h\cdot {\beta }_1+S_w\left(S_h+R_h-N\right)\cdot {\beta }_3$

$T_{comm3}=2R_h{R}_w\cdot {\beta }_2+R_w\left(S_h+R_h-N\right)\cdot {\beta }_3$

$T_{comm1}=\left(N\left(N-S_h-1\right)-R_w{R}_h+S_h{R}_w+S_h+R_h\right)\cdot {\beta }_2+\left(N\left(N-R_h-1\right)-S_w{S}_h+R_h{S}_w+S_h+R_h\right)\cdot {\beta }_1$

By analogy with the SCО algorithm let us get rid of the ${\beta }_3$ coefficient, having received ratio of bandwidths between computational elements $\frac{{\beta }_1}{{\beta }_3},\frac{{\beta }_2}{{\beta }_3}$.

3. Research results

Based on the constructed mathematical model, software was developed in the Java programming language that in text form or via the web interface allows entering the initial parameters (P, R, $\frac{{\beta }_1}{{\beta }_3}$, $\frac{{\beta }_2}{{\beta }_3}$) and determining the theoretical optimal data partitioning shape (Figures 6–8).

Figure 6. Сlass diagram of “parallel matrix computation on heterogeneous processors” web-application.

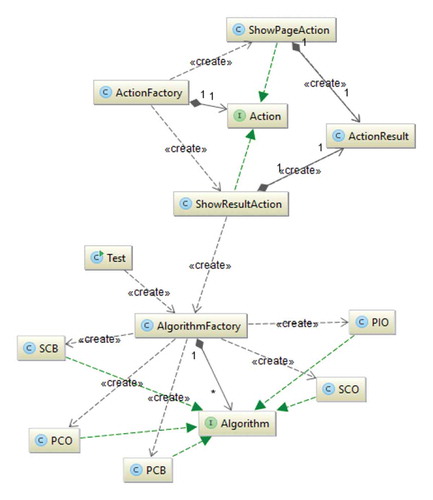
Figure 7. Example of Program Computations for SCB algorithm with different input values of Pr, Rr, ${\beta }_1$, ${\beta }_2,{\beta }_3$.

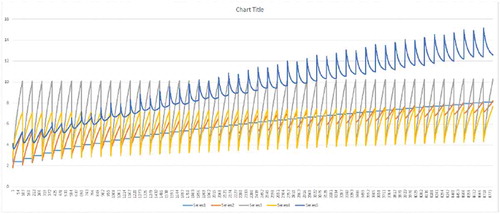
Y axis—execution time; X axis—number of experiments. Series 1—Square Corner; Series 2—Rectangle Corner; Series 3—L Rectangular; Series 4—Block 2D Rectangular; Series 5—Square Rectangle.

Figure 8. Example of program computations for SCB and PCB algorithms with different input values of Pr, Rr, ${\beta }_1$, ${\beta }_2,{\beta }_3$.

Y axis—execution time; X axis—number of experiments. Series shows different types of element partition.

Based on the analysis performed on the basis of calculations obtained according to the constructed mathematical model, the following conclusions were made.

BR, LR, SC and SR partition shapes are optimal for the Serial Communication with Barrier Algorithm. The LR partition shape is optimal at a value of $\frac{{\beta }_1}{{\beta }_3}<1$ and roughly equal powers of the processors P and R, while significantly exceeding the power of the processor S. The SR form is optimal in cases of small values of the coefficients $\frac{{\beta }_1}{{\beta }_3},\frac{{\beta }_2}{{\beta }_3}$ and the powers of the processors P and R, significantly exceeding the power of the processor S. In all other cases, the BR and SC forms are optimal.

As in the case of using the SCB algorithm, only BR, LR, SC and SR forms can be optimal for Parallel Communication with the Barrier Algorithm. LR is optimal only for values of the coefficients $\frac{{\beta }_1}{{\beta }_3}$ = 0,1, $\frac{{\beta }_2}{{\beta }_3}<1$ and roughly equal the powers of processors P and R while being much larger than S. SR is optimal for $\frac{{\beta }_1}{{\beta }_3}\le 2$ and the computing power values of processors P and R are larger than those in the processor S. In other cases, depending on the selected parameters, the forms BR and SC are optimal.

For the Serial Communication with Overlap Algorithm in the same way as in previous algorithms, optimal matrix partitioning shapes may be BR, LR, SC and SR. SR and SC shapes may beoptimalwiththe P processor power values that significantlyexceedpower of the processors R and S. At the same time, for the SR shape, this statement is true only with the coefficient value of $\frac{{\beta }_1}{{\beta }_3}$≥2. The LR shape is optimal with the coefficient value of $\frac{{\beta }_1}{{\beta }_3}<1$ and approximately equal power of the processors P and R that significantly exceeds the power of the processor S. In all other cases, optimal shapes are BR.

For the Parallel Communication with Barrier Algorithm, optimal partitioning shapes may be also only BR, LR, SC and SR. The LR shape is only with the coefficient value of $\frac{{\beta }_1}{{\beta }_3}<$ 0.6, $\frac{{\beta }_2}{{\beta }_3}=<1$ and approximately equal power of the processors P and R. The SR shape may be optimalwith $\frac{{\beta }_1}{{\beta }_3}\le 2$ andpower values of processors P and R that significantly exceed the power of the processor S. The SC shape is optimal with the power of the processor P that significantly exceeds the power of the processors R and S and values $\frac{{\beta }_1}{{\beta }_3}$, $\frac{{\beta }_2}{{\beta }_3}\ge 1.$ In other cases, depending on the chosen parameters,optimal shapes are BR.

4. Conclusion

Based on the results of obtained calculation, it can be concluded that, as in the case of three-processor systems with the same bandwidth between computational elements, the Rectangle Corner and Traditional 1D Rectangular data partitioning shapes are optimal for any set of parameters.

In contrast to the results obtained in matrix (DeFlumere, 2014, p. 85, 88), the L-Rectangle form is optimal with the powers of the processors P and R greatly exceeding the power of the processor S, and approximately equalling each other in the case of $\frac{{\beta }_1}{{\beta }_3}<1$ for the SCB algorithm and $\frac{{\beta }_1}{{\beta }_3}$ = 0,1 for the PCB algorithm. However, in these cases, there is no sense in using a low-power processor S, and the task can be solved on two processors.

The Square Rectangle shape is optimal for small values of the coefficients $\frac{{\beta }_1}{{\beta }_3},\frac{{\beta }_2}{{\beta }_3}$ with the powers of processors P and R significantly exceeding the power of the processor S. With such initial data, the problem can also be solved using two powerful processors.

In other cases, the Square Corner and Block Rectangle forms are optimal in the case of using both algorithms, depending on the values of the coefficients ${\mathrm{P}}_{\mathrm{r}},{\mathrm{R}}_{\mathrm{r}},\frac{{\beta }_1}{{\beta }_3},\frac{{\beta }_2}{{\beta }_3}$.

L-Rectangle shape may be optimal with approximately equal powers of the processors P and R that significantly exceed the power of the processor S and $\frac{{\beta }_1}{{\beta }_3}<1$ for the SCО algorithm, and $\frac{{\beta }_1}{{\beta }_3}<$ 0.6, $\frac{{\beta }_2}{{\beta }_3}=<1$ for the PCО algorithm. But in this case, the problem may be solved by two processors, without engaging the processor S.

Square Rectangle shape may be optimal if both caseswithpower values of the processors P and R that significantly exceed the power of the processor S. With such input data, the problem also may be solved using two powerful processors.

In most cases for both algorithm classes, it is preferable to use the Block Rectangle shape.

The developed software can be used to determine the optimal form of partitioning the matrix elements for certain parameters of a real computing system. The results can be used to implement a specific subject area algorithm, for example, for the analysis of large volumes of data presented in the form of matrices, as well as for the analysis of urban structures in modern metropolitan areas, in particular for determining the reachability between the city districts.

Additional information

Funding

This work was supported by the Ministry of Education and Science of the Republic of Kazakhstan [grant number АР05133699].

Notes on contributors

Ye.G Klyuyeva

Ye.G. Klyuyeva Senior Lecturer, Karaganda State Technical University, Kazakhstan. Research interests: parallel computing, databases, computer networks, software development.

V.V. Yavorskij

V.V. Yavorskij Doctor of Technical Sciences, Professor, Karaganda State Technical University, Kazakhstan. Research interests: mathematical modeling, optimization, intelligent systems.

A.A. Adamov

A.A. Adamov Doctor of Technical Sciences, Professor, Head of the Department of Mathematical and Computer Modeling, L.N. Gumilyov Eurasian National University, Research interests: mathematical modeling, optimization, development of information systems.

I.T. Utepbergenov

I.T. Utepbergenov Doctor of Technical Sciences, Professor, Head of Laboratory of Innovative and Smart Technologies Institute of Information and Computational Technologies CS MES of RK, Kazakhstan. Research interests: ACS, Information technology in education, telecommunications, management, transport.

The research described in the paper was carried out in the framework of the research project grant financing of MES RK AR05133699 “Research and development of innovative telecommunications technologies with the use of modern cyber-technical means for the cities of intelligent transport system”.