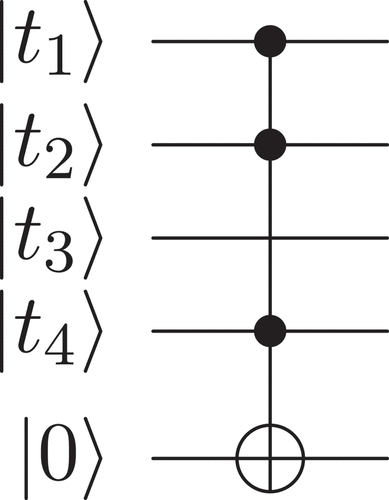Quantum algorithm for solving the test suite minimization problem

Abstract

Test-suite minimization problem is an essential problem in software engineering as its application helps to improve the software quality. This paper proposes a quantum algorithm to solve the test-suite minimization problem with high probability in $O\left(\sqrt{2^n}\right)$, where $n$ is the number of test cases. It generates an incomplete superposition to find the best solution. It also handles the non-uniform amplitudes’ distribution case for the system with multisolutions. The proposed algorithm uses amplitude amplification techniques to search for the minimum number of test cases required to test all the requirements. The proposed algorithm employs two quantum search algorithms, Younes et al. algorithm for quantum searching via entanglement and partial diffusion to prepare incomplete superpositions that represent different search spaces such that the number of test cases is incremented in each search space, and updated Arima’s algorithm to handle the multisolutions case. The updated Arima’s algorithm searches for a quantum state that satisfies an oracle that represent the instance of the test-suite minimization problem.

Keywords:

• Quantum Algorithm
• Test-Suite Minimization
• Superposition Preparation
• Quantum Search

Public Interest Statement

Test-suite minimization problem is an essential software engineering problem that has special importance in software testing. Evolutionary algorithms and other algorithms have been proposed to solve this problem. In this paper, a quantum algorithm is proposed to solve the est-suite minimization problem with high probability. Applying quantum algorithms to software engineering problems gives better results than that obtained using classical methods. This paper proposes a quantum algorithm that uses amplitude amplification techniques to search for the minimum number of test cases required to test all the requirements. The proposed algorithm employs two quantum search algorithms, Younes et al algorithm for quantum searching via entanglement to prepare incomplete superposition, and an updated Arima’s algorithm for searching the prepared search space for a possible solution to the given problem instance.

1. Introduction

Software testing is an essential stage in the software development life cycle. Redundant test cases can arise through the development of software versions. New test cases may arise for new versions of the software that cover the requirements tested by previous test cases for earlier software versions. Thus, software testing minimization techniques are required to reduce the number of test cases that cover the same requirements. Software testing minimization techniques are also required to utilize resources efficiently to reduce the cost and time requirements and to detect software bugs (Harman et al., 2012; Rothermel et al., 1998). There are many metaheuristic algorithms used to solve optimization problems, for example, quantum algorithms, quantum inspired algorithms, genetic algorithms, differential evolution, simulated annealing, ant and bee algorithms, bat algorithm, particle swarm optimization, and others as surveyed (Ahmed, 2016) and discussed next in this section.

Reduction can be performed classically using clustering such as Subashini and Jeyamala in 2014 (Subashini & JeyaMala, 2014) and Wang, Qu, Lu in 2015 (Wang et al., 2015) such that the program can be tested using any one of the clustered test cases. These clusters can be classified with the similarity in profiling (Alian et al., 2016) or by using the data mining approach of clustering (Wang et al., 2015). Many quantum algorithms are proposed to solve minimization problems for various applications, such as Anindita and Anirban (Banerjee & Pathak, 2009) who proposed a minimization algorithm for quantum circuit cost in 2010, where they minimize the number of gates in various selected quantum circuits. This algorithm can be applied on other circuits, but to do so, templates have to be developed for the corresponding gate library or the circuit has to be converted into other gate library with a previously prepared template. In 2020, Hussein, et al. (Hussein et al., 2020) proposed a quantum inspired algorithm that performs better than the classical genetic version of the algorithm. Orsan Ozener and Hasan Sozer (Orsan Ozener & Sozer, 2020) proposed a formulation of the test-suite minimization problem in 2020 that solves the issues in heuristic techniques or integer linear programming focusing on a specific criterion or bi-criteria. In 2020, Yinxing Xue, and Yan Li (Xue & Li, 2020) proved that integer linear programming models multi-criteria test-suite minimization then they proposed a multi-objective integer programming approach to solve it.

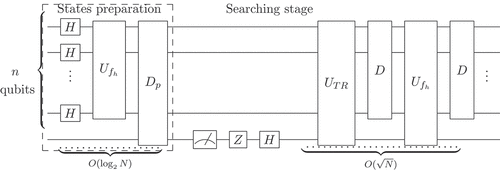
The aim of the paper is to propose a quantum algorithm to solve the test-suite minimization problem. The proposed algorithm consists of two stages: the first stage prepares an incomplete superposition of a search space with certain properties using Younes et al. algorithm for quantum searching via entanglement (Younes et al., 2008). The second stage searches for a solution of the test-suite minimization problem in the prepared incomplete superposition using an updated version of Arima’s algorithm for incomplete superposition searching (Arima et al., 2009).

This paper is organized as follows: Section 2 reviews the required background and discusses the quantum search algorithms used in the proposed algorithm. Section 3 proposes the quantum algorithm to solve the test-suite minimization problem. Section 4 shows the analysis of the searching phase. Section 5 discusses the proposed algorithm. Section 6 concludes the paper and mentions the future work.

2. Background

2.1. Test-Suite minimization problem

The aim of the test-suite minimization problem is to cover a given set of requirements with the smallest number of tests. The problem can be defined as follows (Panda & Mohapatra, 2017).

Given: A test suite $T$ with a set of $n$ test cases {$t_1$, $t_2$, $t_3$, …, $t_n$} and a set $R$ of $m$ test requirements {$R_1$, $R_2$, $R_3$, …, $R_m$} that must be satisfied. Each test case must cover one or more requirements and a requirement can be covered by one or more test cases.

Required: Find the minimum subset of $T$ that tests all the requirements.

For example, Table 1 illustrates a given test suite showing the requirements that are covered by each test case. Many solutions can be found that cover all the requirements, but the target is to find the minimum number of tests that cover all the requirements. For example, all the requirements can be covered with the test set {$t_1$, $t_2$, $t_3$, $t_4$} or {$t_1$, $t_2$, $t_4$}, but the minimum set which covers all the requirements is {$t_1$, $t_2$, $t_4$}. It becomes more complicated with large data sets. The TestNo column represents the test case number, while the $R{ }^{\mathrm{\prime }}$s columns represent the requirements that are satisfied by each test case.

Table 1. Example for test-suite minimization problem

TestNo	$r_1$	$r_2$	$r_3$	$r_4$	$r_5$	$r_6$
$t_1$	0	1	0	1	1	1
$t_2$	0	1	1	0	0	1
$t_3$	0	1	0	1	0	0
$t_4$	1	0	0	1	0	1

A test requirement matrix ($TR$) has to guarantee covering all the requirements, for example, to minimize the number of test cases shown in the test-suite minimization problem shown in Table 1, we start to represent the problem by its $TR$ matrix as follows:

(1) $TR=\left[\begin{array}{cccccc}0& 1& 0& 1& 1& 1\\ 0& 1& 1& 0& 0& 1\\ 0& 1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0& 1\end{array}\right].$(1)

To solve this instance of the test-suite minimization problem that is shown in Table 1, the minimal number of true assignments that satisfy the following Boolean formula should be found as follows:

(2) $f_{TR}=\underset{r_1}{\underbrace{\left(t_4\right)}}\wedge \underset{r_2}{\underbrace{\left(t_1\vee t_2\vee t_3\right)}}\wedge \underset{r_3}{\underbrace{\left(t_2\right)\wedge }}\underset{r_4}{\underbrace{\left(t_1\vee t_3\vee t_4\right)}}\wedge \underset{r_5}{\underbrace{\left(t_1\right)}}\wedge \underset{r_6}{\underbrace{\left(t_1\vee t_2\vee t_4\right)}},$(2)

which is a reduction of the test-suite minimization problem to the SAT problem (satisfiability problem).

2.2. Quantum computing

The elementary unit of data in quantum computing is the quantum bit or qubit. The qubit can be in a superposed state that is a combination of state $|0⟩$ and state $|1⟩$ and when a measurement is performed, the superposition is collapsed to one of the states in a probabilistic way. A combination of $|0⟩$ and $|1⟩$ before measurement is called a superposition as shown in Equation 3(3) $|\psi ⟩=\alpha |0⟩+\beta |1⟩,$(3) where $\alpha ,\beta$ are complex numbers representing the probabilistic amplitudes of $|0⟩$ and $|1⟩$ respectively. The amplitudes must satisfy the condition in Equation 4(4) $|\alpha {|}^2+|\beta {|}^2=1.$(4) :

(3) $|\psi ⟩=\alpha |0⟩+\beta |1⟩,$(3)

and

(4) $|\alpha {|}^2+|\beta {|}^2=1.$(4)

One of the quantum properties is entanglement, which means that each object of the quantum system can’t be described independently, and instead, the quantum state has to be described for the whole system (Menon & Ritwik, 2014). Another feature in quantum computing is the parallelism where it takes a quantum computer a single step to operate on $N$ inputs with a single gate, while the classical computer takes $N$ steps for the same input size. Parallelism does not require additional hardware or to wait for other processes to complete, but it performs multiple operations at a time. Quantum gates are unitary operators, considering that a gate has $s$ inputs, and then it can be represented as $2^s\times 2^s$ unitary matrix assuming that state $|0⟩=\left[\begin{array}{c}1\\ 0\end{array}\right]$ and state $|1⟩=\left[\begin{array}{c}0\\ 1\end{array}\right]$. Examples of such gates are:

The Hadamard gate with the following effect on $|0⟩$ and $|1⟩$:

(5) $H.|0⟩=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{c}1\\ 1\end{array}\right]=\frac{1}{\sqrt{2}}(|0⟩+|1⟩).$(5)

(6) $H.|1⟩=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]=\frac{1}{\sqrt{2}}\left[\begin{array}{c}1\\ -1\end{array}\right]=\frac{1}{\sqrt{2}}(|0⟩-|1⟩).$(6)

The X gate which is equivalent to the NOT gate in classical computers maps $|0⟩$ to $|1⟩$ and $|1⟩$ to $|0⟩$ as shown in the following equation:

(7) $X.|0⟩=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 1\end{array}\right]=|1⟩.$(7)

(8) $X.|1⟩=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]=|0⟩.$(8)

The Z gate that does not change the state $|0⟩$ but it converts $|1⟩$ to $-|1⟩$ as shown in the following equation:

(9) $Z.|0⟩=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]=|0⟩.$(9)

(10) $Z.|1⟩=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}0\\ -1\end{array}\right]=-|1⟩.$(10)

Quantum circuits are combinations of elementary quantum gates to perform a certain task.

2.3. Quantum searching algorithms

The aim of this section is to review the three quantum algorithms that will be used in the proposed algorithm: Grover’s algorithm for searching an unstructured list via phase shift (Younes, 2008), Younes et al. algorithm for searching an unstructured list via entanglement (Younes et al., 2008), and Arima’s algorithm for searching in an incomplete superposition (Arima et al., 2009).

Grover’s algorithm is a fast searching algorithm, Ventura added the feature of searching in a subset of the whole superposition to Grover’s algorithm, Arima amended Ventura’s algorithm to guarantee high probability results, and the Partial diffusion operator that updated Grover’s algorithm to guarantee high probability results in case of having multiple copies of the searched data.

2.3.1. Grover’s Algorithm

Grover’s algorithm can search an unstructured database of size $N$ in $O(\sqrt{N})$ given that $N=2^n$. Grover’s algorithm requires the following initialization (Younes, 2008) of qubits where the first $n$ qubits are initialized to state $|0⟩$ and an extra workspace qubit initialized to state $|1⟩$,

(11) $|{\psi }_{G0}⟩=|{0⟩}^{\otimes n}\otimes |1⟩,$(11)

then it applies $H^{\otimes n+1}$ on each of the $n+1$ qubits so that the first $n$ qubits contain the $N$ states representing the list and the extra qubit will be in state $(|0⟩-|1⟩)/\sqrt{2}$ as follows:

(12) $|{\psi }_{G1}⟩=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}|i⟩\otimes \left[\begin{array}{c}\frac{|0⟩-|1⟩}{\sqrt{2}}\end{array}\right].$(12)

Grover’s algorithm then applies the oracle operator $O_G$ that evaluates a Boolean function $f_G:\{0,1{\}}^n\to \{0,1\}$. The operator $O_G$ gives the amplitudes of the matches a phase shift of $e^{i\pi }$(Younes, 2008) as shown in Equation 13(13) $O_G|x⟩=\left\{\begin{array}{cc}|x⟩,& f_G(x)=0\\ -|x⟩,& f_G(x)=1.\end{array}\right.$(13) , and the system can be written as shown in Equation 14(14) $O_G|{\psi }_{G1}⟩=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}|i⟩\otimes \left[\begin{array}{c}\frac{|0\oplus f_G(i)⟩-|1\oplus f_G(i)⟩}{\sqrt{2}}\end{array}\right].$(14) .

(13) $O_G|x⟩=\left\{\begin{array}{cc}|x⟩,& f_G(x)=0\\ -|x⟩,& f_G(x)=1.\end{array}\right.$(13)

(14) $O_G|{\psi }_{G1}⟩=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}|i⟩\otimes \left[\begin{array}{c}\frac{|0\oplus f_G(i)⟩-|1\oplus f_G(i)⟩}{\sqrt{2}}\end{array}\right].$(14)

Next, it applies the diffusion operator $D$ on the first $n$ qubits. The diffusion operator $D$ is as follows:

(15) $D=H^{\otimes n}(2|{0⟩}^{\otimes n}⟨0{|}^{\otimes n}-I_n)H^{\otimes n},$(15)

where $I_n$ is the identity matrix of size $N\times N$. Consider a general system $|{\psi }_{G2}⟩$ of $n$ qubits as follows:

(16) $|{\psi }_{G2}⟩=\sum _{i=0}^{N-1}{\alpha }_i|i⟩.$(16)

Applying $D$ on the general system $|{\psi }_{G2}⟩$ has the following effect:

(17) $D|{\psi }_{G2}⟩=\sum _{i=0}^{N-1}[-{\alpha }_i+2⟨\alpha ⟩]|i⟩,$(17)

where $⟨\alpha ⟩=\frac{1}{N}{\sum }_{i=0}^{N-1}{\alpha }_i$ represents the mean of the states’ amplitudes.

The oracle operator $O_G$ and diffusion operator $D$ must be iterated approximately $\frac{\pi \sqrt{N}}{4}$ times. Measurement is then performed on the first $n$ qubits to reveal one of the searched items.

2.3.2. Younes et al Algorithm

An unstructured database of size $N$ can be searched with higher probability of success with an algorithm that uses the partial diffusion operator ($D_p$) in $O(\sqrt{N/M})$ where $M$ is the number of matches satisfying $1\le M\le N$. This algorithm amplifies the amplitudes of the solutions via entanglement of the search space with the extra qubit that is useful in the preparation of the incomplete superposition that can be done by applying the measurement on the extra qubit (Younes et al., 2003).

Younes et al. algorithm requires the following initialization of $n+1$ qubits where the $n+1$ qubits are initialized to state $|0⟩$ (Younes et al., 2008):

(18) $|{\psi }_{Y0}⟩=|{0⟩}^{\otimes n}\otimes |0⟩,$(18)

then applies $H$ on the first $n$ qubits as follows:

(19) $|{\psi }_{Y1}⟩=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}|i⟩\otimes |0⟩.$(19)

This algorithm then applies the oracle operator $O_Y$ on $n+1$ qubits where $O_Y$ evaluates the Boolean function $f_Y:\{0,1{\}}^n\to \{0,1\}$ as shown in the following equation:

(20) $O_Y|x,0⟩=\left\{\begin{array}{cc}|x,0⟩,& f_Y(x)=0\\ |x,1⟩,& f_Y(x)=1.\end{array}\right.$(20)

Next, it applies the $D_p$ operator which can be described in the following form (Younes et al., 2008):

(21) $D_p=(H^{\otimes n}\otimes I_1)(2|{0⟩}^{\otimes n+1}⟨0{|}^{\otimes n+1}-I_{n+1})(H^{\otimes n}\otimes I_1),$(21)

where $|0⟩$‘s size is $2N=2^{n+1}$, and the identity matrix $I_k$ is of size $2^k\times 2^k$.

Consider a general system $|{\psi }_{Y2}⟩$ of $n+1$ qubits as follows:

(22) $|{\psi }_{Y2}⟩=\sum _{k=0}^{2N-1}{\delta }_k|k⟩.$(22)

The state $|{\psi }_{Y2}⟩$ can be re-written to

(23) $|{\psi }_{Y2}⟩=\sum _{i=0}^{N-1}{\alpha }_i|i⟩\otimes |0⟩+\sum _{i=0}^{N-1}{\beta }_i|i⟩\otimes |1⟩,$(23)

where ${\alpha }_i={\delta }_k:keven$ and ${\beta }_i={\delta }_k:kodd$.

Applying $D_p$ on the general system has the following effect:

(24) $D_p|{\psi }_{Y2}⟩=\sum _{i=0}^{N-1}(2⟨\alpha ⟩-{\alpha }_i)(|i⟩\otimes |0⟩)-\sum _{i=0}^{N-1}{\beta }_i(|i⟩\otimes |1⟩),$(24)

where $⟨\alpha ⟩={\sum }_{i=0}^{N-1}{\alpha }_i/N$ is the mean of the amplitudes of the subspace entangled with the $|0⟩$ of the extra qubit. The $O_Y$ and $D_p$ operators are iterated $q_y$ times where $q_y$ is as follows:

(25) $q_y=\frac{\pi }{2\sqrt{2}}\sqrt{\frac{N}{M}},1\le M\le N.$(25)

Assume that $\sum \mathrm{\prime }$ is the sum over the desired $M$ matches, while $\sum \mathrm{\prime }\mathrm{\prime }$ represents the sum over the $N-M$ undesired matches. The system after $q_y\ge 1$ iterations can be described as follows:

$|{\psi }_{Y3}⟩=a_q\sum _{i=0}^{N-1}\mathrm{\prime }\mathrm{\prime }(|i⟩\otimes |0⟩)+b_q\sum _{i=0}^{N-1}{ }^{\mathrm{\prime }}(|i⟩\otimes |0⟩)$

(26) $+c_q\sum _{i=0}^{N-1}{ }^{\mathrm{\prime }}(|i⟩\otimes |1⟩),$(26)

where $a_q$, $b_q$, and $c_q$ values are as follows: Let $y=1-\frac{M}{N}$ and $v=\frac{1}{\sqrt{N}}$, and then (Younes et al., 2008),

(27) $⟨{\alpha }_q⟩=y{a}_{q-1}+(1-y)c_{q-1},$(27)

(28) $a_0=v,a_1=v(2y-1),a_q=2⟨{\alpha }_q⟩-a_{q-1},$(28)

(29) $b_0=v,b_1=2vy,b_q=2⟨{\alpha }_q⟩-c_{q-1},$(29)

(30) $c_0=0,c_1=-v,c_q=-b_{q-1}.$(30)

Finally, the first $n$ qubits are measured to get one of the searched items.

2.3.3. Arima’s Algorithm

Grover’s algorithm is effective when the initial amplitude distribution of dataset is uniform, which means that $N$ is equal to the number of stored data, but it is not always effective in the non-uniform cases where $N$ is not equal to the number of stored data. Arima’s algorithm was proposed to solve the search in an incomplete superposition.

Given an incomplete superposition $|{\psi }_{in}⟩$ and an oracle $U_{TR}$ that evaluates to $|1⟩$ for states in $|{\psi }_{in}⟩$, and an oracle $U_{f_h}$. It is required to find any state in $|{\psi }_{in}⟩$ that makes $U_{f_h}$ evaluate to $1$. Arima’s algorithm is summarized as (Arima et al., 2009),

• Initial state $|{\psi }_{in}⟩$.

• Repeat $q_a$ times, where $q_a=\frac{\pi }{4}\sqrt{N}$.

• $|{\psi }_{in}^{\mathrm{\prime }}⟩=U_{TR}|{\psi }_{in}⟩.$

• $\left|{\psi }_{in}⟩=D\right|{\psi }_{in}{ }^{\mathrm{\prime }}⟩$.

• $\left|{\psi }_{in}\mathrm{\prime }⟩=U_{f_h}\right|{\psi }_{in}⟩$.

• $|{\psi }_{in}⟩=D|{\psi }_{in}{ }^{\prime \prime \prime }⟩$.

• Observe the system.

The test-suite minimization problem definition has been illustrated. Quantum computing basics have been shown. Quantum searching algorithms that will be used in the proposed algorithm have been explained in detail.

3. The proposed algorithm

3.1. Methodology

The main idea of the proposed algorithm is to search the power set of the set of test cases in rounds, excluding the empty set since the problem is promised to have a solution. Each round searches simultaneously the set of all subsets from the power set that have the same cardinality, and if no solution is found, then increment the cardinality of the subsets in the search space next round. For example, given the set of test cases {$t_1$, $t_2$, $t_3$, $t_4$}, the first round searches in a search space that contains a single test, i.e. $\left\{\left\{t_1\right\},\left\{t_2\right\},\left\{t_3\right\},\left\{t_4\right\}\right\}$, the second round searches in a search space that contains two tests, i.e. $\left\{\left\{t_1,t_2\right\},\left\{t_1,t_3\right\},\left\{t_1,t_4\right\},\dots ,\left\{t_3,t_4\right\}\right\}$, and so on.

The proposed algorithm prepares an incomplete superposition using Younes et al. algorithm where all the states in the incomplete superposition have the same Hamming distance with the state $|{0⟩}^{\otimes n}$. Starting with hamming distance equals to $1$, the proposed algorithm searches for a state that satisfies the oracle that represents the $TR$ using an updated version of Arima’s algorithm. If the $TR$ oracle is satisfied with a state in the prepared incomplete superposition, then the algorithm terminates and the truth assignment from the incomplete superposition is reported as the minimum solution, and otherwise prepare the next incomplete superposition with an incremented hamming distance and restart the algorithm.

The proposed algorithm has a maximum of $O({log}_{2}N)$ rounds, where the first round will search in ${ }^n{C}_1$ states and the second round will search in ${ }^n{C}_2$ states and so on. After ${log}_{2}N$ rounds in the worst case, the algorithm will search the $N$ states since ${\sum }_{i=0}^{n}n{C}_i=N$, where state $|{0⟩}^{\otimes n}$ is excluded since it is guaranteed that the $m$ requirements will be covered with a subset of the $n$ test cases.

3.2. Problem encoding

Given a test-suite minimization problem as shown in Table 1. Assuming that all the requirements will be satisfied by a subset of the set of test cases, the problem can be represented as $TR$ matrix, for example, the problem shown in XTable 1 can be represented as shown in the $TR$ matrix shown in Equation 1(1) $TR=\left[\begin{array}{cccccc}0& 1& 0& 1& 1& 1\\ 0& 1& 1& 0& 0& 1\\ 0& 1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0& 1\end{array}\right].$(1) . The $TR$ matrix will be the input to the proposed algorithm.

The idea of the proposed algorithm is to represent the tests to be applied as quantum states, for example, given a set of tests {$t_1$, $t_2$, $t_3$, $t_4$}. Applying the subset {$t_1$, $t_2$, $t_4$} is represented as the quantum state $|1101⟩$. The proposed algorithm prepares an incomplete superposition of states with the same Hamming distance as will be illustrated next, for example, $|0001⟩$, $|0010⟩$, $|0100⟩$, and $|1000⟩$ have the same Hamming distance with state $|0000⟩$, which is equal to $1$. The algorithm then searches if the operator representing $f_{TR}$ is satisfied by one of these states, otherwise, increment the number of $1$‘s in the prepared states and repeat the algorithm until a solution with the minimum number of tests is reached.

3.3. Preparation of states with a given hamming distance

A $TR$ matrix of size $n\times m$ is considered as an input, and this means we will need to prepare $n+1$ qubit system. The quantum circuit shown in Figure 1 illustrates the algorithm steps, which will be explained in detail in this section.

Figure 1. Quantum circuit for the proposed algorithm

The algorithm first initializes $n+1$ qubit system to $|0⟩$ so that the system takes the following state:

(31) $|{\psi }_1⟩=|{0⟩}^{\otimes n}\otimes |0⟩,$(31)

then apply $H$ on the first $n$ qubits to prepare the complete superposition. The system will be

(32) $|{\psi }_2⟩=(H^{\otimes n}\otimes I)|{\psi }_1⟩=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}|i⟩\otimes |0⟩.$(32)

The $TR$ matrix shown in Table 1 will be taken as a working example to illustrate the proposed algorithm. Using the working example, the complete superposition stored in $|{\psi }_2⟩$ will be equal to

(33) $\begin{array}{cc}|{\psi }_2⟩& =\frac{1}{4}(|0000⟩+|0001⟩+|0010⟩+|0011⟩+|0100⟩+|0101⟩\\ \hspace{0.17em}& +|0110⟩+|0111⟩+|1000⟩+|1001⟩+|1010⟩+|1011⟩\\ \hspace{0.17em}& +|1100⟩+|1101⟩+|1110⟩+|1111⟩)\otimes |0⟩.\end{array}$(33)

The proposed algorithm prepares superposition of states containing a specific $t$ number of $1$‘s that is $nt$ states. For a set of states that have $t$ number of $1$‘s, define $f_h$ as follows:

(34) $f_h(x)=\left\{\begin{array}{cc}1,& ifham(x)=h,h=1,2,\dots ,n\\ 0,& o.w.\end{array}.\right.$(34)

Using the working example, $f_h$ can be written as follows (Younes & Rowe, 2015), where $n=4$ and $t=3$,

(35) $f_h=(\overline{t_1}\wedge t_2\wedge t_3\wedge t_4)\vee (t_1\wedge \overline{t_2}\wedge t_3\wedge t_4)\vee (t_1\wedge t_2\wedge \overline{t_3}\wedge t_4)\vee (t_1\wedge t_2\wedge t_3\wedge \overline{t_4}).$(35)

This can be represented as Reed–Muller expansion (Younes & Miller, 2004) so it can be represented as follows:

(36) $f_h=(t_2\wedge t_3\wedge t_4)\oplus (t_1\wedge t_3\wedge t_4)\oplus (t_1\wedge t_2\wedge t_4)\oplus (t_1\wedge t_2\wedge t_3),$(36)

then the proposed algorithm applies the oracle $U_{f_h}$ for the function $f_h$ as shown in the quantum circuit in Figure 2 (Younes & Miller, 2004). $U_{f_h}$ is defined as follows:

(37) $U_{f_h}(|x>\otimes |0>)=\left\{\begin{array}{cc}(|x>\otimes |1>),& f_h(x)=1,\\ (|x>\otimes |0>),& f_h(x)=0.\\ \hspace{0.17em}& \hspace{0.17em}\end{array}\right.$(37)

Figure 2. Quantum circuit for the $U_{f_h}$ in .Equation 36(36) $f_h=(t_2\wedge t_3\wedge t_4)\oplus (t_1\wedge t_3\wedge t_4)\oplus (t_1\wedge t_2\wedge t_4)\oplus (t_1\wedge t_2\wedge t_3),$(36) and Equation 37(37) $U_{f_h}(|x>\otimes |0>)=\left\{\begin{array}{cc}(|x>\otimes |1>),& f_h(x)=1,\\ (|x>\otimes |0>),& f_h(x)=0.\\ \hspace{0.17em}& \hspace{0.17em}\end{array}\right.$(37)

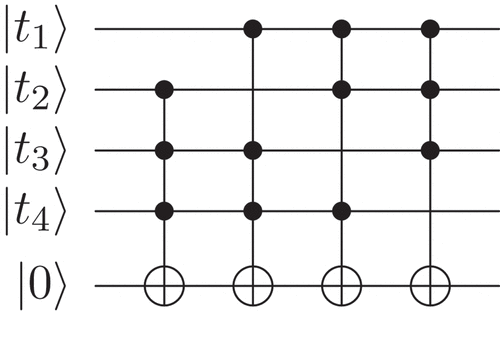
In this paper, the quantum circuits for boolean functions will be represented as Reed–Muller expansions for illustration. In the proposed algorithm, the query complexity will be considered where using a boolean function will be counted once since the optimization of the quantum circuits for boolean functions is a different research area irrelevant to the scope of the paper.

After applying $U_{f_h}$, we apply the partial diffusion operator as will be shown next. The current system can be rewritten as a summation of two subspaces, the subspace of the non-matches that is denoted as $\sum$ and the subspace of the matches that is denoted as $\sum$,

(38) $|{\psi }_3>=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}\mathrm{\prime }\mathrm{\prime }(|i>\otimes |0>)+\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}\mathrm{\prime }(|i>\otimes |1>).$(38)

Let us consider the following equation:

(39) $|{\psi }_y>=|0{>}^{\otimes n}\otimes |0>.$(39)

The proposed algorithm applies $D_p{U}_{f_h}$ for $q$ times, where

(40) $q=\frac{\pi }{2\sqrt{2}}\sqrt{\frac{N}{nt}}.$(40)

Then, the system will be updated to be

$|{\psi }_y^{\mathrm{\prime }}>=\sum _{i=0}^{N-1}\mathrm{\prime }{ }^{\mathrm{\prime }}{a}_q|i>\otimes |0>$

$+\sum _{i=0}^{N-1}\mathrm{\prime }{b}_q|i>\otimes |0>$

(41) $+\sum _{i=0}^{N-1}\mathrm{\prime }{c}_q|i>\otimes |1>.$(41)

Using the working example with $t=3$ and $n=4$, $q$ will be equal to $\frac{\pi }{\sqrt{2}}$, which is approximately $2$ and the system will be updated as follows:

(42) $\begin{array}{cc}|{\psi }_y^{\mathrm{\prime }}>& =\frac{1}{8}(|0000>+|0001>+|0010>+|0011>+|0100>+|0101>+|0110>\\ \hspace{0.17em}& +|1000>+|1001>+|1010>+|1100>+|1111>)\otimes |0>\\ \hspace{0.17em}& +\frac{3}{8}(|0111>+|1011>+|1101>+|1110>)\otimes |0>\\ \hspace{0.17em}& -\frac{1}{4}(|0111>+|1011>+|1101>+|1110>)\otimes |1>.\end{array}$(42)

Then, the proposed algorithm applies measurement on the extra qubit and proceeds by applying $Z$ then $H$ on the extra qubit, if the outcome is $|1>$, otherwise restarts the preparation stage. The probability to get $|1>$ on the extra qubit is $nt|c_q{|}^2$. If the outcome is $|1>$, then the superposition can be represented as

(43) $|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}}>=\frac{1}{\sqrt{nt}}\sum _{f_h(i)=1}|i>\otimes |1>$(43)

Using the working example, assuming that $U_{f_h}$ is an oracle to prepare all possible states with $t=3$, applying $D_p{U}_{f_h}$ for $q=2$ times prepares all the possible solutions with $t=3$ resulting in the following incomplete superposition:

(44) $|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}}>=\frac{1}{2}(|0111>+|1011>+|1101>+|1110>)\otimes |1>.$(44)

3.4. Searching the incomplete superposition

Given an incomplete superposition of states that have a specific $t$ number of $1$‘s, we amended Arima’s algorithm (Arima et al., 2009) to search for the assignment that satisfies $U_{TR}$ in the case of having multisolutions. Considering the given matrix $TR$ in Equation 1(1) $TR=\left[\begin{array}{cccccc}0& 1& 0& 1& 1& 1\\ 0& 1& 1& 0& 0& 1\\ 0& 1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0& 1\end{array}\right].$(1) , $f_{TR}$ can be represented as shown in Equation 2(2) $f_{TR}=\underset{r_1}{\underbrace{\left(t_4\right)}}\wedge \underset{r_2}{\underbrace{\left(t_1\vee t_2\vee t_3\right)}}\wedge \underset{r_3}{\underbrace{\left(t_2\right)\wedge }}\underset{r_4}{\underbrace{\left(t_1\vee t_3\vee t_4\right)}}\wedge \underset{r_5}{\underbrace{\left(t_1\right)}}\wedge \underset{r_6}{\underbrace{\left(t_1\vee t_2\vee t_4\right)}},$(2) (Younes & Rowe, 2015). This can be represented as Reed–Muller expansion (Younes & Miller, 2004) so it can be represented as follows:

(45) $f_{TR}=t_1\vee t_2\vee t_4,$(45)

then use the oracle $U_{TR}$ for the function $f_{TR}$ in the algorithm as shown in the quantum circuit in Figure 3 (Younes & Miller, 2004).

Figure 3. Quantum circuit for the $U_{TR}$

The proposed algorithm amended Arima’s algorithm to search for the states that satisfy $f_{TR}$ in the prepared incomplete superposition in the case of having multisolutions, so we are searching for states recognized by $f_h$ and to satisfy $f_{TR}$ if exists, and otherwise, we prepare another an incomplete superposition with an incremented Hamming distance and repeat the algorithm. The updated Arima’s algorithm is applied for $\frac{\pi \sqrt{N}}{4}$ times and report whether or not the prepared superposition contains a state that satisfies $f_{TR}$.

Using the working example with $t=3$ and $n=4$, the number of iterations of Arima’s algorithm, $q_a=2$. The system of the working example will be updated as follows:

(46) $\begin{array}{cc}|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}>& =\frac{1}{8\sqrt{2}}(|0000>+|0001>+|0010>+|0011>\\ \hspace{0.17em}& +|0100>+|0101>+|0110>-|0111>\\ \hspace{0.17em}& +|1000>+|1001>+|1010>-|1011>\\ \hspace{0.17em}& +|1100>-|1110>+|1111>)\otimes |0>\\ \hspace{0.17em}& +\frac{1}{8\sqrt{2}}(-|0000>-|0001>-|0010>-|0011>\\ \hspace{0.17em}& -|0100>-|0101>-|0110>+|0111>\\ \hspace{0.17em}& -|1000>-|1001>-|1010>+|1011>\\ \hspace{0.17em}& -|1100>+|1110>-|1111>)\otimes |1>\\ \hspace{0.17em}& +\frac{7}{8\sqrt{2}}(|1101>)\otimes |0>-\frac{7}{8\sqrt{2}}(|1101>)\otimes |1>.\end{array}$(46)

The probability of the desired pattern is calculated as in Arima et al., (2009) with a minimized value of the number of stored data because of our incomplete superposition preparation step, which in turn improves the probability. In the working example, the desired pattern of $|1101>$ is obtained with probability $2(\frac{7}{8\sqrt{2}}{)}^2\approx 0.766$.

The methodology of the proposed algorithm has been illustrated. Problem encoding, preparation phase, and searching the incomplete superposition phase have been explained.

4. Analysis of the searching phase

To analyze the dynamics of the searching phase, $|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}>$ can be generalized to the form:

(47) $\begin{array}{cc}|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}>& =\frac{1}{h}\sum _{k=1}^h{\alpha }_k(t_x)(|i>\otimes |1>)\\ \hspace{0.17em}& +\frac{1}{m-h}\sum _{i=h+1}^m{\beta }_i(t_x)(|i>\otimes |0>)\\ \hspace{0.17em}& +\frac{1}{N-m}\sum _{j=m+1}^N{\gamma }_j(t_x)(|i>\otimes |1>)\\ \hspace{0.17em}& =\bar{\alpha }(t_x)(|i>\otimes |1>)+\bar{\beta }(t_x)(|i>\otimes |0>)+\bar{\gamma }(t_x)(|i>\otimes |1>),\end{array}$(47)

where we define the average of the amplitudes of the subspace $\frac{1}{h}{\sum }_{k=1}^h{\alpha }_k(t_x)(|i>\otimes |1>)$ of possible solutions at time $t_x$ by ${\alpha }_k(t_x)$ where $k$ starts with $1$ and increments to $h$ where $h$ representes the number of possible solutions. The average of the amplitudes of the subspace $\frac{1}{m-h}{\sum }_{i=h+1}^m{\beta }_i(t_x)(|i>\otimes |0>)$ of non-solutions by ${\beta }_i(t_x)$ where $i$ takes the range of $h$ to $m$. Thus, ${\alpha }_k(t_x)$ and ${\beta }_i(t_x)$ are the average amplitudes of the subspace $\frac{1}{N-m}{\sum }_{j=m+1}^N{\gamma }_j(t_x)(|i>\otimes |1>)$ of the stored data, while the amplitude of the other data that were not in the prepared superposition at time $t_x$ is defined by ${\gamma }_j(t_x)$ where $j$ takes values from $m$ to $N$.

To calculate the averages of such amplitudes, we use the following equations:

(48) $\bar{\alpha }(t_x)=\frac{1}{h}\sum _{k=1}^h{\alpha }_k(t_x),$(48)

(49) $\bar{\beta }(t_x)=\frac{1}{m-h}\sum _{i=h+1}^m{\beta }_i(t_x),$(49)

(50) $\bar{\gamma }(t_x)=\frac{1}{N-m}\sum _{j=m+1}^N{\gamma }_j(t_x),$(50)

considering that the initial distribution at $t_x=0$ is arbitrary. The weighted average over states is calculated as follows:

(51) $\begin{array}{cc}w(t_x)& =\frac{1}{N}[\sum _{j=m+1}^N{\gamma }_j(t_x)+\sum _{i=h+1}^m{\beta }_i(t_x)-\sum _{k=1}^h{\alpha }_k(t_x)]\\ \hspace{0.17em}& =\frac{1}{N}[(N-m)\bar{\gamma }(t_x)+(m-h)\bar{\beta }(t_x)-(h)\bar{\alpha }(t_x)].\end{array}$(51)

Then, the following relation holds based on (Biron et al., 1998):

(52) $\bar{\alpha }(t_x+1)=2w(t_{x{ }^{\mathrm{\prime }}})+\bar{\alpha }(t_{x{ }^{\mathrm{\prime }}}),$(52)

(53) $\bar{\beta }(t_x+1)=2w(t_{x{ }^{\mathrm{\prime }}})+\bar{\beta }(t_{x{ }^{\mathrm{\prime }}}),$(53)

(54) $\bar{\gamma }(t_x+1)=2w(t_{x{ }^{\mathrm{\prime }}})-\bar{\gamma }(t_{x{ }^{\mathrm{\prime }}}).$(54)

After solving Equation 52(52) $\bar{\alpha }(t_x+1)=2w(t_{x{ }^{\mathrm{\prime }}})+\bar{\alpha }(t_{x{ }^{\mathrm{\prime }}}),$(52) , Equation 53(53) $\bar{\beta }(t_x+1)=2w(t_{x{ }^{\mathrm{\prime }}})+\bar{\beta }(t_{x{ }^{\mathrm{\prime }}}),$(53) , and Equation 54(54) $\bar{\gamma }(t_x+1)=2w(t_{x{ }^{\mathrm{\prime }}})-\bar{\gamma }(t_{x{ }^{\mathrm{\prime }}}).$(54) , the following amplitude averages can be calculated as follows:

(55) $\left[\begin{array}{c}\bar{\alpha }(t_x+1)\\ \bar{\beta }(t_x+1)\\ \bar{\gamma }(t_x+1)\end{array}\right]=\left[\begin{array}{ccc}\frac{N^2-8N+8(m-h)}{N^2}& \frac{8(m-h)(N-m)}{N^2}& \frac{4(N-m)(N-2m-2h+1)}{N^2}\\ \frac{-8(N-(m-h))}{N^2}& \frac{8(m-h)(N-m)-N^2}{N^2}& \frac{4(N-m)(N-2m-2h+1)}{N^2}\\ \frac{-4(N-2(m-h))}{N^2}& \frac{4(m-h)(N-2m)}{N^2}& \frac{-8m(N-m-h+1)+N^2}{N^2}\end{array}\right]\left[\begin{array}{c}\bar{\alpha }(t_x)\\ \bar{\beta }(t_x)\\ \bar{\gamma }(t_x)\end{array}\right].$(55)

The analysis of the searching phase has been explained in detail. The amplitude averages can then be calculated at any given time $t_x$.

5. Discussion

A pseudocode is shown in Algorithm 1 to summarize the proposed algorithm.

Algorithm 1: Pseudocode for the proposed algorithm

1. Prepare $|{\psi }_1>$.

2. Apply $H$ on the first $n$ qubits.

3. for $q=1$ to $\frac{\pi }{2\sqrt{2}}\sqrt{\frac{N}{nt}}$ do

4. Apply $D_p{U}_{f_h}$ on $|{\psi }_2>$.

5. end for

6: Measure the extra qubit.

7. if The outcome is $|1>$ then

8. Apply $Z$ on the extra qubit.

9. Apply $H$ on the extra qubit.

10. for $q_a=1$ to $\frac{\pi }{4}\sqrt{N}$ do

11. Apply $D{U}_{f_h}D{U}_{TR}$ on $|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}}>$.

12. end for

13. else

14. Go to step 2.

15. end if

The target of the proposed algorithm is to search for the best solution for the test-suite minimization problem. Equation 31(31) $|{\psi }_1⟩=|{0⟩}^{\otimes n}\otimes |0⟩,$(31) shows the system initialization. The $n+1$ qubits are initialized to $|0>$ and then $H$ is applied to the first $n$ qubits as shown in Equation 32(32) $|{\psi }_2⟩=(H^{\otimes n}\otimes I)|{\psi }_1⟩=\frac{1}{\sqrt{N}}\sum _{i=0}^{N-1}|i⟩\otimes |0⟩.$(32) . These steps prepares the complete superposition. A superposition of $t$ number of $1$‘s is needed; thus, the oracle $U_{f_h}$ and the partial diffusion operator $D_p$ are applied for $q$ times as shown in Equation 40(40) $q=\frac{\pi }{2\sqrt{2}}\sqrt{\frac{N}{nt}}.$(40) . This step prepares the incomplete superposition that contains a candidate solution we are trying to find. The extra qubit is then measured to amplify the amplitudes of the solutions via entanglement of the search space with this extra qubit. In case that the outcome is $|1>$, $Z$ is applied on the extra qubit, and then $H$ is applied on this extra qubit to update the system to be as shown in Equation 44(44) $|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}}>=\frac{1}{2}(|0111>+|1011>+|1101>+|1110>)\otimes |1>.$(44) . The updated version of Arima’s is then applied to search for the best solution in the prepared incomplete superposition. Equation 47(47) $\begin{array}{cc}|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}>& =\frac{1}{h}\sum _{k=1}^h{\alpha }_k(t_x)(|i>\otimes |1>)\\ \hspace{0.17em}& +\frac{1}{m-h}\sum _{i=h+1}^m{\beta }_i(t_x)(|i>\otimes |0>)\\ \hspace{0.17em}& +\frac{1}{N-m}\sum _{j=m+1}^N{\gamma }_j(t_x)(|i>\otimes |1>)\\ \hspace{0.17em}& =\bar{\alpha }(t_x)(|i>\otimes |1>)+\bar{\beta }(t_x)(|i>\otimes |0>)+\bar{\gamma }(t_x)(|i>\otimes |1>),\end{array}$(47) shows the system after applying the updated Arima’s algorithm $q_a$ times in its general form. Equation 47(47) $\begin{array}{cc}|{\psi }_y^{\mathrm{\prime }{ }^{\mathrm{\prime }}{ }^{\mathrm{\prime }}}>& =\frac{1}{h}\sum _{k=1}^h{\alpha }_k(t_x)(|i>\otimes |1>)\\ \hspace{0.17em}& +\frac{1}{m-h}\sum _{i=h+1}^m{\beta }_i(t_x)(|i>\otimes |0>)\\ \hspace{0.17em}& +\frac{1}{N-m}\sum _{j=m+1}^N{\gamma }_j(t_x)(|i>\otimes |1>)\\ \hspace{0.17em}& =\bar{\alpha }(t_x)(|i>\otimes |1>)+\bar{\beta }(t_x)(|i>\otimes |0>)+\bar{\gamma }(t_x)(|i>\otimes |1>),\end{array}$(47) also shows the average amplitudes for the possible solutions represented by $\bar{\alpha }(t_x)$, the average amplitudes for the non-solutions represented by $\bar{\beta }(t_x)$, and the average amplitudes for the other data that were not in the prepared superposition represented by $\bar{\gamma }(t_x)$ and the weighted averages are shown in Equation 51(51) $\begin{array}{cc}w(t_x)& =\frac{1}{N}[\sum _{j=m+1}^N{\gamma }_j(t_x)+\sum _{i=h+1}^m{\beta }_i(t_x)-\sum _{k=1}^h{\alpha }_k(t_x)]\\ \hspace{0.17em}& =\frac{1}{N}[(N-m)\bar{\gamma }(t_x)+(m-h)\bar{\beta }(t_x)-(h)\bar{\alpha }(t_x)].\end{array}$(51) . The average of the amplitudes can be calculated at any time $t_x$ by Equation 55(55) $\left[\begin{array}{c}\bar{\alpha }(t_x+1)\\ \bar{\beta }(t_x+1)\\ \bar{\gamma }(t_x+1)\end{array}\right]=\left[\begin{array}{ccc}\frac{N^2-8N+8(m-h)}{N^2}& \frac{8(m-h)(N-m)}{N^2}& \frac{4(N-m)(N-2m-2h+1)}{N^2}\\ \frac{-8(N-(m-h))}{N^2}& \frac{8(m-h)(N-m)-N^2}{N^2}& \frac{4(N-m)(N-2m-2h+1)}{N^2}\\ \frac{-4(N-2(m-h))}{N^2}& \frac{4(m-h)(N-2m)}{N^2}& \frac{-8m(N-m-h+1)+N^2}{N^2}\end{array}\right]\left[\begin{array}{c}\bar{\alpha }(t_x)\\ \bar{\beta }(t_x)\\ \bar{\gamma }(t_x)\end{array}\right].$(55) . The proposed algorithm has a maximum of $O({log}_{2}N)$ rounds.

This paper proposes a solution to the test-suite minimization problem. It is crucial to software testing because it helps developers to improve the software quality by finding the minimum test that covers all the requirements. Test sizes increase with software modifications over time in the maintenance phase; thus, the proposed algorithm is significant to find the minimum number of tests through this periodic test size growth. The proposed algorithm saves software testing resources such as time and money by finding the minimum sized solution with high probability.

6. Conclusion and future work

This paper proposed a quantum algorithm to solve the test-suite minimization problem. The proposed algorithm used quantum search algorithms to search for the minimum number of test cases required to test all the requirements. The algorithm encoded a subset of the power set of the set of test cases as quantum states. The two main phases of the algorithm are the states preparation phase and the searching phase. In the preparation phase, the algorithm used Younes et al algorithm for quantum searching via entanglement and partial diffusion to prepare an incomplete superposition that represents a subset of sets from the power set that have the same cardinality. The searching phase was applied by amending Arima’s algorithm to find a possible solution to the given test-suite minimization problem instance in the prepared incomplete superposition. If no solution is found, then the algorithm prepares another incomplete superposition with the cardinality of the subsets in the search space incremented next round. Applying this algorithm to a test-suite minimization problem instance gives the best solution with the minimum required test cases that saves software testing resources such as time and money. The proposed algorithm is crucial while testing the software in the maintenance phase as test sizes increase with software modifications over time. Applying the proposed algorithm is important in case of software growth from a version to another where a requirement that is tested in a previous version will be tested again in the newer version that may result in redundant test cases.

The algorithm needs $O\left(lo{g}_{2}N\right)$ rounds to search the power set of all possible solutions. It was shown that the algorithm can find a solution with high probability in $O\left(\sqrt{2^n}\right)$, where $n$ is the number of test cases.

For future work, we intend to propose efficient quantum algorithms to solve other software engineering problems such as next release problem and the structural test data generation problem (Harman et al., 2012).

Disclosure statement

No potential conflict of interest was reported by the authors.

Data Availability

The data are readily available upon request.

Additional information

Funding

The authors received no direct funding for this research

Notes on contributors

Hager Hussein

Hager Hussein is an Assistant Lecturer in Software Engineering Department, College of Computing and Information Technology (CCIT), Arab Academy for Science, Technology and Maritime Transport (AASTMT). She received her MSc degree in software engineering from CCIT in AASTMT in 2012. Her research interests include quantum algorithms, software engineering.

Ahmed Younes

Ahmed Younes is a Professor of Computer Science at Alexandria University and Honorary Research Fellow at School of Computer Science, University of Birmingham, United Kingdom. He is the founder and leader of Alexandria Quantum Computing Group. He obtained his PhD from University of Birmingham, United Kingdom, in 2004. He published many papers on Quantum Algorithms and Reversible Circuits.

Walid Abdelmoez

Walid M. Abdelmoez is an Associate Professor in Software Engineering Department, CCIT, AASTMT. He received PhD degree in computer engineering at Lane Department of Computer Science and Electrical Engineering, West Virginia University, Morgantown, WV, USA, in 2006. His research interests are software engineering, software quality assurance, software risk assessment.