A graph-based approach for detection degenerate structures in multi-planet gear trains

Abstract

A locked chain is an immovable sub-chain within a kinematic chain. The detection of immovable sub-chains is a critical step in the structural synthesis of planetary gear trains (PGTs). This paper presents a simplified method for the identification of locked chains in PGTs based on the vertex-edge mobility criterion. The vertex-edge mobility criterion is formulated, and the detection method is proposed. A connectivity matrix is developed for the analytical determination of locked chains in multi-planet gear trains. The algorithm is suitable for planetary gear trains with any degree of freedom (DOF). For the automatic identification of locked chains, a MATLAB program is developed. The only input to the program is the adjacency matrix. The result of this work is beneficial for the automation of the structural synthesis of planetary gear trains.

Keywords:

• connectivity matrix
• locked chains
• fundamental geared entity
• mobility criterion
• matrix representation
• planetary gear train
• structural synthesis

PUBLIC INTEREST STATEMENT

Planetary gear trains are commonly used in transmission systems of machines, automobiles, and robots. Because of the graph theory-based representation of a PGT, structural synthesis algorithms have been developed for enumerating all feasible concepts in the form of non-isomorphic graphs. The enumerated PGTs are important to a PGT designer during the conceptual stage of design. The detection and elimination of graphs with degenerate structure/s as subgraphs is a critical step in the structural synthesis. This paper presents a graph theory-based method for detecting degenerate PGT graphs during the enumerated collection. The result of this work is beneficial for the automation of the structural synthesis of planetary gear trains.

1. Introduction

Graph theory is essential for the structural synthesis of planetary gear trains (Buchsbaum & Freudenstein, 1970; C. H. Hsu & Hsu, 1995; Hsu, 1993). Graphs are used to represent planetary gear trains and to generate all their possible structures with the aid of combinatorial analysis. In the graphs of the enumerated PGTs, some locked chains are likely to be formed. A geared kinematic chain is said to be locked when it contains a group of members that have zero degrees of freedom and act as a rigid body within the system. A PGT containing a locked sub-chain should be excluded from further study, as the locked chain can always be replaced by only one link with fewer joints. That is why, before moving on to the next step of design, it becomes necessary to identify and eliminate all of the locked chains.

Using combinatorial analysis, C.H. Hsu & Wu (1997) presented an algorithm for detecting locked chains in PGTs. For a gear train containing (n) fundamental circuits, the vertex sets created by three to n-FCs are checked for degeneracy. Del Castillo (2002) reduced the degeneracy problem to find a group of links rotating at the same speed. Salgado & Del Castillo (2005) identified locked chains by applying the same criteria of C.H. Hsu & Wu (1997) but to combinations of fundamental geared entities rather than to the FCs individually. The main advantage of the Salgado and Del Castillo method (Salgado & Del Castillo, 2005) over the method of C.H. Hsu & Wu (1997) is the reduction of the required combinations. Kamesh et al. (2017) used the presence of an articulation point in the graph of 1-DOF PGT to confirm the existence of the locked chain. There are three shortcomings in this algorithm: the first is that it does not work with PGTs that have multiple DOFs, the second that it does not work with multi-planet PGTs and the third is that according to the counter example given by Yang & Ding (2018), the algorithm is not comprehensive. The method of Shanmukhasundaram et al. (Shanmukhasundaram et al., 2019) also relies on the idea that there is a cut vertex in locked PGT. Sometimes the cut vertex is visible and most of the time it needs to be detected after removal of binary links from the graph. The method of Shanmukhasundaram et al. (Shanmukhasundaram et al., 2019) is an ad hoc method that is based on

1. the visual inspection of a graph to find a cut vertex.

2. deleting binary links.

3. applying vertex selection for subtrees with the same label in such a way that leads to a cut vertex, if any.

4. individually testing the decomposed components (i.e., separated by CVs) for immobile sub-chains.

One of the drawbacks of this method (Shanmukhasundaram et al., 2019) is that there are several methods of arranging the revolute edges on a common level for a single planetary gear train, resulting in many conventional graphs. Another major drawback is that this method is the only method that needs the revolute edges in the graph to be labeled. The labeling step increases the complexity of this method compared to other methods. Yang & Ding (2018) applied the same criteria as (C.H. Hsu & Wu, 1997) to detect locked chains in PGTs. Their method is based on successive combination of FCs and checking of degrees of freedom. The method in Salgado & Del Castillo (2005) is less complex than the method in Yang & Ding (2018), but the method in Yang & Ding (2018) performs in multi-planet FGEs. Based on matroid theory and through a series of deletion operations, Morlin et al. (2021) evaluated decomposed closed-loop sub-chains to identify the locked chain.

All of the available methods for detecting locked chains in PGTs are based on adding the fundamental circuits or their combinations to each other or removing the fundamental circuits from the given PGT graph, in an attempt to find a structure with zero degrees of freedom. Each step in adding or deleting the fundamental circuits requires calculating the degrees of freedom of the resulting structure. In the present work, a different approach is proposed. A new vertex-edge mobility criterion is developed. According to this criterion, any locked chain is a PGT formed by two fundamental geared entities with three or more common edges and/or vertices. The new mobility criterion does not require combinatorial analysis. Recently, Esmail & Juber (2021) introduced a CM matrix called the connectivity matrix, which greatly simplifies the degeneracy detection process. Two fundamental geared entities are said to be locked if they have three elements in common. However, the above method is not sufficient to deal with multi-planet gear trains. The main reason is that multi-planet geared entities may form locked chains by themselves. Here, the notion of multi-planet FGE, which is the union of single-planet FGEs with common gear edge(s), is introduced and a detection algorithm is proposed.

The objective of this paper is to develop an easy algorithm such that any locked chain can be detected from single-planet, multi-planet, single-DOF, or multi-DOF PGTs. The well-known adjacency matrix is used to represent the system and then to detect the locked chain. The main advantage of this algorithm is that a connectivity matrix can be derived without manipulating the equations or the graph of the PGT. A MATLAB program is developed for the automatic identification of locked chains. The locked chain detection is useful for automating the structural synthesis of PGTs.

2. Mathematical model

An F-DOF PGT is an assemblage of N links with $\left(N-1\right)$ revolute joints and $\left(N-F-1\right)$ gear joints (Buchsbaum & Freudenstein, 1971). The numbers of degrees of freedom ($F$) of a PGT can be expressed as follows:

(1) $F=3\times N-2\times J_r-1\times J_g-3,$(1)

where $J_{\mathrm{r}}$ represent the revolute pairs and $J_{\mathrm{g}}$ represent the gear pairs. The number of DOFs in terms of $N$ and $J_g$ is

(2) $F=N-1-J_g.$(2)

Planetary gear trains with multiple DOF are often used in planetary automatic transmissions (Chen & Chen, 2021; Hussen et al., 2020; Esmail et al., 2021; Cammalleri & Castellano, 2021). In the graph representation, an FC is made up of two adjacent gears $i$, $j$ and their carrier $k$. It consists of two edges, a geared edge $\left(i-j\right)$, a revolute edge $\left(j-k\right)$ and a transfer vertex $k$. An FC is denoted as $\left(i,j\right)k$. According to the work conducted by (Chatterjee and Tsai,1996) by all the FCs that have their planet gear and planet carrier in common, a PGT is formed which is called a single-planet fundamental geared entity. If two planet gears with a common carrier are connected by a gear edge, a double-planet FGE is obtained (Hsieh & Tsai, 1996; Hsieh & Tsai 1998: Tsai, 2001) and so on.

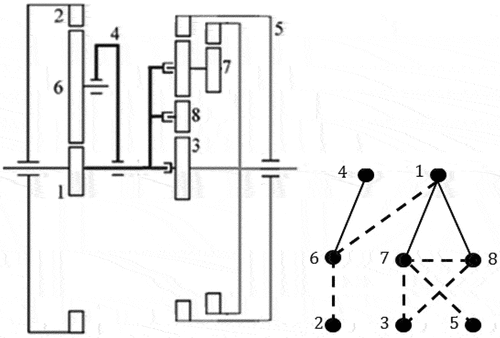
The elements of an adjacency matrix indicate whether the vertices of a graph are adjacent or not (Ali Hussen & Lauibi Esmail, 2021). If vertex $i$ is adjacent to vertex $j$, then $a_{ij}=1$. Otherwise, $a_{ij}=0$ including $a_{ii}$. For example, Figure 1 shows a PGT and its graph and Equation (1)(1) $F=3\times N-2\times J_r-1\times J_g-3,$(1) gives its adjacency matrix.

Figure 1. (a) A PGT (b) its graph.

(3) $A=\left[\begin{array}{cccccccccc}\hspace{0.17em}& v_1& v_2& v_3& v_4& v_5& ⋮& v_6& v_7& v_8\\ v_1& 0& 0& 0& 0& 0& ⋮& 1& 1& 1\\ v_2& 0& 0& 0& 0& 0& ⋮& 1& 0& 0\\ v_3& 0& 0& 0& 0& 0& ⋮& 0& 1& 1\\ v_4& 0& 0& 0& 0& 0& ⋮& 1& 0& 0\\ v_5& 0& 0& 0& 0& 0& ⋮& 0& 1& 0\\ \dots & \dots & \dots & \dots & \dots & \dots & ⋮& \dots & \dots & \dots \\ v_6& 1& 1& 0& 1& 0& ⋮& 0& 0& 0\\ v_7& 1& 0& 1& 0& 1& ⋮& 0& 0& 1\\ v_8& 1& 0& 1& 0& 0& ⋮& 0& 1& 0\end{array}\right]$(3)

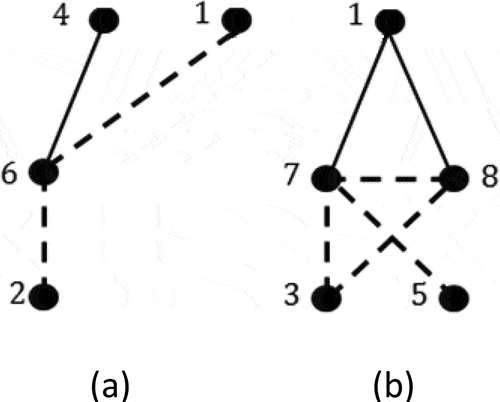
Since $A$ represents the topological structure of a PGT, the fundamental geared entities can easily be achieved from it. There are two fundamental geared entities: a single-planet FGE (FGE1) consists of vertices (1, 2, 4, 6) and a double-planet FGE. The double-planet FGE consists of two single-planet FGEs connected by a gear edge; FGE2 consists of vertices (1, 3, 5, 7); and FGE3 consists of vertices (1, 3, 8). Vertices 7 and 8 are connected by a gear edge. Figure 2 shows these two FGEs.

Figure 2. (a) The single-planet FGE (FGE1) (b) The double planet FGE (FGE2 $\cup$ FGE3).

We can partition the adjacency matrix $\mathrm{A}$ into four submatrices $A_{11}$, ${\mathrm{A}}_{12}$, ${\mathrm{A}}_{21}$, and ${\mathrm{A}}_{22}$ according to the three-row distribution,

(4) $A=\left[\begin{array}{ccc}{A}_{11}& ⋮& A_{12}\\ \cdots & \cdots & \cdots \\ A_{21}& ⋮& A_{22}\end{array}\right],$(4)

where ${\mathrm{A}}_{11}$ contains the vertices of the first and third rows of the graph, while ${\mathrm{A}}_{22}$ contains the vertices of the second row. It is not necessary to adhere to the sequence of vertices.

Let the connectivity of an FGE be defined as the number of vertices and/or edges in common with another FGE. Then, the connectivity matrix $CM$ can be written as

(5) $CM=\left[\begin{array}{c}{A}_{21}\end{array}\right]\left[\begin{array}{c}{A}_{12}\end{array}\right]+\left[\begin{array}{c}{A}_{22}\end{array}\right]$(5)

From this matrix, it can be confirmed whether there is a locked chain especially in multi-planetary FGEs or not. For single-planet FGEs, the latter term of Equation (5)(5) $CM=\left[\begin{array}{c}{A}_{21}\end{array}\right]\left[\begin{array}{c}{A}_{12}\end{array}\right]+\left[\begin{array}{c}{A}_{22}\end{array}\right]$(5) can be dropped. The first term of Equation (5)(5) $CM=\left[\begin{array}{c}{A}_{21}\end{array}\right]\left[\begin{array}{c}{A}_{12}\end{array}\right]+\left[\begin{array}{c}{A}_{22}\end{array}\right]$(5) gives the common vertices between the FGEs, while the second term gives the common edges.

Following the definition of the FGE above and using Equation (5)(5) $CM=\left[\begin{array}{c}{A}_{21}\end{array}\right]\left[\begin{array}{c}{A}_{12}\end{array}\right]+\left[\begin{array}{c}{A}_{22}\end{array}\right]$(5) , we get

(6) $\begin{array}{rl}& CM=\left[\begin{array}{cccccc}\hspace{0.17em}& {\mathrm{v}}_1& {\mathrm{v}}_2& {\mathrm{v}}_3& {\mathrm{v}}_4& {\mathrm{v}}_5\\ {\mathrm{v}}_6& 1& 1& 0& 1& 0\\ {\mathrm{v}}_7& 1& 0& 1& 0& 1\\ {\mathrm{v}}_8& 1& 0& 1& 0& 0\end{array}\right]\left[\begin{array}{cccc}\hspace{0.17em}& {\mathrm{v}}_6& {\mathrm{v}}_7& {\mathrm{v}}_8\\ {\mathrm{v}}_1& 1& 1& 1\\ {\mathrm{v}}_2& 1& 0& 0\\ {\mathrm{v}}_3& 0& 1& 1\\ {\mathrm{v}}_4& 1& 0& 0\\ {\mathrm{v}}_5& 0& 1& 0\end{array}\right]+\\ & \left[\begin{array}{cccc}\hspace{0.17em}& {\mathrm{v}}_6& {\mathrm{v}}_7& {\mathrm{v}}_8\\ {\mathrm{v}}_6& 0& 0& 0\\ {\mathrm{v}}_7& 0& 0& 1\\ {\mathrm{v}}_8& 0& 1& 0\end{array}\right]\end{array}$(6)

The common vertex between FGE₁ and FGE₂ is vertex ${\mathrm{v}}_1$, between FGE₁ and FGE₃ is vertex ${\mathrm{v}}_1$; and between FGE₂ and FGE₃ is vertices ${\mathrm{v}}_1$ and ${\mathrm{v}}_3$. The edge between FGE2 and FGE3 is the only common edge that lies between vertices ${\mathrm{v}}_6$ and ${\mathrm{v}}_7$. The CM matrix can be easily calculated manually, and its off-diagonal elements indicate the number of vertices and/or edges in common. The CM matrix is

(7) $\mathrm{C}\mathrm{M}=\left[\begin{array}{ccc}3& 1& 1\\ 1& 3& 3\\ 1& 3& 2\end{array}\right]$(7)

For example, the element $c{m}_{23}=3$ indicates that FGE₂ and FGE₃ are connected by two vertices and one edge, while $c{m}_{12}=1$ indicates that FGE₁ and FGE₂ are connected by only one vertex.

3. Unification of FGEs

In general, fundamental geared entities are connected to each other by common links and/or joints unless the fundamental geared entity itself stands alone as a PGT. For $N_1$-link and $J_{g1}$-gear edges FGE, $F_1$ can be expressed as

(8) $F_1=N_1-1-J_{g1}.$(8)

Similarly,

(9) $F_2{=}_2-1-J_{g2}.$(9)

The total number of links N of the kinematic chain formed by two FGEs can be written in terms of $N_1$ and $N_2$ as

(10) $N=N_1+N_2-N_c.$(10)

The total number of gear joints $J_g$ can be written in terms of $J_{g1}$ and $J_{g2}$ as

(11) $J_g=J_{g1}+J_{g2}+J_{gc},$(11)

Where $N_c$ and $J_{gc}$ are common links and joints between the two FGEs.

The number of DOFs ($F$) of combined system is

(12) $F=N-1-J_g.$(12)

Substituting Equations (10)(10) $N=N_1+N_2-N_c.$(10) and (11(11) $J_g=J_{g1}+J_{g2}+J_{gc},$(11) ) into Equation (12)(12) $F=N-1-J_g.$(12) yields

(13) $F=N_1+N_2-N_c-1-J_{g1}-J_{g2}-J_{gc}.$(13)

Substituting Equations (8)(8) $F_1=N_1-1-J_{g1}.$(8) and (9(9) $F_2{=}_2-1-J_{g2}.$(9) ) into Equation (13)(13) $F=N_1+N_2-N_c-1-J_{g1}-J_{g2}-J_{gc}.$(13) yields

(14) $F=F_1+F_2-N_c-J_{gc}+1.$(14)

THEOREM 1. Any single-planet fundamental geared entity is a one-DOF PGT. Hence, any single-planet FGE cannot constitute a locked chain.

PROOF.

The number of DOFs in terms of N and Jg is given by Equation (12)(12) $F=N-1-J_g.$(12) .

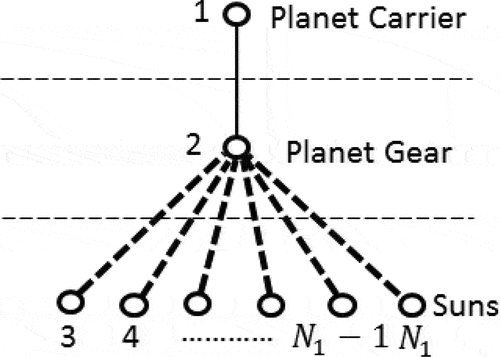
For an N-link single-planet fundamental geared entity, since there is only one planet gear in a single-planet fundamental geared entity, all edges emanating from the planet gear vertex must terminate at the other vertices (see Figure 3). Since each edge has two end vertices, the planet gear vertex is incident by $\left(\mathrm{N}-1\right)$ edges. One of these edges is a revolute edge incident to the planet carrier vertex (solid line), while the others are geared edges (dotted lines). Therefore,

(15) $J_g=N-2.$(15)

Figure 3. A single-planet FGE.

The number of DOFs (F) in terms of $\mathrm{N}$ and ${\mathrm{J}}_g$ is $\mathrm{F}=\mathrm{N}-1-{\mathrm{J}}_g$, and therefore,

(16) $F=N-1-(N-2)=1.$(16)

THEOREM 2. A locked chain is a PGT formed by at least two fundamental geared entities with three common edges and/or vertices.

PROOF. A PGT is said to be locked when it has a zero degree of freedom structure.

If Equation (14)(14) $F=F_1+F_2-N_c-J_{gc}+1.$(14) yields F = 0, the kinematic chain becomes a structure with zero degrees of freedom. For any two single-planet FGEs, ${\mathrm{F}}_1={\mathrm{F}}_2=1$, therefore, we can simplify Equation (14)(14) $F=F_1+F_2-N_c-J_{gc}+1.$(14) to

(17) $F=3-N_c-J_{gc}.$(17)

A locked PGT is the one that has $\mathrm{D}\mathrm{O}\mathrm{F}\le 0$. Hence, from Equation (17)(17) $F=3-N_c-J_{gc}.$(17) ,

(18) $N_c+J_{gc}\ge 3.$(18)

Therefore, the graph of two FGEs with one common edge and two common vertices is a locked chain, with one common edge and two common vertices is a one-DOF PGT, and with one common edge or vertex is a fractionated two-DOF PGT.

For example, Figure 2(b) shows two single-planet FGEs connected by two common vertices and a common edge. Vertices 1 and 3 are the common vertices, while the common edge is the edge connecting vertices 7 and 8. According to Equation (18)(18) $N_c+J_{gc}\ge 3.$(18) : ${\mathrm{N}}_{\mathrm{c}}+{\mathrm{J}}_{\mathrm{g}\mathrm{c}}=2+1=3$. As mentioned above, a locked planetary gear train contains at least one locked chain. The graph of two FGEs with three common edges and/or vertices is a locked chain. Based on this fact, a MATLAB program is developed to automatically identify locked chains.

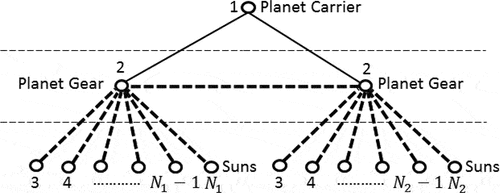
THEOREM 3. If the planet gears of two single-planet fundamental geared entities with a common carrier are connected by a gear edge, a one-DOF double-planet FGE is obtained.

PROOF. Since the degree of freedom for any single-planet FGE is one, then ${\mathrm{F}}_1={\mathrm{F}}_2=1$. Since there is a common carrier, then $N_c=1$. Since the planet gears are connected by a gear edge, then $J_{gc}=1$. Substituting these values in Equation (17)(17) $F=3-N_c-J_{gc}.$(17) yields F = 1, and the double-planet FGE will have one degree of freedom (see Figure 4).

Figure 4. A double -planet FGE.

THEOREM 4. If any two fundamental geared entities, which are part of multi-planet FGE have a common vertex (link), a locked chain is formed. Thus, any multi-planet FGE can form in some of its parts a locked chain.

PROOF. A locked chain is a PGT formed by at least two fundamental geared entities with three common edges and/or vertices.

Since the planet gears are connected by a gear edge, then $J_{gc}=1$. Since there is a common carrier between any two fundamental geared entities, which are part of multi-planet FGE, therefore the existence of an additional common link between the these two FGEs will increase the common vertices to two or $N_c=2$.

Substituting these values in Equation (17)(17) $F=3-N_c-J_{gc}.$(17) yields F = 0, and a locked chain is formed.

4. Detection algorithm

Since any FGE is a one-DOF PGT and according to Equation (17)(17) $F=3-N_c-J_{gc}.$(17) , two FGEs can have the following relationships with each other:

1. They can have two of their vertices in common. The two FGEs constitute a one-DoF PGT.

2. They can have one of their vertices in common. In this case, they form a fractionated two-DoF PGT with the common vertex as the articulation point.

3. They can have one of their vertices and one of their edges in common. In this case, they form a double-planet FGE.

4. They can have two of their vertices and one of their edges in common. The resulting PGT forms a zero-DoF PGT.

5. They can have three of their vertices in common. The resulting PGT forms a zero-DoF PGT.

Based on points 4 and 5, the following detection algorithm is developed:

Step 1. Construct the adjacency matrix (Matrix A) for the graph of the given PGT.

Step 2. Enter the A-matrix to the MATLAB program.

Step 3. Partition the A-matrix into four submatrices $A_{11}$, $A_{12}$, $A_{21}$, and $A_{22}$ according to the vertex-level distribution.

Step 4. Multiply the $A_{21}$ by the $A_{12}$ matrix and add $A_{22}$ to the resulting matrix, and then store the element in the matrix (CM).

Step 5. Check whether the PGT is locked. If we can find at least one off-diagonal element equal to or more than 3 in the connectivity matrix, then the gear train is locked.

Step 6. Obtain the multi-planet FGE that is the union of single-planet FGEs with common gear edge(s).

Step 7. Get the reduced A-matrix ($\tilde{A}$) with the unified FGEs.

Step 8. Multiply the ${\tilde{A}}_{21}$ by the ${\tilde{A}}_{12}$ matrix and store the element in matrix ($\widetilde{CM}$).

Step 10. Repeat step 5.

To explain and validate the algorithm, four examples are used.

Example: 1

The graph “9431Bf” given by Salgado and Del Castillo (Salgado & Del Castillo, 2005) is shown in Figure 5.

Figure 5. The graph “9431Bf” according to Salgado & Del Castillo (2005).

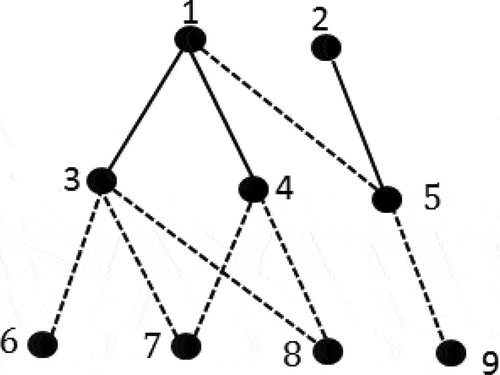
The adjacency matrix is

(19) $\left(A=\begin{array}{ccccccccccc}\hspace{0.17em}& v_1& v_2& v_6& v_7& v_8& v_9& ⋮& v_3& v_4& v_5\\ v_1& 0& 0& 0& 0& 0& 0& ⋮& 1& 1& 1\\ v_2& 0& 0& 0& 0& 0& 0& ⋮& 0& 0& 1\\ v_6& 0& 0& 0& 0& 0& 0& ⋮& 1& 0& 0\\ v_7& 0& 0& 0& 0& 0& 0& ⋮& 1& 1& 0\\ v_8& 0& 0& 0& 0& 0& 0& ⋮& 1& 1& 0\\ v_9& 0& 0& 0& 0& 0& 0& ⋮& 0& 0& 1\\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & ⋮& \dots & \dots & \dots \\ v_3& 1& 0& 1& 1& 1& 0& ⋮& 0& 0& 0\\ v_4& 1& 0& 0& 1& 1& 0& ⋮& 0& 0& 0\\ v_5& 1& 1& 0& 0& 0& 1& ⋮& 0& 0& 0\end{array}\right)$(19)

The connectivity matrix $CM$ is

(20) $CM=\left[\begin{array}{ccccccc}& v_1& v_2& v_6& v_7& v_8& v_9\\ v_3& 1& 0& 1& 1& 1& 0\\ v_4& 1& 0& 0& 1& 1& 0\\ v_5& 1& 1& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}& v_3& v_4& v_5\\ v_1& 1& 1& 1\\ v_2& 0& 0& 1\\ v_6& 1& 0& 0\\ v_7& 1& 1& 0\\ v_8& 1& 1& 0\\ v_9& 0& 0& 1\end{array}\right]$(20)

(21) $CM=\left[\begin{array}{cccc}& FGE1& FGE2& FGE3\\ FGE1& 4& \hspace{0.17em}& 1\\ FGE2& 3& 3& 1\\ FGE3& 1& 1& 3\end{array}\right]$(21)

Since there is an off-diagonal element equal to 3, therefore, FGE1 and FGE2 form a locked chain. FGE1 consists of vertices 1, 3, 6, 7, and 8, while FGE2 consists of vertices 1, 4, 7, and 8.

In this regard, the PGT with the code “9431Bf” was not detected to be locked by Salgado et al. (Salgado & Del Castillo, 2005). In fact, this appears to be an omission rather than a flaw in the method as pointed out by (Esmail & Juber, 2021; Kamesh et al., 2017; Morlin et al., 2021; Shanmukhasundaram et al., 2019; Yang & Ding, 2018). In reality, the reason given by (Shanmukhasundaram et al., 2019) is not true. Although Salgado & Del Castillo (2005) excluded the FGEs from degeneracy testing, the combinations of FCs considered are exhaustive. This was a correct procedure that resulted in the method being shorter. In reality, locked chains can have all their FCs associated with the same transfer vertex.

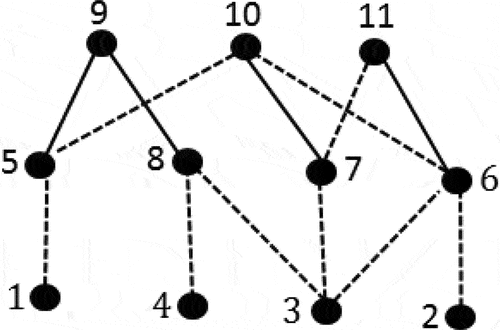
Example 2

Figure 6 shows the graph of an 11-link PGT.

Figure 6. An 11-link PGT.

The adjacency matrix is

(22) $\left[A=\begin{array}{ccccccccccccc}\hspace{0.17em}& v_1& v_2& v_3& v_4& v_9& v_{10}& v_{11}& ⋮& v_5& v_6& v_7& v_8\\ v_1& 0& 0& 0& 0& 0& 0& 0& ⋮& 1& 0& 0& 0\\ v_{{ }_2}& 0& 0& 0& 0& 0& 0& 0& ⋮& 0& 1& 0& 0\\ v_3& 0& 0& 0& 0& 0& 0& 0& ⋮& 0& 1& 1& 1\\ v_4& 0& 0& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 1\\ v_9& 0& 0& 0& 0& 0& 0& 0& ⋮& 1& 0& 0& 1\\ v_{10}& 0& 0& 0& 0& 0& 0& 0& ⋮& 1& 1& 1& 0\\ v_{11}& 0& 0& 0& 0& 0& 0& 0& ⋮& 0& 1& 1& 0\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & ⋮& \cdots & \cdots & \cdots & \cdots \\ v_5& 1& 0& 0& 0& 1& 1& 0& ⋮& 0& 0& 0& 0\\ v_6& 0& 1& 1& 0& 0& 1& 1& ⋮& 0& 0& 0& 0\\ v_7& 0& 0& 1& 0& 0& 1& 1& ⋮& 0& 0& 0& 0\\ v_8& 0& 0& 1& 1& 1& 0& 0& ⋮& 0& 0& 0& 0\end{array}\right]$(22)

The connectivity matrix $CM$ is

(23) $\left[CM=\begin{array}{cccccccc}\hspace{0.17em}& v_1& v_2& v_3& v_4& v_9& v_{10}& v_{11}\\ v_5& 1& 0& 0& 0& 1& 1& 0\\ v_6& 0& 1& 1& 0& 0& 1& 1\\ v_7& 0& 0& 1& 0& 0& 1& 1\\ v_8& 0& 0& 1& 1& 1& 0& 0\end{array}\right]\left[\begin{array}{ccccc}\hspace{0.17em}& v_5& v_6& v_7& v_8\\ v_1& 1& 0& 0& 0\\ v_2& 0& 1& 0& 0\\ v_3& 0& 1& 1& 1\\ v_4& 0& 0& 0& 1\\ v_9& 1& 0& 0& 1\\ v_{10}& 1& 1& 1& 0\\ v_{11}& 0& 1& 1& 0\end{array}\right]$(23)

(24) $CM=\left[\begin{array}{ccccc}& FGE1& FGE2& FGE3& FGE4\\ FGE1& 3& 1& 1& 1\\ FGE2& 1& 4& \hspace{0.17em}& 1\\ FGE3& 1& 3& 3& 1\\ FGE4& 1& 1& 1& 3\end{array}\right]$(24)

Since there is an off-diagonal element equal to 3, therefore, FGE2 and FGE3 form a locked chain. FGE2 consists of vertices 2, 3, 6, 10, and 11, while FGE3 consists of vertices 3, 7, 10, and 11. The common vertices are 3, 10, and 11.

The method in Kamesh et al. (2017) is based on the idea that the existence of a cut vertex between any two FGEs of a PGT is a crucial evidence of locked chain (Table 1). According to Kamesh et al . (2017), since there is no vertex of “count” 2 between the FGEs, the PGT may be misclassified as devoid of locked chain..

Table 1. The degeneracy detecting process according toKamesh et al. (2017) to the PGT shown in Figure 6

	1	2	3	4	5	6	7	8	9	10	11	Count
FGE1 (1,5,9,10)	√				√				√	√		2
FGE2 (2,3,6,10,11)		√	√			√				√	√	3
FGE3 (3,7,10,11)			√				√			√	√	3
FGE4 (3,4,8,9)			√	√				√	√			2

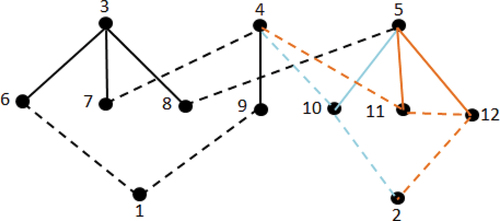
Example 3

Figure 7 shows the graph of a 12-link double-planet PGT.

Figure 7. The degeneracy detection of a 12-link 2-DOF double-planet PGT.

The adjacency matrix is

(25) $\left[A=\begin{array}{cccccccccccccc}\hspace{0.17em}& v_1& v_2& v_3& v_4& v_5& ⋮& v_6& v_7& v_8& v_9& v_{10}& v_{11}& v_{12}\\ v_1& 0& 0& 0& 0& 0& ⋮& 1& 0& 0& 1& 0& 0& 0\\ v_2& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 1& 0& 1\\ v_3& 0& 0& 0& 0& 0& ⋮& 1& 1& 1& 0& 0& 0& 0\\ v_4& 0& 0& 0& 0& 0& ⋮& 0& 1& 0& 1& 1& 1& 0\\ v_5& 0& 0& 0& 0& 0& ⋮& 0& 0& 1& 0& 1& 1& 1\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & ⋮& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ v_6& 1& 0& 1& 0& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_7& 0& 0& 1& 1& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_8& 0& 0& 1& 0& 1& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_9& 1& 0& 0& 1& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_{10}& 0& 1& 0& 1& 1& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_{11}& 0& 0& 0& 1& 1& ⋮& 0& 0& 0& 0& 0& 0& 1\\ v_{12}& 0& 1& 0& 0& 1& ⋮& 0& 0& 0& 0& 0& 1& 0\end{array}\right]$(25)

The connectivity matrix $CM$ is

(26) $CM=\left[\begin{array}{cccccc}\hspace{0.17em}& v1& v2& v3& v4& v5\\ v6& 1& 0& 1& 0& 0\\ v7& 0& 0& 1& 1& 0\\ v8& 0& 0& 1& 0& 1\\ v9& 1& 0& 0& 1& 0\\ v10& 0& 1& 0& 1& 1\\ v11& 0& 0& 0& 1& 1\\ v12& 0& 1& 0& 0& 1\end{array}\right]\left[\begin{array}{cccccccc}\hspace{0.17em}& v6& v7& v8& v9& v10& v11& v12\\ v1& 1& 0& 0& 1& 0& 0& 0\\ v2& 0& 0& 0& 0& 1& 0& 1\\ v3& 1& 1& 1& 0& 0& 0& 0\\ v4& 0& 1& 0& 1& 1& 1& 0\\ v5& 0& 0& 1& 0& 1& 1& 1\end{array}\right]+\left[\begin{array}{cccccccc}\hspace{0.17em}& v6& v7& v8& v9& v10& v11& v12\\ v6& 0& 0& 0& 0& 0& 0& 0\\ v7& 0& 0& 0& 0& 0& 0& 0\\ v8& 0& 0& 0& 0& 0& 0& 0\\ v9& 0& 0& 0& 0& 0& 0& 0\\ v10& 0& 0& 0& 0& 0& 0& 0\\ v11& 0& 0& 0& 0& 0& 0& 1\\ v12& 0& 0& 0& 0& 0& 1& 0\end{array}\right]$(26)

(27) $CM=\left[\begin{array}{cccccccc}& FGE1& FGE2& FGE3& FGE4& FGE5& FGE6& FGE7\\ FGE1& 2& 1& 1& 1& 0& 0& 0\\ FGE2& 1& 2& 1& 1& 1& 1& 0\\ FGE3& 1& 1& 2& 0& 1& 1& 1\\ FGE4& 1& 1& 0& 2& 1& 1& 0\\ FGE5& 0& 1& 1& 1& 3& 2& 2\\ FGE6& 0& 1& 1& 1& 2& 2& 2\\ FGE7& 0& 0& 1& 0& 2& 2& 2\end{array}\right]$(27)

At this stage, it seems that there is no locked chain.

The presence of a double-planet FGE is indicated by the presence in matrix $A_{22}$ of off-diagonal elements of values equal to one. The reduced A-matrix ($\tilde{A}$) with the unified FGEs having a common gear edge is

(28) $A=\left[\begin{array}{ccccccccccccc}\hspace{0.17em}& v1& v2& v3& v4& v5& ⋮& v6& v7& v8& v9& v10& v11,v12\\ v1& 0& 0& 0& 0& 0& ⋮& 1& 0& 0& 1& 0& 0\\ v2& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 1& 1\\ v3& 0& 0& 0& 0& 0& ⋮& 1& 1& 1& 0& 0& 0\\ v4& 0& 0& 0& 0& 0& ⋮& 0& 1& 0& 1& 1& 1\\ v5& 0& 0& 0& 0& 0& ⋮& 0& 0& 1& 0& 1& 1\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & ⋮& \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ v6& 1& 0& 1& 0& 0& ⋮& 0& 0& 0& 0& 0& 0\\ v7& 0& 0& 1& 1& 0& ⋮& 0& 0& 0& 0& 0& 0\\ v8& 0& 0& 1& 0& 1& ⋮& 0& 0& 0& 0& 0& 0\\ v9& 1& 0& 0& 1& 0& ⋮& 0& 0& 0& 0& 0& 0\\ v10& 0& 1& 0& 1& 1& ⋮& 0& 0& 0& 0& 0& 0\\ v11,v12& 0& 1& 0& 1& 1& ⋮& 0& 0& 0& 0& 0& 1\end{array}\right]$(28)

The reduced connectivity matrix $\widetilde{CM}$ is

(29) $\begin{array}{rl}& \stackrel{\sim }{CM}=\left[\begin{array}{cccccc}& v_1& v_2& v_3& v_4& v_5\\ v_6& 1& 0& 1& 0& 0\\ v_7& 0& 0& 1& 1& 0\\ v_8& 0& 0& 1& 0& 1\\ v_9& 1& 0& 0& 1& 0\\ v_{10}& 0& 1& 0& 1& 1\\ v_{11},v_{12}& 0& 1& 0& 1& 1\end{array}\right]\left[\begin{array}{ccccccc}& v_6& v_7& v_8& v_9& v_{10}& v_{11},v_{12}\\ v_1& 1& 0& 0& 1& 0& 0\\ v_2& 0& 0& 0& 0& 1& 1\\ v_3& 1& 1& 1& 0& 0& 0\\ v_4& 0& 1& 0& 1& 1& 1\\ v_5& 0& 0& 1& 0& 1& 1\end{array}\right]+\\ & \left[\begin{array}{ccccccc}& v_6& v_7& v_8& v_9& v_{10}& v_{11},v_{12}\\ v_6& 0& 0& 0& 0& 0& 0\\ v_7& 0& 0& 0& 0& 0& 0\\ v_8& 0& 0& 0& 0& 0& 0\\ v_9& 0& 0& 0& 0& 0& 0\\ v_{10}& 0& 0& 0& 0& 0& 0\\ v_{11},v_{12}& 0& 0& 0& 0& 0& 1\end{array}\right]\end{array}$(29)

or

(30) $\widetilde{CM}=\left[\begin{array}{ccccccc}& FGE1& FGE2& FGE3& FGE4& FGE5& FGE6{\cup }^{F}GE7\\ FGE1& 2& 1& 1& 1& 0& 0\\ FGE2& 1& 2& 1& 1& 1& 1\\ FGE3& 1& 1& 2& 0& 1& 1\\ FGE4& 1& 1& 0& 2& 1& 1\\ FGE5& 0& 1& 1& 1& 3& \hspace{0.17em}\\ FGE6{\cup }^{F}GE7& 0& 1& 1& 1& 3& 4\end{array}\right]$(30)

Since there is an off-diagonal element equal to 3, therefore, FGE6, FGE7 and FGE5 form a locked chain. FGE6 and FGE7 form a double-planet FGE that consists of vertices 2, 4, 5, 11, and 12, while FGE5 consists of vertices 2, 4, 5 and 10. The common vertices are 2, 4, and 5.

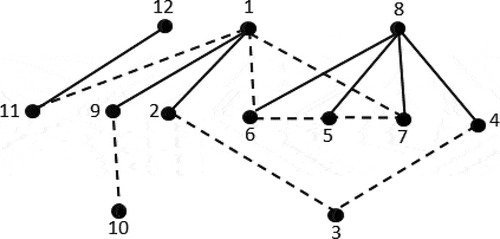
Example 4

Some methods failed to detect the locked chains in multi-planet PGTs. According to Salgado & Del Castillo (2005), a single-planet PGT can be derived from the double-planet PGT by eliminating one of the planet gears and then diagnosing the resulting PGT for degeneration. But sometimes one of the double planets cannot be removed without affecting the kinematic structure of the PGT. This is what causes the method proposed by Salgado & Del Castillo (2005) to lose its comprehensiveness. Figure 8 shows the graph of a counterexample for a 12-link triple-planet PGT.

Figure 8. The degeneracy detection of a 12-link triple-planet PGT.

The adjacency matrix is

(31) $\mathrm{A}=\left[\begin{array}{cccccccccccccc}\hspace{0.17em}& v_3& v_{10}& v_1& v_8& v_{12}& ⋮& v_2& v_4& v_5& v_6& v_7& v_9& v_{11}\\ v_3& 0& 0& 0& 0& 0& ⋮& 1& 1& 0& 0& 0& 0& 0\\ v_{10}& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 0& 1& 0\\ v_1& 0& 0& 0& 0& 0& ⋮& 1& 0& 0& 1& 1& 1& 1\\ v_8& 0& 0& 0& 0& 0& ⋮& 0& 1& 1& 1& 1& 0& 0\\ v_{12}& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 0& 0& 1\\ \dots & \dots & \dots & \dots & \dots & \dots & ⋮& \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ v_2& 1& 0& 1& 0& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_4& 1& 0& 0& 1& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_5& 0& 0& 0& 1& 0& ⋮& 0& 0& 0& 1& 1& 0& 0\\ v_6& 0& 0& 1& 1& 0& ⋮& 0& 0& 1& 0& 0& 0& 0\\ v_7& 0& 0& 1& 1& 0& ⋮& 0& 0& 1& 0& 0& 0& 0\\ v_9& 0& 1& 1& 0& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\\ v_{11}& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$(31)

The reduced A-matrix ($\tilde{A}$)

(32) $\tilde{A}=\left[\begin{array}{ccccccccccccc}\hspace{0.17em}& v_3& v_{10}& v_1& v_8& v_{12}& ⋮& v_2& v_4& v_5,v_6& v_7& v_9& v_{11}\\ v_3& 0& 0& 0& 0& 0& ⋮& 1& 1& 0& 0& 0& 0\\ v_{10}& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 1& 0\\ v_1& 0& 0& 0& 0& 0& ⋮& 1& 0& 1& 1& 1& 1\\ v_8& 0& 0& 0& 0& 0& ⋮& 0& 1& 1& 1& 0& 0\\ v_{12}& 0& 0& 0& 0& 0& ⋮& 0& 0& 0& 0& 0& 1\\ \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\ v_2& 1& 0& 1& 0& 0& ⋮& 0& 0& 0& 0& 0& 0\\ v_4& 1& 0& 0& 1& 0& ⋮& 0& 0& 0& 0& 0& 0\\ v_5,v_6& 0& 0& 1& 1& 0& ⋮& 0& 0& 1& 1& 0& 0\\ v_7& 0& 0& 1& 1& 0& ⋮& 0& 0& 1& 0& 0& 0\\ v_9& 0& 1& 1& 0& 0& ⋮& 0& 0& 0& 0& 0& 0\\ v_{11}& 0& 0& 1& 0& 1& ⋮& 0& 0& 0& 0& 0& 0\end{array}\right]$(32)

The reduced connectivity matrix $\widetilde{CM}$ is

(33) $\widetilde{CM}=\left[\begin{array}{cccccc}\hspace{0.17em}& v_3& v_{10}& v_1& v_8& v_{12}\\ v_2& 1& 0& 1& 0& 0\\ v_4& 1& 0& 0& 1& 0\\ v_5,v_6& 0& 0& 1& 1& 0\\ v_7& 0& 0& 1& 1& 0\\ v_9& 0& 1& 1& 0& 0\\ v_{11}& 0& 0& 1& 0& 0\end{array}\right]\left[\begin{array}{ccccccc}\hspace{0.17em}& v_2& v_4& v_5,v_6& v_7& v_9& v_{11}\\ v_3& 1& 1& 0& 0& 0& 0\\ v_{10}& 0& 0& 0& 0& 1& 0\\ v_1& 1& 0& 1& 1& 1& 1\\ v_8& 0& 1& 1& 1& 0& 0\\ v_{12}& 0& 0& 0& 0& 0& 1\end{array}\right]+\left[\begin{array}{ccccccc}\hspace{0.17em}& v_2& v_4& v_5,v_6& v_7& v_9& v_{11}\\ v_2& 0& 0& 0& 0& 0& 0\\ v_4& 0& 0& 0& 0& 0& 0\\ v_5,v_6& 0& 0& 1& 1& 0& 0\\ v_7& 0& 0& 1& 0& 0& 0\\ v_9& 0& 0& 0& 0& 0& 0\\ v_{11}& 0& 0& 0& 0& 0& 0\end{array}\right]$(33)

or

(34) $\widetilde{CM}=\left[\begin{array}{ccccccc}& FG1& FG2& FGE3{\cup }^{F}GE4& FGE5& FGE6& FGE7\\ FGE1& 2& 1& 1& 1& 1& 1\\ FGE2& 1& 2& 1& 1& 0& 0\\ FGE3{\cup }^{F}GE4& 1& 1& 3& \hspace{0.17em}& 1& 1\\ FGE5& 1& 1& 3& 2& 1& 1\\ FGE6& 1& 0& 1& 1& 2& 1\\ FGE7& 1& 0& 1& 1& 1& 2\end{array}\right]$(34)

Since there is an off-diagonal element equal to 3, therefore, FGE3, FGE4 and FGE5 form a locked chain. FGE3 and FGE4 consist of vertices 1, 5, 6, and 8, while FGE3 consists of vertices 1, 7, and 8. The common vertices are 1 and 8, and the common edge is the edge between vertices 5 and 7.

5. Conclusion

In this paper, a novel criterion for the detection of locked chains is developed. The new vertex-edge mobility criterion is based on the fact that any locked gear structure is a PGT formed by at least two fundamental geared entities with 3 or more common edges and/or vertices. The utility of the method is demonstrated by multiple degrees of freedom, multi-planet, and complex PGTs, including counterexamples found in the literature. The results of the proposed adjacency matrix-based algorithm are useful for the automation of the structural synthesis of PGTs. It is possible that degeneracy detection based on graph theory may contribute to the development of computer-aided design programs for structural synthesis of PGTs.

Nomenclature

A	=	Adjacency matrix
Ã	=	Reduced adjacency matrix
CM	=	Connectivity matrix
$\widetilde{CM}$	=	Reduced connectivity matrix
F	=	Number of DOF
Jg	=	Number of gear joints
Jr	=	Number of revolute joints
Jgc	=	Number of common joints between two FGEs
N	=	Number of links of PGT
Nc	=	Number of common links between two FGEs
vi	=	Vertex i

Abbreviations

DOF	=	Degree of freedom
FC	=	Fundamental circuit
FGE	=	Fundamental geared entity
PGT	=	Planetary gear train

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The authors received no direct funding for this research.

Notes on contributors

Essam L. Esmail

Dr. Essam L. Esmail, was born in 1958 in Iraq. He received B.Sc. and M.Sc. from the Department of Mechanical Engineering, Baghdad University, Baghdad, Iraq, in 1980 and 1985, respectively. His Ph.D. degree in Mechanical Engineering is from the University of Technology in 2009. He is a Professor of University of Al-Qadisiyah, College of Engineering. He laid the foundations for the master’s program in Applied Mechanical Engineering at the College of Engineering at the University of Al-Qadisiyah. His research interests include mechanisms, hybrid transmissions, graph theory and genetic algorithm optimization. He serves as a referee for many well-known journals in his subjects of interest.