Appraisal of the realistic accuracy of molecular dynamics of high-pressure hydrogen

Abstract

Molecular dynamics (MD) is a powerful method for studying the behaviour of materials at high temperature. In practice, however, its effectiveness in representing real systems is limited by the accuracy of the forces, finite size effects, quantization and equilibration methods. In this paper, we report and discuss some calculations carried out using MD on high-pressure hydrogen, reviewing a number of sources of error, of which the neglect of zero-point vibrations is quantitatively the largest. We show that simulations using ab initio MD with the PBE functional predict a large stability field for the molecular Cmca4 structure at pressures just above those achieved in current experiments above the stability range of the mixed molecular layered Phase IV. However, the various errors in the simulation all point towards a much smaller stability range, and the likelihood of a non-molecular phase based on low-coordination networks or chains of atoms.

Keywords:

• high pressure
• hydrogen
• molecular dynamics
• path integral
• lattice dynamics
• metallization
• exchange-correlation
• density functional theory

Public Interest Statement

It is inferred from the magnetic fields of giant planets that at high pressures, hydrogen must become metallic. It is widely assumed that this will occur when the pressure is high enough to break up the molecules and create an atomic solid. This has yet to be achieved experimentally in solid hydrogen, but calculations suggest it is within reach of current technology. Here, we examine the reliability of these calculations in view of the necessary approximations made by current theorists. It now seems likely that the metallic phase will be based on H2 molecules, rather than atomic.

1. Introduction

The theory of molecular dynamics (MD) is well established and MD remains the best way to study high-temperature behaviour of materials, especially dynamical processes such as phase transitions, anharmonic vibrations and diffusion. With classical MD, the number of atoms which can be routinely treated is now well above ${10}^7$. As a consequence, many of the finite size effects which early protagonists wrestled with are eliminated. However, with the advent of ab initio molecular dynamics (AIMD), system sizes have dropped back to ${10}^2$, and the problems met by classical MD in the 1980s have reemerged.

As long ago as 1935, Wigner and Huntington (1935) predicted that with a 10-fold increase in density, metallic hydrogen might be formed at high pressures. Evidence for metallic hydrogen comes from the strong magnetic fields of gas giant planets (Acuna & Ness, 1976; Connerney, 1993). On earth, such pressures are accessible at high temperatures in shock-wave experiments (Fortov et al., 2007; Nellis, Weir, & Mitchell, 1996). There are also at least three distinct liquid structures (Ashcroft, 2000). Compression using diamond anvil cells is now approaching the metallization density predicted by Wigner and Huntington (1935), and the general structure of the phase diagram of hydrogen is becoming established, with tantalizing similarity to other mono- and divalent elements (Arapana, Skorodumova, & Ahuja, 2009; Heine, 2000; Ma et al., 2009; Marqués et al., 2009, 2011; Marques et al., 2011; McMahon & Nelmes, 2004; Reed & Ackland, 2011). At low pressures, “Phase I” adopts a hexagonal close packed of freely rotating (i.e. spherical on average) molecules. As pressure increases, the rotation becomes more correlated between molecules, and at low temperatures a broken symmetry phase freezes in (Phase II). At still higher pressures, electrons begin to delocalize, forming molecular trimer units (Phase III), while at higher T a mixed structure of trimers and hindered rotors appears (Phase IV). At these pressures, the liquid is denser than the solid, so the melt curve has negative slope.

All these qualitative features are captured by AIMD, even using a few hundred atoms. At still higher pressures, it is expected that a transition from molecular to atomic phases will occur. From static calculations, candidate phases above 300 GPa are molecular Cmca or atomic I4/amd (Cs-IV) phases (Geng, Song, Li, & Wu, 2012; Pickard, Martinez-Canales, & Needs, 2012; Pickard & Needs, 2007). However, previous experience in divalent metals suggests that very complicated structures may exist, beyond what can be found in structure searches. Phase IV shows that the high-temperature phase may be very different from the low-T phase.

The classical treatment of nuclei brings a raft of problems which are particularly significant for hydrogen. In particular, energy in MD is divided between classical degrees of freedom according to equipartition, while in quantum reality the degrees of freedom should be populated according to quantum statistics.

Here, we compare and contrast AIMD and two methods for including quantum protons: path integral molecular dynamics (PIMD) which quantizes motion in real space and lattice dynamics which takes phonon occupancy as the good quantum number. We also examine different exchange-correlation functionals to determine the most significant sources of uncertainty in current theory.

2. Calculation details

2.1. Ab initio molecular dynamics

Our MD proceed based on the forces between atoms in the NPH ensemble. In this work, we generate forces using density functional theory and Kohn–Sham Hamiltonian (Kohn & Sham, 1965) implemented in the CASTEP program (Clark et al., 2005; Segall et al., 2002), with norm conserving pseudopotentials and various exchange correlation functionals (Ceperley & Alder, 1980; Perdew, Burke, & Ernzerhof, 1996, Perdew et al., 2008; Perdew & Zunger, 1981).

Figure 1. Definition of angular distribution function (ADF). Cmca4 is molecular, so we build a histogram based on the angles defined by the axis of a reference molecule and neighbour atoms. The histogram is weighted with the fourth power of the distance r such that the further the neighbours, the less they contribute to the distribution.

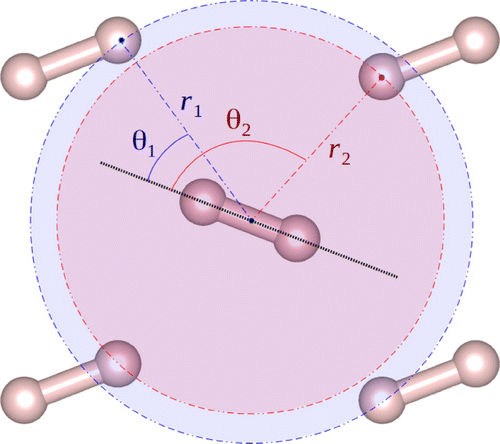
We calculate radial distribution functions (RDF) and angular distribution functions (ADF) (see Figure 1), while our dynamical calculation of phonon density of states (PDOS) is done with a sliding window technique over a simulation of length T (after equilibration) to eliminate dependence on the initial phase of the vibration:(1) $$\begin{array}{c}\hfill g(\mathit{\omega })\propto {\int }_0^T{\int }_0^T\sum _{j=1}^N{e}^{i\mathit{\omega }t}{v}_j(t+\mathit{\tau })v_j(t)d\mathit{\tau }dt\end{array}$$(1)

where $v_j(t)$ is the velocity of atom j at time t in the simulation. This density of states can also be projected onto individual modes, following methods developed by Pinsook and Ackland (1999), to extract specific details from a simulation such as Raman spectra (Magdău & Ackland, 2013) or transition paths. Our simulations are on a small 128 atom cell, which will be subject to finite size effects; in particular, diffusion can be confounded by phase fluctuations. In this case, however, the MSD saturates (Figure 3) and the cell remains stable, indicating that we remain within a single phase. In the absence of any interesting dynamical processes, we contrast thermodynamic properties from these MD simulations with lattice dynamics.

2.2. PIMD calculations

We also carried out PIMD calculations, as implemented in CASTEP. The essence of PIMD (Marx & Parrinello, 1994; Tuckerman, Berne, Martyna, & Klein, 1993) is to treat the nuclei as a set of distinguishable particles and use configurations generated from MD to sample their wavefunction via the Feynman path integral approach. To do this sampling, one runs several replicas of the system (known as “beads”) in conventional molecular dynamics, with the Hellman–Feynman forces augmented by interactions with the “same” atom in other beads. PIMD enables the quantum energy, including zero point, to be evaluated directly at finite temperature. Formally, the atoms are moving in “imaginary time” and sampling a distribution, such that their trajectories have no physical meaning.¹ Nevertheless, the application of PIMD uses standard MD packages which have atoms moving on trajectories, and it is tempting to assign meaning to these trajectories. A technique known as “centroid dynamics” (Cao & Voth, 1994) assigns physical meaning to the motion of the atomic position averaged over all beads with the “imaginary time” treated as real. For a PIMD run with only one bead, centroid dynamics become identical to a classical simulation, giving some weight to the idea that “centroid dynamics” may resemble time-dependent behaviour. ²

2.3. Static relaxation and lattice dynamics

MD follows classical trajectories, yet the actual vibrational motion should be described by quantum mechanics. Lattice dynamics and the harmonic approximation (Born, 1966) provides a simple approach in which the classical vibrational frequencies, extracted by lattice dynamics or Fourier transform of the velocity autocorrelation function (Equation 1), are then treated as 3N-3 quantum harmonic oscillators.

The internal energy (kinetic and potential energy above the ground state) of a classical harmonic crystal, assuming equipartition of energy, is:(2) $$\begin{array}{c}\hfill U=(3N-3)k_{B}T\end{array}$$(2)

whereas the quantized energy of harmonic oscillators is(3) $$\begin{array}{c}\hfill U=\sum _{i=1}^{3N-3}\frac{ħ{\mathit{\omega }}_i}{exp(ħ{\mathit{\omega }}_i/kT)-1}+\frac{ħ{\mathit{\omega }}_i}{2}\end{array}$$(3)

At high temperatures, these differ only by the zero-point energy, so it is helpful to include zero-point energy in the ground state potential energy.(4) $$\begin{array}{c}\hfill U_q=(3N-3){\int }_{\mathit{\omega }=0}^{\infty }\frac{ħ\mathit{\omega }g(\mathit{\omega })}{exp(ħ\mathit{\omega }/kT)-1}+\frac{ħ\mathit{\omega }g(\mathit{\omega })}{2}d\mathit{\omega }\end{array}$$(4)

Conceptually, the phonon density of states, $g(\mathit{\omega })$ is the same classically or quantum mechanically, and can be extracted from AIMD (Equation 1), even for the liquid phase. Thus, it should be possible to include quantum nuclear effects by sampling the classical normal modes. Once we have $g(\mathit{\omega })$, the quantum-correction to the internal energy from a simulation can be readily calculated: $\mathrm{\Delta }U=-(3N-3)k_{B}T+U_q$ (see Figure 2). Other thermodynamic properties also follow, e.g. the heat capacity(5) $$\begin{array}{c}\hfill C_v(T)=3k_B{\int }_0^{\infty }{\left(\frac{ħ\mathit{\omega }}{k_{B}T}\right)}^2\frac{exp\left(\frac{ħ\mathit{\omega }}{k_{B}T}\right)}{exp\left(\frac{ħ\mathit{\omega }}{k_{B}T}\right)-1}g(\mathit{\omega })d\mathit{\omega }\end{array}$$(5)

For hydrogen, the classical limit is well above the melting temperature (e.g. for vibrons $ħ\mathit{\omega }/k_b\approx 6000K$). Consequently, the vibrational entropy in AIMD is an order of magnitude higher than in LD. Furthermore, for hydrogen, zero-point energy is also significant and phase-dependent, and neglecting it will affect phase stability and direct calculation of melting point, e.g. via Z-method (Belonoshko, Skorodumova, Rosengren, & Johansson, 2006) or coexistence (Morris, Wang, Ho, & Chan, 1994).

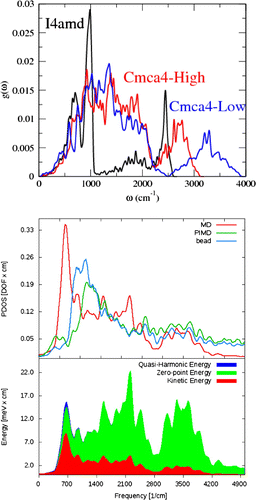
Figure 2. Upper figure, $g(\mathit{\omega })$ (PDOS) for I4amd and two Cmca4 structures from PBESOL harmonic lattice dynamics at a nominal pressure of 400 GPa. Lower figure, top panel shows Cmca4 PDOS extracted from 128-atom (i.e. a supercell with 8 layers of 8 molecules) , 400 GPa, 300K MD, PIMD centroid dynamics and one PIMD bead using Equation 1. The curves are normalized to the degrees of freedom of the system. bottom panel, energy distribution between the modes in MD (red), the zero-point energy obtained by quantizing the molecular dynamics PDOS (green) and the total quasi-harmonic energy (zero point and thermal) (blue).

At the high-N limit, the distribution of frequencies becomes a continuous density of states $g(\mathit{\omega })$ and the quantum free energy becomes:$$F(T)=k_{B}T\int g(\mathit{\omega })ln(2\text{sinh}(ħ\mathit{\omega }/2k_{B}T))d\mathit{\omega }$$

2.4. Validity of exchange-correlation function

The exchange-correlation functional is the main uncontrolled approximation in density functional theory. Probably, the most reliable description of electronic exchange-correlation is Quantum Monte Carlo (QMC) (Azadi & Foulkes, 2013; Azadi, Monserrat, Foulkes, & Needs, 2014). However, due to the computational cost, this is currently not usable in MD. For AIMD there are many different parameterized exchange-correlation functionals in use.

The popular PBE functional has become a de facto standard for AIMD hydrogen calculations, despite evidence that it overbinds molecular states compared with QMC (Azadi & Foulkes, 2013; Azadi et al., 2014). Table 1 gives a detailed comparison of PBE (Perdew et al., 1996) with two similar functionals, PBESOL, which has the same form as PBE but is fitted to a database of solids (Perdew et al., 2008) and the local density approximation (Ceperley & Alder, 1980; Perdew & Zunger, 1981) (LDA) fitted to the free electron gas. We compare the fourfold-coordinated I41/amd structure with two variants of the molecular Cmca4 structure, differing in lattice parameter and internal coordinate, as taken from previous work (Pickard et al., 2012; Pickard & Needs, 2007). We tabulate harmonic calculations corresponding to static relaxation carried out at nominal pressures³ of 300 and 400 GPa; Zero point and thermal pressures should be added to these, so they are overestimates by about 50 GPa. The most notable feature of the table is that PBE strongly favours the molecular phases, and gives lower densities for all phases. PBE disagrees with more accurate QMC calculation (Azadi & Foulkes, 2013; Azadi et al., 2014), a failing which PBESOL was designed to counter.

2.5. Simulation results

To contrast the methods, we have run calculations initiated in Cmca4, and LD calculation contrasting this molecular phase with the atomic I4/amd structure (Table 1).

The LD shows that, independent of exchange-correlation functional, the Cmca4 phase has lower Kohn–Sham energy and much higher zero-point energy. It is interesting that energy minimization finds two metastable variants of Cmca (except with PBE at 300GPa): molecular dynamics can provide a good test as to whether they should be regarded as part of the same “phase” at high temperatures. At 400GPa, Cmca4(low) should be stable in AIMD and unstable in PIMD: However, no transition or phase fluctuation is observed in either case, presumably due to kinetic barriers.

Three RDFs and ADFs are shown: classical AIMD, PIMD-centroid dynamics and RDFs direct from a single PIMD bead (Figures 2–4). The most obvious effect is that the individual beads have an unphysical broad spread of position. Closer inspection shows that the PIMD centroids also have lower, broader peaks than AIMD, due to the combination of thermal and quantum uncertainty. The mean-squared displacement for the three simulations have zero slope at long times, showing there is no diffusion or phase fluctuation. Curiously, the long(imaginary)time atomic MSD is smaller under centroid dynamics despite the wider spread of bondlength.

Figure 3. The radial distribution function (RDF) (top), angular distribution function (ADF) (middle) and mean square-root displacement (MSD) (bottom) for ab initio MD (red), 16-bead PIMD centroid dynamics (green) and PIMD individual bead (blue). Calculations are done for 128 atoms of Cmca4 hydrogen run at 400 GPa and 300 K, using PBE.

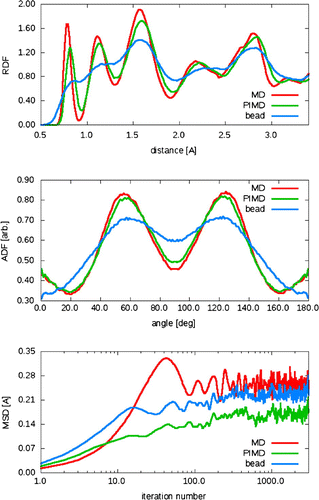
Table 1. Effect of different exchange correlation functionals on volume, Kohn–Sham enthalpy relative to I41–amd, zero-point energy. The three functionals are PBE, PBESOL and LDA; calculations are done based on static relaxations in the harmonic approximation. The relaxed fractional coordinates of the two Cmca4 structures are shown: at 300GPa the Cmca4 (high) (Pickard & Needs, 2007) structure transformed into the Cmca4 structure ($u,v\to \frac{1}{2}-u,\frac{1}{2}-v$.)

Phase	XCF	V/atom	$\mathrm{\Delta }$ H${}_{KS}$ (eV/atom)	ZPE (eV/atom)	v,w
400 GPa
Cmca4	LDA	1.271	-0.003	0.296	0.366 0.435
Cmca4 (high)	LDA	1.258	-0.003	0.286	0.117 0.129
I41-amd	LDA	1.237	0	0.227
Cmca4	PBESOL	1.271	-0.004	0.296	0.366 0.436
Cmca4 (high)	PBESOL	1.257	-0.003	0.286	0.117 0.129
I41-amd	PBESOL	1.228	0	0.226
Cmca4	PBE	1.280	-0.023	0.301	0.368 0.439
Cmca4 (high)	PBE	1.267	-0.014	0.287	0.111 0.131
I41-amd	PBE	1.245	0	0.232
300 GPa
Cmca4	LDA	1.424	-0.045	0.280	0.368 0.441
Cmca4 (high)	LDA	1.408	-0.003	0.270	0.108 0.133
I41-amd	LDA	1.411	0	0.214
Cmca4	PBESOL	1.424	-0.048	0.281	0.368 0.441
Cmca4 (high)	PBESOL	1.407	-0.003	0.269	0.108 0.132
I41-amd	PBESOL	1.410	0	0.211
Cmca4	PBE	1.445	-0.058	0.290	0.371 0.441
Cmca4	PBE	1.445	-0.058	0.290	0.133 0.059
I41-amd	PBE	1.417	0	0.214

Our NPT ensemble allows us to compare thermodynamic properties under the two approximations (Figure 4) under various pressures. The ZPE shift is clear in the figure, and the associated zero-point pressure means that the “PIMD” material is more difficult to compress, and the effect is significant: the PIMD volume is higher by some 6%.

The equilibrium cell volumes in MD contrast with the 0K value of $163{\mathrm{\AA }}^3$, implying a thermal expansivity of $3\times {10}^{-5}{\mathrm{K}}^{-1}$, typical for a metallic solid. From the pressure–volume relation, we can estimate the bulk modulus to be of order ${10}^{12}$ Pa, much higher than any material at ambient conditions.

3. Sources of error in MD

3.1. Definition of a phase

The definition of a phase within MD is not straightforward. The simulation traverses a series of microstates, and in order to define the free energy of a phase, one needs to define which microstate belongs to which phase. Symmetry is of marginal use, since the microstates have no symmetry. If a simulation remains in a single phase, time-averaged quantities can be used to define symmetry, but where there are two distinct “phases” with the same symmetry (e.g. Cmca4). If the simulation changes phase, or undergoes an excursion between phases, this becomes even more problematic. A distinct change in a continuous variable such as pressure or volume over a short time period may define a discontinuous transformation.

3.2. Finite size effect and phase fluctuations

When sampling the phase space, the probability of being in a particular phase is exponentially dependent on the number of atoms. It means that in the thermodynamic limit phase transformations are sharp. However, for a finite size system, the statistical weight of the unstable phase may be significant, even quite far from the phase boundary. Consider for example a typical simulation of hydrogen in Phase IV (Magdău & Ackland, 2014) which should have layer stacking BG’BG”. At 600 K with a free energy difference of 5 meV/molecule between stable and metastable stacking (e.g. BBGB), simulation with 4 layers and 144 atoms could be expected to be in the “wrong” phase 15% of the time. If there is no significant barrier, the dynamics of such a simulation will be dominated by such unphysical transitions, giving unphysical effects like divergent MSD (Goncharov et al., 2013; Magdău & Ackland, 2013, 2014).

It is also possible to have multiple representations of the same phase, so for example a BG’BG” stacking could be represented as any of four permutations: (e.g G”BG’B). A simulation which is “stuck” in a single representation will sample only 1/4th of the phase space compared to one sampling the entire space. This will result in lower entropy $k_{B}ln(4)$: negligible in the thermodynamic limit, but in a simulation with 50 atoms at 600 K, even this is equivalent to a few tenths of meV per atom.

Phase fluctuation problems arise whenever it is kinetically possible for the simulation to transform between phases, either homogeneously or by nucleation of a defect which passes through the entire system. Although this is system dependent, the signature will be a short-lived rearrangement of all the atoms in the system, followed by a period of relative stasis. We have observed this behaviour in some simulations which are therefore of no use in calculating thermodynamic properties and are not reported here.

To obtain a crystal structure in MD, it is necessary to have a number of atoms compatible with the unit cell. This is especially challenging when the unit cell is not known a priori. In hydrogen, even numbers of atoms are always used to allow molecules to form and typically ones with many factors. However, it may still be impossible to obtain complex phases, e.g. there are no MD studies in hydrogen compatible with structures such as the 40 and 88 atom unit cells in lithium (Marqués, 2011), the element adjacent to H in the Periodic Table.

Similarly, simulations run in NVE ensemble are restricted to cells compatible with the box. For anything other than cubic systems, such simulations are inevitably run at inhomogeneous pressure, and any phase transition is strongly inhibited, at best requiring twinning (Kastner & Ackland, 2009; Pinsook & Ackland, 2000). The NPT ensemble (Martoňák, Laio, & Parrinello, 2003; Parrinello & Rahman, 1981). alleviates this somewhat, but unless some bespoke damping method is used, it suffers from a long-lived “ringing mode”.

This is due to poor coupling between the phonon with the same wavelength as the box and other modes, it extends the equilibration period and may affect the dynamics; in NVE the same preequilibration ringing effect can be seen as long-lived oscillations in the pressure.

3.3. Classical treatment of the nuclei

Quantization has a significant effect on energy. AIMD makes a severe approximation treating the nuclei as classical particles. PIMD treats them as distinguishable quantum particles. Lattice dynamics quantize the vibrations.

Figure 2 shows a number of interesting features. The lack of high-frequency modes in I4/amd reduces its zero-point energy enormously in comparison with Cmca4(high). The Cmca4(low) structure has an even higher branch of vibrons around $3400{\mathrm{cm}}^{-1}$, reflecting its more molecular nature. First/second neighbours are at 0.80/1.05Åand 0.88/0.97Åin the two Cmca4 structures (from PBESOL). The consequent 10 meV/atom difference in ZPE would be absent in AIMD: enough to shift the transition pressure between these phases by tens of GPa.

At 300 K for Cmca4/I4amd phases, the quantum heat capacities are typically 0.3R, compared with 1.5R classically. It implies that the vibrational entropy may be overestimated by an order of magnitude in AIMD, which will induce a significant error on phase transition temperatures to high entropy phases. This may be mitigated by the fact that for Phase IV and the melt, a large contribution to the entropy is configurational. In fact, high entropy phases typically have lower zero-point energy, which is an even larger effect than the quantum reduction in heat capacity: reduced heat capacity favours low entropy phases, so there is some cancellation of errors.

Comparison of the two upper panels in Figure 2 shows that molecular vibration frequencies are underestimated in lattice dynamics, compared with MD, and what has been seen experimently (Magdău & Ackland, 2013). So even when ZPE is included via lattice dynamics, its effect may be underestimated. The lowest panel illustrates the size of the effects. At room temperature, ZPE far exceeds the classical kinetic energy, yet the quantum kinetic energy is negligible and visible only in the low energy modes. The three different terms (ZPE, classical and quantum KE) integrate to 327, 77 and 4 meV/atom, respectively. As well as the effects of zero-point energy, zero-point motion is around $0.2\mathrm{\AA }$. If neglected in AIMD, additional thermal motion would be required to initiate diffusion, meaning that the onset of diffusion in the simulation is of order 100 K greater than in reality (Belonoshko, Ramzan, Mao, & Ahuja, 2013).

Since these quantum effects are missing in previous MD simulations (Belonoshko et al., 2013; Magdău & Ackland, 2014), the observation of a wide field of Cmca4 stability may be suspect, perhaps even sampling the wrong Cmca4.

We note a practical problem in calculating $g(\mathit{\omega })$—the phonons are weakly coupled, and even if the perturbations are strong enough to satisfy the KAM theorem (Kolmogorov, 1954), it may take many nanoseconds before equipartition occurs. Most serious of these is the overpopulation of the “ringing mode” described above, which manifests as a long-term oscillation in volume (NPT ensemble) or pressure (NVE). The normalization of the expression for the velocity autocorrelation function $⟨v{(0)}^2⟩$ assumes equipartition. The unresolved dichotomy here is that we assume harmonicity of the quantum mechanics, and require anharmonicity to achieve equipartition.

3.4. Non-harmonic modes: rotons

In Phase I, two degrees of freedom per molecule involve free rotations: “rotons”. In this case, the energy is quantized according to $J(J+1){ħ}^2/2I$, with J a quantum number and I the moment of inertia, as is readily observable in spectroscopy (Howie, Guillaume, Scheler, Goncharov, & Gregoryanz, 2012; Howie, Magdău, Goncharov, Gregoryanz, & Ackland, 2014). A curious feature of the roton energy is that it bears no relation to any frequency which might be measured in MD.

Rotons have no zero-point energy ($J=0$), and for distinguishable atoms are described by a partition function:(6) $$\begin{array}{c}\hfill Z=\sum _{J=0}^{\infty }(2J+1)exp(-J(J+1){ħ}^2/2I{k}_{B}T)\end{array}$$(6)

where $2J+1$ is the degeneracy of each mode. As with the harmonic oscillator, the energy in high T limit is $k_{B}T$ per mode, but significantly lower at low T. For ortho- and para- hydrogen, the degeneracies are different, but the limiting cases are the same. The energy of the $J=1$ state is of order 15meV, so it is thermally excited at room temperature and the quantum energy approaches the classical value.

It is also noteworthy that the ground state $J=0$ wavefunction or the classically tumbling dimer is spherically symmetric, which helps to explain why the favoured structure corresponds to the close packing of spheres.

3.5. Zero-point pressure

As a material is compressed, the zero-point energy increases. This is a contribution to the pressure required to compress the material. It can be readily calculated from ab initio lattice dynamics calculations, and is typically a few tens of GPa.

This effect is completely absent in AIMD calculations. The zero-point pressure can be estimated from Table 1 as the ratio of $\mathrm{\Delta }{U}_{ZPE}$ to $\mathrm{\Delta }V$ e.g. in I41/amd with LDA this is 12.5 GPa. In Figure 4, we see that ZPE pressure is enough to change the volume of Cmca4 by 5%.

Figure 4. Results from MD and PIMD runs in NPT ensemble. Top panels and bottom right panel compare the cell volume, potential energy and total energy, respectively, as extracted from MD, PIMD (for all 128 atoms, at 300 K) and single-point DFT calculation (at 0 K, with arrows showing thermal or ZPE shifts). The total energy in DFT is the same as the potential energy and is only repeated for reference, whereas the total energy in MD is the sum of the DFT energy and vibrational energy (i.e. twice the kinetic energy $(3N-3)k_{B}T$ in the classical harmonic limit). The last panel illustrates the zero-point plus thermal energy calculated from PIMD. The barostat is weak, and we note that all quantities vary with pressure.

It is interesting to note that the zero-point energy in a liquid must be similar to that in a solid, since typical ZPE values around 0.25eV/atom far exceed the thermal energy at the melting temperature.

3.6. Kinetic pressure

Static calculations of energy minimization ignore the pressure effects from the kinetic energy which give rise to thermal expansion. In classical MD, this can be easily estimated from the ideal gas law P=nRT/V. For hydrogen at around 300GPa, we have a density of about one molecule per $2.5{\mathrm{\AA }}^3$, which gives a classical kinetic pressure of around 1.5 GPa at room temperature. The quantum kinetic pressure is much lower for hydrogen at room temperature, since most modes are not excited.

4. Conclusions

We have shown that there is a large degree of uncertainty around the use of MD in the study of high-pressure hydrogen. Various treatments of the exchange-correlation functional give somewhat differing results, accounting for tens of GPa uncertainty in phase boundaries. The problems with finite size and definition of a phase introduce unquantifiable errors. The major uncertainty comes from understanding the quantum behaviour of the protons. In particular, this relates to the zero-point vibrations. These contribute massively to the total energy, and thus also introduce a correction of tens of GPa to the nominal pressure calculated from the Kohn–Sham energy and virial. The energy difference between two phases can be calculated by integrating the forces along a transition path; therefore, in addition to a missing zero-point energy, there are missing zero-point forces and pressures in MD.

Our results also suggest that previous work with classical MD, lattice dynamics and the PBE functionals is likely to have systematically overestimated the stability of this molecular phases relative to low-ZPE structure such as I41amd or its high-temperature variants such as chainlike structures.

In view of all this, one might ask whether there is any point to doing MD. The answer remains a resounding yes, with appropriate modesty about numerical results.

For perturbative effects such as vibrational Frequencies, MD provides the best way to tackle anharmonicity. Even when qualitative accuracy is missing, MD can give indications of relative densities for phase boundary slopes. In the NPH ensemble, MD can transform between crystal phases giving candidate structures for comparison with experiment. Calculated barrier heights can be used to determine when tunnelling effects should augment thermal ones in considering diffusion. MD can give snapshot indications of the structure of the melt. Without MD, the character of Phase IV would be unknown (Liu & Ma, 2013), the liquid structure with its high density would be a mystery and the discrepancy between lattice dynamics and experimental Raman frequency would remain unsolved.

Many material properties remain stubbornly inaccessible to experiment. If density could have been measured as reliably as pressure, Wigner and Huntington’s prediction (Wigner & Huntington, 1935) would be regarded as correct: to avoid their much derided 25 GPa figure, they needed to know that the bulk modulus was 10 times that of steel, while the thermal expansion remains similar. AIMD shows that the interesting behaviour occurs when energy per atom is around 13.5 eV/atom (Figure 4), very close to the energy of a hydrogen atom, i.e. when the total binding energy is close to zero and the atoms are primarily kept together by external pressure.

Cover image

Source: Authors.

Additional information

Funding

Computing time for this work was supported by EPSRC-Support for the UKCP consortium [grant number EP/K01465X/1]. IBM thank EPSRC for a studentship.

Notes on contributors

Graeme J. Ackland

Graeme J. Ackland’s research programme is in understanding the elements at high pressure. He has developed the theory that the group 1 elements, Cs, Rb, K, Na and Li, follow similar structural trends with increasing pressure. At about the pressure where the mechanical work done equals cohesive energy, their structures change dramatically to form highly complex crystals which are either nonmetallic or poor metals: the details all captured by standard electronic structure calculation. He has developed the theory that these crystal structures are determined by their strong scattering at the Fermi wavevector, or, alternately, by efficient packing of ions and electrons to form electrides (as opposed to packing of atoms).

Ioan B. Magdău

Ioan B. Magdau is Romanian PhD student, who has done calculations to extend this theory into hydrogen, concentrating especially on relating calculations to properties which can be directly measured in experiment, using methods pioneered by ACHPR7 chair, Udomsilp Pinsook.

Notes

This article is associated with the 7th Asian Conference on High Pressure Research (ACHPR-7) 2015, Bangkok, Thailand.

1 “PIMD” is something of a misnomer. There are no dynamics, rather the MD technique is used to sample the energy landscape in Wick-rotated imaginary time. There are no molecules: atoms are treated as independent, distinguishable entities, and the integral is replaced by a sum over a typically small number of replicas.

2 Centroid dynamics is a marked improvement on standard MD; however, for hydrogen molecules the assumptions break down. For example, the hydrogen atoms in a molecule cannot be treated as distinguishable (in classical MD, these problems become manifest if the molecule rotates through ${180}^{\circ }$).

3 i.e. the volume differential of the Kohn Sham energy in the Born Oppenheimer approximation