Moving mesh partial differential equations modelling to describe oxygen induced effects on avascular tumour growth

Abstract

The urokinase plasminogen activator (uPA) is a proteolytic enzyme, which over expression by cancer cells is recognized as promoting tumour growth and proliferation. In the early stage of formation, cancer cells grow in the avascular phase and oxygen supply come from surrounding healthy tissue. Using parameters estimated from in vivo experiments on human tumours, we simulate the effects of hypoxic conditions on cancer cell interacting with the uPA system, in the avascular phase. The resulting system of six-coupled partial differential equations is solved over one-dimensional domain implementing an adaptive grid technique, using the finite element method. Our results predict that changes of both diffusion and uptake/decay coefficients for oxygen, because of possible microenvironment changes of cancer cells, induce variations of the invasion velocity, with crowding effects during cell growth and proliferation.

Keywords:

• cancer invasion
• cell locomotion
• avascular growth
• FEM
• MMPDE
• computer modelling

Public Interest Statement

Data on the very early stage of human tumours in situ often are difficult to obtain due to belated clinical recognition. A common feature of most malignancies is a poor perfusion leading to hypoxia, hence modelling avascular tumour growth under hypoxic conditions can help understanding the early stage of malignant proliferations, when clinical evidences of a pathologic condition are not yet disclosed. The interaction of cancer cells dynamics with the urokinase plasminogen activator system has been simulated in a portion of biological tissue, modelling hypoxia using parameters determined in vivo on human tumours. The moving mesh partial differential equations technique applied to the particular biological system gives an improved numerical resolution of the model, while the results allow to predict that, in the early stage, the tumour progression depends on the oxygen diffusion characteristics and on crowding effects due to cell proliferation.

1. Introduction

Modelling avascular tumour growth benefits by the relative ease in obtaining data from in vitro experiments on multi-cellular spheroid systems (Ambrosi & Preziosi, 2002; Byrne, 2003; Byrne & Preziosi, 2003; Chaplain, Ganesh, & Graham, 2001; Sherratt & Chaplain, 2001), together with the availability of ever more performing computers giving the modellers the possibility to build sophisticated mathematical models. A multi-cellular spheroid is usually schematized as follows: (1) an outer shell of active and proliferating cancer cells; (2) an inner shell of quiescent cells holding the ability to activate and proliferate; (3) a core of necrotic non-proliferating cells. The interface among these three phases is not sharp, and the presence of oxygen influences the spheroid dynamics (Sherratt & Chaplain, 2001). In particular, the oxygen distribution in biological tissue is very worth due to its key role as nutrient influencing cells growth (Hubbard & Byrne, 2013; Vaupel, Kallinowski, & Okunieff, 1989). Indeed, in vitro experimental studies performed on multi-cellular spheroids show a decrease in oxygen concentration on going from the outer proliferating shell towards the inner necrotic core, passing across the intermediate quiescent shell (Mueller-Klieser, Freyer, & Sutherland, 1986), although avascular tumour growth in vivo can differ considerably from in vitro proliferation (Sherratt & Chaplain, 2001). During the early stage of human tumour formation, the number of host vessels per unit tumour mass remains constant, with an overall reduction of the available exchange area for oxygen and other nutrients (Vaupel et al., 1989). In particular, tissue oxygenation is a factor markedly modulating the sensitivity of cancer cells to, for example, therapeutic responses, while oxygen deficiency is a common factor of malignancy. In fact, in the very early stages of human tumour formation, relevant structural and functional abnormalities of the surrounding microvasculature are already present, and most of the malignancies are characterized by the presence of hypoxic, or even anoxic, tissue areas heterogeneously distributed within the tumour mass. In general, it is very difficult to obtain in vivo experimental data of the early stage of tumour invasion, even if the oxygen consumption and utilization rates of human tumours in vivo are estimated to be intermediate between healthy tissues with normal metabolic rates and healthy tissues with quite high activities (Vaupel et al., 1989).

Cancer cells dynamics is a multi-scale mechanism involving phenomena occurring over different length scales, requiring a multi-scale approach appropriate for complex modelling (Macklin et al., 2009; Preziosi, 2004; Preziosi & Tosin, 2009): sub-cellular mechanisms influence intercellular interactions both in tumour and healthy cells, which in turn determine the evolution at the tissue level, where cancer cells start to cluster in the avascular phase (Ambrosi & Preziosi, 2002; Byrne, 2003; Byrne & Preziosi, 2003; Chaplain et al., 2001; Sherratt & Chaplain, 2001). Afterwards, the mechanical interaction of tumour with the surrounding tissue (Ambrosi & Mollica, 2002; Breward, Byrne, & Lewis, 2001; Chen, Byrne, & King, 2001), stimulate the angiogenic process causing the formation of new blood vessels (Anderson & Chaplain, 1998; Levine, Pamuk, Sleeman, & Nilsen-Hamilton, 2001; Levine & Sleeman, 2003; McDougall, Anderson, & Chaplain, 2006; McDougall, Anderson, Chaplain, & Sherratt, 2002), and attracting much more nutrients like oxygen and glucose (Folkman, 1974, 1976; Folkman & Klagsbrun, 1987). Metastasis begins when the increased speed of invasion of the healthy cells and the vascularization allows cancer cells to come out from the initial localization, diffusing through the vascular system (Anderson, Chaplain, Newman, Steele, & Thompson, 2000; Chaplain & Anderson, 2003; McDougall et al., 2002; Hanahan & Weinberg, 2000). The literature about mathematical modelling of cancer cell growth and proliferation is expanding rapidly, and recent reviews can be found, among others, in Preziosi (2003), Araujo and McElwain (2004), Astanin and Preziosi (2008), Graziano and Preziosi (2007), Roose, Chapman, and Maini (2007), Tracqui (2009), Lowengrub et al. (2010).

At tissue level, continuum models for avascular tumour growth are expressed as systems of partial differential equations (PDEs) (Hubbard & Byrne, 2013), in which an initial cluster of cancer cells is considered as immersed in the extracellular matrix (ECM), a nutrient-rich aqueous environment where, depending on chemical signalling, the cells start to grow and proliferate (Preziosi, 2004).

Chemotaxis and haptotaxis are motility mechanisms sensible to concentration gradients of chemicals influencing cell migration inside the ECM. The chemotaxis is the movement of cancer cells towards the source of chemicals dissolved in solution. When the attracting chemicals are adhered to some ECM component, the haptotaxis describes the movement of cancer cell, which iteratively make and break bond with such chemicals, jumping towards growing concentration gradient of the attracting molecules adhered to ECM.

Recently, tumour proliferation has been described on the basis of chemotactic and haptotactic stimulated mechanisms, modelling the interaction between the urokinase plasminogen activator (uPA) system and cancer cells dynamics (Andasari, Gerisch, Lolas, South, & Chaplain, 2011; Chaplain & Lolas, 2005). The invasion of the healthy tissue starts from the degradation of the ECM macromolecules, such as the vitronectin (VN) protein. Specifically, cancer cells secrete the pro-uPA inactive enzyme, which is activated to the uPA degrading enzyme, a serine protease catalyzing the proteolysis of ECM macromolecules. uPA is activated by plasmin, another ECM degrading enzyme, being in turn an activated form of the plasminogen ubiquitous protein: both uPA and pro-uPA bind to the receptor uPAR, and this last binds to the cell surface. In order to regulate excess of proteolysis induced by uPA, healthy cells secrete a specific inhibitor, the plasminogen activator inhibitor type-1 (PAI-1) (Chaplain & Lolas, 2005).

The uPA system consists of the uPA enzyme, together with plasmin, VN protein and PAI-1 inhibitor. The analysis of the cancer cells dynamics, and theirs interaction with the uPA system, is performed by using a system of five coupled PDEs, which Andasari et al. (2011) solved using a uniform finite volumes discretization in space and an implicit method for discretization in time, imposing a set of model parameters and suitable initial and boundary conditions. In last years, the solid tumour growth has been reproduced by using adaptive meshing (Cristini, Li, Lowengrub, & Wise, 2009), multi-grid (Wise, Lowengrub, & Cristini, 2011) and hybrid finite volume/finite element (Hubbard & Byrne, 2013) algorithms, in order to improve the effectiveness of the computational techniques. In general, despite the possibility to use finite difference-based numerical methods in order to solve reaction–diffusion–taxis PDEs (Valenti, Denaro, Spagnolo, Conversano, & Brunet, 2015), the finite element method (FEM) (Zienkiewicz & Taylor, 2002) is most attractive due to its ability to handle complicated geometries and boundaries with relative ease, to the better quality of the approximation between grid points, and often to higher approximation quality (see, among others, Fletcher, 1984; Frehner, Schmalholz, Saenger, & Steeb, 2008; Quarteroni, 2009; Simpson & Clement, 2003). In the FEM, the PDE integration domain is discretized in elements delimited by nodes, the mesh points, on which the solution of a variable is found, while its spatial variation inside each element is interpolated by suitable shape functions. Solid tumour progression is characterized by irregular spatio-temporal proliferation patterns (Andasari et al., 2011), with local steep gradients of the domain variables, suggesting that the overall accuracy of the numerical procedure could be influenced by the discretization of the integration domain: in fact, as the spatial positions where cancer cells cluster are a priori unknown, the choice of an appropriate grid of nodes is crucial. In this respect, in a very recent work, we modelled the interaction of the uPA system with cancer cells dynamics in the avascular phase, and the resulting PDE system has been solved implementing the moving mesh partial differential equation (MMPDE) numerical technique, using FEM (Amoddeo, 2015a). Such technique belongs to dynamic, or r-type, adaptive grid techniques, also known as moving mesh techniques (Tang, 2005), and has the peculiarity of keeping constant nodal connectivity and number of mesh points inside the integration domain, moving the mesh points towards regions where more details are required, with no need for external intervention. In the recent past, the MMPDE technique has been successfully applied to the study of highly frustrated dynamical system, characterized by strong temporal and spatial variations of some physical parameters (Amoddeo, 2015b; Amoddeo, Barberi, & Lombardo, 2010, 2011, 2012, 2013), discretizing the integration domain according to the gradient of a control parameter calculated during the solution procedure, driving a non-uniform node distribution. It follows that the node number in the integration domain remains constant, ensuring no waste of computational effort in areas of low spatial variability, where there is no need for finer grids, but adaptive grid techniques, more in general, allow both resolution improvements and computational savings with respect to techniques based on uniform discretization, as reported, for example, in Ramage and Newton (2008). Specifically, in the model investigated in Amoddeo (2015a), the solution of the arising non-linear PDE system has been computed over a one-dimensional integration domain, discretized according to the gradient of the cancer cells concentration, by setting the grid nodes in correspondence with the points of growing cancer cell density. The numerical results, obtained for the cancer cells with low motility values, show that a fine and irregular structure of the tumour invading front is connected to a high degree of malignancy, while a higher motility value causes an increase in the invasion velocity with a smoothing of the invasion front.

In this work, we consider the interaction between the uPA system and cancer cell dynamics, introducing a model for the oxygen supplied to tumour from surrounding healthy tissue. A model for a generic nutrient supply to multi-cellular spheroids has been developed in Sherratt and Chaplain (2001), which takes into account nutrient consumption not only by active cancer cells, but also from quiescent and necrotic ones. We assume, instead, that oxygen utilization comes from proliferating cells only: it results a PDE system in which the reaction–diffusion model equation for oxygen is directly coupled to the evolution equation for cancer cells. In particular, the model parameters for the oxygen supply come from in vivo determinations, aimed at mimicking hypoxic conditions related to typical malignant proliferations (Vaupel et al., 1989). As in Amoddeo (2015a), the model is discretized over a one-dimensional domain and solved using the MMPDE technique implemented by FEM.

The paper has the following organization: In Section 2, we introduce the theoretical model; the numerical technique and results/discussion are presented in Sections 3 and 4, respectively, while we conclude in Section 5.

2. Model theory

The mathematical model we introduce represents a mixture theory formulation for the mass conservation. If Ω ⊂ ℝ³ is a fixed volume domain with S its bounding surface, w = (w₁, …, w_l), in which w_i = w_i(x, t), for i = 1, …, l, represents the concentration of the ith interacting chemical species at time t ∈ (0, T] and position x ∈ Ω, the evolution law for the generic w_i reads as(1) $$\frac{d}{dt}\underset{V}{\int }{w}_i(x,t)dx=-\underset{S}{\int }{\mathit{\phi }}_i(x,t)·dS+\underset{V}{\int }{f}_i(w)dV$$(1)

where φ_i(x, t) is the flux of w_i through S, and f_i accounts for production terms. Using the divergence theorem and considering the domain fixed in time, the PDE describing the evolution of the generic w_i(x, t) is obtained,(2) $$\frac{\mathit{\partial }{w}_i}{\mathit{\partial }t}=-\mathrm{\nabla }·{\mathit{\phi }}_i+f_i(w),i=1,\dots ,l$$(2)

We consider explicitly the concentration evolution of cancer cell, uPA serine protease, PAI-1 inhibitor, VN protein and plasmin degrading enzyme, denoted, respectively, by c(x, t), u(x, t), p(x, t), v(x, t) and m(x, t). The oxygen supply from surrounding tissue to the cells is taken into account by considering its concentration n(x, t). Then Equation (2), with l = 6 to account for the considered chemical species, constitutes a system of six reaction–diffusion-coupled PDEs to be solved in order to describe the dynamics inside the domain Ω, in which cell movement due to chemotaxis and haptotaxis is explicitly considered.

In the evolution equation for cancer cells, the flux vector accounts for movement due to diffusion via D_c, chemotaxis due to the presence of uPA and PAI-1 molecules, respectively, through χ_u and χ_p, and haptotaxis due to VN, through χ_v; the production includes a logistic growth term through the cancer cell proliferation rate μ₁, and the contribution due to oxygen interaction through k₂:(3) $$\frac{\mathit{\partial }c}{\mathit{\partial }t}=\mathrm{\nabla }·\left[D_c\mathrm{\nabla }c-c\left({\mathit{\chi }}_u\mathrm{\nabla }u+{\mathit{\chi }}_p\mathrm{\nabla }p+{\mathit{\chi }}_v\mathrm{\nabla }v\right)\right]+{\mathit{\mu }}_{1}c(1-c)+k_{2}nc$$(3)

Vitronectin, as ECM in general, does not diffuse, but it is degraded by plasmin at a rate δ and neutralized by PAI-1 inhibitor at a rate φ₂₂; in addition, its growth is indirectly supported by the PAI-1/uPA interaction at a rate φ₂₁, while a logistic term accounts for proliferation at a rate μ₂:(4) $$\frac{\mathit{\partial }v}{\mathit{\partial }t}=-\mathit{\delta }vm+{\mathit{\varphi }}_{21}up-{\mathit{\varphi }}_{22}vp+{\mathit{\mu }}_{2}v(1-v)$$(4)

The evolution equation for uPA includes the diffusion at a rate D_u, while, besides the production by cancer cells at a rate α₃₁, the reaction/production term includes the uPA degradation at a rate φ₃₃ via the interaction with its receptor uPAR bounded to cancer cells, and its inhibition at a rate φ₃₁ via the interaction with PAI-1:(5) $$\frac{\mathit{\partial }u}{\mathit{\partial }t}=\mathrm{\nabla }·(D_u\mathrm{\nabla }u)-{\mathit{\varphi }}_{31}pu-{\mathit{\varphi }}_{33}cu+{\mathit{\alpha }}_{31}c$$(5)

Concerning PAI-1 inhibitor, its movement is considered through the diffusion at a rate D_p; it is produced by plasmin at a rate α₄₁, and it is degraded via the interactions with uPA and VN at a rate of, respectively, φ₄₁ and φ₄₂:(6) $$\frac{\mathit{\partial }p}{\mathit{\partial }t}=\mathrm{\nabla }·(D_p\mathrm{\nabla }p)-{\mathit{\varphi }}_{41}pu-{\mathit{\varphi }}_{42}pv+{\mathit{\alpha }}_{41}m$$(6)

The enzyme plasmin moves according to D_m; both PAI-1 binding to VN and uPA binding to cancer cells promote it at a rate, respectively, φ₅₂ and φ₅₃, while it is degraded, or inhibited by its inhibitor α₂-antiplasmin (Andasari et al., 2011), globally at a rate φ₅₄:(7) $$\frac{\mathit{\partial }m}{\mathit{\partial }t}=\mathrm{\nabla }·(D_m\mathrm{\nabla }m)+{\mathit{\varphi }}_{52}pv+{\mathit{\varphi }}_{53}cu-{\mathit{\varphi }}_{54}m$$(7)

Considering the evolution equation for the nutrient oxygen, it diffuses according to a diffusion coefficient D_n, in general it degrades at a rate k₁ and it is utilized by cancer cells at a rate k₂. Denoting with n₀ the initial concentration of oxygen in absence of cancer cells, we admit the oxygen source decrease with cell growth, accounted for by a crowding parameter λ ∈ [0, 1]:(8) $$\frac{\mathit{\partial }n}{\mathit{\partial }t}=\mathrm{\nabla }·(D_n\mathrm{\nabla }n)+k_1{n}_0(1-\mathit{\lambda }c)-k_{1}n-k_{2}nc$$(8)

3. The moving mesh technique and parameters setting

The six coupled Equations 3–8 constitute a PDE system, which we solve over one-dimensional spatial domain using the MMPDE numerical technique based upon the equidistribution principle (Beckett, Mackenzie, Ramage, & Sloan, 2001; de Boor, 1974; Pereyra & Sewell, 1975; Russell & Christiansen, 1978; White, 1979): the discretization of the integration domain Ω, typical of the FEM procedure, is controlled by equidistributing in each domain element a monitor function (Beckett & Mackenzie, 2000; Huang, 2001), assumed as depending on the problem solution and computed during the solution procedure. The method results appropriate in presence of rapidly varying parameters, as in shocks or defects, leading to sharp solution features (Amoddeo et al., 2010, 2011, 2012, 2013).

Denoting as Ω_p = [0, 1] the physical domain over which w(x, t) is a solution of a PDE, with x  Ω_p physical coordinate, and as Ω_c = [0, 1] a computational domain, with ξ  Ω_p computational coordinate, a one-to-one mapping at time t from computational space Ω_c × (0, T] to physical space Ω_p × (0, T], is defined by the coordinate transformation x = x(ξ, t), ξ ∈ Ω_c, t ∈ (0, T], while the reverse, ξ = ξ(x, t), x ∈ Ω_p, t ∈ (0, T], is from physical space Ω_p × (0, T] to computational space Ω_c × (0, T]. A uniform grid ξ_i = i/N, i = 0, 1, …, N imposed on computational space, corresponds to a set of nodes on physical space 0 = x₀(t) < x₁(t) < , …, x_N(t) = 1.

Given a monitor function M = M(w(x, t)), it is equidistributed over the one-dimensional integration domain if(9) $${\int }_0^{x(\mathit{\xi },t)}M(w(s,t))ds=\mathit{\xi }{\int }_0^{1}M(w(s,t))ds$$(9)

or in discrete form(10) $${\int }_{x^{i-1}(t)}^{x^i(t)}M(w(s,t))ds=\frac{1}{N}{\int }_0^{1}M(w(s,t))ds$$(10)

The coordinate mapping x(ξ, t) is obtained by differentiating (9) with respect to ξ, giving the mesh equation(11) $$M(x(\mathit{\xi },t))\frac{\mathit{\partial }}{\mathit{\partial }\mathit{\xi }}x(\mathit{\xi },t)={\int }_0^{1}M(w(s,t))ds=C(t)$$(11)

Equation 10 expresses the equidistribution of the monitor function M(w(x, t)) in each subinterval of Ω, while from Equation 11 we deduce that, at a larger monitor function value corresponds a denser mesh. The optimal choice of the monitor function can depend on the problem being solved, the numerical discretization being used, as well the norm of the error that is to be minimized (Beckett & Mackenzie, 2000). We choose the monitor function appropriate for the kind of problem we are treating (Amoddeo, 2015a) as:(12) $$M(w(x,t))={\int }_0^1{\left(\left|\frac{\mathit{\partial }w(x,t)}{\mathit{\partial }x}\right|\right)}^{1/2}dx+{\left(\left|\frac{\mathit{\partial }w(x,t)}{\mathit{\partial }x}\right|\right)}^{1/2}$$(12)

depending on the gradient of the problem solution, which has been introduced by Beckett et al. (2001), based on the method proposed by Huang, Ren, and Russell (1994). The adaptive solution of the PDE system (3–8) is obtained by the following iterative procedure: (i) a uniform initial grid x_j(0) is generated, and an initial solution w_j(0) for each PDE is calculated using FEM; a temporal loop is done in the time domain, (ii) the monitor function is evaluated at the current time step, the grid is moved from x_j(ν) to x_j(ν + 1) equidistributing the monitor function in each subinterval and a solution w_j(ν + 1) is calculated on the new mesh, for each of the six coupled Equations 3–8, and (iii) the PDE system is put forward on the new mesh x_j(ν + 1) to obtain a numerical approximation w_j(ν + 1) at the new time level.

The FEM discretization of the one-dimensional domain is done via the method of lines, while the Galerkin’s method, associated to a weak formulation of the residual of the differential equations (Zienkiewicz & Taylor, 2002), allowed us to overcome the difficulty related to the non-linearity. Moreover, time discretization has been performed by using an implicit Euler method, and the local distribution of our variables in each element has been interpolated by quadratic shape functions (see Amoddeo et al., 2010, 2011, 2012, 2013, for details). In general, using weighted residual methods, the approximate solution of a differential equation can be obtained introducing a trial function different from the exact solution, containing unknown coefficients to be determined during the solution procedure. Once introduced the trial function into the differential equation, the residual is computed, and the best approximation of the unknown solution is obtained by minimizing the average of the residual over the problem domain, weighted by a test (or weighting) function, determining the unknown constants. In the Galerkin’s method, the test function comes from the chosen trial function (Zienkiewicz & Taylor, 2002), while its reliability is based upon stability and convergence of the problem solution, proper of the method (Quarteroni, 2009). As a consequence, it results a robust and stable numerical technique (Fletcher, 1984; Quarteroni, 2009), relying also on a proper choice of the updating time step (Anderson, Titus, Watson, & Bos, 2000), with recognized efficiency and effectiveness discussed in Amoddeo (2015a), Ramage and Newton (2008).

Most of the involved biological parameters are available in literature, coming from experimental measurements or experimental data fitting, still more estimated by numerical simulations (Chaplain & Lolas, 2005, 2006): often, depending on the technique used for their measurements, have estimate ranges two order of magnitude wide, on average.

For computational reasons, we use dimensionless quantities, obtained by scaling all variables and parameters with reference quantities. In particular, the distance x is rescaled with L = 10⁻¹ cm, i.e. the maximum distance for cancer cells, while D = 1 × 10⁻⁶ cm² s⁻¹ is a representative coefficient for chemical diffusion. As a consequence, the time t is rescaled according to τ = L²D⁻¹. The reference cancer cell concentration, according to Gerisch and Chaplain (2008), is fixed to c₀ = 6.7 × 10⁷ cell cm⁻³. The remaining variables of the uPA system (uPA, VN, PAI-1 and plasmin), are rescaled according to u₀ = 1 nM, v₀ = 1 nM, p₀ = 1 nM, m₀ = 0.1 nM, respectively, which are appropriate reference concentration values coming from estimates obtained in previous work (Andasari et al., 2011; Chaplain & Lolas, 2005, 2006). Finally, the other non-dimensional parameters, estimated in Andasari et al. (2011), McDougall, Watson, Devlin, Mitchell, and Chaplain (2012), Buchwald (2009), are summarized in Table 1.

Table 1. Dimensionless parameter values used in our simulations

Parameter	Value	Description
Dc	3.5 × 10^−4	Cancer cell diffusion coefficient
Du	2.5 × 10^−3	uPA diffusion coefficient
Dp	3.5 × 10^−3	PAI-1 diffusion coefficient
Dm	4.91 × 10^−3	Plasmin diffusion coefficient
χu	3.05 × 10^−2	uPA chemotactic coefficient
χp	3.75 × 10^−2	PAI-1 chemotactic coefficient
χv	2.85 × 10^−2	VN haptotactic coefficient
μ1	0.25	Cancer cell proliferation rate
μ2	0.15	ECM proliferation rate
α31	0.215	uPA production rate
α41	0.5	PAI-1 production rate
δ	8.15	VN degradation rate from interaction with plasmin
φ21	0.75	VN production rate from uPA/PAI-1 interaction
φ22	0.55	VN neutralization rate from interaction with PAI-1
φ31	0.75	uPA inhibition rate from interaction with PAI-1
φ33	0.3	uPA degradation rate from interaction with uPAR
φ41	0.75	PAI-1 degradation rate from interaction with uPA
φ42	0.55	PAI-1 degradation rate from interaction with VN
φ52	0.11	Plasmin production rate from PAI-1/VN interaction
φ53	0.75	Plasmin production rate from cancer cell/uPA interaction
φ54	0.5	Plasmin degradation rate
Dn	2.5, 25	Oxygen diffusion coefficient
k1	0.03, 0.15	Oxygen degradation rate
k2	0.3	Oxygen utilization rate
λ	0, 0.5, 1	Crowding parameter

As reported in McDougall et al. (2012), the diffusion coefficient for oxygen in extracellular retinal tissue, is estimated to be 2.5 × 10⁻⁶ cm² s⁻¹, while for diffusion in other biological media, measured values and estimates, reported in Buchwald (2009), are in the 1.3 × 10⁻⁵ cm² s⁻¹/3.1 × 10⁻⁵ cm²s⁻¹ range: then, we put D_n = 2.5 × 10⁻⁶ cm² s⁻¹ and D_n = 25 × 10⁻⁶ cm² s⁻¹, which in dimensionless form become 2.5 and 25, respectively. Pooled data about oxygen supply for in vivo human tumours, from the review of Vaupel et al. (1989), indicate inadequate oxygen supply to cancer cells. Therefore, we assume the oxygen concentration initially available to cancer cells, acting also as reference for scaling purposes, is fixed to n₀ = 1.37 μM in strongly hypoxic conditions, while the representative oxygen utilization rate for human tumours is set to k₂ = 0.3. Moreover, the degradation coefficient describing the decay of oxygen and its uptake by surrounding host tissue, is set according to Hubbard and Byrne (2013) (k₁ = 0.5 × k₂ = 0.15). In order to consider the utilization rates in normal tissue (Vaupel et al., 1989), we also performed computations with k₁ = 0.1 × k₂ = 0.03. Finally, we analysed the theoretical results obtained for three different values of crowding parameter (λ = 0, 0.5 and 1).

We simulated the proliferation of cancer cells in a one-dimensional portion of biological tissue for x ∈ [0, 4] and t ∈ [0, 300], corresponding to a tissue thickness d = 4 mm and to a time interval of about 35 days. Assuming ε = 0.01, we impose that at t = 0 and x = 0, a cluster of cancer cells is already present, while the remaining portion of the domain is filled by ECM: then, c(x, 0) = exp(−|x|²ε⁻¹), v(x, 0) = 1–0.5c(x, 0). Similarly, as the initial concentrations of uPA and PAI-1 are proportional to the cancer cells concentration, plasmin is not produced yet, and the oxygen concentration is at the initially available concentration, we impose u(x, 0) = 0.5c(x, 0), p(x, 0) = 0.05c(x, 0), m(x, 0) = 0 (Amoddeo, 2015a; Andasari et al., 2011; Chaplain & Lolas, 2005) and n(x, 0) = n₀. Moreover, the components remain confined within the simulated portion of tissue, and then our PDE system, apart from the ordinary differential Equation 4, satisfies zero-flux boundary conditions.

The integration domain in the 0 ≤ x ≤ 4 range is discretized by a mesh of 400 grid points, and the dynamical evolution of the biological system is monitored in the 0 ≤ t ≤ 300 time interval with steps of size δ_t = 0.5. Both the dimensional timescale and the tissue thickness can be recovered multiplying, respectively, t by τ, and x by L. At each time step, the PDE system (3–8) is solved over the grid generated replacing, in Equation 12, the generic solution w(x, t) with c(x, t): during the time evolution, the grid points on which the solution is computed move according ∇c(x, t), see steps (ii) and (iii) of the above algorithm description.

4. Numerical results and discussion

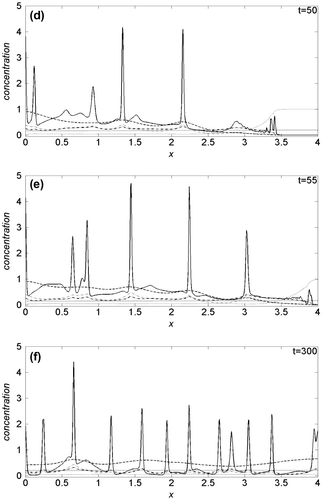
In Figure 1 we show the proliferation pattern built by cancer cells, linearly mapped in a grey-level scale: black and white colours refer, respectively, to zero and maximum cancer cell density. On the horizontal axis the tissue thickness is in the 0 ≤ x ≤ 4 range, while on the vertical axis is reported the time scale of the solution evolution in the 0 ≤ t ≤ 300 interval. Oxygen supply is modelled imposing D_n = 2.5, k₁ = 0.03, k₂ = 0.3, λ = 0 and at t = 0, the cell distribution is prescribed by the initial conditions. For t > 0, the proliferation patterns are very similar to that recently obtained simulating the interaction of the uPA system with cancer cells in absence of oxygen (Amoddeo, 2015a): in fact its reduced presence does not significantly alter the tumour progression, which build heterogeneous branched spatio-temporal pattern, a somehow expected result. Moreover, letting D_n, k₁ and λ to vary, no appreciable differences are observed: the proliferation patterns remain similar to that of Figure 1, hence not shown here. Plots of the domain variables at selected times along the tissue thickness are presented in Figure 2, monitoring the density evolution of the interacting species: on the horizontal axis is reported the tissue thickness, and in the vertical one the concentration of the chemical species. Solid line refers to cancer cells c(x, t), dotted line to VN v(x, t), dash-dotted line to uPA u(x, t), dashed line to PAI-1 p(x, t), thin dash-dotted line to plasmin m(x, t) and heavy dotted line to oxygen n(x, t). We observe that the oxygen concentration decreases as a function of time, even if it remains uniformly distributed along the tissue thickness. The same behaviour is obtained also varying the D_n, k₁ and λ parameters. The spatio-temporal dynamics of the cell density depend on the initial condition (see Figure 2(a)). As a consequence, we observe a broad structure uniformly clustered close x = 0 until t = 15, namely when the density profile starts to change (see Figure 2(b)). Afterwards, the invasion front moves from x = 0, exhibiting a characteristic irregular shape marking the interface between cancer and healthy cells. The interaction of the former with the uPA system causes the evolution of the other chemical densities, and in particular the VN degradation. For t = 25, Figure 2(c), the invading front has penetrated beyond x = 1, while, for t = 50, it reaches about x = 3.5 (see Figure 2(d)), assuming characteristic sharp structures of the density profile corresponding to the branches of Figure 1. This feature indicates the presence of inhomogeneous clustering of cancer cells. The simulated domain is almost completely invaded at t = 55 (see Figure 2(e)). For t > 55, the density profile of cancer cells exhibits repeated sharp peaks (see Figure 2(f)) in correspondence with the heterogeneous pattern shown in Figure 1. This behaviour proves the presence of malignant cells in the tumour (Araujo & McElwain, 2004). We remark as our numerical method allows resolving the fine structure at the boundary between cancer and healthy cells, characterized by the irregular invading front, during the cancer cell invasion.

Figure 1. Surface contour plots of the cancer cells concentration evolution in the 0 ≤ x ≤ 4 spatial domain and in the 0 ≤ t ≤ 300 time interval, imposing D_n = 2.5, k₁ = 0.03, k₂ = 0.3, λ = 0.

Note: The concentration is linearly mapped in a grey-level scale between the black (zero concentration) and white (maximum concentration) colours.

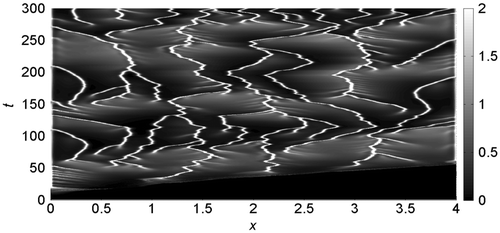
Figure 2. Theoretical distributions for chemical species. The spatial distributions are acquired at six different times: (a) t = 0, (b) t = 15, (c) t = 25, (d) t = 50, (e) t = 55, (f) t = 300. The parameters are set as in Figure 1.

Notes: Cancer cells (solid line); Vitronectin (dotted line); uPA (dash-dotted line); PAI-1 (dashed line); Plasmin (dash-dotted thin line); Oxygen (heavy dotted line).

To emphasize the oxygen induced effects on cancer cell dynamics, in Figure 3(a) and (b) we compare the cancer cell density profiles obtained at t = 25 and t = 50, respectively, imposing k₁ = 0.03. In each panel, the first three curves from the bottom are obtained with D_n = 2.5, while for the three top curves D_n = 25. Moreover, solid curves refer to λ = 0, dashed and dotted ones to, respectively, λ = 0.5 and λ = 1. For t < 25, the density profiles are not appreciably influenced by changes of the simulation parameters, hence we omit to show them. In Figure 3(a), we observe that, for t = 25, the tumour invading front is located above x = 1, with a characteristic sharp and irregular cancer/healthy cells interface. The comparison among the density curves, nevertheless, show that, for fixed value of λ, the velocity of the invading front decreases when D_n increases. On the other hand, given a D_n value, the proliferation is faster according to growing λ, i.e. increasing the cell crowding, and after all, lowering the availability of oxygen even if, for D_n = 25, such behaviour is less evident: globally, the invading front seems to be sharper at low D_n.

Figure 3. Comparison of the cancer cell density profiles obtained at (a) t = 25 and (b) t = 50, for k₁ = 0.03.

Notes: In each panel, the first three curves from the bottom are obtained for D_n = 2.5, while the three top curves are obtained for D_n = 25. The numerical results are reproduced for three different values of crowding parameter: λ = 0 (solid line), λ = 0.5 (dashed line) and λ = 1 (dotted line).

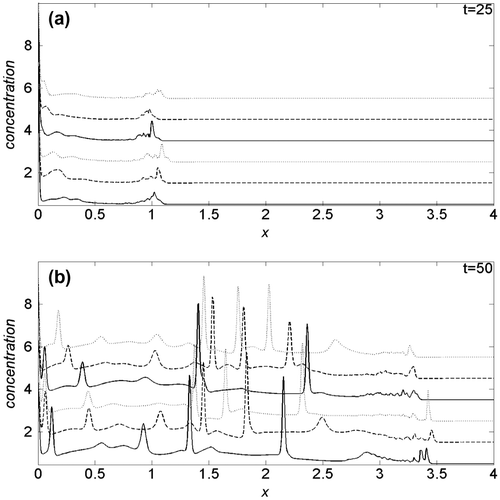
At t = 50 and D_n = 2.5, Figure 3(b), the invading front is near x = 3.5, while for D_n = 25, is around x = 3.3: as for t = 25, the speed of the invasion front is higher at low D_n. The effects of the λ parameter, with respect to t = 25, start to change, and for D_n = 25 are weakly inverted. Also in the present case, the invading front is sharper for the lowest D_n value.

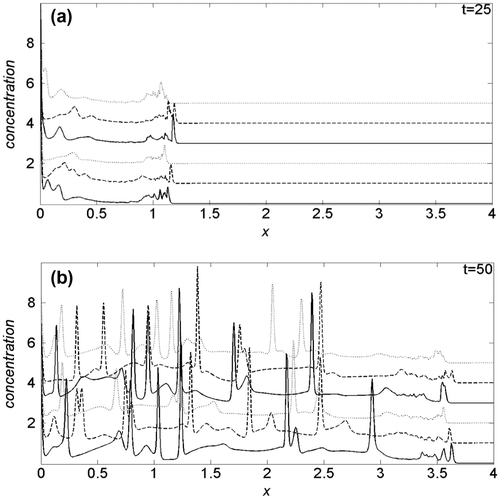
Imposing k₁ = 0.15, in general, the invading front increases its velocity: at t = 25, Figure 4(a), is always well beyond x = 1, and for each D_n value, the maximum velocity of invasion is reached with λ = 0.5, dashed curves, while the velocity is lower for λ = 1 than for λ = 0. Contrary to k₁ = 0.03, given a λ value, an increase in the oxygen diffusion coefficient, three top curves, reflects an increase in the invading front velocity. At t = 50, Figure 4(b), the invading front is above x = 3.5, and for D_n = 2.5, its velocity decrease monotonically according to growing λ. With respect to the simulations performed in Amoddeo (2015a), where the same model parameters for cancer cell dynamics and uPA system have been used, the presence of oxygen induces a marked increase in the invading front velocity, but the cancer/healthy cells interface is less jagged and spiky.

Figure 4. Comparison of the cancer cell density profiles obtained at (a) t = 25 and (b) t = 50, for k₁ = 0.15.

Notes: In each panel, the first three curves from the bottom are obtained for D_n = 2.5, in the three top curves D_n = 25, while the crowding parameter is set to λ = 0 (solid line), λ = 0.5 (dashed line) and λ = 1 (dotted line).

Our results are in agreement with simulations of vascular tumour growth with a generic nutrient supply, performed on a two-dimensional domain (Hubbard & Byrne, 2013); moreover, they are consistent with the avascular tumour growth simulated introducing a model for the interaction between growing tumour and hypoxic microenvironment with vessels remodelling in three spatial dimensions, in which the oxygen consumption expands in enlarged tumour regions (Cai, Wu, Long, Xu, & Li, 2013).

Nevertheless, our simulations allow to predict that oxygen effects are non-obviously modulated during cancer cell growth, depending on oxygen availability, and on its motility. At very strong hypoxic conditions of the cells microenvironment, modelled with a low k₁, cancer cells “sense” more D_n parameter, balancing a lower motility of the nutrient oxygen with an increase in the proliferation speed. Moreover, the reducing of the oxygen-per-cell availability, due to an increase in cancer cell crowding for fixed D_n, promotes a faster invasion in early stage (see Figure 3(a)). When the invasion establishes in a large part of tissue, its velocity is promoted/damped by cell crowding, for low/high oxygen motility (see Figure 3(b)). The increase in k₁ causes an increase in proliferation velocity, while crowding effects are inverted with respect to k₁ = 0.03 (see Figure 4). In particular, both growing oxygen motility and moderate cell crowding, promote the invasion speed in the early stage, Figure 4(a), while at high temporal values, cell crowding induce an overall reduction of the invasion speed, Figure 4(b).

The obtained results confirm the efficiency of the MMPDE numerical technique to solve the proposed mathematical model for cancer growth and proliferation, allowing, with respect to techniques based on uniform discretization of the integration domain, improving the resolution of solution features related to malignancy.

5. Conclusions

In this work, the MMPDE numerical technique has been applied to model the effects induced by oxygen during the interaction of uPA system with cancer cell dynamics. In particular, the study performed shows that the presence of oxygen in human tissue causes an increase in the cancer cell proliferation velocity. This process is observed also for low oxygen concentration. Letting the degrading rate of oxygen to change, due to interaction with surrounding tissue as consequence, for example, of microenvironment changes of in vivo cancer cells (Buchwald, 2009; Vaupel et al., 1989), reflects in a change of the speed of invasion of the tumour front. Moreover, the crowding, due to cell growth and proliferation, gives rise to changes in the invasion velocity with effects depending on both the diffusion coefficient and degradation rate of oxygen. Besides deterministic models like the one presented here, in recent years a series of papers focus on cancer cell dynamics from a stochastic point of view (Chichigina, Valenti, & Spagnolo, 2005; Fiasconaro, Spagnolo, Ochab-Marcinek, & Gudowska-Nowak, 2006; Pizzolato, Persano Adorno, Valenti, & Spagnolo, 2011; Valenti, Schimansky-Geier, Sailer, & Spagnolo, 2006). We are aware that modelling a complete biological system is quasi impossible, due to the number of parameters involved, even if the one-dimensional model devised in the study could shed some light on the challenging problem of cancer cell proliferation.

Cover image

Source: Author.

Additional information

Funding

Funding. The author received no direct funding for this research.

Notes on contributors

Antonino Amoddeo

Antonino Amoddeo is working as a researcher in the Department of Civil, Energy, Environmental and Materials Engineering of the Università ‘Mediterranea’ of Reggio Calabria. His recent research interests concern the physical and mathematical modelling of anisotropic materials. In this respect, he started to study the order tensor dynamics of nematic liquid crystals subjected to mechanical and electric stresses, as well models for avascular tumour growth in the early stage of invasion of biological tissues. Formerly, he was concerned with experimental and theoretical research activities about semiconductors and transition metals surfaces and interfaces, both clean and in presence of adsorbed contaminant species.