A functional renormalization group application to the scanning tunneling microscopy experiment

Abstract

We present a study of a system composed of a scanning tunneling microscope (STM) tip coupled to an absorbed impurity on a host surface using the functional renormalization group (FRG). We include the effect of the STM tip as a correction to the self-energy in addition to the usual contribution of the host surface in the wide band limit. We calculate the differential conductance curves at two different lateral distances from the quantum impurity and find good qualitative agreement with STM experiments where the differential conductance curves evolve from an antiresonance to a Lorentzian shape.

Keywords:

• scanning tunneling microscopy (STM)
• quantum impurity
• functional renormalization group (fRG)
• differential conductance

Public Interest Statement

In the present work, we study an atom on a metallic surface by means of a STM microscope. The electrons flow from the microscope tip to the atom. These electrons can follow different paths: directly from the tip to the atom and through the metallic surface. This effect has consequences over the available states of the atom resulting in a change from an antiresonance to a bell-shaped form of the differential conductance when the STM tip is away from the impurity. The change can be explained by considering the fact that less electrons arrive to the sample when the tip is away and the contribution of the electrons of the metallic surface dominates the shape of the differential conductance which is a measure of the distribution of the electrons in the atom over the energy.

1. Introduction

The coupling of the spin degree of freedom to the electronic degrees of freedom in quantum impurity models leads to a variety of phenomena. One of the correlation phenomena is the Kondo effect arising from the spin-flip scattering between the impurity and the conduction electrons, for temperatures below a characteristic Kondo temperature ($T_K$), this scattering causes the electrons of the host metal to condense into a many-body ground state that collectivelly screens the local spin of the impurity resulting in the anomalous behavior in the resistivity, specific heat, and magnetic susceptibility of the modeled system (Hewson, 1993; White, 1983). While the Kondo effect is well understood for impurities in solids, the scanning tunneling microscope (STM) has revealed new facets of the Kondo physics (Li, 1998; Madhavan, Chen, Jamneala, Crommie, & Wingreen, 1998; Néel et al., 2008; Prüser et al., 2011), such as the Fano-Kondo resonance on the differential conductance when a single magnetic impurity is placed on a metallic surface. The line shape of the observed Kondo resonance in STM experiments (Aynajian et al., 2010; Jiang, Zhang, Cao, Wu, & Ho, 2011; Madhavan et al., 1998) is not Lorentzian but has the asymmetric shape characteristic of a Fano antiresonance (Fano, 1961; Uchoa, Yang, Tsai, Peres, & Castro Neto, 2009). The antiresonances observed in the differential conductance, reflect a dip in the spectral density of conduction electrons near the Fermi level caused by the Kondo effect. In an STM experiment, electrons from a sharp tip tunnel into the material to be studied, creating a tunneling current due to the application of a potential. When a STM tip is away from the impurity it measures the substrate density of states; however, close to the impurity electrons from the tip can tunnel directly to the impurity. The theory of STM is not trivial because electrons from the tip not only tunnel to the impurity but also via the surface states i. e. we have various different channels of tunneling. The line shape can be explained as a result of the interference from the different tunneling paths: one from the STM tip to the substrate and the other from the tip to the impurity and then to the substrate.

In the present work, we approach the correlation problem or the on-site interaction of the impurity’s electrons by the functional renormalization group (FRG) (Bartosch, Freire, Ramos-Cardenas, & Kopietz, 2009; Gezzi, Pruschke, & Meden, 2007; Jakobs, Meden, & Schoeller, 2007; Hedden, Meden, Pruschke, & Schoenhammer, 2004; Jakobs, Pletyukov, & Schoeller, 2010; Metzner, Salmhofer, Honerkamp, Meden, & Schoenhammer, 2012; Schuetz, Bartosch, & Kopietz, 2005). This method leads to an infinite set of coupled ordinary equations (ODEs) for the system’s irreducible n-particle vertex functions ${\mathit{\gamma }}^{(n)}$. The derivation is done in such a way that the effects of high-energy modes above a flowing infrared cutoff parameter $\mathrm{\Lambda }$, are incorporated before the modes below $\mathrm{\Lambda }$. The $\mathrm{\Lambda }$ serves as a flow parameter that controls the RG flow of the $\mathrm{\Lambda }$-dependent vertex functions ${\mathit{\gamma }}_{\mathrm{\Lambda }}^{(n)}$ from an initial cutoff ${\mathrm{\Lambda }}_i$, at which all vertex functions are known to a final cutoff ${\mathrm{\Lambda }}_f$, at which the full theory is recovered. Though this method is exact and in most cases not solvable, one has to truncate the infinite set of ODEs for vertex functions ${\mathit{\gamma }}_{\mathrm{\Lambda }}^{(n)}$ with $n\ge 3$. Nevertheless, the flexibility and relative simplicity of the FRG can lead to useful applications in complex contexts such as the problem of the impurity on a metallic substrate.

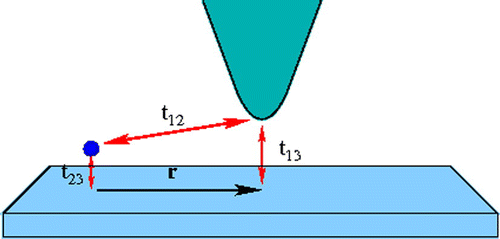
In this work, we investigate the STM differential conductance of an impurity on a metallic surface considering the different channels of tunneling. We choose and Anderson type model (Anderson, 1961) for the impurity, substrate, and STM tip. The STM tip has an additional feature: the tip can move laterally away from the impurity and the differential conductance is calculated for increasing lateral distances (Figure 1). In order to keep things as simple as possible, the surface and tip are modeled as featureless by considering a constant density of states in the wide band limit. The calculation of the self-energy $({\mathit{\gamma }}_{\mathrm{\Lambda }}^1)$ and the effective interaction $({\mathit{\gamma }}_{\mathrm{\Lambda }}^2)$ is based on the Keldysh non-equilibrium FRG in the static approximation.

In Section 2, we present a brief description of the Anderson type model we use, derive the corrections to the self-energy in the presence of the STM tip and write the model in terms of the Keldysh Green functions. In Section 3, we discuss briefly the FRG in its Keldysh version. In Section 4, we discuss the parameters and the numerical results. We conclude with a discussion in Section 5.

Figure 1. STM tip coupled to a host surface with an impurity. Notes: The tunneling matrix elements $t_{12},t_{13}$ and $t_{23}$ represent the couplings tip-impurity, tip-surface and impurity-surface, respectively. The tip-impurity lateral distance is denoted by r.

2. Model Hamiltonian and effective action

We consider a host material with an impurity deposited on the surface. Electrons from an STM’s tip can tunnel to the substrate via (a) direct tunneling tip-to-surface or (b) tunneling via tip-impurity-surface, for a particular bias V. The system’s Hamiltonian is(1) $$\begin{array}{cc}\hfill H& =H_1+H_2+H_3+H_{12}+H_{13}+H_{23},\hfill \\ \hfill H_1& =\sum _p{\mathit{ϵ}}_p{c}_{p\mathit{\sigma }}^{†}{c}_{p\mathit{\sigma }},\hfill \\ \hfill H_2& =\sum _{\mathit{\sigma }}{E}_d{d}_{\mathit{\sigma }}^{†}{d}_{\mathit{\sigma }}+U{n}_{\uparrow }{n}_{\downarrow },\hfill \\ \hfill H_3& =\sum _k{\mathit{ϵ}}_k{c}_{k\mathit{\sigma }}^{†}{c}_{k\mathit{\sigma }}.\hfill \end{array}$$(1)

where $c_p$ is the annihilation operator for electrons in the tip, $c_k$ is the annihilation operator for electrons in the surface, $d_{\mathit{\sigma }}^{†}$ and $d_{\mathit{\sigma }}$ are, respectively, the creation and annihilation operators of the electrons in the impurity. In this work, we focus on an absorbed impurity, described in terms of correlated quantum levels: $E_d=eV-\frac{U}{2}$ where, if we set eV=0 this corresponds to the particle-hole symmetric case, U is the repulsive interaction between electrons in the impurity, and $n_{\mathit{\sigma }}=d_{\mathit{\sigma }}^{†}{d}_{\mathit{\sigma }}$ is the electron occupation in the impurity. The tunneling parts of the Hamiltonian are(2) $$\begin{array}{cc}\hfill H_{12}& =\sum _{p,\mathit{\sigma }}(t_{12}{c}_{p\mathit{\sigma }}^{†}{d}_{\mathit{\sigma }}+t_{12}{d}_{\mathit{\sigma }}^{†}{c}_{p\mathit{\sigma }}),\hfill \\ \hfill H_{13}& =\sum _{k,p,\mathit{\sigma }}(t_{13}{c}_{k\mathit{\sigma }}^{†}{c}_{p\mathit{\sigma }}+t_{13}{c}_{p\mathit{\sigma }}^{†}{c}_{k\mathit{\sigma }}),\hfill \\ \hfill H_{23}& =\sum _{k,\mathit{\sigma }}(t_{23}{c}_{k\mathit{\sigma }}^{†}{d}_{\mathit{\sigma }}+t_{23}{d}_{\mathit{\sigma }}^{†}{c}_{k\mathit{\sigma }}),\hfill \end{array}$$(2)

where $t_{ij}$ is the coupling between the subsystems i and j, with $i,j=1,2,3$. Here the numbers 1, 2, and 3 denote the tip, impurity, and host surface, respectively. The tip and host surface are assumed to be in thermal equilibrium at the temperature T, and to have independent chemical potentials ${\mathit{\mu }}_1$ and ${\mathit{\mu }}_3$ respectively, the difference between them is the bias voltage $eV={\mathit{\mu }}_3-{\mathit{\mu }}_1$. The distribution functions for electrons of the tip and substrate systems are assumed to be equilibrium Fermi distribution functions, $f_1$ and $f_3$. Electronic tunneling matrix elements $t_{13}$ (tip-impurity) and $t_{23}$ (substrate-impurity) give rise to an stationary current between the tip and host surface, and between the impurity and host surface.

In general, the Hamiltonian (1) is a generalization of the well-known interacting Anderson Impurity Model. The Hamiltonian $H_1$ and $H_2$ in Equation (2) describe free electrons in the tip and substrate, respectively, while $H_2$ describes the electrons in the impurity, this contains the $E_d$ levels of the d electrons plus the interaction term $U{n}_{\uparrow }{n}_{\downarrow }$, here we assume the simplest case of an isolated atomic impurity state of energy $E_d$, which has at the most double occupancy with a spin $\uparrow$ and a spin $\downarrow$ electron. The Hamiltonians $H_{12}$ and $H_{23}$ describe the d levels of the impurity hybridized with the conduction electrons in the tip and the host surface, respectively. The Hamiltonian $H_{13}$ describes the hybridization between the electrons in the tip and those of the host surface. To get some insight into the model, let us consider the case where the hybridization energies are set equal to zero, $t_{ij}=0$. Since the d electrons are uncoupled from the conduction electrons in the tip and the host surface. There are three energy configurations for the states in the impurity: zero occupation with total energy $E_0=0$, single occupation with energy $E_{1\mathit{\sigma }}=E_d$ and double occupation with total energy $E_2=2E_d+U$. If the ground state corresponds to single occupation then the state has twofold degeneracy corresponding to 1/2 spin. It will have associated magnetic moments which will give a Curie law contribution to susceptibility. The other two configurations are no magnetic. This is the so called atomic limit. When we set the hybridization energies $t_{ij}\ne 0$ the impurity-level energy is degenerate with the conduction electron energy levels in the host surface and the tip. In this work we assume the hybridizations $t_{ij}$ are small compared to U, Therefore, we expect the ground states of the impurity to be essentially the same of the atomic limit.

The contributions from the substrate and the tip to the self-energy of the impurity’s Green function can be calculated from the inverse free retarded Green’s function $Q(\mathit{\omega })\equiv {[g(\mathit{\omega })]}^{-1}$. On the real frequency axis $Q(\mathit{\omega })$ is given by $Q(\mathit{\omega })=\mathit{\omega }\mathbf{1}-{\widehat{H}}_0$, where ${\widehat{H}}_0$ is the noninteracting part of the Hamiltonian. Written as a matrix $Q(\mathit{\omega })$ is given by

where The inverse of $Q_{\mathit{\sigma }}(\mathit{\omega })$ can be calculated using The free Green’s function on the impurity is obtained from the element(3) $$\begin{array}{c}\hfill g_{d\mathit{\sigma }}(\mathit{\omega })={\left[Q_{\mathit{\sigma }}(\mathit{\omega })\right]}_{1,1}^{-1},\end{array}$$(3)

here one can identify the matrix blocks $A=\mathit{\omega }-E_d$, $B=\left[t_{12}{t}_{23}\right]$, $C={\left[t_{12}^{\ast }{t}_{23}^{\ast }\right]}^T$ and(4) $$\begin{array}{c}\hfill D=\left[\begin{array}{cc}\mathit{\omega }-E_d& t_{13}\\ t_{13}^{\ast }& \mathit{\omega }-{\mathit{ϵ}}_k\end{array}\right],\end{array}$$(4)

after some Matrix Algebra one can obtain an expression for the Green’s function:(5) $$\begin{array}{c}\hfill g_{d\mathit{\sigma }}(\mathit{\omega })={\left(\mathit{\omega }-E_d-\sum _k\frac{|t_{23}{|}^2}{\mathit{\omega }-{\mathit{ϵ}}_k}-\sum _p\frac{|{\tilde{t}}_{12}{|}^2}{\mathit{\omega }-{\mathit{ϵ}}_p}\right)}^{-1},\end{array}$$(5)

where the renormalized tunneling energy between the tip and the impurity is given by(6) $$\begin{array}{c}\hfill {\tilde{t}}_{12}=t_{12}-\sum _k\frac{t_{23}{t}_{13}^{\ast }}{\mathit{\omega }-{\mathit{ϵ}}_k+i{\mathit{\delta }}^{+}}.\end{array}$$(6)

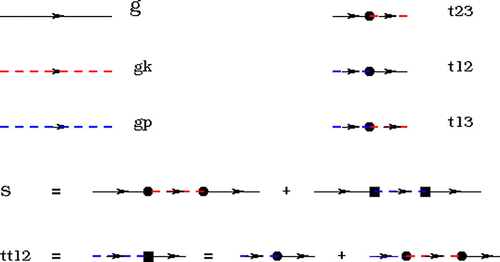
The different contributions to the self-energy are depicted in Figure 2. The vertices $t_{12}$, $t_{23}$, and $t_{13}$ represent the interaction between electrons in the tip-impurity, impurity-host surface, and tip-host surface, respectively. The Green’s functions for free electrons in the impurity, host surface and tip are represented by a black, red, and blue lines. The self-energy has the contributions from the substrate and tip represented by the diagram with a red line and the diagram with a blue line, respectively, where the renormalized hybridization ${\tilde{t}}_{12}$ is represented with a square with an entering blue line and a leaving black line. The first term in the self-energy derives from the hybridization of the electrons in the impurity with the conduction sea of the host metal while the second derives from the hybridization of the electrons with the conduction sea of the tip of the STM.

We model the tip-impurity, tip-surface, and impurity-surface couplings, respectively, by considering(7) $$\begin{array}{cc}\hfill t_{12}& =t_{12}^0{e}^{-r/r_0},\hfill \end{array}$$(7) (8) $$\begin{array}{cc}\hfill t_{13}& =t_{13}^0{e}^{ik·r},\hfill \end{array}$$(8) (9) $$\begin{array}{cc}\hfill t_{23}& =t_{23}^0,\hfill \end{array}$$(9)

We treat the substrate in the wide band limit with a constant density of states ${\mathit{\rho }}_3$ and assume the coupling between the substrate and the impurity does not depend on momentum and spin, and the substrate contribution to the self-energy is(10) $$\begin{array}{c}\hfill \sum _k\frac{|t_{23}{|}^2}{\mathit{\omega }-{\mathit{ϵ}}_k+i{\mathit{\delta }}^{+}}=-i\frac{{\mathrm{\Gamma }}_3}{2},\end{array}$$(10)

where ${\mathrm{\Gamma }}_3=2\mathit{\pi }{|t_{23}^0|}^2{\mathit{\rho }}_3$. The renormalized tunneling ${\tilde{t}}_{12}$ is calculated by using(11) $$\begin{array}{c}\hfill \sum _k\frac{t_{13}^{\ast }}{\mathit{\omega }-{\mathit{ϵ}}_k+i{\mathit{\delta }}^{+}}=R(r,\mathit{\omega })+iI(r,\mathit{\omega }),\end{array}$$(11)

Figure 2. The Green functions of the impurity $g(\mathit{\omega })$, substrate $g_k(\mathit{\omega })$, and tip $g_p(\mathit{\omega })$. Notes: Feynman diagrams for the hybridizations $t_{23}$, $t_{12}$ and $t_{13}$. The self-energy ${\mathrm{\Sigma }}_{tun}$ include two tunneling events: an electron can tunnel from the impurity to the substrate and from the impurity to the tip. The interaction ${\tilde{t}}_{12}$ contains the physical event that an electron from the tip jump to the surface and then to the impurity.

where $R(r,\mathit{\omega })$ and $I(r,\mathit{\omega })$ denote the corresponding real and imaginary parts given by(12) $$\begin{array}{c}\hfill R(r,\mathit{\omega })={\mathit{\rho }}_3{\int }_{-1}^{1}dx\frac{\frac{\mathit{\omega }}{D}-x}{{(\frac{\mathit{\omega }}{D}-x)}^2+{\mathit{\delta }}^2}{J}_0(k_{F}r\sqrt{1+x}),\end{array}$$(12)

and(13) $$\begin{array}{c}\hfill I(r,\mathit{\omega })=-\mathit{\pi }{\mathit{\rho }}_3{J}_0\left(k_{F}r\sqrt{1+\frac{\mathit{\omega }}{D}}\right),\end{array}$$(13)

with $k_F$ being the Fermi wave number and D the band width. In the wide band limit, the real part R and the imaginary part I reduce to(14) $$\begin{array}{c}\hfill R(r)={\mathit{\rho }}_3\frac{k_F^2{r}^2}{2},\end{array}$$(14)

and(15) $$\begin{array}{c}\hfill I(r)=-\mathit{\pi }{\mathit{\rho }}_3{J}_0\left(k_{F}r\right).\end{array}$$(15)

We work in terms of the non-equilibrium Keldysh Green functions therefore expressions are written in a matrix form.

Integrating out the tip and surface electrons, we obtain an effective action for the interacting electrons for the electrons in the impurity.(16) $$\begin{array}{c}\hfill S[\overline{d},d]={\overline{d}}_{\mathit{\alpha }}{\left[G_0^{-1}\right]}_{\mathit{\alpha }\mathit{\beta }}{d}_{\mathit{\beta }}-\frac{1}{4}{\mathit{\nu }}_{\mathit{\alpha }\mathit{\beta }\mathit{\gamma }\mathit{\delta }}{\overline{d}}_{\mathit{\alpha }}{\overline{d}}_{\mathit{\beta }}{d}_{\mathit{\gamma }}{d}_{\mathit{\delta }},\end{array}$$(16)

where the set of indices $\mathit{\alpha }=\left\{k_{\mathit{\alpha }},{\mathit{\omega }}_{\mathit{\alpha }},{\mathit{\sigma }}_{\mathit{\alpha }}\right\}$ contain the Keldysh index, frequency, and spin, and repeated indices are summed or integrated over. In this work, we use the triangular representation of the Keldysh–Green’s functions(17) $$\begin{array}{c}\hfill G_{\mathit{\sigma }}=\left(\begin{array}{ccc}{G}_{\mathit{\sigma }}^r\hfill & & G_{\mathit{\sigma }}^k\\ 0\hfill & & G_{\mathit{\sigma }}^a\end{array}\right),\end{array}$$(17)

and the self-energy(18) $$\begin{array}{c}\hfill {\mathrm{\Sigma }}_{\mathit{\sigma }}=\left(\begin{array}{ccc}{\mathrm{\Sigma }}_{\mathit{\sigma }}^r\hfill & & {\mathrm{\Sigma }}_{\mathit{\sigma }}^k\\ 0\hfill & & {\mathrm{\Sigma }}_{\mathit{\sigma }}^a\end{array}\right).\end{array}$$(18)

The Keldysh-Green’s function in the triangular representation couple together the retarded, advanced, and Keldysh Green’s functions $G_{\mathit{\sigma }}^r$, $G_{\mathit{\sigma }}^a$ and $G_{\mathit{\sigma }}^k$. The direct antysymmetrized electron–electron vertex is given by(19) $$\begin{array}{cc}\hfill {\mathit{\nu }}_{\mathit{\alpha },\mathit{\beta },\mathit{\gamma },\mathit{\delta }}& =2\mathit{\pi }\mathit{\delta }\left({\mathit{\omega }}_{\mathit{\alpha }}+{\mathit{\omega }}_{\mathit{\beta }}-{\mathit{\omega }}_{\mathit{\gamma }}+{\mathit{\omega }}_{\mathit{\delta }}\right)\frac{U}{2}\left({\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\alpha }}}{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\gamma }}}{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\beta }}}{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\delta }}}-{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\alpha }}}{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\delta }}}{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\beta }}}{\mathit{\delta }}_{{\mathit{\sigma }}_{\mathit{\gamma }}}\right){\mathit{\delta }}_{{\overline{\mathit{\sigma }}}_{\mathit{\alpha }}{\mathit{\sigma }}_{\mathit{\delta }}}\hfill \\ \hfill & \times {\left(\begin{array}{ccc}{\left(\begin{array}{ccc}0\hfill & & 1\\ 1\hfill & & 0\end{array}\right)}_{\mathit{\alpha },\mathit{\gamma }}\hfill & & {\left(\begin{array}{ccc}1\hfill & & 0\\ 0\hfill & & 1\end{array}\right)}_{\mathit{\alpha },\mathit{\gamma }}\\ {\left(\begin{array}{ccc}1\hfill & & 0\\ 0\hfill & & 1\end{array}\right)}_{\mathit{\alpha },\mathit{\gamma }}\hfill & & {\left(\begin{array}{ccc}0\hfill & & 1\\ 1\hfill & & 0\end{array}\right)}_{\mathit{\alpha },\mathit{\gamma }}\end{array}\right)}_{\mathit{\beta },\mathit{\delta }},\hfill \end{array}$$(19)

The free retarded Green’s function of the impurity can be written as(20) $$\begin{array}{c}\hfill g_{\mathit{\sigma }}^r(\mathit{\omega })={\left(\mathit{\omega }-{\mathit{ϵ}}_d+i\frac{{\mathrm{\Gamma }}_3}{2}+i\frac{{\tilde{\mathrm{\Gamma }}}_1}{2}\left\{q^2+1\right\}\right)}^{-1},\end{array}$$(20)

where ${\tilde{\mathrm{\Gamma }}}_1=2\mathit{\pi }{\mathit{\rho }}_1{\left[\mathrm{Im}{\tilde{t}}_{12}(r,\mathit{\omega })\right]}^2$ with ${\mathit{\rho }}_1$ the (STM) tip’s density of states and $q=M/N$ is the Fano parameter with $M=\mathrm{Re}{\tilde{t}}_{12}(r,\mathit{\omega })$ and $N=\mathrm{Im}{\tilde{t}}_{12}(r,\mathit{\omega })$. The advanced Green function $G_{\mathit{\sigma }}^a$ and the Keldysh Green function $G_{\mathit{\sigma }}^k$ are given by(21) $$\begin{array}{cc}\hfill g_{\mathit{\sigma }}^a(\mathit{\omega })& =g_{\mathit{\sigma }}^r{(\mathit{\omega })}^{\ast },\hfill \\ \hfill g_{\mathit{\sigma }}^k(\mathit{\omega })& =g_{\mathit{\sigma }}^r(\mathit{\omega }){\mathrm{\Sigma }}_{tun}^k{g}_{\mathit{\sigma }}^a(\mathit{\omega }),\hfill \end{array}$$(21)

with(22) $$\begin{array}{cc}\hfill {\mathrm{\Sigma }}_{tun}^r& =-i{\tilde{\mathrm{\Gamma }}}_1(r,\mathit{\omega })-i{\mathrm{\Gamma }}_3,\hfill \\ \hfill {\mathrm{\Sigma }}_{tun}^k(\mathit{\omega })& =-i\left[1-2f_1(\mathit{\omega })\right]{\tilde{\mathrm{\Gamma }}}_1(r,\mathit{\omega })-i\left[1-2f_3(\mathit{\omega })\right]{\mathrm{\Gamma }}_3,\hfill \\ \hfill f_j& =\frac{1}{e^{(\mathit{\omega }-{\mathit{\mu }}_j)/T_j}+1}.\hfill \end{array}$$(22)

3. Functional renormalization group

After integrating out the tip and surface, we treat the problem of the interacting electrons in the impurity with the functional renormalization group. We use the Keldysh formulation developed in Jakobs et al. ( 2007). We use the hybridization to an auxiliary tip, $\mathrm{\Lambda }$, as the flow parameter and truncate the hierarchy of FRG equations at second order.

The functional renormalization group is set up by making the bare Green’s function $g_{d\mathit{\sigma }}^r$ as depending on a flow parameter $\mathrm{\Lambda }$(23) $$\begin{array}{c}\hfill g_{\mathit{\sigma }\mathrm{\Lambda }}^r(\mathit{\omega })={\left(\mathit{\omega }+i\frac{({\mathrm{\Gamma }}_3+\mathrm{\Lambda })}{2}+i\frac{{\tilde{\mathrm{\Gamma }}}_1}{2}\left\{q^2+1\right\}\right)}^{-1}.\end{array}$$(23)

Most commonly $\mathrm{\Lambda }$ is chosen to suppress Low-energy degrees of freedom. Being functionals of the bare Green’s function $g_{\mathit{\sigma }}^r$, the retarded Green’s function $g_{\mathit{\sigma }}^r$ and higher vertex functions acquire a $\mathrm{\Lambda }$ dependence as well, which are described by an infinite hierarchy of coupled flow equations. In the Keldysh version of the functional renormalization group we need to express the Green’s functions as matrices

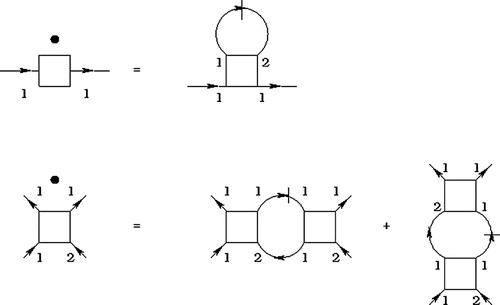
The exact FRG flow equation (Figure 3) for the irreducible vertices can be obtained from the general FRG flow equations given in Metzner et al. (2012), Schuetz et al. (2005), Bartosch et al. (2009), Jakobs et al. (2007,2010), Gezzi et al. (2007).(24) $$\begin{array}{c}\hfill {\mathit{\partial }}_{\mathrm{\Lambda }}{\mathit{\gamma }}_{\mathrm{\Lambda },{\mathit{\alpha }}_1{\mathit{\alpha }}_2}^{(1)}={\int }_{{\mathit{\beta }}_1}{\int }_{{\mathit{\beta }}_2}{\dot{[G_{\mathrm{\Lambda }}]}}_{{\mathit{\beta }}_1{\mathit{\beta }}_2}{\mathit{\gamma }}_{\mathrm{\Lambda },{\mathit{\beta }}_1{\mathit{\beta }}_2{\mathit{\alpha }}_1{\mathit{\alpha }}_2}^{(2)},\end{array}$$(24)

while the four-point vertex or effective interaction(25) $$\begin{array}{c}\hfill {\mathit{\partial }}_{\mathrm{\Lambda }}{\mathit{\gamma }}_{\mathrm{\Lambda },{\mathit{\alpha }}_1{\mathit{\alpha }}_2{\mathit{\alpha }}_3{\mathit{\alpha }}_4}^{(2)}={\int }_{{\mathit{\beta }}_1}{\int }_{{\mathit{\beta }}_2}{\int }_{{\mathit{\beta }}_3}{\int }_{{\mathit{\beta }}_4}{\dot{[G_{\mathrm{\Lambda }}]}}_{{\mathit{\beta }}_1{\mathit{\beta }}_2}{[G_{\mathrm{\Lambda }}]}_{{\mathit{\beta }}_3{\mathit{\beta }}_4}{\mathit{\gamma }}_{\mathrm{\Lambda },{\mathit{\beta }}_2{\mathit{\beta }}_3{\mathit{\alpha }}_3{\mathit{\alpha }}_4}^{(2)}{\mathit{\gamma }}_{\mathrm{\Lambda },{\mathit{\beta }}_4{\mathit{\beta }}_1{\mathit{\alpha }}_1{\mathit{\alpha }}_2}^{(2)},\end{array}$$(25)

where the single-scale propagator is given by(26) $$\begin{array}{c}\hfill {\dot{G}}_{\mathrm{\Lambda }}=-G_{\mathrm{\Lambda }}({\mathit{\partial }}_{\mathrm{\Lambda }}{[g_{\mathrm{\Lambda }}]}^{-1})G_{\mathrm{\Lambda }},\end{array}$$(26)

the elements of this matrix are(27) $$\begin{array}{cc}\hfill {\dot{G}}_{\mathit{\sigma }\mathrm{\Lambda }}^r(\mathit{\omega })& =-\frac{i}{2}{[G_{\mathit{\sigma }\mathrm{\Lambda }}^r(\mathit{\omega })]}^2,\hfill \\ \hfill {\dot{G}}_{\mathit{\sigma }\mathrm{\Lambda }}^a(\mathit{\omega })& ={\dot{G}}_{\mathit{\sigma }\mathrm{\Lambda }}^r{(\mathit{\omega })}^{\ast }\hfill \\ \hfill {\dot{G}}_{\mathit{\sigma }\mathrm{\Lambda }}^k(\mathit{\omega })& =-i\left[1-2f_{eff}(\mathit{\omega })\right]G_{\mathit{\sigma }\mathrm{\Lambda }}^r(\mathit{\omega })G_{\mathit{\sigma }\mathrm{\Lambda }}^a(\mathit{\omega }),\hfill \end{array}$$(27)

Figure 3. Flow equations. Notes: The dots over the vertices indicate a derivative with respect to the flow parameter $\mathrm{\Lambda }$, the lines connecting different vertices are different Green’s functions in the Keldysh formalism. Each of the Green’s functions have a contribution from the self-energy in Figure 2 which is denoted by a contribution $\mathrm{\Gamma }$ to the Green’s function.

with the effective distribution function(28) $$\begin{array}{c}\hfill f_{eff}(\mathit{\omega })=\sum _j\frac{{\mathrm{\Gamma }}_j}{\mathrm{\Gamma }}{f}_j(\mathit{\omega }),\end{array}$$(28)

and the total hybridization(29) $$\begin{array}{c}\hfill \mathrm{\Gamma }={\mathrm{\Gamma }}_1+{\mathrm{\Gamma }}_3.\end{array}$$(29)

The equation for the self-energy Equation (29) is after integration(30) $$\begin{array}{c}\hfill {\mathit{\partial }}_{\mathrm{\Lambda }}{\mathrm{\Sigma }}_{d\mathit{\sigma }}^r=\frac{\overline{U}}{2\mathit{\pi }}\sum _i\frac{{\mathrm{\Gamma }}_i}{\mathrm{\Gamma }}\frac{{\mathrm{\Sigma }}_{\mathit{\sigma }}-{\mathit{\mu }}_i}{{\left({\mathrm{\Sigma }}_{\mathit{\sigma }}-{\mathit{\mu }}_i\right)}^2+{\left(\mathrm{\Lambda }+\mathrm{\Gamma }\right)}^2},\end{array}$$(30)

and for the effective interaction is(31) $$\begin{array}{c}\hfill {\mathit{\partial }}_{\mathrm{\Lambda }}\overline{U}=\frac{{\overline{U}}^2}{\mathit{\pi }}\sum _i\frac{{\mathrm{\Gamma }}_i}{\mathrm{\Gamma }}\frac{{\left({\mathrm{\Sigma }}_{\mathit{\sigma }}-{\mathit{\mu }}_i\right)}^2}{{\left({\left({\mathrm{\Sigma }}_{\mathit{\sigma }}-{\mathit{\mu }}_i\right)}^2+{\left(\mathrm{\Lambda }+\mathrm{\Gamma }\right)}^2\right)}^2}.\end{array}$$(31)

Once the self-energy and the vertex function are determined at the end of the FRG flow, we obtain the differential conductance. We assume that STM tip and the absorbate–substrate complex are each in local equilibrium and use the formula for the calculation of the differential conductance given in Plihal and Gadzuk (2001).(32) $$\begin{array}{c}\hfill \frac{dI}{dV}=2\mathit{\pi }e{\mathit{\rho }}_1\sum _{\mathit{\sigma }}\frac{\mid N{\mid }^2}{\mathrm{Im}{\mathrm{\Sigma }}_{\mathit{\sigma }}^r(eV)}\frac{q^2-1+2q{\mathit{\xi }}_{\mathit{\sigma }}}{{\mathit{\xi }}_{\mathit{\sigma }}^2+1},\end{array}$$(32)

where e is the electron charge, q the Fano parameter, eV the applied bias and(33) $$\begin{array}{c}\hfill {\mathit{\xi }}_{\mathit{\sigma }}=-[\mathit{\omega }-E_d-\mathrm{Re}{\mathrm{\Sigma }}_{\mathit{\sigma }}^r(eV)]/\mathrm{Im}{\mathrm{\Sigma }}_{\mathit{\sigma }}^r(eV).\end{array}$$(33)

Here $\mathit{\xi }$ is the dimensionless energy parameter, and the term$$\begin{array}{c}\hfill \frac{\mid N{\mid }^2}{\mathrm{Im}{\mathrm{\Sigma }}_{\mathit{\sigma }}^r(eV)},\end{array}$$

is the contribution from the tip and surface states that couple to the impurity. The formula for the differential conductance is valid for arbitrary interaction $U\ne 0$ in the Hamiltonian $H_2$ and hold in the Kondo and mixed-valent regimes of the model. The properties of the impurity enter through the impurity Green function $G_{\mathit{\sigma }}$. The problem is thus reduced to finding the one-electron Green’s function $G_{\mathit{\sigma }}$.

4. Parameters and numerical results

In our Calculation, we take ${\mathrm{\Gamma }}_3$ as the energy scale, the impurity on-site interaction $U=10{\mathrm{\Gamma }}_3$, tip chemical potential ${\mathit{\mu }}_1=-eV/2$, host chemical potential ${\mathit{\mu }}_3=eV/2$ and decaying factor of $t_{12}$, $r_0=1/k_F$. The factor $t_{23}$ is taken as ${\mathrm{\Gamma }}_3/\sqrt{10}$ and the ratio $t_{12}/t_{13}=1.5$. The parameter $r_0$ controls how fast the coupling $t_{12}$ decays in space when the tip moves away from the adatom. We take equal to $k_F^{-1}$. 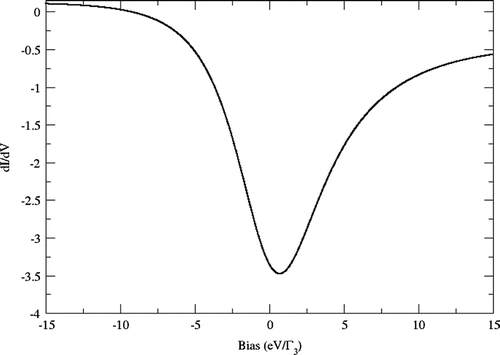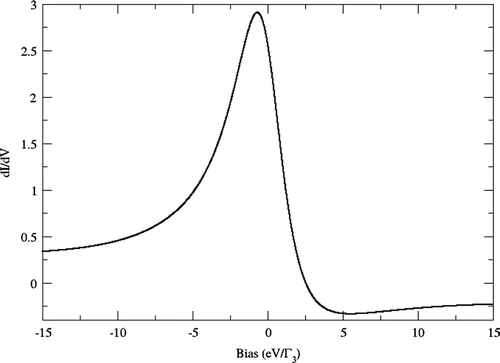Hereafter $k_F^{-1}$ is used as a length scale. With these parameters, the equations for the self-energy and effective interaction (35 and 36) are solved numerically. Figures (4) and (5) show the differential conductance at different lateral distances. We notice that for short distances, the line shape of the differential conductance is an antiresonance. Nevertheless as the distance of the STM distance is increased, the line shape becomes more symmetric and a positive Lorentzian is developed. This can be explained in terms of the amplitude of the interference from the different channels produce the asymmetric form in the differential conductance on and near the impurity becoming a Lorentzian when the tip is away from the impurity. The differential curves reproduce qualitatively the form of the differential conductance when changing its shape from a antiresonance to a Lorentzian shape in different STM experiments but fail to reproduce the strong coupling limit since the static approximation is not sufficient. For a more realistic calculation we have to consider the electronic structure of the surface rather than the very crude wide band limit. In a future work, we would like to extend our calculation to a non-static approximation.

Figure 4. The differential conductance for $r=0$ in units of $k_F^{-1}$. A negative differential conductance develops over the whole range.

Figure 5. The differential conductance for $r=2$ in units of $k_F^{-1}$. A positive Lorentzian is developed when the STM tip is away from the impurity.

5. Discussion and conclusions

We have studied a microscopic theory of a single impurity on a surface starting from the single impurity Anderson model-type Hamiltonian which contains the tip of an STM modeled by a continuum band of electrons coupled to the impurity and to the host surface. We have derived perturbatively expressions for the correction to the self-energy due to the presence of the tip. This correction has been added to the non-interacting Green’s function which in turn has been used in the functional renormalization group in order to calculate the self-energy of the quantum impurity. The calculation of the self-energy has been performed numerically in the case where the on-site energy U is much larger than the hybridization energy ${\mathrm{\Gamma }}_3$.

We have used the functional renormalization group FRG in its Keldysh version that allows to calculate numerically the retarded self-energy as a function of the lateral distance.

In this work, we have made extreme simplifications regarding to the electrons in the tip and the host surface which we consider as a gas of free electrons. A material-specific electronic structure calculation combined with the strongly correlated method FRG is needed. For example in the work Ujsaghy, Kroha, Szunyogh, and Zawadowski (2001), the authors perform calculations using the semi-relativistic, screened Korringa–Kohn–Rostoker method in combination with Non-Crossing Approximation obtained an oscillating line shape with the known Fermi wave numbers of the host-surface. Since in our model the host-surface is structureless we do not obtain such an oscillating line shape. Thus, we expect a quantitative distance dependence of the line shape sensitive to details of the conduction band structure. Instead we obtain a qualitative change when we go from long distances to small distances where the differential conductance changes from an antiresonance to a Lorentzian as the STM moves away from the impurity. We notice that as the distance of the STM tip to the impurity is increased, the lineshape becomes more symmetric and a positive Lorentzian is developed this indicates that the interference between the tip and the impurity is fading away. This means that in Equation (37) the Fano parameter q is becoming large and positive giving rise to a positive Lorentzian. This feature is a characteristic of any theory that starts with free electron wavefunctions.

The differential conductance at $r=0$ in Figure (4) is negative in the whole range since we have taken a structureless surface leading to a Fano parameter which is really small. Physically this means that the contribution from the electrons scattering from the tip to the surface and then from the surface to the impurity is big compared to the contribution of the self-energy, at least in this model.

Our results reproduce qualitatively the features observed in experiments of differential conductance when the differential conductance changes from an antiresonance to a Lorentzian shape of a quantum impurity measured with an STM (Schneider et al., 2005).

Acknowledgements

The authors acknowledge the computing time given on the National Supercomputer Center (CNS-IPICYT, Mexico).

Additional information

Funding

Funding. This work was financially supported by CONACYT [grant number 106437], [grant number 216315].

Notes on contributors

José Juan Ramos Cárdenas

Dr. José Juan Ramos Cárdenas is a theoretical physicist interested in the problems of Condensed Matter Physics specifically in quantummany-body theory. A main emphasis of his theoretical research is on the theory of quantum systems with many degrees of freedom, particularly in the condensed matter context, concerning their static properties, their efficient numerical simulation, as well as their quantum dynamics in nonequilibrium. Characteristic of his work is the guidance by rigor of theoretical techniques but at the same time to be pragmatically and physically motivated by experiments. The work reported is a part of a wider project related to transport in nanostructures.