Classical analogues of a quantum system in spatial and temporal domains: A probability amplitude approach

Abstract

We have simulated the similar features of the well-known classical phenomena in quantum domain under the formalism of probability amplitude method. The identical pattern of interference fringes of a Fabry–Perot interferometer (especially on reflection mode) is obtained through the power-broadened spectral line shape of the population distribution in the excited state with careful delineation of a coherently driven two-level atomic model. In a unit wavelength domain, such pattern can be substantially modified by controlling typical spatial field arrangement in one and two dimensions, which is found complementary to the findings of recent research on atom localization in sub-wavelength domain. The spatial dependence of temporal dynamics has also been studied at a particular condition, which is equivalent to that could be obtained under Raman–Nath diffraction controlled by spatial phase.

Keywords:

• a driven two-level atom
• power-broadened spectrum
• spatial population distribution
• Fabry–Perot fringe like pattern
• spatio-temporal response
• atomic Raman–Nath diffraction

Public Interest Statement

The urge for mapping the various features of the microscopic quantum world to the macroscopic classical arena has resulted in the development of a fascinating research field of quantum–classical analogy exhibiting the similarities and correlation between different macroscopic and microscopic physical phenomena rooted on different paradigms. In the present study, we simulate the similar characteristics of the interference pattern on reflection mode of a Fabry–Perot interferometer in a driven two-level atom and obtain modified patterns by the use of superposition of two or more coherent fields. Spatio-temporal dynamics of the present model are also analyzed in connection with the similar behaviors of a damped harmonic oscillator or classical galvanometer. Equivalence of atomic Raman–Nath diffraction in momentum representation is also demonstrated in case of a driven two-level atom. The results could be useful with applications in high-precision atomic lithography via fluorescence imaging technique and cold-atom optics.

1. Introduction

In the last few decades, there has been tremendous interest to study the coherence effects either in temporal or spatial domain through the absorption spectrum of an atomic or molecular system interacting with one or two laser fields. In general, the signature of coherence in the spectral line shape gets suppressed by the effects of two common broadening phenomena (Demtröder, 1981): (1) broadening due to finite lifetime of the energy levels associated with the atomic transition, which is directly affected by the inter-atomic collision effect when the atomic density is large enough. In presence of such broadening effects, the generated spectral line shape is known as pressure broadened Lorentzian profile, which is specific for static configuration of an atom or molecule. (2) when an atom or molecule is in motion, for different velocity sub-groups, convolution of several Lorentzians as a whole gives rise to Doppler broadened line shape. With the advent of the techniques of “Laser Cooling and Magneto-Optical Trapping of Neutral Atoms” (Letokhov, 2007; Metcalf & van der Straten, 1994) as developed in the last few years, the Doppler shifted-resonance resulting from atomic motion can be almost neglected due to the atom being trapped and cooled at nano-Kelvin temperature. And, at very low gas pressure, effect of pressure broadening on the Lorentzian line shape becomes insignificant. Two other types of broadening effects also affect the line shape, which are known as transit-time broadening and power broadening (Demtröder, 1981). Later is due to the strength of light-matter interaction, which is tacitly embedded in exploring the interesting findings of the present work. In frequency scale, the interaction energy is quantified by the term Rabi frequency which, for an electric dipole allowed transition, is denoted as $\overrightarrow{\mathit{\mu }}.\overrightarrow{E}/ħ$ where $\overrightarrow{\mathit{\mu }}$ is the atomic transition dipole moment and $\overrightarrow{E}$ is the electric field vector of the light field. This phenomenon of broadening evolves due to square of the Rabi frequency i.e. square of the amplitude of the electric field vector, and is named as power broadening. In this article, as the power-broadened Lorentzian spectrum plays the key role to obtain the coherence effects under static atom consideration, laser-cooled atomic environment is much needed.

As the title indicates, this work is aimed at establishing similar characteristics of the physical properties of the classical phenomena in quantum domain. Though, a field-coupled two-level atomic model is available in many literature, the present model is very similar to that depicted in Rand (2010), but not exactly equal in respect of irreversible decay mechanism for both the atomic states. Being inspired by the perturbative response within short time domain as described by the model given in Rand (2010) with decaying ground state, we have considered the present two-level model with quasi-metastable ground state in the first phase of study. Under the methodology of probability amplitude approach in an open two-level atom, such consideration has been justified by examining the possibility of getting “level-saturation” effect, which leads to the generation of an ideal power broadened spectrum in the long time limit. This non-perturbative phenomenon represents the efficacy of the present model, which is not pointed out in Rand (2010).

When the atom is driven resonantly by a spatially modulated coherent field, the power-broadened spectrum has been exploited to observe similar behavior of reflected intensity distribution pattern of a Fabry–Perot (FP) interferometer (Hecht, 2004). This is in contrast to the formation of transmission function of a FP interferometer in a doubly driven three-level atom in respect of localization (Agarwal & Kapale, 2006) based on the concept of coherent population trapping (Arimondo, 1996). The spatially modulated population distribution in our two-level model, which can be envisaged as the intensity distribution of a FP interferometer on reflection mode, is found to be complementary to the simulated FP transmission function implementing atom localization in subwavelength domain as shown in Agarwal and Kapale (2006). At a limiting condition corresponding to perfect metastability of the ground level, the present model is able to produce similar localization characteristics (Agarwal & Kapale, 2006) which are reciprocal to the behavior of simulated FP-interference pattern in reflection mode. Attempt has been made to display how the FP distribution-like pattern as obtained in the present model can be modified by invoking superposed spatial field arrangements (Dutta, Panchadhyayee, & Mahapatra, 2012) in both the one and two dimensions. It is to note that appearance of dips (inverted peaks in the reflected FP- intensity distribution) within one space-period of unit wavelength represents sub-wavelength resolution in the space-localized pattern obtained. The number of dips can be manipulated by varying the spatial field arrangement based on the scheme as mentioned in Dutta et al. (2012). For a typical spatial field arrangement, which is different from that given in Dutta et al. (2012), it has been shown that asymmetry can be introduced in the so-called symmetric FP fringe-like pattern. The way of observing spatial modulation of population distribution from various perspectives is very much interesting in the present study as carried out on the basis of power broadened spectrum in a driven two-level atom. Albeit the phenomenon of level saturation in two-level atom limits to achieve population inversion, the technique of generation of spatially modulated coherence as presented in this article makes it possible even when the system is a closed one. We note that the reciprocity of spatially modulated population distribution through the FP fringe-like pattern in reflection mode is useful for its potential application in demonstrating atom localization by probing fluorescence either from the excited level or by monitoring fluorescence followed by coherent excitation from the ground state as proposed in Agarwal and Kapale (2006). As a whole, the technique of localization finds its importance in high-precision atomic lithography (Johnson et al., 1998).

We have studied the transient response of the present model when the ground state is purely metastable. Such model is very similar to that undertaken in finding coherent features in a driven two-level atom (Wu & Yang, 2007a, 2007b). The transient evolution of the system exhibits characteristics akin to dynamical behaviors of a classical damped harmonic oscillator or a classical galvanometer realizable in quantum domain. The spatial dependence of the transient behavior for different spatial field arrangements has also been investigated. In contrast to the diffraction of cold atoms in Bragg regime (Wu, 2006), this observation is shown to be equivalent to the recent study of atomic Raman–Nath diffraction (Li-Ping, Yan, Jun, Tao, & Bin, 2007). In the present scheme, such interesting phenomenon can be similarly obtained, and modified by means of variation of spatial phase as a controlling parameter at a particular condition of Rabi frequency and detuning of resonance. This study might be helpful for the implementation of opto-atomic phase-grating in atom-optics at the condition of resonant atom-field interaction controlled by spatial phase. In broad spectrum, the present work in a driven two-level atom reflects basically the aspect of recent trend of research, which is equivalent to those (Bai, Hang, & Huang, 2013; Bayal, Panchadhyayee, Dutta, & Mahapatra, 2012; Dragoman & Dragoman, 2004; Garrido Alzar, Martinez, & Nussenzveig, 2002; Gea-Banacloche, 1999; Harden, Joshi, & Serna, 2011; Longhi, 2008; Rodríguez-Lara, Cárdenas, Soto-Eguibar, & Moya-Cessa, 2013; Satpathy, Roy, & Mohapatra, 2012; Spreeuw, van Druten, Beijersbergen, Eliel, & Woerdman, 1990) performed in respect of quantum-classical analogy.

2. Theory and results

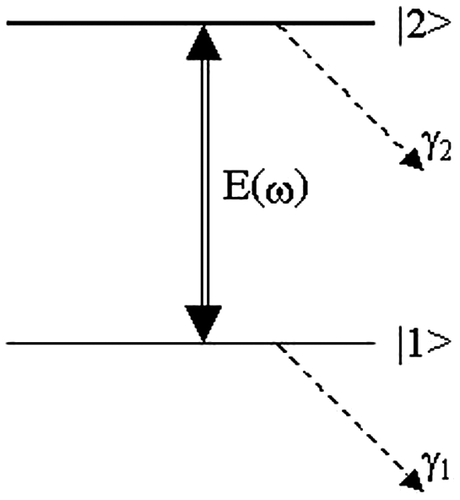
In the beginning of theoretical formulation of the present work, we start with choosing an open two-level atom interacting with a coherent field of frequency ω as shown in Figure 1. The natural decay rates of the ground and excited levels are respectively designated by γ₁ and γ₂. The quantized energy of the atomic level is denoted by ℏω_j(j = 1, 2) i.e. the atomic transition frequency ω₂₁ = ω₂ − ω₁ and the transition is considered to be electric dipole allowed.

Figure 1. Field-coupled energy-level diagram of a two-level atom with associated decay rates.

Under the semi-classical formalism, the field interacting with the atom is defined classically as $\overrightarrow{E}(t)={\overrightarrow{E}}_{0}cos(\mathit{\omega }t)$. The Hamiltonian of the atom-field system is given in following(1) $$H=\sum _{j,k=1}^2<j|H|k>|j><k|\equiv H_0+H^{\prime }$$(1)

where the field-free atomic Hamiltonian(2) $$H_0=\sum _{j=1}^2ħ{\mathit{\omega }}_j$$(2)

and the interaction Hamiltonian(3) $$H^{\prime }=ħ\left(<2|\frac{\overrightarrow{\mathit{\mu }}.\overrightarrow{E}(t)}{ħ}|1>|2><1|+h.c.\right)$$(3)

In the interaction or Dirac picture$$<\mathrm{\Psi }|H^{\prime }|\mathrm{\Psi }>=\left\{<\mathrm{\Psi }|e^{-\frac{i{H}_{0}t}{ħ}}\right\}\left\{e^{\frac{i{H}_{0}t}{ħ}}{H}^{\prime }{e}^{-\frac{i{H}_{0}t}{ħ}}\right\}\left\{e^{\frac{i{H}_{0}t}{ħ}}|\mathrm{\Psi }>\right\}\equiv {(<\mathrm{\Psi }|)}_{\text{int}.}{(H^{\prime })}_{\text{int}.}{(|\mathrm{\Psi }>)}_{\text{int}.}$$

by excluding the counter-rotating term under rotating wave approximation (RWA) (Demtröder, 1981), the interaction Hamiltonian can be written as(4) $${(H^{\prime })}_{\text{int}.}=ħ({\text{Re}}^{i\mathrm{\Delta }t}|2><1|+c.c.)$$(4)

where the Rabi frequency $R=\frac{|<2|\overrightarrow{\mathit{\mu }}|1>\Vert {\overrightarrow{E}}_0|}{2ħ}$ and the detuning parameter Δ = ω₂₁ − ω. Without loss of generality the Rabi frequency is taken to be real. For the wave-vector |Ψ(t) > = C₁(t)| 1 >  + C₂(t)|2 > defined in the interaction picture, one can obtain the dynamical evolution of the probability amplitudes C_j(j = 1, 2) by employing the Schrodinger’s equation of motion(5) $$iħ\frac{\mathit{\partial }|\mathrm{\Psi }{>}_{\text{int}.}}{\mathit{\partial }t}={(H^{\prime })}_{\text{int}.}|\mathrm{\Psi }{>}_{\text{int}.}$$(5)

This is to note here that this equation represents the time evolution dynamics of the system in reversible way. The equations of motion for the two-component wave vector are given by the following coupled equations(6) $${\dot{C}}_1=-i{\text{Re}}^{-i\mathrm{\Delta }t}{C}_2,$$(6) (7) $${\dot{C}}_2=-i{\text{Re}}^{i\mathrm{\Delta }t}{C}_1.$$(7)

On using the unitary transformation, C₂ = B₂e^iΔt, Equations (6) and (7) can be expressed as(8) $${\dot{C}}_1=-iR{B}_2,$$(8) (9) $${\dot{B}}_2=-i\mathrm{\Delta }{B}_2-iR{C}_1.$$(9)

So far as irreversible spontaneous decay mechanism is concerned, the component equations can be rewritten by incorporating phenomenologically the terms involving natural decay of the energy levels. In this respect, firstly we consider the decay from the ground level, which leads to represent Equation (8) as(10) $${\dot{C}}_1=-{\mathit{\gamma }}_1{C}_1-i{\text{Re}}^{-i\mathrm{\Delta }t}{C}_2.$$(10)

Under the transformation $C_1={\tilde{C}}_1{e}^{-{\mathit{\gamma }}_{1}t}$, Equation (10) can be expressed as(11) $${\dot{\tilde{C}}}_1=-iR{B}_2{e}^{{\mathit{\gamma }}_{1}t}.$$(11)

By taking the time derivative on both sides of Equation (9) and then substituting C₁ and ${\dot{\tilde{C}}}_1$, one can obtain the following second-order equation for the probability amplitude B₂ as(12) $${\ddot{B}}_2+({\mathit{\gamma }}_1+i\mathrm{\Delta }){\dot{B}}_2+(R^2+i\mathrm{\Delta }{\mathit{\gamma }}_1)B_2=0.$$(12)

On restricting to the assumptions R > γ₁, $\sqrt{{\mathrm{\Delta }}^2+4R^2}>\mathrm{\Delta }$ and $\sqrt{{\mathrm{\Delta }}^2+4R^2}>{\mathit{\gamma }}_1$, and based on the initial boundary condition B₂(t = 0) = 0, the solution of Equation (12) can be obtained as(13) $$B_2(t)=i(2A)sin\left(\frac{\sqrt{{\mathrm{\Delta }}^2+4R^2}}{2}t\right)e^{-\frac{1}{2}({\mathit{\gamma }}_1+i\mathrm{\Delta })t}$$(13)

where the value of constant A can be found by using Equation (9) set at t = 0, as $A=-R/\sqrt{{\mathrm{\Delta }}^2+4R^2}$. Thus, the transient evolution of population in the excited state is determined by the term $B_2^{*}(t)B_2(t)$. This term denotes the diagonal term ρ₂₂ in the pure state density matrix formalism. As the probability distribution for the exponential decay of population from the excited state is ${\mathit{\gamma }}_2{e}^{-{\mathit{\gamma }}_{2}t}$, the time averaged population in the excited state is given by(14) $$<{\mathit{\rho }}_{22}>={\mathit{\gamma }}_2{\int }_0^{\infty }{e}^{-{\mathit{\gamma }}_{2}t}{|B_2(t)|}^{2}dt=\frac{2{\mathit{\gamma }}_2}{{\mathit{\gamma }}_1+{\mathit{\gamma }}_2}\left(\frac{R^2}{{\mathrm{\Delta }}^2+{({\mathit{\gamma }}_1+{\mathit{\gamma }}_2)}^2+4R^2}\right)$$(14)

where it is worth noting that, for γ₁ = γ₂ = γ, <ρ₂₂> ≈ 1/4 at Δ = 0 when R ≫ γ. While at the same condition of resonance, for γ₁ ≪ γ₂, <ρ₂₂> ≈ 1/2when R >> γ₂. Therefore, it is evident from the expression (14) that the phenomenon of level-saturation can be explained for a two-level atom whose ground state is almost metastable.

2.1. Power broadened line shape

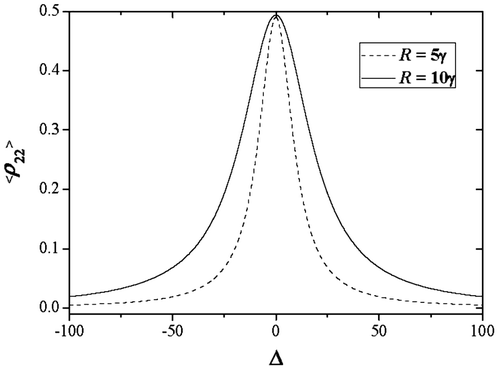
This is important to mention here that laser induced fluorescence from the excited state is proportional to the population pumped to the excited state by the laser field (Demtröder, 1981). Thus, the spectral distribution of population in the excited state as predicted by the expression (14) gives rise to the laser-induced fluorescence spectrum also, which carries the signature of power broadening as the full-width at half-maximum (FWHM) $2\sqrt{{({\mathit{\gamma }}_1+{\mathit{\gamma }}_2)}^2+4R^2}$ is almost of the order of four times of the Rabi frequency in the high field limit. To visualize the effect of power broadening on the spectral line shape, numerical computation of <ρ₂₂> is performed for the chosen parameters: γ₂ = γ, γ₁ = 0.01γ, R = rγ and Δ = δγ i.e. all the rate parameters are scaled by the decay rate γ. Figure 2 shows the power-broadened line shapes by the dashed $(R=5\mathit{\gamma })$ and solid $(R=10\mathit{\gamma })$ curves whose line widths clearly show the dominance of the Rabi frequency over the natural line width. It has been checked that, for γ₁ = 0.001γ, level-saturation will exactly occur at the line center for large values of Rabi frequency.

Figure 2. Plot of excited state population versus detuning parameter for different values of Rabi frequency with unequal values of decay rates (see text). All the rate parameters are scaled by the decay rate γ.

2.2 Formation of Fabry–Perot fringe-like pattern and modification

The purpose of this subsection can be fulfilled if the field interacting with the atom be considered to be a counter-propagating one. For such “stationary-wave”-configuration, the field amplitude is considered to be sinusoidally modulated along x-direction i.e. the spatially modulated Rabi frequency can be redefined as Ω(x) = R sin (kx); k stands for the propagation vector. If the field be operating at exact resonance Δ = 0, the expression of population in the excited state based on the assumption γ₁ ≪ γ₂ transforms into the following form(15a) $$<{\mathit{\rho }}_{22}(x)>=\frac{2{\mathrm{\Omega }}^2(x)}{{\mathit{\gamma }}^2+4{\mathrm{\Omega }}^2(x)}$$(15a)

where γ being equal to γ₂. If we consider the ground state as perfectly metastable in the two-level atom, the decay rate associated with the ground state becomes zero $({\mathit{\gamma }}_2=0)$. In such condition, we can obtain the value of <ρ₁₁(x)> from Equation (15) and the normalization condition $<{\mathit{\rho }}_{22}(x)>+<{\mathit{\rho }}_{11}(x)>=1$ as(15b) $$<{\mathit{\rho }}_{11}(x)>=1-\frac{2{\mathrm{\Omega }}^2(x)}{{\mathit{\gamma }}^2+4{\mathrm{\Omega }}^2(x)}=\frac{{\mathit{\gamma }}^2+2{\mathrm{\Omega }}^2(x)}{{\mathit{\gamma }}^2+4{\mathrm{\Omega }}^2(x)}.$$(15b)

If we express <ρ₂₂(x)> as$$<{\mathit{\rho }}_{22}(x)>=\frac{2\mathrm{\Omega }{(x)}^2}{{({\mathit{\gamma }}_1+{\mathit{\gamma }}_2)}^2+4\mathrm{\Omega }{(x)}^2}=\frac{1}{2}F(x)$$

where(16) $$F(x)=\frac{\tilde{\mathrm{\Omega }}{(sin(kx))}^2}{1+\tilde{\mathrm{\Omega }}{(sin(kx))}^2}$$(16)

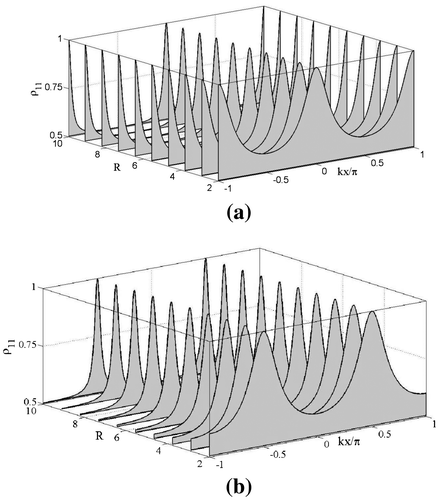
with $\tilde{\mathrm{\Omega }}=4R^2/{\mathit{\gamma }}^2$ which governs the full width at half maximum $(4/\sqrt{\tilde{\mathrm{\Omega }}})$ of the FP fringe-like distribution. Thus, it can be regarded to be equivalent to the entity “finesse”-factor determining the sharpness of fringes in case of FP interference pattern (Hecht, 2004). Here, the function F(x), which represents the similar interference pattern in the reflection mode, is later mentioned as the Fabry–Perot function. Populations of the excited and ground states <ρ₂₂(x)> and <ρ₁₁(x)> are plotted in Figures 3 and 4, respectively, with the variation of normalized position kx/π. From the expression (15) of <ρ₂₂(x)> and <ρ₁₁(x)>, the profiles exhibiting the localization pattern in a unit wavelength domain of the standing-wave field should be complementary in nature. As plotted in Figure 3(a) the population <ρ₂₂(x)> for R = 20γ (solid), 5γ (dashed) shows the behavior of reflected intensity distribution for a FP interferometer. Interestingly, in the present model, the finesse can be controlled by increasing the Rabi frequency, leading to sharper variation in <ρ₂₂(x)> as well as the increase in the resolution of delocalization. For clear understanding of the reciprocal nature of atom-localization reflected by Figure 3(a), we present in Figure 3(b) the feature of subwavelength atom localization for the population transferring to one of the ground states as a result of resonant two-photon process in a Lambda-type atom-field coupling configuration (Agarwal & Kapale, 2006) shown in the inset, which exhibits the spatial distribution similar to the fringe pattern of FP interferometer in transmission mode. It can be noted that the profile of <ρ₁₁(x)> in Figure 4 exhibits the similar interference pattern in the FP-transmission mode. We plot the population <ρ₁₁(x)> versus kx in Figure 4(a) for various values of the R where the population peaks are exhibited at the nodes of the standing-wave field. It is prominent that the peaks are not well defied for small values of the Rabi frequencies resulting no spatial dependence for R = 0 as expected. For larger values of R, the peaks become sharp, which directly lead to the aspect of sub-wavelength localization when compared to the reciprocal distribution pattern obtained in the FP-reflection mode. We find excellent resemblance with the results obtained in case of a Lambda-type configuration (Agarwal & Kapale, 2006). If there involves any initial phase (say, $\mathit{\pi }/2$ in our standing-wave field arrangement, the localization structure changes with the orientation of peaks at the antinodes of the standing-wave field as shown in Figure 4(b).

Figure 3. Plot of state populations versus normalized spatial-modulation parameter kx/π for different values of Rabi frequency (see text).

Notes: Inset of Figure 3(b) shows the level scheme of a Lambda-type configuration akin to the model (Agarwal et al., 2006) in which a strong standing-wave field of Rabi frequency Ω₂ is applied on the transition, | 2 〉 ↔| 1 〉 whereas another weak field of Rabi frequency Ω₁ on the | 2 〉 ↔| 3 〉 transition.

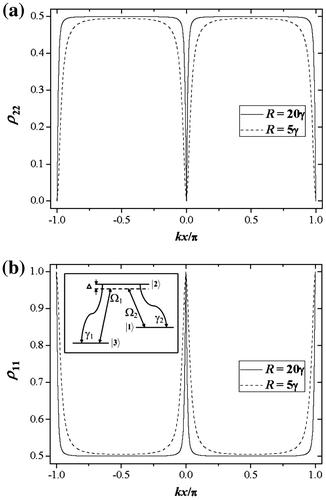
Figure 4. Plot of ground state population versus normalized spatial-modulation parameter kx/π for different values of Rabi frequency.

2.2.1. Effect of field superposition on spatial population distribution

We present Figure 5 to show modification in such FP pattern (reflection mode) easily attainable for another spatial field arrangement which includes two or more fields along the x-direction. In case of two fields, we consider another field E₂ along the x-direction, in which the counter-propagating x-components of two degenerate wave vectors constitute the standing wave which modulates the standing wave generated directly by the counter-propagating field E₁. Thus, we can represent the spatially modulated Rabi frequency as(17) $$\mathrm{\Omega }(x)=R_{1}sin(kx)+R_{2}sin(\mathit{\eta }kx+\mathit{\phi })$$(17)

Figure 5. Plot of simulated Fabry–Perot function [F(x)] versus spatial-modulation parameter kx/π: (a) φ = 0; (b) $\mathit{\phi }=\mathit{\pi }/2$; (c) $\mathit{\phi }=2\mathit{\pi }/3$; (d) φ = π; (e) $\mathit{\phi }=4\mathit{\pi }/3$ with $R_1=R_2=20\mathit{\gamma },\mathit{\eta }=0.6$; and (f) $R_1=\mathit{\gamma },R_2=2\mathit{\gamma },R_3=3\mathit{\gamma }$, ${\mathit{\eta }}_1=0.9,{\mathit{\eta }}_2=0.6$, ${\mathit{\phi }}_1=-\mathit{\pi }/2$ and ${\mathit{\phi }}_2=\mathit{\pi }/2$.

where R₁ and R₂ are the Rabi frequencies of two fields E₁ and E₂ respectively with the angular separation $\mathit{\theta }(\mathit{\eta }=cos\mathit{\theta })$ of the standing waves for two fields E₁ and E₂. φ is the spatially induced phase (Dutta et al., 2012). For three fields along x-direction, we can design another standing-wave field arrangement for which the spatial modulation of Rabi frequency can be written as(18) $$\mathrm{\Omega }(x)=R_{1}sin(kx)+R_{2}sin({\mathit{\eta }}_{1}kx+{\mathit{\phi }}_1)+R_{3}sin({\mathit{\eta }}_{2}kx+{\mathit{\phi }}_2)$$(18)

Here, R₁, R₂, and R₃ are the corresponding Rabi frequencies of three fields E₁, E₂, and E₃, respectively. Along with the respective spatially induced phases φ₁ and φ₂, η₁ and η₂ are the factors related to angular separations of the standing waves for two fields E₂ and E₃ with respect to E₁. Figure 5(a–e) shows the variation of F(x) with respect to kx using Equations (15) and (17) for the Rabi frequencies R₁ = R₂ = 20γ. In all the graphs of space-localized pattern dips occur with sub-wavelength resolution. We are able to manipulate the number and position of the dips by varying suitable parameters as shown in Figure 5(a–e). In Figure 5(a), for η = 0.6 and φ = 0, we attain only one minimum (at central node) in one wavelength regime compared to three minima at central and edge nodes as presented in Figure 3(a). The shift of minima from edge nodes becomes prominent when η assumes larger values. For this particular value of η, we depict the modification in F(x) structures in Figure 5(b–e) varying the spatially induced phase $\mathit{\phi }=\mathit{\pi }/2,2\mathit{\pi }/3,\mathit{\pi }$ and 4π/3, respectively. The respective introduction of phases π/2 and 2π/3 induces asymmetry in F(x) distribution and sets the F(x)-structures having two minima in Figure 5(b) and three minima in Figure 5(c) at the positions other than nodes with uneven separation in a unit wavelength domain of the standing-wave field. The separation between three minima becomes same for $\mathit{\phi }=\mathit{\pi }$. The reverse pattern of F(x) as in Figure 5(c) is obtained and exhibited in Figure 5(e) when φ gets doubled. Figure 5(f) presents us another interesting F(x) pattern with no minima found in one wavelength regime. In this case, we adopt spatial modulation of Rabi frequency by three-field arrangement given in Equation (18$$<{\mathit{\rho }}_{22}(x)>=\frac{2\mathrm{\Omega }{(x)}^2}{{({\mathit{\gamma }}_1+{\mathit{\gamma }}_2)}^2+4\mathrm{\Omega }{(x)}^2}=\frac{1}{2}F(x)$$) and set parameters as $R_1=\mathit{\gamma },R_2=2\mathit{\gamma },R_3=3\mathit{\gamma },$ ${\mathit{\eta }}_1=0.9,{\mathit{\eta }}_2=0.6$, ${\mathit{\phi }}_1=-\mathit{\pi }/2$ and ${\mathit{\phi }}_2=\mathit{\pi }/2$.

In the surface plots as well as density plots of Figure 6 we have investigated the modulation in two-dimensional F(x, y) function by assuming spatially modulated Rabi frequency with two dimensions in the form $\mathrm{\Omega }(x,y)=R_{1}sin({\mathit{\eta }}_{x}kx)+R_{2}sin({\mathit{\eta }}_{y}ky+\mathit{\phi })$ where ${\mathit{\eta }}_y=\sqrt{1-{\mathit{\eta }}_x^2}$ with the symbols used have same meanings as given earlier. We consider the field E₂, along the y-direction, which constitutes the standing-wave regime by the counter-propagating y-components of two degenerate wave vectors modulating that generated by the counter-propagating x-components of field E₁. For all figures of Figure 6 we set R₁ = R₂ = 5γ and obtain the partial pillar-like patterns of F(x, y) function in one space period of unit wavelength domain. In Figure 6(a) $({\mathit{\eta }}_x=0.9,\mathit{\phi }=0)$, the F(x, y) distribution shows two partial pillar-like patterns with decrease in sharpness in its variation and sharpness increases with the decrease in η_x as found in Figure 6(b) $({\mathit{\eta }}_x=0.6,\mathit{\phi }=0)$. As is seen in Figure 6(d) $({\mathit{\eta }}_x=0.6,\mathit{\phi }=\mathit{\pi })$ the same structure of Figure 6(b) is obtained with $\mathit{\pi }/2$ rotation in (kx, ky) space. When φ becomes $\mathit{\pi }/2$, the F(x, y) distribution, as shown in Figure 6(c), includes asymmetry which is prominent with one prominent pattern with other two sub-patterns.

Figure 6. Plot of simulated Fabry–Perot function $[F(x,y)]$ in two dimensions (kx, ky): (a) ${\mathit{\eta }}_x=0.9,\mathit{\phi }=0;$ (b) ${\mathit{\eta }}_x=0.6,\mathit{\phi }=0;$ (c) ${\mathit{\eta }}_x=0.6,\mathit{\phi }=\mathit{\pi }/2$; and (d) ${\mathit{\eta }}_x=0.6,\mathit{\phi }=\mathit{\pi }$. Here R₁ = R₂ = 5γ.

2.3. Transient dynamics of the quantum system

To study the transient behavior of the system, we recall the coupled equations of motion of the probability amplitudes with the phenomenological inclusion of decay rate at the excited state considering the ground state to be a perfectly metastable one. So, Equation (9) can be written at the condition of exact atom-field resonance as(19) $${\dot{B}}_2=-\mathit{\gamma }{B}_2-iR{C}_1$$(19)

From Equations (8) and (19), it is straightforward to derive the following equation(20) $${\ddot{B}}_2+\mathit{\gamma }{\dot{B}}_2+R^2{B}_2=0$$(20)

On using the trial solution $B_2(t)={\tilde{B}}_2(t)e^{-\mathit{\gamma }t/2}$, one can simplify Equation (20) as given in following:(21) $${\ddot{\tilde{B}}}_2+(R^2-{\mathit{\gamma }}^2/4){\tilde{B}}_2=0$$(21)

The analytical solution of Equation (21) can be derived as follows:(22) $$B_2(t)=A\left\{e^{\sqrt{{(\mathit{\gamma }t/2)}^2-R^{2}t}}-e^{-\sqrt{{(\mathit{\gamma }/2)}^2-R^{2}t}}\right\}{e}^{-\mathit{\gamma }t/2}$$(22)

where $A=-iR/2\sqrt{{(\mathit{\gamma }/2)}^2-R^2}$.

For the three distinct conditions $R<,\approx ,>\mathit{\gamma }/2$, we can use the expression of Equation (22) and obtain the population in the excited state ρ₂₂ from $B_2^{*}(t)B_2(t)$.

In aiming at better comprehension with a deep physical insight in the above cases of the problem, we attempt to analyze those in a simplified way with respect to the initial boundary condition:

(1)	$R<\mathit{\gamma }/2$, the solution for B2(t) is given by(23) $$B_2(t)=A\left(e^{\sqrt{{\mathit{\gamma }}^2/4-R^{2}t}}-e^{-\sqrt{{\mathit{\gamma }}^2/4-R^{2}t}}\right)e^{-\frac{\mathit{\gamma }}{2}t}.$$(23) For simplicity of the problem, one can approximate $\sqrt{{\mathit{\gamma }}^2/4-R^2}\approx \mathit{\gamma }/2$ for $\mathit{\gamma }/2>>R$. Then, by setting the constant, A = 1, one can have the following expression of transient population in the excited state:(24) $${\mathit{\rho }}_{22}=1-2e^{-\mathit{\gamma }t}+e^{-2\mathit{\gamma }t}.$$(24)
(2)	$R=\mathit{\gamma }/2$, by choosing the integration constant as γ, the population term can be expressed in a symmetric form like(25) $${\mathit{\rho }}_{22}={(\mathit{\gamma }t)}^2{e}^{-\mathit{\gamma }t}.$$(25)
(3)	$R>\mathit{\gamma }/2$, one could represent(26) $${\mathit{\rho }}_{22}={sin}^2\left((\sqrt{R^2-{\mathit{\gamma }}^2/4})t\right)e^{-\mathit{\gamma }t}.$$(26) Here, the population oscillation with frequency $\sqrt{R^2-{\mathit{\gamma }}^2/4}$ will die out rapidly for the exponential decay.

Hence, on the basis of the transient features obtained by the analytical calculations (Equation 22) corresponding to the conditions mentioned in the above cases (1 and 2), we can reach at the analogy between a two-level system and a damped classical oscillator in overdamped and critically damped conditions. It is to note that, for such equivalence, some deviation may occur, but it is not supported for a quantum system with decaying upper level. Usually, deviation from the behavior of exponential decay in a quantum system is referred to as the well-known Zeno effect (Bayal et al., 2012). In this situation, such characteristics derived by the analytical calculation can be envisaged as a paradoxical truth in the realm of quantum physics.

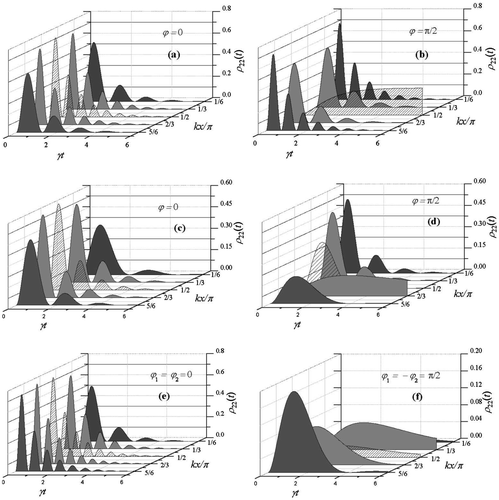
2.3.1. Spatio-temporal dynamics

Based on the condition (3) $(R>\mathit{\gamma }/2$, where ρ₂₂ includes the Rabi frequency in the simplified expression (Equation 26), we present the transient evolution of ρ₂₂ in Figure 7(a–f) on considering spatially modulated Rabi frequency R = R₁ sin (kx + φ) for Figure 7(a and b), R in the form of Equations (17) and (18) for Figure 7(c and d) and (e and f), respectively. We present the oscillations in transient variation of ρ₂₂ with respect to γt in Figure 7(a–e) for phase-independent condition, whereas phase dependent cases in Figure 7(b, d, f). In Figure 7(a), the amplitudes and number of oscillations for R₁ = 5 are found gradually decreasing when kx value is shifted from $kx=\mathit{\pi }/2$. But for $\mathit{\phi }=\mathit{\pi }/2$ in Figure 7(b), the variation of oscillations in ρ₂₂ occurs in reverse order with kx as mentioned in Figure 7(a). Surprisingly, at $kx=\mathit{\pi }/2$, ρ₂₂ assumes 25% population throughout the time scale. On introducing the two-field spatial arrangement $(R_1=1,R_2=2,\mathit{\eta }=0.9,\mathit{\phi }=0)$, we obtain the profile of oscillations in Figure 7(c), where oscillations become less pronounced with the same qualitative variation with kx. For $\mathit{\phi }=\mathit{\pi }/2$ (Figure 7(d)), ρ₂₂ follows same variation (as shown in Figure 7(b)) with kx up to $kx=\mathit{\pi }/2$. One interesting observation, which needs special attention, is that the respective features obtained in Figure 7(b) for $kx=2\mathit{\pi }/3$ and $5\mathit{\pi }/6$ show overdamped and critically damped characters even in the limit $R>\mathit{\gamma }/2$. In case of the three-field arrangement the oscillations of ρ₂₂ with greater amplitudes and frequencies are observed in Figure 7(e) compared to that in Figure 7(a) when the parameters are $R_1=1,R_2=2,R_3=3,{\mathit{\eta }}_1=0.9,{\mathit{\eta }}_2=0.6$ and φ = 0. But when φ values are increased to $\mathit{\pi }/2$, i.e. ${\mathit{\phi }}_1=\mathit{\pi }/2,{\mathit{\phi }}_2=-\mathit{\pi }/2$, the temporal variation of ρ₂₂ mimics only the qualitative behavior of overdamped and critically damped conditions for $R>\mathit{\gamma }/2$. The transient features of the driven two-level atom as shown in Figure 7 may be also comparable to the characteristics of a moving-coil galvanometer or dc transient response of a series LCR circuit (during charging of the capacitor) in overdamped, critically damped and underdamped conditions.

Figure 7. Plot of spatio-temporal dynamics of excited state population: (a) $R_1=5,\mathit{\phi }=0$; (b) $R_1=5,\mathit{\phi }=\mathit{\pi }/2$; (c) $R_1=1,R_2=2,\mathit{\eta }=0.9,\mathit{\phi }=0$; (d) $R_1=1,R_2=2,\mathit{\eta }=0.9,\mathit{\phi }=\mathit{\pi }/2$; (e) $R_1=1,R_2=2,R_3=3,{\mathit{\eta }}_1=0.9,{\mathit{\eta }}_2=0.6,\mathit{\phi }=0$; and (f) $R_1=1,R_2=2,R_3=3$, ${\mathit{\eta }}_1=0.9$, ${\mathit{\eta }}_2=0.6,\mathit{\phi }=\mathit{\pi }/2$.

2.3.2. Equivalence of atomic Raman–Nath diffraction

Lastly, the present work offers a possibility to show the equivalence of atomic Raman–Nath diffraction, which is similar to that attained in momentum representation. Following the expression of ρ₂₂ as in Equation (26) (condition (3) $(R>\mathit{\gamma }/2)$), we can express the probability amplitude of the excited state as,(27) $$B_2(t)=sin(R_{G}t)e^{-\mathit{\gamma }t/2}$$(27)

where $R_G=\sqrt{R^2-{(\mathit{\gamma }/2)}^2}$.

To incorporate spatial dependence in Rabi frequency R_G, we consider $R_G=R_{G0}sin(kx+\mathit{\phi })$. φ indicates the induced spatial phase. By using the following transformation (Ghatak & Thyagrajan, 1994),$$e^{-i(R_{G0}t)sin(kx)}=J_0(R_{G0}t)+2\sum _{n=1}^{\infty }{J}_{2n}(R_{G0}t)cos\left[2n(kx)\right]-2i\sum _{n=1}^{\infty }{J}_{2n-1}(R_{G0}t)sin\left[(2n-1)kxt\right],$$

J_2n or J_2n−1 being first Bessel Functions, we obtain(28) $$B_2(x,t)=2\sum _{n=1}^{\infty }{J}_{2n-1}(R_{G0}t)e^{-\mathit{\gamma }t/2}{e}^{i\mathit{\phi }}sin\left[(2n-1(kx+\mathit{\phi })\right]$$(28)

The expression of B₂(x, t) is reshaped as

$B_2(x,t)=2{\sum }_{m=1}^{\infty }{J}_m(R_{G0}t)e^{-\mathit{\gamma }t/2}{e}^{i\mathit{\phi }}sin(m(kx+\mathit{\phi }))$ where m is only odd integers.

If we take Fourier series expansion for $B_2(x,t)=\sum _{m=1}^{\infty }{B}_m(t)sin(m(kx+\mathit{\phi }))$, m being odd integers, we find(29) $$B_m(t)=2J_m(R_{G0}t)e^{-\mathit{\gamma }t/2}.$$(29)

For exclusion of decay factor, this is almost identical to that obtained in Li-Ping et al. (2007) for momentum space representation of atomic Raman–Nath diffraction. In contrast to the findings of the work presented in Li-Ping et al. (2007), this article represents spatial phase induced variation of atomic Raman–Nath diffraction for a decaying atom, which can be perceived by observing the various plots as given in Figure 7. More specifically, the spatio-temporal behaviors as depicted in Figure 7, basically display the spatial phase variation of atomic Raman–Nath diffraction in coordinate representation through the spatial phase dependent population distribution. The technique of spatial phase variation as adopted in our study is an addition to the earlier scheme (Li-Ping et al., 2007).

4. Conclusion

First of all, we have studied the evolution of power broadened spectrum in a two-level atom with quasi-metastable ground state under the methodology of probability amplitude approach. Through the power broadened line shape, similar characteristics of the interference pattern on reflection mode of a FP interferometer have been simulated by spatial modulation of coherent field. Complementarity of such pattern, which is analogous to the features of one dimensional atom-localization obtained in a three-level atom, is shown to be achievable with possible modification in the present model. Simulated FP interference-like pattern on reflection mode in quantum domain is shown to have the possibility to be modified in various ways based on superposition of two or more coherent fields in both the one and two dimensions. The results, as presented in the paper, might have great impact on further studies regarding applications in atomic lithography via fluorescence imaging technique.

Within the scope of the present work, spatio-temporal dynamics of the present model are also analyzed for a number of physical aspects, which gives rise to the similar behaviors of a damped harmonic oscillator or classical galvanometer. We have pointed out the usefulness of this study by representing the equivalence of atomic Raman–Nath diffraction in momentum representation under the control of spatial phase. This is an interesting aspect for finding its applications in the field of cold-atom-optics.

Acknowledgments

The authors would like to express their utmost thanks to Prof. Ying Wu, Prof. Abhijit Mookerjee, and Prof. Prasanta K. Mahapatra for their encouragement and helpful discussions. The authors are also grateful to the Learned Reviewers for theirs intuitive comments to improve the manuscript.

Additional information

Funding

Pradipta Panchadhyayee and Nityananda Das gratefully acknowledge the University Grants Commission, New Delhi, India, for financial support [grant number F. PSW-136/13-14], and [grant number F. PSW-125/14-15], respectively.

Notes on contributors

Pradipta Panchadhyayee

Pradipta Panchadhyayee is presently an assistant professor in the Department Physics (UG & PG) of P. K. College, Contai, West Bengal, India. His research interests include the fields of opto-quantum analogy, quantum optics, and tunneling in semiconductor nanostructures.

Nityananda Das

Nityananda Das is an associate professor in the Department Physics of J. K. College, Purulia, West Bengal, India. His research field encompasses quantum-classical analogy, condensed matter physics, cellular manufacturing, and micromechanics.