Neuronal avalanches in complex networks

Abstract

Brain networks are neither regular nor random. Their structure allows for optimal information processing and transmission across the entire neural substrate of an organism. However, for topological features to be appropriately harnessed, brain networks should implement a dynamical regime which prevents phase-locked and chaotic behaviour. Critical neural dynamics refer to a dynamical regime in which the system is poised at the boundary between regularity and randomness. It has been reported that neural systems poised at this boundary achieve maximum computational power. In this paper, we review recent results regarding critical neural dynamics that emerge from systems whose underlying structure exhibits complex network properties.

Keywords:

• neuronal avalanches
• self-organised criticality
• complex networks
• phase transitions
• scale-free networks
• small-world networks
• complex collective dynamics of the brain

PACS numbers:

• 05.65.+b
• 05.70.Fh
• 05.70.Jk

Public Interest Statement

It is not merely the sheer amount of nerve cells and synaptic connections between them that is responsible for the immense capabilities of a brain. More important are the intricate patterns of connectivity which are unlikely to be specified in detail by genetic or environmental information. We study effects of such connectivity patterns on the activity dynamics and consider in particular the phenomenon of criticality which refers to the brain's ability to remain flexible and responsive for a large diversity of sensory inputs. While we and other authors have proposed a number of mechanisms how a brain can manage a critical state, the role of the specific connection patterns is less well understood. Here, we discuss several classes of network structures and show how they enhance critical behaviour in the brain. It remains an interesting question whether these structures are the cause or the consequence of a critical dynamics.

1. Introduction

A healthy brain is a well-connected brain. Intelligence requires the capacity to process information in an efficient and robust manner. Thus, the brain should exhibit an architecture that enables optimal information transmission across its many regions. Additionally, the architecture would have to provide mechanisms to enable structural modifications that are essential for memory, learning and recovery when its function is damaged. Neuronal plasticity incorporates such structural changes including the establishment or removal of existing connections among nerve cells. It is accompanied by modulatory mechanisms at the level of individual synapses. The changes of brain structure are tightly intertwined with the dynamics occurring within them in such a way that structure affects collective dynamics, and vice versa—thus creating a loop that is responsible for the rich repertoire of functions that neural systems perform.

In recent years, the importance of studying neural systems within the framework of network theory has been stated, and research in this direction has been carried out with considerable success. The discovery of structural and functional connections among brain areas is an important, prolific and promising field of research in neuroscience. Charts of brain connectivity, from their structural or functional perspective, can be constructed nowadays thanks to the capacity to collect, store and analyse large brain databases. Neuroscience has thus entered the age of big data.

Brain networks can be described as graphs that are composed of nodes representing neural elements such as single neurons or brain regions which are connected by links denoting either physical or functional connectivity (Bullmore & Sporns, 2009). Here, the direction of the edges denotes the flow of information transmission across the network. The Human Connectome Project sponsored by the National Institutes of Health in the United States is a project whose goal is to build a map of the whole brain connectivity in the same spirit as the genome project had the objective of mapping the entire human genome. Similar efforts are being carried out in Europe with the Human Brain Project, and in China, with the Brainnetome Project. These ventures reflect the current restlessness in trying to understand the dynamics of the brain through understanding its structural properties.

Recent results in neuroimaging seem to imply that the brain’s structural and functional systems exhibit features of complex networks, such as small-world topology, modularity and highly connected nodes suggesting power-law degree distributions (Sporns, 2010; Sporns, Chialvo, Kaiser, & Hilgetag, 2004). The study of brain networks under the perspective of network theory is devoted to analyse particular network statistics that might reveal the mechanisms of particular brain functions. However, which network measures are most appropriate for the analysis of brain networks is still an open question (Rubinov & Sporns, 2010).

The brain exhibits features commonly associated to complex networks. Recently, it has been reported the existence of a rich-club organisation of the human brain, which is characterised by the presence of neocortical hubs that have a tendency to connect to other brain hubs rather than to poorly connected regions (van den Heuvel & Sporns, 2011). These brain hubs play a key role in the integration and propagation of global information giving rise to a backbone for global communication (van den Heuvel, Kahn, Goni, & Sporns, 2012). Moreover, these observations have been applied to the study of brain pathologies such as Alzheimer’s disease and schizophrenia, suggesting that these conditions imply abnormalities in brain topology (Bullmore & Sporns, 2009). Researchers have found that these diseases are associated with alterations in brain structure. For instance, they have found that such conditions are associated with a reduction of the small-world property in specific brain regions along with loss in hierarchical organisation (Bullmore & Sporns, 2009).

Experimental evidence in this direction seems to lead to the same conclusion, that the architecture of the brain is not random (Song, Sjöström, Reigl, Nelson, & Chklovskii, 2005). And although when we are born the brain is densely connected, its architecture evolves towards a sparse topology through the programmed death of cells that do not imply any benefit to brain function. Moreover, the brain is expensive in terms of the costs of neural tissue and metabolic consumption. Therefore, its dynamics and architecture must be the result of an economic trade-off between the network’s physical cost and the adaptive value of its structure which translates into functional connectivity (Bullmore & Sporns, 2012).

Structure leads to function, for instance, the small-world property provides the structural requirements to allow synchronisation in brain networks (Yu, Huang, Singer, & Nikolic, 2008). The brain is a very powerful computing machine which is performing complex calculations all the time, from the most abstract ones required for mathematical thinking, to the most habitual ones such as walking down a staircase without looking at every step. For these complex computations to take place, the brain must implement dynamics that take out the best from its efficient structure.

Recently, it has been put forward the idea that brain computations are carried out at the edge of chaos (Beggs, 2008). This means that the dynamics of brain networks are undergoing a phase transition similar to those that occur in inorganic matter when a parameter is finely tuned (e.g. liquid water turning into vapour). A typical signature of a phase transition is the power-law distribution of event sizes, which implies that at the critical point, the dynamics of a system do not exhibit a particular scale. Power-law distributions in the activity of brain tissue have been detected in a modality of neuronal activity previously unknown whose modus operandi is avalanches of bursts of activity. These neuronal avalanches were first detected in cortical and acute slices of rat cortex (Beggs & Plenz, 2003, 2004). Since their first observation they have spawned subsequent research in various experimental settings which seem to suggest that these neuronal avalanches are the main modality of the brain at rest (Barbieri & Shimono, 2012; Bellay, Klaus, Seshadri, & Plenz, 2015; Friedman et al., 2012; Klaus, Yu, & Plenz, 2011; Petermann et al., 2009; Shew et al., 2015). Model implementations of neuronal avalanches have elucidated the potential benefits of neuronal networks teetering at the edge of chaos. It is in this boundary between order and randomness, known as the critical point, that brain networks reach maximum computational power (Bertschinger & Natschläger, 2004; Haldeman & Beggs, 2005; Kinouchi & Copelli, 2006).

However, the idea of critical brain dynamics has not been received without some scepticism (Touboul & Destexhe, 2010), which includes the unjustified enthusiasm regarding the ubiquity of power-law distributions in nature (Clauset, Shalizi, & Newman, 2009; Stumpf & Porter, 2012). Moreover, it has been reported that brain dynamics are not precisely in the critical regime but instead they are wandering about it (Priesemann et al., 2014). Nevertheless, experimental evidence of the scale-invariant nature of neuronal avalanches in brain networks either in vivo or in vitro keeps piling up, implying that this is an active and promising field of research.

Another question regarding this modality of brain function refers to its mechanism of emergence. It is known from the theory of critical phenomena that the control parameter of systems that exhibit critical behaviour needs to be fine-tuned in order to give rise to this particular type of dynamics. However, under certain circumstances, some systems are able to reach this state without the need of external tuning, which implies that the system implements some sort of feedback mechanism that gives it control over its parameters. Self-organised criticality (SOC) was proposed as a theory to explain the underlying mechanisms of this kind of systems, and at the same time, provide explanations to the apparent ubiquity of 1/f fluctuations and power-law distributions of events that are observed in phenomena as diverse as the dynamics of plate tectonics, solar flares, stock market crashes, mass extinctions, and forest fires, among others (Bak, 1997). Therefore, the concept of SOC has been put forward as a mechanism by which complexity arises in nature.

Self-organised critical models of neuronal networks have been developed to explain the emergence of power-law distribution of events and other observables that would imply that these networks are at the edge of a phase transition. These models can be divided in two categories, those that explain the emergence of critical behaviour through plasticity mechanisms such as spike-timing-dependent plasticity (Meisel & Gross, 2009; Shin & Kim, 2006) or short-term plasticity (Levina, Herrmann, & Geisel, 2007) or another Hebbian-like plasticity process (de Arcangelis, Perrone-Capano, & Herrmann, 2006), and those that explain it through non-plastic mechanisms like axonal re-wiring (Bornholdt & Röhl, 2003; Bornholdt & Rohlf, 2000) or the balance between neuronal excitation and inhibition (Beggs & Plenz, 2003).

A healthy brain is a well-connected brain, and this results in optimal neuronal information processing. Recently, it has been pointed out that critical dynamics are a signature of healthy brain systems (Massobrio, de Arcangelis, Pasquale, Jensen, & Plenz, 2015). This hypothesis rests on the idea that a critical brain can show the fastest and most flexible adaptation to environments where unpredictability abounds. In such environment, we not only require fast, robust and reliable cognitive functions, but also sensory systems that can adapt quickly to changes in the environment, and provide responses that maximise the diversity of stimuli found in the world (Chialvo, 2006; Tagliazucchi & Chialvo, 2011). Moreover, it has been proposed that one of the purposes of sleep is to tune the brain for criticality (Pearlmutter & Houghton, 2009). The suggestion that criticality is a signature of a healthy brain implies a novel perspective to study brain disease whose effects result in a deviation from critical (or close-to-critical) dynamics.

In this paper, we briefly examine the relationship between network topology and critical neural dynamics. We focus particularly in complex topologies identified by the presence of the small-world property and the existence of network hubs, and describe how these properties influence the onset of the critical state.

2. A Model for Neuronal Avalanches

A simple and convenient model for neuronal avalanches is the one proposed by Eurich and colleagues (Eurich, Herrmann, & Ernst, 2002). The model resembles the original sand-pile model from Bak and coworkers (Bak, Tang, & Wiesenfeld, 1988). The model for neuronal avalanches consists of N non-leaky integrate-and-fire nodes. Each node j is characterised by a continuous variable known as the membrane potential h_j, which is updated in discrete time according to the equation:(1) $$h_j(t+1)=h_j(t)+\sum _{i=1}^N{A}_{ij}{w}_{ij}{s}_i(t)+I_{ext}$$(1)

where A denotes the adjacency matrix with entries A_ij = 1 if node i sends and edge to node j, and A_ij = 0 otherwise, w_ij denotes the synaptic weight from node i to node j, s_i(t) ∊ {1, 0} represents the state of node i (active or quiescent, respectively) at time t, and I_ext denotes external input which is supplied to a node depending on the state of the system at time t. This mechanism of external driving works as follows: if there is no activity at time t, then a node is chosen uniformly at random and its membrane potential is increased by a fixed amount through the variable I_ext. If h_i(t) exceeds the threshold θ, then node i emits a spike, which changes the state of this node to active (s_i(t) = 1) and propagates its activity through its synaptic output. Afterwards, the node is reset, i.e. h_i(t + 1) = 0.

The coupling strength w_ij for every node i sending an edge to node j is set according to the equation:

(2) $$w_{ij}=\frac{\mathit{\alpha }}{⟨e⟩}$$(2)

where α is the control parameter of the model, and 〈e〉 denotes the mean degree of the network.

The model gives rise to cascading behaviour. Here, avalanches take the form of neuronal activity being propagated as a domino effect. While the system is relaxing, external drive stops. This guarantees that relaxation time occurs at a different time scale as the external driving. This corresponds to an infinite separation of time scales between external driving and relaxation dynamics that has been suggested as a necessary condition for critical behaviour (Jensen, 1998).

For a particular interval of the control parameter α in Equation (2(2) $$w_{ij}=\frac{\mathit{\alpha }}{⟨e⟩}$$(2) ), the sizes of the neuronal avalanches (identified as the number of nodes that become active in between two quiescent periods) and their durations (identified as the number of time steps in between two quiescent periods) can be approximated by a power-law. In analytical examinations, the exponents derived for such distributions are γ = −3/2 and δ = −2 for avalanches sizes and durations, respectively, in the thermodynamic limit of fully connected networks. Interestingly, this model, which was proposed before neuronal avalanches were reported in brain data, predicted accurately the critical exponents found by Beggs and Plenz in neuronal tissue (Beggs & Plenz, 2003).

Thus, a simple and straightforward way to look for criticality is to inspect the distribution of avalanche sizes and durations of a system for different values of the control parameter α. If the distribution resembles a power-law distribution, then we have reasons to suspect that the system is undergoing a phase transition. For this purpose, one can assess the quality of such a power-law through the mean-squared deviation from the best-matching power law with exponent γ obtained through regression in log–log scales. This results in an error function that has been called Δγ function elsewhere (Levina et al., 2007). When this error function is at its minimum, that is, when the data are best approximated by a power-law distribution of avalanche sizes with exponent γ, is when the system is at a purported critical state.

A power-law fit of the distribution of avalanche sizes is by no means a sufficient condition for a system to be critical, but it is a necessary one. Other tests for criticality that can be performed are:

(1)	Observation of the trichotomy of critical behaviour: It has been pointed out the relative ease to produce power-laws through natural or artificial means (Touboul & Destexhe, 2010). In other words, there are power-law distributions without criticality. However, real critical systems exhibit a trichotomy of dynamical regimes that is non-existent in other contexts where power-law distributions can be found. These three dynamical regimes are the sub-, super- and critical regimes (see Figure 2(a)). For a system that features the presence of power-law behaviour to be critical, it should exhibit as well this dynamical trichotomy when the control parameter is properly tuned (Beggs & Timme, 2012).
(2)	Analysis of the largest eigenvalue Λ associated to the matrix of synaptic weights: Larremore and colleagues studied the spectral decomposition of the weight matrix of a system at criticality, and concluded through analytical inspections along with numerical simulations that the largest eigenvalue of the weight matrix governs the network’s dynamic range. When this value is unity, the system is in a critical state and its dynamic range is maximised (Larremore, Shew, & Restrepo, 2011).
(3)	Analysis of the relationships between critical exponents of avalanche sizes and their lifetimes: From the theory of critical phenomena, we know that at criticality, the distribution of several observables follows power-laws with mathematical expressions linking each other (Sornette, 2004). In particular, there is a power-law positive correlation between avalanche sizes and their lifetimes which only occurs at criticality (Beggs & Timme, 2012; Bellay et al., 2015; Shew et al., 2015).
(4)	Analysis of data collapse: At criticality, the dynamics of a system show no particular scale, thus resulting in a fractal geometry of its observables (Kadano, 2010; Sornette, 2004). A standard procedure to analyse the critical regime in a model of neuronal avalanches is to observe if avalanches exhibit a fractal structure. To this purpose, the average “shape” of avalanches is estimated by keeping track of the lifetime of an avalanche and the number of nodes involved at each avalanche step. If the system is at criticality, then avalanches of different sizes would exhibit the same shape up to a scaling function, in such a way that data could be collapsed in order to observe how avalanche shapes resemble each other (Friedman et al., 2012).

The list above is not exhaustive and some other tests can be carried out following the theory of critical phenomena from statistical physics. Some of these tests are easier to perform in computational models than in real brain data. Therefore, their application depends strongly in the research scenario.

Lastly, while studying the dynamics of the above model of neuronal avalanches, we can introduce a local measure of the performance of a node during simulation time: the node success.

The node success of node i at time t is the fraction of out-neighbours of this node that become active at time t + 1 when node i spikes at time t, in other words:

(3) $${\mathit{\phi }}_i(t)=\frac{\sum _{j=1}^N{A}_{ij}{s}_j(t+1)}{\sum _{j=1}^N{A}_{ij}}$$(3)

Thus, node success measures the performance of an individual spike in terms of the subsequent spikes triggered by such initial activation, which occur within the out-neighbourhood of a given node. In contrast to other network statistics (e.g. degree distribution, mean shortest path length, mean clustering coefficient, etc.), node success is a local measure of performance.

Through this statistic we are able to track the type of nodes that contribute more to the critical state of the system (e.g. highly or lowly connected nodes). Moreover, we are able to know what type of network structure yields the most successful nodes during the critical state (e.g. fully connected, random or scale-free networks). This type of analysis is only possible when considering a local measure instead of a global one.

In Figure 1, we show the development of the dynamics of a six-node graph. There we also present the value of the node success φ for nodes that become active throughout the simulation. As mentioned earlier, external driving occurs when there is no node active in the system. A node is chosen uniformly at random and its membrane potential is increased by a fixed amount of energy I_ext. As soon as a node’s membrane potential goes beyond threshold as a result of the external driving, relaxation dynamics take place in the form of an avalanche of node activations (that is, spike propagation). During this process, the driving is stopped. This results in a separation of time scales between driving and relaxation dynamics which is required for criticality to occur in a system. When there is no node being triggered by spike propagation, the system reaches a metastable state and external driving resumes. The size of the avalanche is the number of nodes that became active during the avalanche, whereas its duration is the number of time steps until the avalanche stops.

Figure 1. Avalanche dynamics. External inputs drive system when there are no active nodes and are assumed to stop as soon as an avalanche starts. At time t_i, a node becomes active and propagates a spike to its out-neighbours. The number of out-neighbours that become active as a result of spike propagation is captured by the node success statistic φ (3). The avalanche ends when all nodes have returned to a state below the firing threshold. The second avalanche may continue after t_i+7. The success φ(t_i+7) for the only active node at this time step is estimated based on the number of nodes active at t_i+8.

3. Critical Neuronal Avalanches and Complex Networks

A complex network is a structure that captures the interaction among dynamical units, whose number is so large that a graphical representation of such interaction becomes cumbersome. Unlike a graph, a complex network is a structure in which a process takes place, and most of the time, this process affects the connectivity of the elements responsible for the process, creating, thus, a feedback loop. Thus, we should not only consider the dynamics on the network, but also the dynamics of the network (Gross & Blasius, 2008; Gross & Sayama, 2009).

Previous studies involving models of critical neuronal avalanches and complex networks considered network statistics such as assortativity, which measures the preference of nodes to connect to other nodes with similar (or dissimilar) degree, as well as locally tree-like networks, which can be loosely defined as networks with a low number of cliques (Larremore, Shew, & Restrepo, 2014).

In a recent study, we considered complex-directed networks as the underlying network structure in which the model described in the last section gives rise to neuronal avalanches. The complex network features we were interested in introducing to the model are the small-world property identified by a high-mean clustering coefficient paired up with a low-mean characteristic path length (Watts & Strogatz, 1998), and the presence of highly connected nodes (hubs) identified by a power-law degree distribution. Networks of the latter type are known as scale-free networks (Barabasi & Albert, 1999). As mentioned in the Introduction, such features have been observed in brain structures. Therefore, we would expect that these topological features exert some influence over the system’s critical dynamics. For the purpose of testing this hypothesis, we analysed and compared how the system reaches the critical state when its underlying structure is either fully connected, random or scale-free. For the latter type, we considered out-degree scale-free networks, that is, networks whose out-degree distribution follows a power-law and results in the presence of nodes with a large number of outgoing connections which we call broadcasting hubs. As well, we considered in-degree scale-free networks, which feature the presence of nodes with a large number of incoming connections which we call absorbing hubs.

Furthermore, as the small-world property is not a binary one, rather there exists a degree of what we would call small-world-ness, we considered two “levels” of the small-world property in our scale-free networks by tuning the mean clustering coefficient in them. This resulted in in-degree and out-degree scale-free networks with high and low levels of the small-world property.

The heterogeneity in the structure of scale-free and random networks has an impact on the collective dynamics which is captured by the shape of the Δγ function when considering the value of the fitting error in function of the control parameter α. While for fully connected networks, this function exhibits a smooth shape as the value of α varies (Figure 2(b)), in scale-free and random networks the Δγ function exhibits abrupt transitions and long plateaus where the error is at its minimum (Figure 3).

Figure 2. Distribution P(S, α) of avalanche sizes S as a function of the synaptic parameter α in double logarithmic plots, and Δγ curve and exponent γ for fully connected network of size N = 128. Error is minimised for values of α ∊ (0.9, 0.95). The inset shows the exponent γ of the best matching power-law distribution for different values of α. In the region where the error is minimal, the exponent γ takes values between −1.5 and −1.

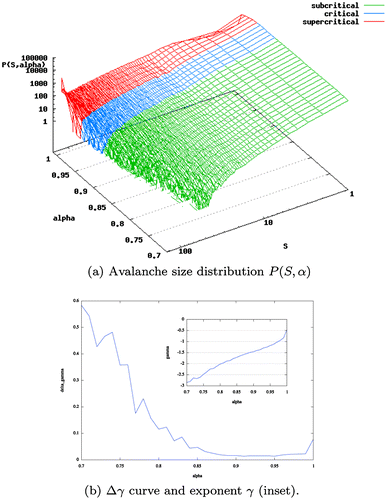
Figure 3. Deviation from the best-matching power law is described by the Δγ curve for random and scale-free networks of size N = 256. Abrupt changes in the shape of the curve occur when the system goes from one regime to the other. A plateau appears and within it the function reaches its minimum. Outsets show this behaviour for random and out-degree scale-free networks with high- and low-mean degrees of the small-world property, whereas insets show the same for in-degree scale-free networks.

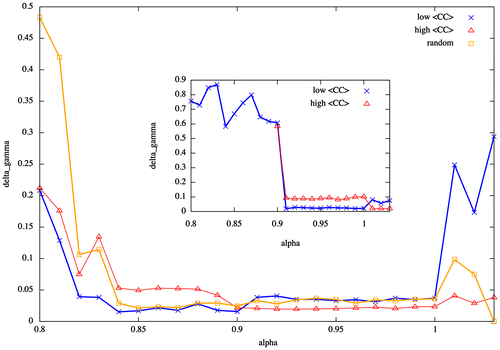
The existence of such plateaus might be related to the presence of Griffith phases as a result of the collective dynamics of the system. The existence of Griffith phases in models of neuronal avalanches has been suggested as a mechanism by which neural systems extend their “range of criticality”, which implies that the critical point is replaced by an extended critical region (Moretti & Munoz, 2013). This hypothesis has been proven in hierarchical-modular networks, which resemble the structure of brain networks. Here, we suggest that this phenomenon might also be observed in random and scale-free networks due to sparsity in the system. Therefore, neural systems “in the wild” might prefer sparse complex topologies such as scale-free networks in order to extend the critical region, and at the same time, obtain the benefits of a scale-free structure such as robustness (Albert, Jeong, & Barabási, 2000).

The question regarding the node type that contributes more to avalanche behaviour becomes reasonable only when going beyond homogeneous topologies like fully connected networks or lattices in which every node has exactly the same number of connections. It is only when facing heterogeneity in node connectivity when makes sense to study the node type that participates more in the avalanche behaviour of the system. In this sense, absorbing hubs in in-degree scale-free networks, that is nodes with many incoming edges, emit the largest number of spikes than any other kind of node. At first, this could be explained by the large number of nodes connecting to them. However, this would also predict that nodes in fully connected networks behave in a similar fashion due to the large number of incoming connections in them, which is maximal. This is not the case, and nodes in fully connected networks are being affected by a phenomenon that we call spike jamming, which refers to the obstruction of spike triggering that results from nodes being connected completely among each other. This dampening does not occur in heterogeneous networks due to sparsity in the structure. Because this sparsity in scale-free networks is not random, there is a positive correlation between node in-degree and spike emission.

Therefore, scale-free networks take advantage of the heterogeneity of their structure to yield nodes that achieve a larger firing rate in a sparse topology. Moreover, we observe that as the small-world property increases in scale-free networks, the correlation between in-degree and spike emission becomes quadratic. Thus, as the amount of clustering in a scale-free network increases, the spiking activity within the system grows non-linearly without taking the system out of the critical regime.

Spiking is not all that matters, since we should also consider the fate of a spike that has just been emitted. Here, we consider a successful spike one that triggers subsequent spikes from the nodes in the out-neighbourhood of the node where the initial spike originated. As we are interested in the propagation of activity within the system, we would like to observe the sustained activation of nodes in subsequent time steps. With Equation (3(3) $${\mathit{\phi }}_i(t)=\frac{\sum _{j=1}^N{A}_{ij}{s}_j(t+1)}{\sum _{j=1}^N{A}_{ij}}$$(3) ), we defined the success of a node i at time t as the fraction of out-neighbours of i that become active at time t + 1 when node i spiked at time t. With the node success in mind, we define the mean node success of the system as the mean of the mean node success 〈φ〉_i for all nodes in the system as:

(4) $$⟨\mathit{\phi }⟩=\frac{1}{N}\sum _{i=1}^N{⟨\mathit{\phi }⟩}_i$$(4)

In-degree scale-free networks with high-mean clustering coefficient (therefore, high degree of the small-world property) is a topology in which nodes achieve larger success. In this type of structure, the spikes emitted by nodes are more successful at triggering subsequent spikes in their neighbourhood without compromising the critical state of the system. On the contrary, fully connected networks, which are affected by the spike-jamming effect, are structures in which nodes perform the worst (Figure 4).

Figure 4. Mean node success per network structure and all sizes considered: fully connected (FC), random (RN), out-degree scale-free networks with low-mean clustering coefficient (SF[outdeg, lowCC]), high-mean clustering coefficient (SF[outdeg, highCC]) and in-degree scale-free networks with similar features (SF[indeg, lowCC] and SF[indeg, highCC]). In-degree scale-free network is the type of structure that maximises the success of spikes emitted by nodes, whereas fully connected structures perform the worst.

Note: High/low mean clustering coefficient implies high/low degree of the small-world property.

Additionally, scale-free and random networks exhibit non-Hamiltonian avalanches. In the context of graph theory, a path in a graph (or network) refers to a sequence of edges in which two consecutive edges possess a vertex in common. A Hamiltonian path is defined as a path in a directed (or undirected) graph or network that visits each vertex exactly once. Thus, a Hamiltonian avalanche is an avalanche in which no nodes are active more than once for the entire duration of the avalanche.

It has been reported previously that fully connected networks exhibit only Hamiltonian avalanches, that is, avalanches in which no node is active more than once in a single avalanche. Furthermore, it has been proven that the only situation in which the opposite occurs, that is, when a node is active more than once in a single avalanche, occurs only when the system is in the supercritical regime related with avalanches larger than the size of the system (Eurich et al., 2002).

The situation in complex networks looks quite different, and in fact, non-Hamiltonian avalanches are the norm in this type of networks at criticality. This kind of systems exhibit the properties associated with the critical state, namely power-law distributions, correlations among critical exponents, data collapse, etc., but these systems also exhibit avalanches in which nodes can be active more than once in a single avalanche, which is incompatible with criticality in fully connected networks.

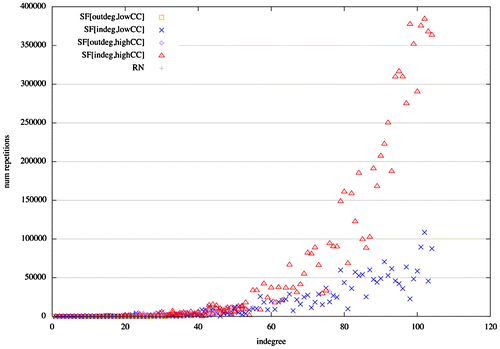
Non-Hamiltonian avalanches imply nodes that become active more than once in a single avalanche. Node in-degree is positively correlated with the number of re-activations of a node in a single avalanche in heterogeneous structures (Figure 5). Thus, in-degree scale-free networks, which feature the presence of absorbing hubs, are the type of network that exhibit more re-active nodes and therefore more non-Hamiltonian avalanches. The larger the in-degree a node has the more it is susceptible to re-activate in a single avalanche. Moreover, clustering has also an effect on node re-activations. A higher mean clustering coefficient, which implies a larger degree of small-world-ness, results in a quadratic trend between in-degree and node re-activation. Thus, if a network possesses absorbing hubs and exhibits the small-world property, then avalanches will exhibit re-activation of nodes without leaving the critical regime.

Figure 5. Scatter plot of in-degree vs. number of node re-activations for scale-free and random networks. Nodes with largest in-degree have also the largest number of re-activations in a single avalanche. Therefore, in-degree scale-free networks possess nodes with the largest number of re-activations, and thus, the largest number of non-Hamiltonian avalanches. (Labelling as in Figure 4)

4. Discussion

Neural tissue is expensive in terms of metabolic consumption; therefore, the brain must do the best with a sparse architecture (Bullmore & Sporns, 2012). Scale-free networks that possess the small-world property provide the structural requirements for robustness and fast communication across brain regions due to the presence of hubs and long-range connections (Albert et al., 2000; van den Heuvel et al., 2012). However, these properties refer only to the underlying structure of brain networks. The brain would additionally require a dynamical regime that takes advantage of this optimal architecture, in the same way that a highway system across a country would also require high-speed vehicles that speed up traffic, along with other logistics that maximise transportation. In this sense, criticality is a dynamical regime in which neural computation is optimised in terms of maximum information storage, transmission, robustness and sensitivity to stimuli (Beggs, 2008).

Here, we briefly presented some of our results regarding the influence of network complexity over the critical regime in a model of neuronal avalanches. The features of network complexity that we focused on were the small-world property, and the presence of hubs. By comparing networks with these features against random and fully connected structures, we confirm that such properties exert a considerable effect in the system particularly in terms of spiking activity and the success of spikes in terms of their capacity to trigger subsequent activations. Therefore, we stress the importance of network heterogeneity over the collective dynamics of a critical system. The presence of hubs and high clustering improves the overall network performance than when nodes are all the same as in fully connected networks, or when there is no particular pattern of connectivity as in random networks.

The introduction of the analysis of the success of a spike through the node success statistic (Equation (3(3) $${\mathit{\phi }}_i(t)=\frac{\sum _{j=1}^N{A}_{ij}{s}_j(t+1)}{\sum _{j=1}^N{A}_{ij}}$$(3) )) allowed us to study how different node types contribute to the critical state of the system, as well as allowing us to find the network structure in which nodes’ spikes are more successful. This statistic can be applied seamlessly to other contexts where the propagation of activity within the system requires that agents in a network go beyond a given threshold in order to release energy or any other physical quantity. For instance, a spike can be thought of the transmission of an infection among contacts, the death of a species in models of ecosystems, the failure of a power generator in power networks, etc. In all these contexts, the fate of a “spike” is as relevant to the collective dynamics as is the network topology. The combination of individual dynamics of nodes and topology determines the success of the spikes that spread across the system.

Lastly, in scale-free and random networks, the critical regime is extended by the presence of a plateau. We suggest that this might be related to the presence of Griffith phases in neural systems (Moretti & Munoz, 2013). This hypothesis is interesting as it proposes that brain networks “prefer” sparse heterogeneous structures such as scale-free small-world networks not only for the benefits that these structures imply in terms of robustness, information processing and transmission, but also because it allows the system to extend the range in parameter space in which the critical state is reached.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Victor Hernandez-Urbina

Victor Hernandez-Urbina completed his PhD in Neuroinformatics at the University of Edinburgh. He studied criticality in neural systems, complex networks and synaptic plasticity under the supervision of Michael Herrmann. 

J. Michael Herrmann

Having received a Doctorate from the University of Leipzig in 1993, J. Michael Herrmann continues to work on computational neuroscience and theoretical aspects of artificial neural networks. He has contributed to establish the concept of criticality in these fields and has been active to apply approaches related to criticality also in the emerging field of neurorobotics. As a Lecturer for Robotics at the School of Informatics, University of Edinburgh, his research interests include also self-organisation, robot learning, neural avalanches, auditory system, bio-medical data analysis, metaheuristic optimisation and information theory.