The multifunctional process of resonance scattering and generation of oscillations by nonlinear layered structures

Abstract

The paper focuses on the development of a mathematical model, an effective algorithm and a self-consistent numerical analysis of the multifunctional properties of resonant scattering and generation of oscillations by nonlinear, cubically polarizable layered structures. The multifunctionality of such layered media is caused by the nonlinear mechanism between interacting oscillations—the incident oscillations (exciting the nonlinear layer from the upper and lower half-spaces) as well as the scattered and generated oscillations at the frequencies of excitation/scattering and generation. The study of the resonance properties of scattering and generation of oscillations by a nonlinear structure with a controllable permittivity in dependence on the variation of the intensities of the components of the exciting wave package is of particular interest. In the present paper, we extend our former results, and furthermore we analyze the realizability of multifunctional properties of nonlinear electromagnetic objects with a controllable permittivity. The results of our investigations (i) demonstrate the possibility to control the scattering and generation properties of the nonlinear structure via the intensity of the incident field, (ii) indicate the possibility of increasing the multifunctionality of electronic devices, of designing frequency multipliers, and other electrodynamic devices containing nonlinear dielectrics with controllable permittivity.

Keywords:

• resonance scattering
• cubic polarizability
• generation of oscillations
• wave packets
• self-consistent analysis

Public Interest Statement

Nonlinear dielectrics with controllable permittivity are intensively investigated and begin to find broad applications in device technology. The development of new types of dielectrics, the introduction, and production of modern functional electronic devices require a comprehensive knowledge about the properties of these materials. In this context, the properties of such solid and liquid nonlinear materials are of important, which practically enable the conversion of energy or information, modulation, detection, amplification, recording, storing, displaying, and other types of conversion of electrical, magnetic, and optical signals carrying information. The paper is devoted to the mathematical and computational investigation of a model of resonance scattering and generation of waves by an isotropic, nonmagnetic, nonlinear, layered, dielectric structure which is excited by two-sided acting packets of plane waves in the resonance frequency range. In particular, an algorithm for the numerical determination of the eigenfrequencies (resonance frequencies) and eigenfields is developed.

1. Introduction

Nonlinear dielectrics with controllable permittivity are subject of intense studies and begin to find broad applications in device technology and electronics, where both the radio and optical (Akhmediev & Ankevich, 1997; Chernogor, 2004; Kivshar & Agrawal, 2003; Miloslavsky, 2008; Shen, 1984) frequency ranges are of interest. We present a model of resonance scattering and generation of waves by an isotropic, nonmagnetic, nonlinear, layered, dielectric structure which is excited by packets of plane waves in the resonance frequency range in a self-consistent formulation (Angermann, Shestopalov, & Yatsyk, 2013; Angermann & Yatsyk, 2011a, 2011b; Angermann, Yatsyk, & Yatsyk, 2013; Yatsyk, 2011, 2012, 2013). We consider two-sided acting wave packets consisting of both strong electromagnetic fields at the excitation frequency of the nonlinear structure, leading to the generation of waves, and of weak fields at multiple frequencies, which do not lead to the generation of harmonics but influence on the process of scattering and generation of waves by the nonlinear structure. A self-consistent numerical algorithm is developed. Based on the linearization of nonlinear problems of scattering and generation of waves by cubically polarizable, layered structures, we provide suitable spectral problems and formulate an algorithm for the numerical determination of the eigenfrequencies and eigenfields. We restrict our considerations to dispersionless nonlinear dielectrics, however, this is not essential but only simplifies the explanations.

We discuss numerical results for the problem of third harmonic generation by resonant scattering of the wave packet by single nonlinear layers having either decanalizing or canalizing properties as well as by a three-layer structure consisting of layers with canalizing–decanalizing–canalizing properties of energy dissipation. Within the framework of a self-consistent formulation of the problem we see that the induced imaginary part of the permittivity of the layer is determined by the nonlinear part of the polarization and characterizes the loss of energy in the nonlinear medium which is spent for the generation of the electromagnetic field of the third harmonic (Angermann & Yatsyk, 2011a, 2011b; Angermann, Yatsyk, et al., 2013; Yatsyk, 2012, 2013). The consideration of weak fields at multiple frequencies leads only to an increase of the portion of generated energy (Angermann, Kravchenko, Pustovoit, & Yatsyk, 2013a; 2013b; Angermann & Yatsyk, 2012, 2013a, 2013b). In particular, the investigation of a nonlinear single-layered decanalizing structure disclosed the effect of type-conversion of the generated oscillations in the case of an increasing amplitude of the incident field at the excitation frequency. In the range of third harmonic generation, this effect is also observed in the case of an increasing amplitude of the weak field at double frequency (Angermann & Yatsyk, 2012, 2013a, 2013b; Angermann, Krevchenko, et al., 2013a, 2013b). In this paper, for the first time two-sided acting fields at the scattering frequency are investigated and type-conversions by variation of the amplitude of the two-sided acting excitation fields were found.

The numerical computations of the eigenfrequencies and eigenfields of the linearized problems show that the resonant scattering and generation properties of a nonlinear structure are determined by the proximity of the excitation frequencies of the nonlinear structure to the complex eigenfrequencies of the corresponding homogeneous linear spectral problems with an induced nonlinear dielectric permittivity of the medium. In this paper, we propose an effective method to describe the processes of generation of oscillations via the variation of the relative magnitude of the Q-factor of the eigenoscillations corresponding to the eigenfrequencies of the scattering and generating structure when the intensity of the excitation field changes.

2. Formulation of the boundary-value problems of scattering and third harmonic generation of oscillations

In the framework of a self-consistent formulation, we investigate the problem of resonant scattering and generation of waves by a nonlinear, nonmagnetic, isotropic, cubically polarizable, linearly E-polarized $\mathbf{E}={\left(E_1,0,0\right)}^{\mathrm{T}}$, $\mathbf{H}={\left(0,H_2,H_3\right)}^{\text{T}}$ layered, dielectric structure (see Figure 1), which is excited by packets of plane stationary electromagnetic waves, where the time dependency of the fields is of the form $exp\left(-in\mathit{\omega }t\right)$, n ∊ N, and the vector of cubic polarization is given as ${\mathbf{P}}^{\left(\text{NL}\right)}={\left(P_1^{\left(\text{NL}\right)},0,0\right)}^{\mathrm{T}}$. Here, the variables x, y, z, t denote dimensionless spatial–temporal coordinates such that the thickness of the layer is equal to $4\mathit{\pi }\mathit{\delta };$ nω = nκc are the dimensionless circular frequencies and nκ are dimensionless frequency parameters such that $n\mathit{\kappa }=n\mathit{\omega }/c={2\mathit{\pi }/\mathit{\lambda }}_{n\mathit{\kappa }}$. These parameters characterize the ratios of the true thickness h of the layer to the lengths of the incident waves ${\mathit{\lambda }}_{n\mathit{\kappa }}$, i.e. $h/{\mathit{\lambda }}_{n\mathit{\kappa }}=2n\mathit{\kappa }\mathit{\delta }$, where $c={({\mathit{\epsilon }}_0{\mathit{\mu }}_0)}^{-1/2}$ denotes a dimensionless parameter, equal to the absolute value of the speed of light in the medium containing the layer, $\text{Im}c=0$. ɛ₀ and μ₀ are the material parameters of the medium. The absolute values of the true variables $x^{\prime },y^{\prime },z^{\prime },t^{\prime },{\mathit{\omega }}^{\prime }$ are given by the formulas ${\left(x^{\prime },y^{\prime },z^{\prime },t^{\prime }\right)}^{\mathrm{T}}=\frac{h}{4\mathit{\pi }\mathit{\delta }}{\left(x,y,z,t\right)}^{\mathrm{T}}$ and ${\mathit{\omega }}^{\prime }=\frac{4\mathit{\pi }\mathit{\delta }}{h}\mathit{\omega }$.

Figure 1. The nonlinear dielectric layered structure.

We consider packets of plane waves consisting of strong fields at the frequency κ (which generate a field at the triple frequency 3κ) and of weak fields at the frequencies 2κ and 3κ (having an impact on the process of third harmonic generation due to the contribution of weak electromagnetic fields):$${\left\{{\overline{E}}_1^{\text{inc}}\left(n\mathit{\kappa };y,z\right)\right\}}_{n=1}^3\cup {\left\{{\underline{E}}_1^{\text{inc}}\left(n\mathit{\kappa };y,z\right)\right\}}_{n=1}^3,$$

where$${\left\{\left\{\begin{array}{c}{\overline{E}}_1^{\text{inc}}\left(n\mathit{\kappa };y,z\right)\\ {\underline{E}}_1^{\text{inc}}\left(n\mathit{\kappa };y,z\right)\end{array}\right\}=\left\{\begin{array}{c}{a}_{n\mathit{\kappa }}^{\text{inc}}\\ b_{n\mathit{\kappa }}^{\text{inc}}\end{array}\right\}exp\left[i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y\mp {\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z\mp 2\mathit{\pi }\mathit{\delta }\right)\right)\right],z\begin{array}{c}>\\ <\end{array}\pm 2\mathit{\pi }\mathit{\delta }\right\}}_{n=1}^3$$

with δ > 0, amplitudes ${\left\{a_{n\mathit{\kappa }}^{\text{inc}},b_{n\mathit{\kappa }}^{\text{inc}}\right\}}_{n=1}^3$; angles of incidence ${\left\{{\mathit{\varphi }}_{n\mathit{\kappa }},\mathit{\pi }-{\mathit{\varphi }}_{n\mathit{\kappa }}\right\}}_{n=1}^3$, $\left|{\mathit{\varphi }}_{n\mathit{\kappa }}\right|<\mathit{\pi }/2$ (cf. Figure 1) and frequencies nκ, $n=1,2,3$. Here Φ_nκ = nκ sin ϕ_nκ are the longitudinal propagation constants and ${\mathrm{\Gamma }}_{n\mathit{\kappa }}=\sqrt{{\left(n\mathit{\kappa }\right)}^2-{\mathrm{\Phi }}_{n\mathit{\kappa }}^2}$ are the transverse propagation constants, where ϕ_nκ is the given angle of incidence of the exciting field at the frequency nκ (cf. Figure 1). The upper/lower excitation fields of the nonlinear layer are denoted by overlined/underlined symbols.

Subject to Kleinman’s rule (i.e. the equality of all coefficients ${\mathit{\chi }}_{1111}^{(3)}$ at multiple frequencies (Kleinman, 1962; Miloslavsky, 2008), the problem under consideration can be reduced to the following system of boundary value problems with respect to the complex Fourier amplitudes of the scattered and generated fields(1) $$\begin{array}{c}{E}_1\left(n\mathit{\kappa };y,z\right)=\mathit{\chi }\left(z-2\mathit{\pi }\mathit{\delta }\right){\overline{E}}_1^{\text{inc}}\left(n\mathit{\kappa };y,z\right)+\mathit{\chi }\left(-z-2\mathit{\pi }\mathit{\delta }\right){\underline{E}}_1^{\text{inc}}\left(n\mathit{\kappa };y,z\right)+E_1^{\text{scat/gen}}\left(n\mathit{\kappa };y,z\right):\\ \left[\mathrm{\Delta }+{\left(n\mathit{\kappa }\right)}^2{\mathit{\epsilon }}_{n\mathit{\kappa }}\left(z,\mathit{\alpha }\left(z\right),E_1\left(\mathit{\kappa };y,z\right),E_1\left(2\mathit{\kappa };y,z\right),E_1\left(3\mathit{\kappa };y,z\right)\right)\right]E_1\left(n\mathit{\kappa };y,z\right)\\ =-{\mathit{\delta }}_n^1{\mathit{\kappa }}^2\mathit{\alpha }\left(z\right)E_1^2\left(2\mathit{\kappa };y,z\right)E_1^{*}\left(3\mathit{\kappa };y,z\right)\\ -{\mathit{\delta }}_n^3{\left(3\mathit{\kappa }\right)}^2\mathit{\alpha }\left(z\right)\left\{E_1^3\left(\mathit{\kappa };y,z\right)/3+E_1^2\left(2\mathit{\kappa };y,z\right)E_1^{*}\left(\mathit{\kappa };y,z\right)\right\},n=1,2,3,\end{array}$$(1)

where χ(z) = {0, z < 0; and 1, z ≥ 0}–the Heaviside function, $\mathrm{\Delta }=\mathit{\partial }{}^2/\mathit{\partial }y{}^2+\mathit{\partial }{}^2/\mathit{\partial }{z}^2$, ${\mathit{\delta }}_n^k$—Kronecker’s symbol,(2) $$\begin{array}{c}{\mathit{\epsilon }}_{n\mathit{\kappa }}=\left\{1,\left|z\right|>2\mathit{\pi }\mathit{\delta };\text{and}{\mathit{\epsilon }}^{\left(\text{L}\right)}+{\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)},\left|z\right|\le 2\mathit{\pi }\mathit{\delta }\right\},\\ {\mathit{\epsilon }}^{\left(\text{L}\right)}=1+4\mathit{\pi }{\mathit{\chi }}_{11}^{\left(1\right)}\left(z\right),\\ {\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)}=\mathit{\alpha }\left(z\right)\left[\sum _{m=1}^3{\left|E_1\left(m\mathit{\kappa };y,z\right)\right|}^2+\left\{{\mathit{\delta }}_n^1\frac{{\left[E_1^{*}\left(\mathit{\kappa };y,z\right)\right]}^2}{E_1\left(\mathit{\kappa };y,z\right)}+{\mathit{\delta }}_n^2\frac{E_1^{*}\left(2\mathit{\kappa };y,z\right)}{E_1\left(2\mathit{\kappa };y,z\right)}{E}_1\left(\mathit{\kappa };y,z\right)\right\}{E}_1\left(3\mathit{\kappa };y,z\right)\right],\end{array}$$(2)

–the dielectric permittivity, $\mathit{\alpha }\left(z\right)=6\mathit{\pi }{\mathit{\chi }}_{1111}^{\left(3\right)}\left(z\right)$—the function of cubic susceptibility of the nonlinear medium, ${\mathit{\chi }}_{11}^{\left(1\right)}$ and ${\mathit{\chi }}_{1111}^{\left(3\right)}$—components of the susceptibility tensors of the nonlinear medium.

The scattered and generated field in a transversely inhomogeneous, non-linear dielectric layer excited by a plane wave is quasi-homogeneous along the coordinate y; hence, it can be represented as follows:

Condition 1. $E_1\left(n\mathit{\kappa };y,z\right)=U\left(n\mathit{\kappa };z\right)exp\left(i\mathrm{\Phi }{}_{n\mathit{\kappa }}y\right)$, $n=1,2,3$.

Here $U\left(n\mathit{\kappa };z\right)$ and Φ_nκ = nκ sin ϕ_nκ denote the complex-valued transverse component of the Fourier amplitude of the electric field and the value of the longitudinal propagation constant (longitudinal wave-number) at the frequency nκ, respectively.

The dielectric permittivities of the layered structure at the multiple frequencies nκ are determined by the values of the transverse components of the Fourier amplitudes of the scattered and generated fields, i.e. by the redistribution of energy of the electric fields at multiple frequencies, where the angles of incidence are given and the nonlinear structure under consideration is transversely inhomogeneous. The condition of the longitudinal homogeneity (along the coordinate y) of the nonlinear layered structure (2) can be written as follows:$${\mathit{\epsilon }}_{n\mathit{\kappa }}\left(z,\mathit{\alpha }\left(z\right),E_1\left(\mathit{\kappa };y,z\right),E_1\left(2\mathit{\kappa };y,z\right),E_1\left(3\mathit{\kappa };y,z\right)\right)={\mathit{\epsilon }}_{n\mathit{\kappa }}\left(z,\mathit{\alpha }\left(z\right),U\left(\mathit{\kappa };z\right),U\left(2\mathit{\kappa };z\right),U\left(3\mathit{\kappa };z\right)\right),n=1,2,3.$$

Having used the representation (2) for ${\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)}$ and the Condition 1, we obtain the following physically consistent requirement, which we call the condition of the phase synchronism of waves:

Condition 2. ${\mathrm{\Phi }}_{n\mathit{\kappa }}=n{\mathrm{\Phi }}_{\mathit{\kappa }}$ or ϕ_nκ = ϕ_κ, $n=1,2,3$.

It has been shown in detail in Angermann and Yatsyk (2011), Yatsyk (2011) that the Condition 2 is a formal consequence of Condition 1 and Equation (2) but not an independent assumption. We note that in view of Condition 2 the nonlinear layered structure remains longitudinally homogeneous. In this case, the quasi-homogeneous plane waves exciting the nonlinear layer at a set of multiple frequencies ${\left\{n\mathit{\kappa }\right\}}_{n=1}^3$ impinge on the nonlinear layer at the angles ${\left\{{\mathit{\varphi }}_{n\mathit{\kappa }},\mathit{\pi }-{\mathit{\varphi }}_{n\mathit{\kappa }}\right\}}_{n=1}^3$, $\left|{\mathit{\varphi }}_{n\mathit{\kappa }}\right|<\mathit{\pi }/2$ with equal values ϕ_nκ = ϕ_κ, but the amplitudes ${\left\{a_{n\mathit{\kappa }}^{\text{inc}},b_{n\mathit{\kappa }}^{\text{inc}}\right\}}_{n=1}^3$ of these waves may be arbitrary (cf. Condition 2 and Figure 1).

In addition, we pose the following conditions:

Condition 3. The tangential components ${\mathbf{E}}_{\text{tg}}\left(n\mathit{\kappa };y,z\right)$ and ${\mathbf{H}}_{\text{tg}}\left(n\mathit{\kappa };y,z\right)$ of the intensity vectors of the full electromagnetic fields $\mathbf{E}$ and $\mathbf{H}$ are continuous at the boundaries of the layered structure.

Condition 4. $E_1^{\text{scat/gen}}\left(n\mathit{\kappa };y,z\right)=\left\{\begin{array}{c}{a}_{n\mathit{\kappa }}^{\text{scat/gen}}\\ b_{n\mathit{\kappa }}^{\text{scat/gen}}\end{array}\right\}exp\left[i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y\pm {\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z\mp 2\mathit{\pi }\mathit{\delta }\right)\right)\right],z\begin{array}{c}>\\ <\end{array}\pm 2\mathit{\pi }\mathit{\delta }$, for $\text{Im}{\mathrm{\Gamma }}_{n\mathit{\kappa }}\equiv 0$ and $\text{Re}{\mathrm{\Gamma }}_{n\mathit{\kappa }}>0$—the radiation condition w.r.t. the scattered and generated fields.

The sought complex Fourier amplitudes of the total scattered and generated fields in the problem (1) incl. Conditions 1–4 at the multiple frequencies ${\left\{n\mathit{\kappa }\right\}}_{n=1}^3$ can be represented in the form(3) $$\begin{array}{c}{E}_1\left(n\mathit{\kappa };y,z\right)=U\left(n\mathit{\kappa };z\right)exp\left(i{\mathrm{\Phi }}_{n\mathit{\kappa }}y\right)\\ =\left\{\begin{array}{cc}{a}_{n\mathit{\kappa }}^{\text{inc}}exp\left(i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y-{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z-2\mathit{\pi }\mathit{\delta }\right)\right)\right)+a_{n\mathit{\kappa }}^{\text{scat/gen}}exp\left(i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y+{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z-2\mathit{\pi }\mathit{\delta }\right)\right)\right),\hfill & z>2\mathit{\pi }\mathit{\delta },\hfill \\ U\left(n\mathit{\kappa };z\right)exp\left(i{\mathrm{\Phi }}_{n\mathit{\kappa }}y\right),\hfill & \left|z\right|\le 2\mathit{\pi }\mathit{\delta },\hfill \\ b_{n\mathit{\kappa }}^{\text{inc}}exp\left(i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y+{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z+2\mathit{\pi }\mathit{\delta }\right)\right)\right)+b_{n\mathit{\kappa }}^{\text{scat/gen}}exp\left(i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y-{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z+2\mathit{\pi }\mathit{\delta }\right)\right)\right),\hfill & z<-2\mathit{\pi }\mathit{\delta }.\hfill \end{array}\right.\end{array}$$(3)

Taking into consideration (3), the nonlinear system (1) incl. Conditions 1–4 is equivalent to a system (see Angermann & Yatsyk, 2011a, 2011b) of nonlinear boundary-value problems of Sturm–Liouville type(4) $$\begin{array}{c}\left[d^{2}d{z}^2+{\mathrm{\Gamma }}_{n\mathit{\kappa }}^2-\left(n\mathit{\kappa }\right){}^2\left\{1-{\mathit{\epsilon }}_{n\mathit{\kappa }}\left(z,\mathit{\alpha }\left(z\right),U\left(\mathit{\kappa };z\right),U\left(2\mathit{\kappa };z\right),U\left(3\mathit{\kappa };z\right)\right)\right\}\right]U\left(n\mathit{\kappa };z\right)\\ =-\left(n\mathit{\kappa }\right){}^2\mathit{\alpha }\left(z\right)\left({\mathit{\delta }}_n^1{U}^2\left(2\mathit{\kappa };z\right)U^{*}\left(3\mathit{\kappa };z\right)+{\mathit{\delta }}_n^3\left\{U^3\left(\mathit{\kappa };z\right)/3+U^2\left(2\mathit{\kappa };z\right)U^{*}\left(\mathit{\kappa };z\right)\right\}\right),\left|z\right|\le 2\mathit{\pi }\mathit{\delta },\\ \left[i{\mathrm{\Gamma }}_{n\mathit{\kappa }}-d/dz\right]U\left(n\mathit{\kappa };2\mathit{\pi }\mathit{\delta }\right)=2i{\mathrm{\Gamma }}_{n\mathit{\kappa }}{\overline{U}}^{\text{inc}}\left(n\mathit{\kappa };2\mathit{\pi }\mathit{\delta }\right),\\ \left[i{\mathrm{\Gamma }}_{n\mathit{\kappa }}+d/dz\right]U\left(n\mathit{\kappa };-2\mathit{\pi }\mathit{\delta }\right)=2i{\mathrm{\Gamma }}_{n\mathit{\kappa }}{\underline{U}}^{\text{inc}}\left(n\mathit{\kappa };-2\mathit{\pi }\mathit{\delta }\right),n=1,2,3,\\ \end{array}$$(4)

and also to a system of one-dimensional nonlinear integral equations w.r.t. the unknown functions $U\left(n\mathit{\kappa };·\right)\in L_2\left(-2\mathit{\pi }\mathit{\delta },2\mathit{\pi }\mathit{\delta }\right)$,(5) $$\begin{array}{c}U\left(n\mathit{\kappa };z\right)+\frac{i{\left(n\mathit{\kappa }\right)}^2}{2{\mathrm{\Gamma }}_{n\mathit{\kappa }}}\underset{-2\mathit{\pi }\mathit{\delta }}{\overset{2\mathit{\pi }\mathit{\delta }}{\int }}exp\left(i{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left|z-\mathit{\xi }\right|\right)\left[1-{\mathit{\epsilon }}_{n\mathit{\kappa }}\left(\mathit{\xi },\mathit{\alpha }\left(\mathit{\xi }\right),U\left(\mathit{\kappa };\mathit{\xi }\right),U\left(2\mathit{\kappa };\mathit{\xi }\right),U\left(3\mathit{\kappa };\mathit{\xi }\right)\right)\right]U\left(n\mathit{\kappa };\mathit{\xi }\right)d\mathit{\xi }\\ =\frac{i{\left(n\mathit{\kappa }\right)}^2}{2{\mathrm{\Gamma }}_{n\mathit{\kappa }}}\underset{-2\mathit{\pi }\mathit{\delta }}{\overset{2\mathit{\pi }\mathit{\delta }}{\int }}exp\left(i{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left|z-\mathit{\xi }\right|\right)\mathit{\alpha }\left(\mathit{\xi }\right)\left[{\mathit{\delta }}_n^1{U}^2\left(2\mathit{\kappa };\mathit{\xi }\right)U^{*}\left(3\mathit{\kappa };\mathit{\xi }\right)\right.\\ +\left.{\mathit{\delta }}_n^3\left\{U^3\left(\mathit{\kappa };\mathit{\xi }\right)/3+U^2\left(2\mathit{\kappa };\mathit{\xi }\right)U^{*}\left(\mathit{\kappa };\mathit{\xi }\right)\right\}\right]d\mathit{\xi }+{\overline{U}}^{\text{inc}}\left(n\mathit{\kappa };z\right)+{\underline{U}}^{\text{inc}}\left(n\mathit{\kappa };z\right),n=1,2,3.\\ \end{array}$$(5)

Here ${\overline{U}}^{\text{inc}}\left(n\mathit{\kappa };z\right)=a_{n\mathit{\kappa }}^{\text{inc}}exp\left[-i{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z-2\mathit{\pi }\mathit{\delta }\right)\right]$, ${\underline{U}}^{\text{inc}}\left(n\mathit{\kappa };z\right)=b_{n\mathit{\kappa }}^{\text{inc}}exp\left[+i{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z+2\mathit{\pi }\mathit{\delta }\right)\right]$, $n=1,2,3$.

The solution of the problem (1) incl. Conditions 1–4, represented in (3), can be obtained from (4) or (5) using the formulas $U\left(n\mathit{\kappa };2\mathit{\pi }\mathit{\delta }\right)=a{}_{n\mathit{\kappa }}^{\text{inc}}+a{}_{n\mathit{\kappa }}^{\text{scat/gen}}$, $U\left(n\mathit{\kappa };-2\mathit{\pi }\mathit{\delta }\right)=b_{n\mathit{\kappa }}^{\text{inc}}+b_{n\mathit{\kappa }}^{\text{scat/gen}}$, $n=1,2,3$.

3. Self-consistent analysis of the system of nonlinear equations and eigenoscillations

According to Angermann and Yatsyk (2011a, 2011b, 2012, 2013a, 2013b), Angermann, Yatsyk, et al. (2013), Angermann, Krevchenko, et al. (2013a, 2013b), Yatsyk (2012, 2013), the application of suitable quadrature rules to the system (5) leads to a system of complex-valued nonlinear algebraic equations of the second kind(6) $$\begin{array}{c}\left[\mathbf{I}-{\mathbf{B}}_{n\mathit{\kappa }}\left({\mathbf{U}}_{\mathit{\kappa }},{\mathbf{U}}_{2\mathit{\kappa }},{\mathbf{U}}_{3\mathit{\kappa }}\right)\right]{\mathbf{U}}_{n\mathit{\kappa }}\\ ={\mathit{\delta }}_n^1{\mathbf{C}}_{\mathit{\kappa }}\left({\mathbf{U}}_{2\mathit{\kappa }},{\mathbf{U}}_{3\mathit{\kappa }}\right)+{\mathit{\delta }}_n^3{\mathbf{C}}_{3\mathit{\kappa }}\left({\mathbf{U}}_{\mathit{\kappa }},{\mathbf{U}}_{2\mathit{\kappa }}\right)+{\overline{\mathbf{U}}}_{n\mathit{\kappa }}^{\text{inc}}+{\underline{\mathbf{U}}}_{n\mathit{\kappa }}^{\text{inc}},n=1,2,3,\\ \end{array}$$(6)

where ${\mathbf{U}}_{n\mathit{\kappa }}={\left\{U_l\left(n\mathit{\kappa }\right)\right\}}_{l=1}^N\approx {\left\{U_{n\mathit{\kappa }}\left(z_l\right)\equiv U\left(n\mathit{\kappa };z_l\right)\right\}}_{l=1}^N$—the vectors of the unknown approximate values of the solution, $\left\{{\left\{z_l\right\}}_{l=1}^N:z_1=-2\mathit{\pi }\mathit{\delta }<...<z_l<...<z_N=2\mathit{\pi }\mathit{\delta }\right\}$—a discrete set of interpolation nodes, $\mathbf{I}={\{{\mathit{\delta }}_l^m\}}_{l,m=1}^N$—the identity matrix, ${\mathbf{B}}_{n\mathit{\kappa }}\left({\mathbf{U}}_{\mathit{\kappa }},{\mathbf{U}}_{2\mathit{\kappa }},{\mathbf{U}}_{3\mathit{\kappa }}\right)$—nonlinear matrices, ${\mathbf{C}}_{\mathit{\kappa }}\left({\mathbf{U}}_{2\mathit{\kappa }},{\mathbf{U}}_{3\mathit{\kappa }}\right)$, ${\mathbf{C}}_{3\mathit{\kappa }}\left({\mathbf{U}}_{\mathit{\kappa }},{\mathbf{U}}_{2\mathit{\kappa }}\right)$—the vectors of the right-hand sides determined by the choice of the quadrature rule, and ${\overline{\mathbf{U}}}_{n\mathit{\kappa }}^{\text{inc}}={\left\{a_{n\mathit{\kappa }}^{\text{inc}}exp{\left[-i{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z_l-2\mathit{\pi }\mathit{\delta }\right)\right]}^{}\right\}}_{l=1}^N$, ${\underline{\mathbf{U}}}_{n\mathit{\kappa }}^{\text{inc}}={\left\{b_{n\mathit{\kappa }}^{\text{inc}}exp{\left[+i{\mathrm{\Gamma }}_{n\mathit{\kappa }}\left(z_l+2\mathit{\pi }\mathit{\delta }\right)\right]}^{}\right\}}_{l=1}^N$—the vectors induced by the incident wave packets. A solution of (6) can be found iteratively by the help of a block Jacobi method, where at each step a system of linearized algebraic equations is solved.

The analytic continuation of the linearized nonlinear problems into the region of complex values of the frequency parameter allows us to switch to the analysis of spectral problems (Angermann & Yatsyk, 2011, 2012, 2013a, 2013b; Angermann, Yatsyk, et al., 2013; Shestopalov & Sirenko, 1989; Shestopalov & Yatsik, 1997; Yatsyk, 2000, 2001, 2013). The problem of finding the eigenfrequencies κ_n and the eigenfields ${\mathbf{U}}_{{\mathit{\kappa }}_n}$ reads as follows (cf. (6)):(7) $$\left\{\begin{array}{cc}{f}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)=det\left[\mathbf{I}-{\mathbf{B}}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)\right]=0\hfill & \\ \left[\mathbf{I}-{\mathbf{B}}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)\right]{\mathbf{U}}_{{\mathit{\kappa }}_n}=\mathbf{0}\hfill & \mathit{\kappa }\equiv {\mathit{\kappa }}^{\text{inc}};{\mathit{\kappa }}_n\in {\mathrm{\Omega }}_{n\mathit{\kappa }}\subset {\mathrm{H}}_{n\mathit{\kappa }},\hfill \end{array}\right.$$(7)

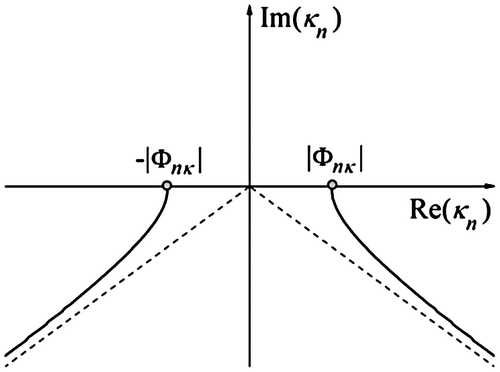
where ${\mathit{\kappa }}_n\in {\mathrm{\Omega }}_{n\mathit{\kappa }}\subset {\mathrm{H}}_{n\mathit{\kappa }}$, at $\mathit{\kappa }\equiv {\mathit{\kappa }}^{\text{inc}}$, $n=1,2,3$, Ω_nκ are the sets of eigenfrequencies and ${\mathrm{H}}_{n\mathit{\kappa }}$ denote two-sheeted Riemann surfaces (cf. Figure 2), ${\mathbf{U}}_{{\mathit{\kappa }}_n}={\left\{U_l\left({\mathit{\kappa }}_n\right)\right\}}_{l=1}^N\approx {\left\{U\left({\mathit{\kappa }}_n;z_l\right)\right\}}_{l=1}^N$–the vector of unknown values of the nontrivial solution at the nodes in the layer corresponding to the eigenfrequency κ_n, ${\mathbf{B}}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)={\mathbf{B}}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n;{\mathbf{U}}_{\mathit{\kappa }},{\mathbf{U}}_{2\mathit{\kappa }},{\mathbf{U}}_{3\mathit{\kappa }}\right)$–the matrix with the given vectors ${\mathbf{U}}_{n\mathit{\kappa }}$ (cf. (6)).

Figure 2. The geometry of the two-sheeted Riemann surfaces H_nκ.

We mention that the radiation condition to the eigenfield (cf. Condition 4)$$E_1\left({\mathit{\kappa }}_n;y,z\right)=\left\{\begin{array}{c}{a}_{{\mathit{\kappa }}_n}\\ b_{{\mathit{\kappa }}_n}\end{array}\right\}exp\left[i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y\pm {\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)\left(z\mp 2\mathit{\pi }\mathit{\delta }\right)\right)\right],z\begin{array}{c}>\\ <\end{array}\pm 2\mathit{\pi }\mathit{\delta },n=1,2,3$$

for real values of the parameters κ_n and Φ_nκ is consistent with the physically justified requirement of the absence of waves coming from infinity z = ± ∞ in the radiation field:(8) $$\text{Im}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)\ge 0,\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)·\text{Re}{\mathit{\kappa }}_n\ge 0,\text{for}\text{Im}{\mathrm{\Phi }}_{n\mathit{\kappa }}=0\text{Im}\mathit{\kappa }{}_n=0,n=1,2,3.$$(8)

The nontrivial solutions of the spectral problem (7) allow us to write the electric components of the eigenfield as follows:(9) $$\begin{array}{c}{E}_1\left({\mathit{\kappa }}_n;y,z\right)=U\left({\mathit{\kappa }}_n;z\right)exp\left(i{\mathrm{\Phi }}_{n\mathit{\kappa }}y\right)\\ =\left\{\begin{array}{cc}{a}_{{\mathit{\kappa }}_n}exp\left[i\left({\mathrm{\Phi }}_{n\mathit{\kappa }}y+{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)\left(z-2\mathit{\pi }\mathit{\delta }\right)\right)\right],\hfill & z>2\mathit{\pi }\mathit{\delta },\hfill \\ U\left({\mathit{\kappa }}_n;z\right)exp\left(i{\mathrm{\Phi }}_{n\mathit{\kappa }}y\right),\hfill & \left|z\right|\le 2\mathit{\pi }\mathit{\delta },\hfill \\ b_{{\mathit{\kappa }}_n}exp\left[i\left(\mathrm{\Phi }{}_{n\mathit{\kappa }}y-{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)\left(z+2\mathit{\pi }\mathit{\delta }\right)\right)\right],\hfill & z<-2\mathit{\pi }\mathit{\delta },\hfill \end{array}\right.\\ {\mathit{\kappa }}_n\in {\mathrm{\Omega }}_{n\mathit{\kappa }}\subset {\mathrm{H}}_{n\mathit{\kappa }},n=1,2,3.\\ \end{array}$$(9)

Here: $\mathit{\kappa }\equiv {\mathit{\kappa }}^{\text{inc}}$–a given constant value equal to the excitation frequency of the nonlinear structure, $a_{{\mathit{\kappa }}_n}=U\left({\mathit{\kappa }}_n;2\mathit{\pi }\mathit{\delta }\right)$ и $b_{{\mathit{\kappa }}_n}=U\left({\mathit{\kappa }}_n;-2\mathit{\pi }\mathit{\delta }\right)$–the radiation coefficients of the eigenfield, ${\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)={\left({\mathit{\kappa }}_n^2-{\mathrm{\Phi }}_{n\mathit{\kappa }}^2\right)}^{1/2}$–the functions of the transverse propagation (depending on the complex spectral frequency parameters κ_n), ${\mathrm{\Phi }}_{n\mathit{\kappa }}=n\mathit{\kappa }sin\left({\mathit{\varphi }}_{n\mathit{\kappa }}\right)$—the given real values of the longitudinal propagation constants.

The range of variation of the spectral frequency parameters is completely determined by the boundaries of the possible analytic continuation of the canonical Green’s functions (i.e. the Green’s functions for the unperturbed quasi-homogeneous problems with ${\mathit{\epsilon }}_{n\mathit{\kappa }}\equiv 1$, $n=1,2,3$) into the complex spaces of the spectral frequency parameters κ_n (Angermann & Yatsyk, 2011, 2012, 2013a, 2013b; Angermann, Yatsyk, et al., 2013; Shestopalov & Sirenko, 1989; Shestopalov & Yatsik, 1997; Yatsyk, 2000, 2001, 2013).$$G_0^{(QH)}\left({\mathit{\kappa }}_n;y,z,z_0\right)=\frac{i}{2}exp\left\{i\left[\mathrm{\Phi }{}_{n\mathit{\kappa }}y+{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)\left|z-z_0\right|\right]\right\}/{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right),n=1,2,3.$$

These complex spaces are two-sheeted Riemann surfaces ${\mathrm{H}}_{n\mathit{\kappa }}$ (see Figure 2) with real algebraic branch points of second-order ${\mathit{\kappa }}_n{}^{\pm }:{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n{}^{\pm },{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)=0$ (i.e. ${\mathit{\kappa }}_n{}^{\pm }=\pm |{\mathrm{\Phi }}_{n\mathit{\kappa }}|$, $n=1,2,3$) and cuts along the lines(10) $${(\text{Re}{\mathit{\kappa }}_n)}^2-{(\text{Im}{\mathit{\kappa }}_n)}^2-{\mathrm{\Phi }}_{n\mathit{\kappa }}{}^2=0,\text{Im}{\mathit{\kappa }}_n\le 0,n=1,2,3.$$(10)

The first, proper (or physical) sheets (i.e. the pair of values $\left\{{\mathit{\kappa }}_n,{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)\right.\}$) on each of the surfaces ${\mathrm{H}}_{n\mathit{\kappa }}$, $n=1,2,3$, are completely determined by the condition (8) and the cuts (10). At the first sheets ${\mathrm{H}}_{n\mathit{\kappa }}$ the signs of the pairs $\left\{{\mathit{\kappa }}_n,\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\right\}$ and $\left\{{\mathit{\kappa }}_n,\text{Im}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\right\}$ are distributed as follows: $\text{Im}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}>0$ for $0<arg{\mathit{\kappa }}_n<\mathit{\pi }$, $\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\ge 0$ for $0<arg{\mathit{\kappa }}_n<\mathit{\pi }/2$ and $\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\le 0$ for $\mathit{\pi }/2\le arg{\mathit{\kappa }}_n<\mathit{\pi }$. For points κ_n with $3\mathit{\pi }/22\le arg{\mathit{\kappa }}_n\le 2\mathit{\pi }$ the function values (where ${(\text{Re}{\mathit{\kappa }}_n)}^2-{(\text{Im}\mathit{\kappa }{}_n)}^2-{\mathrm{\Phi }}_{n\mathit{\kappa }}^2>0$) are determined by the condition $\text{Im}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}<0$, $\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}>0$, for the remaining points κ_n the function ${\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\left({\mathit{\kappa }}_n,{\mathrm{\Phi }}_{n\mathit{\kappa }}\right)$ is determined by the condition $\text{Im}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}>0$, $\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}\le 0$. In the region $\mathit{\pi }<arg{\mathit{\kappa }}_n<3\mathit{\pi }/2$ the situation is similar to the previous one up to the change of the sign of $\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}$. The second, improper (or unphysical) sheets of the surfaces ${\mathrm{H}}_{n\mathit{\kappa }}$, $n=1,2,3,$ are different from the proper ones in that, for each κ_n, the signs of both $\text{Re}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}$ and $\text{Im}{\mathrm{\Gamma }}_{{\mathit{\kappa }}_n}$ are reversed.

The eigenfrequencies ${\mathit{\kappa }}_n\in {\mathrm{\Omega }}_{n\mathit{\kappa }}\subset {\mathrm{H}}_{n\mathit{\kappa }}$, $n=1,2,3$, i.e. the characteristic numbers of the dispersion equations of problem (7), are obtained by solving the corresponding dispersion equations $f_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)=det\left(\mathbf{I}-{\mathbf{B}}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)\right)=0$ using Newton’s method or a modification of it. The nontrivial solutions ${\mathbf{U}}_{{\mathit{\kappa }}_n}$ of the homogeneous systems $\left(\mathbf{I}-{\mathbf{B}}_{n\mathit{\kappa }}\left({\mathit{\kappa }}_n\right)\right)·{\mathbf{U}}_{{\mathit{\kappa }}_n}=\mathbf{0}$ of linear algebraic equations (7) corresponding to these characteristic numbers are the eigenfields (9) of the linearized nonlinear layered structures with an induced dielectric permittivity (2). Obviously, the solutions ${\mathbf{U}}_{{\mathit{\kappa }}_n}$ are sought up to an arbitrary multiplicative constant. Therefore, we have required that $U\left({\mathit{\kappa }}_n;2\mathit{\pi }\mathit{\delta }\right)=a_{{\mathit{\kappa }}_n}\equiv 1$, $n=1,2,3$, in the representation (9) of ${\mathbf{U}}_{{\mathit{\kappa }}_n}$.

Finally, we mention that the classification of scattered, generated, or eigenfields of the dielectric layer by the H_m,l,p-type adopted in our paper is identical to that given in (Angermann & Yatsyk, 2012, 2013a, 2013b; Shestopalov & Sirenko, 1989; Shestopalov & Yatsik, 1997; Yatsyk, 2000, 2001, 2011). In the case of E-polarization, H_m,l,p (or TE_m,l,p) denotes the type of polarization of the wave field under investigation. The subscripts indicate the number of local maxima of $\left|E_x\right|$ (or $\left|U\right|$, as $\left|U\right|=\left|E_x\right|$, see (3), (9)) in the dielectric layer, i.e. along the coordinate axes x, y и z (see Figure 1). Since the considered waves are homogeneous along the x-axis and quasi-homogeneous along the y-axis, we actually study fields of the type H_0,0,p (or TE_0,0,p), where the subscript p is equal to the number of local maxima of the function $\left|U\right|$ of the argument z in $\left[-2\mathit{\pi }\mathit{\delta },2\mathit{\pi }\mathit{\delta }\right]$.

4. Numerical results

In order to describe the scattering and generation properties of the nonlinear structure, we introduce the following notation:(11) $$R_{n\mathit{\kappa }}^{+}={\left|a_{n\mathit{\kappa }}^{scat/gen}\right|}^2/\sum _{s=1}^3\left({\left|a_{s\mathit{\kappa }}^{inc}\right|}^2+{\left|b_{s\mathit{\kappa }}^{inc}\right|}^2\right)\text{if}z>2\mathit{\pi }\mathit{\delta },$$(11)

and(12) $$R_{n\mathit{\kappa }}^{-}={\left|b_{n\mathit{\kappa }}^{scat/gen}\right|}^2/{\sum }_{s=1}^3\left({\left|a_{s\mathit{\kappa }}^{inc}\right|}^2+{\left|b_{s\mathit{\kappa }}^{inc}\right|}^2\right)\text{if}z<-2\mathit{\pi }\mathit{\delta }.$$(12)

The quantities $R_{n\mathit{\kappa }}^{+},$ $R_{n\mathit{\kappa }}^{-}$ are called scattering/generation (or radiation) coefficients of the waves w.r.t. the total intensity of the incident packet. (Note that alternatively the radiation coefficients can be chosen according to ${\left(R_{n\mathit{\kappa }}^{\pm }\right)}^{1/2}$).

We define by$$W_{n\mathit{\kappa }}={\left|a_{n\mathit{\kappa }}^{\text{scat/gen}}\right|}^2+{\left|b_{n\mathit{\kappa }}^{\text{scat/gen}}\right|}^2,n=1,2,3$$

the total energy of the scattered and generated fields at the frequencies nκ and consider the quantity(13) $$W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}=\frac{W_{3\mathit{\kappa }}\left(a_{3\mathit{\kappa }}^{\text{scat/gen}},b_{3\mathit{\kappa }}^{\text{scat/gen}}\right)}{W_{\mathit{\kappa }}\left(a_{\mathit{\kappa }}^{\text{scat/gen}},b_{\mathit{\kappa }}^{\text{scat/gen}}\right)}$$(13)

which characterizes the portion of energy generated in the third harmonic in comparison to the energy scattered in the first harmonic.

In the case of problem (1) incl. Conditions 1–4, for nonabsorbing media with $\text{Im}\left[{\mathit{\epsilon }}^{\left(\text{L}\right)}\left(z\right)\right]\equiv 0$, the validity of the energy balance law$${\sum }_{n=1}^3\left[R_{n\mathit{\kappa }}^{+}+R_{n\mathit{\kappa }}^{-}\right]=1$$

has been verified numerically. Computational experiments for the processes of scattering and generation of oscillations without any impact of weak fields $a_{2\mathit{\kappa }}^{inc}=a_{3\mathit{\kappa }}^{inc}=0$ have shown that the error of the energy balance law$$W^{\left(\text{Error}\right)}=1-{\sum }_{n=1}^3\left[R_{n\mathit{\kappa }}^{+}+R_{n\mathit{\kappa }}^{-}\right]$$

does not exceed the value $\left|W^{\left(\text{Error}\right)}\right|<{10}^{-8}$. The consideration of weak fields $a_{n\mathit{\kappa }}^{inc}\ne 0$, $n=2,3$ in the investigation of the same scattering and generation processes can lead to errors in the balance equation of a few percent (Angermann & Yatsyk, 2012, 2013a, 2013b; Angermann, Krevchenko, et al., 2013a, 2013b). This indicates that the amplitudes of the weak fields $a_{n\mathit{\kappa }}^{inc}\ne 0$, $n=2,3$ are sufficiently large, and that these fields can serve as a source of generation of oscillations themselves. In such situations the presented mathematical model (1) incl. Conditions 1–4 (cf. also (6)) and the linearized spectral problems (7) should take into account the complex Fourier amplitudes of oscillations at frequencies nκ with numbers n larger than three.

4.1. Decanalizing and canalizing nonlinear media

Consider a decanalizing ($\mathit{\alpha }\left(z\right)<0$) and a canalizing ($\mathit{\alpha }\left(z\right)>0$) nonlinear dielectric structure with the parameters ${\mathit{\epsilon }}^{\left(\text{L}\right)}\left(z\right)=16$, $\mathit{\alpha }\left(z\right)=\mp 0.01$, δ = 0.5. The excitation of the nonlinear layer takes place from above by only one strong top electromagnetic field at the basic frequency, i.e. $\left\{a_{\mathit{\kappa }}^{\text{inc}}\ne 0,a_{2\mathit{\kappa }}^{\text{inc}}=0,a_{3\mathit{\kappa }}^{\text{inc}}=0\right\},$ $\left\{b_{\mathit{\kappa }}^{\text{inc}}=0,b_{2\mathit{\kappa }}^{\text{inc}}=0,b_{3\mathit{\kappa }}^{\text{inc}}=0\right\}$ and $\mathit{\kappa }={\mathit{\kappa }}^{\text{inc}}=0.375$.

The study of the scattering and generation properties of the nonlinear layers is carried out by means of consideration of the eigenmodes. The computational results are shown in Figures 3–8 pairwise, for media with a value of the cubic susceptibility α = −0.01 (left column) and α = +0.01 (right column).

Figure 3. Relative portion of energy generated in the third harmonic $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$, the scattering $R_{\mathit{\kappa }}^{+},R_{\mathit{\kappa }}^{-}$ and generation $R_{3\mathit{\kappa }}^{+}{R}_{3\mathit{\kappa }}^{-}$ coefficients for α = −0.01 (left top/bottom) and for α = +0.01 (right top/bottom).

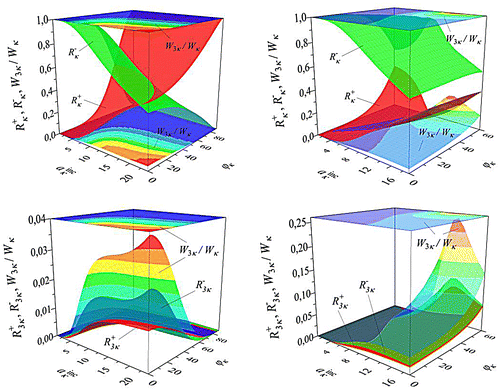
Figure 4. Curves at $a_{\mathit{\kappa }}^{\text{inc}}=24$, ϕ_κ = 0° for α = −0.01 (left) and at $a_{\mathit{\kappa }}^{\text{inc}}=14$, ϕ_κ = 66° for α = +0.01 (right): 1 – ${\mathit{\epsilon }}^{\left(\text{L}\right)}$, 2 – $\left|U\left(\mathit{\kappa };z\right)\right|$, 3 – $\left|U\left(3\mathit{\kappa };z\right)\right|$, 4 – $\text{Re}\left({\mathit{\epsilon }}_{\mathit{\kappa }}\right)$, 5 – $\text{Im}\left({\mathit{\epsilon }}_{\mathit{\kappa }}\right)$, 6 – $\text{Re}\left({\mathit{\epsilon }}_{3\mathit{\kappa }}\right)$, 7 – $\text{Im}\left({\mathit{\epsilon }}_{3\mathit{\kappa }}\right)\equiv 0$.

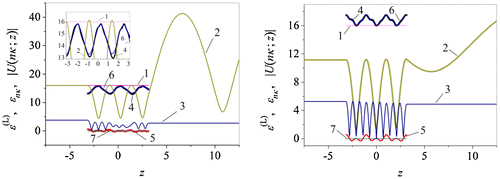
Figure 5. Scattered $\left|U_{\mathit{\kappa }}\left[a_{\mathit{\kappa }}^{\text{inc}},z\right]\right|$ and generated $\left|U_{3\mathit{\kappa }}\left[a_{\mathit{\kappa }}^{\text{inc}},z\right]\right|$ fields in the nonlinear layer at ϕ_κ = 0° for α = −0.01 (left) and ϕ_κ = 60° for α = +0.01 (right).

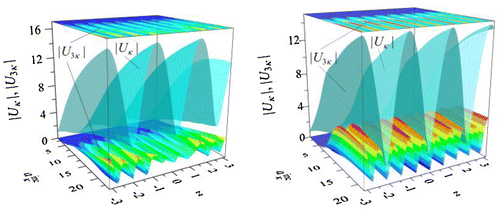
Figure 6. Curves at ϕ_κ = 0°, for α = −0.01 (left) and at ϕ_κ = 60° for α = +0.01 (right): 1 – $R_{\mathit{\kappa }}^{+}$, 2 – $R_{\mathit{\kappa }}^{-}$, 3 – $R_{2\mathit{\kappa }}^{+}\equiv 0$, 4 – $R_{2\mathit{\kappa }}^{-}\equiv 0$, 5 – $R_{3\mathit{\kappa }}^{+}$, 6 – $R_{3\mathit{\kappa }}^{-}$, 7 – $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$.

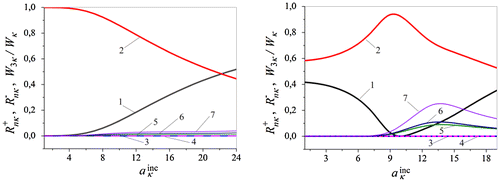
Figure 7. Curves at ϕ_κ = 0° (left) and ϕ_κ = 60° (right): 1 … $\mathit{\kappa }={\mathit{\kappa }}^{\text{inc}}=0.375$, 2 … $3\mathit{\kappa }={\mathit{\kappa }}^{\text{gen}}=3{\mathit{\kappa }}^{\text{inc}}$; 3.1 … $\text{Re}\left({\mathit{\kappa }}_1^{\left(\text{L}\right)}\right)$, 3.2 … $\text{Im}\left({\mathit{\kappa }}_1^{\left(\text{L}\right)}\right)$, 4.1 … $\text{Re}\left({\mathit{\kappa }}_3^{\left(\text{L}\right)}\right)$, 4.2 … $\text{Im}\left({\mathit{\kappa }}_3^{\left(\text{L}\right)}\right)$ for α ≡ 0; 5.1 … $\text{Re}\left({\mathit{\kappa }}_1^{\left(\text{NL}\right)}\right)$, 5.2 … $\text{Im}\left({\mathit{\kappa }}_1^{\left(\text{NL}\right)}\right)$, 6.1 … $\text{Re}\left({\mathit{\kappa }}_3^{\left(\text{NL}\right)}\right)$, 6.2 … $\text{Im}\left({\mathit{\kappa }}_3^{\left(\text{NL}\right)}\right)$ for α = −0.01 (left) and for α = +0.01 (right).

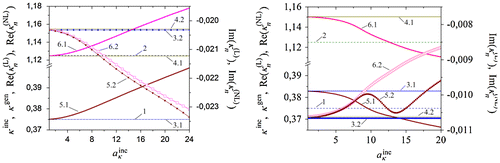
Figure 8. The Q-factor and the relative Q-factor. Curves: 1 … $Q_{{\mathit{\kappa }}_1}$, 3 … $Q_{{\mathit{\kappa }}_3}$, and … $Q_{{\mathit{\kappa }}_1}/Q_{{\mathit{\kappa }}_3}$ at ${\mathit{\kappa }}^{\text{inc}}=0.375$, ${\mathit{\kappa }}_n={\mathit{\kappa }}_n^{\left(\text{NL}\right)}$, $n=1,3$, for ϕ_κ = 0°, α = −0.01 (left top/bottom) and for ϕ_κ = 60°, α = +0.01 (right top/bottom).

In the case of decanalizing media in Figure 3 (left column), the maximal portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is observed for $a_{\mathit{\kappa }}^{\text{inc}}=24$ and normal excitation ϕ_κ = 0° of the nonlinear layer. In the investigated range of amplitudes and incident angles $a_{\mathit{\kappa }}^{\text{inc}}\in \left[1,24\right]$, ${\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)$, an increase of $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is observed for parameters corresponding to the closest values of the scattering coefficients $R_{\mathit{\kappa }}^{+}\approx R_{\mathit{\kappa }}^{-}$. The maximal portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}=0.039$ does not exceed 4%.

In the case of canalizing media in Figure 3 (right column) in the range of $a_{\mathit{\kappa }}^{\text{inc}}\in \left[1,19\right]$, ${\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ },{60}^{\circ }\right]$ the maximal value $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}=0.2505$ for $a_{\mathit{\kappa }}^{\text{inc}}=14$ and ϕ_κ = 60° reaches 25%. The increase of the portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is achieved by increasing the amplitude $a_{\mathit{\kappa }}^{\text{inc}}$at incident angles ϕ_κ which lie slightly above the canalizing angle. The latter corresponds to the greatest possible transparency of the scattering at the frequency κ, where the reflection coefficient $R_{\mathit{\kappa }}^{+}$ is minimal and the transmission coefficient $R_{\mathit{\kappa }}^{-}$ is maximal.

We can state that in the case of canalizing layers the portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is maximal in the region of higher transparency of the nonlinear structure, see Figure 3 (top right), where the radiation coefficients $R_{3\mathit{\kappa }}^{+}$ and $R_{3\mathit{\kappa }}^{-}$ at the generation frequency are close each to the other on both sides of the canalizing layer, see Figure 3 (bottom right).

The radiation fields and the induced nonlinear permittivity of the nonlinear decanalizing and canalizing layers, corresponding to the eigenmodes depicted in Figure 3, are shown in Figure 4. The graphs no. 1 show the values of the linear part of the dielectric permittivity ${\mathit{\epsilon }}^{\left(\text{L}\right)}$ of the nonlinear structure. The values of the dielectric permittivity of the nonlinear structure at the excitation frequency are represented by the graphs no. 4 and no. 5, whereas the graphs no. 6 and no. 7 illustrate the values of the dielectric permittivity of the nonlinear structure at the generation frequency.

The nonlinear components ${\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)}$ of the dielectric permittivities ɛ_nκ at each of the frequencies κ и 3κ are determined by the magnitudes of the fields $U\left(\mathit{\kappa };z\right)$ and $U\left(3\mathit{\kappa };z\right)$. For nonabsorbing media $\text{Im}{\mathit{\epsilon }}^{\left(\text{L}\right)}\left(z\right)\equiv 0,$ taking into account the cubic susceptibility $\mathit{\alpha }\left(z\right)$, the equality $\text{Im}{\mathit{\epsilon }}_{n\mathit{\kappa }}\left(z\right)=\text{Im}{\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)}\left(z\right)$ holds, see (2). The increase of the amplitude $a_{\mathit{\kappa }}^{\text{inc}}$ of the incident field at the frequency κ leads to the generation of the third harmonic field $U\left(3\mathit{\kappa };z\right)$. In the case under study the quantity $\text{Im}{\mathit{\epsilon }}_{\mathit{\kappa }}^{\left(\text{NL}\right)}\left(z\right)$ (or $\text{Im}{\mathit{\epsilon }}_{\mathit{\kappa }}\left(z\right)$ if $\text{Im}{\mathit{\epsilon }}^{\left(\text{L}\right)}\left(z\right)\equiv 0$) takes positive as well as negative values along the height of the nonlinear layer (see Figure 4, graphs no. 5). The described situation of varying $\text{Im}{\mathit{\epsilon }}_{\mathit{\kappa }}^{\left(\text{NL}\right)}\left(z\right)$ characterizes that portion (the “loss”) of energy in the nonlinear medium (at the excitation frequency κ) which is spent for the generation of the electromagnetic field of the third harmonic (at the frequency 3κ) (Angermann & Yatsyk, 2011a, 2011b, 2012, 2013a, 2013b; Angermann,Yatsyk, et al., 2013; Angermann, Krevchenko, et al., 2013a, 2013b; Yatsyk, 2012, 2013). The generated fields at the frequency 3κ are weak. They do not give any energy to generate new harmonics. Here, $\text{Im}{\mathit{\epsilon }}_{3\mathit{\kappa }}^{\left(\text{NL}\right)}\left(z\right)\equiv 0$ (see Figure 4, graphs no. 7, $\text{Im}{\mathit{\epsilon }}_{3\mathit{\kappa }}\left(z\right)\equiv 0$ if $\text{Im}{\mathit{\epsilon }}^{\left(\text{L}\right)}\left(z\right)\equiv 0$).

Furthermore, in Figure 4 the absolute values of the amplitudes $\left|U\left(\mathit{\kappa };z\right)\right|$ of the total scattered field of type H_0,0,4 at the excitation frequency κ (graphs no. 2 left/right) and $\left|U\left(3\mathit{\kappa };z\right)\right|$ of the generated field at the frequency 3κ of type H_0,0,9 (left graph no. 3) and type H_0,0,10 (right graph no. 3) are shown. The values $\left|U\left(\mathit{\kappa };z\right)\right|$ и $\left|U\left(3\mathit{\kappa };z\right)\right|$ are given in the nonlinear structure $\left|z\right|\le 2\mathit{\pi }\mathit{\delta }$, as well as in the zones of radiation (reflection z > 2πδ and transmission z < −2πδ). In Figure 4, we see a symmetry violation in the generated field in the radiation zone (graphs no. 3, left/right). This effect is more distinct in the case of a decanalizing layer, compare the values of the generated fields $\left|U\left(3\mathit{\kappa };z\right)\right|$ in the radiation zones $\left|z\right|>2\mathit{\pi }\mathit{\delta }$ and in the nonlinear layer $\left|z\right|\le 2\mathit{\pi }\mathit{\delta }$. In particular, inside the decanalizing layer the symmetry violation is accompanied by the presence of an inflection point z ≈ 1, 25, where $\left|U\left(3\mathit{\kappa };z\right)\right|=1,81$ for $a_{\mathit{\kappa }}^{\text{inc}}=24$, see graph no. 3 in Figure 4 (left) and the surface $\left|U_{3\mathit{\kappa }}\left[a_{\mathit{\kappa }}^{\text{inc}},z\right]\right|$ in Figure 5 (left).

Figure 5 shows the surfaces $\left|U_{\mathit{\kappa }}\left[a_{\mathit{\kappa }}^{\text{inc}},z\right]\right|$ and $\left|U_{3\mathit{\kappa }}\left[a_{\mathit{\kappa }}^{\text{inc}},z\right]\right|$ reflecting the dynamics of the behavior of the scattered $\left|U\left(\mathit{\kappa };z\right)\right|$ and generated $\left|U\left(3\mathit{\kappa };z\right)\right|$ fields in a decanalizing (left) and in a canalizing (right) nonlinear layer. In the considered ranges of amplitudes $a_{\mathit{\kappa }}^{\text{inc}}$, the plane waves exciting the nonlinear layer under the angle ϕ_κ produce a scattered field U_κ of the type H_0,0,4.

The generated field U_3κ of a canalizing layer, observed in the range $a_{\mathit{\kappa }}^{\text{inc}}\in \left[5,22\right]$, has the type H_0,0,10, Figure 5 (right). In the case of a decanalizing layer, the generated field U_3κ changes its type with increasing amplitude $a_{\mathit{\kappa }}^{\text{inc}}$. The generation of a third harmonic field U_3κ is observed in the range $a_{\mathit{\kappa }}^{\text{inc}}\in \left[4,24\right]$, Figure 5 (left). Here, it is of the type H_0,0,10 for $a_{\mathit{\kappa }}^{\text{inc}}\in \left[4,23\right)$ and of the type H_0,0,9 for $a_{\mathit{\kappa }}^{\text{inc}}\in \left[23,24\right]$. The type-conversion of the generated oscillations from H_0,0,10 to H_0,0,9 with increasing $a_{\mathit{\kappa }}^{\text{inc}}$ is due to the loss of one maximum point of the function $\left|U\left(3\mathit{\kappa };z\right)\right|$ for $z\in \left[-2\mathit{\pi }\mathit{\delta },2\mathit{\pi }\mathit{\delta }\right]$ at the inflection point z = 1.15 for $a_{\mathit{\kappa }}^{\text{inc}}=23$, see the point with coordinates $\left(a_{\mathit{\kappa }}^{\text{inc}}=23,z=1.15,\left|U_{3\mathit{\kappa }}\right|=1.61\right)$ on the surface $\left|U_{3\mathit{\kappa }}\left[a_{\mathit{\kappa }}^{\text{inc}},z\right]\right|$, Figure 5 (left).

The increase in the intensity of the excitation field leads to critical inflection points of the function (the absolute value of the amplitude of the scattered/generated field) identifying the type of oscillation. If in these points the local maximum of the function along the characteristic spatial coordinate of the investigated structure (the transverse coordinate along the height of the nonlinear layer) is lost, then the effect of type-conversion of the radiation field occurs. The amplitudes of the incident field, for which the described effect is observed, can be called the threshold of the considered types of oscillations.

The violation of symmetry in the excitation of the nonlinear structure $a_{\mathit{\kappa }}^{\text{inc}}\ne b_{\mathit{\kappa }}^{\text{inc}}$ $(a_{\mathit{\kappa }}^{\text{inc}}=const\ne 0$, $b_{\mathit{\kappa }}^{\text{inc}}=0)$ leads to a violation of symmetry of the radiation coefficients $R_{\mathit{\kappa }}^{\pm }\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$ at the scattering frequencies κ or $R_{3\mathit{\kappa }}^{\pm }\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$ at the generated frequencies 3κ, see Figure 3.

In the case of a decanalizing layer and under the condition of symmetry of the scattered energy $R_{\mathit{\kappa }}^{+}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)=R_{\mathit{\kappa }}^{-}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$, there is a significant difference in the portion of generated energy $R_{3\mathit{\kappa }}^{+}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)<<R_{3\mathit{\kappa }}^{-}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$ in the half-spaces above and below the layer, see Figure 3 (left). This can lead to a type-conversion effect in the oscillations of the radiation field U_3κ. In the case of normal excitation, ϕ_κ = 0° of a decanalizing layer as described above the effect of type-conversion of the generated field U_3κ is detected at the threshold amplitude $a_{\mathit{\kappa }}^{\text{inc}}=23$, where the condition of equality of the scattering coefficients $R_{\mathit{\kappa }}^{+}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)=R_{\mathit{\kappa }}^{-}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$ is satisfied, see Figure 5 (left) and the intersection of the surfaces in Figure 3 (top left). The portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ increases with increasing $a_{\mathit{\kappa }}^{\text{inc}}$ for a normal excitation ϕ_κ = 0°, see Figure 3 (left).

For a canalizing structure, at the scattering frequency the portion of reflected energy is less than the portion of transmitted energy $R_{\mathit{\kappa }}^{+}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)<R_{\mathit{\kappa }}^{-}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$, and at the generation frequency the portion of radiated energy in the transmission zone slightly dominates the radiated energy in the reflection zone $R_{3\mathit{\kappa }}^{+}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)\le R_{3\mathit{\kappa }}^{-}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$, see Figure 3 (right). The maximal generation $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is achieved if the amplitude $a_{\mathit{\kappa }}^{\text{inc}}$ increases at incident angles ϕ_κ slightly above the canalizing angle (the angle of the greatest possible transparency of the structure at the scattering frequency κ), see Figure 3 (right).

4.2. Qualitative analysis of the generation properties of nonlinear layers

We discuss a possible mathematical model for the qualitative analysis of the generation properties of nonlinear decanalizing and canalizing layers. We consider the surfaces $R_{n\mathit{\kappa }}^{+}$, $R_{n\mathit{\kappa }}^{-}$, $n=1,3$ and $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ described previously in Section 4.1 as well as the characteristic properties of the scattering and generation of oscillations by nonlinear layers, see Figure 3. In Figure 6 (left and right) we depict the cross-sections of these surfaces with the planes ϕ_κ = 0° for a decanalizing layer and ϕ_κ = 60° for a canalizing layer.

The particular features of the dynamics of the scattering and generation characteristics of oscillations by the nonlinear layer are caused by the proximity of the eigenfrequencies κ_n of the linearized problems (7) to the scattering (excitation) frequencies ${\mathit{\kappa }}^{\text{scat}}\equiv {\mathit{\kappa }}^{\text{inc}}=\mathit{\kappa }$ and to the generation frequencies ${\mathit{\kappa }}^{\text{gen}}=3\mathit{\kappa }$ of waves. The branches of the eigenfrequencies ${\mathit{\kappa }}_n={\mathit{\kappa }}_n^{\left(\text{NL}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$ of the nonlinear layers with dielectric permittivities induced by the excitation field at the frequencies of scattering and generation are depicted by the graphs no. 5.1, 5.2, 6.1, 6.2 in Figure 7. In addition, the curves nos. 3.1, 3.2, 4.1, 4.2 show the values of the eigenfrequencies ${\mathit{\kappa }}_n={\mathit{\kappa }}_n^{\left(\text{L}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)=const$ of the corresponding linear problems (for α ≡ 0). The eigenfrequencies ${\mathit{\kappa }}_n^{\left(\text{L}\right)}$ do not depend on the amplitude characteristics of the field, in particular, the equation $\underset{a_{\mathit{\kappa }}^{\text{inc}}\to 0}{lim}{\mathit{\kappa }}_n^{\left(\text{NL}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)={\mathit{\kappa }}_n^{\left(\text{L}\right)}$ holds, see Figure 7.

In the case of a canalizing/decanalizing layer the increase of the excitation amplitude $a_{\mathit{\kappa }}^{\text{inc}}$ leads to an increase/decrease of $\text{Re}\left({\mathit{\kappa }}_1^{\left(\text{NL}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)\right)$, $\text{Re}\left({\mathit{\kappa }}_3^{\left(\text{NL}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)\right)$ (graphs no. 5.1, 6.1), decrease/increase of $\text{Im}\left({\mathit{\kappa }}_3^{\left(\text{NL}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)\right)$ (graphs no. 6.2) and increase/decrease–decrease/increase of $\text{Im}\left({\mathit{\kappa }}_1^{\left(\text{NL}\right)}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)\right)$ (graphs no. 5.2), Figure 7 (left/right). The interval of monotonic decrease of the graph no. 5.2 is localized in a range of amplitudes $a_{\mathit{\kappa }}^{\text{inc}}$ which is determined by a closeness condition of the eigenfrequencies to the frequencies of scattering and generation, see the amplitudes corresponding to the intersection of the graphs no. 5.1 with no. 1 and no. 6.1 with no. 2 in Figure 7 (right). In this range of amplitudes, an outburst of generation of energy in the third harmonic is observable, see graph no. 7 in Figure 6 (right).

In order to describe the branches of the eigenfrequencies of the linearized problems, we use the concept of the Q-factor (Reed & Simon, 1978; Shestopalov & Sirenko, 1989; Vainstein, 1966; Voitovich, Katsenelenbaum, & Sivov, 1977)$$Q_{{\mathit{\kappa }}_n}=-\frac{\text{Re}\left({\mathit{\kappa }}_n\right)}{2\text{Im}\left({\mathit{\kappa }}_n\right)}.$$

It is convenient to perform the analysis of coupled regimes of the scattered and generated fields (3) induced by the dielectric permittivity (2) of nonlinear electrodynamic structures within the framework of a self-consistent process of exchange of energy by the help of the concept of the relative magnitude of the radiated energy, see e.g. (11), (12), (13). Similarly, spectral approaches for the description of the generation of oscillations by nonlinear structures can be effectively applied if the concept of the Q-factor of the eigenregimes is used:(14) $$Q_{{\mathit{\kappa }}_1}/Q_{{\mathit{\kappa }}_3}=\frac{Q_{{\mathit{\kappa }}_1}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)}{Q_{{\mathit{\kappa }}_3}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)}.$$(14)

The Q-factors $Q_{{\mathit{\kappa }}_1}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$ and $Q_{{\mathit{\kappa }}_3}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$ corresponding to oscillations with eigenfrequencies as indicated in Figure 7 (left and right) are shown in Figure 8 (top left and right). It also depicts the corresponding values of the relative Q-factors $Q_{{\mathit{\kappa }}_1}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)/Q_{{\mathit{\kappa }}_3}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$, Figure 8 (bottom left and right). We can see the intervals of local decrease of the values $Q_{{\mathit{\kappa }}_1}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)/Q_{{\mathit{\kappa }}_3}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$ caused by the decrease of $Q_{{\mathit{\kappa }}_1}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$ at the scattering frequency. This is particularly emphasized in Figure 8 (right top and bottom). The mentioned intervals of the local decrease of the relative Q-factor $Q_{{\mathit{\kappa }}_1}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)/Q_{{\mathit{\kappa }}_3}\left(a_{\mathit{\kappa }}^{\text{inc}}\right)$ can be correlated with a range of amplitudes of the incident field where an outburst of energy generation in the third harmonic is observable–compare the results of the calculations in Figure 8 (bottom left and right) with the graphes no. 5, 6, 7 in Figure 6 (left and right) and with the results in Figure 3 (bottom left) for ϕ_κ = 0° and (bottom right) for ϕ_κ = 60°.

We note that the proposed approach to describe the outburst of energy of oscillations by means of the relative variation of the Q-factor (14) is quite effective. It can be successfully applied for both a suffiently weak and a strong generation of energy in ranges from a few percent (Figure 3, bottom left) to dozens percents (Figure 3, bottom right) of generated energy, respectively.

4.3. A three-layer nonlinear dielectric structure

Consider a nonlinear structure with the parameters: $\left\{{\mathit{\epsilon }}^{\left(\text{L}\right)}\left(z\right),\mathit{\alpha }\left(z\right)\right\}=\left\{\left\{{\mathit{\epsilon }}^{\left(\text{L}\right)}=16,\mathit{\alpha }={\mathit{\alpha }}_1\right\}\right.$, $z\in \left[-2\mathit{\pi }\mathit{\delta },\right.$$\left.-2\mathit{\pi }\mathit{\delta }/3\right);$ $\left\{{\mathit{\epsilon }}^{\left(\text{L}\right)}=64,\mathit{\alpha }={\mathit{\alpha }}_2\right\},$ $z\in \left(-2\mathit{\pi }\mathit{\delta }/3,\right.\left.2\mathit{\pi }\mathit{\delta }/3\right);$ $\left\{{\mathit{\epsilon }}^{\left(\text{L}\right)}=16,\right.\left.\mathit{\alpha }={\mathit{\alpha }}_3\right\},$ $\left.z\in \left[2\mathit{\pi }\mathit{\delta }/3,2\mathit{\pi }\mathit{\delta }\right)\right\}$ at δ = 0.5,  ${\mathit{\alpha }}_1={\mathit{\alpha }}_3=+0.01,$ α₂ = −0.01.

The excitation takes place from above and below by electromagnetic fields at the basic frequency at incidence angles $\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}$ for amplitudes $\left\{a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}\right\}$ accordingly. The Figures 9 and 10 show the properties of the nonlinear layered structure at the parameters: $\mathit{\kappa }={\mathit{\kappa }}^{\text{inc}}=0.25$, ${\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ },{90}^{\circ }\right)$, $a_{\mathit{\kappa }}^{\text{inc}}\ne 0$, $b_{\mathit{\kappa }}^{\text{inc}}=\text{const}$ and $a_{2\mathit{\kappa }}^{\text{inc}}=b_{2\mathit{\kappa }}^{\text{inc}}=a_{3\mathit{\kappa }}^{\text{inc}}=b_{3\mathit{\kappa }}^{\text{inc}}=0$.

Figure 9. The properties of the nonlinear structure at incidence angles $\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}$ with ${\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)$ for amplitudes $\left\{a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}\right\}$: (top left/right) $a_{\mathit{\kappa }}^{\text{inc}}\ne 0$, $b_{\mathit{\kappa }}^{\text{inc}}=0$; (middle left/right) $a_{\mathit{\kappa }}^{\text{inc}}=38$, $b_{\mathit{\kappa }}^{\text{inc}}\ne 0$; (bottom left/right) $a_{\mathit{\kappa }}^{\text{inc}}=b_{\mathit{\kappa }}^{\text{inc}}$ here $R_{n\mathit{\kappa }}^{+}=R_{n\mathit{\kappa }}^{-}$, $n=1,3$.

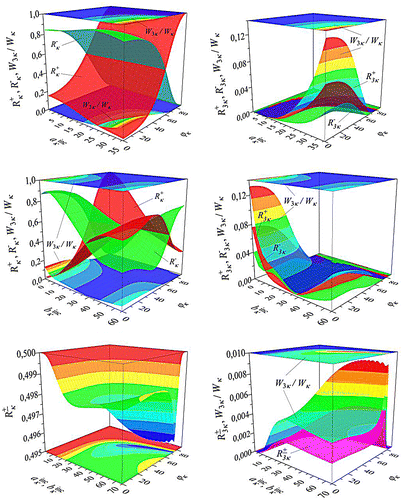
Figure 10. Curves: 0 – $\left|U\left(\mathit{\kappa };z\right)\right|$ for $\mathit{\alpha }\left(z\right)\equiv 0$, 1 – ${\mathit{\epsilon }}^{\left(\text{L}\right)}$, 2 – $\left|U\left(\mathit{\kappa };z\right)\right|$, 3 – $\left|U\left(3\mathit{\kappa };z\right)\right|$, 4 – $\text{Re}\left({\mathit{\epsilon }}_{\mathit{\kappa }}\right)$, 5 – $\text{Im}\left({\mathit{\epsilon }}_{\mathit{\kappa }}\right)$, 6 – $\text{Re}\left({\mathit{\epsilon }}_{3\mathit{\kappa }}\right)$, 7 – $\text{Im}\left({\mathit{\epsilon }}_{3\mathit{\kappa }}\right)\equiv 0$, at $\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}$ with ϕ_κ = 0° and (top left): $\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=0\right\}$; (top right): $\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=20\right\}$; (bottom left): $\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=30\right\}$; (bottom right) $\left\{a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}\right\}$ with $a_{\mathit{\kappa }}^{\text{inc}}=b_{\mathit{\kappa }}^{\text{inc}}=38$.

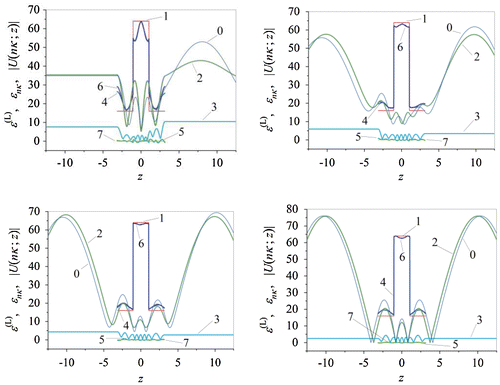
A three-layer structure consisting of a decanalizing layer which is located between two canalizing layers possesses novel properties of scattering and generation of oscillations. They partially resemble those properties which are inherent decanalizing and canalizing layers. Thus, in the case of a one-sided excitation $a_{\mathit{\kappa }}^{\text{inc}}\ne 0$, $b_{\mathit{\kappa }}^{\text{inc}}=0$ investigated in the range of amplitudes $a_{\mathit{\kappa }}^{\text{inc}}\in \left[1,38\right]$ and incident angles ${\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)$ of the layered structure the increase of the portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ with increasing amplitude $a_{\mathit{\kappa }}^{\text{inc}}$ is observed at normal excitation ϕ_κ = 0°, see Figure 9 (top). This is typical also for decanalizing structures, see Figure 3 (left). Moreover, in the case under consideration, the increase of $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is accompanied by an increase in the transparency of the layered structure. A canalization of energy is observed at the minimum value of the reflection coefficient $R_{\mathit{\kappa }}^{+}=0.0172$ for the $a_{\mathit{\kappa }}^{\text{inc}}=38$ at normal excitation ϕ_κ = 0°, Figure 9 (top left). This is typical for canalizing layers, Figure 3 (top right). The difference between the investigated situation and the numerical experiments for layers which canalize and decanalize energy is that the portion of energy generated in the region above the structure exceeds the portion of energy generated below the structure $R_{3\mathit{\kappa }}^{+}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)>R_{3\mathit{\kappa }}^{-}\left(a_{\mathit{\kappa }}^{\text{inc}},{\mathit{\varphi }}_{\mathit{\kappa }}\right)$, compare Figure 9 (top right) with Figure 3 (bottom left and right).

The energy characteristics for the case of a two-sided excitation $a_{\mathit{\kappa }}^{\text{inc}}=38$, $b_{\mathit{\kappa }}^{\text{inc}}\ne 0$ of the layered structure are depicted in Figure 9 (middle). Here, in the range of amplitudes ${\left.\left\{a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}\right\}\right|}_{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}\in \left[0,65\right]}$ and angles ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)}$, there are two local maxima of the portion of generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ corresponding to the incident angles ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}=0^{\circ }}$. The first of these corresponds to a one-sided excitation with the amplitudes $a_{\mathit{\kappa }}^{\text{inc}}=38$, $b_{\mathit{\kappa }}^{\text{inc}}=0$ at ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}=0^{\circ }}$, where $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}=0.1319$, see Figure 9 (top and middle). The increase of the amplitude $b_{\mathit{\kappa }}^{\text{inc}}$ leads to the equality of the scattering $R_{\mathit{\kappa }}^{+}=R_{\mathit{\kappa }}^{-}$ and generating $R_{3\mathit{\kappa }}^{+}=R_{3\mathit{\kappa }}^{-}$ characteristics at equal amplitudes of excitation $b_{\mathit{\kappa }}^{\text{inc}}=a_{\mathit{\kappa }}^{\text{inc}}=38$ in the whole range of incident angles ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)}$. This is due to the symmetry of both the excitation and the investigated structure. The maximum portion of generated energy ${\left.W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}\right|}_{{\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}={57}^{\circ }}}=0.0078$ for $b_{\mathit{\kappa }}^{\text{inc}}=a_{\mathit{\kappa }}^{\text{inc}}=38$ does not exceed 0.8%, see Figure 9 (middle and bottom). A further increase of $b_{\mathit{\kappa }}^{\text{inc}}$ leads to the violation of symmetry of excitation $b_{\mathit{\kappa }}^{\text{inc}}>a_{\mathit{\kappa }}^{\text{inc}}=38$. The properties of the scattering and generation characteristics change from $R_{n\mathit{\kappa }}^{+}\ge (or\le )R_{n\mathit{\kappa }}^{-}$, when $b_{\mathit{\kappa }}^{\text{inc}}<a_{\mathit{\kappa }}^{\text{inc}}=38$, to $R_{n\mathit{\kappa }}^{+}\le (or\ge )R_{n\mathit{\kappa }}^{-}$, when $b_{\mathit{\kappa }}^{\text{inc}}>a_{\mathit{\kappa }}^{\text{inc}}=38$, for $n=1,3$, see Figure 9 (middle).

The second local maximum $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}=0.0457$ corresponds to a two-sided normal excitation ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}=0^{\circ }}$ with amplitudes $a_{\mathit{\kappa }}^{\text{inc}}=38$, $b_{\mathit{\kappa }}^{\text{inc}}=65$, see Figure 9 (middle). Here the increase of the generation $R_{3\mathit{\kappa }}^{-}$, $R_{3\mathit{\kappa }}^{+}$, $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}$ is caused by the observed canalizing properties of the layered structure near the minimum of the radiation coefficient $R_{3\mathit{\kappa }}^{-}=0.2302$ for $a_{\mathit{\kappa }}^{\text{inc}}=38$, $b_{\mathit{\kappa }}^{\text{inc}}=65$ and ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}={40}^{\circ }}$, see Figure 9 (middle).

Numerical results for the characteristics of scattering and generation of oscillations in the case of a two-sided ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)}$ symmetric $a_{\mathit{\kappa }}^{\text{inc}}=b_{\mathit{\kappa }}^{\text{inc}}$ excitation of the nonlinear layered structure are shown in Figure 9 (bottom). Here, equal values of the scattering and generation coefficients can be observed $R_{n\mathit{\kappa }}^{+}=R_{n\mathit{\kappa }}^{-}$, $n=1,3$. This is due to the symmetry of both the excitation $a_{\mathit{\kappa }}^{\text{inc}}=b_{\mathit{\kappa }}^{\text{inc}}$ and of the nonlinear dielectric structure under investigation with respect to the plane y = 0. Here, in the whole range of amplitudes $a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}\in \left[0,75\right]$ and angles ${\mathit{\varphi }}_{\mathit{\kappa }}\in \left[0^{\circ }\right.,\left.{90}^{\circ }\right)$, we observe the following. The coefficient of the relative portion of scattered energy lies in the range $0.4954<R_{\mathit{\kappa }}^{\pm }\le 0.5$, the corresponding coefficient of generated energy $R_{3\mathit{\kappa }}^{\pm }<0.0046$ does not exceed 0.46%, and the portion of the total generated energy $W_{3\mathit{\kappa }}/W_{\mathit{\kappa }}<0.0093$ does not exceed 0.93%, see Figure 9 (bottom).

The absolute values of the amplitudes of the total scattering $\left|U\left(\mathit{\kappa };z\right)\right|$ and generation $\left|U\left(3\mathit{\kappa };z\right)\right|$ fields, for different variants of one-sided $\left\{a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}=0\right\}$ and two-sided $\left\{a_{\mathit{\kappa }}^{\text{inc}},b_{\mathit{\kappa }}^{\text{inc}}\right\}$ normal ${\left.\left\{{\mathit{\varphi }}_{\mathit{\kappa }},{180}^{\circ }-{\mathit{\varphi }}_{\mathit{\kappa }}\right\}\right|}_{{\mathit{\varphi }}_{\mathit{\kappa }}=0^{\circ }}$ excitation of the nonlinear structure, corresponding to some effects depicted in Figure 9, are illustrated by the graphs no. 2 and no. 3 in Figure 10. They may be identified as oscillations of the types ${\left.\left\{H_{0,0,4}\text{and}{H}_{0,0,9}\right\}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=0\right\}}$ (top left), ${\left.\left\{H_{0,0,4}\text{and}{H}_{0,0,9}\right\}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=20\right\}}$ (top right), ${\left.\left\{H_{0,0,3}\text{and}{H}_{0,0,9}\right\}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=30\right\}}$ (bottom left), and ${\left.\left\{H_{0,0,3}\text{and}{H}_{0,0,9}\right\}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=38\right\}}$ (bottom right). We mention a resonance effect of type-conversion of the total scattered field ${\left.\left\{H_{0,0,4}\text{and}{H}_{0,0,9}\right\}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=0\right\}}\iff {\left.\left\{H_{0,0,3}\text{and}{H}_{0,0,9}\right\}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=38\right\}}$ for both a nonsymmetric $\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=0\right\}$ and a symmetric $\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=38\right\}$ excitation of the nonlinear layered structure.

The total scattered fields ${\left.\left\{\left|U\left(\mathit{\kappa };z\right)\right|\right\}\right|}_{\mathit{\alpha }\left(z\right)\equiv 0}$ for the investigated variants of excitation of a linear structure are also shown. They can be related to oscillations of the types ${\left.H_{0,0,4}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=0\right\}}$ (top left), ${\left.H_{0,0,3}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=20\right\}}$ (close to the transition $H_{0,0,4}\iff H_{0,0,3}$ at the inflection point z ≈ 1, 22, where $\left|U\left(\mathit{\kappa };z\right)\right|\approx 13.4321$) (top right), ${\left.H_{0,0,3}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=30\right\}}$ (bottom left), and ${\left.H_{0,0,3}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=38\right\}}$ (bottom right), see graphs no. 0 in Figure 10. We detect an interference mechanism of resonant type-conversion of oscillations ${\left.H_{0,0,4}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=0\right\}}\iff {\left.H_{0,0,3}\right|}_{\left\{a_{\mathit{\kappa }}^{\text{inc}}=38,b_{\mathit{\kappa }}^{\text{inc}}=38\right\}}$, see graphs no. 0 in Figure 10.

The resonant type-conversion of oscillations, which is observed for the two-sided excitation of both linear and nonlinear structures, occurs if the symmetry of the excitation is violated. The fundamental difference in the occurrence of this effect between the nonlinear and the linear situations consists in the presence of the nonlinear part ${\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)}$ of the dielectric permittivity ɛ_nκ, $n=1,3$, see (2). The behavior of the quantity ${\mathit{\epsilon }}_{n\mathit{\kappa }}^{\left(\text{NL}\right)}={\mathit{\epsilon }}_{n\mathit{\kappa }}-{\mathit{\epsilon }}^{\left(\text{L}\right)}$ can be estimated easily by the help of the graphs nos. 4, 5, 6, 7 and 1 in Figure 10. The graph no. 1 depicts the dielectric permittivity ${\mathit{\epsilon }}^{\left(\text{L}\right)}$ of a linear nonabsorbing $\text{Im}\left({\mathit{\epsilon }}^{\left(\text{L}\right)}\right)\equiv 0$ structure. The graphs nos. 4, 5, 6, 7 show the real and imaginary parts of the nonlinear dielectric permittivity ɛ_nκ, $n=1,3$, for the excitation variants under consideration, see Figure 10. In particular, $\text{Im}\left({\mathit{\epsilon }}_{\mathit{\kappa }}^{\left(\text{NL}\right)}\right)$ takes positive and negative values along the height of the nonlinear layer, for all the considered excitation variants of the nonlinear structure. The variation of this quantity characterizes the energy consumption of the nonlinear medium which is spent for the third harmonic generation.

The dependence of the nonlinear dielectric structure on the amplitude characteristics of the scattered and generated fields together with a spectral approach to the analysis of the linearized problems near the critical points of the branches of the amplitude–phase dispersion can be used as the basis of numerical and analytical methods for the synthesis and analysis of nonlinear structures with anomalous scattering and generation properties.

The numerical results for the scattereing and generation of a wave package by a nonlinear cubically polarizable layer are obtained by means of the solution of the system of integral equations (4). Applying Simpson′s quadrature rule, the system (4) is reduced to a system of nonlinear algebraic equations (6). The numerical solution of (6) is carried out using a self-consistent iterative algorithm based on a block Jacobi method (Angermann & Yatsyk, 2011a, 2011b, 2012, 2013a, 2013b; Angermann, Yatsyk, et al., 2013; Angermann, Krevchenko, et al., 2013a, 2013b; Yatsyk, 2012, 2013). The spectral problems (7) are solved by the help of Newton′s method. In the investigated range of problem parameters, the dimension of the algebraic systems was 301 and 501 in the case of single-layered and three-layered structures, respectively. The relative error of the calculations did not exceed 10⁻⁷.

4. Conclusion

The problem of scattering and generation of waves by an isotropic, nonmagnetic, linearly polarized, nonlinear dielectric structure consisting of a cubically polarizable medium is investigated in the range of resonance frequencies, where the excitation is induced by wave packets consisting of plane waves at multiple frequencies. In extension of our previous work, here the case of two-sided acting fields is treated. The mathematical model of the boundary value problem is transformed into a system of one-dimensional nonlinear integral equations. The numerical solution of the problem is performed by the help of quadrature formulas in conjunction with an iterative method, where at each step a linear system of equations is solved. The analytic continuation of the linearized nonlinear problems into the region of complex values of the frequency parameter allows to switch to the analysis of spectral problems. That is, the eigenfrequencies and the corresponding eigenfields of homogeneous linear problems with an induced nonlinear dielectric permittivity are to be determined. Single-layered structures with both negative and positive values as well as three-layer structures with piecewise constant positive–negative–positive values of the coefficient of the cubic susceptibility of the nonlinear medium are investigated. The layers under consideration have different properties. In particular, nonlinear layers with a negative value of the cubic susceptibility show decanalizing properties, layers with a positive value of the cubic susceptibility—canalizing properties. The investigations were restricted to the third harmonic generation. The paper presents the results of the numerical analysis characterizing the scattering/generation and spectral properties of the considered structures. An effective way to describe the processes of generation of oscillations via the variation of the relative Q-factor of the eigenoscillations corresponding to the eigenfrequencies of the scattering and generating structures, when the intensity of the excitation field changes, is given. Moreover, the proposed approach applies equally well for sufficiently weak/strong energy generation in ranges from a few percent to dozens percents of generated energy. For the first time, two-sided acting fields at the scattering frequency were taken into account and a type-conversion of the oscillations could be observed. The latter effect was observed at a symmetry violation of the nonlinear problem caused by different amplitudes of the excitation fields. This effect may serve as a basis for numerical and analytical methods for the synthesis and analysis of nonlinear structures in the vicinity of critical points of the amplitude–phase dispersion, similar to the approach developed in the papers (Shestopalov & Yatsik, 1997; Yatsyk, 2000, 2001). That is, mathematical models for the control of anomalous scattering and generation properties of nonlinear structures via the variation of amplitudes in a two-sided excitation of a nonlinear structure at scattering and generation frequencies near the resonance frequencies of the linearized spectral problems can be created.

Additional information

Funding

Funding. The authors acknowledge support by Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of Clausthal University of Technology.

Notes on contributors

Lutz Angermann

The authors perform joint research about scattering and generation of electromagnetic waves on nonlinear structures since more than 10 years.

Lutz Angermann is a professor of Numerical Mathematics at the Department of Mathematics of the Clausthal University of Technology since 2001. His research is concerned with the mathematical analysis of numerical algorithms for partial differential equations with special interests in finite-volume and finite-element methods and their application to problems in Physics and Engineering. He is the author of more than 100 research papers.

Vasyl V. Yatsyk

Vasyl V. Yatsyk is a senior scientist at the O.Ya. Usikov Institute for Radiophysics and Electronics of the National Academy of Sciences of Ukraine (O.Ya. Usikov IRE NASU) 1998, Kharkiv, Ukraine. He authored more than 100 papers. His research interests include scattering and generation effects on nonlinear materials, numerical–analytical methods of electromagnetic theory, resonant interaction, and dispersion of waves.