Phononic band gap and wave propagation on polyvinylidene fluoride-based acoustic metamaterials

Abstract

In the present work, the acoustic band structure of a two-dimensional phononic crystal (PC) containing an organic ferroelectric (PVDF-polyvinylidene fluoride) and topological insulator (SnTe) was investigated by the plane-wave-expansion (PWE) method. Two-dimensional PC with square lattices composed of SnTe cylindrical rods embedded in the PVDF matrix is studied to find the allowed and stop bands for the waves of certain energy. Phononic band diagram ω = ω(k) for a 2D PC, in which non-dimensional frequencies ωa/2πc (c-velocity of wave) were plotted vs. the wavevector k along the Г–X–M–Г path in the square Brillouin zone shows five stop bands in the frequency range between 10 and 110 kHz. The ferroelectric properties of PVDF and the unusual properties of SnTe as a topological material give us the ability to control the wave propagation through the PC over a wide frequency range of 10³–10⁶ Hz. SnTe is a discrete component that allows conducting electricity on its surface but shows insulator properties through its bulk volume. Tin telluride is considered as an acoustic topological insulator as the extension of topological insulators into the field of “topological phononics”.

Keywords:

• phononic crystals
• acoustic band gaps
• topological insulator
• wave propagation

Public Interest Statement

Phononic crystals (PCs) are composite materials that are artificially manufactured structures with special properties regarding wave propagation, known as acoustic metamaterials. The most interesting aspect of such materials arises from the presence of phononic band gaps (PBGs). It is important to understand phononic behavior of polymeric materials combined with topological materials, such as PVDF/SnTe. These types of structures can be regarded as smart materials and be utilized for energy harvesting and they may be useful to the improvements in the design of acoustic phononic crystals. Many smart structures are periodically made up of two or more distinct constituents, and due to their combined properties, they may have potential engineering applications such as vibration/noise insulation, waveguides, or acoustic wave filtering. They provide some perspectives in a way for designing acoustic filters or insulators.

1. Introduction

Phononic crystals (PCs) and acoustic metamaterials have generated increasing scientific interest for very diverse technological applications ranging from sound abatement to ultrasonic imaging to telecommunications to thermal management and thermoelectricity (Pennec, Djafari-Rouhani, Larabi, Vasseur, & Hladky-Hennion, 2009). PCs and acoustic metamaterials are artificially structured composite materials that enable the manipulation of the dispersive properties of vibrational waves in ways that are not possible in conventional materials. This new class of materials may achieve a zero, or even negative, refractive index for sound and give new possibilities for acoustic lenses, acoustic imaging, and the control of energy funneling by hyperbolic materials (García-Chocano, Christensen, & Sánchez-Dehesa, 2014; Kaina, Lemoult, Fink, & Lerosey, 2015). PCs are made of periodic distributions of inclusions (polymer in water, narrow band semiconductor in air, etc.) embedded in a matrix. In addition, it is well known that, with such a structure, the band gaps of PCs may appear and are independent of the direction of propagation of the incident elastic wave. PCs are designed to control the dispersion of waves through Bragg scattering, the scattering of waves by a periodic arrangement of scatterers with dimensions and periods comparable to the wavelength (Cummer, Chritensen, & Alui, 2016). Acoustic metamaterials have the added feature of local resonance, and although often designed as periodic structures, their properties do not rely on periodicity. Since the geometric dimensions are orders of magnitude smaller than the wavelength, the degree of periodicity is not needed to create a metamaterial with designed properties. Instead, disordered structures of localized resonant structures can be described with effective values of density and elasticity, including unusual negative values (Lucklum, 2014). Finally, the study of PCs and acoustic metamaterials has also extensively relied on a combination of theory and experiments that have shown extraordinary complementarity (Tanaka & Tamura, 1998).

Due to their interesting property, the phononic structures have extensive practical applications by suppressing sound waves for a given frequency range. Therefore, the application of PCs can be mainly determined by manipulating the regulation performance level of the band gap. The condition of controlling and tuning band gap in conventional research is primarily met by changing the geometry of lattice, filling fraction, and orientation of scatterers in a PC (Kuang, Hou, Liu, & Li, 2005; Kushwaha, Halevi, Dobrzynski, & Djafari-Rouhani, 1993; Wang, Wang, Gu, & Yang, 2001). The characteristics of PCs can be altered by changing the geometry of the inclusions or by varying the elastic characteristics of the constitutive materials. The geometry of the inclusion in most band gap studies is principally regular-shape geometries, such as circle, squares, and so on. However, material selection has a great effect on manipulating sound and hypersound frequencies. Therefore, different materials are needed to fabricate phononic structures to obtain reachable frequencies for the energy band gaps from about kilohertz to megahertz range and even to ultra-high frequencies (very high-frequency sound, with f < 1 GHz) (Olsson & El-Kady, 2009). Polymer materials might have a possible future in PCs as constitutive materials with their good mechanical properties (Pichard, Duclos, Groby, Tournat, & Gusev, 2012; Qian, Jin, Li, & Kishimoto, 2008; Walker, Sharp, Akimov, & Kent, 2010). They can also be used to harness their anisotropic elasticity across particle–polymer interface in densely polymer-tethered colloidal particles as phononic hybridization gap materials (Alonso-Redondo et al., 2015). Today, it is seen that an increasing number of systems appear to gather energy from different types of motion, such as vibratory motion of typical mechanical systems. PVDF materials could be good candidates for mechanical energy harvesting as an acoustic energy harvester component for real applications (Li, Laviage, You, & Kim, 2013; Lv, Tian, Wang, & Li, 2013). PVDF films are flexible piezoelectric materials with an effective piezoelectric constant. This polymer is a fluorinated thermoplastic material that has high resistance to many mineral and organic acids. However, investigations in the band structures of PCs, including piezoelectric materials, have increased because of their high mechanical quality factor, low acoustic impedance, and electromechanical coupling coefficients (Gaur & Rana, 2015).

The effect of the acoustic impedance of constituent materials on the band structure and dependence of pass band on the thickness/strain were investigated (Wang, Song, Sun, Zhang, & Cao, 2014). In this study, some types of simplification allow us to model the sound waves as pressure waves propagating through the crystal that validates the acoustic pressure wave modeling with PCs. One important simplification made in the theoretical calculations is to neglect the piezoelectric effect of the material. The piezoelectric effect on the band gap characteristics in the polymer-based PCs, especially for low-frequency regions can be tolerated (Wang et al., 2008). Another simplification process is to treat polyvinylidene fluoride polymer as a fluidic acoustic material. Therefore, in numerical calculations, we have only considered the case of the propagation of a longitudinal wave in a PC structure.

2. The model and calculation method

The wave propagation in a homogeneous medium can be strongly changed by inserting periodical inclusions with different elastic constants. The periodic arrangement in these so-called PCs induces a wave scattering, and destructive interferences can appear in some frequency ranges thereby leading to forbidden band gaps. Total reflection is then expected in these frequency ranges. PCs can be generally classified into two main categories as acoustic PCs (Kushwaha et al., 1993; Ruffa, 1992; Sigalas & Economou, 1992, 1993) and elastic PCs (Martínez-Sala et al., 1995). The system in our study was modeled as a solid–fluid PC. The advantage of this type of modeling is to assume that mechanical waves propagate as acoustic waves. This approximation is reasonable because, in these PCs, it can be considered that mechanical waves propagate mainly through the fluid region due to the rigidity of the cylinders. We consider a 2D system consisting of infinitely long cylinders aligned along the z direction and any material-based parameters to be independent of the z direction (Chen & Ye, 2001; Sánchez-Pérez et al., 1998). The PC also extends infinitely in the x–y plane. Therefore, the mechanical properties of the PC vary periodically in the x–y plane. Acoustic waves propagate within the solid–fluid PCs as Bloch waves. In this study, we only consider the longitudinal polarization and, therefore, the propagation of acoustic wave is assumed to be only in the x–y plane. The acoustic wave equation in such a system is written as:(1) $$\mathit{\rho }\frac{{\mathit{\partial }}^2\overrightarrow{u}}{\mathit{\partial }{t}^2}=\overrightarrow{\mathrm{\nabla }}·\left(\mathit{\rho }{c}_l^2\overrightarrow{\mathrm{\nabla }}·\overrightarrow{u}\right)$$(1)

where $c_l=\sqrt{C_{11}/\mathit{\rho }}$ is the longitudinal speed of sound, C₁₁ is the longitudinal elastic constant, ρ is the mass density of element, and $\overrightarrow{\mathrm{\nabla }}$ is the two-dimensional nabla operator. Introducing a scalar quantity such that $\mathit{\rho }\overrightarrow{u}=\mathrm{\nabla }p\left(\overrightarrow{r},t\right)$, where p is the pressure, Equation (1(1) $$\mathit{\rho }\frac{{\mathit{\partial }}^2\overrightarrow{u}}{\mathit{\partial }{t}^2}=\overrightarrow{\mathrm{\nabla }}·\left(\mathit{\rho }{c}_l^2\overrightarrow{\mathrm{\nabla }}·\overrightarrow{u}\right)$$(1) ) can be rewritten as:(2) $${\left(C_{11}\right)}^{-1}\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{t}^2}=\overrightarrow{\mathrm{\nabla }}·\left({\mathit{\rho }}^{-1}\mathrm{\nabla }p\right)$$(2)

the pressure p in Equation (2(2) $${\left(C_{11}\right)}^{-1}\frac{{\mathit{\partial }}^{2}p}{\mathit{\partial }{t}^2}=\overrightarrow{\mathrm{\nabla }}·\left({\mathit{\rho }}^{-1}\mathrm{\nabla }p\right)$$(2) ) can be written as:(3) $$p\left(\overrightarrow{r},t\right)=e^{i\left(\overrightarrow{K}·\overrightarrow{r}-\mathit{\omega }t\right)}{p}_{\overrightarrow{K}}\left(\overrightarrow{r}\right)$$(3)

where $p_{\overrightarrow{K}}$ is a periodic function with the same periodic structure as $\sum _{\overrightarrow{G}}p\left(\overrightarrow{G}\right)e^{i\overrightarrow{G}.\overrightarrow{r}}$, and K is the Bloch vector taking advantage of the two-dimensional periodicity in the x–y plane, the quantities $\mathit{\rho }\left(\overrightarrow{r}\right)$ and $C\left(\overrightarrow{r}\right)$ can be expanded in the Fourier series as given below:(4) $$C_{11}^{-1}\left(\overrightarrow{r}\right)=\sum _{\overrightarrow{G}}\mathit{\tau }\left(\overrightarrow{G}\right)e^{i\overrightarrow{G}.\overrightarrow{r}}\text{and}{\mathit{\rho }}^{-1}\left(\overrightarrow{r}\right)=\sum _{\overrightarrow{G}}\mathit{\sigma }\left(\overrightarrow{G}\right)e^{i\overrightarrow{G}.\overrightarrow{r}}$$(4)

where $\overrightarrow{G}=\left(\frac{2\mathit{\pi }{n}_x}{a}\right)\widehat{x}+\left(\frac{2\mathit{\pi }{n}_y}{a}\right)\widehat{y}$ is the 2D reciprocal lattice vector and r is the direct lattice vector. The Fourier transforms of these functions:(5) $$\mathit{\sigma }\left(\overrightarrow{G}\right)=\left\{\begin{array}{cc}{\mathit{\rho }}_a^{-1}f+{\mathit{\rho }}_b^{-1}\left(1-f\right)=\overline{{\mathit{\rho }}^{-1}}\hfill & \text{for}\overrightarrow{G}=0\hfill \\ \left({\mathit{\rho }}_a^{-1}-{\mathit{\rho }}_b^{-1}\right)F\left(\overrightarrow{G}\right)=\mathrm{\Delta }\left({\mathit{\rho }}^{-1}\right)F\left(\overrightarrow{G}\right)\hfill & \text{for}\overrightarrow{G}\ne 0\hfill \end{array}\right.$$(5) (6) $$\mathit{\tau }\left(\overrightarrow{G}\right)=\left\{\begin{array}{cc}{C}_a^{-1}f+C_b^{-1}\left(1-f\right)=\overline{C^{-1}}\hfill & \text{for}\overrightarrow{G}=0\hfill \\ \left(C_a^{-1}-C_b^{-1}\right)F\left(\overrightarrow{G}\right)=\mathrm{\Delta }\left(C^{-1}\right)F\left(\overrightarrow{G}\right)\hfill & \text{for}\overrightarrow{G}\ne 0\hfill \end{array}\right.$$(6) (7) $$F\left(\overrightarrow{G}\right)=\frac{1}{A_c}\underset{a}{\int }{e}^{-i\overrightarrow{G}.\overrightarrow{r}}{d}^{2}r=2f{J}_1\left(Gr\right)/\left(Gr\right)$$(7)

where f is the filling fraction of the cylindrical rods with lattice constant a, $F(\overrightarrow{G})$ is the structure factor, J(x) is the Bessel function of the first kind of order one. A_c is the area of a unit cell, and r₀ is the cylinder’s radius. The integral in $F(\overrightarrow{G})$ is over the cross-sectional area of cylinder of radius r. By applying some algebra:(8) $$\sum _{{\overrightarrow{G}}^{\prime }\ne \overrightarrow{G}}\left[\mathit{\sigma }\left(\overrightarrow{G}-{\overrightarrow{G}}^{\prime }\right)\left(\overrightarrow{K}+\overrightarrow{G}\right)·\left(\overrightarrow{K}+\overrightarrow{G}\right)-\mathit{\tau }\left(\overrightarrow{G}-{\overrightarrow{G}}^{\prime }\right){\mathit{\omega }}_K^2\right]p_{\overrightarrow{K}}\left({\overrightarrow{G}}^{\prime }\right)=0$$(8)

Equation (8(8) $$\sum _{{\overrightarrow{G}}^{\prime }\ne \overrightarrow{G}}\left[\mathit{\sigma }\left(\overrightarrow{G}-{\overrightarrow{G}}^{\prime }\right)\left(\overrightarrow{K}+\overrightarrow{G}\right)·\left(\overrightarrow{K}+\overrightarrow{G}\right)-\mathit{\tau }\left(\overrightarrow{G}-{\overrightarrow{G}}^{\prime }\right){\mathit{\omega }}_K^2\right]p_{\overrightarrow{K}}\left({\overrightarrow{G}}^{\prime }\right)=0$$(8) ) is an N × N matrix equation and it is obtained using a finite number of Fourier components in the expansion. The solution of the secular equation gives the $\mathit{\omega }\left(\overrightarrow{k}\right)$ eigenvalues and $p\left(\overrightarrow{G}\right)$ eigenvectors. For software implementation and numerical calculation, the code written by Elford (2010) was used with some modification such that it was executed for Γ–X, X–M, and Γ–M directions to obtain eigenvalues and eigenvectors of the system.

Here, we focus on the acoustic wave propagation through a periodic array of cylindrical scatterers. Despite the fact that one of the media is a solid structure, we will assume the matrix as a fluid medium to take advantage of the solid/fluid approximation. Such approximation is reasonable if we only consider that the waves propagate as longitudinal waves by means of adiabatic compression and decompression. Assuming a homogeneous and isotropic medium, we can separate the wave modes and use methods based on acoustic wave theory. The separation can be carried out by the PWE method due to its simplicity. The advantage of the PWE method is that it must neglect the transverse mode existing in solid and simply treat the solid as an artificial “fluid”. It must be noted that one of the advantages of PVDF like materials is that they can be fluid-processed as a melt. Based on these assumptions, the solid matrix can be considered as a fluid but with the material parameters of actual PVDF. The considered system is a 2D PC composed of SnTe inclusions in a PVDF host in a square lattice.

3. Results and discussion

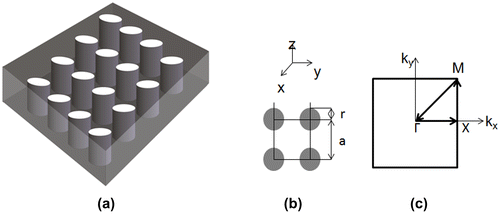
Figure 1(a) shows the 2D PC array structure. The cylindrical materials and their environment around them can be set to different materials. Numerical calculation in this study has the parameters with the column radius of 16.5 mm and the lattice size of a = b = 33 mm for an array of circular SnTe cylinders embedded in a PVDF background material. This results in a filling ratio of approximately 78%. The phononic material parameters used in the calculations are ρ_PVDF = 1,780 kg/m³, ρ_SnTe = 6,383 kg/m³, C_PVDF = 1,300 m/s, and C_SnTe = 4,138 m/s. The unit cell of the system is a square lattice in the Brillouin zone and its first irreducible Brillouin zone corresponding to this periodic structure is shown in Figure 1(b) and (c), respectively.

Figure 1. Schematics of the structure composed of a periodic square array of circular cylinders in polymer matrix (a), unit cell of the structure (b), and the Brillouin zone for a 2D square lattice (c).

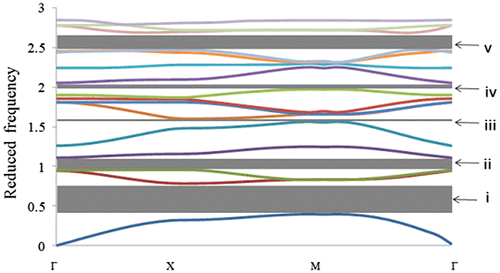
The values of n_x and n_y in the reciprocal vector G were permitted to take integer values between −9 and +9 (3 6 1 plane waves). This resulted in a very good convergence. In order to show the feature appearing in the band structures of the proposed structure, we illustrate the dispersion curves for a typical circular hole with an r/a = 0.5 in Figure 2 which corresponds to the maximum filling ratio. The plots are given in terms of the reduced frequency Ω = ωa/2πc_l, which is the vertical axis and the horizontal axis is the reduced wave vector. All of the parameters are independent of the z direction. That means the 2D PC structure is invariant along the z direction. The first 18 bands for propagation in the x–y plane were computed while the irreducible triangle Γ–X–M–Γ of the Brillouin zone along its periphery was scanned. For band structure calculations, moving along the high symmetry axes of the first Brillouin zone was good enough. Figure 2 shows full band gaps, numbered by Roman numerals I through V, along the right-handed triangle Г–X–M–Г with vertices at Г = (0, 0), X = (π/a, 0), and M = (π/a, π/a). This helps us cover the entire angular range of the wave propagation direction.

Figure 2. The band structure of the studied 2D PVDF/SnTe PC calculated in the first Brillouin zone.

4. Equi-frequency surface and group velocity

Because the momentum conservation law is satisfied at the reflection and refraction of waves, it is convenient to analyze the reflection and refraction of a certain wave in the space of wave numbers by introducing the equi-frequency surface (EFS) of the wave. This surface is directly described by the dispersion relation of the anisotropic medium at the fixed frequency ω. Then, the group velocity of the wave in an anisotropic medium can be found as the frequency gradient in the space of wave vectors (Lock, 2008). It is known that for a wave propagating in an isotropic medium with a fixed frequency ω, the EFS represents a sphere. In this case, the wave vector and group velocity vector, which determines the ray direction, are always parallel. However, EFS is not spherical for anisotropic media and the vectors are not parallel. By analogy with 3D case, the propagation, reflection, and refraction of the wave in 2D structure can be described in terms of the equi-frequency dependence that can be considered as the section of the dispersion surface in the space of variables by the plane corresponding to constant frequency. It is well known that the analysis of equi-frequency dependences is most efficient in the studies of 2D geometries, especially in solving problems when only orientations of the vector of incident, reflected, and refracted waves are of interest, and are not the amplitudes of the reflected and refracted rays. The equi-frequency dependence has a simple physical meaning for the analysis of 2D geometries: since this dependence describes all the possible waves with the given frequency ω and various wave vectors, the directions of the reflected and the refracted rays can be determined by simply finding the points in the equi-frequency dependences of media that satisfy the momentum conservation law at a known orientation of the boundary and a given angle of incidence of the wave. Now, we present some numerical examples for our PC structures. In all of these examples, we exploit symmetry to calculate the EFSs over the irreducible Brillouin zone of the entire Brillouin zone. First, we consider the EFS of a square lattice of SnTe layers in PVDF medium. Here, the map was discretized using 441 points per edge of the unit cell for the first band in Figures 3 and 4. Each point on the surface gives the possible eigen solutions that consist of all allowed wave vectors in the first Brillouin zone. Therefore, the plots retain detailed information but they are difficult to analyze. Figures 3(b) and 4(b) show contours of ω(k_x, k_y) with values on the contours given. Note that they are the reduced form of the EFSs for a two-dimensional crystal. The EFCs are at the intersection of the 3D dispersion curves with a horizontal plane and they provide an essential source of information. The equi-frequency contours (EFCs) are something that is more meaningful and easier to analyze. The plots basically indicate the contours of the energy flow which may allow us to identify irregularities in refraction and they are also very helpful in understanding the propagation effects within the crystal. In Figure 3(b), some contours are nearly circular and they imply that the propagation of the energy is radially symmetric (no dependence on direction). Deviation from the circular shape depends on the radial amplitude that is a function of the incident frequencies.

Figure 3. (a) The dispersion, ω(k), relation (band-diagram) for the first mode of the square PC, calculated for all k-vectors in the first Brillouin zone and (b) the equifrequency contours for the first mode.

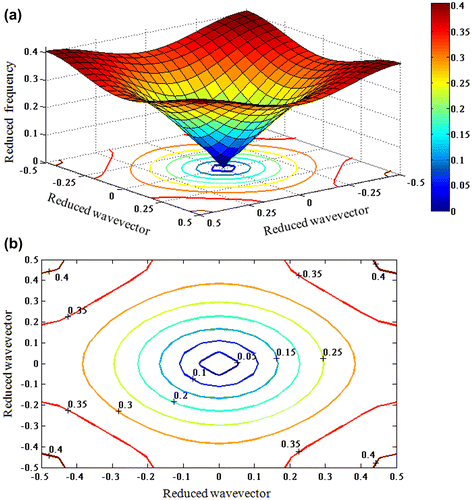
Figure 4. (a) The dispersion, ω(k), relation (band-diagram) for the second mode, of the square PC, calculated for all k-vectors in the first Brillouin zone and (b) the equi-frequency contours for the first mode.

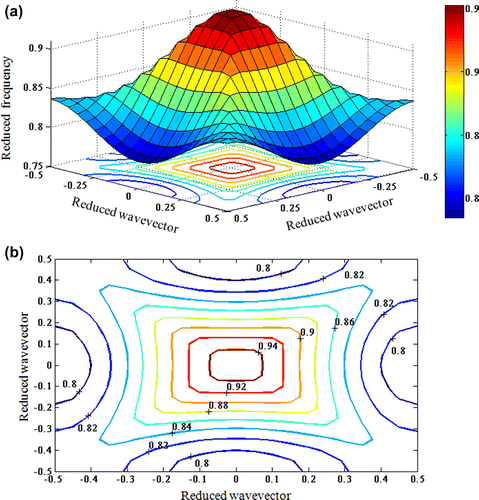
The EFSs of the incident wave along the Γ–X–M–Γ direction in Figure 4(a) shows that the local curvature of the EFCs deviates from circular symmetry. The case of a non-circular EFCs, however, indicates anisotropic behavior. On the other hand, a square-like contour also reflects some symmetry in a particular direction. This could especially be advantageous and even be more effective if the self-collimation property of the PC is considered.

A pulse of waves propagating along the PC let the pulse be finite in dimension along the direction of propagation. Theoretically, such a pulse can be represented as a wave packet formed as a superposition of the modes, but with a different propagation constant (Lock, 2008; Spitsyn & Glinskiĭ, 2008). From Lock (2008) and Spitsyn and Glinskiĭ (2008), it follows that the envelope of the wave packet propagates with the velocity $V_g^z={\mathit{\omega }}_n(\mathit{\beta })$, where β is a propagation constant. The direct calculation of the derivative of the dispersion relation calculated numerically is not always convenient and can give an error. As shown in Yariv and Yeh (2006), the group velocity of the wave packet $V_g^z$ is equal to the velocity of energy transfer by the mode nβ. Thus, using the results of Kildishev and Shalaev (2011), the group velocity can always be calculated with more accuracy, irrespective of the number of points in the dispersion curve. Figure 5 shows the results of calculations of the group velocity of the wave packet formed of the differently localized modes in PC with SnTe structure in a PVDF background. Figure 4 shows variation in reduced velocity for several modes along the M–Γ–X direction is shown in (c).

Figure 5. The first four branch group velocity, ∂ω/∂k, calculated along high symmetry directions of the first irreducible Brillouin zone.

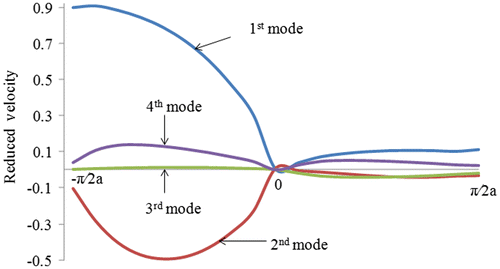
From Figure 5, it is evident that the components of the group velocity vs. the high symmetry direction (0–π/2a) vary over wide limits. The dependences, which describe the wave packets of the localized modes of any polarization and any order, exhibit (generally) a maximum at certain propagation constants. This means that the dispersion of the group velocity can be positive, negative, or zero (Burov, Voloshinov, Dmitriev, & Polikarpova, 2011; Craster & Guenneau, 2013; Kildishev & Shalaev, 2011). It is worth mentioning that the group velocity of the waves is zero at the high symmetric point X meaning that there is no energy transfer at this point.

5. Conclusions

In the present paper, we initially discussed the band structure of two-dimensional PC composed of a topological material embedded in a polymer host. We used the plain wave expansion method to calculate band gaps in the acoustic band structure of the locally resonant PC. The results of this study illustrate that the width of the first band decreases and more phononic stop bands appear under the assumption of the fluid/solid approach. The topological properties of the material SnTe with PVDF composing a PC may have an important effect on its dispersion characteristics. Such a combination can alter the propagation characteristics of acoustic waves within the system. Therefore, SnTe can be viewed as an acoustic topological insulator and could be useful for acoustic waves to improve a novel device with new functionalities for acoustic systems that are unique and robust. The topological distribution of the material phases inside the unit cell composing a PC has a significant effect on its dispersion characteristics. The findings of this paper may be useful to the improvements in the design of acoustic PCs and they provide some perspectives in a way for designing acoustic filters or insulators.

Acknowledgment

The author (Ekmel Ozbay) acknowledges partial support from the Turkish Academy of Sciences.

Additional information

Funding

Funding. This work is supported by the projects DPT-HAMIT, DPT-FOTON, and NATO-SET-193 as well as TUBITAK [project number 113E331], [project number 109A015], [project number 109E301].

Notes on contributors

Amirullah M. Mamedov

Dr Amirullah M Mamedov, Emeritus Professor and Seniour Researcher, is in Nanotechnology Research Center (NANOTAM) at Bilkent University in Turkey. He received his PhD Degree in Solid State Physics at the Ioffe Phys. Techn. Institute Academy Sci. of the USSR (1974, St. Petersburg) and received his Doctor of Habilitatus (Doctor of Sciences) in Optics and Spectroscopy at the Latvian State University (1984, Riga, Latvia). His current research interest focuses on Nonlinear Optics, Electro-Optics and Guidance Systems, Metamaterials and Nanostructures, and Electronic Properties of Topological insulators and Ferroelectric Materials. The research reported in this paper relates to understanding of complex structures to create materials with enhanced properties that can be tailored to a particular application.