Some novel exponential function structures to the Cahn–Allen equation

Abstract

In this manuscript, we consider the Bernoulli sub-equation function method for obtaining new exponential prototype structures to the Cahn–Allen mathematical model. We obtained new results using this technique. We plotted two- and three-dimensional surfaces of the results using Wolfram Mathematica 9. At the end of this manuscript, we submitted a conclusion in a comprehensive manner.

Keywords:

• Cahn–Allen equation
• Bernoulli sub-equation function method
• exponential function solution
• rational function solution

Publıc Interest Statement

Finding new travelling wave solutions to the nonlinear partial differential equations, especially, some important mathematical models have been significant for public statement. For example, the mathematical models such as AIDS, HIV, AEROCPACE and OPTICAL STRUCTURES attract attention from all over the world. Obtaining new travelling wave solutions to such models give new ideas to scientists and experts. Finding new types of solutions require a knowledge about the properties of new methods because they give us new properties of mathematical models. This paper is devoted to the mathematical investigation of the Cahn–Allen equation in terms of new travelling wave solutions using Bernoulli sub-equation function method.

1. Introduction

Many well-known phenomena in mathematical physics and engineering fields are described using nonlinear partial differential equations (NPDEs). Furthermore, NPDEs are widely used to describe complex phenomena in various fields of sciences, especially in optical science, engineering, applied science and physics.

Hedayati, Jafari, and Batebi (2016) have investigated the free-electron dynamics and a free-electron laser based on the laser-pumped wiggler. Salik, Hanif, Wang, and Zhang (2016) have studied on the laser-based diagnostics of slaked lime plasma. Tseng and Hsu (1990) have analysed the repair of radiation-induced DNA double-strand breaks. Manafian (2016), Manafian and Lakestani (2016a, 2016b) have searched for significant properties of some NPDEs in terms of optical aspect. Baumann (1978) have found some properties of the Hodgkin–Huxley model of electrical excitability.

In recent years, some researchers have focused on elastic rods. For example, Umetani, Schmidt, and Stam (2014) have submitted to the literature a novel method to simulate complex bending and twisting of elastic rods. Miller et al. (2015) have studied on Buckling of a thin elastic rod inside a horizontal cylindrical constraint. Asymptotic methods have been used for bending–stretching model in adhesive contact for elastic rods by Rodríguez-Arós and Viaño (2015). Murphy (2015) has observed the stability of thin, stretched and twisted elastic rods. Luo, Xie, Xie, Cai, and Gu (2014) have published an article based on Kirchhoff elastic rod, and so many researchers have studied on important NLPDEs (Altan Koç, Baskonus, & Bulut, 2016; Atangana, 2013a, 2013b; Atangana & Alabaraoye, 2013; Atangana & Bildik, 2013; Atangana & Oukouomi Noutchie, 2013; Baskonus, 2016; Baskonus & Bulut, 2015, 2016a, 2016b; Baskonus, Bulut, & Atangana, 2016; Bulut & Baskonus, 2016; Ciancio, 2007; Ciancio, Ciancio, & Farsaci, 2007, 2008; Ciancio & Quartarone, 2013; Özpinar, Baskonus, & Bulut, 2015; Zheng, 2012).

The paper is organized as follows: In Section 2, we describe the Bernoulli Sub-Equation function method (BSEFM). We consider the following NLPDEs defined by:$$u_t=u_{xx}-u^n+u.$$

If we take as n = 3, we obtain the following Chan–Allen equation defined by Taşcan and Bekir (2009):(1) $$u_t=u_{xx}-u^3+u.$$(1)

Moreover, in Section 3 we give the physical interpretations and remarks of the solutions obtained by BSEFM. Also, a comprehensive conclusion is given in Section 4.

2. Fundamental properties of Bernoulli sub-equation function method

An approach to the mathematical models including partial differential equations will be presented in this sub-section of paper. The steps of this technique which are partially modified can be taken as follows (Baskonus, Bulut, & Kayhan, 2015; Zheng, 2012).

Step 1: We consider the following nonlinear partial differential equation (NLPDE) in two variables and a dependent variable u:(2) $$P\left(u_x,u_t,u_{xt},u_{xx},\cdots \right)=0,$$(2)

and take the travelling wave transformation(3) $$u\left(x,t\right)=U\left(\mathit{\eta }\right),\mathit{\eta }=x-ct,$$(3)

where c ≠ 0. Substituting Equation (3) in Equation (2) yields a nonlinear ordinary differential equation (NLODE) as following:(4) $$N\left(U,U^{\prime },U^{″},\cdots \right)=0,$$(4)

where $U=U\left(\mathit{\eta }\right),U^{\prime }=\frac{dU}{d\mathit{\eta }},U^{″}=\frac{d^{2}U}{d{\mathit{\eta }}^2},\cdots .$

Step 2: Take trial equation of solution for Equation (4) as following:(5) $$U\left(\mathit{\eta }\right)=\sum _{i=0}^n{a}_i{F}^i=a_0+a_{1}F+a_2{F}^2+\cdots +a_n{F}^n,$$(5)

and(6) $$F^{\prime }=bF+d{F}^M,b\ne 0,d\ne 0,M\in \mathbb{R}-\left\{0,1,2\right\},$$(6)

where $F\left(\mathit{\eta }\right)$ is Bernoulli differential polynomial. Substituting Equation (5) along with Equation (6) in Equation (4) yields an equation of polynomial $\mathit{\Omega }\left(F\left(\mathit{\eta }\right)\right)$ of $F\left(\mathit{\eta }\right)$ as follows:(7) $$\mathrm{\Omega }\left(F\left(\mathit{\eta }\right)\right)={\mathit{\rho }}_{s}F{\left(\mathit{\eta }\right)}^s+\cdots +{\mathit{\rho }}_{1}F\left(\mathit{\eta }\right)+{\mathit{\rho }}_0=0.$$(7)

According to the balance principle, we can obtain a relationship between n and M.

Step 3: Let the coefficients of $\mathit{\Omega }\left(F\left(\mathit{\eta }\right)\right)$ all be zero yielding an algebraic equations system:(8) $${\mathit{\rho }}_i=0,i=0,\cdots ,s.$$(8)

Solving this system, we will specify the values of a₀, ⋯, a_n.

Step 4: When we solve Equation (6), we obtain the following two situations according to b and d:(9) $$F\left(\mathit{\eta }\right)={\left[\frac{-d}{b}+\frac{E}{e^{b\left(M-1\right)\mathit{\eta }}}\right]}^{\frac{1}{1-M}},b\ne d,$$(9) $$F\left(\mathit{\eta }\right)={\left[\frac{\left(E-1\right)+\left(E+1\right)tanh\left(\frac{b\left(1-M\right)\mathit{\eta }}{2}\right)}{1-tanh\left(\frac{b\left(1-M\right)\mathit{\eta }}{2}\right)}\right]}^{\frac{1}{1-M}},b=d,E\in \mathbb{R}.$$

Using a complete discrimination system for polynomial, we obtain the solutions to Equation (4) with the help of Wolfram Mathematica 9 programming and classify the exact solutions to Equation (4). For a better understanding of results obtained in this way, we can plot two- and three-dimensional surfaces of solutions by taking into consideration suitable values of parameters.

3. Implementation of the BSEFM

In this section, we have successfully considered the BSEFM to the Cahn–Allen equation for getting some new travelling wave solutions.

Application: When we consider the travelling wave transformation and perform the transformation $u\left(x,t\right)=U\left(\mathit{\eta }\right),\mathit{\eta }=x-ct$ in which c is constant, we obtain NLODE as follows:(10) $$U^{″}+c{U}^{\prime }-U^3+U=0.$$(10)

When we consider to Equations (5) and (6) for balance principle between U′′ and U³, we obtain the following relationship between n and M:(11) $$M=n+1.$$(11)

This relationship gives us some new different analytical solutions for Equation (1).

Case 1: If we take as n = 2 and M = 3 in Equation (11), we can write following equations:

(12) $$U=a_0+a_{1}F+a_2{F}^2,$$(12)

(13) $$U^{\prime }=a_{1}bF+a_{1}d{F}^3+2a_{2}b{F}^2+2a_{2}d{F}^4,$$(13)

and(14) $$\begin{array}{c}{U}^{″}=a_1{b}^{2}F+4a_2{b}^2{F}^2+2a_{1}bd{F}^3+14a_{2}bd{F}^4+3a_1{d}^2{F}^5+8a_2{d}^2{F}^6,\hfill \\ ⋮.\hfill \end{array}$$(14)

where $a_2\ne 0,b\ne 0,d\ne 0$. When we substitute Equations (12)–(14) in Equation (10), we obtain a system of algebraic equations for Equation (13). Therefore, we obtain a system of algebraic equations from these coefficients of polynomial of F. Solving this system with the help of Wolfram Mathematica 9, we find the following coefficients and solutions:

Case 1.1: For b ≠ d, it can be considered the following coefficients:(15) $$a_0=-1,a_1=0,b=\frac{1}{2\sqrt{2}},d=-\frac{a_2}{2\sqrt{2}},c=\frac{3}{\sqrt{2}}.$$(15)

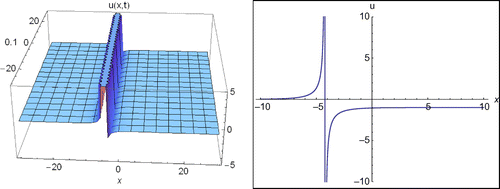
Substituting these coefficients in Equation (12) along with Equation (9), we obtain the following new exponential function solution for Equation (1(1) $$u_t=u_{xx}-u^3+u.$$(1) ) (see Figure 1):(16) $$u_1\left(x,t\right)=-E{\left[E+a_2{e}^{-\frac{3t}{2}+\frac{x}{\sqrt{2}}}\right]}^{-1}.$$(16)

Figure 1. The 2D and 3D surfaces of Equation (16) under the values of a₂ = −7, E = 8, −15 < x < 15, −15 < t < 15 and t = 0.01 for 2D surfaces.

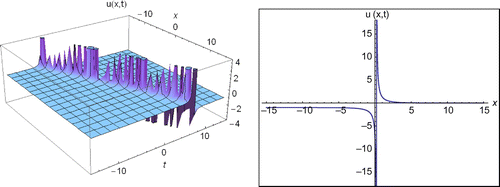
Case 1.2: Another coefficients for Equation (1) and for b ≠ d, it can be considered follows:(17) $$a_0=a_1=0,b=\frac{1}{2\sqrt{2}},d=-\frac{a_2}{2\sqrt{2}},c=-\frac{3}{\sqrt{2}}.$$(17)

When we regulate Equation (12) under the terms of Equations (9) and (17), we find the other new exponential function solution for Equation (1) (see Figure 2):(18) $$u_2\left(x,t\right)=1-E{\left[E+a_2{e}^{\frac{3t}{2}+\frac{x}{\sqrt{2}}}\right]}^{-1}.$$(18)

Figure 2. The 2D and 3D surfaces of Equation (18) under the values of a₂ = 7, E = −8, −15 < x < 15, −15 < t < 15 and t = 0.01 for 2D surfaces.

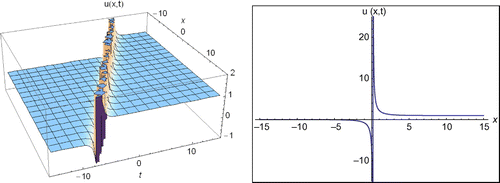
Case 1.3: Another coefficients to the Equation (1) for b ≠ d, it can be considered as follows:(19) $$a_0=1,a_1=0,b=-\frac{1}{2\sqrt{2}},d=-\frac{a_2}{2\sqrt{2}},c=\frac{-3}{\sqrt{2}}.$$(19)

Considering these coefficients in Equation (12) along with Equations (9) and (19), we gain other new exponential function solution to Equation (1) (see Figure 3):(20) $$u_3\left(x,t\right)=1+{\left[-1+\frac{E}{a_2}{e}^{\frac{3t}{2}+\frac{x}{\sqrt{2}}}\right]}^{-1}.$$(20)

Figure 3. The 2D and 3D surfaces of Equation (20) under the values of a₂ = −1, E = −18, −15 < x < 15, −15 < t < 15 and t = 0.01 for 2D surfaces.

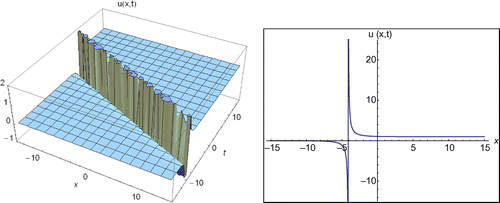
Case 1.4: For b ≠ d, another new coefficients to the Equation (1), it can be considered as follows:(21) $$a_0=-1,a_1=0,a_2=-2\sqrt{2}d,c=\frac{3}{\sqrt{2}},b=\frac{1}{2\sqrt{2}}.$$(21)

If Equation (21) is substituted in Equation (12) along with Equation (9), we gain the same travelling wave solution as the solution obtained by Taşcan and Bekir (2009) for Equation (1) (see Figure 4) as follows:(22) $$u_4\left(x,t\right)=\left[\frac{E}{2\sqrt{2}d{e}^{\left(\frac{-3t}{2}+\frac{x}{\sqrt{2}}\right)}-E}\right].$$(22)

Figure 4. The 2D and 3D surfaces of Equation (22) under the values of d = 17, E = 8, −15 < x < 15, −15 < t < 15 and t = 0.01 for 2D surfaces.

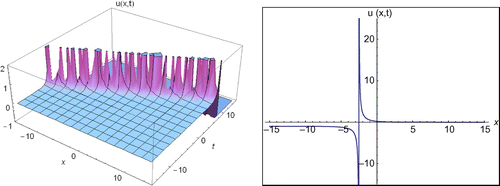
Case 2: If we take n = 3 and M = 4 in Equation (14), we can write as follows:(23) $$U=a_0+a_{1}F+a_2{F}^2+a_3{F}^3,$$(23) (24) $$U^{\prime }=a_{1}bF+a_{1}d{F}^3+2a_{2}b{F}^2+2a_{2}d{F}^4+3a_{3}b{F}^3+3a_{3}d{F}^6,$$(24)

and(25) $$\begin{array}{c}{U}^{″}=a_1{b}^{2}F+4a_2{b}^2{F}^2+2a_{1}bd{F}^3+14a_{2}bd{F}^4+3a_1{d}^2{F}^5+8a_2{d}^2{F}^6+9a_3{b}^2{F}^3+9a_{3}bd{F}^6+18a_{3}db{F}^{5}F+18a_3{d}^2{F}^9,\hfill \\ ⋮.\hfill \end{array}$$(25)

where $a_3\ne 0,b\ne 0,d\ne 0$. When we substitute Equations (23)–(25) in Equation (10), we obtain a system of equations. Therefore, we attain a system of algebraic equations from the coefficients of polynomial of F. Solving this system with the help of Wolfram Mathematica 9, we find the following coefficients:

Case 2.1: Forb ≠ d,  other coefficients to the Equation (1), it can be considered as follows:(26) $$a_0=-1,a_1=0,a_2=0,a_3=-3\sqrt{2}d,c=\frac{3}{\sqrt{2}},b=\frac{1}{3\sqrt{2}}.$$(26)

When Equation (26) is substituted in Equation (12) along with Equation (9), we obtain the same travelling wave solution as the solution obtained by Taşcan and Bekir (2009) as following for Equation (1(1) $$u_t=u_{xx}-u^3+u.$$(1) ) (see Figure 5):(27) $$u_5\left(x,t\right)=E{\left[-E+3\sqrt{2}d{e}^{\frac{-3t}{2}+\frac{x}{\sqrt{2}}}\right]}^{-1}.$$(27)

Figure 5. The 2D and 3D surfaces of Equation (27) under the values of d = 30, E = 17, −20 < x < 20, −20 < t < 20 and t = 0.1 for 2D surfaces.

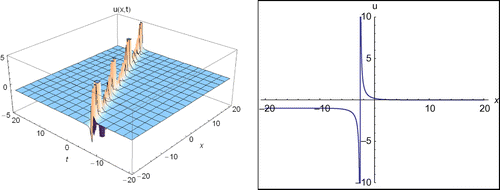
Case 2.2: Forb ≠ d,  other coefficients to the Equation (1), it can be considered as following:(28) $$a_0=a_1=a_2=0,a_3=3\sqrt{2}d,c=\frac{-3}{\sqrt{2}},b=\frac{1}{3\sqrt{2}}.$$(28)

When Equation (28) is substituted in Equation (12) along with Equation (9(9) $$F\left(\mathit{\eta }\right)={\left[\frac{-d}{b}+\frac{E}{e^{b\left(M-1\right)\mathit{\eta }}}\right]}^{\frac{1}{1-M}},b\ne d,$$(9) ), we obtain new travelling wave solution as following for Equation (1) (see Figure 6):(29) $$u_6\left(x,t\right)=-1+{\left[1-\frac{3\sqrt{2}d}{E}{e}^{\frac{3t}{2}+\frac{x}{\sqrt{2}}}\right]}^{-1}.$$(29)

Figure 6. The 2D and 3D surfaces of Equation (29) under the values of d = 20, E = 5, −10 < x < 10, −10 < t < 10 and t = 0.1 for 2D surfaces.

4. Conclusions

The solutions such as Equations (22) and (27) obtained using BSEFM are the same solutions for Equation (1) when we compare with the paper submitted to the literature by Taşcan and Bekir (2009). Moreover, the travelling wave solutions such as Equations (16), (18), (20) and (29) obtained using BSEFM are the new exponential function solutions for Equation (1) when we compare with the paper submitted to the literature by Taşcan and Bekir (2009). It has been observed that all solutions have verified the Equation (1) using Wolfram Mathematica 9. To the best of our knowledge, the application of BSEFM to the Equation (1) has not been previously submitted to the literature.

The method proposed in this paper can be used to seek more travelling wave solutions of NLEEs because the method has some advantages such as easy calculations, writing programme for obtaining coefficients and many.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Hasan Bulut

Hasan Bulut, PhD, is currently an associate professor of Mathematics in Firat University, Elazig, Turkey. He has published more than 100 articles in various journals. His research interests include stochastic differential equations, fluid and heat mechanics, finite element method, analytical methods for nonlinear differential equations, mathematical physics and computer programming.

Sibel Sehriban Atas

Sibel Sehriban Atas is a master’s student under the suprvision of Hasan Bulut. Her research interests include analytical methods such as Bernoulli sub-ODE method, and improved version of it for the nonlinear partial differential equations with integer order.

Haci Mehmet Baskonus

Haci Mehmet Baskonus, PhD, is currently an assistant professor of computer Engineering in Munzur University, Tunceli, Turkey. He has published more than 50 articles in various journals. His research interests include analytical and numerical methods such as sumudu transform method, homotopy perturbation method, improved Bernoulli sub-ODE method and modified exponential function method for the nonlinear partial differential equations with integer order and fractional order.