Ab-initio study on structural, elastic, electronic and optical properties of iron-based superconductor

Abstract

Using the plane-wave ultrasoft pseudo-potential technique, which is based on the first-principle density functional theory with generalized gradient approximation, the structural, elastic, electronic, and optical properties of FeSe are investigated. The calculated structural parameters show a good agreement with the experimental and other theoretical results. The optimized lattice parameters, independent elastic constants (C₁₁, C₁₂, C₁₃, C₃₃, C₄₄, and C₆₆), bulk modulus B, compressibility K, shear modulus G, and Poisson’s ratio ν, as well as the band structures, total and atom projected densities of states, and finally the optical properties of FeSe have been evaluated and discussed. The band structure and density of states show that this phase has metallic behavior and the major contribution comes from Fe-3d states. Further, the first time investigated optical functions reveal that the reflectivity is high in the IR-UV region up to 19.5 eV, showing this to be promising coating material.

Keywords:

• FeSe
• first-principles
• crystal structure
• elastic properties
• electronic properties
• optical properties

Public Interest Statement

In this research article, we have studied the structural, elastic, electronic, and optical properties of iron-based superconductor FeSe using the plane-wave ultrasoft pseudo-potential technique, which is based on the first-principle density functional theory with generalized gradient approximation. This is the quantitative theoretical prediction of the electronic, elastic, and optical properties of this compound. We hope that this research will help to investigate the different properties of other materials of this group.

1. Introduction

The phenomenon of superconductivity has a rich and interesting history, starting in 1911 when Kamerlingh Onnes discovered that upon cooling elemental mercury to very low temperatures, the electrical resistance suddenly and completely vanished below a critical temperature T_c of 4 K (−452°F) (Timmer, 2011). This resistanceless state enables persistent currents to be established in circuits to create enormous magnetic fields, and to stock and transport energy without dissipation. Superconductors have other unique characteristics such as the ability to expel and screen magnetic fields, and quantum oscillations controlled by the magnetic field that provide extraordinary measurement sensitivity. Over the intervening years, the number of superconducting materials has grown, with higher critical temperatures and enriched metallurgical properties, and these have found their way into a number of high-tech applications such as MRI imaging systems for the health care industry.

Iron-based superconductors (FeSe) are iron-containing chemical compounds whose superconducting properties were discovered in 2006 by Hosono’s group, and boosted in 2008 by the superconducting transition temperature, T_c, of 26 K in LaFeAsO_1−xF_x. Since then, enormous researches have been done on the materials, with T_c reaching as high as 55 K. These iron-based superconductors have initiated a flurry of activity as researchers try to understand the origin of the superconductivity in these new materials, as well as develop them for prospective use in devices (Kamihara, Watanabe, Hirano, & Hosono, 2008; Kamihara et al., 2006). Discovery of iron-based superconductors have attracted a lot of attention due to their unique properties (Kamihara et al., 2008). Through these studies, a binary superconducting compound FeSe (11) with the simplest structure has been discovered soon (Hsu et al., 2008). FeSe has several advantages compared with iron pnictide superconductors, such as lower toxicity and less sensitivity to atmosphere of starting materials. Research activity directed towards the applications of this superconductor has been under way because of its high upper critical field (Patel et al., 2009).

In this research paper, we have used plane-wave pseudo-potential density functional theory method (DFT) with generalized gradient approximation (GGA) for investigating the structural, elastic, and optical properties of iron-based superconductor of FeSe. The rest parts of this paper are arranged as follows. The computation details are given in Section 2. In Section 3, the results and discussion are presented. Finally, a summary of our work is shown in Section 4.

2. Computational method

The First-principles investigations were carried out using the plane-wave pseudo-potential method based on the density-functional theory (Kohn & Sham, 1965) implemented in the CASTEP code (Clark et al., 2005). The exchange-correlation energy is treated within the GGA using Perdew-Burke-Ernzerhof (PBE) scheme (Perdew, Burke, & Ernzerhof, 1996). In our present calculations, the ultrasoft pseudo-potentials were used, and the plane-wave cut-off energy was used 500 eV for FeSe. For the sampling of the Brillouin zone a Monkhorst-Pack grid (Monkhorst & Pack, 1976) of 10 × 10 × 12 k-points for FeSe were used. The equilibrium crystal structures are obtained via geometry optimization in the Broyden-Fletcher-Goldfarb-Shanno minimization scheme (Fischer & Lmlof, 1992). Geometry optimization was performed using with the total energy of 1 × 10⁻⁵ eV/atom, maximum force of 0.002 eV/Å, maximum stress of 0.05 GPa, and the maximum atomic displacement of 1 × 10⁻³ Å. Also the Mulliken bond populations, electronic density of states (DOS), elastic constants Cij, and optical properties were calculated by using the CASTEP code (Clark et al., 2005).

3. Results and discussion

3.1. Structural properties

The iron-based superconductor FeSe belongs to tetragonal structure with the space group P4/nmm (No. 129). The equilibrium lattice parameters of FeSe have a value of a = 3.775 Å and c = 5.512 Å (Yeh et al., 2008). By minimizing the total energy, the lattice constants and atomic positions have been optimized as a function of normal stress. Figure 1 shows the optimized structures of FeSe. The calculated values of the structural properties of FeSe are presented in Table 1 along with the available experimental and other theoretical values. Our present theoretical results are very close to both experimental and other theoretical results as evident from Table 1.

Figure 1. The crystal structures of FeSe (a) the conventional cubic cell and (b) the primitive cell.

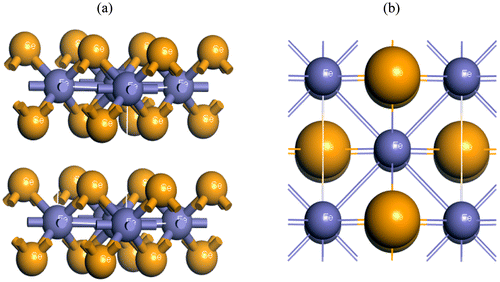
Table 1. The calculated lattice parameters, atomic positions, unit cell volume (V), and bulk modulus (B) of superconductor FeSe

Compound	Lattice parameters (Å)	Unit cell volume V (Å^3)	Bulk modulus B (GPa)	Atomic positions	Ref.
FeSe	a = 3.867, 3.775*	91.48	67.66	Fe (0, 0, 0)	Present
	c = 5.607, 5.512*			Se (0.5,0,0.266)	Yeh et al. (2008)

* Experimental value, Yeh et al. (2008).

3.2. Elastic properties

The elastic properties of materials provide with useful information about the bonding character between adjacent atomic planes, the anisotropic character of the bonding, the structural stability, and the stiffness of materials. The interatomic potentials, interatomic bonding, thermal expansion, Debye temperature, phonon spectra, and specific heat capacity also provided by these properties (Bouhemadou, Khenata, Chegaar, & Maabed, 2007; Pan, Xia, Ye, & Ding, 2012; Ponce, Casali, & Caravaca, 2008). Elastic constants are defined by means of a Taylor expansion of the total energy namely the derivative of the energy as a function of a lattice strain (Clark et al., 2005; Perdew & Zunger, 1981). The elastic constants C_ij, bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν, and the anisotropic factor A have been calculated and are presented in Table 2 in order to study the elastic properties of FeSe. The tetragonal crystal like FeSe has six independent elastic coefficients C_ij, i.e. C₁₁, C₁₂, C_13, C₃₃, C₄₄, and C₆₆. The six independent elastic constants C_ij should satisfy the following Born–Huang criteria (Roknuzzaman & Islam, 2013) for a stable tetragonal structure:(1) $$C_{11}>0;C_{33}>0;C_{44}>0;C_{66}>0$$(1) (2) $$(C_{11}-C_{12})>0;(C_{11}+C_{33}-2C_{13})>0$$(2) (3) $$2[(C_{11}+C_{12})+C_{33}+4C_{13}]>0$$(3)

Table 2. The calculated elastic constants C_ij (in GPa), the shear anisotropic factors A, and k_c/k_aof iron-based superconductor FeSe

Compound	C11	C12	C13	C33	C44	C66	A	kc/ka	Ref.
FeSe	161	62	41	89	50	78	1.010	2.93	Present

The elastic constants listed in Table 2 are positive and satisfy the above conditions. This suggests that this superconductor is mechanically stable compound. The elastic anisotropy of a crystal is the orientation dependence of the elastic moduli or sound velocities. A proper description of elastic anisotropy in crystals has an important implication in engineering science as well as in solid state (crystal) physics. Physicists use the term anisotropy to describe direction-dependent properties of materials. Magnetic anisotropy, for example, may occur in a plasma, so that its magnetic field is oriented in a preferred direction. Plasmas may also show “filamentation” (such as that seen in lightning or a plasma globe) that is directional. Many crystals are anisotropic to light (“optical anisotropy”), and exhibit properties such as birefringence. To quantify the elastic anisotropy of tetragonal structure, FeSe, Zener anisotropic factor defined by A = 2C₄₄/(C₁₁−C₁₂) have been evaluated. The calculated Zener anisotropic factor of FeSe is presented in Table 2. To measure the degree of elastic anisotropy in solids, the Zener anisotropy factor A is used. For a completely isotropic material, the value of A = 1 and for anisotropic material A is smaller or greater than one. The value of A for FeSe listed in Table 2 indicates that the material is elastically anisotropic material. There are another anisotropy parameter defined by the ratio between linear compressibility coefficients along the c and a axis for tetragonal crystal is $k_c/k_a=(C_{11}+C_{12}-2C_{13})/(C_{33}-C_{13})$. The compressibility along both directions is same i.e. the crystal is isotropic if the value of this parameter is unit but any value less (or greater) than unity indicates that the compressibility along the c axis is either smaller or larger than that along the a axis. Our result reveals that the compressibility along the c axis is slightly larger than that along the a axis. This factor also indicates that the material FeSe is anisotropic.

We have estimated the bulk modulus (B) and shear modulus (G) of polycrystalline aggregates from individual elastic constants, C_ij, by the well-known Voigt (Monkhorst & Pack, 1976) and the Reuss (Reuss & Angew, 1929) approximations that are recurrently used in averaging the single-crystal elastic constants for polycrystalline manners. Voigt assumes the uniform strain throughout a polycrystalline aggregate and Reuss assumes the uniform stress. The bulk modulus B_V and shear modulus G_V in the Voigt approximation for the tetragonal lattice are expressed as:(4) $$B_V=\frac{1}{9}[2(C_{11}+C_{12})+4C_{13}+C_{33}]$$(4) (5) $$G_V=\frac{1}{30}(C_{11}+C_{12}+2C_{33}-4C_{13}+12C_{44}+12C_{66})$$(5)

In the Reuss approximation, the bulk modulus B_R and shear modulus G_R are expressed as:(6) $$B_R=\frac{(C_{11}+C_{12})C_{33}-2C_{13}^2}{C_{11}+C_{12}+2C_{33}-4C_{13}}$$(6) (7) $$G_R=\frac{5C_{44}{C}_{66}[(C_{11}+C_{12})C_{33}-2C_{13}^2]}{2[3B_V{C}_{44}{C}_{66}+\{(C_{11}+C_{12})C_{33}-2C_{13}^2\}(C_{44}+C_{66})]}$$(7)

The Voigt and Reuss assumptions are true only for isotropic crystals, but for an anisotropic crystal their assumptions become immediately invalid. Hill (1952) shown that for an anisotropic crystals the Voigt and Reuss assumptions result in theoretical maximum and minimum values of the isotropic elastic moduli of the polycrystalline crystals, respectively, and suggested that the actual effective moduli of anisotropic polycrystalline crystals could be approximated by the arithmetic mean of the two values. According to Hill approximation, the bulk modulus B and shear modulus G are given by:(8) $$B=\frac{1}{2}(B_R+B_V)\text{and}G=\frac{1}{2}(G_R+G_V)$$(8)

Again, from the calculated bulk modulus B and shear modulus G we can estimate the Young’s modulus Y and Poisson’s ratio ν by the following relations:(9) $$Y=\frac{9BG}{3B+G}\text{and}\mathit{\nu }=\frac{3B-2G}{2(3B+G)}$$(9)

Bulk modulus B_R, B_V, B, shear modulus G_R, G_V, G, Young’s modulus Y, compressibility K, and Poisson’s ratio ν calculated using Equations (4)–(9) are listed in Table 3. It is seen that the difference between B_V and B_R as well as G_V and G_R is comparatively small. According to Hill, the difference between these limiting values may be proportional to the degree of elastic anisotropy of crystal. A material should be brittle if its G/B > 0.5, otherwise it should be ductile according to Pugh’s criteria (Pugh, 1954). Our calculations show that G/B > 0.5, hence the material FeSe should behave in brittle manner. The knowledge of the Young’s modulus and Poisson’s ratio are very important for the industrial and technological applications. Useful information about the measure of the stiffness of the solids is provided by the Young’s modulus provides, i.e. the larger the value of Y, the stiffer is the material. The Poisson’s ratio provides the information about the characteristics of the bonding forces. The values of ν are typically 0.1 to 0.25 and interatomic forces are non-central forces for covalent materials. Also the lower and upper limits of ν are 0.25 and 0.5 for ionic crystals and the interatomic forces are central forces. For a brittle material, the Poisson’s ratio is very small, whereas for a ductile metallic material it is typically 0.33 (Clark et al., 2005). This value is smaller than 0.33 for FeSe. So that material FeSe possesses the property of brittleness.

Table 3. The calculated Bulk moduli (B_R, B_V, B in GPa), shear moduli (G_R, G_V, G in GPa), Young’s modulus (Y in GPa), compressibility (K in GPa⁻¹), G/B, and Poisson’s ratio (ν) of FeSe

Compound	BR	BV	B	GR	GV	G	Y	K	G/B	ν	Ref.
FeSe	69.56	77.67	73.62	53.24	59.10	56.17	134.34	0.007	0.563	0.196	Present
	–	–	39	–	–	32	73	–	0.82	0.179	Chandra and Islam (2010)

3.3. Electronic properties

The DOS plays vital role in the analysis of the physical properties of materials. In solid-state and condensed matter physics, the DOS of a system describes the number of states per interval of energy at each energy level that are available to be occupied. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. The total DOS is written as a sum over atomic contributions. The DOS is calculated using the following expression(10) $$n(\in )=s\sum _{n,k}\mathit{\delta }(\in -{\in }_n^k)=(2/V_{BZ})-\sum _n\int \mathit{\delta }(\in -{\in }_n^k)dk$$(10)

And the number of electron in the unit cell is given by(11) $$\underset{-\infty }{\overset{{\in }_F}{\int }}n(\in )d(\in )$$(11)

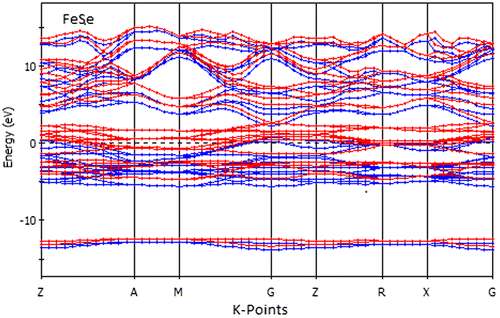
Here, we perform an analysis for the electronic band structure of FeSe. We illustrate the investigated partial density of states (PDOS) and total density of states (TDOS) at normal pressure. The calculated electronic band structures of FeSe along the high symmetry directions in the Brillouin zones are shown in Figure 2. Here, we have treated Fe-3d⁶4s² and Se-4s²4p⁴ as valence electrons. From Figure 2, it is noticed that the compound under study is metallic because a number of valance and conduction bands are overlapping at the Fermi level.

Figure 2. Electronic band structure of FeSe along high symmetry direction in the Brillouin zones.

Mulliken overlap population is a great quantitative criterion for investigating the covalent and ionic nature of bonds. In Table 4, we have listed the atomic Mulliken population of FeSe compound. A high value of the bond population indicates a covalent bond, whereas a low value denotes the ionic bonds. A value of zero indicates a perfectly ionic bond and the values greater than zero indicate the increasing levels of covalency (Segall, Shah, Pickard, & Payne, 1996).

Table 4. Mulliken electronic populations of FeSe

Species	s	p	d	Total	Charge	Bond	Population	Lengths
Fe	0.58	0.94	6.45	7.98	0.02	Fe-Se	0.18	2.47
Se	1.64	4.39	0.00	6.02	−0.02

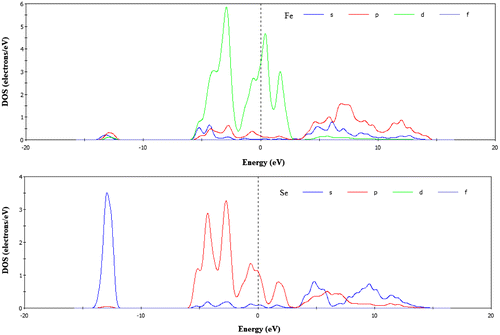
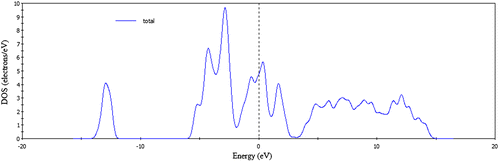
From Table 4, we see that the bond population of FeSe is 0.18 indicating that the bond Fe-Se is covalent. The calculated total and PDOS for FeSe are presented in Figures 3 and 4. For the phase FeSe the total DOS at the Fermi level is 4.8 states per unit cell per eV and at the Fermi level the DOS mainly originates from the Fe-3d states and this states is responsible for the conduction properties of FeSe. Se has a poor contribution at the Fermi level.

Figure 3. Calculated partial density of states of FeSe.

Figure 4. Calculated total density of states of FeSe.

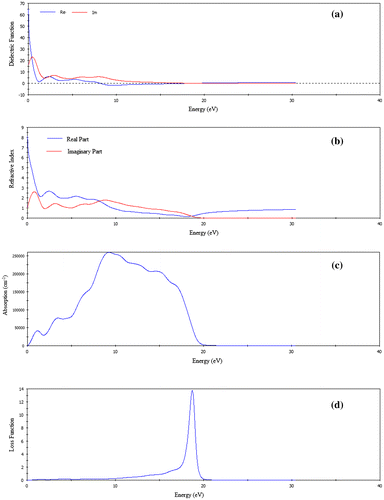
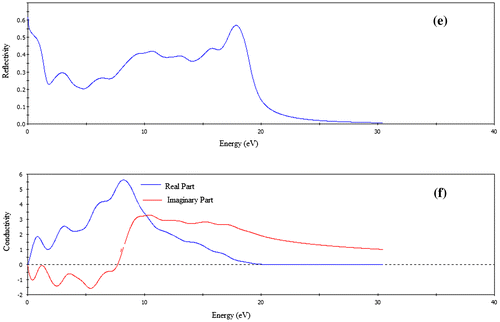
Figure 5. The optical functions (a) dielectric function, (b) refractive index, (c) absorption, (d) loss function, (e) reflectivity, and (f) conductivity of FeSe for polarization vector [1 0 0].

3.4. Optical properties

The study of the optical functions helps to give a better understanding of the electronic structure of different materials. With different photon energies, the optical properties of FeSe are calculated by the frequency-dependent dielectric function, $\mathit{\epsilon }(\mathit{\omega })={\mathit{\epsilon }}_1(\mathit{\omega })+i{\mathit{\epsilon }}_2(\mathit{\omega })$, which is closely related to the electronic band structure. The imaginary part ${\mathit{\epsilon }}_2(\mathit{\omega })$ of the dielectric function is expressed as the momentum matrix elements between the occupied and the unoccupied electronic states and can be calculated directly using (Materials Studio CASTEP manual © Accelrys, 2010):(12) $${\mathit{\epsilon }}_2(\mathit{\omega })=\frac{2e^2\mathit{\pi }}{\mathrm{\Omega }{\mathit{\epsilon }}_0}\sum _{k,v,c}{\left|〈{\mathit{\psi }}_k^c\left|\widehat{u}·\overrightarrow{r}\right|{\mathit{\psi }}_k^v〉\right|}^2\mathit{\delta }(E_k^c-E_k^v-E)$$(12)

where ω is the light frequency, e is the electronic charge, $\widehat{u}$ is the vector defining the polarization of the incident electric field, and ${\mathit{\psi }}_k^c$ and ${\mathit{\psi }}_k^v$ are the conduction and valence band wave functions at k, respectively. From the imaginary part ${\mathit{\epsilon }}_2(\mathit{\omega }),$, the real part ${\mathit{\epsilon }}_1(\mathit{\omega })$ of the dielectric function is derived through the Kramers-Kronig relations. All the other optical properties, such as refractive index, absorption spectrum, loss-function, reflectivity, and conductivity (real part) are derived from the formalism developed in Materials Studio CASTEP manual © Accelrys (2010).

The optical functions of FeSe calculated for photon energies up to 40 eV for polarization vector [1 0 0] are shown in Figure 2. We have used a 0.5 eV Gaussian smearing for all calculations because this smears out the Fermi level, so that k-points will be more effective on the Fermi surface. The most general property of solids is the dielectric function which modifies the incident electromagnetic wave of light. The dielectric function describes what an electric field such as an oscillating light wave does to material. The polarization and absorption properties of the material are described by it. The quantity ${\mathit{\epsilon }}_1(\mathit{\omega })$ represents how much a material becomes polarized when an electric field is applied due to creation of electric dipoles in the material. The quantity ${\mathit{\epsilon }}_2(\mathit{\omega })$ represents absorption in a material. When a material is transparent ${\mathit{\epsilon }}_2(\mathit{\omega })$ is zero, but becomes nonzero when absorption begins. Figure 5(a) illustrates the dielectric functions of FeSe as a function of photon energy. It is observed from Figure 5(a) that the value of ε₂ becomes zero at about 31 eV for FeSe indicating that this material becomes transparent above 31 eV. For FeSe, the value of the static dielectric constant is 65 indicating that this compound is promising dielectric material.

In optics, the refractive index of an optical medium is a dimensionless number that describes how light or any other radiation propagates through that medium. The refractive index of FeSe is shown in Figure 5(b) as function of photon energy. The static refractive index of the phase for polarization direction [1 0 0] is 8. The refractive index of this compound is high in the infrared region and gradually decreased in the visible and ultraviolet region as evident from Figure 5(b).

Important information about optimum solar energy conversion efficiency is provided by the absorption coefficient and it indicates how far light of a specific energy or wavelength can penetrate into the material before being absorbed. The absorption spectrum of FeSe for the direction [1 0 0] is shown in Figure 5(c) which begins at zero photon energy due to metallic nature of this compound. For the phase FeSe, the absorption spectrum arises sharply up-to 18 eV and the highest peak for polarization direction [1 0 0] appear at 9 eV and then decrease drastically up to 20 eV. There is no absorption above 20 eV.

Figure 5(d) shows the energy loss function of FeSe as a function of photon energy, which explains the energy loss of a fast electron traversing the material (Hossain, Ali, & Islam, 2012). It is defined by the bulk plasma frequency ω_p which occurs at ε₂ < 1 and ε₁ = 0. We see in the energy-loss spectrum that the effective plasma frequency ω_p of the phase FeSe is equal to 18 eV. The material becomes transparent when the incident photon frequency is higher than ω_p.

Figure 5(e) illustrates the reflectivity spectrum of FeSe as a function of photon energy. Starting with a value of 0.62, the reflectivity of FeSe at first decreases and then rises again to reach maximum value of ~0.58 in the energy range 10–18 eV. Thus, both the phases have roughly similar reflectivity spectra, show promise as good coating materials between 10 and 28 eV regions.

The photoconductivity is an optoelectronic phenomenon in which electrical conductivity in a material increases due to the absorption of electromagnetic radiation. Since the material has no band gap as evident from band structure, the photoconductivity starts with zero photon energy as shown in Figure 5(f). As a result of absorbing photons, the photoconductivity and hence electrical conductivity of the materials increases. The compound is highly electrically conductive at energy 8.17 eV. When the photon energy is higher than 19 eV, there is no photoconductivity for FeSe.

4. Conclusions

The structural, elastic, electronic, and optical properties of the superconducting phase FeSe have been investigated by the first-principles calculations based on DFT. The calculated lattice parameter of this compound is in good agreement with the experimental finding. We have calculated the independent elastic constants, bulk modulus, shear modulus, Young’s modulus, and elastic anisotropy factor. The material is shown to be mechanically stable, elastically anisotropic, and brittle. The calculated band structures and DOS show that the phase is metallic and at the Fermi level the main contribution comes from the Fe atom for FeSe phase. The first time study of optical properties such as dielectric function, refractive index, absorption spectrum, energy-loss function, reflectivity, and photoconductivity are determined and analyzed in detail. The optical properties such as refractive index, reflectivity, and photoconductivity are found to be polarization dependent. FeSe is potential candidate material for coating to reduce solar heating as evident from the reflectivity spectrum. The photoconductivity and hence electrical conductivity of this material increases as a result of absorbing photons.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Uttam Kumar Chowdhury

Our research groups have studied to observe the different properties such as structural, elastic, electronic, optical, and thermodynamic properties of different materials at ambient condition and under pressure. All the calculations have performed using the plane-wave pseudo-potential technique based on the density functional theory (DFT) implemented in the CASTEP code with the generalized gradient approximation (GGA). Very recently our groups have also worked to prepare crystalline powder by solid-state reaction method by carbolite furnace. The composition and crystalline phase will be confirmed by the X-ray powder diffraction (XRD). We have also synthesized the single crystals of oxide materials by Bridgman method using modified horizontal Bridgman furnace.