Revisiting the ground state phase stability of super-heavy element Flerovium

Abstract

We apply density-functional theory (DFT) using full potential linearized augmented plane wave (FP-LAPW) method to revisiting the electronic structure properties of super-heavy element 114, namely Flerovium (Fl). For the structural properties, among the four phases investigated here (fcc, bcc, hcp, and sc), we found that the face-centered-cubic phase is the ground state of Fl, discarding the hexago- nal-close-packed ground state phase found previously. Interestingly, it is found that the bcc phase competes strongly with the fcc phase for the ground stability, since the total energy difference between the fcc and bcc structures are extremely small (~1 meV). The other structures (i.e. hcp and sc) remain energetically higher, and thus do not compete for the phase stability of this element. The lattice dynamics calculations provide strong support for the calculated static ground state phase of super-heavy element 114, capturing the dynamical stability of the face-centered cubic phase and the dynamical instability of the body-centered cubic phase.

Keywords:

• element 114
• DFT
• ground state properties

Public Interest Statement

We explore here a recently discovered element, namely Flerovium. This new atom is still not well-known even for the most intrinsic properties. For a better use, we should understand deeply the various properties of this element. We have then investigated with a maximum of accuracy the entire properties such as atomic structure, optical, and electronic properties. To this end, we have used a powerful theoretical method called density-functional theory (DFT). The latter was initially developed by Walter Kohn (Nobel Price of Chemistry). The obtained results contribute highly to the knowledge of Flerovium, what should stimulate further studies on the matter.

1. Introduction

Neptunium (Np) has an atomic number of Z = 93 and it was the first heavy element created in laboratory. Neptunium was discovered by McMillan and Abelson (1940) in 1940 at Berkeley Radiation Laboratory of the University of California. Scientists have since discovered more elements called superheavy elements (SHE), each one heavier and with a shorter half-life than the one before it.

The existence of SHE is fundamentally due to shell effects with the atomic nucleus. Analogously to the electron shells in atoms, closed nucleon shells with magic numbers of protons and neutrons in nuclei bring additional stabilization. The building blocks of an atomic nucleus, proton, and neutron, arrange themselves in shell. Ignoring the stabilizing effect, atomic nuclei of SHE would disintegrate due to the drastic repulsion between their many protons.

This notion of shell stabilization leads to the prediction of an “island of stability” (IS). The IS describes the possibility of long-lived elements with particularly stable “magic numbers” of protons and neutrons, previously predicted to be centered on Z = 108, N = 162, and Z = 114, and N = 184. Production of SHE with Z ≥ 112 and neutron numbers closer to the predicted spherical shell closure at N = 184, was pioneered at the Flerov Laboratory of Nuclear Research (FLNR) about a decade ago. Five new elements with Z = 113–116 and 118 were identified among the products of heavy-ion fusion reactions (Oganessian, 2007). Recently a new chemical element with atomic number Z = 117 was reported (Oganessian et al., 2010).The recent observation of superheavy elements Z = 112–118 has not only neared this island of stability but has given a new dimension to the periodic Table of elements in addition to the fundamental excitement that these discoveries have generated.

In December 1998, scientists at Dubna (Joint Institute for Nuclear Research) in Russia created element 114 (old appellation Ununquadium, abbreviated as Uuq; new appellation, Flerovium, Fl). Ognessian et al. bombarded a ²⁴⁴Pu target with ⁴⁸Ca ions. A single atom of Flerovium, decaying by 9.67 MeV alpha-emission with a half-life of 30 s, was produced and assigned to ²⁸⁹Fl (Oganessian et al., 1999, 2000).

Due to the instability of isotopes of these elements, to the short lifetimes (second, or less) of the SHE, and low production rates (one at time), experimental physical and chemical investigations are problematic, and require the development of several new techniques to study such chemical properties. Theoretical calculations can provide valuable information for such experiments and in many cases may be the only way for an electronic structure investigation. However, these calculations are not trivial because of the huge number of electrons involved, and the central role of relativistic effects in systems, including superheavy elements.

In the past few years, a number of first-principles calculations have been made for Flerovium. The electronic and ground state properties of element 114 were investigated previously by means of pseudopotential method (Hermann, Furthmüller, Gäggeler, & Schwerdtfeger, 2010; Noffsinger & Cohen, 2010). Noffsinger and Cohen (2010) (NC) predicted that Flerovium is metallic and crystallize in fcc structure. Hermann et al. (2010) extended Noffsinger and Cohen’s work, and predicted that this element adopts the hexagonal-close-packed (hcp) structure, which is contrasting with the results of NC. The reason was attributed to relativistic effects, namely spin-orbit interaction disregarded in the Noffsinger–Cohen work.

While first-principles pseudopotential method was routinely used for semiconductors and heavy elements (Zaoui, Belabbes, Ahuja, & Ferhat, 2011), this method was not sufficiently tested for “puzzling” superheavy elements in comparison with others light of heavy elements. From a theoretical point of view, relativistic effects are arduous to be determined accurately and it is therefore necessary to analyze the accuracy of the method used. This is especially the case of the pseudopotential method used exclusively in the calculations involving superheavy element 114. This method is based on the well-known idea that only the valence electrons are of chemical importance, while the core electrons and the nucleus are replaced by an effective core potential that is chosen to describe the valence electrons in the spatial valence region. In this context, one question is of particular interest: How the pseudopotential scheme can accurately treat systems with such large number of electrons and high nuclear charge? Hence further different method is crucially needed to explore more accurately the electronic structure properties of Flerovium.

Here we report first-principles electronic structure calculations of element Z = 114. We used the stat of the art full potential linearized augmented plane wave method (FP-LAPW) to revisit the phase stability of super-heavy element 114. The FP-LAPW has proven to be one of the most accurate methods for the computation of the electronic properties of solids, and it is supposed to be more accurate than the pseudopotential method, since the both core and valence electrons are taken into account. We used two FP-LAPW methods, encoded within the elk, and the wien2k codes.

2. Method and results

All calculations are based on the density functional theory (DFT). We have used the full potential linearized augmented plane wave (FP-LAPW) method as encoded in the elkpackage (The Elk FP-LAPW Code, xxxx). The exchange and correlation effects were treated using the local density approximation (LDA) (Perdewand & Wang, 1992), and the generalized gradient approximation (GGA) (Perdew, Burke, & Ernzerhof, 1996). The basis function are expanded up to R_MTK_MAX = 10 (R_MT is the muffin-tin radii; K_MAX is the maximum modulus for the reciprocal lattice vectors). The maximum value of partial waves inside atomic sphere is l_max = 10. Fully relativistic approximation is used for core electrons, and scalar relativistic approximation is used for valence electrons, with the inclusion of spin–orbit interaction. Muffin-tin radii (R_MT) of 2.80 bohr were chosen for Fl. Significant accurate Brillouin zone (BZ) integrations are performed using the standard special k-points technique of Monkhorst and Pack (Monkhorst & Pack, 1976) (MP). For the simple cubic (sc), body-centered-cubic (bcc), and face-centered-cubic (fcc) phases, we have used a 12 × 12 × 12 MP meshes; while for the hexagonal-close-packed (hcp) phase, we have used 10 × 10 × 8 MP meshes. The corresponding integrating points over the irreducible Brilloun zone are 242 k points for the sc, bcc, and fcc phases, and 260 k points for the hcp phase. Total energy was converged to within 0.1 meV/cell.

Figure 1 shows the total energy as a function of the volume of element 114 for the sc, fcc, hcp, and bcc phases with the elk-FP-LAPW method within the LDA and GGA approximations. The calculated total energies are fitted with Murnaghan’s equation of state (Blaha, Schwarz, Madsen, Kvasnicka, & Luitz, 2001), to obtain structural parameters. The calculated structural parameters for ground state phases, namely the equilibrium lattice parameters, and the bulk modulus are given in Table 1, with available theoretical values.

Figure 1. Total energy, vs. volume for the sc, fcc, bcc, and hcp phases of element 114, using the elk-FP-LAPW method with GGA (a) and LDA (b).

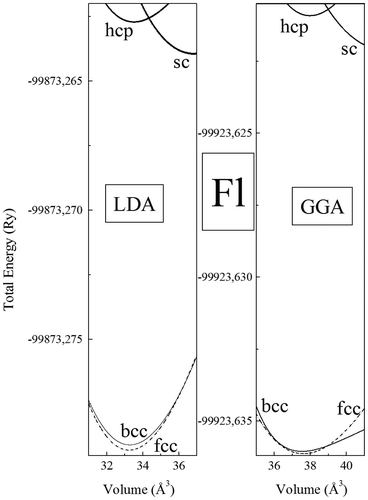
Table 1. Calculated lattice parameters (a and c), and bulk modulus B, for element 114 compared to previous calculations

	GGA	a(Å)	c(Å)	B(GPa)
Fcc	Present elk-FLAPW	5.317		27.97
	Present wien2k-FLAPW	5.196		32.52
	Pseudopotential^a	5.511		12.48
	Pseudopotential^b	5.101		48.00
Bcc	Present elk-FLAPW	4.217		21.69
	Present wien2k-FLAPW	4.130		35.67
	Pseudopotential^a	4.375		12.82
Hcp	Present elk-FLAPW	3.792	6.070	38.67
	Pseudopotential^a	4.126	6.014	14.57
Sc	Present elk-FLAPW	3.481		21.20
	Pseudopotential^a	3.641		9.40
	LDA
Fcc	Present elk-FLAPW	5.103		46.02
	Present wien2k-FLAPW	4.957		40.61
	Pseudopotential^a	4.897		37.48
Bcc	Present elk-FLAPW	4.051		42.86
	Present wien2k-FLAPW	3.954		32.83
Hcp	Present elk-FLAPW	3.627	5.858	55.96
	Pseudopotential^a	4.126	6.014	14.57
Sc	Present elk-FLAPW	3.325		32.12

^a Hermann et al. (2010).

^b Noffsinger and Cohen (2010).

We find that the fcc phase is the most stable for both LDA and GGA approximations. However, we find strong competition between the bcc and fcc phases for the phase stability (E_fcc−E_bcc~ −1 meV for the GGA, and E_fcc−E_bcc~ −2.7 meV for the LDA); while the sc and the hcp phases remain higher in energy. Our results disagree the recent Herman et al. first-principles pseudopotential calculations (Hermann et al., 2010) of structural stability of element 114, where over the four structures considered, the hexagonal close packed (hcp) was found to be the ground state of Fl.

In order to examine the competition between fcc and bcc phases for the static stability of Fl, we carried out a state of the art FP-LAPW calculations within the wien2k code. The exchange and correlation effects were treated using both the GGA and LDA approximations. We further increase slightly the parameters used in the elk-FP-LAPW calculations. Namely, we expand the basis function up to R_MTK_MAX = 12. The maximum value of partial waves inside atomic sphere is l_max = 12. Fully relativistic approximation is used for core electrons, and scalar relativistic approximation is used for valence electrons. Spin–orbit coupling is included using the second-variation method. The second variation energy cutoff is taken as E_cut = 6 Ry. The corresponding integrating points over the irreducible Brillouin zone of the MP mesh are 242 k points for the sc, bcc, and fcc phases, and 260 k points for the hcp phase.

Figure 2 shows the total energy as a function of volume of element 114 for the fcc and bcc phases within the LDA and GGA approximations. The calculated total energies are fitted with the Murnaghan’s equation of state (Murnaghan, 1944) to obtain structural parameters. The calculated structural parameters for ground state phases, namely the equilibrium lattice parameters and the bulk modulus Bare given in Table 1, with available theoretical values.

Figure 2. Total energy, vs. volume for the fcc, and bcc phases of element 114, using the Wien2k-FP-LAPW method with GGA (a) and LDA (b).

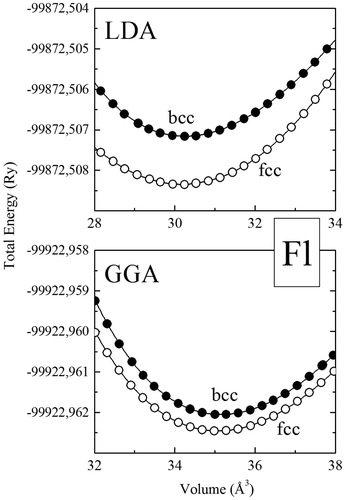
Figure 2 clearly demonstrates that the face-centered-cubic phase is the lowest-energy structure of Fl, within the GGA and the LDA approximations, which is in agreement with our previous elk-FP-LAPW calculations. We note that the total energy difference between the fcc and bcc phase is still extremely small, for the GGA(LDA) approximations, we obtain E_fcc−E_bcc~ −5 meV(E_fcc−E_bcc~ −1 meV).

The very good agreement between our elk and wien2k FP-LAPW calculations for the calculated structural ground phase of element 114 (i.e., the fcc phase) and for the calculated lattice parameters (difference less than 1%) strongly support the present findings. Moreover, we note that there is a small disagreement between our calculated equilibrium lattice parameter for the fcc, bcc, and sc phases, comparing our FP-LAPW (elk and wien2k methods) and first-principles pseudopotential calculations of Hermann et al. (2010). However, we notice at the same time a significant disagreement regarding the lattice parameter of the hcp phase (~8%).

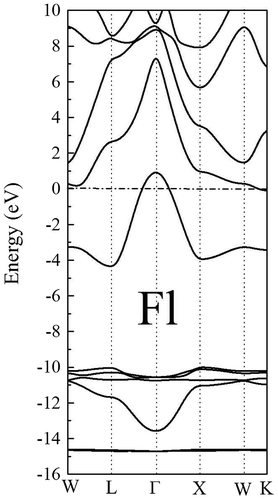
The electronic band structure of element 114 for the fcc structure is shown in Figure 3. Our results indicate that the Flerovium is metallic, which is in agreement with the recent first-principles calculations (Hermann et al., 2010; Noffsinger & Cohen, 2010). The lowest valence bands derived principally from 6d and 7s orbitals. The region close to the Fermi level originates principally from the 7p states. Moreover, the influence of relativistic effects, namely the spin–orbit interaction is strong for element 114. We found that the 5d5/2 and 5d3/2 strongly split by 5 eV; and the 6p3/2 and 6p1/2split by approximately 7 eV.

Figure 3. Calculated band structure of the fcc phase of element 114.

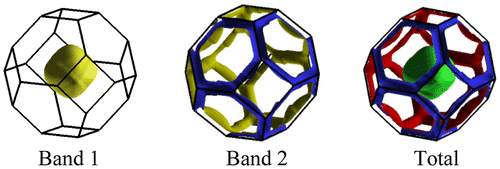
The calculated Fermi surface (FS) structures from bands that cross Fermi level are shown in Figure 4. The FS of Flerovium is made of two sheets (two bands are crossing Fermi level), one of them (band 1) consist of a large hole pocket centered at Γ point, whereas the next band (band 2) show electron “tube”-like sheets along the faces.

Figure 4. Calculated Fermi surface of element 114.

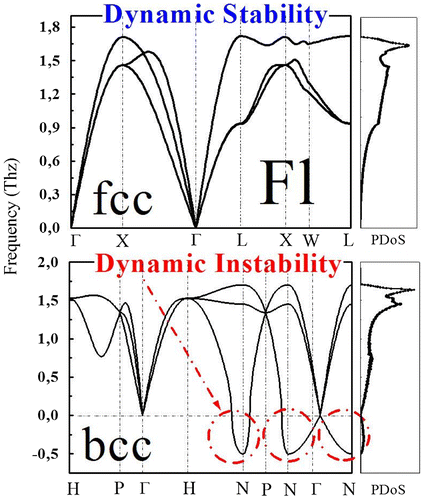
Since we have noticed that the total energy difference between the fcc and the bcc phases calculated with the elk-FP-LAPW and wien2k-FP-LAPW is very week (no more than 5 meV), which is at the border of the accuracy of best to date ab initio methods. So in such conditions, where two phases have almost the same energy, how one can predict which one is the real, and which hypothetical future experiment can follow? In order to have a deeper knowledge about the global dynamical stabilities of the bcc and fcc phases of element 114, we have investigated the phonon properties. To this end, a supercell method implemented in the elk-FP-LAPW code based on the GGA was applied to the fcc and bcc phases at the calculated equilibrium lattice parameter of both phases within a 2 × 2 × 2 q-point mesh.

The phonon dispersion curve of the fcc and bcc structures are shown in Figure 5. The bcc phase shows strong dynamic instability over a large portion of the BZ (i.e., imaginary phonon modes); while the fcc phase that presents the absolute minimum is found to be dynamically stable (only positive phonon modes). Clearly, the phonon calculations show excellent agreement with static total-energy calculations in confirming (discarding) ground state fcc (bcc) phase.

Figure 5. Calculated phonon dispersion curve of element 114 within the GGA for the fcc phase (a) and the bcc phase (b).

3. Conclusion

We have shown that both elk FP-LAPW and wien2k FP-LAPW methods show through total energy calculations, that there is a strong competition between the body-centered-cubic and face-centered-cubic structures for the ground state phase stability of super-heavy element 114. The face-centered-cubic structure is found to be the ground state phase of Flerovium, while the simple cubic, and the hexagonal-close-packed phases remain higher in energy. Furthermore, we presented dynamical calculations that provide strong support for the calculated ground state phase stability of Fl. Our calculations indicate a large dynamical instability of the bcc phase, and a dynamical stability of the fcc phase.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

H. Maiz Hadj Ahmed

This work was achieved by the group of professor Zaoui from the University of Lille (France) and the one of professor Ferhat from Oran (Algeria). Both groups collaborate since several years on various studies regarding computational materials applied to different kind of systems. The idea of developing such project follows some preceding works achieved by the two groups. Indeed the use of such theoretical approach allows a perfect prediction of behaviors for the unknown or even no existing materials. Here, the focus was on the 114 element, which is a recently discovered atom.