Detecting differentially expressed genes of heterogeneous and positively skewed data using half Johnson’s modified t-test

Abstract

Background: Microarray technology allows simultaneously detecting thousands of genes within one single experiment. The Student’s t-test (for a two-sample situation) can be used to compare the mean expression of a gene, taken from replicate arrays, to detect differential expression under the conditions being studied, such as a disease. However, a general statistical test may have insufficient power to correctly detect differentially expressed genes of heterogeneous and positively skewed data. Methods: Here we define a differentially expressed gene as with significantly different expression in means, variances, or both between the two groups of microarray. Monte Carlo simulation shows that the “half Johnson’s modified t-test” maintains quite accurate type I error rates in normal and non-normal distributions. And the half Johnson’s modified t-test was more powerful than the half Student’s t-test overall when the ratio of standard deviations between case and control groups is greater than 1. Results: Analysis of a colon cancer data shows that when the false discovery rate (FDR) is controlled at 0.05, the half Johnson’s modified t-test can detect 429 differentially expressed genes, which is larger than the number of differentially expressed genes (i.e. 344) detected by the half Student’s t. To target 100 priority genes, the half Johnson’s modified t only set FDR to 4.28 × 10⁻⁸, but for the half Student’s t, it is set to 5.39 × 10⁻⁴. Conclusions: The half Johnson’s modified t-test is recommended for the detection of differentially expressed genes in heterogeneous and ONLY positively skewed data.

Keywords:

• gene expression
• positively skewed data
• Johnson’s modified t-test

Public Interest Statement

Gene expression has been a popular research topic in recent years. Student’s t-test is commonly adopted to screen disease-related genes. However, when the researches are focused on heterogeneous and positively skewed expression data, the means of gene expression levels between case and control groups may be similar, and thus, the difference would be insignificant using conventional Student’s t-test. This study proposed half Johnson’s modified t-test to correctly detect differentially expressed genes of heterogeneous and positively skewed data. Test statistics of half Johnson’s modified t-test only considers sample standard deviation of control group, while that of case group is not included. After controlling false discovery rate (cut-off point set to 0.05) of colon cancer gene expression data, half Johnson’s modified t-test could detect 364 more significant genes than conventional Student’s t-test. Half Student t-test is worth recommending as a method for detecting differentially expressed genes in heterogeneous and positively skewed data.

Competing Interest

The authors declare no competing interest.

1. Introduction

Microarray technology allows simultaneously detecting thousands of genes within one single experiment (Templin et al., 2002). One of the main goals of microarray data analysis is to detect the differentially expressed genes, which is a two-step process. The first step involves selecting a statistic to rank the genes by expression data. The second step is to set a criterion (critical value) to consider which of the ranked genes is differentially expressed. The overall aim of this process is to identify a number of candidate genes for further studies, such as using molecular biological techniques. Statistical knowledge is often necessary for the analysis of microarray data, as researchers deal with massive amounts of data with various sources of variability in order to identify important genes. For example, fold change is often used in determining change in the expression level of individual gene for detecting differentially expressed genes in a microarray (Chen, Dougherty, & Bittner, 1997). For simplicity, researchers often use Student’s t-test to compare the mean expression of a gene, taken from replicate arrays, to detect differential expression under the conditions being studied, such as a disease (Dudoit, Yang, Callow, & Speed, 2002; Pan, 2002).

However, a general statistical test may have insufficient power to correctly detect differentially expressed genes in heterogeneous disease. A heterogeneous disease may encompass a multitude of etiological entities that have different morphological features and clinical behavior. Examples of heterogeneous diseases are otosclerosis (Van Den Bogaert et al., 2002), rheumatoid arthritis (van der Pouw Kraan et al., 2003), primary thyroid lymphoma (Thieblemont et al., 2002), and acute lymphoblastic leukemia (Yeoh et al., 2002). A gene may be overexpressed in some cases, but may be expressed normally or even underexpressed in other cases of heterogeneous diseases. This phenomenon (multimodality) will present itself in a higher variance of case group. That is, the variance (or standard deviation) of gene expression values in diseased individuals (cases) is more than that of non-diseased individuals (controls). This particular gene provides useful information and belongs to the differentially expressed class because of heterogeneity in disease. Further, mean expression values may have a small apparent difference in case and control groups, and the gene expression values may follow a positively skewed distribution (Newton, Kendziorski, Richmond, Blattner, & Tsui, 2001). In such instances, the conventional t-test or the “half Student’s t-test” (Hsu & Lee, 2010) would not be applicable to detect the gene. The original t-test may have less power under conditions of heterogeneity, while the “half Student’s t-test” may be powerful; however, neither test is suitable for non-normal data. (Note that here we assume there are some patient subgroups, at least more than one entity, but we don’t know how many subgroups exist and how to define and characterize each of them. Otherwise, we can reconstruct the diseased subjects according to different “disease entities” rather than simply different “diseases.” Then, we can perform a stratified analysis if we have known the patient subgroup structure).

In the statistical genomic field, for the last fifteen years, many researchers have developed innovative alternatives relying upon either parametric or nonparametric approaches (Tusher, Tibshirani, & Chu, 2001) which are based on frequentism or Bayesianism (Smyth, 2004). Moreover, the question of data transformation has been extensively discussed by statisticians (Johnson, 1978; Tukey, 1977) and has been widely considered with highly relevant implications for microarray. In order to determine differentially expressed genes in heterogeneous and positively skewed data, we propose the “half Johnson’s modified t-test.” The half Johnson’s modified t-test is used to correct the t variables for heterogeneity and non-normality of the population distribution, without abandoning the Student’s t distribution as a criterion. Here, the null compliance hypothesis would be that two groups (i.e. case group and control group) have the same distribution of gene expression data. The alternative hypothesis would be that means, variances, or both for the gene expression data are different between the two groups. (Note that we assume that a case effect on mean response is expected to be accompanied by an increase in variability).

Finally, a Monte Carlo simulation was performed to exhibit the statistical characteristics of the half Johnson’s modified t-test in this study, and a colon cancer gene expression data-set (Alon et al., 1999) was analyzed for demonstration.

2. Methods

Let the sample size, the sample mean, and the sample standard deviation of gene expression for case group separately be n₁, ${\overline{X}}_1$, and s₁. The corresponding notations of control group are n₀, ${\overline{X}}_0$, and s₀, respectively. The ordinary test statistic t_s of the Student’s t-test is as follows:$$t_s=\frac{{\overline{X}}_1-{\overline{X}}_0}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_0}}}$$

where $s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_0-1)s_0^2}{n_1+n_0-2}}$ represented the pooled standard deviation. Under normality assumption, t_s follows a Student’s t distribution with n₁ + n₀ − 2 degrees of freedom (d.f.).

Welch’s t-test does not require the variances to be equal (Welch, 1947). Therefore, it is a more robust test than the original Student’s t-test. Welch’s t-test uses case and control groups’ standard deviations separately. The test statistic t_w of Welch’s t-test is as follows:$$t_w=\frac{{\overline{X}}_1-{\overline{X}}_0}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_0^2}{n_0}}}$$

Under normality assumption, t_w follows a Student’s t distribution with d.f. being $\mathit{\nu }\approx \frac{{\left(\frac{s_1^2}{n_1}+\frac{s_0^2}{n_0}\right)}^2}{\frac{{\left(\frac{s_1^2}{n_1}\right)}^2}{n_1-1}+\frac{\left(\frac{s_0^2}{n_0}\right)}{n_0-1}}$

The two-sample Student’s t-test can be used in such occasions (i.e. heterogeneous diseases) to gauge statistical significances. However, when the diseases under study are heterogeneous (van der Pouw Kraan et al., 2003; Thieblemont et al., 2002; Van Den Bogaert et al., 2002; Yeoh et al., 2002), t_s or t_w may be underpowered to detect differentially expressed genes.

To tackle the heterogeneity problem, the half Student’s t-test, t_h, proposed in (Hsu & Lee, 2010) is presented as follows:$$t_h=\frac{{\overline{X}}_1-{\overline{X}}_0}{s_0\sqrt{\frac{1}{n_1}+\frac{1}{n_0}}}$$

which only uses the standard deviation of the control group. Hence, the test statistic t_h is named as the half Student’s t-test. Note that t_h has the same numerator but a different denominator as t_s. Under normality assumptions, t_h follows a Student’s t distribution with d.f. = n₀ − 1.

In case of one sample, the Johnson’s modified t-test (Cressie & Whitford, 1986) was proposed to correct t variables (for one sample) if population distribution is not normal, but not abandon the Student’s t distribution as a criterion. The form of the Johnson’s modified t-test is derived by using Cornish-Fisher expansion and the first few terms of inverse Cornish-Fisher expansion. To correct nonzero skewness of t_w, Johnson’s one-sample modified t-test was extended to deal with two-sample test (Johnson, 1978), and the modified test for t_w is:$$t_{wJ}=\left[({\overline{X}}_1-{\overline{X}}_0)+\frac{{\widehat{\mathit{\mu }}}_3}{6{\left(\sqrt{\frac{s_1^2}{n_1}+\frac{s_0^2}{n_0}}\right)}^2}+\frac{{\widehat{\mathit{\mu }}}_3{({\overline{X}}_1-{\overline{X}}_0)}^2}{3{\left(\sqrt{\frac{s_1^2}{n_1}+\frac{s_0^2}{n_0}}\right)}^4}\right]·{\left(\frac{s_1^2}{n_1}+\frac{s_0^2}{n_0}\right)}^{-1/2}$$

where ${\widehat{\mathit{\mu }}}_3=\frac{1}{n_1^2}{\sum }_{i=1}^{n_1}\frac{{(X_{1i}-{\overline{X}}_1)}^3}{n_1}-\frac{1}{n_0^2}{\sum }_{i=1}^{n_0}\frac{{(X_{0i}-{\overline{X}}_0)}^3}{n_0}$ is the sample third central moment for ${\overline{X}}_1-{\overline{X}}_0$, while ${\sum }_{i=1}^{n_1}\frac{{(X_{1i}-{\overline{X}}_1)}^3}{n_1}$ and ${\sum }_{i=1}^{n_0}\frac{{(X_{0i}-{\overline{X}}_0)}^3}{n_0}$ are the sample third central moments for the case and control groups, respectively. The d.f. of t_wJ is the same as that for t_w.

For the two-sample situation (one case group vs. one control group) (Johnson, 1978), in order to integrate the features of the aforementioned two modified tests, t_wJ and t_h, we propose to only consider the standard deviation of control group in t_wJ. Then, the half Johnson’s modified t-test would be as follows:$$t_{hJ}=\left[({\overline{X}}_1-{\overline{X}}_0)+\frac{{\widehat{\mathit{\mu }}}_3}{6{\left(s_0\sqrt{\frac{1}{n_1}+\frac{1}{n_0}}\right)}^2}+\frac{{\widehat{\mathit{\mu }}}_3{({\overline{X}}_1-{\overline{X}}_0)}^2}{3{\left(s_0\sqrt{\frac{1}{n_1}+\frac{1}{n_0}}\right)}^4}\right]·{\left[s_0^2\left(\frac{1}{n_1}+\frac{1}{n_0}\right)\right]}^{-1/2}$$

The rejection region is $t_{hJ}>t_{n_0-1,\mathit{\alpha }/2}$ or $t_{hJ}<-t_{n_0-1,\mathit{\alpha }/2}$. The significance level is denoted as α in this study.

2.1. Monte Carlo simulation

We used free R software (R Development Core Team, 2008) for testing and analysis. The two test procedures studied were the half Student’s t-test and the half Johnson’s modified t-test. The analyses were performed on two sample sizes: 40 (n₀ = n₁ = 20) and 120 (n₀ = n₁ = 60). The difference in means of gene expression data between case and control groups was denoted as d, being set to 0, 15, and 25. The standard deviation ratio of case group to control group was denoted as r, being set to 1, 1.5, 2, and 2.5. The standard deviation for the control group was set to 30. Let γ₃ = E(X − μ)³/σ³ be the skewness coefficient. In addition, γ₃ > 1, 0.6 < γ₃ ≤ 1, and 0 < γ₃ ≤ 0.6 correspond to high, moderate, and minor positive skewness, respectively. For the completeness of study, a normality scenario and three non-normality scenarios were incorporated: (1) normal distribution; (2) uniform distribution (non-normal but symmetric distribution); (3) Gamma distribution (positively skewed and γ₃ = 0.6); and (4) negatively skewed distribution (γ₃ = −0.6). Note that to generate from (4), a random number from (3) was first simulated, multiplied by −1, and added by twice of the mean of Gamma distribution.

For each scenario, the half Student’s t-test and the half Johnson’s modified t-test were performed under 1,000,000 simulations. It is essential to understand that the null hypothesis corresponds to the ratio and difference of r = 1 and d = 0. As for other settings, any exception of the null hypothesis would be the alternative one.

2.2. A colon cancer example

A colon cancer data-set consists of 40 tumor tissue samples (case group) and 22 normal colon tissue samples (control group). Oligonucleotide arrays provide a broad picture of the state of the cell through monitoring the expression level of thousands of genes simultaneously. Tissue and hybridization were analyzed by using an Affymetrix oligonucleotide Hum6000 array complementary to more than 6,500 human genes. Probes being complementary to the sequence of interest are perfect match (PM), while mismatch (MM) happens for homomeric base change at a specific position. A probe pair is a combination of a PM and an MM. Each probe pair in a probe set plays potential role in determining the signal value. The real signal value is estimated by taking LOG transformation of the PM intensity after subtracting the slide estimates. Affymetrix arrays give absolute expression values for a given gene. 2,000 genes were further analyzed as they crossed the minimal intensity across samples. The average sample skewness of the case group is 1.39, while it is 0.74 for the control group. We also use R software to demonstrate the application of the proposed test.

3. Results

3.1. Main findings

Table 1 shows type I error rates that were calculated under significance level (α-level) of 0.05, 0.01, 0.005, and 0.001. The half Johnson’s modified t-test and the half Student’s t-test maintained fairly precise type I error rates in all four distributions and at each significance level when sample size of case and control groups was larger (n₁ = n₀ = 60). When sample size of case and control groups was small (n₁ = n₀ = 20), the half Student’s t-test maintained fairly precise type I error rates under normal and uniform distribution. Under uniform distribution, type I error rates of half Johnson’s modified t-test are much smaller than significance levels for small samples, whereas they are close to but still smaller than significance levels for larger sample sizes. Although the type I error rate of both tests was mildly inflated at small significance levels such as 0.005 or 0.001 under skewed distributions, such outcome was in line with our expectations due to departure from normality and homogeneity of variance (Adusah & Brooks, 2011).

Table 1. Type I error rates for the half Student’s t-test and half Johnson’s modified t-test

	n0 = n1 = 20		n0 = n1 = 60
Significance level	Half Student’s t-test	Half Johnson’s modified t-test	Half Student’s t-test	Half Johnson’s modified t-test
Normal distribution
0.05	0.0492	0.0494	0.0513	0.0510
0.01	0.0102	0.0106	0.0114	0.0113
0.005	0.0051	0.0056	0.0056	0.0057
0.001	0.0010	0.0013	0.0012	0.0012
Non-normal but symmetric distribution (γ3 = 0)
0.05	0.0470	0.0382	0.0496	0.0464
0.01	0.0094	0.0053	0.0096	0.0079
0.005	0.0047	0.0020	0.0047	0.0037
0.001	0.0010	0.0002	0.0010	0.0007
Positively skewed distribution (γ3 = 0.6)
0.05	0.0534	0.0557	0.0514	0.0528
0.01	0.0126	0.0166	0.0104	0.0115
0.005	0.0068	0.0107	0.0052	0.0062
0.001	0.0017	0.0043	0.0010	0.0016
Negatively skewed distribution (γ3 = −0.6)
0.05	0.0529	0.0570	0.0508	0.0523
0.01	0.0122	0.0166	0.0113	0.0122
0.005	0.0071	0.0106	0.0059	0.0068
0.001	0.0021	0.0048	0.0015	0.0020

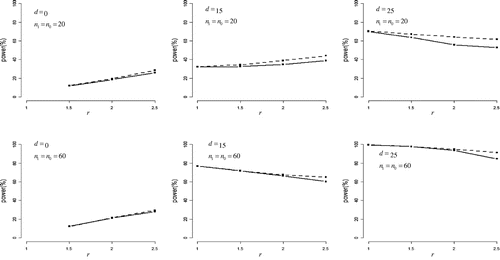
Figure 1 presents the statistical powers of the half Johnson’s modified t-test (solid lines) and the half Student’s t-test (dashed lines) with normal distribution. For r > 1 and d > 0, the half Student’s t-test was more powerful than the half Johnson’s modified t-test overall. Note that the maximal difference in power between these two tests was 9%. Also note that under d = 0, both tests had some power for detecting difference between variances, with power increasing in r. For d > 0, powers of both tests decreased marginally as r increased, except for a condition (d = 15, n₀ = n₁ = 20), power increased as r increased.

Figure 1. Statistical power in normal distribution.

Notes: Solid line: half Johnson’s modified t; dash line: half Student’s t.
The difference in means between case and control groups (denoted as d) was set to 0, 15, and 25. The ratio of standard deviations for case group to control group (denoted as r) was set to 1, 1.5, 2, and 2.5.

Under non-normal but symmetric such as uniform distribution, Figure 2 shows the statistical powers of the two tests. When n₀ = n₁ = 20, the half Student’s t-test was more powerful than the half Johnson’s modified t-test for r > 1, and the largest difference in power was 19%. When n₀ = n₁ = 60, both tests had almost the same power when d > 0.

Figure 2. Statistical power in non-normal but symmetric distribution.

Notes: solid line: half Johnson’s modified t; dash line: half Student’s t.
The difference in means between case and control groups (denoted as d) was set to 0, 15, and 25. The ratio of standard deviations for case group to control group (denoted as r) was set to 1, 1.5, 2, and 2.5.

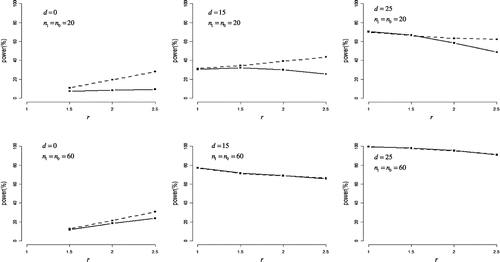
Figure 3 summarizes the statistical powers under positively skewed distributions. What was noteworthy was that the half Johnson’s modified t-test was more powerful than the half Student’s t-test when r > 1 under each of other settings, with the largest difference in power being 12%. The power performances of the two tests were similar when r = 1. For d = 0, both tests had some power to detect difference between variances, with power increasing in r for both tests. For d > 0, powers of both tests decreased with r increased, except for a case (d = 15, n₀ = n₁ = 20), power increased in r.

Figure 3. Statistical power in positively skewed distribution.

Notes: solid line: half Johnson’s modified t; dash line: half Student’s t.
The difference in means between case and control groups (denoted as d) was set to 0, 15, and 25. The ratio of standard deviations for case group to control group (denoted as r) was set to 1, 1.5, 2, and 2.5.

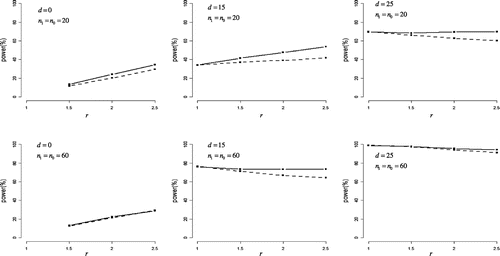
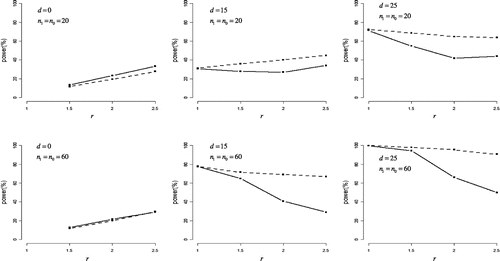
Figure 4 shows the statistical powers under negatively skewed distributions. For r > 1 and d > 0, the half Student’s t-test was more powerful than the half Johnson’s modified t-test overall. For d = 0, both tests also had some power for detecting the difference in variances between case and control groups with power increasing in r, and half Johnson’s modified t-test had a little more power than half Student’s t-test under n₀ = n₁ = 20. However, the half Johnson’s modified t-test could not do so when d > 0 and r > 1.5.

Figure 4. Statistical power in negatively skewed distribution.

Notes: solid line: half Johnson’s modified t; dash line: half Student’s t.
The difference in means between case and control groups (denoted as d) was set to 0, 15, and 25. The ratio of standard deviations for case group to control group (denoted as r) was set to 1, 1.5, 2, and 2.5.

3.2. Extensive study results

We also conducted extensive simulations to evaluate the performance of different tests. The results are summarized below. (For more details, refer to Supplementary Methods).

3.2.1. Unequal sample sizes

We examined the situations of unequal sample sizes. We found that the half Johnson’s modified t-test also maintained fairly precise type I error rates under four situations of equal and unequal sample sizes. The half Johnson’s modified t-test was also more powerful than the half Student’s t-test in a positively skewed scenario for both equal and unequal sample sizes. Notice that type I error rates of both tests was marginally inflated at a small significance level of 0.005 or 0.001 under skewed distribution with small control sample and large case sample. It has been discussed that the type I error would be inflated at the nominal significance levels for unequal sample sizes (Adusah & Brooks, 2011).

3.2.2. Unequal skewness

We examined the situation of increasing difference in skewness between the control and case groups (skewness of the case group is greater than skewness of the control group in most situations). We found that difference in power (between half Johnson’s t-test and half Student’s modified t-test) increased as difference in skewness increased. However, it should be cautioned that type I error rates were inflated in scenarios (of r and d) departing from normality and homogeneity of variance. We also observed that half Johnson’s modified t-test was more powerful than the other tests. The results suggested that half Johnson’s modified t-test can overcome heterogeneity and non-normality simultaneously when 0.3 ≤ γ₃ ≤ 0.6 for the control group.

3.2.3. Powers of tests

We examined the power performances of Student’s t-test, half Student’s t-test, Johnson’s modified t-test, and half Johnson’s modified t-test. We found that half Johnson’s modified t performs best among these tests. It’s no surprise to understand that half Johnson’s modified t-test can overcome heterogeneity (a higher variance for case group) and non-normality simultaneously under minor positive skewness (0.3 < γ₃ < 0.6 for the control group).

3.2.4. Combined test

We examined the power performances of a combined test which simultaneous testing means (using Student’s t-test) and variances (using F-test) for the control and case group with a Bonferroni correction. For comparison of this combined test and two half tests, we found that the Johnson’s modified t doesn’t outperform the half Student’s t under r ≤ 1.5 for small sample size normal data. The half Student’s t outperforms this combined test when there is a difference in means between the case group and the control group under r ≤ 1.4.

3.3. Main findings for colon cancer data

Table 2 presents the numbers (percentages) of differentially expressed genes detected using the half Johnson’s modified t, half Student’s t, Welch’s t, and Wilcoxon rank-sum tests (Wilcoxon, 1945), respectively. We set significance levels at 0.05, 0.01, 0.005, and 0.001 in this study. The half Johnson’s modified t-test detected more differentially expressed genes than the half Student’s t-test at all significance levels.

Table 2. Number (percentage) of differentially expressed genes of studied test methods in colon cancer data

	Test methods
	Half Student’s t-test	Half Johnson’s modified t-test	Welch’s t-test	Wilcoxon test
Significance level
0.05	577 (28.9%)	632 (31.6%)	355 (17.8%)	275 (13.8%)
0.01	360 (18.0%)	422 (21.1%)	192 (9.60%)	141 (7.05%)
0.005	299 (15.0%)	368 (18.4%)	147 (7.35%)	99 (4.95%)
0.001	214 (10.7%)	292 (14.6%)	74 (3.70%)	45 (2.25%)
False discovery rate
0.05	344 (17.2%)	429 (21.5%)	117 (5.85%)	48 (2.40%)
0.005	185 (9.25%)	278 (13.9%)	3 (0.15%)	5 (0.25%)

Since a total of 2,000 genes were selected, we consider controlling the false discovery rate (FDR) (Benjamini & Hochberg, 1995; Storey & Tibshirani, 2003) to reduce the problem of multiple testing. The FDR (Benjamini & Hochberg, 1995; Storey & Tibshirani, 2003) was set to 0.05 and 0.005, respectively. From Table 2, half Johnson’s modified t-test still detected more differentially expressed genes than the other tests. For instance, setting FDR to be 0.05, there are 429 differentially expressed genes determined by half Johnson’s modified t-test, while 344 differentially expressed genes are determined by half Student’s t-test.

4. Discussion

We found that half Johnson’s modified t-test maintains the nominal α level and is fairly precise for normal and skewed distributions when standard deviation of case group is larger than that of control group. Further, half Johnson’s modified t-test is more powerful than half Student’s t-test for a positively skewed distribution. This means that half Johnson’s modified t-test is suitable for studying positively skewed microarray gene expression data of heterogeneous diseases. In a heterogeneous disease, there is more than one entity that causes various clinical pictures and etiologies. Thus, the ratio of standard deviation between case group and control group is greater than 1 (that is the case group’s standard deviation is larger). However, if the expression data for a heterogeneous disease is not positively skewed distributed, half Johnson’s modified t will not achieve good power; instead, there may be power loss. Theoretically, half Johnson’s modified t can test for the difference in the means and the difference in the variances simultaneously. From simulation results (refer to Supplementary Methods for details), half Johnson’s modified t has very low power for testing the difference in two variances when means are equal or about the same (even with less power than half Student’s t). But this shortcoming can be overcome since one can combine Student’s t and F-test to achieve better power when the case group and the control group differ mainly in their variances. Therefore, half Johnson’s modified t is mainly a test of equality of two means in heterogeneous diseases.

An overlap analysis was designed to match the baseline (selected as the Student’s t-test) detection outcome (Supplement Table 4). These methods detected at least 92% overlap in differentially expressed genes. Under significance level of 0.05, the half Johnson’s modified t-test had a 95.6% overlap and detected the most novel differentially expressed genes (i.e. 260). Researchers may be concerned about FDR settings when studying a large number of genes. Half Johnson’s modified t-test provided a more rigorous FDR setting than the half Student’s t-test for targeting the same number of priority genes. For example, to target 100 priority genes, the FDR for half Johnson’s modified t-test was set to 4.28 × 10⁻⁸, but for the half Student’s t, it was set to 5.39 × 10⁻⁴.

In practice, one may calculate the standard deviation of case and control to determine the status prior to applying the proposed test, the half Johnson’s modified t-test. We suggest researchers carry out both half Student’s t-test and the half Johnson’s modified t-test to compare their results for heterogeneous and minor skewed gene expression data. However, if researchers have no prior idea about heterogeneity and skewness of gene expression data, then we suggest not using both tests simultaneously in the beginning. When detecting differentially expressed genes, type I error rate of both tests is mildly inflated at a strict significance level under skewed distribution. Slight inflation of type I error rate had no bearing on the findings of the present study. If researchers have enough resources to investigate more genes, we suggest they initially choose a moderate significance level (i.e. 0.05) for detecting differentially expressed genes.

In conclusion, half Johnson’s modified t-test maintains fairly precise type I error rates in simulation scenarios, when the ratio of standard deviation between case group and control group is large (r > 1), and the distribution of gene expression in each group has positive skewness. In summary, half Johnson’s modified t-test is recommended for detecting differentially expressed genes in heterogeneous and ONLY positively skewed data.

Funding

This study was partly supported by a grant from the Ministry of Science and Technology, Taiwan [MOST 105-2325-B-002-027].

Additional information

Notes on contributors

I-Shiang Tzeng

I-Shiang Tzeng is a doctoral researcher in the National Translational Medicine and Clinical trial Resource Center (NTCRC) composed by Academia Sinica, National Taiwan University and National Yang-Ming University, Taiwan. He currently serves as a bioinformatics and biostatistics consultant in NTCRC. He also is an adjunct assistant professor in the department of statistics, National Taipei University, Taiwan. His area of research includes biostatistics and epidemiologic method and further studies proposing the potential powerful method to detect differential expressed genes. His research interests include the field of age-period-cohort (APC) modeling from social issues to biological issues as well as the analysis of the APC models that arise in all these applications.