Stochastic modelling for financial bubbles and policy

Abstract

In this paper, we draw upon the close relationship between statistical physics and mathematical finance to develop a suite of models for financial bubbles and crashes. By modifying previous approaches, we are able to derive novel analytical formulae for evaluation problems and for the expected timing of future change points. In particular, we help to explain why previous approaches have systematically overstated the timing of changes in market regime. The list of potential empirical applications is deep and wide ranging, and includes contemporary housing bubbles, the Eurozone crisis and the Crash of 2008.

Keywords:

• econophysics
• bubbles
• crashes
• expected crash-time

Public Interest Statement

By drawing upon close links between statistical physics and mathematical finance, we provide a mathematical description of bubbles and crashes. From an academic perspective by refining previous approaches, we are able to make a contribution to the underlying theory. However, this research provides support to both policy-makers and academicians. This is reinforced by the list of potential applications which includes housing bubbles, the Eurozone crisis and the Crash of 2008.

1. Introduction

Work by Bachelier and by Black–Scholes–Merton hints at close links between mathematical finance and statistical physics, and there is a fascinating history of joint work straddling the two areas (Weatherall, 2013). This has led to the development of a field called econophysics which has seen the large-scale application of tools and techniques from statistical physics to model financial and economic phenomena (Bouchaud & Potters, 2003; Voit, 2005). At the core of this approach is the development of complex systems theory whereby system-level behaviour becomes dominated by the interaction by a multitude of microscopic components (Sornette, 2003). The resultant system-level behaviour is also much richer than the individual components when viewed in isolation. This simple observation means that conventional macroeconomic models based on microfoundations are thus liable to miss important features of the real world. As far as finance is concerned, a key ingredient to the story is that developments in complex systems theory have also occurred alongside notable increases in computing power and the growth of many very large and readily accessible financial databases.

This new field of econophysics has much to offer. In several ways, econophysics techniques may be viewed as potentially more informative than conventional economic approaches (Buchanan, 2013). In particular, econophysics may also offer novel insights into market stability and regulation which is what most interests us here. Here, further links between “econophysics” and mainstream economic models such as Zeira (1999) are also of interest.

In thermodynamics, a phase transition occurs when there is a singularity in the free energy or one of its derivatives in some thermodynamic system (Yeomans, 1992). Typically, one sees a visibly sharp change in the properties of the system such as a transformation from liquid to gas. However, phase transition behaviour has been recorded in a vast range of physical and human systems, including finance (Sornette, 2003). This analogy between financial crashes and phase transitions in critical phenomena in statistical physics is now well established (Johansen, Ledoit, & Sornette, 2000; Sornette, 2003) and has recently been explicitly linked (Fry, 2012, 2014). As a consequence, many papers discuss the sometimes controversial subject of log-periodic precursors to financial crashes (Bree, Challet, & Perrano, 2013; Chang & Feigenbaum, 2006, 2008; Feigenbaum, 2001a, b; Zhou & Sornette, 2008, 2009). For recent reviews of the relevant literature, see (Geraskin & Fantazzini, 2013; Sornette, Woodard, Wanfeng Yan, & Zhou, 2013). Clearly, financial bubbles and crashes are too important a subject to ignore and the academic literature has begun to recognize the importance of the area. Despite their origins being firmly based in statistical physics, log-periodic models have also begun to appear in several well-respected mainstream finance journals in recent years (Bree & Joseph, 2013; Geraskin & Fantazzini, 2013; Jiang et al., 2010; Kurz-Kim, 2012; Lin, Ren, & Sornette, 2014; Lin & Sornette, 2013).

Financial markets operate by balancing risk and return (Markowitz, 1971). As discussed in Fry (2012, 2014), there is a sense in which the prevailing class of log-periodic models omits a crucial second-order related to market overconfidence. Interestingly, there is thus a sense in which the academic literature reflects wider popular failings prior to the 2008 crisis (Peston & Knight, 2012). Here, by using a better “physical” model, which makes the link between finance and phase-transition behaviour more explicit, we can also extend the range of possible financial and economic applications.

Bubbles and anti-bubbles (Zhou & Sornette, 2005) are a core theme explored by log-periodic and related models although a wide range of alternative applications are possible (Fry, 2014). Recent advances include modelling unpredictable market shocks (Fry, 2012) and the development of elementary technical trading strategies (Fry, 2014). Here we explore further links between an economic model for informational overshooting in Zeira (1999) and develop a suite of related univariate and multivariate models. This ability to fit multivariate models to data is significant. Multivariate models enable the simultaneous modelling of multiple markets. This is important as previous work has often studied different types of financial markets (Guo, Zhou, Cheng, & Sornette, 2011; Sornette & Cauwels, 2014; Zhou & Sornette, 2004) or multiple regional markets (Adila, 2014). Multivariate models also allow for a more systematic approach for studying contagion (McNeil, Frey, & Embrechts, 2005; Sornette & Cauwels, 2006). The inherently practically minded nature of our approach is reinforced by the empirical estimates for the level of over-pricing and the level of under-pricing that we are able to provide.

The empirical analyses in this paper are interesting and important in their own right. Firstly, we apply our model to London property prices. Recently, there has been intense media speculation over whether or not there is currently a bubble in London property prices. The potential policy ramifications are obvious as the economic impact of house-price crashes can be particularly severe (Black, Fraser, & Hoesli, 2006; Hott & Monnin, 2008). Secondly, we analyse the effect of unpredictable market shocks on Greek government bond yields that occurred as part of the recent Eurozone crisis. Thirdly, we are able to show that the 2008 crash was preceded by both a speculative bubble in the US stock market and a detectable decline in lending quality amongst major financial institutions.

The layout of this paper is as follows. Section 2 introduces a univariate model for bubbles and anti-bubbles – here termed endogenous shocks. By slightly modifying the formulation of our model, we can derive novel analytical formulae for valuation and for the expected changepoint time. Further, our model is able to generate a plausible mechanism to explain why similar methods have systematically overestimated the timing of future changepoints (Voit, 2005). Section 3 develops a model for unpredictable market shocks. These unpredictable shocks may be either endogenous or exogenous in nature. Section 4 then shows how the models in Sections 2 and 3 can be applied to bond yields and interest rates. Section 5 discusses an extension of the basic model to multivariate bubbles and anti-bubbles. Some sample empirical applications are discussed in Section 6. Section 7 concludes.

2. Endogenous shocks: bubbles and anti-bubbles

Markets work by balancing risk and return. The level of risk and return remains stable even in the face of technological innovation or an influx of new investors (Zeira, 1999). These assumptions do not rely on complicated mathematics and avoid dubious assumptions such as the “riskless hedge” of the Black–Scholes model (Bouchaud & Potters, 2003). Our model makes several observable predictions for market crashes. Inter alia speculation-induced crashes are preceded by an unsustainable super-exponential growth coupled with a detectable increase in market overconfidence.

Let $P_t$ denote the price of an asset at time $t$ and let $X_t=log{P}_t$. The set up of the model is as follows:

Assumption 1

(Intrinsic Rate of Return) The intrinsic rate of return is assumed constant and equal to $\mathit{\mu }$:(1) $$\begin{array}{c}\hfill E[X_{t+\mathrm{\Delta }}-X_t|X_t]=\mathit{\mu }\mathrm{\Delta }+o(\mathrm{\Delta })\end{array}$$(1)

Assumption 2

(Intrinsic Level of Risk) The intrinsic level of risk is assumed constant and equal to ${\mathit{\sigma }}^2$:(2) $$\begin{array}{c}\hfill \text{Var}[X_{t+\mathrm{\Delta }}-X_t|X_t]={\mathit{\sigma }}^2\mathrm{\Delta }+o(\mathrm{\Delta })\end{array}$$(2)

As in Johansen et al. (2000) our starting point is the equation(3) $$\begin{array}{c}\hfill P(t)=P_1(t){(1-\mathit{\kappa })}^{j(t)}\end{array}$$(3)

where $P_1(t)$ satisfies(4) $$\begin{array}{c}\hfill d{P}_1(t)=\left[\mathit{\mu },(t),+,{\mathit{\sigma }}^2,(t),/,2\right]P_1(t)dt+\mathit{\sigma }(t)P_1(t)d{W}_t\end{array}$$(4)

where $W_t$ is a Wiener process and $j(t)$ is a jump process satisfying(5) $$\begin{array}{c}\hfill j(t)=\left\{\begin{array}{c}0\text{before the crash}\\ 1\text{after the crash}\end{array}\right.\end{array}$$(5)

When a crash occurs $\mathit{\kappa }\%$ is automatically wiped off the value of the asset. Prior to a crash, $P(t)=P_1(t)$ and $X_t=log(P(t))$ satisfies(6) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }(t)dt+\mathit{\sigma }(t)d{W}_t-vdj(t),\end{array}$$(6)

where $v=-ln[(1-\mathit{\kappa })]>0$.¹ Assumptions 1 and 2 show that crashes are outliers and can, in principle, be predicted based on anomalous behaviour in the drift and volatility in Equation (6). In a bubble regime, a representative investor is compensated for the crash risk by an increased rate of return with $\mathit{\mu }(t)>\mathit{\mu }$ the long-term rate of return. This is accompanied by a decrease in the volatility function ${\mathit{\sigma }}^2(t)$ – a result which at first glance may appear counterintuitive but, in fact, represents market overconfidence (Fry, 2012; 2014).

Suppose that a crash has not occurred by time $t$. In this case, we have that(7) $$\begin{array}{cc}\hfill E[j(t+\mathrm{\Delta })-j(t)]& =\mathrm{\Delta }h(t)+o(\mathrm{\Delta }),\hfill \end{array}$$(7) (8) $$\begin{array}{cc}\hfill \text{Var}[j(t+\mathrm{\Delta })-j(t)]& =\mathrm{\Delta }h(t)+o(\mathrm{\Delta }),\hfill \end{array}$$(8)

where $h(t)$ is the hazard rate. Hence, it follows from (1) and (7) that(9) $$\begin{array}{c}\hfill \mathit{\mu }(t)-vh(t)=\mathit{\mu };\mathit{\mu }(t)=\mathit{\mu }+vh(t)\end{array}$$(9)

Equation (9) thus returns the first-order model – namely that the rate of return must increase in order to compensate a representative investor for the risk of a crash.

Second-order condition. This condition stipulates that in order for a bubble to develop a rapid growth in prices is not sufficient in isolation. The perceived price risk must also diminish. From Equations (2) and (8), it follows that(10) $$\begin{array}{c}\hfill {\mathit{\sigma }}^2(t)+v^{2}h(t)={\mathit{\sigma }}^2;{\mathit{\sigma }}^2(t)={\mathit{\sigma }}^2-v^{2}h(t)\end{array}$$(10)

Equation (10) thus describes a collective market overconfidence that arises as a result of the bubble and leads to an underestimation of the true long-term level of volatility. We note that from a mathematical perspective Equation (10) holds some wider significance (Fry, 2012) since it satisfies a phase-transition condition delineating between random and deterministic behaviour in prices:(11) $$\begin{array}{c}\hfill \underset{t}{min}{\mathit{\sigma }}^2(t)=0\end{array}$$(11) Post-crash increase in volatility. Further to the above Discussion, Equation (10) also predicts that volatility increases after the crash – in line with the predictions of several related models (see e.g. Sornette & Helmstetter, 2003). Before the market crashes, in the bubble regime, we have that(12) $$\begin{array}{c}\hfill {\tilde{\mathit{\sigma }}}^2=\text{Var}(X_{t+\mathrm{\Delta }}|X_t)=\mathrm{\Delta }[{\mathit{\sigma }}^2-v^{2}h(t)]+o(\mathrm{\Delta })\end{array}$$(12)

whilst after the crash(13) $$\begin{array}{c}\hfill \text{Var}(X_{t+\mathrm{\Delta }}|X_t)=\mathrm{\Delta }[{\tilde{\mathit{\sigma }}}^2+v^{2}h(t)]+o(\mathrm{\Delta })\end{array}$$(13)

Equations (9) and (10) show that specification of the hazard function $h(t)$ completes the model. In contrast to previous work Fry (2012; 2014) here we follow (Zeira, 1999) in assuming that the time of the crash follows a uniform $U[0,\overline{T}]$ distribution. This gives(14) $$\begin{array}{c}\hfill h(t)=\frac{f(t)}{1-F(t)}={(\overline{T}-t)}^{-1}\end{array}$$(14)

In order that the volatility function, ${\mathit{\sigma }}^2(t)$ remains positive we need that(15) $$\begin{array}{c}\hfill {\mathit{\sigma }}^2-\frac{v^2}{\overline{T}-t};t_c=\overline{T}-\frac{v^2}{{\mathit{\sigma }}^2}\end{array}$$(15)

Thus, from Equation (15), our model remains valid only in the region $0\le t\le \overline{T}$.

Expected crash time. Unlike previous approaches, (Fry, 2012, 2014) assuming $h(t)$ has the from given by Equation (14) means that we can estimate the time when a crash is most likely. Suppose that a crash has not occurred by time $T_{end}$. We have that the time of the crash is distributed according to $U(T_{end},t_c)$. This suggests that(16) $$\begin{array}{c}\hfill \text{Expected Crash Time}=\frac{t_c+T_{end}}{2}<t_c\end{array}$$(16)

Equation (16) may thus help to explain why a range of previous approaches have systematically overestimated the time of the crash (Voit, 2005).

As laid out above, our model can be used to empirically test for the presence of bubbles in a given price series. However, our model also enables us to estimate the speculative bubble component present within observed prices. Under fundamental price dynamics with $v=0$(17) $$\begin{array}{c}\hfill P_F(t):=E(P(t))=P(0)e^{\tilde{\mathit{\mu }}t}\end{array}$$(17)

where $\tilde{\mathit{\mu }}=\mathit{\mu }+{\mathit{\sigma }}^2/2$. In empirical work, we can use Equation (17) to estimate fundamental value – an approach which recreates the widespread phenomenology of approximate exponential growth in economic time series (Campbell, Lo, & MacKinlay, 1997). Define(18) $$\begin{array}{c}\hfill H(t):={\int }_0^{t}h(u)du=ln\left(\frac{\overline{T}}{\overline{T}-t}\right)\end{array}$$(18)

Under a speculative bubble, with $v>0$, we have that(19) $$\begin{array}{c}\hfill X_t\sim N(X_0+\mathit{\mu }t+vH(t),{\mathit{\sigma }}^{2}t-v^{2}H(t))\end{array}$$(19)

Hence, it follows from (19) that(20) $$\begin{array}{c}\hfill P_B(t):=E(P(t))=P(0)e^{\tilde{\mathit{\mu }}t+\left(v,-,\frac{v^2}{2}\right)H(t)}=P_F(t){\left(\frac{\overline{T}}{\overline{T}-t}\right)}^{v-\frac{v^2}{2}}\end{array}$$(20)

Equations (17)–(20) lead to the following estimate of the speculative bubble component defined as the “average distance” between fundamental and bubble prices:(21) $$\begin{array}{cc}\hfill \text{Bubble Component}& =1-\frac{1}{T}{\int }_0^T\frac{P_F(t)}{P_B(t)}dt\hfill \\ \hfill & =1+\frac{\overline{T}}{T\left(v,-,\frac{v^2}{2},+,1\right)}\left[{\left(1,-,\frac{T}{\overline{T}}\right)}^{v-\frac{v^2}{2}+1},-,1\right]\hfill \end{array}$$(21)

As defined Equation (21) gives a fraction in $(0,1)$. In Fry (2010), a similar approach gave a value of 0.202 for UK house prices over the years 2002–2007 suggesting that the bubble accounted for around 20% of observed prices – closely matching a subsequent fall in UK house prices of around 20% in 2008–2009.

An anti-bubble represents the mirror image of a speculative bubble (Yan et al., 2012). Just as speculative bubbles result in dramatic price rises anti-bubbles can result in dramatic price falls. Anti-bubbles can be modelled by replacing $v$ with $-v$ in the above. In the case of an anti-bubble, analogous reasoning leads to an estimate of the level of under-pricing. Define$$\begin{array}{c}\hfill P_{AB}(t):=E(P(t))=P(0)e^{\tilde{\mathit{\mu }}t-\left(v,+,\frac{v^2}{2}\right)H(t)}=P_F(t){\left(\frac{\overline{T}-t}{\overline{T}}\right)}^{v+\frac{v^2}{2}}\end{array}$$

It follows that(22) $$\begin{array}{cc}\hfill \text{Anti-bubble Component}& =1-\frac{1}{T}{\int }_0^T\frac{P_F(t)}{P_{AB}(t)}dt\hfill \\ \hfill & =1+\frac{\overline{T}}{T(1-v-\frac{v^2}{2})}\left[{\left(1,-,\frac{T}{\overline{T}}\right)}^{1-v-\frac{v^2}{2}},-,1\right]\hfill \end{array}$$(22)

Similarly, (22) should yield a fraction in $(-1,0)$. E.g. a value of $-0.1$ would suggest that prices are undervalued by roughly 10%.

3. Unpredictable market shocks

Suppose that the market is exposed to an unpredictable shock. The timing of the shock is assumed to be completely unpredictable. If the shock is exogenous in nature then its affect is merely transitory (Sornette & Helmstetter, 2003). In contrast, the after-effects of an endogenous shock are potentially much longer lasting.

The shock occurs at time 0 and results in an initial decrease in drift by the amount ${\mathit{\mu }}_0$ and an initial increase in volatility by the amount ${\mathit{\sigma }}_0^2$. As an arbitrage opportunity has to be eliminated, the market recovers at the random time $t_0$ – the drift increases by ${\mathit{\mu }}_0$ and volatility decreases by ${\mathit{\sigma }}_0^2$. The time $t_0$ of the market recovery is a random variable with hazard function $h(t)$. Since the effect of an exogenous shock is transitory it follows that in this case $h^{\prime }(t)>0$, since as time progresses a market rebound becomes increasingly likely. Also, since the shock is assumed to happen at $t=0$ it follows that we must also have $h(0)=0$:(23) $$\begin{array}{c}\hfill h^{\prime }(t)>0;h(0)=0\end{array}$$(23)

The price dynamics prior to the market recovery are described by the following equation(24) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }(t)dt+\mathit{\sigma }(t)d{W}_t+dj(t),\end{array}$$(24)

where $j(t)$ satisfies(25) $$\begin{array}{c}\hfill dj(t)={\mathit{\mu }}_0\mathit{\delta }(t-t_0)dt+i{\mathit{\sigma }}_0\mathit{\delta }(t-t_0)d{W}_t\end{array}$$(25)

where $i=\sqrt{-1}$ and $\mathit{\delta }(·)$ denotes Dirac’s delta function. When a recovery happens, the effect is an increase in drift and a decrease in the variance, hence the introduction of $i=\sqrt{-1}$. Prior to the recovery we have that(26) $$\begin{array}{c}\hfill E[X_{t+\mathrm{\Delta }}-X_t|X_t]=(\mathit{\mu }(t)+{\mathit{\mu }}_{0}h(t))\mathrm{\Delta }+o(\mathrm{\Delta })\end{array}$$(26)

Thus, from Equation (1) it follows that(27) $$\begin{array}{c}\hfill \mathit{\mu }(t)=\mathit{\mu }-{\mathit{\mu }}_{0}h(t)\end{array}$$(27)

Equation (54) shows that the shock reduces the level of return. The risk (variance) associated with Equation (24(24) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }(t)dt+\mathit{\sigma }(t)d{W}_t+dj(t),\end{array}$$(24) ) is(28) $$\begin{array}{c}\hfill \text{Var}\left(X_{t+\mathrm{\Delta }},-,X_t,|,X_t\right)=\text{Var}\left[\mathit{\sigma },(t),\left(W_{t+\mathrm{\Delta }},-,W_t\right)\right]+\text{Var}\left[j,(,t,+,\mathrm{\Delta },),|,j,(,t,),=,0\right]\end{array}$$(28)

This gives(29) $$\begin{array}{cc}\hfill \text{Var}\left(X_{t+\mathrm{\Delta }},-,X_t,|,X_t\right)& ={\mathit{\sigma }}^2(t)\mathrm{\Delta }+\text{Var}[E(j(t+\mathrm{\Delta })|j(t)=0)]\hfill \end{array}$$(29) (30) $$\begin{array}{cc}& +E[\text{Var}(j(t+\mathrm{\Delta })|j(t)=0)]+o(\mathrm{\Delta });\hfill \end{array}$$(30) (31) $$\begin{array}{cc}\hfill \text{Var}\left(X_{t+\mathrm{\Delta }},-,X_t,|,X_t\right)& =\left({\mathit{\sigma }}^2,(t),+,\left({\mathit{\mu }}_0^2,-,{\mathit{\sigma }}_0^2\right),h,(t)\right)\mathrm{\Delta }+o(\mathrm{\Delta })\hfill \end{array}$$(31)

Similarly, it follows from (2) that(32) $$\begin{array}{c}\hfill {\mathit{\sigma }}^2(t)+\left({\mathit{\mu }}_o^2,-,{\mathit{\sigma }}_0^2\right)h(t)={\mathit{\sigma }}^2;{\mathit{\sigma }}^2(t)={\mathit{\sigma }}^2+\left({\mathit{\sigma }}_0^2,-,{\mathit{\mu }}_0^2\right)h(t)\end{array}$$(32)

If ${\mathit{\sigma }}_0^2\ge {\mathit{\mu }}_0^2$ the shock affects volatility more than it does the drift. The shock thus results in an increase in market volatility alongside a decrease in drift. If ${\mathit{\sigma }}_0^2\le {\mathit{\mu }}_0^2$ the shock actually results in a reduction in volatility. However, irrespective of the effect upon market volatility the shock decreases the rate of return so is still likely to remain bad news for investors. If ${\mathit{\sigma }}_0^2={\mathit{\mu }}_0^2$ market volatility remains unaffected.

In empirical work, we choose(33) $$\begin{array}{c}\hfill h(t)=\mathit{\lambda }[1-{(1+t)}^{-\mathit{\alpha }}]\end{array}$$(33)

Not only does $h(t)$ in (33) satisfy (23) but the special case $\mathit{\alpha }=0.5$ in (43) recreates both the empirical power-law reported in Sornette, Malevergne, and Muzy (2003) and related phenomenology in Sornette and Helmstetter (2003). Equation (33) also provides a natural empirical test for the presence of an exogenous/endogenous shock (see below).

From (33), it follows that(34) $$\begin{array}{c}\hfill {\mathit{\sigma }}^2(t)={\mathit{\sigma }}^2+\mathit{\beta }[1-{(1+t)}^{-\mathit{\alpha }}]\end{array}$$(34)

where $\mathit{\beta }=\mathit{\lambda }({\mathit{\sigma }}_0^2-{\mathit{\mu }}_0^2)$. The case $\mathit{\alpha }=0$ corresponds to the case of an efficient market where price changes are completely unpredictable and we are left with the classical random walk or Black–Scholes model:(35) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }dt+\mathit{\sigma }{dW}_t\end{array}$$(35)

The link with statistical physics gives two main cases of interest.

Endogenous shock. If $\mathit{\beta }<0$ and $\mathit{\alpha }<0$ then ${\mathit{\sigma }}^2(t)$ increases without bound. This represents the fundamental uncertainty related to an endogenous shock (Fry, 2014).

Exogenous shock. If $\mathit{\beta }<0$ and $\mathit{\alpha }>0$ the market recovery becomes the inevitable phase transition between random and deterministic behaviour with(36) $$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{\mathit{\sigma }}^2(t)=0\end{array}$$(36)

This suggests that(37) $$\begin{array}{c}\hfill {\mathit{\sigma }}^2+\mathit{\beta }=0;{\mathit{\sigma }}^2=-\mathit{\beta }\end{array}$$(37)

4. Shocks to bond yields

It is easy to show that an anti-bubble in the price of the underlying asset leads to a bubble in the corresponding Bond yields (Fry, 2014). Following the standard approach, (Hillier, Ross, Westerfeld, Jaffe, & Jordan, 2010) write(38) $$\begin{array}{c}\hfill P(t)=M{e}^{-y(t)T}\end{array}$$(38)

where $y(t)$ is the yield, $T$ is the maturity date, $M$ is the constant value of the bond at maturity, and $P(t)$ is the price of the underlying asset. It follows that $X(t)=lnP(t)$ satisfies(39) $$\begin{array}{c}\hfill X(t)=lnM-y(t)T\end{array}$$(39)

Under the equation for an anti-bubble, we have that(40) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }(t)dt+\mathit{\sigma }(t)d{W}_t+vdj(t)\end{array}$$(40)

where(41) $$\begin{array}{cc}\hfill \mathit{\mu }(t)& =\mathit{\mu }-vh(t),\hfill \\ \hfill {\mathit{\sigma }}^2(t)& ={\mathit{\sigma }}^2-v^{2}h(t)\hfill \end{array}$$(41)

Combining Equations (39)–(41) it follows that the bond yields $y(t)$ satisfy(42) $$\begin{array}{c}\hfill dy(t)=-\frac{\mathit{\mu }(t)}{T}dt+\frac{\mathit{\sigma }(t)}{T}d{W}_t^{\prime }-\frac{v}{T}dj(t)\end{array}$$(42)

where $W_t^{\prime }=-W_t$. Thus it follows that (42) gives the formula for a speculative bubble since $W_t^{\prime }\stackrel{d}{=}{W}_t$. Similarly Equations (23)–(25) and (39) show that an exogenous shock would also affect observable bond yields in the same way.

5. Multivariate bubbles and anti-bubbles

In this subsection, we discuss multivariate models for bubbles. Thus, we are able to simultaneously describe multiple markets. This is significant for empirical applications across different countries (McNeil et al., 2005; Sornette & Malevergne, 2006) and different regions.

Let $P_t$ denote the prices $(P_t^1,\dots ,P_t^p)$ of a basket of $p$ assets at time $t$. Define $X_t=(X_t^1,\dots ,X_t^p)$ where $X_t^i=log{P}_t^i$. For the multivariate model, Assumptions 1 and 2 are replaced by their vector/matrix analogues.

Assumption 3

(Intrinsic Rate of Return) The intrinsic rate of return is assumed constant and equal to $\mathit{\mu }$:(43) $$\begin{array}{c}\hfill E[X_{t+\mathrm{\Delta }}-X_t|X_t]=\mathit{\mu }\mathrm{\Delta }+o(\mathrm{\Delta })\end{array}$$(43)

Assumption 4

(Intrinsic Level of Risk) The intrinsic level of risk is assumed constant and equal to $\mathrm{\Sigma }$:(44) $$\begin{array}{c}\hfill \text{Var}[X_{t+\mathrm{\Delta }}-X_t|X_t]=\mathrm{\Sigma }\mathrm{\Delta }+o(\mathrm{\Delta })\end{array}$$(44)

Co-ordinatewise our starting Equation (3) becomes(45) $$\begin{array}{c}\hfill p^i(t)=p_1^i(t)(1-{\mathit{\kappa }}^i)j(t)\end{array}$$(45)

and before the crash $X_t$ satisfies the vector-valued equation(46) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }(t)dt+\sqrt{\mathit{\sigma }(t)}d{W}_t-vdj(t)\end{array}$$(46)

where $v$ is the diagonal matrix satisfying $v_{ii}=-ln(1-{\mathit{\kappa }}_i)=v_i$. Assumption 1 above yields a vector-valued re-statement of Equation (9):(47) $$\begin{array}{c}\hfill \mathit{\mu }(t)-vh(t)=\mathit{\mu };\mathit{\mu }(t)=\mathit{\mu }+vh(t)\end{array}$$(47)

Similarly, Assumption 2 shows that the second-order condition now becomes(48) $$\begin{array}{c}\hfill \mathrm{\Sigma }(t)+v{\mathrm{\Sigma }}_j{v}^{T}h(t)=\mathrm{\Sigma };\mathrm{\Sigma }(t)=\mathrm{\Sigma }-v{\mathrm{\Sigma }}_j{v}^{T}h(t)\end{array}$$(48)

where ${\mathrm{\Sigma }}_j$ denotes the correlation matrix of $j(t)$. Equation (48) thus shows how correlation in the bubble process is transferred to prices prior to the crash. Genuinely high-dimensional and multivariate models are possible though it seems that these may lose some interpretability. Since bivariate models are by far the most convenient and natural to use in applications in the sequel we restrict to a bivariate model.

5.1. A bivariate model

In a bivariate extension of the preceding univariate and multivariate models, Equation (46) becomes(49) $$\begin{array}{c}\hfill d{X}_t=\mathit{\mu }(t)dt+\sqrt{\mathrm{\Sigma }(t)}d{W}_t-vdj(t)\end{array}$$(49)

where $X_t={(X_1(t),X_2(t))}^T$ denotes the log-price of Assets 1 and 2 at time $t$, $\mathrm{\Sigma }(t)$ is the instantaneous covariance and $W_t$ is standard bivariate Brownian motion. Assumption 1 gives(50) $$\begin{array}{c}\hfill {\mathit{\mu }}_1(t)={\mathit{\mu }}_1+v_{1}h(t);{\mathit{\mu }}_2(t)={\mathit{\mu }}_2+v_{2}h(t)\end{array}$$(50)

Assumption 2 gives(51) $$\begin{array}{cc}\hfill \mathrm{\Sigma }(t)& =\left(\begin{array}{cc}{\mathit{\sigma }}_1^2& {\mathit{\sigma }}_{12}\\ {\mathit{\sigma }}_{12}& {\mathit{\sigma }}_2^2\end{array}\right)-\left(\begin{array}{cc}{v}_1& 0\\ 0& v_2\end{array}\right)\left(\begin{array}{cc}1& \mathit{\rho }\\ \mathit{\rho }& 1\end{array}\right)\left(\begin{array}{cc}{v}_1& 0\\ 0& v_2\end{array}\right)h(t),\hfill \end{array}$$(51) (52) $$\begin{array}{cc}& =\left(\begin{array}{cc}{\mathit{\sigma }}_1^2& {\mathit{\sigma }}_{12}\\ {\mathit{\sigma }}_{12}& {\mathit{\sigma }}_2^2\end{array}\right)-\left(\begin{array}{cc}{v}_1^2& \mathit{\rho }{v}_1{v}_2\\ \mathit{\rho }{v}_1{v}_2& v_1^2\end{array}\right)h(t).\hfill \end{array}$$(52)

In addition to Equation (10) the phase-transition condition also gives(53) $$\begin{array}{c}\hfill \underset{t}{min}\mathrm{\Sigma }(t)=0;\underset{t}{min}{\mathit{\sigma }}_{12}-\mathit{\rho }{v}_1{v}_{2}h(t)=0\end{array}$$(53) Historical Estimation Bias. Equation (52) when taken together with Equations (9(9) $$\begin{array}{c}\hfill \mathit{\mu }(t)-vh(t)=\mathit{\mu };\mathit{\mu }(t)=\mathit{\mu }+vh(t)\end{array}$$(9) ) and (10(10) $$\begin{array}{c}\hfill {\mathit{\sigma }}^2(t)+v^{2}h(t)={\mathit{\sigma }}^2;{\mathit{\sigma }}^2(t)={\mathit{\sigma }}^2-v^{2}h(t)\end{array}$$(10) ) serve to highlight possible dangers regarding historical estimation bias – an issue with specific relevance to the CDO crisis (see e.g. MacKenzie & Spears, 2014). We have already seen that during a bubble regime prices may be rising at artificially high rates with comparatively little volatility compared to the underlying long-term values. Equation (52) is also useful in highlighting that using historical prices in a bubble regime may lead to under-diversified portfolios as a consequence of under-estimating long-term correlation levels in returns series. If a crash occurs at time $t_0$, in addition to an increase in marginal volatility, the covariance of $\mathrm{\Delta }{X}_1(t_0)$ and $\mathrm{\Delta }{X}_2(t_0)$ increases by a factor of $\mathit{\rho }{v}_1{v}_{2}h(t_0)$ (from ${\mathit{\sigma }}_{12}-\mathit{\rho }{v}_1{v}_{2}h(t_0)$ to its equilibrium value of ${\mathit{\sigma }}_{12}$).

Contagion. The above discussion leads naturally to an empirical test for contagious effects that arise as part of the bubble process. As discussed below this involves testing the hypothesis shown in Equation (57). Suppose we have two assets whose prices are given by $e^{X(t)}$ and $e^{Y(t)}$. Let $\mathrm{\Delta }{X}_t=X_{t+1}-X_t$. Under the model (49), knowledge of $Y(t)$ reduces uncertainty in $X(t)$ by(54) $$\begin{array}{cc}\hfill \text{Var}[\mathrm{\Delta }X(t)]-\text{Var}[\mathrm{\Delta }X(t)|\mathrm{\Delta }Y(t)]& =\text{Var}[\mathrm{\Delta }{X}_t]-(1-{\text{Cor}}^2(\mathrm{\Delta }{X}_t,\mathrm{\Delta }{Y}_t))\text{Var}[\mathrm{\Delta }{X}_t]\hfill \\ \hfill & ={\text{Cor}}^2(\mathrm{\Delta }{X}_t,\mathrm{\Delta }{Y}_t)\text{Var}[\mathrm{\Delta }{X}_t]\hfill \end{array}$$(54)

Similarly, knowledge of $X(t)$ reduces uncertainty in $Y(t)$ by the amount(55) $$\begin{array}{c}\hfill \text{Var}[\mathrm{\Delta }Y(t)]-\text{Var}[\mathrm{\Delta }Y(t)|\mathrm{\Delta }X(t)]={\text{Cor}}^2(\mathrm{\Delta }{X}_t,\mathrm{\Delta }{Y}_t)\text{Var}[\mathrm{\Delta }{Y}_t]\end{array}$$(55)

The constraints ${\mathit{\sigma }}_X^2(t)\ge 0$ and ${\mathit{\sigma }}_Y^2(t)\ge 0$ imply that(56) $$\begin{array}{c}\hfill {\mathit{\sigma }}_X^2=\frac{v_X^2}{\overline{T}-t_c};{\mathit{\sigma }}_Y^2=\frac{v_Y^2}{\overline{T}-t_c}\end{array}$$(56)

Contagion from $Y(t)$ to $X(t)$ occurs if $Y(t)$ is more informative about $X(t)$ than $X(t)$ is about $Y(t)$. From Equations (54) and (55) contagion from $Y(t)$ to $X(t)$ occurs if(57) $$\begin{array}{cc}\hfill {\text{Cor}}^2(\mathrm{\Delta }{X}_t,\mathrm{\Delta }{Y}_t)\text{Var}[\mathrm{\Delta }{X}_t]& <{\text{Cor}}^2(\mathrm{\Delta }{X}_t,\mathrm{\Delta }{Y}_t)\text{Var}[\mathrm{\Delta }{Y}_t]\hfill \\ \hfill \text{Var}[\mathrm{\Delta }{X}_t]& <\text{Var}[\mathrm{\Delta }{Y}_t]\hfill \\ \hfill v_X^2\left[\frac{1}{\overline{T}-t_c},+,ln,\left(\frac{\overline{T}-t}{\overline{T}-t+1}\right)\right]& <v_Y^2\left[\frac{1}{\overline{T}-t_c},+,ln,\left(\frac{\overline{T}-t}{\overline{T}-t+1}\right)\right]\hfill \\ \hfill v_X^2& <v_Y^2\hfill \end{array}$$(57)

Equation (57) is significant as it shows that contagion occurs as the overall bubble process becomes dominated by price rises and speculation in Asset $Y$. Similarly in an anti-bubble contagion from $Y(t)$ to $X(t)$ occurs as speculation that drives down the price of $Y(t)$ becomes the dominant effect.

6. Empirical applications

6.1. Is there a bubble in London property prices?

Amid intense speculation in the media, and anecdotal evidence of speculative pressures forcing buyers to place bids in excess of the asking price, it is of interest to determine whether or not London property prices are currently in a bubble. Whilst recent price hikes do look dramatic they do need to be adjusted for inflation in order to gain a more complete picture. This simple procedure can nonetheless have a dramatic effect. Information from actual price-paid may also be needed to provide a more realistic assessment of the evidence for a bubble. In view of the above, it is also important to recognize that the debate about a possible bubble occurs against the backdrop of wider structural problems. Recent figures released suggest that the average London house price is now eight times the average first-time buyer’s salary.

Figure 1. Inflation-adjusted London house prices.

Table 1. Results testing the null hypothesis of no speculative bubble.

Date	LR-statistic	$p$-value
March 2009 – March 2014	1.075	0.141
March 2010 – March 2014	1.394	0.119
March 2011 – March 2014	1.431	0.116
Jan 2012 – March 2014	1.226	0.134

A plot of average London property prices obtained from the Land Registry, based on actual price-paid data and adjusted for inflation, is shown below in Figure 1. To some extent prices appear to be simply recovering from past price falls although the recent price rises that have occurred are clearly far from trivial. Results for the test of speculative bubbles are shown below in Table 1. Irrespective of the time window chosen our model suggests that there is currently no evidence of a bubble.

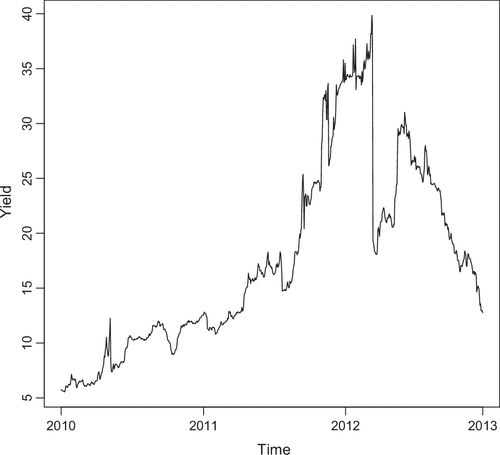
6.2. The Greek Eurozone crisis

We illustrate our model with an application to the ongoing Eurozone crisis. A time series plot of Greek government bond yields is shown below in Figure 2. For a number of years, Greek government bond yields were very stable before spiking upwards from late 2009 onwards as the crisis took hold. The precise chronology of the crisis is discussed in Choi, Gulati, and Posner (2011). Following established methodology (Fry, 2012; Johansen & Sornette, 2010; Sornette et al., 2003) we test for the presence of an exogenous shock in the first 100 trading days following a putative shock – and cross-check these results with Choi et al. (2011). Results are summarized in Table 2.

Figure 2. Greek government bond yields 2010–2012.

Table 2. Results for the test of endogenous vs. exogenous shocks (Section 3).

Start date	5/11/2009
$\widehat{\mathit{\alpha }}$	-0.535
e.s.e. $\widehat{\mathit{\alpha }}$	0.207
$t$-value	2.585
$p$-value	0.010
Conclusion	Significant evidence of an endogenous shock

In Choi et al. (2011) Greece’s announced plan to cut its budget deficit on 5/11/2009 is heralded as the start of the crisis. Results in Table 2 suggest that this event did indeed have a statistically significant effect upon Greek bond yields. Moreover, our results classify the Greek crisis as an endogenous shock associated with fundamental weaknesses in the economies of the Eurozone countries (Blundell-Wagnall, 2011).

6.3. US bubbles prior to the crash of 2008

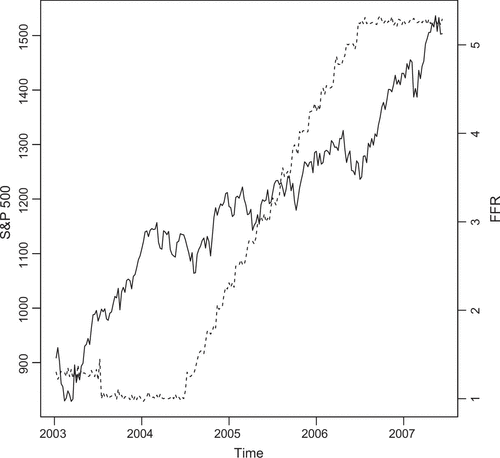
We illustrate our multivariate bubble models with an application to a data set consisting of the S& P 500 and the Federal Funds Rate (FFR). The joint behaviour of US interest rates is much studied (Guo, Zhou, Cheng, & Sornette, 2011; Sornette & Cauwels, 2014; Zhou & Sornette, 2004) and is also of wider interest amid concern that loose US monetary policy has inflated a succession of recent bubbles (Sornette & Cauwels, 2014).

The FFR is the interest rate at which depositing institutions actively trade balances held at the Federal Reserve. In particular, data published as the FFR effective rate represent the weighted averaged across all such transactions. As the rate increases, it becomes more expensive for financial institutions to borrow funds. One feature of interest is whether or not the FFR increases as a symptom of wider problems with credit worthiness. In a similar vein to the original model in Johansen et al. (2000) increases in the FFR may compensate lending institutions for the Credit Risk that they bear. It is well known that such structural problems and anti-bubbles in the underlying can lead to dramatic increases and bubbles in the associated interest rates (Fry, Fry (2014)) – see Section 4.

Figure 3. S& P 500 (solid lines) and Federal Funds Rate (FFR) (dashed lines).

Table 3. Results for the statistical tests for bubbles

Univariate bubble model
	LR-statistic	$p$-value
S& P 500	7.454	0.001
FFR	14.601	0.000
Multivariate bubble model
	11.189	0.001
Test for contagion
	$t$-value	$p$-value
	0.746	0.456

Following a similar approach in Guo et al. (2011) we analyse weekly data from January 2003 to June 2007. A plot of the S& P 500 and the FFR is shown below in Figure 3. Both series show a rapid growth over time consistent with earlier suggestions of a bubble in both series. Results in Table 3 give conclusive evidence of a bubble in both univariate series. This is subsequently confirmed by the statistical significance of the bivariate bubble model. Further, the test for contagion in Equation (57) suggests no evidence for contagion running from the FFR to the S& P 500 and what we have instead is co-dependence. This tallies with aspects of the account of debt-fuelled bubbles in Sornette and Cauwels (2014). In the lead in to the crisis the FFR increased to unsustainably high levels as a symptom of generally decreasing credit quality in the wider financial system. This also fed into, and was also influenced by, an unsustainable bubble in the US stock market.

7. Conclusions and further work

This paper discusses models for financial bubbles and crashes adding to several recent developments in the area (Fry, 2012, 2014). Bubbles occur as the price rises to compensate a representative investor for the risk of a crash. Similarly, anti-bubbles occur as the price decreases as compensation for the risk associated with a subsequent market correction. This is accompanied by a detectable increase in market overconfidence akin to phase-transition behaviour in statistical physics (Borland, 2012). Not all crashes are predictable however. Throughout history, financial and economic systems have remained at the mercy of fundamental uncertainties (Machado & Mata, 2013; Reinhart & Rogoff, 2009). However, our model does enable us to track the effects of unpredictable market shocks.

Our model allows for a more systematic approach in empirical applications. We develop statistical tests for bubbles, anti-bubbles and endogenous shocks. Simple adjustments also enable us to track related effects on bond markets and interest rates. Our multivariate models enable us to compare multiple markets simultaneously and all for a more considered approach to analysing contagion. Beyond the purely operational, our model highlights a possible issue with historical estimation bias. Relying on historical prices only may overestimate gains (losses) during a bubble (anti-bubble), may underestimate the true level of long-term risk and may also underestimate long-term correlation levels potentially leading to under-diversified portfolios (MacKenzie & Spears, 2014).

The empirical analyses in this paper are interesting and important in their own right and may help to shed light on areas related to economic policy. Firstly, our model refutes recent claims of a bubble in London house prices. Secondly, our model classifies the announcement of Greek plans to cut their budget deficit as an endogenous shock reflecting deep underlying economic factors. This appears in line with the interpretation in Choi et al. (2011). Thirdly, our model finds evidence of speculative bubbles in the S& P 500 and in the FFR prior to the Crash of 2008. This suggests that prior to 2008 a stock market bubble and a decline in lending quality occurred simultaneously and fed off each other.

The models in this paper are potentially very rich. Further applications include financial resilience (Coaffee, 2003), economic policy (Carnot, Koen, & Tissot, 2011) and market psychology and trading (Plummer, 2006). Future work will examine bitcoin and crypto-currencies and the UK housing market amid concerns that conventional approaches may understate the true extent of the North-South divide in the UK (Rowthorn, 2010).

Additional information

Funding

The author has received no direct funding for this research.

Notes on contributors

John Fry

John Fry has a PhD in Probability and Statistics, and an MSc in Statistics and a BSc in Mathematics and Statistics from the University of Newcastle-upon-Tyne. His research interests are in mathematical finance, econophysics, and operational research. He is a member of the Centre for Research into Accounting and Finance in Context (CRAFiC) at Sheffield University Management School.

Notes

1 In the sequel we note that the case of an anti-bubble is the same basic model but with $v$ replaced by $-v$ throughout Yan, Woodard, and Sornette (2012).