Don’t use quotients to calculate performance

Abstract

Quotients, ratios, are among the most applied tools for measuring performance of mutual funds and investment portfolios, the Jensen index being an exception to the general rule. In this paper, we show some problems that arise when quotients are applied, closely related to their statistical meaning, which is too often forgotten. We also raise some advantages of the use of linear penalization, introducing a little known methodology for performance measurement. With this purpose, this paper’s approach is comprehensive: we conceptually analyze performance indexes’ geometric and statistical meaning, complementing this with a numerical example and empirical testing that confirm our view. This paper’s main contribution is to demonstrate and empirically test how the use of quotients to measure performance may create problems due to their denominators, which may be solved by applying linear penalization.

Video Abstract

Read the transcript

Watch the video on Vimeo

© 2015 The Author(s). This open access article is distributed under a Creative Commons Attribution (CC-BY) 4.0 license

Keywords:

• performance
• ratio
• risk
• linear penalization

JEL Classifications:

• G11
• G23

Public Interest Statement

Academics, practitioners, and general public very often apply quotients, like the ratio between return and risk, to measure the performance of their investments (e.g. the Sharpe and Treynor indexes or the Information Ratio). In this paper, we show how the application of these quotients may have problems and could lead analysts to take wrong investment decisions, partially due to the statistical implications of these quotients’ use. We propose linear penalization by risk as an interesting alternative and introduce a little known methodology for performance measurement. With this purpose, this paper’s approach is comprehensive including conceptual, geometric, and statistical analyses that we complement with a numerical example and empirical testing. We think that the explained ideas are especially interesting under the current economic environment, in which optimal prioritization of investments and accurate analysis of balance between return and risk are a must.

1. Introduction

In order to calculate the performance of investment portfolios and to evaluate whether a mutual fund outperformed the market or its peer funds, we use several ex-post performance measures, usually based on the average return obtained and the risk assumed. As we consider that investors prefer more wealth to less, and that they are risk averse, we understand that performance improves as return increases and it worsens as risk grows (some nuances to this general affirmation may be seen in Gómez-Bezares & Gómez-Bezares, 2012). Many performance indexes have been developed since the classical ones proposed in the 1960s by Sharpe, Treynor, and Jensen. A frequently used idea is to calculate the excess of average return above the risk-free rate and divide it by a risk measure, just as Sharpe and Treynor ratios do. There are many other options to measure performance depending on the method applied to calculate risk (some quite well-known ones can be seen in Eling, 2008).

Despite their appearance being somewhat different, the M² index (proposed by Modigliani & Modigliani, 1997) and the M²_{for beta} (proposed by Modigliani, 1997) are equivalent to the Sharpe and Treynor indexes, respectively. On the other hand, the information ratio (IR), which can be defined as the average tracking error divided by the standard deviation of tracking error¹, will have similar characteristics to other indexes that are calculated through a quotient. Definitively, many of the indexes we apply are “ratios,” that is, quotients (the Jensen index is an exception).

The problem is that quotients, ratios, have some peculiarities that make them less attractive for their use in performance measuring, and this is what we want to show in the current paper. Some studies have affirmed that the application of one or another performance index has little relevance (i.e. Eling, 2008, after analyzing several indexes and obtaining similar results, tends to prefer the Sharpe ratio), but we disagree and will provide empirical evidence that supports our view. Many studies (Eling’s one among them) affirm that different indexes rank investments performance almost identically, with minor differences in ordering; but we think that quantitative differences must be considered apart from the strict rank ordering. On the other hand, there could be few but dramatic changes in rank ordering that can be very interesting for an analyst.

There is a wide literature facing this topic of performance measuring and we have cited a few authors already. Only to mention some of the many who use the three classical indexes, we have Chua and Koh (2007) who use the Sharpe ratio, Hodges, Taylor, and Yoder (2003) or Hübner (2007) who use the Treynor ratio, and Sainz, Grau, and Doncel (2006), Lin (2006), Fama and French (2010), or Miralles, Miralles, and Lisboa (2012) who use the Jensen index. On the other hand, practitioners use them continuously, and there exist empirical studies analyzing which are the most commonly applied indexes, as the one by Amenc, Goltz, and Lioui (2011).

Literature has analyzed, among other topics, what happens when the numerator of the Sharpe ratio is negative (Ferruz Agudo & Sarto Marzal, 2004; Israelsen, 2005, 2009, with different solutions to this situation). However, in this paper, we want to study a different matter, as we focus on denominators of quotient-based indexes and find advantages in applying linear indexes.

This paper contributes by giving an integrated comparative view, both from a geometric and from a statistical perspective, of the Sharpe, Treynor, Jensen, M², M²_{for beta}, and IR indexes. The paper also adds an original proposal to measure performance that was developed by the authors and allows seeing advantages of linear penalization. All this is corroborated with a numerical example and empirical testing. Such popular indexes as Sharpe, Treynor, or the IR may cause relevant problems if applied to compare performance of funds and their denominators take certain values. At the same time, linear indexes show higher consistency. Practitioners must be aware of this.

We will now proceed to review the mentioned indexes, introducing a complementary and less known one: the penalized internal rate of return (PIRR). We will see the indexes’ geometric and statistical meaning, as well as their main weaknesses. We will then analyze some empirical results and reach our final conclusions.

2. Indexes review and proposal of the PIRR

We begin by reviewing the three classical indexes, including their geometric explanation. Their formulae are the following:(1) $$\text{Sharpe}\left(1966\right):\text{S}=\left(\mathit{\mu }-r_0\right)/\mathit{\sigma }$$(1) (2) $$\text{Treynor}\left(1965\right):\text{T}=(\mathit{\mu }-r_0)/\mathit{\beta }$$(2) (3) $$\text{Jensen}\left(1968,1969\right):\text{J}=\mathit{\mu }-r_0-({\mathit{\mu }}_{\text{m}}{\text{- r}}_0)\mathit{\beta }$$(3)

where S, T, and J are the corresponding values of the Sharpe, Treynor, and Jensen indexes; μ is the average return of the investment in a certain period; r₀ is the risk-free rate of return; σ is the standard deviation of the investment return in the period of analysis; β is the respective systematic risk; and μ_m is the average return of the market portfolio during the period.

Consequently, we can observe that we have two indexes defined as ratios (Sharpe and Treynor) and one defined as a difference, and therefore linear (Jensen). At the same time, we have one index (the Sharpe ratio) that penalizes return with total risk (σ), while the other two (Treynor and Jensen) apply systematic risk (β). Focusing on the type of risk considered, it would seem more adequate to use Sharpe when we analyze the performance of a mutual fund with a vocation to diversify or when we analyze an investor’s total portfolio (in these cases, diversifiable risk should have been eliminated, and if not, performance will be negatively affected by penalization with total risk). Treynor and Jensen would be more adequate to analyze a specialized investment fund or a specific investment, understanding that systematic risk is the only one to be observed in these cases, as the diversifiable risk will be eliminated at another level.

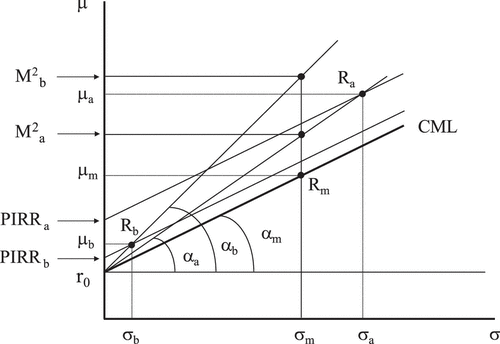
If we observe Figure 1, we may geometrically see the Sharpe ratio: on a μ–σ map of ex-post returns, we can draw the result of the market portfolio (R_m) with its average return (μ_m) and risk (σ_m); starting from the risk-free rate (r₀) and passing through R_m, we have the capital market line (CML), whose slope (tangent of α_m angle) is the market Sharpe (Formula 1 applied to the market case). For the case of portfolios R_a and R_b (with their respective values of μ and σ), their corresponding Sharpe ratios will be the tangents of α_a and α_b (as it is obtained from the application of Formula 1). We see how the Sharpe ratio, for being a quotient, is a tangent.

Figure 1. Geometric view of Sharpe, M², and PIRR indexes drawn on a μ–σ map of ex-post returns.

If we now want, with the same Figure 1, to reason as Modigliani and Modigliani (1997) did in order to obtain their M² index, we can do the following: starting from the result of one portfolio (R_b), we can leverage the investment (by borrowing) at the risk-free rate, until obtaining the same risk as the market (σ_m); we get to this by moving up along the straight line that starts from the risk-free rate (r₀) and passes through R_b until we position ourselves on the vertical of σ_m, reaching an average return equal to M²_b. We can do the same with the result of the other portfolio (R_a) by deleveraging the investment (lending) at the risk-free rate up to obtain a risk level of σ_m; we get to this by moving down from R_a along the straight line that links R_a with r₀, until we position ourselves on the vertical of σ_m, reaching an average return of M²_a. Modigliani and Modigliani propose these M² values as performance measures, and it is clear that their ranking must coincide exactly with Sharpe’s ordering (in our case: α_b > α_a > α_m and M²_b > M²_a > M²_m = μ_m). Therefore, those problems associated to the Sharpe ratio, which we will explain later, will also be applicable to M². This index has the advantage of being measured in points of return, while at the same time, its logic endorses Sharpe ratio’s validity: the best portfolio or investment fund for M² (which coincides with the best one for Sharpe) will be the one that, after matching its risk with the market, obtains a better return (thanks to the process of leveraging/deleveraging).

We can do a very similar reasoning with Figure 2 to geometrically see the Treynor ratio and its equivalent the M²_{for beta} index (proposed by Modigliani, 1997); consequently, we will give a much shorter explanation. The reader can see how, by applying Formula 2, the Treynor ratios of portfolios with results R_a, R_b, and R_m will, respectively, be the tangents of angles α_a, α_b, and α_m on a μ–β map, where betas of different portfolios and the security market line (SML) appear².

Figure 2. Geometric view of Treynor, M²_{for beta}, and PIRR_{for beta} indexes drawn on a μ–β map of ex-post returns.

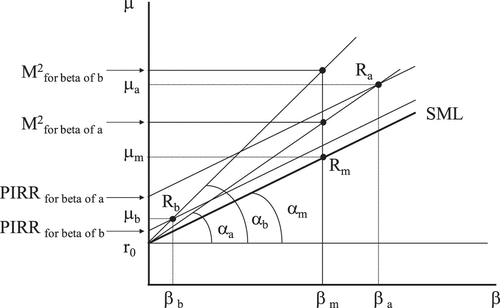
Starting now from R_b and leveraging (or deleveraging from R_a) up to reach the vertical of β_m, the market beta (equal to one), we will obtain the M²_{for beta} values of these portfolios. This index is equivalent to the Treynor ratio (it gets to an identical performance ranking), and it will therefore suffer the same problems we will mention on the use of quotients, while at the same time, it has the advantages already explained when commenting the M² and Sharpe indexes.

From the review of these indexes, it is easily deduced that one is missing: an index that applies linear penalization (as Jensen does) and refers to the total risk (as Sharpe does). This is what Gómez-Bezares, Madariaga, and Santibáñez (2004) did, arriving at the PIRR. The formulation could be:(4) $$\text{PIRR}=\mathit{\mu }-t.\mathit{\sigma }$$(4)

where we need to obtain the t value. With that purpose, we can reason this way: the PIRR would be like a certainty equivalent of a risky investment (characterized by μ–σ values); considering that the risk-free rate (r₀) is the certainty equivalent of the market portfolio (R_m) with its average return (μ_m) and risk (σ_m), we could write, by applying Formula 4, r₀ = μ_m−t.σ_m, so:(5) $$\text{t =}\left({\mathit{\mu }}_{\text{m}}-{\text{r}}_0\right)/{\mathit{\sigma }}_{\text{m}}$$(5)

which coincides with the market Sharpe ratio, this is, the tangent of angle α_m in Figure 1 and the slope of the CML. In consequence, applying the PIRR is geometrically equivalent to moving along parallel to the CML straight lines, giving as certainty equivalent (the PIRR value) the crossing point with the y-axis of the straight line parallel to the CML that passes through the corresponding portfolio. The PIRR values for portfolios with results R_a and R_b can be seen in Figure 1. Substituting the t value of Formula 5 in the formula of the PIRR index (Formula 4), we have:(6) $$\text{PIRR}=\mathit{\mu }-[({\mathit{\mu }}_{\text{m}}{\text{- r}}_0)/{\mathit{\sigma }}_{\text{m}}]\mathit{\sigma }$$(6)

The reader can confirm (geometrically or by applying Formula 6) that the PIRR of the market portfolio is the risk-free rate (r₀): we assume that the market as a whole is indifferent between the market portfolio and the risk-free rate, and this is why it combines both investments³.

If we understand that the CML slope represents the price for risk, the return increase that the market demands per each unit of risk growth, the functioning of the PIRR (in Formula 6) is absolutely logical. The reader may also confirm that the ranking derived from the PIRR in Figure 1 is different to the one obtained from the Sharpe ratio.

If we applied the PIRR methodology to the systematic risk, subtracting t betas from μ and giving to t the market Treynor value (which can be reasoned in an identical manner as we did before to use the market Sharpe ratio as t value), we would get to:(7) $${\text{PIRR}}_{\text{for beta}}=\mathit{\mu }-t.\mathit{\beta }=\mathit{\mu }-[({\mathit{\mu }}_{\text{m}}-r_0)/{\mathit{\beta }}_{\text{m}}]\mathit{\beta }=\mathit{\mu }-({\mathit{\mu }}_{\text{m}}-r_0)\mathit{\beta }$$(7)

On this Formula, we could make very similar comments to those mentioned above about the PIRR, and the corresponding results may be seen in Figure 2. Analyzing Formulae 3 and 7, it is evident that the PIRR_{for beta} exactly coincides in its ranking with the Jensen index (this is reasonable, as both apply linear penalization using systematic risk), but applying the PIRR logic (concept of certainty equivalent, price for risk, etc.) allows us to understand the classical Jensen index in a new way. Additionally, it is clear that for many individual investors, who cannot consider diversifiable risk elimination as something given and are therefore interested in the trade-off between obtained returns and total assumed risk (including both systematic and diversifiable risk), applying an index like the PIRR (using σ as the relevant risk measure) can be more realistic than applying the Jensen index (which ignores diversifiable risk behavior).

3. Some problems of quotients

The geometric view of the Sharpe ratio shows us that it is a slope in a μ–σ map, more specifically the slope of the straight line starting from r₀ and passing through the corresponding portfolio. If we assume a normal distribution of returns, the value of that slope has a clear statistical meaning: it indicates the probability of the portfolio return falling below r₀⁴. Therefore, when we rank mutual funds by their Sharpe ratio, we are actually ranking them by the probability of their return to fall below r₀ in a period; mutual funds will be more attractive if they have a lower probability of having a return below r₀. This seems very reasonable at first sight, but it is not obvious that a mutual fund with a probability, let’s suppose, of falling below r₀ of one ten-thousandth, is necessarily worse than a mutual fund with a probability of one hundred-thousandth. It is clearly better to have a low probability of falling below r₀, but if both investments show small probabilities, it is likely that the investor may also consider other aspects. Even when not having such low probabilities, we do not find logical that investors exclusively consider this point. This is precisely what happens in Figure 1: for the Sharpe ratio, R_b is better to R_a (the tangent of α_b is bigger than the tangent of α_a), but many investors will prefer R_a to R_b (this is what the PIRR sustains: PIRR_a > PIRR_b, which may help to intuitively see the advantages of linear penalization).

In any case, this is more clearly seen with small probabilities; assuming two mutual funds with the following data (in percentage):$$\text{Mutual fund C}:{\mathit{\mu }}_{\text{C}}=5;{\mathit{\sigma }}_{\text{C}}=1$$$$\text{Mutual fund D}:{\mathit{\mu }}_{\text{D}}=1.9;{\mathit{\sigma }}_{\text{D}}=0.1$$

If we assume r₀ = 1.5, the Sharpe ratios will be: S_C = (5−1.5)/1 = 3.5; and S_D = (1.9−1.5)/0.1 = 4, so mutual fund D is better to C for the Sharpe ratio, when we think that C would definitively be preferred by most investors⁵.

In consequence, the statistical meaning of the Sharpe ratio warns us about its correctness when ranking mutual funds by their performance, and we can intuitively see that too little standard deviations may take the Sharpe ratio to exaggerated values, assigning excellent Sharpe ratios to mediocre mutual funds.

We could reason in a similar way with the Treynor ratio, as we have seen in Figure 2 that it is a slope as well⁶. However, in this case, the situation is even more serious, as it is relatively easy to find betas close to zero (which would increase the ratio values extremely) or even with negative values (which would change the sign of the ratio)⁷.

We can also reason in a similar way with the IR that we have defined as the tracking error average divided by the standard deviation of tracking error. We could draw a tracking error μ–σ map (similar to the existing one in Figure 1) and we would see that the IR of a portfolio is the slope of the straight line starting from the origin of coordinates and passing through the corresponding point for that portfolio. If we assume that the tracking error follows the normal distribution, we can make a statistical interpretation similar to that one we made for the Sharpe index: the IR shows us the probability of the tracking error to be below zero for a period, and ranks portfolios by their probability of the tracking error to be positive (the best one is that portfolio with the smallest probability of falling below zero). We could repeat here the criticism we made of the Sharpe ratio, which could mostly be extended to other ratios applied to measure performance.

It is argued as one advantage of the Sharpe ratio that, just as with the M², we can leverage or deleverage our portfolios up to reach that, for a determined risk, the portfolio with a bigger Sharpe outperforms the others. However, borrowing or lending at the risk-free rate is not easy for particular investors, neither is it possible to fall into debt without limit; on the other hand, performance results are obtained ex-post, when leverage cannot be modified already. It can also be argued that linear penalization (as in the case of the PIRR), when considering as indifferent two mutual funds at the same vertical distance to the CML, does not treat risk adequately. It is not the same to exceed the CML in 2% with a low risk than with a high risk; in the second case, for instance, this is easier to happen by chance. However, the Jensen index has the same problem and is profusely used.

One advantage of the PIRR indexes is that, as it occurs with the M² indexes, they are measured in points of return, which makes them easier to understand for the standard investor. And above all, they avoid the evident problems of quotient-based measures.

4. Empirical results

In order to test whether any of the above-mentioned problems occur in practice, we took the 413 largest equity mutual funds in the USA, with the data series running from August 2006 to the same month in 2011 and Bloomberg being the utilized source⁸. We calculated the monthly returns of the mutual funds⁹, their averages, standard deviations, and betas (using the S&P 500 total returns as market portfolio, which was also used to obtain μ_m and σ_m); the Treasury Bill 1M was used as risk-free rate. We calculated the S, T, J, and PIRR indexes for each mutual fund, and the Pearson and Spearman correlations. Results can be seen in Table 1 (and a summary including key statistical parameters of the analyzed data is included in Appendix A).

Table 1. Pearson and Spearman correlation coefficients (including initial 413 mutual funds)

	S	T	J	PIRR
Pearson
S	1.0000	−0.0311	0.9570	0.9519
T	−0.0311	1.0000	0.0093	0.0145
J	0.9570	0.0093	1.0000	0.9997
PIRR	0.9519	0.0145	0.9997	1.0000
Spearman
S	1.0000	0.9848	0.9882	0.9848
T	0.9848	1.0000	0.9752	0.9730
J	0.9882	0.9752	1.0000	0.9990
PIRR	0.9848	0.9730	0.9990	1.0000

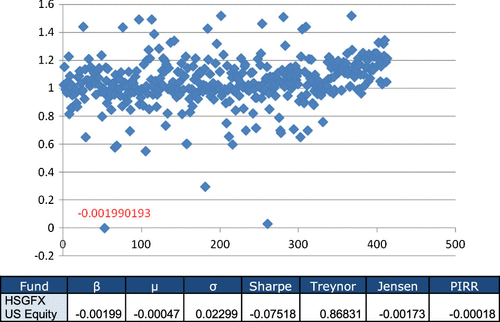
We see that in Table 1, there appears one negative Pearson correlation coefficient, more specifically between the Treynor and Sharpe ratios; as well as this, the values of the Pearson correlations between Treynor and the other indexes are extremely low, which is surprising. However, if we focus on the Spearman coefficients, they are all quite high, above 0.97. From this we can deduce that rank correlation may hide very serious problems, and above all, that something unexplained must be happening to find so strange coefficients. We analyzed the data and found a mutual fund with a negative beta value and very small in absolute terms, this was fund number 53 by order of capitalization. This is the case of a fund with an objective of long-term value creation, focused on capital preservation under adverse market conditions. As the analyzed period has a negative market Sharpe, this fund’s negative beta is reasonable (see Figure 3).

Figure 3. β value of mutual funds by fund number and details of a mutual fund with a negative β.

This very small and negative value of the beta for fund number 53 is precisely what is causing a very high and positive value of the Treynor ratio and what is totally distorting the Pearson correlations. We then thought of repeating the exercise excluding fund number 53, and we reached Table 2.

Table 2. Pearson and Spearman correlation coefficients (initial 413 mutual funds excluding fund number 53)

	S	T	J	PIRR
Pearson
S	1.0000	0.8936	0.9573	0.9524
T	0.8936	1.0000	0.9369	0.9416
J	0.9573	0.9369	1.0000	0.9997
PIRR	0.9524	0.9416	0.9997	1.0000
Spearman
S	1.0000	0.9993	0.9881	0.9848
T	0.9993	1.0000	0.9888	0.9859
J	0.9881	0.9888	1.0000	0.9990
PIRR	0.9848	0.9859	0.9990	1.0000

Results are surprising. By excluding one single fund, all the Pearson coefficients become close to or higher than 0.9 and Spearman coefficients exceed 0.98. We repeat the exercise with the largest 100 funds, reaching Table 3, and if we exclude the fund with negative beta, we reach Table 4.

Table 3. Pearson and Spearman correlation coefficients (100 largest mutual funds)

	S	T	J	PIRR
Pearson
S	1.0000	−0.1725	0.9626	0.9551
T	−0.1725	1.0000	−0.0964	−0.0860
J	0.9626	−0.0964	1.0000	0.9996
PIRR	0.9551	−0.0860	0.9996	1.0000
Spearman
S	1.0000	0.9401	0.9896	0.9857
T	0.9401	1.0000	0.9326	0.9315
J	0.9896	0.9326	1.0000	0.9990
PIRR	0.9857	0.9315	0.9990	1.0000

Table 4. Pearson and Spearman correlation coefficients (100 largest mutual funds excluding fund number 53)

	S	T	J	PIRR
Pearson
S	1.0000	0.8641	0.9641	0.9573
T	0.8641	1.0000	0.9520	0.9581
J	0.9641	0.9520	1.0000	0.9996
PIRR	0.9573	0.9581	0.9996	1.0000
Spearman
S	1.0000	0.9995	0.9896	0.9858
T	0.9995	1.0000	0.9908	0.9874
J	0.9896	0.9908	1.0000	0.9991
PIRR	0.9858	0.9874	0.9991	1.0000

If fund number 53 is not excluded (Table 3), results are even worse for the Treynor ratio, as all its Pearson coefficients become negative, which is reasonable having one fund with an illogical Treynor ratio within a smaller sample. The Spearman coefficients are high, while smaller than with the 413 funds sample. Repeating the same exercise excluding fund number 53 (Table 4), problems get solved.

The analyzed period (August 2006–August 2011) gives a negative market Sharpe (−0.01265); so, we considered it convenient to extend the time period, taking August 2003–August 2011, and we obtained a positive market Sharpe (0.03952). We focused on the largest 100 funds (same ones as before) and we calculated their performance indexes in the same way. Fund number 53 that previously had a negative beta now has a small but positive value (β = 0.00348), which is consistent with the goals of the fund. Based on our previous exercise’s experience, we first analyzed whether there was any fund with a negative or very small beta. This was only the case of fund 53 (positive but very small beta), and we also analyzed the standard deviations. We can see the σ values of the 100 funds in Figure 4, and we observe there are four funds with smaller values, which may cause problems in the Sharpe ratio; as they have a very small denominator, the index value could be abnormally high.

Figure 4. σ value of mutual funds by fund number and details of mutual funds with a smaller σ (extended period).

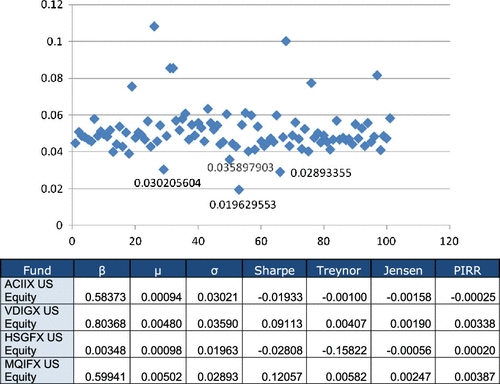
If we ignore those four funds, we also eliminate the fund with a very small beta; so, we decided to make the analysis both with all the 100 funds (Table 5) and with 96 funds (excluding those four funds with a smaller σ), and we reached Table 6.

Table 5. Pearson and Spearman correlation coefficients (100 largest mutual funds, extended period)

	S	T	J	PIRR
Pearson
S	1.0000	0.3512	0.9194	0.9561
T	0.3512	1.0000	0.2770	0.2867
J	0.9194	0.2770	1.0000	0.9872
PIRR	0.9561	0.2867	0.9872	1.0000
Spearman
S	1.0000	0.9521	0.9873	0.9879
T	0.9521	1.0000	0.9423	0.9375
J	0.9873	0.9423	1.0000	0.9970
PIRR	0.9879	0.9375	0.9970	1.0000

Table 6. Pearson and Spearman correlation coefficients (100 largest mutual funds, excluding 4 with smaller σ, extended period)

	S	T	J	PIRR
Pearson
S	1.0000	0.8423	0.9272	0.9631
T	0.8423	1.0000	0.9681	0.9383
J	0.9272	0.9681	1.0000	0.9871
PIRR	0.9631	0.9383	0.9871	1.0000
Spearman
S	1.0000	0.9993	0.9875	0.9861
T	0.9993	1.0000	0.9901	0.9862
J	0.9875	0.9901	1.0000	0.9992
PIRR	0.9861	0.9862	0.9992	1.0000

The Pearson coefficient, in the analysis with 100 funds, gives low values for Treynor (despite being higher than before, they are still unusually low); the Spearman coefficient keeps hiding the problem. Making the analysis with 96 funds, the coefficients clearly improve, as the problems caused by abnormally small denominators have been avoided.

Summarizing, in this empirical section, we took a sample of the most important equity mutual funds in the USA and calculated their performance indexes (S, T, J, and PIRR). Expectations would be, according to most of the literature, that relations among these indexes were high. However, Pearson correlation coefficient has abnormally low values for the Treynor index. The problem is mainly caused by a fund with a negative beta value; by excluding this fund, the problem is solved. We have repeated the exercise with the 100 most important funds, reaching substantially similar results. Considering that the time period of the selected sample had a negative market Sharpe, and in order to get more robust results, we have repeated the same analyses with a longer time period and with a positive market Sharpe, concluding that problems of applying quotients persist.

All these calculations support the theoretical argumentation made at the beginning, summarized in the problems caused by applying quotients to measure performance. It is clear that a negative beta may lead us to error if we use the Treynor ratio, but we have seen that we can also make a mistake in case of a very low beta. This is the problem of using ratios. In the sample we have used, there were no cases with very small σ, which is reasonable in a complicated investment period analyzing equity mutual funds; this is why the Sharpe ratio did not show major problems. Even with this, when excluding funds with lower σ, its Pearson coefficients improve a little, and it is clear that we could have searched for funds with σ close to zero, which would have caused unusual Sharpe indexes and therefore lower Pearson coefficients. We preferred not to do this in order to avoid falling in a data mining exercise (one of the major problems of current financial research; see Gómez-Bezares & Gómez-Bezares, 2006); and this is why we have described in detail the followed path to execute the different analyses while looking for robustness in our results. In any case, we consider we have shown clearly enough that the use of ratios may cause problems, which is what we wanted to prove.

On the other hand, it is important to emphasize the high correlations that usually exist between the Jensen and PIRR indexes, despite them using different risk measures (β and σ, respectively), which proves the great importance of the penalization methodology.

5. Conclusion

Given that many authors show how the Sharpe ratio is the most commonly applied (Amenc et al., 2011; Eling, 2008), and that IR or Treynor and other quotient-based ratios are also widely used (Amenc et al., 2011), this paper’s title may be considered provocative. Should we not use these ratios anymore?

We have tried to warn the analyst, the fund manager, about some important failures these ratios may have, which does not imply that these ratios must not be used or that other indexes do not have any problems of their own. They must simply be used cautiously, especially under certain circumstances, as we have explained along this paper.

Contrary to Eling’s view (2008), we think that the way in which we measure performance does have its importance, at least in some cases, and it is not enough with finding high Spearman correlations among the indexes because this may be hiding the reality.

Our empirical results show problems with the Treynor ratio in some cases, but not with the Sharpe ratio, as we have not used funds with too small σ values. However, this does not mean that the Sharpe ratio cannot have problems in other samples, as we have explained with a numerical example. It has been said that the Sharpe ratio is not valid if returns do not follow the normal distribution; but, even following the normal distribution, the statistical explanation that we have given forces us to be cautious with the interpretation of the Sharpe ratio.

In general, we must be careful when applying quotients for performance measurement, especially when denominators have very low values; in these cases, it is advisable to use additional performance measures, at least to complete the analysis. In case of having negative beta values, the most prudent practice is to disregard the Treynor index for those funds. The PIRR index, as it is not a quotient but a difference, does not have these problems.

Finally, we want to emphasize that we have worked with indexes that are easy to calculate and understand; among these, linear penalization, in the way we have presented it, is an interesting option.

Acknowledgments

The authors want to thank the editor, referees, and other colleagues for their comments and suggestions, which have undoubtedly contributed to the improvement of the present paper.

Additional information

Funding

Funding. The authors received no direct funding for this research.

Notes on contributors

Fernando Gómez-Bezares

Fernando Gómez-Bezares, as professor of Finance at the Deusto Business School, has written 25 books and many papers in academic and professional journals related to the topic faced in this paper: risk treatment and value creation.

Fernando R. Gómez-Bezares

Fernando R. Gómez-Bezares, as a practitioner, currently at The Boston Consulting Group and previously at Morgan Stanley, knows the importance given daily to the performance indexes analyzed in this paper. Apart from the works mentioned below, he has published in the “Revista Española de Capital Riesgo” (Spanish Journal of Venture Capital).

Both authors have published together the following papers: “On the use of hypothesis testing and other problems in financial research” in “The Journal of Investing,” “Classic performance indexes revisited: axiomatic and applications” in “Applied Economics Letters,” “An analysis of risk treatment in the field of finance” as a chapter in the “Encyclopedia of Finance, 2nd edition,” edited by Springer, and “The efficiency-CAPM paradigm” in the Spanish journal “Análisis Financiero”.

Notes

1. Taking the tracking error definition applied by Roll (1992): difference between portfolio’s return and benchmark’s return for the same period of time, and applying the IR definition proposed by Modigliani and Modigliani (1997).

2. In this approach, the capital asset pricing model (CAPM) logic is underlying. A recent test of this model in the Spanish market can be seen in Gómez-Bezares, Ferruz, and Vargas (2012).

3. We can also give a statistical meaning to the t value. From Formula 4, we get to (PIRR−µ)/σ = −t; so, if return follows a normal distribution, the −t value would leave at its left a probability in the standard normal distribution equal to the probability for the actually obtained return of the mutual fund or portfolio in a certain period to be less than the PIRR. In this sense, an investor may look for a different t value from the one offered by the market (we have seen that this is the market Sharpe ratio). For instance, a t value of 1 would leave a probability (in the standard normal distribution tables) equal to 0.1587, which means that the PIRR would be a “guaranteed value” with a probability of (1−0.1587) = 0.8413. We could also interpret the straight lines, parallel to the CML, as indifference straight lines, giving a greater value to the portfolio or mutual fund that reaches the highest straight line; but, this would lead us to another type of reasoning that would take us away from this paper’s goal.

4. Taking Formula 1 (Sharpe ratio), (µ−r₀)/σ is also, changed its sign, the standardized value of r₀, which we call t. This t, searching in the tables of the standard normal distribution, shows us the probability of the return to fall below the risk-free rate in a certain period.

5. A t = 3.5 implies, in the tables of the standard normal distribution, a 0.00023 probability of the return falling below r₀, and a t = 4 would result in a probability of 0.00003; the latter is smaller, but both are insignificant. On the other hand, the probability of C mutual fund return falling below the average return of D would be obtained this way: t = (5−1.9)/1 = 3.1, with a corresponding probability of 0.00097, which makes mutual fund C clearly more attractive.

6. Its statistical meaning is not so obvious, but assuming that diversifiable risk will be eliminated by diversification, the β will be proportional to the resulting σ, and we can maintain the same reasoning.

7. There is a lack of logic in the negative value obtained for Treynor when we have a mutual fund with a positive risk premium and a negative beta. A more detailed explanation can be seen in Gómez-Bezares and Gómez-Bezares (2012).

8. We want to show our gratitude to Norbolsa (Broker), Raquel Arechabala, and Manu Martín-Muñío for their help to obtain the required data. We also want to specially thank Alba Díaz Gómez for her support with the information processing.

9. Based on variations of net asset value.

Appendix A

Summarized statistical parameters of the analyzed data (base period)

Table

Number of mutual funds		413	(Largest equity mutual funds in the USA)
Mutual funds returns
(Mean of monthly net asset value variations Aug2006–Aug2011 for each fund)
Maximum	0.020494
Minimum	−0.003642
Average	0.003174
Median	0.002967
Mutual funds risk measures
(Considering returns variations in the period for each fund)
	σ	β
Maximum	0.113217	1.516710
Minimum	0.009749	−0.001990
Average	0.058197	1.040882
Median	0.056492	1.035236
Benchmark returns
(S&P 500)
Average	0.000603	Standard deviation: 0.051857
Risk-free rate returns
(Treasury Bill 1M)
Average	0.001259
Mutual funds performance measures
	Sharpe	Treynor	Jensen	PIRR
Maximum	0.169899	0.868313	0.019717	0.021927
Minimum	−0.082367	−0.004694	−0.004172	−0.002889
Average	0.030617	0.004025	0.002598	0.003910
Median	0.028801	0.001646	0.002428	0.003713
Standard deviation	0.049674	0.042779	0.003123	0.003173