Oil and non-energy commodity markets: An empirical analysis of volatility spillovers and hedging effectiveness

Abstract

Although a large number of empirical papers have examined the price spillover in global oil and non-energy commodity markets, very little is known about the volatility transmission between these two markets. The present study aims to conceal this gap by investigating the volatility cross effects between oil and three different non-energy commodity markets. Using the bivariate VAR-GARCH models, we do not find any evidence of volatility linkage between oil and agricultural product markets during the sample period used. We, however, document that oil market sends volatility to both metal and non-energy aggregate markets. This finding is not surprising, since petroleum-related products are one of the major production inputs in metal industries and hence the production process of metals largely depends on the crude oil market. Since various financial assets are traded on the basis of commodity markets, our results are beneficial for portfolio diversification and hedging decisions. Policy-makers could also use the findings of this research to reduce the impact of oil price uncertainty on metal and agricultural markets.

Keywords:

• oil market
• non-energy commodity markets
• volatility transmission
• hedging effectiveness
• VAR-GARCH model

Public Interest Statement

This paper investigates the impact of oil price fluctuations on different non-energy commodity markets. In particular, we consider agriculture, metal, and aggregate non-energy price indices to serve our purpose. Using standard econometric models, we document those variations in oil prices account for the movements in the non-energy commodity prices. Our findings are not surprising, since oil is one of the major production inputs in agriculture and metal markets, and hence oil price shocks impact these non-energy commodity markets. Investors could use our results for making proper investment decisions. In addition, policy-makers, on the basis of our results, could take appropriate measures to limit the effect of oil price uncertainty.

1. Introduction

A growing body of literature documents that important commodity markets such as agriculture and metal markets are highly sensitive to oil price shocks. For instance, Ewing and Malik (2013) show that oil price volatility directly impacts the gold market and thus affects the performance of the overall economy. Chen, Kuo, and Chen (2010) report that changes in crude oil price would cause the variations in different grain prices. The authors argue that bio-fuel firms may have an incentive to produce ethanol or bio-diesel if the crude oil price remains at a higher level. Hence, an increase in crude oil price has induced a higher derived demand for corn or soybeans and has resulted in higher prices of corn and soybeans. Additionally, Mensi, Hammoudeh, Nguyen, and Yoon (2014) contend that higher oil prices can make the production of agricultural goods more expensive by raising the costs of mechanical cultivation, energy-related inputs like fertilizers and pesticides, and transportation of both inputs and outputs. Ji and Fan (2012) also find that the crude oil market has significant volatility spillover effects on non-energy commodity markets, which demonstrates its core position among the commodity markets.

Although several empirical papers (e.g. Narayan, Narayan, & Zheng, 2010; Sari, Hammoudeh, & Soytas, 2010; Soytas, Sari, Hammoudeh, & Hacihasanoglu, 2009) have investigated the linkage between oil and non-energy commodity markets at price level, inspecting how shocks and volatility are transmitted between these two markets is still limited. Such investigations are crucial in several aspects. First, the agriculture sector largely depends on the transportation sector for the shipment of food grains and such products. Now, a rise in oil price will result in increased prices of gasoline which is produced from crude oil. Consequently, the price of shipping goes up. Thus, fluctuations in oil price volatility do account for raising food and grain prices in general. Second, due to high external dependency on oil, oil price volatility seems to impact the relevant industries and hence the overall economy of a specific country or region. For instance, Zhang and Tu (2016), report that metal industry is highly oil-intensive and hence oil price volatility certainly affects the metal markets. Third, understanding volatility spillover mechanism plays a vital role in making optimal portfolio allocation decisions. Ewing and Malik (2013), for example, argue that since many financial assets are traded on the basis of gold and oil, it is important for financial market participants to understand the volatility transmission mechanism over time and across these series in order to facilitate proper decisions. Ji and Fan (2012) also document that research on volatility spillover is a key concept for portfolio diversification strategies.

Therefore, the aim of our study is to extend this limited literature by assessing the volatility transmission mechanism between global oil and non-energy commodity markets. In particular, we attempt to investigate whether volatility spills over from oil market to agriculture, metal and aggregate non-energy commodity markets. Although the paper by Ji and Fan (2012) is the closet to the present study, ours still extends this prior work in several aspects.

First, we consider the application of the bivariate vector autoregressive–generalized autoregressive conditional heteroskedastic (VAR-GARCH) models to estimate the shock and volatility spillover effects. Such approach, proposed by Ling and McAleer (2003), is advantageous as it captures the effect on current volatility of both own innovation and lagged volatility shocks deriving from within a given market and cross-innovation and volatility transmission from interrelated markets.

Second, we find minimum variance portfolio weights using the estimated results of our VAR-GARCH model. This finding will be useful to examine whether the combination of oil and non-energy commodities reduces the portfolio risk.

Third, in contrast to the previous studies, which have used only the symmetric VAR-GARCH model to estimate the volatility spillover effects across different financial markets, we also consider the application of the asymmetric VAR-GARCH (VAR-AGARCH) methodology proposed by McAleer, Hoti, and Chan (2009). Employing this method is beneficial, since it allows us to explore whether negative return innovations affect volatility more than positive shocks.

The results of our VAR-GARCH models suggest that volatility is significantly transmitted from global oil prices to majority of the non-energy commodity indices considered. To be specific, we document that both metal and aggregate non-energy commodity indices are the recipients of volatility from the oil market. However, we do not find any evidence of volatility linkage between oil and agriculture price indices. One could expect that the agriculture sector has adopted some effective strategies to get insulated from the influence of oil market shocks and volatility. Our findings are robust in that both the VAR-GARCH as well as the VAR-AGARCH models infer the same.

The rest of the paper will proceed as follows. The next section reviews the relevant literature. Section 3 explains the data and their properties. Section 4 outlines the VAR-GARCH model. Results are discussed in Section 5. Section 6 assesses the robustness of our results obtained from the VAR-AGARCH model. Section 7 concludes.

2. Related literature

Several researchers study whether oil market has any significant influences over non-energy commodity markets. Hammoudeh and Yuan (2008), for example, consider the application of GARCH family models to inspect the volatility behavior of three strategic commodities: gold, silver, and copper, in the presence of crude oil and interest rate shocks. The empirical results indicate that past oil shock does not impact all three metals similarly. To be more specific, oil volatility mainly affects the precious metals. Harri, Nalley, and Hudson (2009) investigate the price relationship through time of the primary agricultural commodities, exchange rates, and oil prices. Using overlapping time periods, the authors inspect the co-integration relationship between prices to determine changes in the strength of the link between markets through time. The results reveal that prices of commodities such as corn, cotton, and soybeans are significantly affected by oil prices. The study also documents that exchange rates have a major role in the association of prices over time.

Moreover, Sari et al. (2010) study the co-movements and information transmission among the spot prices of four precious metals (gold, silver, platinum, and palladium), oil price, and the US dollar/euro exchange rate. The study reports a weak evidence of long-run equilibrium relationship but strong feedbacks in the short run. The authors further show that the spot precious metal markets respond significantly (but temporarily) to a shock in any of the prices of the other metal prices and the exchange rate. Nazlioglu and Soytas (2011) assess the short- and long-run interdependence between world oil prices, lira–dollar exchange rate, and individual agricultural commodity prices (wheat, maize, cotton, soybeans, and sunflower) in Turkey. The impulse–response analysis shows that oil price and exchange rate shocks do not have any impact on the Turkish agricultural prices in the short-run. In addition, the long-run causality analysis suggests that the changes in oil prices and appreciation/depreciation of the Turkish lira are not transmitted to agricultural commodity prices in Turkey.

Besides, Ji and Fan (2012) study the effect of the crude oil market on non-energy commodity markets before and after the 2008 financial crisis. By introducing the US dollar index as exogenous shocks, the authors examine the price and volatility spillover between commodity markets by building a bivariate EGARCH model with time-varying correlation construction. Their findings suggest that the crude oil market has significant volatility spillover effects on non-energy commodity markets, which demonstrates its core position among commodity markets. Ewing and Malik (2013) employ the univariate and bivariate GARCH models to assess the volatility of gold and oil futures incorporating structural breaks using daily returns from 1 July 1993 to 30 June 2010. They report strong evidence of significant transmission of volatility between gold and oil returns when structural breaks in variance are taken into account in the model.

A recent study by Zhang and Qu (2015) investigates the effect of global oil price shocks on agricultural commodities in China, including strong wheat, corn, soybean, bean pulp, cotton, and natural rubber. Considering the oil price volatility process as a combination of continuous process and jump process, the authors document that the oil price is characterized by volatility clustering and jump behavior. In addition, oil price shocks have different effects on agricultural commodities and these shocks on most agricultural commodities are found to be asymmetric. Furthermore, only natural rubber was under influence of the jump intensity of the oil price, in contrast to strong wheat, corn, soybean, bean pulp, and cotton. More recently, Zhang and Tu (2016) examine the impacts of global oil price shocks on the Chinese metal markets. The study considers the whole metal market as well as two typical metal markets: copper and aluminum. Employing ARJI-GARCH models, the authors show that crude oil price shocks have significant impacts on China’s metal markets and the impacts are symmetric. Additionally, when compared with aluminum, copper is more easily affected by oil price shocks.

3. Data

In this study, we use daily data for West Texas Intermediate (WTI) as the measure of oil price. WTI is a primary crude stream which is traded on the domestic spot market at the Cushing, Oklahoma center. In addition, we use S&P GSCI (Goldman Sachs Commodity Index) data which measure the level of nearby commodity prices. Three different GSC spot price indices have been considered to represent the agriculture, metal and aggregate non-energy commodity markets, respectively. Our sample period goes from 2 January 1986 to 31 December 2015, yielding a total of 7,826 observations. We collect all these data from the Thomson Reuters DataStream database.

3.1. Descriptive statistics

Table 1 indicates the descriptive statistics for each of the return series considered in the present study. Interestingly, the average return for each of the indices is positive and it is highest in the metal market followed by the rest. In addition, the oil market shows higher volatility than the commodity markets, while among the commodity indices, agriculture market is more volatile than metal and aggregate commodity markets. Besides, all the indices exhibit negative skewness implying that large negative stock returns are more common than large positive returns in these markets. Moreover, each of the indices is leptokurtic which is a normal case in high-frequency financial time series data. Figures 1^{Figure 2Figure 3}–4, where the return indices are plotted, also show the presence of volatility clustering and hence the GARCH process, proposed by Engle (1982) and Bollerslev (1986), has been opted for modeling the return series. Furthermore, the Jarque–Bera test rejects the null hypothesis of normality for all the indices under review. However, this Jarque–Bera test has some concerns regarding its properties. Bai and Ng (2005), for instance, report that this test is influenced by serial correlation.

Table 1. Descriptive statistics

Market	Mean	Standard deviation	Skewness	Kurtosis	Jarque-Bera test
WTI oil	0.000048	0.0248	−0.7349	17.92	73,349.01 (0.00)***
Agriculture	0.000035	0.0111	−0.0969	6.28	3,523.22 (0.00)***
Metal	0.000150	0.0106	−0.3497	9.99	16,102.12 (0.00)***
Aggregate	0.000055	0.0078	−0.2775	7.35	6,292.88 (0.00)***

Notes: This table reports the main descriptive statistics for various return indices studied. The values in parentheses denote the p-values.

*** Indicates statistical significance at 1% level.

Figure 1. Return index for the oil market.

Figure 2. Return index for the agriculture market.

Figure 3. Return index for the metal market.

Figure 4. Return index for the aggregate market.

4. Methodology

We employ a multivariate GARCH (MGARCH) model in order to detect the volatility transmission linkages among different return indices. Popular multivariate GARCH specifications include BEKK, CCC, and DCC GARCH models. The current literature documents that all these models perform fairly well in empirical modeling of volatility spillovers (see, for example, Arouri, Jouini, & Nguyen, 2011; Hammoudeh, Yuan, & McAleer, 2009; Malik & Ewing, 2009). However, in this study we propose to use the VAR(1)-GARCH(1,1) model to investigate the return and volatility transmission linkages. We prefer the VAR-GARCH model to the BEKK-GARCH specification, since the BEKK model does not have a VAR attached to it. Therefore, using the BEKK model does not allow us to estimate the price/return spillover effects among the markets under consideration. Hammoudeh et al. (2009) also prefer the VAR(1)-GARCH(1,1) approach to the BEKK model arguing that the BEKK-VAR distribution has not theoretically been analyzed. Besides, Arouri et al. (2011) document that when analyzing the diversification benefits and hedging effectiveness, the VAR-GARCH model outperforms several competing multivariate GARCH models including the dynamic conditional correlation (DCC)-GARCH, the constant conditional correlation (CCC)-GARCH, and the BEKK-GARCH. Since one of our purposes is to find the optimum portfolio weights and hedge ratios, we consider the application of the VAR-GARCH model in our empirical analysis.

Now, on the basis of Akaike information criterion (AIC) and Schwartz information criterion (SIC), we have selected the optimal number of lags and employ the following bivariate VAR(1)-GARCH (1,1) model defined as follows:(1) $$R_t=V+\mathit{\theta }{R}_{t-1}+{\mathit{\epsilon }}_t$$(1) $${\mathit{\epsilon }}_t=D_t^{1/2}{\mathit{\eta }}_t$$

Within this framework, R_t denotes a 2 × 1 vector of daily returns on oil and commodity market indices at time t, V refers to a 2 × 1 vector of constants, θ is a 2 × 2 matrix of parameters measuring the impacts of own-lagged and cross-mean transmissions between two markets, ε_t is the residual of the mean equation for the oil and commodity returns at time t, η_t indicates a 2 × 1 vector of independently and identically distributed innovations and $D_t^{1/2}=\text{diag}\left(\sqrt{h_t^c},\sqrt{h_t^o}\right)$, where, $h_t^c$ and $h_t^o$, which indicate the conditional variances of commodity and oil returns, respectively, are defined as follows:

(2) $$h_t^c=v_c^2+b_{11}^2{h}_{t-1}^c+b_{21}^2{h}_{t-1}^o+a_{11}^2{\mathit{\epsilon }}_{c,t-1}^2+a_{21}^2{\mathit{\epsilon }}_{o,t-1}^2$$(2) (3) $$h_t^o=v_o^2+b_{12}^2{h}_{t-1}^c+b_{22}^2{h}_{t-1}^o+a_{12}^2{\mathit{\epsilon }}_{c,t-1}^2+a_{22}^2{\mathit{\epsilon }}_{o,t-1}^2$$(3)

where c denotes the non-energy commodity market which takes the value a for the agriculture market, the value m for the metal market and the value n for the aggregate non-energy commodity market, respectively. Equations (2) and (3) allow us to examine how shocks and volatility spillover across time as well as across the return indices. Moreover, the conditional covariance between oil and commodity returns is estimated as follows:

(4) $$h_t^{\text{co}}={\mathit{\rho }}_t\sqrt{h_t^c}\sqrt{h_t^o}$$(4)

where ρ_t denotes the conditional correlation between oil and commodity returns at time t.

Now, in order to capture the non-normality associated with oil and commodity prices, we apply the quasi-maximum likelihood estimation technique to obtain the estimates of the parameters of our VAR(1)-GARCH (1,1) model. These findings are then used to compute the optimal weights and hedge ratios.

5. Empirical results

In this section, we present the findings of our empirical analyses. We first implement the augmented Dickey and Fuller test (ADF) (1979, 1981), Phillips and Perrron test (PP) (1988), and ADF-GLS test (Elliott, Rothenberg, & Stock, 1996) to assess the stationarity conditions for each of the return indices under study. The next sub-section includes the results of the VAR-GARCH models which shed light on the volatility transmission relationship between oil and each of the commodity markets considered. We then discuss the time-varying correlations between oil price changes and different non-energy price indices used. The outcomes of optimum portfolio weights and hedging effectiveness take place in the following sub-section. We finally explain the results of the GARCH-jump model.

5.1. Unit root tests

Table 2 reports the results of the unit root tests. All the tests used confirm that the null hypothesis of no unit root holds suggesting that all the price indices appear to be non-stationary. However, the first differenced series are stationary implying that all the individual return indices tend to have unit roots. These outcomes are essential, since the stationarity condition gives us the authority to employ the autoregressive process for modeling the returns.

Table 2. Results of unit root tests

Sector	ADF tests		PP tests		ADF-GLS tests
	Level	1st difference	Level	1st difference	Level	1st difference
Oil	−1.59 (0.48)	−90.73*** (0.00)	−1.58 (0.49)	−90.95*** (0.00)	−1.33 (0.18)	−3.93*** (0.00)
Agriculture	−1.76 (0.39)	−85.36*** (0.00)	−1.83 (0.36)	−85.44*** (0.00)	−1.54 (0.12)	−2.99*** (0.00)
Metal	−0.85 (0.80)	−89.57*** (0.00)	−0.82 (0.81)	−89.58*** (0.00)	−0.22 (0.82)	−8.61*** (0.00)
Aggregate	−1.22 (0.66)	−87.33*** (0.00)	−1.27 (0.64)	−87.36*** (0.00)	−0.75 (0.45)	−3.42*** (0.00)

Notes: This table shows the results for the ADF, PP, and ADF-GLS tests. The values in parentheses denote the p-values.

*** Indicates statistical significance at 1% level.

5.2. Price and volatility spillovers between oil and non-energy commodity markets

The estimated outcomes of the bivariate VAR(1)-GARCH(1,1) models are shown in Tables 3–5. These results are useful for assessing the connotation between first- and second-order moments of global oil market and different commodity markets used. In Tables 3–5, $h_{t-1}^o$ measures the conditional variance of the oil market at time t − 1 and $h_{t-1}^c$ indicates the conditional variance of a particular commodity market at time t − 1. In addition, $r_{t-1}^c$ refers to the return for commodity market at time t − 1 and $r_{t-1}^o$ denotes the same for the oil market. The squared error terms ${\mathit{\epsilon }}_{c,t-1}^2$ and ${\mathit{\epsilon }}_{o,t-1}^2$ measure the effects of unexpected news or shocks in commodity and oil markets, respectively. In these Tables, Panel A contains the results for mean equations and Panel B shows the same for variance equations.

Table 3. Results of the oil–agriculture model

Independent variable	Agriculture	Oil
Panel A: mean equation
$r_{t-1}^a$	0.0411 (0.00)***	0.0257 (0.17)
$r_{t-1}^o$	−0.0084 (0.03)**	−0.0233 (0.02)**
Panel B: variance equation
${\mathit{\epsilon }}_{a,t-1}^2$	0.0420 (0.00)***	0.0002 (0.51)
${\mathit{\epsilon }}_{o,t-1}^2$	1.4e10^−6 (0.74)	0.0686 (0.00)***
$h_{t-1}^a$	0.9467 (0.00)***	6.1e10^−7 (0.39)
$h_{t-1}^o$	2.7e10^−7 (0.93)	0.9254 (0.00)***

Notes: This table reports the VAR(1)-GARCH(1,1) outcomes for the oil–agriculture model. Panel A contains the results of the mean equation, while Panel B shows the same for variance equation. $r_{t-1}^a$ refers to the return on agriculture index at time t − 1 and $r_{t-1}^o$ denotes the same for oil market. In addition, $h_{t-1}^o$ measures the conditional variance of the oil market returns at time t − 1 and $h_{t-1}^a$ indicates the conditional variance of agriculture index returns at time t − 1. The squared error terms ${\mathit{\epsilon }}_{a,t-1}^2$ and ${\mathit{\epsilon }}_{o,t-1}^2$ measure the effects of unexpected news or shocks in agriculture and oil markets, respectively. The values in parentheses denote the p-values.

** Indicate statistical significance at 5% level.

*** Indicate statistical significance at 1% level.

Table 4. Results of the oil–metal model

Independent variable	Metal	Oil
Panel A: mean equation
$r_{t-1}^m$	−0.0184 (0.11)	−0.0075 (0.70)
$r_{t-1}^o$	0.0103 (0.01)**	−0.0304 (0.00)***
Panel B: variance equation
${\mathit{\epsilon }}_{m,t-1}^2$	0.0309 (0.00)***	2.2e10^−6 (0.59)
${\mathit{\epsilon }}_{o,t-1}^2$	0.0011 (0.01)**	0.0789 (0.00)***
$h_{t-1}^m$	0.9662 (0.00)***	4.9e10^−7 (0.32)
$h_{t-1}^o$	0.0001 (0.00)***	0.9158 (0.00)***

Notes: This table reports the VAR(1)-GARCH(1,1) outcomes for the oil–metal model. Panel A contains the results of the mean equation, while Panel B shows the same for variance equation. $r_{t-1}^m$ refers to the return on metal index at time t − 1 and $r_{t-1}^o$ denotes the same for oil market. In addition, $h_{t-1}^o$ measures the conditional variance of the oil market returns at time t − 1 and $h_{t-1}^m$ indicates the conditional variance of metal index returns at time t − 1. The squared error terms ${\mathit{\epsilon }}_{m,t-1}^2$ and ${\mathit{\epsilon }}_{o,t-1}^2$ measure the effects of unexpected news or shocks in metal and oil markets, respectively. The values in parentheses denote the p-values.

** Indicate statistical significance at 5% level.

*** Indicate statistical significance at 1% level.

Table 5. Results of the oil–aggregate model

Independent variable	Aggregate	Oil
Panel A: Mean equation
$r_{t-1}^n$	0.0358 (0.00)***	0.0335 (0.11)
$r_{t-1}^o$	−0.0027 (0.32)	−0.0251 (0.02)**
Panel B: Variance equation
${\mathit{\epsilon }}_{n,t-1}^2$	0.0309 (0.00)***	0.0006 (0.74)
${\mathit{\epsilon }}_{o,t-1}^2$	0.0008 (0.28)	0.0745 (0.00)***
$h_{t-1}^n$	0.9643 (0.00)***	1.4e10^−8 (0.83)
$h_{t-1}^o$	0.0001 (0.04)**	0.9196 (0.00)***

Notes: This table reports the VAR(1)-GARCH(1,1) outcomes for the oil–aggregate non-energy model. Panel A contains the results of the mean equation, while Panel B shows the same for variance equation. $r_{t-1}^n$ refers to the return on non-energy commodity index at time t − 1 and $r_{t-1}^o$ denotes the same for oil market. In addition, $h_{t-1}^o$ measures the conditional variance of the oil market returns at time t − 1 and $h_{t-1}^n$ indicates the conditional variance of non-energy commodity index returns at time t − 1. The squared error terms ${\mathit{\epsilon }}_{n,t-1}^2$ and ${\mathit{\epsilon }}_{o,t-1}^2$ measure the effects of unexpected news or shocks in non-energy commodity and oil markets, respectively. The values in parentheses denote the p-values.

^** Indicates statistical significance at 5% level.

^*** Indicates statistical significance at 1% level.

Table 3 reports the findings of our oil–agriculture model. The results suggest that for each of these two markets, past returns can be used to forecast the current returns. This result indicates the short-term predictability in both markets. In addition, we find that lagged oil returns have a significant impact on agriculture market. This finding is not surprising, since the agriculture sector is sensitive to changes in the cost of inputs and oil is one of the major production inputs. Thus, variations in crude oil market are likely to account for any possible changes in agricultural commodity prices. Now, the findings of the variance equations reveal that the agriculture market does not receive volatility from the global oil market and vice versa. Moreover, we do not find any evidence of shock transmission between these markets. Most probably, the agriculture sector has developed appropriate hedging strategies which limit the effects of adverse oil price movements. Furthermore, both the commodity as well as oil markets are affected by their own one-period lagged news and volatility. Such outcomes indicate strong GARCH effects in these markets.

The results of the oil–metal model are reported in Table 4. Reviewing these outcomes shows that current oil returns are significantly affected by the past oil returns, whereas this is not the case for metal market. Furthermore, the past oil returns have significant and positive impacts on the current returns of the metal market. This finding is consistent with that reported by Zhang and Tu (2016) who document that changes in oil prices will affect the costs of the production process directly, further resulting in the changes of metal prices. One interesting output is that past metal returns cannot forecast the current returns in metal market. With reference to the conditional variance equation, the findings confirm that there exists a unidirectional volatility transmission from oil to metal market. This volatility linkage could be attributed to the high degree of oil usage in metal markets. Besides, crude oil affects the metal industry due to transportation costs as well. The significant coefficient on ${\mathit{\epsilon }}_{o,t-1}^2$ further reveals that metal market returns are affected by the news stemming from the oil market. We also document that both oil and metal markets are substantially influenced by their own-lagged news as well as own past volatility.

Table 5 displays the outcomes of our third and final model which includes the oil and aggregate non-energy commodity markets. These findings document that past returns are useful for the prediction of current returns in both oil and aggregate markets. Such findings designate the short-term predictability in both markets. Surprisingly, the current aggregate non-energy commodity returns are not significantly affected by the lagged returns on the oil market. This finding is consistent with that obtained by Ji and Fan (2012) who report that returns on aggregate market are mainly dependent on their own past values. Such price spillover results confirm that the oil market is more strongly associated with the agriculture and metal markets, while it does not have firm relationship with the aggregate market. The results of our empirical analysis further confirm that oil market volatility significantly transmits to the corresponding commodity index implying that such market is highly oil-intensive and hence oil price volatility affects the aggregate non-energy commodity returns. In addition, we do not find any sign of shock and volatility spillover from the non-energy commodity market to the crude oil market. Furthermore, like the previous two models, the own-lagged news and own past volatility seem to affect the current volatility of oil and aggregate non-energy commodity markets.

To sum up, the results of our empirical investigation suggest significant mean and volatility transmission from the oil market to most of the commodity markets under study. Such volatility cross-effects might be useful for investors and traders participating in these markets for their optimum asset allocation and hedging decisions. It is also noteworthy that compared to the effects of own-lagged shocks and volatilities, the amount of cross-market shocks and volatilities is reported to be much smaller. These findings reveal that the impacts of own past news as well as volatility are more important in predicting current volatility in the oil and commodity markets.

5.3. Time-varying correlation analysis

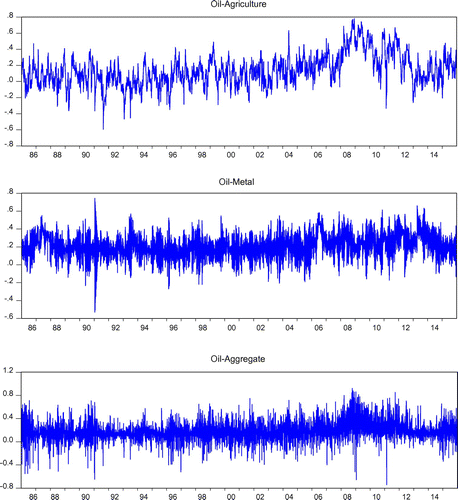
We now discuss the time-varying correlation between oil prices and non-energy commodity market returns. Figure 2 presents the time-varying plots for the considered sample period. Additionally, we report the descriptive statistics of the correlation series in Table 6.

Table 6. Descriptive statistics of time-varying correlations

	Agriculture	Metal	Aggregate
Mean	0.137600	0.207388	0.183717
Median	0.117615	0.206970	0.164480
Maximum	0.783139	0.743472	0.921721
Minimum	−0.593876	−0.530356	−0.742010
Std. dev.	0.193498	0.143393	0.148395
Skewness	0.474424	−0.079192	0.309573
Kurtosis	3.447998	3.258070	6.241869

On the whole, our results suggest that the mean correlations are positive for all the series under investigation. However, the correlations between oil prices and various non-energy return indices do change over time indicating that such correlations are not constant. Although the plots shown in Figure 5 behave differently, they share a common feature in the way that all these correlations swing in both positive and negative levels. Besides, the numbers exhibited in Table 6 indicate high volatilities in the time-varying correlation between oil price changes and different non-energy price indices under study. This latter finding is not surprising, since the agricultural as well as the metal sectors are highly sensitive to oil price fluctuations.

Figure 5. Time-varying correlations between oil and different non-energy markets.

5.4. Economic implications of the results

The results of our bivariate VAR(1)-GARCH(1,1) model can be used to examine whether oil price risk can be hedged effectively against the adverse movements in commodity price. Suppose, an investor is holding a portfolio of commodity assets and he would like to assess whether investing in oil market could reduce the risk of the resulting portfolio. Following Kroner and Ng (1998), the optimal portfolio weight can be constructed as follows:

(5) $${\mathit{\omega }}_t^{\text{co}}=\frac{h_t^c-h_t^{\text{co}}}{h_t^o-2h_t^{\text{co}}+h_t^c}$$(5)

and,

$${\mathit{\omega }}_t^{\text{co}}=\left\{\begin{array}{cc}0,\hfill & \text{if}{\mathit{\omega }}_t^{\text{co}}<0\hfill \\ {\mathit{\omega }}_t^{\text{co}},\hfill & \text{if}0\le {\mathit{\omega }}_t^{\text{co}}\le 1\hfill \\ 1,\hfill & \text{if}{\mathit{\omega }}_t^{\text{co}}>1\hfill \end{array}\right.$$

where ${\mathit{\omega }}_t^{\text{co}}$ indicates the weight of commodity in a one-dollar portfolio consisting of crude oil and commodity at time t, $h_t^c$ and $h_t^o$ are the conditional variances of commodity and oil markets, respectively, and $h_t^{\text{co}}$ refers to the covariance term between commodity and oil returns at time t. The weight for the non-energy commodity market is given by $(1-{\mathit{\omega }}_t^{\text{co}})$.

Additionally, we use our results to compute optimal hedge ratios for the portfolios considered. According to Kroner and Sultan (1993), to minimize the risk of a portfolio, an investor should short β_t dollar in the commodity market which is one dollar long in the oil market, where β_t is given by

(6) $${\mathit{\beta }}_t^{\text{co}}=\frac{h_t^{\text{co}}}{h_t^c}$$(6)

Table 7 reports the average values of optimum portfolio weights $({\mathit{\omega }}_t^{\text{co}})$ and hedge ratios $({\mathit{\beta }}_t^{\text{co}})$. The outcomes suggest that the optimal weights vary from 4% for aggregate non-energy commodity market to 11% for agricultural product market. Such results imply that for a $1 portfolio, on average 11 cents should be invested in the oil market and the remaining 89 cents should be invested in the agricultural product market. For the metal market, these weights are 9 and 91%, respectively. We hence document that investors holding assets in commodity markets should invest more in commodities than in oil with a view to minimizing the portfolio risk without reducing the expected return.

Table 7. Portfolio weights and hedge ratios

Portfolio	${\mathit{\omega }}_t^{\text{co}}$	${\mathit{\beta }}_t^{\text{co}}$
Panel A: time-varying
Agriculture/Oil	0.11	0.43
Metal/Oil	0.09	0.45
Aggregate/Oil	0.04	0.63
Panel A: constant
Agriculture/Oil	0.12	0.41
Metal/Oil	0.09	0.49
Aggregate/Oil	0.02	0.78

Notes: The findings in Panel A show the average optimal portfolio weights along with hedge ratios calculated from time-varying moments, while the outcomes in Panel B simply indicate the constant weights and hedge ratios computed from unconditional moments. We use data from WTI to present the oil asset, while several S & P GSC spot series are considered to represent the commodity prices.

The average values of the hedge ratios, on the other hand, tend to be high for all the portfolios. These findings reveal that hedging does not seem highly effective in the non-energy commodity markets considered in this study. For example, a $1 long position in oil can be hedged for 45 cents with a short position in the metal market. These results are inconsistent with those reported by Ewing and Malik (2013) who show that oil can be used as an effective hedge against the adverse movements in gold price.

It is notable that Table 7 also indicates the constant weights and hedge ratios computed from unconditional moments. These results, shown in Panel B, are quite similar to those documented in Panel A, albeit the hedge ratio values do vary slightly.

6. Robustness test

In order to assess the robustness of the results obtained from the VAR-GARCH approach, we also apply the bivariate VAR-AGARCH model proposed by McAleer et al. (2009). The bivariate model assumes the following form:

(7) $$h_t^c=d_c^2+b_{11}^2{h}_{t-1}^c+b_{21}^2{h}_{t-1}^o+a_{11}^{2}A{({\mathit{\epsilon }}_{c,t-1})}^2+a_{21}^{2}A{({\mathit{\epsilon }}_{o,t-1})}^2+B[({\mathit{\epsilon }}_{c,t-1})\times (({\mathit{\epsilon }}_{c,t-1})<0)]$$(7)

(8) $$h_t^o=d_o^2+b_{12}^2{h}_{t-1}^c+b_{22}^2{h}_{t-1}^o+a_{12}^{2}A{({\mathit{\epsilon }}_{c,t-1})}^2+a_{22}^{2}A{({\mathit{\epsilon }}_{o,t-1})}^2+B[({\mathit{\epsilon }}_{o,t-1})\times (({\mathit{\epsilon }}_{o,t-1})<0)]$$(8)

Within this framework, A(ε_c,t − 1)² and B[(ε_c,t − 1) × ((ε_c,t − 1) < 0)] along with A(ε_o,t − 1)² and B[(ε_o,t − 1) × ((ε_o,t − 1) < 0)] signify the relationship between a market’s volatility and own-lagged positive as well as negative returns, respectively.

Table 8 displays the results of our bivariate VAR-AGARCH model. It is interesting to note that the findings of this table mirror those exhibited in Tables 3–5. That is, we still find a significant volatility linkage between global oil and metal market return indices. In addition, consistent with the previous results, we do not report any sort of volatility spillover effect between oil and agricultural commodity markets. The results further indicate that the multivariate asymmetric effects are mainly significant for the non-energy commodity market returns. Besides, positive return innovations affect volatility more than negative shocks, as evidenced by corresponding size of the coefficients. We conclude that our findings are quite robust, since they are not sensitive to various bivariate GARCH models considered in our empirical analyses.

Table 8. Results of VAR-AGARCH model

Independent variable	Agriculture	Oil	Metal	Oil	Aggregate	Oil
$r_{t-1}^c$	0.0456 (0.00)***	0.0119 (0.44)	−0.0128 (0.29)	−0.0093 (0.67)	0.0445 (0.00)***	−0.00231 (0.43)
$r_{t-1}^o$	−0.0084 (0.06)*	−0.0286 (0.02)**	0.0106 (0.02)**	−0.0304 (0.00)***	−0.0008 (0.21)	0.0093 (0.49)
A(εc,t-1)^2	0.0647 (0.00)***	0.0225 (0.03)**	0.0523 (0.00)***	0.0076 (0.25)	0.1255 (0.00)***	0.0002 (0.18)
A(εo,t-1)^2	0.0001 (0.13)	0.0821 (0.00)***	0.0005 (0.08)*	0.0745 (0.00)***	0.0246 (0.02)**	0.1331(0.00)***
B[(εc,t-1) × ((εc,t-1) < 0)]	0.0222 (0.00)***		0.0328 (0.00)***		0.0204 (0.00)***
B[(εo,t-1) × ((ɛo,t-1 < 0)]		0.0023 (0.75)		0.0117 (11)		0.0082 (0.02)**
$h_{t-1}^c$	0.9358 (0.00)***	0.0002 (0.17)	0.9627 (0.00)^***	0.0007 (0.23)	0.8466 (0.00)***	0.0001 (0.69)
$h_{t-1}^o$	0.0138 (0.30)	0.9123 (0.00)***	0.0180 (0.02)**	0.9166 (0.00)***	0.0052 (0.00)***	0.8300 (0.00)***

Notes: The results of this table assess the robustness of our initial findings. $r_{t-1}^c$ refers to the return on non-energy commodity market at time t − 1 and $r_{t-1}^o$ denotes the same for oil market. $h_{t-1}^o$ measures the conditional variance of the oil market at time t − 1 and $h_{t-1}^c$ indicates the conditional variance for different non-energy commodity markets at time t − 1. The squared error terms ${\mathit{\epsilon }}_{c,t-1}^2$ and ${\mathit{\epsilon }}_{o,t-1}^2$ measure the effects of unexpected news or shocks in non-energy commodity and oil markets, respectively. The values in parentheses denote the p-values.

* Indicate statistical significance at 10% level.

** Indicate statistical significance at 5% level.

*** Indicate statistical significance at 1% level.

7. Conclusion

In this paper, we study the mean and volatility transmission mechanism between global oil and non-energy commodity markets. Three different non-energy commodity price indices are used to serve our purpose. These include agriculture, metal, and aggregate non-energy commodity return series. At the empirical stage, we employ the bivariate VAR-GARCH model to estimate the volatility spillover effects. This VAR-GARCH model has been preferred over other popular multivariate GARCH models such as BEKK specifications, since the former produces more accurate results in terms of portfolio diversification and hedging effectiveness (Arouri et al., 2011). Besides, the VAR(1) version of BEKK has not theoretically been analyzed as well (Hammoudeh et al., 2009). Taking all these issues into account, we consider the application of the VAR-GARCH approach in our empirical investigation.

The findings of the present study reveal that volatility is significantly transmitted from global oil prices to most of the non-energy commodity indices considered. More specifically, we report that both metal and aggregate non-energy commodity indices are the recipients of volatility from the oil market. We do not find any evidence of volatility cross effects between oil and agriculture price indices. It is likely that the agriculture sector is insulated from the influence of oil market shocks and volatility. In order to check the robustness of our results, we also employ the asymmetric VAR-GARCH (VAR-AGARCH) model. Our findings are robust, since the employed methods lead to similar conclusions.

We extend the prior literature in several aspects. First, while earlier studies mainly examine the possible link between oil and commodity returns and little attention has been paid to the volatility linkage between these two markets, this study aims to contribute to the standing literature by assessing the association between the second moments of oil and non-energy commodity markets. Investigating the volatility spillover effects between these two markets is often important for building precise models in order to forecast future return and volatility of both markets. Second, we apply two recently developed bivariate VAR-GARCH methods which are quite advantageous for studying the mean and volatility linkages between the markets under consideration. Third, the results obtained by employing the VAR-GARCH model are useful to address important issues regarding optimal portfolio allocation and hedging strategies.

Moreover, the outcomes of our analysis carry important implications for investors and policymakers. For instance, the volatility transmission relationships between oil and non-energy commodity markets might help the financial market participants to make optimum portfolio allocation decisions. The findings could be useful for predicting the financial market return volatility as well.

Further, we report that oil price and agricultural product price are independent of each other and hence agriculture policies should be independent and policy-makers should take into account the detachment of energy and agriculture policies. In addition, metal industry policymakers could utilize our results for finding better strategies or schemes to minimize the impacts of oil market uncertainty. One possible policy is to promote the use of alternative energy or bioenergy. In order to increase the practice of such environmentally friendly energies, governments in different oil-intensive economies can tax the fossil fuel usage. Sadorsky (2012), for instance, argue that fossil fuel consumption taxes and carbon taxes should help reduce the impact of oil price risk on the financing and investment activities of renewable energy companies. Additionally, governments could benefit from building their strategic petroleum reserves, as the oil reserve is essential for those countries which are highly dependent on imported oil (Zhang & Tu, 2016). Taking all these measures into account might help the metal and agricultural industries to limit the effects of global oil price shocks.

Funding

The authors received no direct funding for this research.

Additional information

Notes on contributors

Anupam Dutta

Anupam Dutta is working as an assistant professor in the Accounting & Finance Department of Vaasa University (Finland). He completed his PhD in May 2015 in the field of Financial Economics. In his doctoral thesis, he has proposed a new approach to measure long-run anomalies after corporate events such as IPOs, SEOS. He has a number of publications in the area of long-run event studies and energy finance. His other research interests include energy market volatility, financial market integration, and asset pricing.

Md Hasib Noor

Md Hasib Noor is presently working as an assistant professor in the Faculty of Engineering, American International University Bangladesh. He has published several articles in the field of volatility transmission among financial markets. His current research areas include energy economics and financial market integration.