Empirical measures of symmetry of market sentiments

Abstract

The analysis of asset return series of equity prices and stock indices is a well-researched problem tackled by economists, business and financial analysts in the last few decades. It has captured the fancy of financial economists, global and local portfolio investment consultants, foreign investment institutions and the trading man in the street. In this paper a strong case is made to follow a new approach for any investor to foray into an unknown stock market. This approach is the market sentiment approach. We introduce the concept of market sentiments, their definitions and different constructs one may propose vis-a-vis asset return series. We formulate several concepts of symmetry of market sentiments and propose empirical measures to validate such types of symmetric market sentiments. The efficacies of these measures are evaluated using extensive simulation studies and the efficient measures are identified. As an application, we explore the nature of absolute market sentiments that prevailed in weekly mean asset returns of two domestic companies registered in Botswana Stock Exchange during the trading period: 4 January 2016 to 30 December 2016. Our analysis indicates that both companies are characterised by the presence of complete symmetric absolute market sentiments.

Keywords:

• asset return series
• classification rules
• equity prices
• empirical measures
• market sentiments
• concept of symmetry

JEL classifications:

• C 19
• G13
• G 14

Public Interest Statement

Many financial data analyses are focused on prediction of the future prices of security and as such are model based strategies. It is believed that security prices exhibit considerable variations from time to time and these variations can be captured by well-defined market volatility phenomena. Researchers in financial data analysis followed the classical approach when dealing with stock return volatility from an investor’s perceptive. However, the existing approaches and analyses are a natural follow-up once the investor has entered the market and these approaches are relevant to an investor “post-market-entry”. The questions of substantive interest are “What drive a prospective investor into a market?” “What should be the guiding principles that help a prospective investor to enter into a market?” This paper attempts to address these questions by introducing the concept of “market sentiments” and advance some formulations and theories vis-à-vis the new concept. We formulate several concepts of symmetry of market sentiments and corresponding empirical measures. The efficacies of these measures are evaluated using extensive simulation studies.

1. Introduction

Suppose that we have a financial time series data denoted by $\left\{X_t\right\},t=1,2,\dots$. In a classical financial data analysis approach a researcher is primarily concerned with modelling and the related inferential problems such as the estimation of the parameters of the model, tests of hypotheses about the parameters, forecasting the future value of the time series and testing the adequacy of the fitted model etc. The analysis of financial data has been a well-researched problem tackled by economists, business and financial analysts in the last few decades. There have been several approaches to the analysis of financial data. Notable among these, from a statistical point of view, are those based on the theories of multiple regression and time series analysis.

The natural up and down patterns of the daily stock prices are indicative of the stochastic nature of the financial markets. Despite such price movements investors risk their funds in the stocks with the expectation of making more future returns. The variation in the stock returns due to daily price changes is generally termed as volatility that is measured by the standard deviation of the returns. Investors in stock market are interested in the volatility of stock prices as high volatility could be interpreted as huge losses or profits at the expense of greater uncertainty (Gujarati, 2003). Volatility is something good but that can only be bad if the stock price swings are unusually very high and rapid over short time periods as it makes financial planning difficult (Islam, 2013). This means that high fluctuations in stock prices can possibly increase both risk and uncertainty about the future returns. Since prediction of stock is part and parcel of stock trading, if the market performance is unstable then investors will be clueless as what the future holds for them and hence increased uncertainty about future price changes. As a result of uncertainty investors can fear to take risk and continue to fund their investments.

A volatile market inhibits individual retailers and companies to raise funds in the capital markets. Islam (2013) cited that uncertainty causes loss of investor confidence that is essential in trading of stocks particularly in encouraging further investment and leverage decision. He further mentions that uncertainty can aggravate volatility. The knowledge of volatility is of crucial importance in many areas of finance in enabling investors to manage risks and optimise profits (Hull, 2003). The fluctuations in the asset prices are widely believed to be the cause of changes in the economic and geo political environmental factors such as stocks, bonds, exchange rates, tradable options and banking instruments among others. The perceived knowledge of the aforementioned contributing factors along with analysis of data gives a player in any stock market a strong and reliable tool to trade.

Most of the financial data analyses are focused on prediction of the future prices of security and as such they are model-based strategies. These models can be understood and serve the needs of well-informed market players on ground that includes individual investors, financial institutions and mutual fund managers. These market players are well grounded in a market and exercise their trading options from time to time possibly guided by predictions of how well stocks are performing or going to perform in the near future. It is widely believed that security prices exhibit considerable variations from time to time and these variations can be objectively captured more or less by well-defined market volatility phenomena. The concept of volatility is imperative in the analysis of financial time series data. Broadly speaking, it is the unpredictable change of a variable over time. In the context of finance and economics, volatility refers to the unstable states of economic and financial variables, these variables include, stock prices, exchange rates, inflation rates, volume of trade, currency returns etc. Generally speaking, volatility could be defined as the changeability of the market trends. Another approach followed by many researchers in financial data analysis is to deal with stock return volatility from an investor’s perceptive. In some of the studies related to this approach, researchers preferred to use the terminology investor sentiment rather than the “market sentiment”. It is pertinent to point out that the existing approaches and analyses are a natural follow-up once the investor entered the stock market and assumes the role of an active stakeholder. In a sense, these approaches are relevant to an investor “post-market-entry”. The questions of substantive interest one may ask then are: “What drives a prospective investor into a market?” “What should be the guiding principles that help a prospective investor to enter into a market?” In this paper, an attempt is made to address these questions by introducing the concept of “market sentiments” and advance some formulations and theories vis-à-vis the new concept.

In the new approach suggested here volatility in stock returns is conceived in terms of suitable function of the observed data and then based on this function, it is classified into market sentiments. A fairly accurate knowledge of such states of market sentiments in asset returns will be of great help to a prospective investor to foray into a stock market and become part and parcel of active stock traders.

1.1. Objectives and implications of the study

A usual assumption in applying GARCH type models to financial data is that the conditional return series is conditionally normally distributed. In practice, however, the shape of the daily distribution of return series is much broader than the commonly assumed Gaussian distribution. Some alternatives have been applied in the likes of truncated Levy distribution, Student’s distribution and log normal distribution among others. For comprehensive application of GARCH models to these distributions we refer to Bouchaud and Potters (2003). Gourieroux (1997) made some observations that the applications of standard GARCH models to stock returns would produce good estimation results under stable market conditions, but often fail to fully capture the heavy tails commonly observed in asset return series. Conventional asset allocation frameworks typically make a range of assumptions about the normality of asset returns. Empirically, Sheikh and Qiao (2010) observed that in many cases returns are not independent, and in all cases they are not normally distributed. It follows that there is need for alternative measures that will capture the non-normality of the market returns in order to minimise inaccuracies in estimation of portfolio risk. Investors and traders should be supplied with accurate information regarding their investment portfolios. Fund managers must rely on correct statistics to advise them. As such, this forms the basis for our paper. It is pertinent that we do not assume any specific form of the probability distribution for stock return series. Thus, we adopt a nonparametric approach to pursue the objectives of our study.

The major contribution of this paper is that it suggests an alternative approach for modelling and related analysis of stock returns. In the new approach suggested here volatility in weekly means of stock returns is conceived to be a function of the mean and its standard error and the perceived volatility is classified into various market sentiment states. Thus a fairly accurate knowledge of such states of volatility in stock returns will be of great help to a prospective or an existing market player in assessing their investment portfolios. The main objectives of the paper are as follows:

(i)	To advance the notion of market sentiment as a propelling mechanism for a prospective investor to rely on before entering into a stock market.
(ii)	To appreciate the distinction between absolute and relative market sentiments that govern stock return data.
(iii)	To devise suitable data driven rules to classify volatility in stock returns into market sentiment states.
(iv)	To propose different patterns of market sentiments that prevail in a stock market.
(v)	To construct different empirical measures of symmetry of market sentiments.
(vi)	To run simulation studies to compare the efficacy of proposed measures.

The implications of the current work are many folds. A few among these are stated below:

(i)	The results in this paper indicate an alternative approach to analyse financial data, namely, the market sentiment approach, as opposed to the volatility approach that is in vogue.
(ii)	The proposed approach and measures are robust in the sense that they are non-parametric in character as they do not depend on the underlying probability distribution of the data.
(iii)	It is established that normed measures among the proposed different measures have high efficacies and deemed to be efficient to analyse market sentiments.
(iv)	Any decision-making that an investor takes on to enter the stock market is heavily dependent on the direction of the market sentiments. Signed norm measures proposed in this paper are geared to assist in decision-making and future planning of investment portfolio.
(v)	Due to the novelty of the proposed approach, it is hoped that the line of analysis suggested here will be of interest to both academicians and stock market players.

To the best of our knowledge, no attempt seems to have been made to define market sentiments in precise quantitative terms and analyse those using the empirical approach advocated in this paper.

The rest of the paper is organised as follows. In Section 2, we provide a literature review detailing the classical approach to volatility studies and our own market sentiment approach. The Section 3 deals with the main contributions of this article. This section includes the definitions of absolute and relative market sentiments, their constructs for a typical equity index data, types of market sentiments and their measures and the related properties of these measures. Sections 4 and 5 discuss the performance of the measures of equi-symmetry and complete-symmetric market sentiments in terms of extensive simulation studies. In Section 6, using the concepts and the measures we developed in this paper, we examine the weekly market sentiments of stock prices for the period: 4 January 2016 to 30 December 2016 of two typical domestic companies registered under Botswana Stock Exchange (BSE). Some general conclusions are outlined in Section 7.

2. Literature review

The literature on economic and financial variable data analysis is indeed quite extensive. Forecasts of the distribution of such variables like asset returns are of great importance in the context of financial risk management. In pricing options, anticipated volatility over the life of the option is the crucial unknown parameter. One of the most popular tools used to explain volatility clustering in option pricing is the Auto-Regressive Conditional Heteroscedasticity (ARCH) class of models which was invented by Engle in 1982. The theoretical frame work of modelling volatility advocated by Engle captures the time-variability of the variance of returns by imposing an autoregressive structure on the conditional second moment of returns. Over the years there have been a number of extensions to the basic ARCH model. The most important of these is the generalised ARCH (or GARCH) model developed by Bollerslev in 1987 which includes lagged values of the conditional variance as extra regressors. Subsequently, many other ARCH-type processes have been developed to capture various dynamics. For additional references and expository studies using ARCH type of models and also for exhaustive theoretical treatment of volatility models, we refer to Blake (2005) and Sheldon (1994).

Generally, market sentiments are perceived to be either absolute or relative. Absolute market sentiments can be defined with reference to a base period greater than a month such as a quarter or bi-annual or annual. In this case, market sentiments are constructed based on the entirety of data corresponding to the base period. For example, the weekly market sentiments can be constructed based on the daily stock prices of a given year. It may be pointed out that absolute market sentiments are useful to compare the movements in market sentiments over blocks of years and hence may be of use to players with long-term interest. In other words, absolute market sentiment captures the long- term impact on volatility. Relative market sentiments are defined with reference to shorter base period such a week or month. In this case, market sentiments are more dynamic in the sense that constructs compare weekly or monthly data from time to time. Relative market sentiments are seen to be useful to an active player with short-term interest. A large share of overall movement of an individual stock has been attributed to market sentiments. Forecasting market sentiments in financial data such as stock indices, volume of trade is a formidable area of research in financial economics. There are innumerable causes, as mentioned earlier, that propel market sentiments in a financial data. Classically, market sentiment is monitored by a variety of technical and statistical methods such as the number of advancing vs. declining stocks and new highs vs. new lows comparisons.

There are multiple of studies dealing with stock return volatility from an investor’s perceptive. In most of these studies, researchers preferred to use the terminology investor sentiment rather than the “market sentiment”. For the sake of completeness, we outline a few of these, keeping in mind that none of these studies follow the approach that is advocated in this paper.

Within the scope of behavioural finance, many studies have gone on to analyse factors relating to the mentality of investors, chief among others being volatility. An exhaustive review of the prior studies based on the role of market sentiments in the financial markets was investigated by Shiller (1999) who examined the behaviour of investors in the financial markets; Hirshleifer and Shumway (2003) demonstrated, from the psychological point of view, that since investors have acute shortage of information, investor sentiment is a factor for consideration in the formulation of any investment strategy. In other words, when investors lack complete information regarding their investment, they tend to make their choices based on unreasonable behaviour and personal considerations.

Lee, Jiang, and Indro (2002) investigated the relationship between volatility, stock returns and investor sentiments. They applied a GARCH-in-mean model which includes contemporaneous shifts in investor sentiment in the mean equation and lagged shifts in investor sentiment in the conditional volatility variance equation. They used the survey indicators provided by investors’ intelligence to examine the impact of changes in investor sentiment on the conditional volatilities and indices. They made observations that bullish (bearish) changes in investor sentiment result in downward (upward) adjustments in volatility.

Wang, Keswani, and Taylor (2006) and Lee et al. (2002) showed that the index of investor sentiment has no predictive power in the stock market return, or at best very limited ability. This has not diluted the appeal by the majority of studies. Within the prior studies by Brown (1999), Fisher and Statman (2000), Lee et al. (2002), Baker and Wurgler (2004), Baker and Stein (2004), Brown and Cliff (2004), and Lee and Kumar (2006) tend to agree that there is correlation between the investor sentiment index and stock market returns, and this could be used to predict the index of return within the stock market. Yoshinaga and de Castro (2012) estimated a pricing model that relates stock rate of return to market sentiment index and other factors and the results confirm that the sentiment variable plays a relevant role.

Recently, Rao and Moseki (2009) advocated a new approach based on the market sentiments to analyse financial data rather than the traditional approach based on volatility measures. According to them, the market sentiment is the general prevailing attitude of the market that enables investors as to the anticipated price development in a market. Thus, market sentiment is inbuilt in any financial data subject to volatility. The volatility in asset prices naturally manifests in several layers of price movements; called market sentiment states. For example, if there is an upward price movement in the stock market, the sentiment is said to be bullish. On the contrary, if the market sentiment is bearish, it is natural to expect downward price movement. Thus market sentiments may be construed as the manifestation of intense volatility into perceptible categories and this leads to a possible definition of market sentiment as perceived in this article as some kind of partitioned market volatility or some kind of transformation of the underlying continuous distribution of the asset return series into discrete multinomial distribution.

A large share of overall movement of an individual stock has been attributed to market sentiment. Many traditional econometric methods forecast asset returns by a point prediction of volatility.

According to researchers, the market sentiments approach as an alternative to volatility model approach can be either empirical or probabilistic. The purpose of this paper is to focus on the first approach, namely the empirical approach, in which no assumptions are made on the process which generates the daily financial data i.e. the observed data, is assumed to be a realisation of population data on the time axis and the observed data can be grouped into market sentiment states according to certain classification rules. On the other hand, in a probability model-based approach, market sentiment states are assumed to follow a certain discrete distribution. Rao and Moseki (2009) provided the basic idea of analysing financial data in terms of market sentiments. Their approach to market sentiment analysis was probability model based as opposed to the empirical approach considered in this paper. They primarily dealt with relative market sentiments and considered the data on Domestic Company Indices of Botswana Stock Exchange. In this paper, our focus is on absolute market sentiments and the data we consider is the Daily Domestic Company return indices rather than the daily Domestic Company Indices. The exchange rate market sentiments of major global currencies were analysed in Rao and Ramachandran (2014). In these researches the authors primarily considered relative market sentiments and the two probability model based indices, namely chi-square and likelihood ratio, were proposed as measures of symmetric relative market sentiments. Rao and Moseki (2011), Rao and Ramachandran (2016) furthermore demonstrated the Markovian approach to analyse the market sentiments of daily Domestic Company Indices and major global currencies, respectively. In a recent paper, Moseki and Rao (2017) provided few other model-based measures of complete symmetric market sentiments. In the earlier works carried out by Rao and Moseki (2009, 2011), Rao and Ramachandran (2014) and Moseki and Rao (2017), albeit references have been made to absolute and relative market sentiment; but we provide precise definitions of these concepts and provide illustrative examples. Two more types of market sentiments namely, equi-symmetric and partial symmetric market sentiments are introduced in this work besides the complete symmetric market sentiments considered by these authors in their earlier works.

3. Methodology

3.1. Data description

The basic data to be considered here refer to the daily stock price of two domestic companies NAP (New African Properties) and STANCHART (Standard Chartered Bank), registered under Botswana Stock Exchange for the period: 3 January 2016 to 30 December 2016. The absolute market sentiments are calculated for the weeks assuming that each starting and ending weeks in a calendar year have at least two trading days. The movements in stock price log returns are classified in to the five states S₁, S₂, …, S₅ based on the classification rule described by (5). The primary data related to the daily trading of stocks of the two companies can be obtained from the first author. The detailed calculations of weekly averages and standard deviations of weekly stock log returns are not reported in this paper, but may be obtained from the first author on request.

The notations used in this paper are as follows: “n” - total number of days in the study period; “t” - refers to the day; “W” - total number of weeks in a study period; “w” - refers to the week; “P_t”, $t=1,2,\dots ,n$ - the DCI at time “t”; “n_w” - denotes the number of trading days in a week. Here, n_w varies between 1 and 5 in a typical stock trading market. “r_t”, t = 2, … n, DCI log return at time “t”.

The Table 1 displays the time series data related to DCI.

Table 1. The daily domestic company indices and log returns

Day t:	1	2	3	…	t	…	n − 1	n
DCI Pt:	P1	P2	P3	…	Pt	…	Pn−1	Pn
Log return index $r_t=\ell ln\left(\frac{P_t}{P_{t-1}}\right)$	–	$\ell ln\left(\frac{P_2}{P_1}\right)$	$\ell ln\left(\frac{P_3}{P_2}\right)$	…	$\ell ln\left(\frac{P_t}{P_{t-1}}\right)$	…	$\ell ln\left(\frac{P_{n-1}}{P_{n-2}}\right)$	$\ell ln\left(\frac{P_n}{P_{n-1}}\right)$

For analysing weekly DCI returns, for a week w = 1, …, W, we define the weekly average return by ${\overline{r}}_w$ = $\frac{1}{n_w}\sum _{\ell =1}^{n_w}{r}_{\ell }$, and the weekly variance by $s_w^2=\frac{1}{(n_w-1)}\sum _{\ell =1}^{n_w}{\left(r_{\ell }-{\overline{r}}_w\right)}^2$. The combined mean and the variance, are respectively given by ${\overline{r}}_c=\frac{1}{W}\sum _{w=1}^W{n}_w{\overline{r}}_w$ and $S_c^2=\frac{1}{W}\sum _{w=1}^W{n}_w{\left(\overline{r_w}-{\overline{r}}_c\right)}^2$.

3.2. Constructs and types of market sentiments

Market sentiments states can be defined purely on the basis of perceptions. A simple market sentiment analysis that deals with daily trading series may be the one based on the “percentage rise or fall in stock prices”. For example, in a five state market sentiment analysis, we may respectively denote above 10% fall or rise as states 1 and state 5, between 10 and 5% fall or rise as state 2 and 4 and between 5% fall and 5% rise as state 3. As a second example, in a seven state market sentiment analysis, we may respectively denote above 10% fall or rise as states 1 and state 7, between 10 and 7.5% fall or rise as state 2 and 6 and between 7.5 and 5% fall or rise as state 3 and 5 and between 5% fall and 5% rise as state 4.

An alternative simple market sentiment analysis that deals with daily trading series is the one based on the well-known “pivotal theory” (Edwards et al., 2001). In this analysis, current day’s market sentiment is arrived based on the pivot point which is simply defined as the average of high, low and closing prices. In a seven point system, the three sentiments above the pivot point sentiment are classified as “resistance 3” (= high + 2 (pivot-low)), “resistance 2” (= pivot+(high-low)) and “resistance 1” (= 2 pivot-low)). Similarly, the three sentiments below the pivot point sentiments are “support 1” (= 2 pivot-high)), “support 2” (= pivot-(high-low)) and “support 3” (= low- 2 (high-pivot)). Similarly, in a five point pivot system one uses the previous day’s high, low and close, along with two support levels and two resistance levels to derive a pivot point.

The internet portals of financial service providers and newspapers, world over, carry such investor friendly market sentiments for the prospective traders dealing with exchange rates, stocks and shares. Such market sentiments as technical indicators are widely available on a day-to-day basis. While an indicator of market sentiments on a day-to-day basis has its own advantages and limitations, there seems to be very little work done on extending these ideas to capture market sentiments based on weekly and monthly data. The need for studying market sentiments based on the weekly and monthly data are many folds. For example, weekly and monthly sentiments are more stable and provide decisive clues as how the market is responding to the economic variables of interest. Further, they also indicate when to trade and what securities to trade with.

Market sentiments in general can be perceived to be either absolute or relative; depending on the type of the constructs used in their definitions. Absolute market sentiments are designed to capture the overall state of market sentiments of a financial data over a fixed period of time. In other words, absolute market sentiments are defined with reference to a base period which is usually greater than a month such as a quarter or bi-annual or annual. In this case, market sentiments constructs are based on the entirety of data corresponding to the base period. An example would be a study of weekly market sentiments based on the stock prices in a given year. It may be pointed out that absolute market sentiments are useful to compare the movements in market sentiments over a block of years and hence may be of use to players with long term investment interest. On the other hand, relative market sentiments are designed to capture the dynamic state of market as they evolve over a period of time. Thus, relative market sentiments are defined from one period to another with a shorter base period such as a week or a month. In this case, market sentiments constructs are based on weekly or monthly data. Relative market sentiments are seen to be useful to an active player with short term interest.

We give below the definition of absolute and relative market sentiments states for daily return indices.

Definition 3.2.1.

Absolute Market Sentiments

Let ${\Im }_k=\left(S_1,\dots ,S_k\right)$ be a class of states for the daily return indices data-set $\underline{r}=\left(r_2,\dots ,r_n\right)$. Then ${\Im }_k$ is said to be a class of absolute market sentiments states if the state S_i, i = 1, …, k, ⊂ ${\Im }_k$, is induced by a classification rule that compares each r_j, j = 2, …, n in $\underline{r}=\left(r_2,\dots ,r_n\right)$ with a suitable measure constructed using a function of r_j−1 and the entire data-set $\underline{r}=\left(r_2,...,r_n\right)$.

The above definition implies that the absolute market sentiments are generated by simply mapping $\underline{r}=\left(r_2,\dots ,r_n\right)$ into ${\Im }_k=\left(S_1,\dots ,S_k\right)$ using the classification rule R(i) based on its immediate past along with a function of the entire data-set $\underline{r}=\left(r_2,\dots ,r_n\right)$. We give below a few examples of classification rules that generate absolute market sentiments.

Example 3.2.1.

Suppose that k = 3 and $\tilde{r}$ be the range of the data-set $\underline{r}=\left(r_2,\dots ,r_n\right)$ and $f_s\left(r_{j-1},\tilde{r}\right),s=1,2$, be suitable functions of r_j−1 and $\tilde{r}$. Then the states S₁, S₂ and S₃ are said to be absolute market sentiments states if the classification rules corresponding to these states are respectively given by: For j = 2, …, n,

(1) $$R(1)=\left\{r_j<f_1\left(r_{j-1},\tilde{r}\right)\right\},R(2)=\left\{f_1\left(r_{j-1},\tilde{r}\right)\le r_j<f_2\left(r_{j-1},\tilde{r}\right)\right\},R(3)=\left\{r_j\ge f_2\left(r_{j-1},\tilde{r}\right)\right\}.$$(1)

For instance, we may set, $f_1\left(r_{j-1},\tilde{r}\right)=r_{j-1}-\frac{\tilde{r}}{\sqrt{n}},f_2\left(r_{j-1},\tilde{r}\right)=r_{j-1}+\frac{\tilde{r}}{\sqrt{n}}$ in (1) to deduce the classification rule $R\left(i\right)$ that defines the state S_i, i = 1, 2, 3.

Example 3.2.2.

Let T₁, T₂ be respectively suitable measures of central tendency and dispersion of return indices data-set $\underline{r}=\left(r_1,\dots ,r_n\right)$ and $f_i\left(T_1,T_2\right),i=1,\dots ,k$ be suitable functions of T₁ and T₂. Then the data $\underline{r}$ can be partitioned into k states defined by the class ${\Im }_k$ using the following rules of classification: For $j=1,\dots ,n,$

(2) $$\begin{array}{c}R(1):\{r_j<f_1(T_1,T_2)\}\hfill \\ R(i):\{f_{i-1}(T_1,T_2)\le r_j<f_i(T_i{T}_2\},i=2,\dots ,k-1,\hfill \\ R(k):\{r_j>f_k(T_1,T_2)\}\hfill \end{array}$$(2)

We observe that the rule of classification for the data $\underline{r}$ is empirical as it is compared with suitable functions of the return indices data $\underline{r}=\left(r_1,\dots ,r_n\right)$. On the other hand one may have rules of classification which may be purely subjective, for example based percentages. Such an example is provided below:

Example 3.2.3.

Suppose that Y_j denotes the observed percentage increase or decrease in r_j as compared to $r_{j-1},j=2,\dots ,n$. In other words, $Y_j=100\frac{r_j}{r_{j-1}}$. Let p₁, …, p_k be the pre-assigned percentages. Then the data $\underline{r}$ can be partitioned into k states defined by the class ${\Im }_k$ using the following classification rule $R\left(i\right)$ given by:

For $j=2,\dots ,n,$(3) $$\begin{array}{c}R(1):\{Y_j<p_1\}\hfill \\ R(i):\{p_i\le Y_j<p_{i+1}\},i=1,\dots ,k-1,\hfill \\ R(k):\{Y_j>p_k\}\hfill \end{array}$$(3)

Market sentiments based on weekly and monthly return indices can be analogously defined. For example, in a weekly absolute market sentiment analysis, a particular week’s average return indices may be compared based on a measure which is a function of the aggregate mean and standard error of the average weekly return indices of the entire reference period, which can be a one year period or more.

Definition 3.2.2.

Relative Market Sentiments

Let ${\Im }_k=\left(S_1,\dots ,S_k\right)$ be a class of states for the daily return indices data-set $\underline{r}=\left(r_2,\dots ,r_n\right)$. Then, ${\Im }_k$ is said to be a class of relative market sentiments states if the state S_i ⊂ ${\Im }_k$ is induced by a classification rule R(i) that compares each r_j+1, j = 2, …, n − 1 in $\underline{r}=\left(r_2,\dots ,r_n\right)$ with its immediate past along with a suitable measure based on the p-lagged data-set $\underline{r_p^{\ast }}=\left(r_{j-t},\dots ,r_j\right),1\le t\le p$.

Example 3.2.4.

Suppose that k = 3, p = 2 and $\widehat{r}$ and r¹ be respectively the sample median and the range of the lagged data-set ${\underline{r}}_2^{\ast }=\left(r_j,r_{j-1}\right),$ and $f_s\left(\widehat{r},r^1\right),\text{for}s=1,2,3$ be suitable functions of $\widehat{r}$and r¹. Then, ℑ₃ is said to be a class of relative market sentiment states if the classification rules are given by:

(4) $$R(1)=\left\{r_{j+1}<f_1(\widehat{r},r^1)\right\},R(2)=\left\{f_1(\widehat{r},r^1)\le r_{j+1}<f_2(\widehat{r},r^1)\right\},R(3)=\left\{r_{j+1}\ge f_2(\widehat{r},r^1)\right\}.$$(4)

As an illustration of such intervals we may set, $f_1\left(\widehat{r},r^1\right)=\widehat{r}-\frac{r^1}{\sqrt{2}},f_2\left(\widehat{r},r^1\right)=\widehat{r}+\frac{r^1}{\sqrt{2}}$ in (4) to deduce the classification rule $R\left(i\right)$ that defines the state $S_i,i=1,2,3,$ with $\widehat{r}=\text{Median}\left(r_{j-1},r_j\right),r^1=\text{Range}\left(r_{j-1},r_j\right),$provided r_j-1, r_j exist.

Conditional on the given classification rule R(i) and the associated class of states ${\Im }_k=\left(S_1,\dots ,S_k\right)$, k being arbitrary, it is assumed that the observed frequency distribution associated with the weekly return index series $\underline{r}=\left(r_2,\dots ,r_W\right)$, where “W” is the number of weeks in the study period can be represented as in Table 2.

Table 2. Table of states and observed frequencies

States	S1	·	·	·	Si	·	·	·	Sk	Total
Observed frequency	f1	·	·	·	fi	·	·	·	fk	$W=\sum _{i=1}^k{f}_i$

Our primary interest is to analyse observed frequency distribution of market sentiments in terms certain characteristics they might possess. Towards this, we propose a few empirical definitions which characterise states of market sentiments in terms of the observed frequencies of the states.

Definition 3.2.3.

Equi-symmetric market sentiments

A k state market sentiments class ${\Im }_k=\left(S_1,\dots ,S_k\right)$ with the observed data vector $\underline{f}=\left(f_1,\dots ,f_k\right)$, with $W=\sum _{i=1}^k{f}_i=a.k,$ a being an integer is said to be equi-symmetric if and only if $f_i=\frac{W}{k},i=1\dots ,k$.

In case of an equi-symmetric market sentiment states, the market sentiments remain uniform over the period of study. In such a market, the investor has very little opportunity to book profit should he decide to foray into the stock market.

Definition 3.2.4.

Complete-symmetric market sentiments

A k state market sentiments class ${\Im }_k=\left(S_1,\dots ,S_k\right)$ with the observed data vector $\underline{f}=\left(f_1,\dots ,f_k\right)$ is said to be complete-symmetric if and only if $f_i=f_{k-i+1},i=1,\dots ,k$.

In case of a complete-symmetric market sentiment states, the market sentiments states located at equi distant from the middle are symmetric over the period of study. In such a market, the investor has every opportunity to book profit should he decide to foray into the stock market and strike a deal at an appropriate time point.

Definition 3.2.5.

Partial-symmetric market sentiments

A k state market sentiments class ${\Im }_k=\left(S_1,\dots ,S_k\right)$ with the observed data vector $\underline{f}=\left(f_1,\dots ,f_k\right)$ is said to be partial-symmetric if and only if for some predetermined t, $f_i=f_{k-i+1}$, for some $i=1,\dots ,t<k$.

In case of a partial-symmetric market sentiment states, a known number of market sentiments states located at equi distant from the middle are symmetric over the period of study. In such a market, the investor has some opportunity to book profit should he decide to foray into the stock market and strike a deal at an appropriate time point.

Definition 3.2.6.

Degenerate market sentiment

Let $t_j,t_j\in \left\{1,\dots ,k\right\}$ denote the market sentiment state for period j = 1, …, n., Then a k state market sentiment class ${\Im }_k=\left(S_1,\dots ,S_k\right)$ with the observed data vector $\underline{f}=\left(f_1,\dots ,f_k\right)$ is said to be degenerate if and only if $t_j=\frac{\left(k+1\right)}{2},\text{for}\text{all}$ j; when k is odd, or $t_j=\frac{k}{2}\text{or}\frac{\left(k+2\right)}{2},\text{for}\text{all}j;$ when k is even.

In case of a degenerate market sentiment state, there is no movement in sentiment states. In such a market, the investor has no incentive to foray into the stock market.

3.3. The empirical approach to absolute market sentiments

In this paper, our focus will be on absolute market sentiments. In an empirical approach to absolute market sentiments analysis, we assume that either a frequency count of various absolute market sentiment states corresponding to the weekly return indices r_t or a set of classification rules that enable construction of absolute sentiments states is available. To be precise, consider weekly return indices $\underline{r}=\left(r_2,\dots ,r_W\right)$. Let ${\Im }_k=\left(S_1,S_2\dots ,S_k\right)$ be a set of mutually exclusive and collectively exhaustive states. Assume that the data $\underline{r}$ is partitioned into states defined by ${\Im }_k$. We assume that the class ${\Im }_k$ is so formed such that the state S_i is defined according to the classification rule $R(i),i=1,\dots ,k$, where R(i) is a rule that maps $\underline{r}$ into S_i based on a certain well-defined function $f_s(.),s=1,\dots k$ of $\underline{r}$. We say that the state S_i occurs if the $\left(w+1\right)\text{th}$ observation r_w+1, w = 1, …, W − 1, satisfy the rule of classification $R_{i}i=1,\dots k$.

Given the data as in Table 1 of Section 3.2, we shall specify the following classification rules to arrive at ℑ₅, the class of absolute market sentiments with the five states, S₁, …, S₅.

For a week (w + 1), w = 1, …, W − 1, the equity index is said to belong to $$(\text{i})\text{State}{S}_1,\text{if}{\overline{r}}_{w+1}<{\overline{r}}_w-2\frac{s_c}{\sqrt{W}}$$$$(\text{ii})\text{State}{S}_2,\text{if}{\overline{r}}_w-2\frac{s_c}{\sqrt{W}}\le {\overline{r}}_{w+1}<{\overline{r}}_w-\frac{s_c}{\sqrt{W}}$$(5) $$(\text{iii})\text{State}{S}_3,\text{if}{\overline{r}}_w-\frac{s_c}{\sqrt{W}}<{\overline{r}}_{w+1}\le {\overline{r}}_w+\frac{s_c}{\sqrt{W}}$$(5) $$(\text{iv})\text{State}{S}_4,\text{if}{\overline{r}}_w+\frac{s_c}{\sqrt{W}}\le {\overline{r}}_{w+1}<{\overline{r}}_w+2\frac{s_c}{\sqrt{W}}$$$$(\text{v})\text{State}{S}_5,\text{if}{\overline{r}}_{w+1}\ge {\overline{r}}_w+2\frac{s_c}{\sqrt{W}}$$

The different states of market sentiments may be named subject to the perception of the seller in the market. As an example, we prefer to name the states in a five-state market sentiment analysis as follows:

S₁: The bearish sentiment.

This is a state in which the equity index witnesses a significant downward trend, enough to cause frustration to a seller holding stocks. This may lead to an offloading exercise of stocks and undermine investor confidence. Moreover, raising funds from the capital market may be adversely affected.

S₂: The downward/decline sentiment.

This is a state in which the equity index witnesses a gradual fall, enough to sound a warning to an investor. This may lead to an offloading exercise of stocks and may dent investor confidence. Sustained attempts may be needed to raise funds from the capital market.

S₃: The tranquil sentiment.

This is a state in which the equity index witnesses normal swings. The investor continues to be an active player in the stock market. This state may also be called “range bound” or “uncertain”.

S₄: The upward/incline sentiment.

This is a state in which the equity index witnesses a gradual upward swing enough to cause a feeling of encouragement to an investor. The environment for fund raising may be encouraging.

S₅: The bullish sentiment.

This is a state in which the equity index witnesses a significant upward swing; propelling speculation by a seller holding stocks. Further, raising funds from the capital market may be easy.

3.4. Empirical measures of symmetry of market sentiments

Having defined various types of symmetry associated with empirical frequencies of market sentiment states, we propose the following intuitive measures of (i) equi-symmetry (ii) complete symmetry (iii) partial symmetry and (iv) degenerate symmetry. The measures are proposed on intuitive basis by considering the divergence between the empirical frequencies and the hypothesised frequencies under the assumption of underlying type of the market sentiments. These measures will be indicators of various types of market sentiments that may obtain in a typical stock market over time.

3.4.1. Measures of equi-symmetric market sentiments

As measures of equi-symmetric market sentiments we propose the following:

(6) $$ESD{M}_E=\frac{1}{k}\sum _{i=1}^k{\left(f_i-\frac{W}{k}\right)}^2$$(6)

(7) $$ESAD{M}_E=\frac{1}{k}\sum _{i=1}^k\left|f_i-\frac{W}{k}\right|$$(7)

(8) $$ESN{M}_E=\frac{1}{k}\sum _{i=1}^k\left|\frac{k{f}_i}{W}-1\right|$$(8)

(9) $$ESSN{M}_E=\frac{1}{k}\sum _{i=1}^{k}sign\left(\frac{k{f}_i}{W}-1\right)\left|\frac{k{f}_i}{W}-1\right|$$(9)

(10) $$ESSD{M}_E=\frac{1}{k}\sum _{i=1}^{k}sign\left(f_i-\frac{W}{k}\right){\left(f_i-\frac{W}{k}\right)}^2,$$(10)

where the sign function is defined as $sign\left(x\right)=1,\text{if}x>0,=-1,\text{if}x<0,=0,\text{if}x=0.$

We state and prove a few lemmas related to the properties of these measures below:

Lemma 3.4.1.

A class of market sentiment states ${\Im }_k$ is said to be equi-symmetric if and only if

(i) ESDM_E = 0, (ii) ESADM_E = 0, (iii) ESNM_E = 0.

Proof of (i). The if part follows from the fact that in the case of equi-symmetry, by definition 3.2.3, $f_i=\frac{W}{k},i=1,\dots ,k$, so that ESDM_E = 0.

The only if part follows from the fact that$$ESD{M}_E=0\Rightarrow \frac{1}{k}\sum _{i=1}^k{\left(f_i-\frac{W}{k}\right)}^2=0\iff \sum _{i=1}^k{\left(f_i-\frac{W}{k}\right)}^2=0\iff \left(f_i-\frac{W}{k}\right)=0\iff f_i=\frac{W}{k},i=1,...,k.$$

In other words, ${\Im }_k$ is equi-symmetric. □

Proof of (ii) and (iii). The proofs of (ii) and (iii) are similar to the proof of (i).

Lemma 3.4.2.

For a class of equi-symmetric market sentiment states ${\Im }_k$, ESSDM_E = 0 = ESSNM_E.

Proof.

The proof follows from the fact that in the case of equi-symmetry, by Definition 3.2.3, $f_i=\frac{W}{k},i=1,\dots ,k$, so that ESSDM_E = 0 = ESSNM_E.□

Remark 3.4.1. Unlike the measures, ESDM_E, ESADM_E and ESNM_E, the measures ESSNM_E and ESSDM_E do not characterise equi-symmetry. To see this, suppose we take, W = 6, k = 3, f₁ = 1, f₂ = 2, f₃ = 3. Clearly, ESSDM_E = 0 = ESSNM_E, but $f_i\ne \frac{W}{k}=2,i=1,2,3.$ However, in the absence of equi-symmetry these two measures are sensitive to the direction of asymmetry. In a sense, they are measures of non-equi-symmetry rather than the equi-symmetry.

Lemma 3.4.3.

For any class of equi-symmetric market sentiment states ${\Im }_k$, $ESN{M}_E\le ESAD{M}_E\le ESD{M}_E.$

Proof. Consider $ESN{M}_E=\frac{1}{k}\sum _{i=1}^k\left|\frac{k{f}_i}{W}-1\right|=\frac{1}{k}\sum _{i=1}^k\frac{k}{W}\left|f_i-\frac{W}{k}\right|\le \frac{1}{k}\sum _{i=1}^k\left|f_i-\frac{W}{k}\right|=ESAD{M}_E,\text{since}\frac{k}{W}<1.$ Next, to show that ESADM_E ≤ ESDM_E, we let $b_i=f_i-\frac{W}{k},i=1,\dots ,k.$ It is sufficient to show that $\sum _{i=1}^k\psi \left(b_i\right){\text{b}}_i^2\le \sum _{i=1}^k{\text{b}}_i^2.$ We note that $\left|\psi \left(b_i\right){\text{b}}_i^2\right|\le \left|\psi \left(b_i\right)\right|\left|{\text{b}}_i^2\right|\le {\text{b}}_i^2$. The equality in the lemma holds when ${\Im }_k$ is equi-symmetric. Hence the Lemma. □

Lemma 3.4.4.

For any class of equi-symmetric market sentiment states ${\Im }_k$,

$$ESSN{M}_E\le ESN{M}_E,ESSD{M}_E\le ESD{M}_E.$$

Proof.

Consider

$$ESSN{M}_E=\frac{1}{k}\sum _{i=1}^{k}sign\left(\frac{k{f}_i}{W}-1\right)\left|\frac{k{f}_i}{W}-1\right|\le \frac{1}{k}\sum _{i=1}^k\left|sign\left(\frac{k{f}_i}{W}-1\right)\right|\left|\frac{k{f}_i}{W}-1\right|=\frac{1}{k}\sum _{i=1}^k\left|\frac{k{f}_i}{W}-1\right|=ESN{M}_E.$$

The equality holds when ${\Im }_k$ is equi-symmetric. The proof of ESSDM_E ≤ ESDM_E is similar.□

3.4.2. Measures of complete symmetry

We propose the following measures of complete symmetric market sentiments:

Let $r=\frac{k}{2}$ or $r=\frac{k+1}{2}$ according as k is even or odd. As measures of complete symmetric market sentiments we propose the following:

(11) $$CSD{M}_C=\frac{1}{k}\sum _{i=1}^r{\left(f_{k-i+1}-f_i\right)}^2$$(11)

(12) $$CSAD{M}_C=\frac{1}{k}\sum _{i=1}^r\left|f_{k-i+1}-f_i\right|$$(12)

(13) $$CSN{M}_C=\frac{1}{k}\sum _{i=1}^r\left|\frac{f_{k-i+1}}{f_i}-1\right|$$(13)

(14) $$CSSN{M}_C=\frac{1}{k}\sum _{i=1}^r\left|\frac{f_{k-i+1}}{f_i}-1\right|sign\left(\frac{f_{k-i+1}}{f_i}-1\right)$$(14)

(15) $$CSSD{M}_C=\frac{1}{k}\sum _{i=1}^{r}sign\left(f_{k-i+1}-f_i\right){\left(f_{k-i+1}-f_i\right)}^2,$$(15)

where the sign function is defined as $sign\left(x\right)=1,\text{if}x>0,=-1,\text{if}x\le 0,=0,\text{if}x=0.$

We state and prove a few lemmas related to the properties of these measures below.

Lemma 3.4.5.

A class of market sentiment states ${\Im }_k$ is said to be complete symmetric if and only if

(i) CSDM_C = 0, (ii) CSADM_C = 0, (iii) CSNM_C = 0.

Proof of (i). The if part follows by noting that, by Definition 3.2.4, for complete symmetry we have f_i = f_k-i+1, i = 1, \ldots, k so that CSDM_C = 0.The only if part follows from the fact that $$CSD{M}_C=0\Rightarrow \frac{1}{k}\sum _{i=1}^r{\left(f_{k-i+1}-f_i\right)}^2=0\iff {\left(f_{k-i+1}-f_i\right)}^2=0\iff f_i=f_{i-k+1},i=1,\dots ,r.$$

In other words, ${\Im }_k$ is complete symmetric. □

Proof of (ii), (iii). The proofs are similar to the proof of (i).

Lemma 3.4.6.

For a class of complete symmetric market sentiment states ${\Im }_k$, CSSDM_C = 0 = CSSNM_C.

Proof.

The proof follows by noting that, by Definition 3.2.4, for complete symmetry we have f_i = f_k-i+1, i = 1, …, k so that CSSDM_C = 0 = CSSNM_C.□

Remark 3.4.2.

Unlike the measures CSDM_C, CSADM_C and CSNM_C, the measure CSSDM_C and CSSNM_C are not characterising measures of complete symmetry. To see this, suppose we take, W = 11, k = 5, f₁ = 2, f₂ = 3, f₃ = 1, f₄ = 4, f₅ = 1. Clearly, CSSDM_C = 0 = CSSNM_C but f_i ≠ f_6-i = 2, i = 1, 2, 3. However, in the absence of complete-symmetry these two measures are sensitive to the direction of asymmetry. In a sense, these are measures of complete asymmetry rather than the complete symmetry.

Lemma 3.4.7.

For any class of symmetric market sentiment states ${\Im }_k$,

$$CSN{M}_C\le CSAD{M}_C\le CSD{M}_C.$$

Proof.

First, we shall prove that CSNM_C ≤ CSADM_C. We have

$$CSN{M}_C=\frac{1}{k}\sum _{i=1}^r\left|\frac{f_{k-i+1}}{f_i}-1\right|=\frac{1}{k}\sum _{i=1}^r\left|\frac{f_{k-i+1}-f_i}{f_i}\right|=\frac{1}{k}\sum _{i=1}^r\frac{1}{f_i}\left|f_{k-i+1}-f_i\right|\le \frac{1}{k}\sum _{i=1}^r\left|f_{k-i+1}-f_i\right|=CSAD{M}_C.$$

Next, we shall prove that CSADM_C ≤ CSDM_C. Toward this, let c_i = (f_k-i+1 − f_i), i = 1, …, r. It is sufficient to show that ${\sum }_{i=1}^r\psi \left(c_i\right)c_i^2\le {\sum }_{i=1}^r{c}_i^2.$ We note that, $\left|\psi \left(c_i\right)c_i^2\right|\le \left|\psi \left(c_i\right)\right|\left|c_i^2\right|\le c_i^2$. Hence, CSADM_C ≤ CSDM_C. Combining the two parts, the lemma follows. The equality holds when ${\Im }_k$ is complete symmetric.□

Lemma 3.4.8.

For any class of symmetric market sentiment states ${\Im }_k$,

$$CSSN{M}_C\le CSN{M}_C,CSSD{M}_C\le CSD{M}_C.$$

Proof.

The proof is similar to the proof of Lemma 3.4.4. □

3.4.3. Measures of partial symmetry

We propose the following measures of partial symmetric market sentiments:

Let $r=\frac{k}{2}$ or $r=\frac{k+1}{2}$ according as k is even or odd. As measures of partial symmetric market sentiments we propose the following:

(16) $$PSD{M}_P=\frac{1}{t}\sum _{i=1}^t{\left(f_{k-i+1}-f_i\right)}^2+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2$$(16)

(17) $$PSAD{M}_P=\frac{1}{r}\sum _{i=1}^t\left|f_{k-i+1}-f_i\right|+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2$$(17)

(18) $$PSN{M}_P=\frac{1}{t}\sum _{i=1}^t\left|\frac{f_{k-i+1}}{f_i}-1\right|+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2$$(18) (19) $$PSSN{M}_P=\frac{1}{t}\sum _{i=1}^t\left|\frac{f_{k-i+1}}{f_i}-1\right|sign\left(\frac{f_{k-i+1}}{f_i}-1\right)+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2$$(19) (20) $$PSSD{M}_P=\frac{1}{t}\sum _{i=1}^{t}sign\left(f_{k-i+1}-f_i\right){\left(f_{k-i+1}-f_i\right)}^2+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2,$$(20)

where the sign function is defined as $sign\left(x\right)=1,\text{if}x>0,=-1,\text{if}x<0,=0,\text{if}x=0.$

We state and prove a few lemmas related to the properties of these measures below.

Lemma 3.4.9.

For a class of partial market sentiment states ${\Im }_k$,

$$(\text{i})PSD{M}_P=PSAD{M}_P=PSN{M}_P=PSSN{M}_P=PSSD{M}_P.$$

Proof.

By Definition 3.2.5, for partial symmetry we have f_i = f_k-i+1, i = 1, …, t., so that $f_{k-i+1}-f_i=0,i=1,\dots ,t;$ in which case all the measures are identically equal to $\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2.$□

Lemma 3.4.10.

For any class of partial market sentiment states ${\Im }_k$,

$$PSN{M}_P\le PSAD{M}_P\le PSD{M}_P.$$

Proof.

First, we shall prove thatPSNM_C ≤ PSADM_C. We have

$$\begin{array}{c}PSN{M}_P=\frac{1}{t}\sum _{i=1}^t\left|\frac{f_{k-i+1}}{f_i}-1\right|+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2\\ =\frac{1}{t}\sum _{i=1}^t\left|\frac{f_{k-i+1}-f_i}{f_i}\right|+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2\\ =\frac{1}{t}\sum _{i=1}^t\frac{1}{f_i}\left|f_{k-i+1}-f_i\right|+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2\\ \le \frac{1}{t}\sum _{i=1}^t\left|f_{k-i+1}-f_i\right|+\frac{1}{\left(k-2t\right)}\sum _{i=t+1}^{k-t}{f}_i^2\\ =PSAD{M}_P\\ \end{array}$$

Next, we shall prove that PSADM_P ≤ PSDM_P. Toward this, let c_i = (f_k-i+1 − f_i), i = 1, …, t. It is sufficient to show that $\sum _{i=1}^r\psi \left(c_i\right)c_i^2\le \sum _{i=1}^r{c}_i^2.$ We note that, $\left|\psi \left(c_i\right)c_i^2\right|\le \left|\psi \left(c_i\right)\right|\left|c_i^2\right|\le c_i^2$. Hence, PSADM_C ≤ PSDM_C. Combining the two parts, the lemma follows. The equality holds when ${\Im }_k$ is partial symmetric.□

Lemma 3.4.11.

For any class of partial market sentiment states ${\Im }_k$,

$$PSSN{M}_P\le PSN{M}_P,PSSD{M}_P\le PSD{M}_P.$$

Proof.

The proof is similar to the proof of Lemma 3.4.4. □

3.4.4. A measure of degenerate state market sentiments

Let W denotes the number of weeks in a year and $t_w,w=1,\dots ,W;t_w\in \left\{1,\dots ,k\right\}$ denote the market sentiment state corresponding to the week w. A measure of degenerate state market sentiments is given by the following:(21) $$DSM{S}_D=\frac{1}{W}\sum _{w=1}^W{\left(t_w-\frac{k+1}{2}\right)}^2,\text{if}k\text{is odd},$$(21)

(22) $$DSM{S}_D=\frac{1}{W}\sum _{w=1}^W{\left(t_w-\frac{k}{2}\right)}^2\text{or}\frac{1}{W}\sum _{w=1}^W{\left(t_w-\frac{k+2}{2}\right)}^2,\text{if}k\text{is even}$$(22)

The following lemma provides an upper bound for the measure DSMS_D.

Lemma 3.4.5.

For a degenerate market sentiments state,

$$0\le DSM{S}_D\le \left\{\begin{array}{c}\frac{{\left(k-1\right)}^2}{4},\text{if}k\text{is odd}\\ \frac{{\left(k-2\right)}^2}{4}\text{or}\frac{k^2}{4},\text{if}k\text{is even}\text{.}\\ \end{array}\right.$$

Proof.

The proof for lower bound is trivial. Note that t_w = i, for some i = 1, …, k. For example, if t₁ = 2, then for the first week, the sentiment state is “2”, if t₂ = 5; then for the second week, the sentiment state is “5” and so on. Then by Definition 3.2.6, $t_w=\frac{\left(k+1\right)}{2}\text{for all w},$ when k is odd. Further, in the extreme cases, either t_w = 1 or t_w = k for all w = 1, …, W. Substituting for t_w in (21), we have

(23) $$DSM{S}_D=\frac{1}{W}\sum _{w=1}^W{\left(t_w-\frac{k+1}{2}\right)}^2=\frac{1}{W}\sum _{w=1}^W{\left(1-\frac{k+1}{2}\right)}^2\text{or =}\frac{1}{W}\sum _{w=1}^W{\left(k-\frac{k+1}{2}\right)}^2=\frac{{\left(k-1\right)}^2}{4}.$$(23)

On the other hand, when k is even by Definition 3.2.6, we have either $t_w=\frac{k}{2}$ or $t_w=\frac{\left(k+2\right)}{2}$. Using the fact that, in the extreme case, either t_w = 1 or t_w = k for all w = 1, …, W, using (22) we get, when t_w = 1,

$$\begin{array}{c}DSM{S}_D=\frac{1}{W}\sum _{w=1}^W{\left(t_w-\frac{k}{2}\right)}^2\text{=}\frac{1}{W}\sum _{w=1}^W{\left(1-\frac{k}{2}\right)}^2\text{or}\frac{1}{W}\sum _{w=1}^W{\left(1-\frac{k+2}{2}\right)}^2\\ =\frac{1}{W}\sum _{w=1}^W{\left(\frac{k-2}{2}\right)}^{2}or\frac{1}{W}\sum _{w=1}^W{\frac{k}{4}}^2=\frac{{\left(k-2\right)}^2}{4}\text{or}\frac{k^2}{4}.\\ \end{array}$$

Similarly, when t_w = k, $DSM{S}_D=\frac{k^2}{4}\text{or}\frac{{\left(k-2\right)}^2}{4}.$This completes the proof of the lemma. □

Remark 3.4.3.

Note that each of the ten empirical measures of market sentiments (6) to (15) in above is zero when the market sentiments are equi/complete symmetric. A large value of the measure indicates significant departure from equi/complete symmetric market sentiments. These measures can be used to compare prevailing market sentiments with respect to two or more stock prices. For example, given two series of stock prices of company A and B, we say that market sentiments of stock A are more near to equi/complete symmetry than stock B if the corresponding measures for stock A is less than that of stock B and is very close to zero. An advantage with the measures corresponding to (9), (10), (14) and (15) is that these give us an indication of the direction of the drift from the equi/complete symmetric market sentiments. A need for empirical verification of partial symmetry may arise for example, when one wishes to ascertain whether the two extreme market sentiments are symmetric.

Remark 3.4.4.

In the case of each of the five measures of partial symmetry, the first expression in their formulae becomes zero. Therefore, a large value of the first expression indicates significant departure from partial symmetry.

Remark 3.4.5.

Turning to the measure given by (21) and (22), it is seen that for a degenerate market sentiment state, DSMS_D = 0. On the other hand, if the sentiments swing on either side of the normal threshold state, DSMS_D will be significantly different from 0. Thus, the greater the values of DSMS_D, more dispersed are the weekly sentiments from the degenerate state. It is to be noted that the measure DSMS_D is an absolute measure of swings in market sentiments, but fails to measure symmetry of market sentiments. It may appear that in a dynamic market scenario, a degenerate market sentiment may be a hypothetical situation; but more often than not it is a practical reality. As we see in Section 6, in the context of domestic companies registered under Botswana Stock Exchange, there are companies which operate with degenerate market sentiments.

4. Comparison of measures of equi symmetry

In this section, we shall compare the performance of various measures of symmetry proposed in Section 3.4. In particular, we shall discuss the performance of equi-symmetric measures proposed in Section 3.4.1 in terms of a simulation study. We shall consider a five state market sentiments under equi-symmetry and non-equi-symmetry scenarios. In each scenario, the number of weeks$\left(W\right)$will be equal to 50, 100 and 150 weeks. For the equi-symmetry scenario, the following three sets of hypothesised empirical frequency configurations are considered:

(a)	$f_1=10,f_2=10,f_3=10,f_4=10,f_5=10$
(b)	$f_1=20,f_2=20,f_3=20,f_4=20,f_5=20$
(c)	$f_1=30,f_2=30,f_3=30,f_4=30,f_5=30$

In each of the above three cases, it can be seen that all the five measures of equi- symmetry are zero and these values are indicated within brackets of the respective measures in the first column of Table 3. To carry out the simulation, for a given W, and hypothesised empirical frequency configuration, we generate simulated frequency counts of assumed five state market sentiments and compute each of these measures. Then, the process is repeated with a simulation run $\left(N\right)$of 1,000, 2,000 and 5,000 trials. For example, when W = 50, N = 1,000, we generate 1,000 sets of 50 random numbers between 01 and 50 and correspond the numbers between 01 and 10 to state S₁, between 11 and 20 to state S₂, between 21 and 30 to state S₃, between 31 and 40 to state S₅ and between 41 and 50 to state S₅. For each of the simulation run, we compute simulated bias (simulated value of the measure – actual value of measure), mean absolute deviation (MAD) (mean of the absolute deviation between the simulated and the actual value of the measure) and the standard deviation (S.D) (mean of the sum squares of the deviation between the simulated values and the actual value of the measure). The simulated bias and MAD will be the same under the equi-symmetric scenarios. The proposed measures are then compared using the criteria of Bias, MAD and S.D. The results are displayed in Table 3. We can make the following conclusions based on the simulation study as reported in Table 3:

(i)	The dispersion measure ESDME seems to be appreciably biased and it is seen in general that, the bias, MAD and S.D keep increasing with the increase in W and simulation run N. As opposed to this, the signed measure exhibit relatively smaller bias, MAD and the S.D.
(ii)	The absolute dispersion measure ESADME performs better than the measure ESDME but continues to be biased though by a smaller magnitude. However, the bias, MAD and S.D tend to increase marginally with increase in W and N.
(iii)	The normed measure, ESNME has very small bias and MAD; which decrease with increase in N; while S.D decreases with increase in both W and N. Further, it is to be noted that across the values of W and N, the S.D’s are indeed very small.
(iv)	The signed normed measure, ESSNME reports negligible bias and MAD and small S.D; all of which decrease with increase in both W and N. However, while it has smaller bias than the measure ESNME, the corresponding S.D’s are slightly higher than that of ESNME.
(v)	Of the fiver measures proposed here, in terms of the three criteria used, ESNME measure is a natural choice, followed by ESSNME, ESADME. Even though, ESSDME does not perform as well as the others, it has the advantage of detecting the direction of asymmetry in case of the absence of equi-symmetric market sentiments.

Table 3. Simulated values of bias, MAD and S.D of measures of equi-symmetry for equi-symmetric market sentiments

No. of weeks (W)		50			100			150
Measure	Criteria	Simulation run (N)
		1,000	2,000	5,000	1,000	2,000	5,000		1,000	2,000	5,000
ESDME (0)	BIAS	8.0	7.9	8.0	15.6	15.9	15.8		24.3	23.6	24.3
	MAD	8.0	7.9	8.0	15.6	15.9	15.8		24.3	23.6	24.3
	S.D	5.24	5.50	5.64	11.21	11.12	11.19		17.53	16.59	17.28
ESADME (0)	BIAS	2.24	2.23	2.23	3.14	3.17	3.16		3.91	3.86	3.93
	MAD	2.24	2.23	2.23	3.14	3.17	3.16		3.91	3.86	3.93
	S.D	0.82	0.85	0.86	1.20	1.20	1.19		1.47	1.45	1.47
ESNME (0)	BIAS	0.22	0.22	0.22	0.16	0.16	0.16		0.13	0.13	0.13
	MAD	0.22	0.22	0.22	0.16	0.16	0.16		0.13	0.13	0.13
	S.D	0.08	0.08	0.09	0.06	0.06	0.06		0.05	0.05	0.05
ESSAME (0)	BIAS	−0.02	−0.03	−0.03	−0.023	−0.020	−0.020		−0.011	−0.008	−0.018
	MAD	0.02	0.03	0.03	0.023	0.020	0.020		0.011	0.008	0.018
	S.D	0.23	0.23	0.21	0.23	0.23	0.23		0.23	0.23	0.24
ESSDME (0)	BIAS	0.37	0.45	0.44	0.71	0.59	0.68		0.75	0.60	0.72
	MAD	0.37	0.45	0.44	0.71	0.59	0.68		0.75	0.60	0.72
	S.D	2.30	2.40	2.39	4.86	4.85	4.71		7.14	6.88	7.01

Next, turning to the non-equi-symmetric market sentiment scenario, the following three sets of hypothesised empirical frequency configurations are considered:

(a)	$f_1=20,f_2=4,f_3=2,f_4=4,f_5=20$
(b)	$f_1=20,f_2=10,f_3=40,f_4=10,f_5=20$
(c)	$f_1=20,f_2=25,f_3=30,f_4=35,f_5=40$

The three sets of scenarios considered have the presence of non-equi-symmetry in varying magnitude. It can be verified that for the cases (a), (b) and (c) indicated above, the computed values of these measures respectively are given below and these are indicated within brackets of the respective measures in the first column of Table 4.$$ESD{M}_E=67.2,ESAD{M}_E=8.0,ESN{M}_E=0.8,ESSN{M}_E=0,ESSD{M}_E=128.8,$$$$ESD{M}_E=120.0,ESAD{M}_E=8.0,ESN{M}_E=0.4,ESSNME=0,ESSD{M}_E=0.5.$$$$ESD{M}_E=50.0,ESAD{M}_E=6.0,ESN{M}_E=0.2,ESSN{M}_E=0,ESSD{M}_E=0.$$

Table 4. Simulated values of bias, MAD and S.D of measures of equi-symmetry for non-equi-symmetry market sentiments

No. of weeks		50			100			150
Measure	Criteria	Simulation run
		1,000	2,000	5,000	1,000	2,000	5,000	1,000	2,000	5,000
ESDME (67.2, 120, 50)	BIAS	6.63	6.65	6.52	16.72	13.67	14.35	24.65	24.75	23.42
	MAD	73.83	73.85	73.72	136.72	133.67	134.35	74.65	74.75	73.42
	S.D	18.72	19.69	19.13	48.49	47.43	48.49	39.14	37.04	37.70
ESADME (8, 8, 6)	BIAS	0	0	0	1.33	1.26	1.24	1.19	1.19	1.11
	MAD	8.00	7.99	7.99	9.33	9.25	9.24	7.19	7.19	7.11
	S.D	1.09	1.14	1.12	1.65	1.63	1.63	2.04	1.96	2.01
ESNME (0.8, 0.4, 0.2)	BIAS	0	0	0	0.07	0.06	0.06	0.04	0.04	0.04
	MAD	0.80	0.80	0.80	0.47	0.46	0.46	0.24	0.24	0.24
	S.D	0.11	0.11	0.11	0.08	0.08	0.08	0.06	0.06	0.06
ESSNME (0, 0, 0)	BIAS	−0.20	−0.20	−0.20	−0.21	−0.20	−0.21	−0.02	−0.02	−0.02
	MAD	0.20	0.20	0.20	0.21	0.20	0.21	0.02	0.02	0.02
	S.D	0.040	0.034	0.034	0.241	0.237	0.244	0.224	0.231	0.230
ESSDME (128.8, 0.5, 0)	BIAS	15.5	15.8	15.6	42.1	40.4	41.7	3.50	3.22	3.42
	MAD	15.67	15.88	15.75	42.21	40.52	41.80	3.49	3.22	3.42
	S.D	7.60	7.84	7.46	30.74	30.09	31.57	17.62	16.85	17.20

The simulated Bias, MAD and S.D of the five measures of equi-symmetry market sentiments under the non-equi-symmetric market sentiment scenario for various combinations of Wand Nare reported in the Table 4. We can make the following conclusions based on the simulation study as reported in Table 4:

(i)	The measure ESDME and ESSDME, do not seem to be encouraging as they have significant percentage of relative bias. Moreover, they also report large MAD and S.D.
(ii)	In the case of the measure,ESADME, the relative bias ranges between 0 and 19%; while the MAD and S.D are relatively smaller than those for ESDME and ESSDME and remain stable with increase in W and N.
(iii)	Turning to the measure ESNME, the relative bias is either zero or almost negligible; while the MAD is very small and is stable across the row; while the S.D is of order 10−1 or less across the row.
(iv)	The measure ESSNME has negligible relative bias across the values of Wand N; but has smaller MAD and S.D consistently across the values of Wand N as compared to that of the measure ESNME.
(v)	In terms of relative bias, the measures ESADME, ESNME and ESSNME are equally sensitive to detect the non-equi-symmetric market sentiments, but in terms of MAD and SD, ESNME and ESSNME seem to be performing reasonably well in detecting non-equi-symmetric market sentiments.

It may be pointed out that, the simulation study was carried with extended values of W such as W = 200(50), 500 and simulation run N such as 6,000(1,000)15,000 for both equi-symmetric and non-equi-symmetric scenarios considered above. The findings in these cases were similar to the conclusions (i) to (iv) outlined for each of the sentiment scenarios considered. For these reasons, the simulated bias, MAD and S.D for these configurations of W and simulation trials N are not reported in Tables 3 and 4.

5. Comparison of measures of complete symmetry

In this section, we shall compare the performance of complete symmetric measures proposed in Section 3.4.2 in terms of a simulation study. We shall consider a five state market sentiments scenario with (i) complete symmetry and (ii) complete asymmetry. In each scenario, the number of weeks $\left(W\right)$ will be 50, 100 and 150 weeks. For the complete symmetry scenario, the following three sets of hypothesised empirical frequency configurations are considered:

(a)	$f_1=12,f_2=10,f_3=6,f_4=10,f_5=12$
(b)	$f_1=30,f_2=15,f_3=10,f_4=15,f_5=30$
(c)	$f_1=30,f_2=35,f_3=20,f_4=35,f_5=30$

In each of the above three cases, it can be seen that all the five measures of complete market symmetry are zero and these values are indicated within brackets of the respective measures in the first column of Table 5. The scheme of simulation, the choice of W, N and comparison criteria are similar to the one discussed in Section 4. The results are displayed in Table 5. We can make the following conclusions based on the simulation study as reported in Table 5:

(i)	In the case of the dispersion measure, it is seen in general that, the bias, MAD and S.D keep increasing with the increase in W and simulation run N. As opposed to this, the signed measure exhibits relatively smaller bias and MAD, while the S.D is more or less of the same order as that of dispersion measure.
(ii)	In the case of the absolute measure, the bias, MAD and S.D are small; however tend to increase marginally with increase in W and N.
(iii)	In the case of the normed measure, the bias, MAD appear to be very small and decreasing with increase N; while S.D decreases with increase in both W and N. It is to be noted that across the values of W and N, the S.D’s are indeed very small.
(iv)	The measure CSSAMC has uniformly a smaller bias and MAD as compared to CSNMC and is as good as the measure CSNMC in terms of S.D; being very small.
(v)	Of the five measures proposed here, in terms of the three criteria used, CSNMC and CSSNMC measures appear to be natural choice, followed by CSADMC. The measures CSDMC and CSSDMC do not seem to be as good as the other three measures.

Table 5. Simulated values of Bias, MAD and S.D of measures of complete symmetry for complete symmetric market sentiments

No. of weeks (W)		50			100			150
Measure	Criteria	Simulation run (N)
		1,000	2,000	5,000	1,000	2,000	5,000	1,000	2,000	5,000
CSDMC (0)	BIAS	9.00	8.95	8.82	18.77	18.31	17.76	26.28	27.02	26.38
	MAD	9.00	8.95	8.82	18.77	18.31	17.76	26.28	27.02	26.38
	S.D	8.77	8.91	8.48	20.0	18.79	18.72	26.53	26.14	26.66
CSADMC (0)	BIAS	1.52	1.51	1.50	2.16	2.13	2.10	2.60	2.64	2.58
	MAD	1.52	1.51	1.50	2.16	2.13	2.10	2.60	2.64	2.58
	S.D	0.80	0.81	0.80	1.16	1.14	1.13	1.36	1.39	1.38
CSNMC (0)	BIAS	0.16	0.16	0.16	0.11	0.11	0.11	0.08	0.08	0.08
	MAD	0.16	0.16	0.16	0.11	0.11	0.11	0.08	0.08	0.08
	S.D	0.11	0.13	0.12	0.08	0.07	0.07	0.05	0.05	0.05
CSSAMC (0)	BIAS	0.05	0.05	0.05	0.02	0.02	0.02	0.01	0.01	0.01
	MAD	0.05	0.05	0.05	0.02	0.02	0.02	0.01	0.01	0.01
	S.D	0.19	0.17	0.17	0.10	0.10	0.10	0.08	0.07	0.07
CSSDMC (0)	BIAS	0	−0.24	−0.03	0.18	0.53	−0.37	−0.64	−0.38	−0.25
	MAD	0	0.24	0.03	0.18	0.53	−0.37	0.64	0.38	0.25
	S.D	10.92	10.92	10.4	24.14	23.35	22.99	32.78	32.18	32.21

Next, turning to the asymmetric market sentiment scenario, the following three sets of hypothesised frequency configurations are considered:

(a)	$f_1=30,f_2=10,f_3=4,f_4=3,f_5=3$
(b)	$f_1=100,f_2=10,f_3=10,f_4=20,f_5=10$
(c)	$f_1=130,f_2=50,f_3=5,f_4=10,f_5=5$

It can be verified that for the cases (a), (b) and (c) indicated above, the computed values of these measures respectively are given below and these are indicated within brackets of the respective measures in the first column of Table 6.$$CSD{M}_C=155.6,CSAD{M}_C=6.8,CSN{M}_C=0.32,CSSN{M}_C=-0.32,CSSD{M}_C=155.6,$$$$CSD{M}_C=1640.0,CSAD{M}_C=20.0,CSN{M}_C=0.38,CSSN{M}_C=0.002,CSSD{M}_C=-1600.$$$$CSD{M}_C=3445.0,CSAD{M}_C=33.0,CSN{M}_C=0.352,CSSN{M}_C=-0.352,CSSD{M}_C=3445.0.$$

Table 6. Simulated values of Bias, MAD and S.D of measures of complete symmetry for asymmetric market sentiments

No. of weeks		50			100			150
Measure	Criteria	Simulation run
		1,000	2,000	5,000	1,000	2,000	5,000	1,000	2,000	5,000
CSDMC (155.6, 1,640, 3,445)	BIAS	5.9	6.3	5.6	16.9	12.6	12.6	−3.5	−13.9	−0.6
	MAD	161.5	161.9	161.2	441.9	437.6	437.6	1,636.5	1,626.2	1,639.35
	S.D	44.7	45.1	45.2	105.2	106.3	106.2	269.9	260.0	270.9
CSADMC (6.8, 20, 33)	BIAS	0	0	0	0.1	0	0	2.7	2.7	2.7
	MAD	6.9	6.8	6.8	11.1	11.0	11.0	18.7	18.7	18.7
	S.D	1.0	1.4	1.0	1.4	1.5	1.5	1.6	1.5	1.6
CSNMC (0.32, 0.38, 0.352)	BIAS	0	0	−0.1	0	0	0	0.24	0.24	0.24
	MAD	0.3	0.3	0.3	0.3	0.3	0.3	0.3	0.3	0.3
	S.D	0.1	0.1	0.1	0.04	0.04	0.04	0.1	0.1	0.1
CSSNMC (−0.32, −0.002, −0.352)	BIAS	−0.62	−0.63	−0.63	−0.55	−0.55	−0.55	−0.27	−0.27	−0.27
	MAD	0.30	0.30	0.30	0.27	0.27	0.27	0.15	0.15	0.15
	S.D	0.07	0.06	0.06	0.04	0.04	0.04	0.11	0.14	0.12
CSSDMC (155.6, −1,600, 3,445)	BIAS	5.9	6.3	5.6	16.8	12.4	12.5	32.6	21.9	35.31
	MAD	161.5	161.9	161.1	441.8	437.4	437.4	1,632.6	1,621.8	1,635.3
	S.D	44.8	45.1	45.2	105.3	106.4	106.2	270.1	260.5	271.2

The simulated Bias, MAD and S.D of the four measures of complete symmetry market sentiments under the asymmetric market sentiment scenario for various combinations of Wand N are reported in the Table 6. We can make the following conclusions based on the simulation study as reported in Table 6:

(i)	In the case of the measures CSDMC and CSSDMC, the maximum relative bias varies between 1 and 4%; while the MAD and S.D are almost the same and in general seem to increase with increase with W and N.
(ii)	In the case of the measure, CSADMC, the relative bias is either zero or almost negligible; while the MAD despite being very small marginally increases with increase in W and N. However, the S.D is almost stable with small magnitude.
(iii)	Turning to the measures CSNMC and CSSNMC, the relative bias is either zero or almost negligible; while the MAD is very small and is stable across the row; while the S.D is of order 10−1 or less across the row.
(iv)	In terms of relative bias, the four measures are equally sensitive to detect the asymmetric market sentiments, but in terms of MAD and SD, CSADMC, CSNMC and CSSNMC seem to be performing reasonably well in detecting asymmetric market sentiments. However, the choice CSNMC and CSSNMC seems to be the best.

As in the case of equi-symmetric simulation study, the simulation study was carried with extended values of W such as W = 200(50), 500 and simulation run N such as 6,000(1,000)15,000 for both symmetric and asymmetric scenarios considered earlier. The findings in these cases were similar to the conclusions (i) to (iv) outlined for each of the sentiment scenario considered. For these reasons, the simulated bias, MAD and S.D for these configurations of W and simulation trials are not reported in Tables 5 and 6.

A simulation study on similar lines as that of equi-symmetry and complete symmetry market sentiments was conducted to assess the performance of the measures of partial symmetry. The conclusions more or less mimic the findings of those complete symmetric market sentiments and for this reason the detailed tables are not reported here. The findings suggest that PSNM_P and PSSNM_P are the preferred measures to be considered to detect the partial symmetric market sentiments.

6. Applications to BSE data

As an application, we will attempt to explore the nature of absolute market sentiments that prevailed in weekly mean asset returns of two domestic companies, NAP and STANCHART registered in Botswana Stock Exchange (BSE) during the trading period: 4 January 2016 to 30 December 2016.

Before proceeding further with the formal analysis of the absolute market sentiments, we conducted the preliminary analysis à la the classical model based approach of the asset return series for the two listed companies in BSE and the results are presented below.

The results from the descriptive statistics reported in Table 7 compare two companies namely NAP and STANCHART. They show that returns distributions are highly skewed in different directions though. For both companies there is excess kurtosis that suggests departure from normality of the return distributions. The Jarque–Bera (JB) test of normality significantly rejects the null hypothesis of normality as informed by the smallest significance level that is below 0.01. All company returns are non-normal; as a consequence of which; inference based on the classical approach may be untenable.

Table 7. Summary statistics for domestic company weekly return indices

Statistics	NAP	STANCHART
Mean	0.0001828	−0.0006268
Maximum	0.0039420	0.0000
Minimum	0.00000	−0.012350
Std. Dev.	0.000602	0.001952
Skewness	4.891232	−4.559608
Kurtosis	26.58265	22.92539
Jarque-Bera (JB)	1,888.7	1,434
Probability	0.0000	0.0000
ADF-test statistics	−3.3792	−3.3665
Probability	0.06874	0.07073
No. of observations	51	51

6.1. Data stationarity test (unit root test)

In order to assess whether the financial time series (returns) are stationary or not the researchers have applied the Augmented Dickey–Fuller (ADF) test. The results show that the ADF test statistics rejected the null hypothesis of the existence of the unit root in NAP and STANCHART return series at the level of significance standing at 10% as indicated by the significant value (<0.1) of the associated probability of the ADF test statistic. The test summarises that the return series of the two companies investigated in the study are stationary and therefore the application of the stochastic models to return series is appropriate to examine the dynamic behaviour of volatility over time.

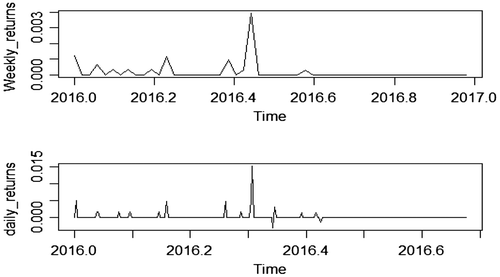
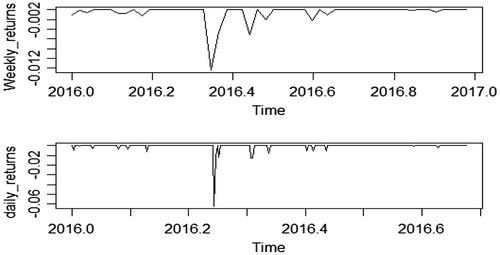
It can be observed that the graphs displayed in Figures 1 and 2 exhibit moderate swings or volatility in the return series over the study year. The spikes in the return plots are the graphical evidence implying that the volatility is time varying conditional variance. It also indicates the presence of volatility clustering effect in the return series of the company, that is to say, the series exhibit some periods of high volatility followed calm volatility around zero. Volatility clustering is a sign of positive autocorrelation in the squared returns.

Figure 1. Weekly and daily returns for NAP from January 2016 to December 2016.

Figure 2. Weekly and daily returns for STANCHART from January 2016 to December 2016.

The measure DSMS_D proposed in Section 3.4.4 picks up degenerate market sentiments. There are a number of companies that are examples of degenerate market sentiments in the likes of OLYMPIA, a domestic company listed in BSE, and a couple of them including INVESTEC and ANGLO, foreign companies at least for the year 2016.

We computed empirical measures of absolute market sentiments as discussed in Sections 3.4.1 and 3.4.2 for the two domestic companies considered and these are presented in Table 8.

Table 8. Empirical measures of market symmetry

Measures	NAP	STANCHART
CSDMC	0.4	0.4
CSADMC	0.4	0.4
CSNMC	0.09	0.14
CSSNMC	0.01	0.14
CSSDMC	0	0.4
ESDME	606	146
ESADME	44	9.6
ESNME	4.4	0.96
ESSNME	4.4	0.96
ESSDME	606	146

The results provide evidence of near complete symmetry of market sentiments for both NAP and STANCHART. For complete symmetry, one would expect the computed measures to be close to zero and the empirical analysis provides the estimates that are almost zero. Trading of shares from these companies for 2016 can offer a possibility of symmetric trading in which an investor can either gain or loss with the same margin. Furthermore for departure from complete symmetry, the signed measures (CSSNM_C and CSSDM_C) suggest to STANCHART as a company that there is some positive investment returns. In other words, the asset yields satisfactory performance even though not high extent as compared to greedy or bullish sentiments. However, the utility of the signed measures is more pronounced when the market sentiments are asymmetric.

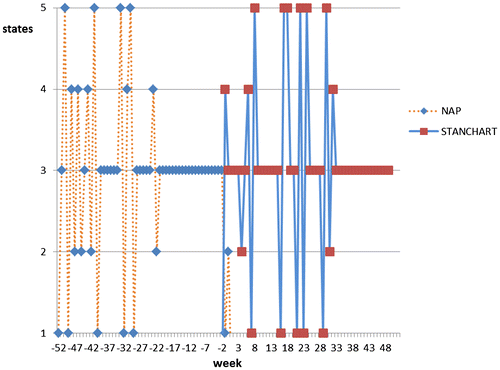
Figure 3 shows the plot absolute market sentiment states for the NAP and STANCHART companies for the year 2016. The weekly market sentiments are shown in Tables 9 and 10 in Appendix 1. The detailed computations that lead to the sentiment states are available from the first author on request. For the two companies there seems to be some popular high frequency of states 3 that describes the calm state of the stock market returns. On the other hand we see a few intermittent states appearing over the period of study.

Figure 3. Plot of NAP and STANCHART absolute market sentiment states for year 2016.

7. Conclusions

In this paper, we revisit the classical problem of analysing stock market data via the market sentiment analysis approach first suggested by Rao and Moseki (2009) and in their other subsequent works. We refine the definition of market sentiments by clearly distinguishing between absolute and relative market sentiments. Four typical types of market sentiments, namely, equi-symmetric, complete-symmetric, partial-symmetric and degenerate-state are formulated. We propose five empirical measures each to assess the presence of equi-symmetric and complete-symmetric and partial-symmetric types of market sentiments. The properties of these measures are also discussed. A measure of degenerate-state market sentiment has also been proposed. The performance of the empirical measures of equi-symmetric and complete-symmetric market sentiments have been discussed in terms of extensive simulation studies under different scenarios using the criteria of Bias, Mean Absolute Deviation and the Standard Deviation. The simulated values suggest that under a complete- symmetric market sentiment scenario, the CSNMc and CSSNMc perform relatively better than the other measures for this can be observed at different number of weeks and simulation trials. It is observed that for an increase in the number of weeks and simulation runs the measures keep improving on performance. In other words, as the number of weeks increase together with simulation runs both the criteria of BIAS, MAD and SD become reduced pushing towards the value of zero thereby identifying a complete symmetric market sentiment state. CSADMc is reasonably closer in terms of performance to CSNMc in comparative terms, while the CSDMc and CSSDMc are failing to produce the desirable outcomes under complete symmetric market state.

In case of the asymmetric market sentiment states scenario, the simulation results perceive CSNMc and CSSNMc as relatively better as compared to other measures proposed. Although CSADMc compares closely with CSNMc, but it is absolutely inferior in terms of the descriptive statistics of BIAS, where the two have same value of zero between 50 and 100 weeks inclusive and SD, where CSNMc performs better than CSADMc for 150 weeks.

In summary, CSNMc and CSSNMc yield absolutely good results and can be used as a preferred choice for analysing market sentiment states for both cases of symmetry and asymmetry scenarios.

Similarly, in the case of equi-symmetric measures, the simulation studies indicate that ESNM_E and ESSNM_E are the preferred empirical measures. On application of these measures, CSNM_C is preferred for symmetric market sentiments while for equi-symmetric market sentiments ESNM_E presents good results.

The proposed market sentiment approach to the analysis of return series is applied to the weekly trading return series of two domestic companies NAP and STANCHART registered with the Botswana Stock Exchange. The recommended measures ESNM_E and ESSNM_E ruled out the presence of equi-symmetric sentiments for the two companies considered while, the measures CSNM_E and CSSNM_E emphatically established the fact of complete market symmetry sentiments that prevailed during the trading period 4 January 2016 to 30 December 2016.

On application of the proposed data driven measures to NAP and STANCHART, in relative terms, one can infer that over the study period, the company NAP was seen to display some complete symmetric market sentiments in nature as evidence provided by the complete norm measure estimate near zero, a quantity for theoretical background under complete symmetric market sentiment. Subjected under the same measure STANCHART proved to be non-symmetric market sentiments. Instead it operated under equi-symmetric market sentiments. The interpretation of the estimates imply that any prospective investor would make a profit if was interested in investing in NAP, while for STANCHART one would not expect to book a profit if wanted to invest in the company at least for the proposed study period. It is imperative to know the historic performance of a company before you become a part ownership. This type of market sentiment analysis is necessary especially for Foreign Direct Investors who intend to put money in a country’s economic development since they are of a long term investment prospect.

It has been empirically proven that under no circumstance would the market sentiments become strictly complete or equi-symmetric in nature but the estimates serve as guiding principle.

Funding

The authors received no direct funding for this research.

Additional information

Notes on contributors

K.K. Moseki

Mr K.K. Moseki is a lecturer in the Department of Statistics, University of Botswana. He is pursuing his PhD degree in Statistics at the same department. He has published research papers in regional and international journals. His research interests include financial data analysis, time series, among others.

K.S. M. Rao

Prof K.S. M. Rao is a Professor in the Department of Statistics, University of Botswana. He has published extensively in national, regional and international peer reviewed journals with high impact factors. His research areas include parametric and nonparametric inference, empirical likelihood, mathematical finance and data analysis related to research areas in atmospheric, biological and social sciences.

Table 9. Weekly absolute market sentiment states for NAP

Table

Week	State	Week	State	Week	State	Week	State
2	S1	17	S3	32	S2	47	S3
3	S3	18	S3	33	S3	48	S3
4	S5	19	S3	34	S3	49	S3
5	S1	20	S5	35	S3	50	S3
6	S4	21	S1	36	S3	51	S3
7	S2	22	S4	37	S3	52	S3
8	S4	23	S5	38	S3
9	S2	24	S1	39	S3
10	S3	25	S3	40	S3
11	S4	26	S3	41	S3
12	S2	27	S3	42	S3
13	S5	28	S3	43	S3
14	S1	29	S3	44	S3
15	S3	30	S4	45	S3
16	S3	31	S2	46	S3

Table 10. Weekly absolute market sentiment states for STANCHART

Table

Week	State	Week	State	Week	State	Week	State
2	S4	16	S3	30	S3	44	S3
3	S3	17	S3	31	S3	45	S3
4	S3	18	S3	32	S1	46	S3
5	S3	19	S1	33	S5	47	S3
6	S3	20	S5	34	S2	48	S3
7	S2	21	S5	35	S4	49	S3
8	S3	22	S3	36	S3	50	S3
9	S4	23	S3	37	S3	51	S3
10	S1	24	S1	38	S3	52	S3
11	S5	25	S5	39	S3
12	S3	26	S1	40	S3
13	S3	27	S5	41	S3
14	S3	28	S3	42	S3
15	S3	29	S3	43	S3