Returns and volatility of water investments

Abstract

This study analyzes the stock returns and volatility of the global water industry in different (full, pre-GFC, GFC and post-GFC) periods. The study estimates ARMA (1, 1)-GARCH (1, 1) and EGARCH (1, 1) models on the World Water index (WOWAX), S-Network Global Water Index (S-Net), S&P Global Water Index (S&P), and MSCI ACWI Water Utilities Index (MSCI ACWI), the Asia, Europe, Latin America and US water markets, Pictet Global Water Fund (Pictet), and KBC Eco Water Fund (KBC Eco) for the period 2004–2014. In this study, the EGARCH (1, 1) model results suggest the existence of persistence of volatility from four water indices, four water markets and two water funds in different periods and asymmetric volatility (leverage) for Asia and US, S-Net and Pictet in full, pre-GFC and GFC periods and for WOWAX in GFC and post-GFC periods. The WOWAX is not highly correlated with water markets and water funds, which suggests that it may provide a possible opportunity for portfolio diversification in different periods.

Keywords:

• water investments
• water indices
• water markets
• volatility

Subjects:

• Investment and securities
• Mathematics and statistics
• Water

Public Interest Statement

Water is the most essential life-sustaining substance and the only commodity that is needed for life. However, many parts of the world are facing chronic water shortages. For water shortages around the globe, water investment is now an issue of growing concern for companies and countries around the globe as the demand for this finite resource is increasing at an accelerated rate. There exist a number of water indices, water markets and water funds, which have had significant impacts on the global water industry. The results of this study provide a guideline for water investors to take their investment decision in the global water industry.

1. Introduction

Water is the most essential life-sustaining substance and the only commodity that is needed for life, agriculture, and industry over the world (Reza, Tularam, & Li, 2017; Summit Global Management, 2017; Tularam & Reza, 2016). However, climate change recently has further compounded the problems of water scarcity (Tularam & Hassan, 2016; Tularam & Murali, 2015; Tularam & Properjohn, 2011). Together, the climate change effect and population growth has led to a water deficit, which in turn has posed major challenges to many parts of developed and developing countries including Bangladesh, Pakistan, Southern India, Northern China, Central Asia, the Middle East, the Sub-Sahara Africa, Southern Spain, Midwest United States, Mexico and the Andes, which are facing chronic drinking water scarcities (Jin, Li, Roca, & Wong, 2016; Reza et al., 2017; Roca & Tularam, 2012; Roca, Tularam, & Reza, 2015; Tularam & Marchisella, 2014; Wild, Francke, Menzli, & Schon, 2010, 2007). Water shortages occur due to rapid economic development and lack of water infrastructure finance (Reza et al., 2017; Tularam, 2014; Tularam & Illahee, 2010; Tularam & Keeler, 2006; Tularam & Krishna, 2009; Tularam & Reza, 2016; Tularam & Singh, 2009). There are shortages of the water necessary to sustain daily life, leading to serious food shortages caused by effects on the ecosystems (Beppu, 2007; Jones, 2009; Tularam & Hassan, 2016). Demand for water far surpasses the sustainable yield of both conventional and non-conventional water resources. The resulting demand-supply gap is being bridged through groundwater diminution (Ouda, 2014; Tularam & Marchisella, 2014; Tularam & Reza, 2017). Clearly, groundwater is important because 90% of irrigation water comes from the ground, as does 75% of drinking water (Roca et al., 2015; White et al., 2010). By 2025, nearly two-thirds of the world’s population will be water stressed due to greater demands placed on freshwater resources by a burgeoning human population (http://www.energyandcapital.com/resources/water-investments). According to the 2030 Water Resources Group (2006), global water requirements would grow from 4,500 billion m³ to 6,900 billion m³ by 2030.

Currently, 20% of the world’s population (1.1 billion people) do not have reliable access to an improved supply of drinking water and some 2.6 billion do not have access to basic sanitation (Jin et al., 2016; Roca et al., 2015; Tularam & Murali, 2015). By 2050, more than 4 billion people, nearly half the world’s population, are expected to live in countries that are chronically short of water (WHO & UNICEF, 2006). Back in 1970, the amount of water desalinated was less than 0.8 million m³ water per day globally. In 2009, this figure has increased to be well over 59 million m³ per day (Wild et al., 2007, 2010). The demand for water derives from agriculture, production of energy, industrial uses, and human consumption. In recent decades, water consumption has dramatically increased. Today, 10% of water is used for domestic purposes, 70% for agriculture, and 20% for industrial production (Roca et al., 2015; Societe Generale, 2006; Wild et al., 2007, 2010). For the above reasons, water utility owners and managers must be willing to critically examine water scarcity and water security in a changing climate, where energy costs and greenhouse emissions could influence water supply options (CSIRO, 2009; Tularam & Properjohn, 2011).

The motivation for the current study is also derived from the need to understand that water asset prices exhibit volatility persistence and asymmetric effect that could imply potential spillovers from water markets that will be observed by water indices and water funds. This study, therefore, provides knowledge on the financial volatility among water indices, water markets, and water funds around the world. Water indexes (WOWAX, S&P Global Water Index, MSCI World Water Index and S-Net Global Water Index), water markets (US, Europe, Asian, and the Latin American Water Market) and water funds (Pictet Water Fund and KBC Eco Water Fund) are very new in the finance literature.

The main goal of this study is to conduct a univariate analysis of water indices, water markets, and water funds to understand how the global water industry incorporates water indices, water markets and water funds into investment decision-making. The study purports to predict the relationships among water indices, water markets and water funds using return and volatility information. Specifically, this study asks, to what extent the returns of investing in different financial instruments (water indices, water markets, and water funds) are associated with water; is it profitable to invest in water and how risky is it?

Some important findings of this study are noted as follows. We find that water indices, water markets, and water funds are correlated with each other. However, the results show that WOWAX provides an opportunity of portfolio diversification benefits to investors in different (full, pre-GFC, GFC, and post-GFC) periods which is in line with Jin, Roca, Li, Wong, and Cheung’s (2015) results. It is notable that the ARMA (1, 1)-GARCH(1, 1) model results show that the conditional volatility process GARCH (1, 1) has a positive effect on the serial autocorrelation of squared residuals for water indices, water markets and water funds in full, GFC and post-GFC periods. Again, EGARCH (1, 1) model results show the significance of β and γ, suggesting persistence of volatility from four water indices, four water markets, and two water funds in different periods (full, pre-GFC, GFC and post-GFC) and asymmetric volatility (leverage) for S-Net, Asia and US and Pictet in the full, pre-GFC and GFC periods, and WOWAX in the GFC and post-GFC periods.

This study has a number of significant contributions to the current literature. Firstly, it is the first study to investigate the relationships between returns and volatility of the water indices, water markets, water funds, and water markets in different (full, pre-GFC, GFC, and post-GFC) periods. Secondly, this study searches for the existence of correlations and dynamic relationships in water indices, water markets and water funds with shareholders’ value in the global water industry. Thirdly and importantly, in a qualitative manner, this study addresses the value relevance of markets, which has a profound impact on the water industry in relation to water funds, water indices, and their components.

The rest of this paper is organized as follows. Section 2 presents a further institutional background. Section 3 reviews the related literature. Section 4 discusses our research hypothesis. Section 5 outlines the data and methodologies employed in the study. Section 6 analyzes the empirical results while Section 7 concludes.

2. Institutional background

Water investment is now an issue of growing concern for companies and countries around the globe as the demand for this finite resource is increasing at an accelerated rate. There are a number of water indices, water markets, and water funds that have had significant impacts on the global water industry (Jin et al., 2015; Roca et al., 2015). Investments in water indices, water markets, and water funds appear to be in an underinvestment phase in the water industry today. Thus, this investment plays a lower than significant role in longer term backing to expand water infrastructures. It is clear that the water sector is expanding and the market appears to be economically resilient, and consequently investments in this industry should lead to better financial returns in the future (Jin, Li, Roca, & Wong, 2014; Roca et al., 2015).

The importance of the water industry is increasing day by day and investors are encouraged to participate in the water sector. In this context, water indices are performing a great role for investors interested in this market. The ZWI is an equally weighted index comprised of companies engaging in the fundamental activities of the global water industry, such as distribution, filtration, pumps and pipes, and treatment (Geman & Kanyinda, 2007; Roca & Tularam, 2012). Following the publication of the ZWI, two exchange traded funds (ETFs), Power Shares Water Resources (PHO) and Power Shares Global Water (PIO) were successively introduced to investors to assist them to keep track of companies included in the ZWI (Keenan, 2008; Roca et al., 2015; Tularam & Reza, 2016). As such, there are other ETFs available to investors, for example, Guggenheim S&P Global Water Fund which is based on the S&P Global Water Index, and First Trust ISE Water (FIW) which is based on the ISE Water Index (Atkinson, 2009). However, often a number of companies included in these water indices generate only a small portion of their revenue from water-related products or services. Questions were raised as to whether these water ETFs can be defined as pure water funds (Kearney, 2008; Tularam & Reza, 2016). Water funds also have been created for investors so that they can have opportunities to invest their money in the water market. US investors are offered the Pictet Global Water Fund by Swiss banker Pictet & Cie for the Pictet Global Water Fund (Roca, Li, & Wong, 2013; Roca & Tularam, 2012). In 2000, Pictet Asset Management in Geneva launched the first water fund in the world, which is the largest specialist water fund around the globe and has risen by 25% since 2006 (Geman & Kanyinda, 2007; Global Water Intelligence, 2007; Roca et al., 2015; Roca & Tularam, 2012).

Recently, water funds have flourished throughout the world. Several well-known specialized water funds include Pictet Water Fund, SAM Sustainable Water Fund, Sarasin Sustainable Water Fund, Swisscanto Equity Fund Global Water Invest, and Tareno Water fund. Several structured water products offered by major investment banks include ABN Amro Water Stocks Index Certificate, BKB Water Basket, ZKB Sustainable Basket Water, Wagelin Water Shares Certificate, UBS Water Strategy Certificate, and Certificate on Vontobel Water Index (Global Water Intelligence, 2007). Table A1 shows water fund’s name, launch date and funds description in the Appendix A.

3. Literature review

Stock market volatility is related to the general health of the economy. It can be used to measure the market risk of a single instrument or an entire portfolio of instruments. The volatility in water prices, such as those for water indices, water managed funds, water exchange traded funds (ETFs), and water markets, is similar in various aspects to financial volatility as it relates to the risk and returns associated with the global water industry. Nevertheless, as the characteristics of water industry may be different from those of financial markets, the results are subject to empirical risk analysis, and need to be investigated.

A number of studies have examined the relationship between stock market volatility (risk) and returns in the US, European, and Asian stock and bond markets. The findings of these studies, however, are inconclusive. Researchers have investigated the time series behavior of stock prices in terms of volatility using generalized autoregressive conditional heteroskedasticity (GARCH) models. Pindyck (1986) and Chou (1988) claim that much of the decline in stock prices during the 1970s is directly related to the increase in volatility. Poterba and Summers (1986), French, Schwert, and Stambaugh (1987), Baillie and DeGennaro (1990) and Poon and Taylor (1992) find a weak relationship between stock market volatility and expected returns. Glosten, Jagannathan, and Runkle (1993) and Nelson (1991), on the other hand, report that positive unanticipated returns reduce conditional volatility whereas negative unanticipated returns increase conditional volatility.

Several studies have been conducted on the asymmetry in news impact. In the finance literature, Black (1976), French et al. (1987), Schwert (1990), Nelson (1991), Bae and Karolyi (1994), Koutmos and Booth (1995), Koutmos (1996), Tularam, Wong, and Roca (2009), Krishnamurti, Tian, Xu, and Li (2013) and others are well known for their studies on the asymmetric effect. French et al. (1987) state that “leverage effect” may not be the only explanation for the asymmetric impact of news on volatility. Many GARCH models that allow for asymmetric impact have been developed. The exponential GARCH (EGARCH) model (Pagan & Schwert, 1990; Nelson, 1991) and the GJR-GARCH model (Glosten et al., 1993) are highly used in asymmetric GARCH models.

A summary of the findings of these studies with regard to different equity and bond markets and their relationship between returns and volatility with GARCH models is shown below.

3.1. Returns and volatility from stock and bond markets around the world

With regard to the asymmetry of volatility, Gallo and Pacini (2000) investigate the effect of trading activity on market volatility by applying an EGARCH (1, 1) model. They find that ARCH effects in the stock market and persistence of volatility are due to the opening price and the closing price of the previous day’s accounts. Chen and Kuan (2002) also study US stock index returns, applying the GARCH and EGARCH models based on daily stock indices data on the Korean KOSPI, the Japanese Nikkei, and the Taiwanese SE weighted index for the period 1980–1997, and the Singaporean Straits Times price index (ST) for the period 1985–1997. The authors conclude that the time irreversibility of these four index returns may be largely attributed to volatility asymmetry, and that such asymmetry may be captured using a proper EGARCH model. Bradant and Jones (2006) study some asymmetry between market returns and volatility, and they find that the EGARCH models significantly improve the in-sample fit and accuracy of out-of-sample forecasts.

Because of the importance of understanding the relationship between return and volatility, Basher, Hassan, and Islam (2007) only investigate the time-varying risk-return relationship for Bangladesh, which is a small but economically booming country. They examine the impact of institutional factors such as a circuit breaker on volatility for the Dhaka Stock Exchange (DSE) of Bangladesh by applying the GARCH-M (1, 1) model. Their results also show a significant relationship between conditional volatility and the DSE stock returns, but the risk-return parameter is found to be both negative and positive. Like Basher et al. (2007), Alberg, Shalit, and Yosef (2008) apply GARCH, EGARCH, GJR and APARCH models to examine the mean return and conditional variance of the Tel Aviv Stock Exchange. They find that the EGARCH model gives better forecasts than the GARCH model, while the APARCH and GJR models give the poorest forecasts.

Karunanayake and Valadkhani (2011) investigate the interdependence of return and co-volatility across four highly integrated international stock markets in Australia, Singapore, the UK and the US by applying GARCH and MGARCH models. Their results are in line with the findings of Theodossiou and Lee (1993). Abdalla (2012) also investigates returns and volatility of exchange rates in a series of 19 Arabian countries during the period of 1 January 2000 to 19 November 2011 by applying GARCH (1, 1) and EGARCH (1, 1) models. The author shows that EGARCH (1, 1) captures leverage effects for all currencies except for the Jordanian dinar. This study also applies an autoregressive moving average ARMA (1, 1) model, as the conditional mean in the returns series is employed as an initial regression test, and does not find ARCH effects in the residual series.

More recently, Krishnamurti et al. (2013) apply EGARCH (1, 1) and EGARCH-GED models to examine the relationship between intra-day volatility and trading volume by using the intra-day Shanghai A-Share Index data from 2004 to 2006. They find that the asymmetric volatility phenomenon is reversed in the Shanghai Stock Exchange during bull markets. This means that volatility increases more with good news than with bad news.

Gil-Alana and Tripathy (2014) examine the volatility persistence and across six ferrous metal spots and future series (aluminum, copper, lead, nickel, zinc, and tin) in India for the period of 1 January 2009 to 30 June 2012 by applying TARCH, GARCH, EGARCH, and TGARCH models. Their results confirm the symmetric, asymmetric, and leverage effect by GARCH, TGARCH, and EGARCH, respectively. Dedi and Yavas (2016) analyze the relationship between five countries’ (Germany, the United Kingdom, China, Russia and Turkey) equity market returns and volatility using MARMA, GARCH, GARCH-in-mean, and EGARCH models by applying daily data on country exchange-traded funds (ETF) based on the MSCI indices from 31 March 2011 to 11 March 2016. They show that the EGARCH (1, 1) model captures a leverage effect with returns, and markets are more sensitive to the “bad” news than to the “good” news.

Furthermore, McAleer and Hafner (2014), McAleer (2014), Lux, Segnon, and Gupta (2016), Tsuji (2016), Epaphra (2017), Fadzil, O’Hara, and Ng (2017) also find that “leverage effect” for the asymmetric impact of news on volatility using GARCH, EGARCH and TGARCH models.

3.2. Returns and volatility within the water industry

To the best of our knowledge, very few studies have been conducted on returns and volatility in the water industry. Morana and Sawkins (2000) use daily share price data for ten English and Welsh water and sewerage companies for the period from December 1989 to March 1998 to investigate the water industry’s periodic review of prices by applying both AR-GARCH and stochastic volatility models. They find that a significant reduction in the volatility of share prices for eight of the ten water and sewerage companies follows the announcement of revised industry price-caps. Furthermore, Pescetto (2008) investigates the impact of regulation on the systematic risk of 10 water companies in England and Wales using dynamic GARCH model and finds that systematic risk does not appear to have been altered by regulatory action over the sample period. Similarly, Buckland and Williams (2013) study the returns on securities issued by regulated water companies in the differently regulated economies of the UK and the US, using data from 1976 to 2010. They find that the levels of systematic risk in the equities of US listed water utilities are low and investors experience systematic risks that are appreciably lower than those used by US regulators in historic rate cases; and they are lower than the betas estimated for UK water utilities. Nevertheless, the systematic risk experienced by the US and the UK investors in water stocks has increased since 2000. Mirroring the results from the 1990s, the results suggest that UK regulators chronically overestimate the risks borne by investors in water utilities, resulting in lax pressure on permitted returns and higher prices than are needed to provoke efficient supply. Their examination confirms that there are striking differences between the regulatory risks and patterns of returns for water utilities in the US and the UK.

Recently, Tularam and Reza (2016) examine the links between idiosyncratic risk and return among four water exchange traded funds (PowerShares Water Resources Portfolio, Power Shares Global Water, First Trust ISE Water Index Fund, and Guggenheim S&P Global Water Index ETF) using a Markov switching model for the period 2007–2015. They show the idiosyncratic risk for most of the exchange traded funds move from low volatility (Regime 2) to very low volatility (Regimes 1 and 3).

Perhaps the study by Geman and Kanyinda (2007) is the best attempt in the water investment research field. They measure the performance and volatility of the World Water Index (WOWAX) between December 2003 and June 2006, and find that the index increased by more than 80% during this period. Meanwhile, the volatility is remarkably low (consistently less than 12% for more than the half year from December 2005 to August 2006). Additionally, they compare the WOWAX’s performance in relation to the three major commodity investments (i.e. Dow Jones-AIG total return index, Dow Jones-AIG Energy Sub-index and Dow Jones-AIG Petroleum Sub-index). Their results indicate that the WOWAX outperforms the Dow Jones-AIG total return index, which itself has since the year 2000 been a particularly successful investment. They also suggest that the WOWAX, and hence the water sector, is a good investment choice. However, their study only examines the WOWAX’s performance for two and a half years.

3.3. Literature review summary and research gap

In terms of the relationship between returns and volatility, finance researchers employ data of a standardized index of stock markets, energy markets, real-estate markets, social responsible investment markets, etc., in a wide variety of different countries’ stock exchanges. Most of the studies use ARCH, GARCH, EGARCH and multivariate GARCH models. Some studies find a positive relationship between stock market volatility and expected returns. From the literature review in this article, it can be seen that other studies find that there is no significant relationship between stock market volatility and expected returns. Some studies also capture the asymmetry and leverage effect with returns and volatility, and find that markets are more sensitive to “bad” news than to “good” news. It is noted that there are only two studies (Morana & Sawkins, 2000; Tularam & Reza, 2016) which are undertaken from the perspective of a water investor.

From the above literature review, we find that some studies have found that a negative (weak) relationship exists between stock market volatility and expected returns. On the contrary, other studies show a positive relationship. To the best of our knowledge, there are no studies on the volatility of water indices, water funds and water markets in relation to stock markets. The present study seeks to close this gap by applying ARMA, ARMA-GRACH and EGARCH models. The only study which investigates the UK water industry’s periodic review of prices by applying both AR-GARCH and stochastic volatility models is that by Morana and Sawkins (2000). In addition, and more significantly, in terms of the motivation for this present study, none of this research on financial volatility has focused on the water sector, the water indices, water funds or water equity markets. The motivation for our study is also derived from the need to understand that water asset prices exhibit volatility persistence and asymmetric effects that could imply potential spillovers from water markets, which will be observed by water indices and water funds.

4. Hypothesis to be tested

Due to prior lack of attention, our study examines the relationships between water indices, water markets and water funds and their dynamics using time series methods. Although the water asset class might have weak relationships (low risk and low correlation) with other assets (Berlant, 2007; Jin et al., 2014), it is nevertheless important to examine whether a cyclical nature exists in the data sets and/or whether a simple trend relationship exists between water indices, water markets and water funds that may be exploited by water investors and companies. Hence, to answer this, our study empirically investigates the relationships among water indices, water funds and water markets using return and volatility information. In this study, there are two main hypotheses that are to be tested. The null and alternative hypotheses in the first case are:

H₀: There is no trend among water indices, water markets and water funds in the context of the global water industry in different periods (full, pre-GFC, GFC and post-GFC) periods.

H₁: There are trends among water indices, water markets and water funds in the context of the global water industry in different (full, pre-GFC, GFC and post-GFC) periods.

Investment decisions relating to the water indices and water funds are dependent on the “good” or “bad” performance of water companies in various environmental, social and corporate governance sectors, as well as being based on ethical criteria (Nikolaou, Kourouklaris, & Tsalis, 2014). Although the water industry is anticompetitive in nature, water firms have a tendency to remain somewhat stable and the global water market is not likely to be easily affected by the volatility of economic conditions. Nevertheless, water investment risks have gained much attention recently (Nikolaou et al., 2014). To date, the risk or volatility in the global water industry has not been critically investigated, even when volatility in the industry is one of the economically significant determinants of stock prices. An investigation into volatility and stock returns can highlight the ways in which the financial structure of a firm can have a significant impact on the risk and returns of water firms’ stocks. The understanding of risk and return is important not only in the assessment of the price of a stock, but also for the evaluation of different managerial actions such as managerial investment and financing decisions. Therefore, the second hypothesis is formulated as follows:

H₀: Stock returns are not affected by volatility in the water indices, water funds and water markets in different (full, pre-GFC, GFC and post-GFC) periods.

H₁: Stock returns are affected by volatility in the water indices, water funds and water markets in different (full, pre-GFC, GFC and post-GFC) periods.

5. Data and methodology

5.1. Data

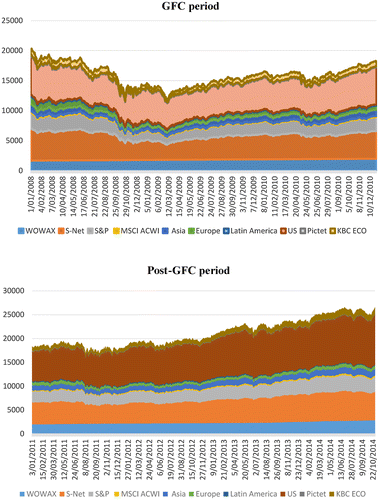
Our study utilizes the World Water Index (WOWAX), the S-Network Global Water Index (S-Net), the S&P Global Water Index (S&P), the MSCI ACWI Water Utilities Index (MSCI ACWI); and the DS Water Index for the Asia, Europe, Latin America and the US, and the Pictet Water Fund (Pictet) and the KBC Eco Water Fund (KBC Eco). The data are obtained from the Thomson Reuters DataStream database except for the data relating to WOWAX, which is obtained from the Societe Generale website. These water indices, water markets and water funds data have been selected based on the completeness of data starting from 1 January 2004 to 31 October 2014. There are four indices, four water markets and two water funds in this data-set. The overall sample period is divided into three sub-periods. Figure 1 shows the trend in water sock prices in different periods. Figure 1 helps the investors to determine whether the water indices, water markets and water funds are appreciating or depreciating in price and understanding the behavior normally or abnormally of water stocks and water funds during the full, pre-GFC, GFC, and post-GFC periods. Daily data are transformed to the form of R_t = ln(Price_t/Price_t−1) × 100 and the prices are in US dollars.

5.2. Methodology

Morana and Sawkins (2000) study is the only one which has investigated the volatility of share prices in the water industry in particular. They use eight water and sewerage companies in the UK and apply AR (1)-GARCH (1, 1) and stochastic volatility models to analyze their data. Models such as the autoregressive moving average (ARMA), combined ARMA (1, 1)-GARCH (1, 1), and EGARCH (1, 1) models appear to have hardly ever been applied in water industry research, and therefore such time series models, when appropriately applied, can help provide critical analysis and in-depth information regarding the modeling relationship in the water research area.

5.2.1. Autoregressive moving average (ARMA) model

A time series univariate analysis is also conducted for an individual series for volatility of changes. The study examines and analyzes the dynamic relationships among water indices, water markets and water funds using the general ARMA (p, q) model (Tularam, 2010; Tularam & Saeed, 2016; Zhou, He, & Sun, 2006) with the conditional mean being applied to all variance models. The origin of the ARMA model is the autoregressive AR model of order p; MA, the moving average framework of order q; and the expressions for the AR, MA and ARMA models are:$$\text{AR}\text{model:}{y}_t={\phi }_i{y}_{t-1}+{\phi }_i{y}_{t-2}+\dots +{\phi }_i{y}_{t-p}+{\mathrm{\xi }}_t=\sum _{i=1}^p{\phi }_i{y}_{t-i},$$$$\text{MA}\text{model:}{y}_t={\lambda }_j{\mathrm{\xi }}_{t-1}+{\lambda }_j{\mathrm{\xi }}_{t-2}+\dots +{\lambda }_j{\mathrm{\xi }}_{t-p}+{\mathrm{\xi }}_t=\sum _{j=1}^q{\lambda }_j{\mathrm{\xi }}_{t-j},$$$$\text{ARMA}\text{model:}{y}_t=\mu +\sum _{i=1}^p{\phi }_i{y}_{t-i}+\sum _{j=1}^q{\lambda }_j{\mathrm{\xi }}_{t-j}+{\mathrm{\xi }}_t$$

This equation can also be written in compact form as follows:$$\phi (L)(y_t-\mu )=\varphi (L){\mathrm{\xi }}_t$$

when all the roots of $\gamma (z)=1-{\gamma }_{1}z-{\gamma }_{2}z,\dots -{\gamma }_{p}z=0$, ARMA (p, q) process are stationary, and invertible if the roots of the characteristic equations are $\phi (z)$.

5.2.2. ARMA-GARCH model

The ARMA-GARCH model is a combination of an ARMA model which is used to model mean behavior, and an ARCH model which is used to model the ARCH effect in the residual series from the ARMA model. Following Wang, Gelder, Vrijling, and Ma (2005) and Tularam (2010), one can write the whole ARMA (p, q)-GARCH (p, q) model as follows:$$\phi (L)(y_t-\mu )=\varphi (L){\mathrm{\xi }}_t$$$${\sigma }_t^2=\omega +\sum _{i=1}^p{\alpha }_i{\sigma }_{t-1}^2+\sum _{j=1}^q{\beta }_j{\rho }_{t-j}^2+={\mathrm{\xi }}_t$$

where $\phi (L)$ is lag polynomials, and $\mathrm{\xi }=Z_t{\rho }_t$. Importantly, ${\alpha }_i\dots ,{\alpha }_p,{\beta }_i,\dots ,{\beta }_p$ are constant coefficients. A fact that should be mindful when modeling conditional variances is that $\omega$, ${\alpha }_i$and ${\beta }_j$ are non-negative.

5.2.3. Exponential GARCH (EGARCH) model

In order to examine the asymmetric effects in time series analysis, the exponential GARCH (EGARCH) model is introduced by Nelson (1991). The EGARCH model allows for the asymmetric effects of the good news and bad news on conditional variances. Our study uses the EGARCH (p, q) model as an exponential function when p = 1, q = 1 which is:$$log({\sigma }_t^2)=w+\beta log({\sigma }_t^2-1)+\gamma \frac{{\epsilon }_{t-1}}{\sqrt{{\sigma }_t^2-1}}+\alpha \left(\frac{\left|{\epsilon }_{t-1}\right|}{{\sqrt{\sigma }}_t^2-1}-\sqrt{\frac{2}{\pi }}\right)$$

The advantage of the EGARCH model is that the conditional variance is positive; and the parameters can be allowed to take negative values. The asymmetric positive and negative shocks $({\epsilon }_{t-1})$on conditional variance and $\frac{{\epsilon }_{t-1}}{\sqrt{{\sigma }_t^2-1}}\sim N,(0,1)$ are captured in the parameter $\gamma$. The negative coefficient of $\gamma$ indicates that volatility rises more than the positive coefficient $\gamma$. The parameter $\gamma$ (a negative sign) ensures that bad news generates more volatility than good news. The coefficient of α captures the assembling effects of the volatility.

6. Empirical results

6.1. Descriptive statistics

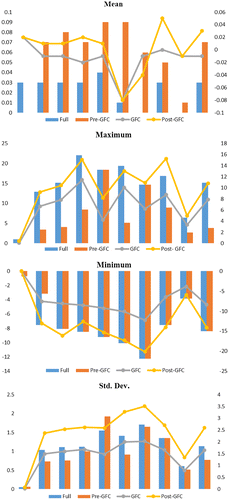
Table 1 shows that stock returns are positive except for Pictet. Asia has the highest positive mean return (0.04) while the lowest positive mean return (−0.00) is for Pictet in the full period. During the pre-GFC period, stock returns are positive except for WOWAX. However, all stock returns are negative except for WOWAX during the GFC period. Europe, Latin America and Pictet stock returns are not positive in the post-GFC period. During the full period, the skewness values of S&P, Europe, Latin America and KBC Eco are in generally negative asymmetric tail. However, WOWAX S-Net, MSCIACWI, Asia, US and Pictet are in positive i.e. asymmetric tail in the pre-GFC period. During the GFC period, the skewness values are related to the symmetric (WOWAX, MSCI ACWI, Europe, and Pictet) and asymmetric (S-Net, S&P, Asia, Latin America, and KBC Eco) tails that are positive and negative value. The skewness values are related to the asymmetric tail that extends towards more negative values than the positive ones for the pre-GFC period. The kurtosis values of all water indices, water markets and water funds statistics are higher than three, suggesting that all time series are fat-tailed for the full period and three sub-sample periods. Subsequently, the Jarque-Bera results are statistically significant. Thus, the assumption of normal distribution is not fulfilled.

Table 1. Descriptive statistics

	WOWAX	S-Net	S&P	MSCI ACWI	Asia	Europe	Latin America	US	Pictet	KBC Eco
Full period: January 2004–October 2014
Mean	0.03	0.03	0.03	0.03	0.04	0.01	0.00	0.03	−0.00	0.03
Median	0.02	0.07	0.08	0.04	0.00	0.01	0.07	0.00	0.00	0.06
Maximum	0.72	9.27	10.90	15.86	13.27	13.96	10.54	12.14	4.61	10.92
Minimum	0.00	−7.55	−8.07	−8.52	−9.23	−10.09	−12.25	−7.56	−3.84	−8.42
Std. Dev.	0.05	1.04	1.11	1.21	1.55	1.41	1.71	1.35	0.61	1.14
Skewness	4.60	−0.43	−0.33	0.41	0.40	−0.04	−0.53	0.35	0.13	−0.31
Kurtosis	36.24	10.84	11.86	17.67	8.19	10.91	7.89	10.10	6.37	12.60
Jarque-Bera	140,135.3	7333.34	9,317.92	25,460.85	3,259.47	7,382.23	2,952.22	5,998.03	1,349.24	10,905.00
Probability	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Observations	2,827	2,827	2,827	2,827	2,827	2,827	2,827	2,827	2,827	2,827
Pre-GFC period: January 2004–December 2007
Mean	−0.0	0.07	0.08	0.07	0.09	0.09	0.06	0.05	0.01	0.07
Median	−0.02	0.11	0.116	0.07	0.00	0.09	0.10	0.00	0.01	0.08
Maximum	0.000	2.50	2.92	6.08	13.27	3.71	10.54	6.44	1.95	2.75
Minimum	−0.72	−3.17	−3.51	−5.06	−6.63	−3.25	−8.16	−7.39	−1.73	−3.35
Std. dev.	0.06	0.73	0.76	1.00	1.92	0.91	1.65	1.35	0.52	0.77
Skewness	−4.06	−0.42	−0.29	0.09	0.77	−0.07	−0.13	−0.29	0.01	−0.33
Kurtosis	26.99	4.10	4.14	4.96	6.73	3.88	6.18	5.84	3.79	4.57
Jarque-Bera	27,903.69	84.14	72.56	170.02	711.34	35.07	445.35	366.6973	27.62	128.35
Probability	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Observations	1,043	1,043	1,043	1,043	1,043	1,043	1,043	1,043	1,043	1,043
GFC period: January 2008–December 2010
Mean	0.02	−0.01	−0.01	−0.02	−0.01	−0.08	−0.01	−0.00	−0.01	−0.01
Median	0.01	0.05	0.07	0.02	0.00	−0.05	0.10	0.00	−0.00	0.06
Maximum	0.10	9.27	10.90	15.86	5.83	13.96	8.65	12.14	4.61	10.92
Minimum	0.00	−7.55	−8.07	−8.52	−9.23	−10.09	−12.25	−6.45	−3.84	−8.42
Std. Dev.	0.02	1.49	1.60	1.68	1.48	2.00	2.03	1.66	0.79	1.65
Skewness	1.60	−0.28	−0.17	0.63	−0.58	0.18	−0.92	0.81	0.27	−0.14
Kurtosis	5.77	8.07	8.79	15.91	7.72	8.50	8.93	10.08	6.21	9.16
Jarque-Bera	586.69	853.15	1,100.60	5498.51	774.98	994.49	1263.38	1728.09	347.98	1,244.69
Probability	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Observations	784	784	784	784	784	784	784	784	784	784
Post-GFC period: January 2011–October 2014
Mean	0.0	0.02	0.02	0.04	0.02	−0.00	−0.03	0.05	−0.00	0.04
Median	0.01	0.03	0.04	0.03	0.00	0.00	0.02	0.02	0.00	0.06
Maximum	0.48	3.58	3.61	5.06	6.56	4.12	6.49	9.05	2.31	4.08
Minimum	0.00	−5.50	−5.51	−4.07	−6.07	−7.21	−7.89	−7.56	−2.10	−5.70
Std. Dev.	0.05	0.88	0.94	0.94	1.11	1.27	1.48	1.04	0.55	0.95
Skewness	3.51	−0.40	−0.41	−0.11	−0.15	−0.34	−0.26	0.39	−0.07	−0.39
Kurtosis	21.74	6.53	6.27	4.72	5.57	5.108	4.96	12.70	4.57	6.22
Jarque-Bera	16,703.68	548.06	476.57	126.52	280.13	205.0	172.54	3,954.23	104.48	458.75
Probability	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
Observations	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000

Notes: This table reports the descriptive statistics for four water indices-World Water Index (WOWAX), S-Net Global Water Index (S-Net), S&P Global Water Index (S&P) and MSCI ACWI Water Utilities Index (MSCI ACWI) and four water markets-Asia, Europe, Latin America and US water markets, and two water funds-Pictet Global Water Fund (Pictet) and KBC ECO Water Fund (KBC Eco). Descriptive statistics include daily mean, maximum, minimum, standard deviation (std.dev.), and performance-related statistics in different (full, pre-GFC, GFC, and post-GFC) periods.

Data are collected from the Thomson Reuters DataStream database. Daily data are transformed to the form of R_t = ln(Price_t/Price_t−1) × 100 and the prices are in US dollars.

Table 1 shows that stock returns are positive for all the water indices and water markets during full, pre-GFC and post-GFC periods. However, during the GFC period, stock returns are only positive for WOWAX. For all the periods the kurtosis values of all water stock index and water market index returns are higher than 3, so the returns distribution could be fat-tailed. The skewness values are related to the asymmetric tail that extends towards more negative values than the positive ones for the full period and three sub-sample periods. Since the Jacque-Bera results are statistically significant, the analysis rejects the null hypothesis of a normal distribution for all stock returns. The difference in the returns would be important for analysis. Table 1 results have been summarized as graphs for mean, maximum, minimum and standard deviation movements during full, Pre-GFC, GFC, and post-GFC periods in Figure 2.

Figure 1. Movements of four water indices (S-Net, WOWAX, S&P, and MSCI ACWI), four water markets (Asia, Europe, Latin America and US) and two water funds (Pictet and KBC Eco).

Notes: This figure presents the four water indices, four water markets and two water funds share prices movements during the full, pre-GFC, GFC, and post-GFC periods. Source: Thomson Reuters DataStream database.

Figure 2. Movements of mean, maximum, minimum, and standard deviation during full, pre-GFC, GFC, and post-GFC periods.

Notes: Mean Maximum, Minimum and Std. Dev results are summarized as graphs here for different (full, pre-GFC, GFC and post-GFC) periods in Table 2. Source: Thomson Reuters DataStream database.

6.2. Analysis based on correlations

In Table 2, we conduct a preliminary analysis of correlations between water equites (water indices water markets) and water mutual funds. The results show that water equities and water mutual funds are correlated with each other. S-Net and S&P, S-Net and KBC Eco, and S&P and KBC Eco are highly correlated in the different periods (full, pre-GFC, GFC, and post-GFC periods). However, WOWAX has low correlation with the other three water indices, four water markets and two water funds in full period. During the pre-GFC period, WOWAX is significantly negatively correlated with four water indices, four water markets and two water funds. WOWAX is significantly positively correlated with MSCI ACWI, Europe and Pictet but significantly negatively correlated with S-Net, S&P, Asia, Latin America, US and KBC Eco in the GFC period. During the pre-GFC period, WOWAX is significantly negatively correlated with MSCI ACWI and US. Nevertheless, WOWAX is positively correlated with S-Net, S&P, Asia, Europe Latin America, Pictet, and KBC Eco. From these results, some doubts arise on the assumption that investing in the 20 component stocks of WOWAX which can bring investors diversification benefits in different (full, pre-GFC, GFC, and post-GFC) periods. Jin et al.’s (2015) results also indicate that WOWAX has the capacity to produce diversification effects in portfolios. We find that Pictet and KBC Eco significantly correlates with Asia, Latin America, and US water markets during the full, pre-GFC, GFC, and post-GFC periods. The results of the correlation analysis, therefore, indicate the trend of positively correlated returns between water equities and water funds over the years.

Table 2. Correlation matrix among water indices, water markets and water funds

	WOWAX	S-Net	S&P	MSCI ACWI	Asia	Europe	Latin America	US	Pictet	KBC Eco
Full period: January 2004–October 2014
WOWAX	1
S-Net	0.01	1
S&P	0.01	0.94	1
MSCI ACWI	0.01	0.67	0.71	1
Asia	0.01	0.29	0.26	0.14	1
Europe	0.02	0.71	0.79	0.72	0.18	1
Latin America	0.02	0.58	0.56	0.40	0.21	0.42	1
US	0.01	0.54	0.49	0.48	0.07	0.27	0.28	1
Pictet	0.02	0.42	0.47	0.35	0.13	0.54	0.27	0.09	1
KBC ECO	0.01	0.93	0.91	0.64	0.24	0.68	0.53	0.52	0.41	1
Pre-GFC period: January 2004–December 2007
WOWAX	1
S-Net	−0.036	1
S&P	−0.02	0.88	1
MSCI ACWI	−0.03	0.61	0.62	1
Asia	−0.00	0.30	0.27	0.10	1
Europe	−0.03	0.68	0.76	0.82	0.14	1
Latin America	−0.03	0.56	0.50	0.32	0.17	0.37	1
US	−0.05	0.48	0.39	0.24	0.03	0.19	0.23	1
Pictet	−0.02	0.34	0.40	0.40	0.05	0.49	0.17	0.06	1
KBC ECO	−0.04	0.88	0.85	0.58	0.22	0.68	0.49	0.46	0.39	1
GFC period: January 2008–Dec ember 2010
WOWAX	1
S-Net	−0.03	1
S&P	−0.02	0.96	1
MSCI ACWI	0.01	0.71	0.76	1
Asia	−0.00	0.36	0.34	0.21	1
Europe	0.01	0.71	0.79	0.69	0.29	1
Latin America	−0.00	0.65	0.66	0.50	0.27	0.50	1
US	−0.03	0.56	0.51	0.61	0.14	0.28	0.31	1
Pictet	0.00	0.42	0.48	0.32	0.24	0.57	0.34	0.06	1
KBC ECO	−0.04	0.95	0.94	0.68	0.33	0.69	0.60	0.55	0.41	1
Post-GFC period: January 2011–October 2014
WOWAX	1
S-Net	0.01	1
S&P	0.01	0.95	1
MSCI ACWI	−0.04	0.63	0.72	1
Asia	0.01	0.25	0.22	0.09	1
Europe	0.01	0.73	0.81	0.75	0.12	1
Latin America	0.00	0.51	0.51	0.36	0.20	0.37	1
US	−0.04	0.61	0.61	0.59	0.04	0.36	0.33	1
Pictet	0.02	0.49	0.54	0.36	0.12	0.56	0.26	0.19	1
KBC ECO	0.01	0.92	0.90	0.59	0.21	0.68	0.49	0.57	0.46	1

Notes: This table reports the correlation results among four water indices, four water markets and two water funds during full, pre-GFC, GFC, and post-GFC periods. This table shows that S-Net is highly and significantly correlated with S&P, and MSCI ACWI is also highly and positively correlated with Europe in different (full, pre-GFC, GFC, and post-GFC) periods.

6.3. ARMA (1, 1) model

Our study uses the Akaike information criterion (AIC) and the Bayesian Schwarz criterion (BIC) to choose the ARMA term, which minimize the corresponding value of the criteria. Our study has selected the ARMA(1, 1) model of the conditional mean, and the estimated results of ARMA (1, 1) are found to have a significant p-value for the coefficients of water indices, water markets and water funds in different periods. The orders p and q of the ARMA models are identified and estimated for both series using Box and Jenkins’ methodology. Table 3 displays the results of the fitted ARMA models. To examine the relative forecasting power of ARMA model, our study attempts to use forecast statistics so that this study can consider predictor, which is optimal in the sense that they minimize the Root Mean Squared Error (RMSE), the Mean Absolute Error Deviation (MAE) and Mean Absolute Percent Error (MAPE) for the forecasts of the ARMA model. The smaller the values of RMSE, MAE, and MAPE, the more accurate or the better, on average, the forecast of a model. It is noted that the proposed model has been able to do well in forecasting for the sample period. The forecast figures (not shown here) for the water indices, water markets and water funds are available from the authors upon request.

Table 3. ARMA (1, 1) model

	WOWAX	S-Net	S&P	MSCI ACWI	Asia	Europe	Latin America	US	Pictet	KBC Eco
Full period: January 2004–October 2014
Constant	0.03	−0.00	0.03	0.01	0.03	−0.01	−0.02	0.00	−0.00	0.00
	(0.00)	(0.72)	(0.40)	(0.24)	(0.19)	(0.15)	(0.22)	(0.99)	(0.61)	(0.62)
AR(1)	0.98	0.22	−0.07	0.67	0.18	−0.91	0.52	0.67	0.97	0.30
	(0.00)***	(0.09)*	(0.06)*	(0.09)*	(0.21)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
MA (1)	0.91	0.35	−0.22	0.69	0.30	−0.86	0.59	0.74	0.98	0.54
	(0.00)***	(0.00)***	(0.05)**	(0.08)*	(0.03)**	(0.00)***	(0.00)***	(0.00)***	(0.00)****	(0.00)***
R-Squared	0.16	0.93	0.93	0.63	0.12	0.75	0.35	0.41	0.33	0.89
Pre-GFC period: January 2004–December 2007
Constant	−0.05	0.00	0.08	0.01	0.09	0.01	−0.05	0.05	0.01	−0.00
	(0.00)	(0.27)	(0.00)	(0.40)	(0.07)	(0.28)	(0.20)	0.10	(0.33)	(0.52)
AR(1)	0.99	0.24	0.23	0.87	0.01	−0.96	0.89	0.87	0.75	0.18
	(0.00)***	(0.14)	(0.25)	(0.00)***	(0.97)	(0.00)***	(0.00)***	(0.00)***	(0.02)**	(0.06)*
MA (1)	0.94	0.41	0.08	0.90	0.09	−0.98	0.91	0.90	0.78	0.46
	(0.00)***	(0.01)***	(0.68)	(0.00)***	(0.80)	(0.00)***	(0.00)***	(0.00)***	(0.01)**	(0.00)***
R-Squared	0.11	0.88	0.85	0.70	0.15	0.81	0.33	0.32	0.26	0.83
GFC period: January 2008–December 2010
Constant	0.02	−0.00	−0.01	−0.03	−0.01	−0.07	−.00	.017	0.00	0.01
	(0.00)	(0.49)	(0.77)	(0.46)	(0.81)	(0.16)	(0.57)	(0.76)	(0.92)	(0.47)
AR(1)	0.01	0.94	−0.18	0.73	−0.99	−0.85	0.01	0.74	−0.57	0.98
	(0.00)***	(0.00)***	(0.24)	(0.00)***	(0.00)***	(0.00)***	(0.93)	(0.07)*	(0.42)	(0.00)***
MA(1)	0.02	0.98	−0.38	0.77	−1.00	−0.76	0.19	0.77	−0.60	1.00
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.33)	(0.05)**	(0.38)	(0.00)***
R-Squared	0.01	0.96	0.96	0.70	0.17	0.75	0.47	0.52	0.36	0.92
Post-GFC period: January 2011–October 2014
Constant	0.03	−0.00	0.00	0.05	0.02	−0.04	−0.07	0.02	−0.00	0.01
	(0.00)	(0.46)	0.79	(0.01)	0.39	(0.08)	0.11	(0.40)	(0.76)	0.16
AR(1)	0.97	−0.05	0.05	−0.98	0.71	0.93	0.43	−0.72	−0.76	0.08
	(0.00)***	(0.80)	(0.86)	(0.00)***	(0.00)***	(0.00)***	(0.42)	(0.00)***	(0.00)***	(0.52)
MA (1)	0.86	0.07	0.15	−0.97	0.77	0.92	0.47	−0.60	−0.79	0.31
	(0.00)***	(0.74)	(0.64)	(0.00)***	(0.00)***	(0.00)***	(0.36)	(0.00)***	(0.00)***	(0.01)**

Notes: The estimation results from this table denotes the forecast for four water indices, four water markets and two water funds in different (full, pre-GFC, GFC, and post-GFC) periods which is derived from the ARMA(1, 1) model. p-values are given in brackets.

*Represent significance at the 10% level.

**Represent significance at the 5% level.

***Represent significance at the 1% level.

At the end of each day, we run the following model using daily stock returns in different (full, pre-GFC, GFC, and post-GFC) periods:

AR model: $y_t={\phi }_i{y}_{t-1}+{\phi }_i{y}_{t-2}+\dots +{\phi }_i{y}_{t-p}+{\mathrm{\xi }}_t=\sum _{i=1}^p{\phi }_i{y}_{t-i}$,

MA model: $y_t={\lambda }_j{\mathrm{\xi }}_{t-1}+{\lambda }_j{\mathrm{\xi }}_{t-2}+\dots +{\lambda }_j{\mathrm{\xi }}_{t-p}+{\mathrm{\xi }}_t=\sum _{j=1}^q{\lambda }_j{\mathrm{\xi }}_{t-j}$,

ARMA model: $y_t=\mu +\sum _{i=1}^p{\phi }_i{y}_{t-i}+\sum _{j=1}^q{\lambda }_j{\mathrm{\xi }}_{t-j}+{\mathrm{\xi }}_t$

6.4. Ljung–Box Q test

The Ljung-Box Q test tests whether a significant correlation is present in order to perform a lack-of-fit hypothesis test for model misspecification by being applied to the residuals and squared residuals of the fitted ARMA-GARCH model. According to the results (not tabulated here but available from the authors upon request), most of the p-values are above 0.05 which indicates the acceptance of the null hypothesis of model accuracy under the 5% significance level. Therefore, the models are specified, in that there is a good fit of the daily stock return data-sets of four water indices, four water markets, and two water funds.

6.5. ARMA (1, 1)-GARCH (1, 1) model

In our study, a new water investment prediction model has been proposed which is based on non-linear time series ARMA (1, 1)-GARCH (1, 1) models. This model is a combination of the linear time series ARMA model and the nonlinear GARCH model. In this research, the ARMA (1, 1)-GARCH (1, 1) model is used to model the four water indices, four water markets and two water funds. The models are based on the conditional volatility process during the different periods. Table 4 shows that parameters for the S-Net, S&P and Pictet AR (1) are not significant in the full period. During the pre-GFC period, all parameters are significant. However, the MA (1) results are not significant in the case of Asia, the US and Pictet. The parameters for the S-Net, S&P and Asia, in the case of MA (1) are not significant for the GFC period. During the post-GFC period, only Latin America market’s MA (1) parameter is not significant. The parameter estimates that are not significant are kept because omitting orders of the AR (p) and MA (q) process results in a higher AIC-value. The parameters of GARCH (1, 1) are significant. This is important because the conditional variance facilitates the comparison between the ARMA and the GARCH models. In the ARMA (1, 1)-GARCH (1, 1) model, α and β show a high degree of persistency in the conditional volatility of stock returns concerning the water indices, water markets and water funds, which means an “explosive” volatility. The coefficient of ARMA (1, 1)-GARCH (1, 1) results confirm that the conditional volatility process GARCH (1, 1) has a positive effect on the serial autocorrelation of squared residuals for water indices, water market indices and water funds in full, GFC and post-GFC periods. These results are consistent with those of Jánský and Rippel (2011). However, in pre-GFC periods, the p-value of the S&P indicates the acceptance of the null hypothesis.

Table 4. ARMA-GARCH (1, 1) model

	WOWAX	S-Net	S&P	MSCI ACWI	Asia	Europe	Latin America	US	PICTET	KBC EcO
Full period: January 2004–October 2014
µ	0.99	0.04	−0.16	−0.80	0.47	−0.84	0.60	0.41	0.50	0.17
	(0.00)***	(0.75)	(0.43)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.02)**	(0.75)	(0.00)***
φ	−0.77	−0.181	0.07	0.78	−0.55	0.83	−0.64	−0.49	−0.51	−0.37
	(0.00)***	(0.17)	(0.72)	(0.00)****	(0.00)****	(0.00)***	(0.00)***	(0.00)***	(0.05)**	(0.00)***
α	1.99	0.05	0.05	0.02	0.07	0.04	0.09	0.04	0.02	0.28
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	0.31	0.92	0.93	0.96	0.92	0.95	0.72	0.95	0.96	0.46
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)****	(0.00)***	(0.00)****
ω	0.00	0.00	0.00	0.00	0.01	0.00	0.35	0.00	0.00	0.03
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
Pre-GFC period: January 2004–December 2007
µ	0.99	0.38	0.94	0.87	0.31	−0.96	0.90	0.25	0.61	0.07
	(0.00)***	(0.01)**	(0.00)***	(0.00)***	(0.11)	(0.00)***	(0.00)***	(0.47)	(0.34)	(0.52)
φ	−0.94	−0.53	−0.96	−0.90	−0.45	0.97	−0.92	−0.33	−0.63	−0.34
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.01)**	(0.00)***	(0.00)***	(0.329)	(0.30)	(0.00)
α	0.34	0.05	0.12	0.12	0.04	0.16	0.08	0.16	0.01	0.23
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	0.72	0.84	0.19	0.48	0.93	0.40	0.62	0.19	0.97	0.34
	(0.00)***	(0.00)***	(0.08)*	(0.00)***	(0.00)	(0.00)***	(0.00)***	(0.09)*	(0.00)**	(0.00)**
ω	0.00	0.00	0.05	0.12	0.08	0.06	0.54	0.81	0.00	0.04
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.23)	(0.00)
GFC period: January 2008–December 2010
µ	0.98	−.002	−0.45	0.70	0.31	−0.78	0.33	−0.57	0.98	0.32
	(0.00)***	(0.94)	(0.09)*	(0.00)***	(0.40)	(0.00)***	(0.21)	(0.14)	(0.00)***	(0.01)**
φ	−0.97	−0.09	0.34	−0.76	−0.40	0.69	−0.46	0.62	−0.97	−0.54
	(0.00)***	(0.76)	(0.22)	(0.00)***	(0.27)	(0.00)***	(0.05)**	(0.09)*	(0.00)***	(0.00)***
α	0.05	0.03	0.07	0.03	0.15	0.04	0.08	0.09	0.05	0.34
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	0.80	0.96	0.92	0.96	0.82	0.94	0.82	0.88	0.80	0.55
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
ω	0.00	0.00	0.00	0.00	0.04	0.00	0.19	0.03	0.00	0.02
	(0.02)	(0.50)	(0.02)	(0.64)	(0.00)	(0.20)	(0.00)	(0.00)	(0.01)	(0.00)
Post-GFC period: January 2011–October 2014
µ	0.98	−0.15	0.07	−0.97	0.75	0.94	0.37	−0.70	0.54	−0.08
	(0.00)***	(0.56)	(0.80)	(0.00)***	(0.00)***	(0.00)***	(0.62)	(0.00)***	(0.63)	(0.73)
φ	−0.92	0.03	−0.17	0.96	−0.83	−0.94	−0.41	0.64	−0.52	−0.04
	(0.00)***	(0.90)	(0.54)	(0.00)***	(0.00)***	(0.00)***	(0.58)	(0.00)***	(0.65)	(0.87)
α	0.11	0.06	0.12	0.10	0.09	0.05	0.07	0.14	0.03	0.33
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.04)	(0.00)	(0.00)	(0.00)	(0.00)
β	0.89	0.88	−0.00	0.66	0.87	−0.11	0.82	0.56	0.94	0.10
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.76)	(0.00)***	(0.00)***	(0.00)***	(0.11)
ω	0.00	0.00	0.03	0.06	0.03	0.36	0.16	0.13	0.00	0.06
	(0.00)	(0.021)	(0.00)	(0.00)	(0.01)	(0.00)	(0.00)	(0.00)	(0.06)	(0.00)

Notes: This table presents the estimation results of an ARMA-GARCH (1, 1) model for four water indices, four water markets and two water funds returns and volatility in different (full, pre-GFC, GFC, and post-GFC) periods. p-values are given in brackets.

*Represent significance at the 10% level.

**Represent significance at the 5% level.

***Represent significance at the 1% level.

Model: At the end of each day, we run the following model using daily stock returns in different (full, pre-GFC, GFC, and post-GFC) periods:

$\sigma (L)(y_t-\mu )=\sigma (L){\mathrm{\xi }}_t$

${\sigma }_t^2=\omega +\sum _{i=1}^p{\alpha }_i{\sigma }_{t-1}^2+\sum _{j=1}^q{\beta }_j{\rho }_{t-j}^2+{\mathrm{\xi }}_t$

where $\sigma (L)$ is lag polynomials, and ${\mathrm{\xi }}_t=Z_t{\rho }_t$. Importantly, ${\alpha }_i,\dots ,{\alpha }_p,{\beta }_i,\dots ,{\beta }_p$ are constant coefficients. A fact that should be mindful when modeling conditional variances is that $\omega$, ${\alpha }_i$ and ${\beta }_j$ are non-negative.

6.6. EGARCH (1, 1) model

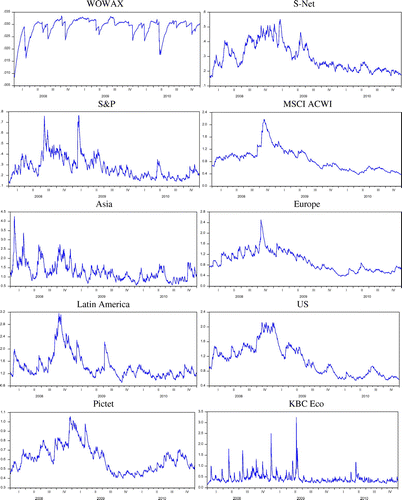
To understand the volatility of water indices, water markets and water funds, the parameter estimation results for the EGARCH (1, 1) model are shown in Table 5. Based on the minimum AIC, the EGARCH (1, 1) model is selected. Therefore, EGARCH (1, 1) provides a better fit for water indices, water markets and water funds instead of a GJR-style GARCH model, i.e. TGARCH (GRJ). Because the volatility response from the TGARCH (GJR) model displays only the negative market shocks, it is not always easy to optimize a TGARCH (GJR) model. The TGARCH (GRJ) results are included in Table A2 in the Appendix A. However, because the EGARCH model is asymmetric, its use avoids the need for parameter constraints and provides more flexible parameters than other ARCH models (Dedi & Yavas, 2016; Tularam et al., 2009). During the full period, the EGARCH (1, 1) results show that the parameter γ does not present the leverage effect on the volatility of the water indices, water markets and water funds except for the US water market. However, during the pre-GFC period, the US water market has a significant leverage effect. The parameter β coefficient of Europe and Pictet are negative and statistically significant at the 1% level of significance in the pre-GFC period. The parameter γ coefficient of the WOWAX and Pictet, and the S-Net and Pictet are negative and statistically significant at the 1% level of significance as well in the GFC and post-GFC periods, respectively. The parameter β estimates for the EGARCH (1, 1) model confirms that bad news generates the volatility of the WOWAX, S-Net, Europe and Pictet during the pre-GFC, GFC, and post-GFC periods. The results are similar to those of Cheung and Ng (1992), Koutmos (1992), Poon and Taylor (1992), and Asteriou and Begiazi (2013). Figure 3 reveals more information regarding the volatility of four water indices, four water markets and two water funds during the GFC period. The EGARCH (1, 1) model forecast figures for the water indices, water market indices and water funds in different periods are included in Figure B2 in the Appendix B.

Table 5. EGARCH (1, 1) model

	WOWAX	S-Net	S&P	MSCI ACWI	Asia	Europe	Latin America	US	Pictet	KBC Eco
Full period: January 2004–October 2014
	0.07	−0.12	−0.16	−0.00	−0.12	−0.07	0.04	−0.10	−0.00	−0.49
w	(0.00)	(0.00)	(0.00)	(0.08)	(0.00)	(0.00)	(0.00)	(0.00)	(0.01)	(0.00)
β	1.00	0.98	0.98	0.99	0.17	0.99	0.94	0.99	0.99	0.74
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	0.27	−0.01	−0.00	0.07	−0.01	0.00	0.10	−0.00	0.06	0.52
	(0.00)***	(0.07)*	(0.00)***	(0.35)	(0.07)*	(0.74)	(0.00)***	(0.73)	(0.00)***	(0.00)***
	0.11	0.11	0.15	0.00	0.17	0.10	−0.05	0.13	0.00	−0.03
α	(0.00)***	(0.00)***	(0.00)***	(0.94)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.18)	(0.00)***
Pre-GFC period: January 2004–December 2007
w	−0.11	−0.04	−1.05	−0.47	0.03	−3.79	0.16	0.11	−2.78	−1.16
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	1.00	0.03	0.25	0.60	0.97	−0.98	0.74	0.55	−0.72	0.49
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	1.50	−0.02	−0.07	0.31	0.08	0.02	0.21	0.32	−0.04	0.60
	(0.00) ***	(0.02)**	(0.02)**	(0.00)***	(0.00)***	(0.00)***	(0.001)***	(0.00)*	(0.33)	(0.00)***
α	1.68	0.99	0.65	−0.00	0.04	−0.02	−0.04	0.08	−0.03	−0.06
	(0.00)***	(0.01)***	(0.00)***	(0.98)	(0.00)***	(0.00)***	(0.18)	(0.00)***	(0.21)	(0.05)**
GFC period: January 2008–December 2010
w	−14.44	0.00	−0.00	0.00	0.02	0.00	0.00	0.01	−0.95	−0.16
	(0.00)	(0.46)	(0.47)	(0.18)	(0.00)	(0.38)	(0.03)	(0.00)	(0.00)	(0.00)
β	−0.84	1.00	0.98	1.00	0.96	0.99	0.98	0.98	−094	0.57
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	−0.07	0.07	0.12	0.06	0.30	0.06	0.03	0.18	−0.00	0.83
	(0.09)*	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.44)	(0.00) ***
α	−0.00	−0.00	−0.09	0.03	−0.01	−0.06	−0.07	−0.07	−0.06	−0.25
	(0.91)	(0.91)	(0.00)***	(0.00)***	(0.50)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
Post-GFC period: January 2008–October 2014
w	−0.11	−5.94	−3.10	−0.26	−0.04	−1.96	0.02	−0.16	−3.22	−1.58
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	1.00	−0.93	0.02	0.79	0.09	−0.83	0.94	0.79	−0.97	0.58
	(0.00)***	(0.00)***	(0.93)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	−0.89	0.05	0.25	0.19	0.03	0.04	0.03	0.28	−0.01	−0.08
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.01)***	(0.16)	(0.00)***	(0.00)***	(0.38)	(0.00)***
α	1.05	−0.04	0.03	0.03	0.97	0.01	−0.09	−0.01	0.00	0.49
	(0.00)***	(0.00)***	(0.43)	(0.17)	(0.00)***	(0.64)	(0.00)***	(0.70)	(0.57)	(0.00)***

Notes: This table presents the estimation results of an asymmetric EGARCH (1, 1) model for four water indices, four water markets, and two water funds leverage in different (full, pre-GFC, GFC, and post-GFC) periods.

*Represent significance at the 10% level.

**Represent significance at the 5% level.

***Represent significance at the 1% level.

Model: At the end of each day, we run the following model using daily stock returns in different (full, pre-GFC, GFC, and post-GFC) periods:

$log({\sigma }_t^2)=w+\beta log({\sigma }_{t-1}^2)+\gamma \frac{{\epsilon }_{t-1}}{\sqrt{{\sigma }_{t-1}^2}}+\alpha \left(\frac{\left|{\epsilon }_{t-1}\right|}{\sqrt{{\sigma }_{t-1}^2}}-\sqrt{\frac{2}{\pi }}\right)$

where the asymmetric positive and negative shocks ${(\epsilon }_{t-1})$on conditional variance and $\frac{{\epsilon }_{t-1}}{\sqrt{{\sigma }_t^2-1}}\sim N,(0,1)$ are captured in the parameter$\gamma$. The negative coefficient of γ indicates that volatility rises more than the positive coefficient $\gamma$. The parameter $\gamma$ (a negative sign) ensures that bad news generates more volatility than good news. The coefficient of α captures the assembling effects of the volatility.

Figure 3. Estimated volatility of EGARCH (1, 1) model during GFC period.

Notes: This figure presents the estimated volatility of daily returns of the four water indices, four water markets, and two water funds which reveals more information regarding the volatility during GFC periods. Source: Thomson Reuters DataStream database.

6.7. Discussion of results

One of the objectives of our study is to analyze the relationship among water indices, water markets and water funds and their volatility and returns in different (full, pre-GFC, GFC, and post-GFC) periods. Our study, therefore, uses a number of statistical methodologies. Firstly, in our study, the correlation results show that the S-Net, S&P, MSCI ACWI, and KBC Eco are highly correlated in different periods. Based on the minimum AIC and the significance of the estimated univariate ARMA (p, q) models, the coefficients criteria leads to the ARMA (1, 1) model of the conditional mean. Hence, the ARMA (1, 1) model is successfully used to decompose autoregressive process and moving average components, and then to obtain stationary residuals. The LB-Q statistics (Ljung & Box, 1978) of the residuals are statistically highly significant. The fitted values are used to estimate the expected and unexpected volatility. The results show that significant ARMA (1, 1)-GARCH (1, 1) model effects appear in the data in different periods. The results show that the S-Net, S&P, Asia, Latin America and Pictet AR (1) and MA (1) parameters are not significant in different periods. The ARMA (1, 1)-GARCH (1, 1) model results (α and β) show that the water indices, water markets and water funds capture the “extremely” high level of stock return volatility in different periods (full, pre-GFC, GFC and post-GFC). These results are unlike those of Geman and Kanyinda (2007), who report that the WOWAX has a higher return but lower risk. Jin et al.’s (2015) results also confirm Geman and Kanyinda’s (2007) results (also their belief that the water sector can be considered as an alternative investment asset class). However, Tularam and Reza (2016) report that water investment has a lower systematic risk and a positive effect on the water exchange traded index funds returns during different regimes. The results of the EGARCH (1, 1) model indicate that all the estimated coefficients of four water indices, water markets, and water funds are statistically significant at the 1% level in different (full, pre-GFC, GFC, and post-GFC) periods. The asymmetric (leverage) effect is captured by the negative sign of parameter estimate which is statistically significant in full, pre-GFC and GFC periods. The existence of the leverage effect is observed in the returns of the US water market, the S-Net, and the Asian water market, and the WOWAX in full, pre-GFC and GFC periods, respectively. However, the overall results of the EGARCH (1, 1) model show that global water industry is more sensitive to “good” news than to “bad” news. Unlike previous related studies, our study explicitly accounts for potential asymmetries that may exist in the volatility transmission mechanism.

7. Conclusion

In this study, we analyze the stock returns and volatility of the four water indices, four water markets and two water funds in different (full, pre-GFC, GFC and post-GFC) periods with the purpose of investigating the profitability of water-related investments using ARMA (1, 1)-GARCH (1, 1) and EGARCH (1, 1) model for the period 2004–2014. ARMA-GARCH (1, 1) models are developed to take into accounts both volatility and returns of the daily time series data. More importantly, in terms of the motivation of this study, it is derived from the need to understand the returns and volatility the global water industry; whether or not water indices, water markets and water funds are desirable tools for water investment; that is, whether water investors can gain highly positive returns from investing in the global water industry.

In terms of correlation analysis, our results show that the S-Net, S&P and KBC Eco are highly correlated with each other in different periods. During the GFC periods, WOWAX is negatively correlated with three water indices, four water markets and two water funds. During the GFC period, WOWAX is significantly negatively correlated with S-Net, S&P, Asia, Latin America, US and KBC Eco in GFC period. During the post-GFC period, WOWAX is significantly negatively correlated with MSCI ACWI and US in post-GFC period. Hence, there is a still possible scope for achieving international portfolio diversification. Therefore, water investors may be able to gain benefits from international portfolio diversification throughout investment periods.

In our study, the ARMA (1, 1) model is used for the daily returns of four water indices, four water markets and two water funds. ARMA-GARCH (1, 1) models are developed to take into account both the volatility and the returns of the daily time series data. Importantly, the motivation for our study is derived from the need to understand the returns and volatility of the global water industry; whether or not water indices, water markets and water funds are desirable tools for water investment. Thus, water investors can gain an understanding into the prospect of higher positive returns from investment in the global water industry. The findings suggest that asymmetric effects can be captured using an EGARCH (1, 1) model, which is the better model in the time series data. The EGARCH (1, 1) model’s results show the significance of β and γ suggesting persistence of volatility from four water indices, four water markets and two water funds in different periods; and a coefficient of γ for asymmetric volatility (leverage) for Asia and the US, the S-Net and Pictet in full, pre-GFC and GFC periods, and the WOWAX in GFC and post-GFC periods. Thus, the investment performance of the global water industry clearly shows that leverage also has an impact on water indices, water markets and water funds returns in different (full, pre-GFC, GFC, and post-GFC) periods. Hence, the results of our study have implications for investors in the water industry and for international institutions in their decision-making regarding the influence of water investment in their portfolios. The results of this research also could be helpful to academics, researchers, policymakers and water investors around the world. The asymmetric volatility phenomenon points to the fact that institutional factors are the major driving forces behind empirical regularities in the water markets. If governments decide to improve the water infrastructure through public–private partnership, they must realize that private water investors expect to be reimbursed for any volatility in the market. It is important to note that the WOWAX is selected to represent the water asset class in our study. Since the inception of the WOWAX can only be traced back to January 2004, the data pertaining to the performance of water-related assets prior to 2004 were not available. Our study can also be extended in several directions. For example, future research can evaluate the relationship between financial risk and return of water indices, water funds and water ETFs using new financial real option theory.

Funding

The authors received no direct funding for this research.

Additional information

Notes on contributors

Rajibur Reza

Rajibur Reza is a PhD candidate at the Department of Accounting, Finance and Economics, Griffith Business School, Griffith University, Australia. His research expertise in water investment.

Gurudeo Anand Tularam

Gurudeo Anand Tularam is a senior lecturer in Mathematics/Statistics in the Griffith Sciences–Science, Environment, Engineering and Technology, and a senior researcher at the Environmental Futures Institute, Griffith University, Australia. His research expertise in time series and stochastic calculus methods in business and finance applications such as investment, portfolio analysis and risk assessment. He has published more than hundred papers in reputed international journals.

Bin Li

Bin Li is a senior lecturer in Finance at the Department of Accounting, Finance and Economics, Griffith University, Brisbane, Australia. His research is in the areas of empirical asset pricing, investments and portfolio management, applied financial econometrics, market efficiency, and volatility modeling. Li has published more than 50 articles in peer-reviewed journals.

Appendix A.

Table A1. Global water funds around the world

Table

Manager	Fund	Launch date	Description
Pictet AM	Pictet Water Fund	2000	Luxembourg-based global managed fund
	Nomura Water Fund	2004	Mirror of Pictet Luxembourg fund
	Criterion Water Inf. Fund	2007	Mirror of Pictet Luxembourg fund
SAM	Sustainable Water Fund	2001	Global managed fund
	Nikko Global Water Fund	2007	Mirror of SAM Sustainable Water Fund
Power Shares	Water Portfolio	2005	Tracks Palisades US water index
	Global Water Portfolio	2007	Tracks Palisades Global water index
KBC AM	Eco Water Fund	2000	Korean mirror fund
	Samsung Global Water Fund	2007	US-based global hedge fund
Summit Global	Summit Master Water Equity Fund	1999	US-based global hedge fund
Credit Suisse	PL100 World Water Trust	2007	Australian investment trust
Aqua Terra AM	Praetor Water Fund	2005	Euro-denominated managed fund
	Kinetics Water Inf. Fund	2007	US-denominated debt and equity fund
	Claymore Global Water UIT	2005	Investment trust with fixed global portfolio
	Claymore US Water UIT	2005	Investment trust with fixed US portfolio
Water AM	The Reservoir Fund	2006	US-based global hedge fund
Terrapin AM	Water Fund	2005	US-based global hedge fund
S&P Indices	Guggenheim S&P Global Water Fund	2007	US fund tracking S&P Water Index
	KDB S&P Global Water Fund	2007	Korean fund tracking S&P Water Index
	iShares Global Water Fund	2007	UK fund tracking S&P Water Index
	ABN AMRO Water Certificate	2005	Unit trust with 10 stocks selected by S&P
Wessex AM	Wessex Global Water Fund	2007	UK-based managed fund
MFS Aqua Man.	MFS Water Fund (Australia)	2007	Australian managed fund

Source: Global Water Intelligence (2007).

Table A2. TGARCH (1, 1) model

Table

	WOWAX	S-Net	S&P	MSCI ACWI	Asia	Europe	Latin America	US	Pictet	KBC Eco
Full period: January 2004–October 2014
w	0.07	−0.12	−0.16	−0.00	−0.12	−0.07	0.04	−0.10	−0.00	−0.49
	(0.00)	(0.00)	(0.00)	(0.08)	(0.00)	(0.00)	(0.00)	(0.00)	(0.01)	(0.00)
β	1.00	0.98	0.98	0.99	0.17	0.99	0.94	0.99	0.99	0.74
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)	(0.00)***	(0.00)***	(0.00)***	(0.00)***
	0.27	−0.01	−0.00	0.07	−0.01	0.00	0.10	−0.00	0.06	0.52
	(0.00)***	(0.07)*	(0.00)***	(0.35)	(0.07)*	(0.74)	(0.00)***	(0.73)	(0.00)***	(0.00)***
γ	0.11	0.11	0.15	0.00	0.17	0.10	−0.05	0.13	0.00	−0.03
	(0.00)***	(0.00)***	(0.00)***	(0.94)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.18)	(0.00)***
Pre-GFC period: January 2004–December 2007
w	−0.11	−0.04	−1.05	−0.47	0.03	−3.79	0.16	0.11	−2.78	−1.16
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	1.00	0.03	0.25	0.60	0.97	−0.98	0.74	0.55	−0.72	0.49
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	1.50	−0.02	−0.07	0.31	0.08	0.02	0.21	0.32	−0.04	0.60
	(0.00) ***	(0.02)**	(0.02)**	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.33)	(0.00)***
α	1.68	0.99	0.65	−0.00	0.04	−0.02	−0.04	0.08	−0.03	−0.06
	(0.00)***	(0.01)***	(0.00)***	(0.98)	(0.00)****	(0.00)***	(0.18)	(0.00)***	(0.21)	(0.05)**
GFC period: January 2008-December 2010
w	−14.44	0.00	−0.00	0.00	0.02	0.00	0.00	0.01	−0.95	−0.16
	(0.00)	(0.46)	(0.47)	(0.18)	(0.00)	(0.38)	(0.03)	(0.00)	(0.00)	(0.00)
β	−0.84	1.00	0.98	1.00	0.96	0.99	0.98	0.98	−094	0.57
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	−0.07	0.07	0.12	0.06	0.30	0.06	0.03	0.18	−0.00	0.83
	(0.09)*	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)**	(0.00)***	(0.44)	(0.00) ***
α	−0.00	−0.00	−0.09	0.03	−0.01	−0.06	−0.07	−0.07	−0.06	−0.25
	(0.91)	(0.91)	(0.00)***	(0.00)***	(0.50)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
Post-GFC period: January 2008–October 2014
w	−0.11	−5.94	−3.10	−0.26	−0.04	−1.96	0.02	−0.16	−3.22	−1.58
	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)	(0.00)
β	1.00	−0.93	0.02	0.79	0.09	−0.83	0.94	0.79	−0.97	0.58
	(0.00)***	(0.00)***	(0.93)	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.00)***
γ	−0.89	0.05	0.25	0.19	0.03	0.04	0.03	0.28	−0.01	−0.08
	(0.00)***	(0.00)***	(0.00)***	(0.00)***	(0.01)**	(0.16)	(0.00)***	(0.00)***	(0.38)	(0.00)***
α	1.05	−0.04	0.03	0.03	0.97	0.01	−0.09	−0.01	0.00	0.49
	(0.00)***	(0.00)****	(0.43)	(0.17)	(0.00)	(0.64)	(0.00)***	(0.70)	(0.57)	(0.00)***

Notes: This table presents the estimation results of an asymmetric TGARCH (1, 1) model for four water indices, four water markets and two water funds leverage in different (full, pre-GFC, GFC, and post-GFC) periods.

Model: At the end of each day, we run the following TGARCH (1, 1) model (Poon & Granger, 2003) using daily stock returns in different (full, pre-GFC, GFC, and post-GFC) periods:$${ħ}_t=\omega +\alpha {\epsilon }_{t-1}^2+\delta I_{t-1}{\epsilon }_{t-1}^2+\beta {ħ}_{t-1}$$$$I_{t-1}=\left\{\begin{array}{ccc}1\hfill & \text{if}\hfill & {\epsilon }_{t-1}<0\hfill \\ 0\hfill & \text{if}\hfill & {\epsilon }_{t-1}\ge 0\hfill \end{array}\right.$$

Symbols *, **, and *** represent significance at the 10, 5, and 1% levels, respectively; and p-values are given in brackets.

Appendix B.

Figure B1. The EGARCH (1, 1) model forecasts for the water indices, water markets and water funds in different periods.

Full period: January 2004–October 2014

Pre-GFC period: January 2004–December 2007

GFC period: January 2008–December 2010

Post-GFC period: January 2008–December 2010

Notes: This figure presents the forecast values of the four water indices, four water markets and four water funds, which are derived from the EGRACH (1, 1) model during full, pre-GFC, GFC, and post-GFC periods.

Source: Thomson Reuters DataStream database.